1 Introduction

The simultaneous growth of three distinct phases from the liquid allows for a broad variety of different phase arrangements far beyond the typical microstructures of rods, lamellae and labyrinths in binary eutectics. Hence, it has been a topic of interest for both experimentalists as well as theoreticians. In addition, their study provides for a fundamental understanding of principle mechanisms which are of general importance for the development of multicomponent alloys for advanced technical applications. Experimental investigations of ternary alloys has been carried out for both metallic [1] and inorganic alloys [2] for thin-film solidification conditions, and bulk solidification of three-phase growth has been studied in separate works [3–9]. However, theoretical investigations of three-phase growth have been few, where Himemiya and Umeda [10] have worked out analytical expressions for undercooling as a function of spacings for different three-phase configurations, while modeling efforts for thin-film and bulk-solidification patterns were carried out by [11, 12].

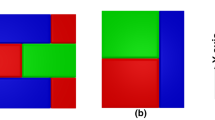
One of the widely studied alloys in this regard is the Ag–Al–Cu alloy [13–19] which classically shows patterns of the type as shown in Fig. 1a. While variations from this structure are seen upon changes in the solidification velocity, the major feature of the patterns is the formation of lamellae of a single phase in combination with lamellae formed out of a combination of the other two-phases.

Fig. 1
figure 1

In a a typical microstructure in a directionally solidified Ag–Al–Cu ternary eutectic alloy [19], white: Ag2Al, grey: Al2Cu, black: Al. In b a phase-field simulation of a representative alloy showing similar morphological characteristics

Full size image

Similarly, there are other systems such as in the Nb–Al–Ni ternary eutectic system [20], which show patterns quite different in characteristics from those seen in the Ag–Al–Cu alloy. So it is an interesting question as to which material/processing parameters lead to the differences in structure formation.

Therefore, the central question we wish to address is how to characterize the influence of these two parameters: volume fraction of the phases and the solid–liquid surface energies. To quantitatively identify the influence of each of the parameters, it is useful to start from a purely symmetric ternary eutectic, with equal volume fractions of the phases and equal surface energies of all interfaces, and then perturb the system. For our phase-field simulations we utilize the state of the art phase-field model based on the grand-potential functional [21]. We perform this study upon variation of both the surface energies of the solid–liquid interface and the volume fractions, in order to independently access the influence of each of these parameters on structure formation. Thereafter, we utilize the model for simulating a typical microstructure derived from the phase-field simulation Fig. 1b using an asymmetric phase diagram and asymmetric interfacial energies.

2 Material Data and Thermodynamic Functions

In this section we describe a method for incorporating thermodynamic information in the multi-phase field model [21] with the possibility of even coupling to thermodynamic databases. The required inputs include the slopes of the liquidus and the equilibrium compositions of the solid and the liquid phases at a given temperature. Using these, we construct simple free-energy polynomial forms around the given equilibrium compositions. The change in the equilibrium compositions as a function of the change in temperature, is encoded into the parameterization of the free-energy density using local thermodynamic extrapolation around the equilibrium compositions of interest. In the following, we briefly describe the scheme of construction of the free-energy density of the phases.

The simplest form of the free-energy density that can retrieve the correct Gibbs–Thomson coefficient as in the databases and the correct slopes of the liquidus and solidus phases are of polynomials of second order of the following form,

$$\begin{aligned} f^{\alpha }\left( {\varvec{c}}\right)&= \dfrac{1}{V_m}\Big (\sum _{i<j}^{K,K}A_{ij}^{\alpha }c_ic_j + \sum _j^{K} B_j^{\alpha } c_j + C^{\alpha }\Big ), \end{aligned}$$
(1)

where the coefficients \(A^{\alpha }, B^{\alpha }\) and \(C^{\alpha }\) are the respective coefficients, \(V_m\) is the molar volume that is assumed equal for all the phases in the present discourse and K is the number of independent components. The coefficients \(A_{ij}\) are linked to the curvatures of the free-energy curves and hence are related to an effective susceptibility. This matrix can be directly obtained from the databases for real material simulations by using the information of the free-energies \(G^{\alpha }\) for each of the phases; as \(\left( \dfrac{\partial ^2 G^{\alpha }}{\partial c_i\partial c_j}\right) _{{\varvec{c}}^{\alpha }_{eq}}\) and \({\varvec{c}}^{\alpha }_{eq}\) are the equilibrium compositions of the components in the \(\alpha -\)phase that is in equilibrium with a given phase, which is presently chosen to be a liquid. Assuming \(B_j^{l}\) and \(C^{l}\) to be zero for the liquid phase, the conditions of equilibrium (equal diffusion potential and equal grand-potentials ) allows to determine the other coefficients \(B_j^{\alpha }\) and \(C^{\alpha }\) for any of the solid-phases, such that the equilibrium between the solid phase \(\alpha\) and the liquid phase is reproduced at the respective equilibrium compositions. Thus, one can derive for a given temperature \(T^{*}\),

$$\begin{aligned}&B_{j}^{\alpha } = 2(A_{jj}^{l}c_{eq,j}^{l} - A_{jj}^{\alpha }c_{eq,j}^{\alpha }) + \sum _{j\ne i}\left( A_{ij}^{\alpha } c_{eq,i}^{\alpha } - A_{ij}^{l} c_{eq,i}^{l}\right) \end{aligned}$$
(2)
$$\begin{aligned}&C^{\alpha } = \sum _{i\le j }\left( A_{ij}^{\alpha } c_{eq,i}^{\alpha }c_{eq,j}^{\alpha } - A_{ij}^{l} c_{eq,i}^{l}c_{eq,j}^{l}\right) \end{aligned}$$
(3)

For describing the driving force as a result of small undercoolings, we utilize the slopes of the liquidus \(m_i^{l}\) and the solidus \(m_{i}^{\alpha }\) , which can be introduced from known thermodynamics, and can be incorporated in the construction of the respective free-energy densities of the phases. The equilibrium co-existence lines and their variation as a function of temperature are reproduced, according to the approximation that the tie-lines are preserved for smaller undercoolings, i.e. the change in the phase-coexistence is assumed to occur in a self-similar manner, such that the resultant equilibrium compositions at a given undercooling, also exist along the same initial tie-line. This allows to write the variation of equilibrium phase concentrations of both phases \(\alpha ,l\) as,

$$\begin{aligned} \dfrac{c_{eq,i}^{\alpha ,l}\left( T\right) - c_{eq,i}^{\alpha ,l}\left( T^*\right) }{c_{eq,i}^{\alpha }\left( T^*\right) - c_{eq,i}^{l}\left( T^*\right) }&=\dfrac{c_{eq,j}^ {\alpha ,l}\left( T\right) -c_{eq,j}^{\alpha ,l}\left( T^*\right) }{c_{eq,j}^ {\alpha }\left( T^*\right) -c_{eq,j}^{l}\left( T^*\right) } \nonumber \\&\quad \forall \quad i,j \in 1 \ldots K. \end{aligned}$$
(4)

The extent of extrapolation \(\Delta T=(T-T^{*})\) can be expressed as the departure from the equilibrium compositions from the chosen set at temperature \(T^*\),

$$\begin{aligned} \sum _{i}m_i^{\alpha ,l}\left( c_{eq,i}^{\alpha ,l}\left( T\right) - c_{eq,i}^{\alpha ,l}\left( T^*\right) \right) = (T-T^*). \end{aligned}$$

Combining the two preceding relations, we derive the equilibrium concentrations of either phase as functions of temperature along a given tie-line by,

$$\begin{aligned} c_{eq,i}^{\alpha ,l}\left( T\right)&= c_{eq,i}^{\alpha ,l}\left( T^*\right) + \dfrac{\left( T-T^*\right) \left( c_{eq,i}^{\alpha }\left( T^*\right) -c_{eq,i}^{l}\left( T^*\right) \right) }{\Delta T_f^{\alpha ,l}}, \end{aligned}$$
(5)

where \(\Delta T_f^{\alpha ,l}\) is given by,

$$\begin{aligned} \Delta T_f^{\alpha ,l}&= \sum _{i}m_i^{\alpha ,l}\left( c_{eq,i}^{\alpha }\left( T^*\right) - c_{eq,i}^{l}\left( T^*\right) \right) . \end{aligned}$$

Using the above relations for the temperature variations of the equilibrium compositions of the phases along a chosen tie-line, one can determine the coefficients \(B_j^{\alpha }\left( T\right)\) and \(C^{\alpha }\left( T\right)\) using Eqs. 2 and 3, such that the equilibrium co-existence lines are reproduced for small variations of both the composition and the temperature around the chosen equilibrium compositions \({\varvec{c}}_{eq}\) and temperature \(T^{*}\).

For a ternary eutectic alloy with three solid phases in equilibrium with the liquid, we consider the ternary eutectic composition of the liquid and the respective equilibrium compositions of the solid phases at the ternary eutectic composition for determining the respective simplified free-energy densities as described previously. The required grand-potential densities of the phases are thereafter computed using the Legendre transform as (\(\Psi ^{\alpha } = f^{\alpha }-\sum _{i=1}^{K}\dfrac{\tilde{\mu }_i^{m}}{V_m}c_i^{\alpha }\)).

The relaxation coefficients for the solid–liquid interfaces \(\tau _{\alpha l}\) for all the solid-phases are determined from the thin-interface analysis as described in [21] and extended for the case of multi-component systems [22], such that the solidification is purely diffusion-controlled. The relaxation constants of the solid–solid interfaces are set as the lowest value among the calculated solid–liquid interface relaxation coefficients. The atomic diffusivity matrix in the present description is assumed to be diagonal, with equal diffusivities for the components, and is non-zero only in the liquid with a value given by \(D_l\).

3 Influence of Volume Fractions and Solid–Liquid Interfacial Energies

An useful starting point to understand the influence of the volume fractions and the surface energy, is to start from a model symmetric ternary eutectic system with phases α, β, γ, l and independent components A, B, which can be created using the following coefficients matrix \(A_{ij}\) and the slopes \(m_i^{l}\),

$$A_{{ij}}^{{\alpha ,\beta ,\gamma ,l}} = \left( {\begin{array}{*{20}c} {} & A & B \\ A & {1.0} & {1.0} \\ B & {1.0} & {1.0} \\ \end{array} } \right)$$
(6)

The liquidus slopes are assumed as,

$$\begin{gathered} m_{i}^{\alpha } = \left( {\begin{array}{*{20}c} {A:} & {0.45} \\ {B:} & 0 \\ \end{array} } \right)\;m_{i}^{\beta } = \left( {\begin{array}{*{20}c} {A:} & 0 \\ {B:} & {0.45} \\ \end{array} } \right), \hfill \\ m_{i}^{\gamma } = \left( {\begin{array}{*{20}c} {A:} & { - 0.45} \\ {B:} & { - 0.45} \\ \end{array} } \right) \hfill \\ \end{gathered}$$
(7)

where we utilize the assumption of parallel liquidus and solidus lines along the chosen tie-line containing the ternary eutectic composition. The ternary eutectic composition is set to give equal volume fractions of the three phases in equilibrium with the liquid. The surface energies of all interfaces is assumed to be 1.0 and the diffusivity is considered to be one-sided with the diffusivity matrix taken to be an identity matrix. The ternary eutectic temperature is set to be \(T_{E}=1.0\), and the molar volume \(V_m\) is set to be 1.0. The set of equilibrium compositions of the phases is given by, \({\varvec{c}}_{eq}^{\alpha }\left\{ A,B \right\} = \left\{ 0.70691, 0.146545\right\}\), \({\varvec{c}}_{eq}^{\beta }\Big \lbrace A,B\Big \rbrace =\Big \lbrace 0.146545, 0.70691\Big \rbrace\) , \({\varvec{c}}_{eq}^{\gamma }\Big \lbrace A,B\Big \rbrace =\) \(\Big \lbrace 0.146545, 0.146545\Big \rbrace\) and the eutectic composition \({\varvec{c}}_{eq}^{liquid}\left\{ A,B \right\} =\) \(\left\{ 0.333333333, 0.333333333\right\}\). With this thermodynamic setting we first set out to explore the influence of the composition and surface energy on the microstructural characteristics.

3.1 Influence of Composition

While in binary alloys, the situation from a completely symmetric (50-50 distribution) can be perturbed by only decreasing the volume fraction of one phase while simultaneously increasing the volume fraction of the remaining phases, in a three phase growth model, where, the volume fractions of the phases can be perturbed along multiple composition paths. In the following, we adopt two such composition pathways, one in which the volume fractions of two phases remain equal but gradually decreases, while the volume fraction of the remaining solid phase increases (Path I in Fig. 2); second in which the volume fraction of one of the phases remains fixed while among the remaining two phases, one of them increases in volume fraction while the other decreases (Path II in Fig. 2).

Fig. 2
figure 2

Schematic of the liqiudus projections (magenta) and solidus projections of the three solid phases, along with the two composition pathways for which the simulations were performed. (Color figure online)

Full size image

To determine the change in microstructures upon change of composition along either of the pathways, we perform a continuous simulation, wherein, the composition of the far-field liquid is changed periodically after sufficient time-intervals during which patterns at a given composition of the liquid is allowed to go reasonably close to steady-state evolution. Figure 3,

Fig. 3
figure 3

Series of microstructures that are obtained upon changing the volume fractions along a composition pathway along which volume fractions of two phases (red and green) remain equal (Path I). The volume fractions corresponding to the images are listed in order for (red, green, blue) phases as a (0.31,0.31,0.38), b (0.22,0.22,0.56), c (0.2,0.2,0.6). (Color figure online)

Full size image

displays the series of microstructures obtained, where starting from the polygonal state near the eutectic composition, the morphology decomposes into a structure of higher connectivity for the larger volume fractions of one of the phases. Similarly, the simulations in Fig. 4 are performed along the pathway where the volume fractions of one of the phases remains intact. Here again, the brick-like structure is obtained at the end, showing that there exists a topological pathway from the polygonal state to the brick-like state, which can be achieved from such a composition variation. Intermediate states among both pathways, leads to each of the phases assuming hexagonally packed rod-like configuration, with the structural change occurring through the gradual coalescence of the rods of the larger volume fraction phase, thus forming the lamellar morphology. All the simulations are performed with an uniform undercooling of \(\Delta T=0.035\).

Fig. 4
figure 4

Series of microstructures that are obtained upon changing the volume fractions along a composition pathway, wherein the volume fractions of one of the phases (green) remains constant (Path II). The volume fractions corresponding to the images are listed in order for (red, green, blue) phases as a (0.31,0.33,0.36), b (0.21,0.33,0.46), c (0.12,0.33,0.55). (Color figure online)

Full size image

3.2 Influence of Solid–Liquid Surface Energy

The second way to perturb the symmetry of the ternary eutectic system is by changing the surface energies. Here we investigate microstructure evolution under two separate conditions. First, while keeping the equilibrium volume fractions symmetric, we change the solid–liquid interfacial energies of one of the solid-phases, (red phase in Fig. 5a). This phase has a solid–liquid interfacial energy lower than the other solid-phases. The solid–liquid surface energies of the three-phases in order (red, green, blue) are thus (0.8, 1.0, 1.0). In a second perturbation, we introduce an asymmetry both in the volume fractions and the surface energies. Here, we choose the equilibrium volume fraction of one of the phases to be larger than the other two phases with equal volume fractions. This phase with larger equilibrium volume fraction is also assigned to have the lowest solid–liquid interfacial energy. In Fig. 5b, the blue phase has the largest volume fraction and also the lowest solid–liquid interfacial energy, such that three solid–liquid interfaces represented by the colors (red, greeen, blue) read (0.32, 0.32, 0.36), while the equilibrium volume fractions are chosen as (0.8, 1.0, 1.0). This leads to the blue-phase assuming a more lamellar type of structure, with high degree of connectivity. The simulations are performed starting from random rods of the different phases distributed with the respective equilibrium volume fractions.

Fig. 5
figure 5

In a phase-fractions corresponding to the ternary eutectic composition in the equilibrium phase diagram are equal, while one of the phases (red) has a solid–liquid interfacial energy lower than the other phases. In b the equilibrium volume fractions of two of the phases (red and green) is smaller than the blue phase, which is also the least stiff. (Color figure online)

Full size image

4 Simulations of a Representative Pattern in a Real Alloy

In the previous section we elaborated on the influence of the interfacial energies and volume fractions on pattern formation. We have seen that asymmetries in either of these properties influences the symmetry of microstructure during solidification. As a final example, we present simulations of a representative alloy that exhibits asymmetry both with respect to the equilibrium volume fractions as well as the interfacial energies.

The surface energies of the interfaces are described by the following matrices;

$$\gamma \alpha \beta = \left( {\begin{array}{*{20}c} {} & \alpha & \beta & \gamma & l \\ \alpha & \times & {0.74} & {0.5} & {0.64} \\ \beta & {0.74} & \times & {0.7} & {0.64} \\ \gamma & {0.5} & {0.7} & \times & {0.4526} \\ l & {0.64} & {0.62} & {0.4526} & \times \\ \end{array} } \right)$$
(8)

The equilibrium compositions of the phases are chosen as: \({\varvec{c}}_{eq}^{\alpha }\left\{ A,B \right\} =\left\{ 0.015629, 0.951626\right\}\), \({\varvec{c}}_{eq}^{\beta }\left\{ A,B\right\} =\left\{ 0.583447, 0.385855\right\}\), \({\varvec{c}}_{eq}^{\gamma }\left\{ A,B\right\} =\left\{ 0.000436, 0.676705\right\}\) and the eutectic composition \({\varvec{c}}_{eq}^{l}\left\{ A,B \right\} =\left\{ 0.180961, 0.691171\right\}\). The coefficient matrix \(A_{ij}\) reads:

$$\begin{gathered} A_{{ij}}^{\alpha } = \left( {\begin{array}{*{20}c} {} & A & B \\ A & {0.92} & {0.83} \\ B & {0.83} & {0.71} \\ \end{array} } \right)\;A_{{ij}}^{\beta } = \left( {\begin{array}{*{20}c} {} & A & B \\ A & {4.4} & {3.52} \\ B & {3.52} & {9.4} \\ \end{array} } \right) \hfill \\ A_{{ij}}^{\gamma } = \left( {\begin{array}{*{20}c} {} & A & B \\ A & {146.6} & { - 0.3565} \\ B & { - 0.3565} & {6.46} \\ \end{array} } \right)\;A_{{ij}}^{l} = \left( {\begin{array}{*{20}c} {} & A & B \\ A & {0.725} & {0.6857} \\ B & {0.6857} & {1.00} \\ \end{array} } \right) \hfill \\ \end{gathered}$$
(9)

while the liquidus slopes read,

$$\begin{aligned} m_{i}^{\alpha } &= \left( {\begin{array}{*{20}c} {A:} & {0.7026} \\ {B:} & {1.099} \\ \end{array} } \right)\;m_{i}^{\beta } = \left( {\begin{array}{*{20}c} {A:} & {0.681} \\ {B:} & { - 0.2648} \\ \end{array} } \right) \hfill \\ m_{i}^{\gamma } & = \left( {\begin{array}{*{20}c} {A:} & { - 0.85243} \\ {B:} & { - 0.8} \\ \end{array} } \right) \hfill \\ \end{aligned}$$
(10)

(For details of the determination of coefficients \(A_{ij}\) and the non-dimensionalization see Appendix 1, 2.)

The results from the phase-field simulation are highlighted in Fig. 6 that depicts the microstructures during the various stages of evolution. The 3D simulation is performed starting from a random-state of rods (size 10 × 10 × 20 in grid units), which represent the early nuclei of the solids in the liquid, that eventually establish a steady-state pattern during directional solidification.

Fig. 6
figure 6

Series of images highlighting the evolution of a microstructure from a random state. The colors represent red: α, green: β and blue: γ. t is non-dimensional time. (Color figure online)

Full size image

The simulated microstructure in Fig. 6d, illustrates close resemblance to the experimental image in Fig. 1a.

5 Conclusions

There are three-main conclusions that we can derive from our work:

  • The asymmetry in the volume fractions is one of the key factors determining the co-ordination/connectivity among the phases.

  • The influence of the solid–liquid surface energies is exhibited in two ways: first the shape of the different phase clusters is modified on account of the shape of the quadruple junctions, and second the coupling with the volume fractions through the change in the solid- compositions on account of the Gibbs-Thomson shifts. The latter should become less effective for smaller solidification speeds and therefore larger microstructural scales.

  • A representative structure in the Ag–Al–Cu alloy can be derived by incorporating an asymmetry both in the volume fractions as well as in the solid–liquid interfacial energies.