Introduction

During the directional solidification of a ternary eutectic composition, the melt transforms into three solid phases. These three phases can form various patterns, which influence the mechanical properties of the macroscopic component.[1,2,3] Gaining a deeper understanding of the pattern formation process is therefore of high technical and scientific interest.

Experiments of directionally solidified eutectic systems show that the lamellar spacing of the solid phases correlates with the velocity of the solidification front.[4,5,6,7]

In 1966, Jackson and Hunt[8] derived an analytical approach for the correlation between the lamellar spacing, the solidification velocity, and the average front undercooling below the temperature of the eutectic point in binary systems, which occurs during lamellar and rod eutectic growth. Further extensions for the directional solidification of binary eutectics and eutectoids are presented in References 9,10,11,12. Himemiya and Umeda,[13] as well as Himemiya,[14] extended the approach of Jackson and Hunt[8] for special patterns in ternary eutectic systems, which is referred to as HU1999 in the following. In their study, they derived analytical approaches for a two-dimensional \(\alpha \)-\(\beta \)-\(\alpha \)-\(\gamma \) pattern and for three-dimensional chain-like and hexagonal patterns. A generalized derivation for arbitrary lamellar arrangements of ternary eutectics in 2D sections is presented by Choudhury et al. in Reference 15, which is called CPN2011 in the following.

To study the effect of the undercooling on the pattern formation process in complex spatial arrangements, the phase-field method has been established in recent years.[17,18,19,20] Phase-field simulations allow to investigate the undercooling depending on physical parameters and process conditions. For a directionally solidified binary eutectic, a Jackson–Hunt-like behavior is found by Folch and Plapp[16] in 2D phase-field simulations. In CPN2011, a quantitative accordance is found between 2D phase-field simulations, based on a free energy model of Reference 17 and the derived analytical approaches. In continuation, binary eutectoid growth is considered in Reference 12 for a comparison between an extended Jackson and Hunt approach and 2D phase-field simulations.

Two-dimensional phase-field simulations of ternary eutectic alloys, based on the minimization of the free energy, are presented in Reference 21, for \(\mathrm {In}\)-\(\mathrm {Bi}\)-\(\mathrm {Sn}\), in Reference 22, for \(\mathrm {Al}\)-\(\mathrm {Ag}\)-\(\mathrm {Cu}\), and in References 23 and 24, for \(\mathrm {Mo}\)-\(\mathrm {Si}\)-\(\mathrm {B}\). The simulations in Reference 21 predict the average undercoolings, and in Reference 23, an accordance with the analytical approach of Reference 15 is found. In experiments, directional solidification takes place in three dimensions. In Reference 25, a Jackson–Hunt-like behavior is shown for a 3D phase-field study of the directional solidification of binary eutectics, with the model from Reference 16. However, the results from the simulation studies of References 16 and 25 are not compared with the analytical predictions following Jackson and Hunt.

Three-dimensional phase-field simulations of the pattern formation process during the directional solidification of three-phase ternary eutectics are studied for idealized systems in References 15, 17, and 26,27,28 and for the ternary eutectic system \(\mathrm {Al}\)-\(\mathrm {Ag}\)-\(\mathrm {Cu}\) in References 22, 27, and 29,30,31. Jackson–Hunt-like behaviors in 3D phase-field studies of the directional solidification of ternary systems, with a model based on the grand potential approach,[29,32,33] are discussed in References 28 and 35.

A dependence of the arising patterns on the average front undercooling is reported in Reference 15, from 2D simulations. During the three-dimensional growth of ternary eutectics, a wide range of different microstructures can evolve. Due to the assumed correlation between the arising patterns and the resulting undercooling, the quantitative investigation is of high interest to identify the fundamental parameters that control the morphology development in multiphase, multicomponent systems. This correlation of three-phase ternary eutectic systems, during 3D directional solidification, has not previously been studied with phase-field simulations.

Therefore, this study focuses on the quantitative comparison of the undercooling in three-dimensional ternary eutectic phase-field simulations with analytical results derived by HU1999, and with a newly derived analytical theory based on a combination of HU1999 and CPN2011. For the comparison with theory, the lamellar spacings and the growth velocities are varied systematically. The purpose of this study is to conduct a quantitative comparison between the analytical approaches and the phase-field model in 3D. For this reason, the undercooling–spacing relationship of a ternary eutectic alloy is investigated for a 3D pattern. Previous studies focused on two-dimensional simulations. Gaining a better understanding of this relation is essential to elucidate the complex pattern arrangement mechanisms in ternary eutectic alloys,[34] and to predict the microstructure which forms during three-dimensional growth.

In the studies, the thermodynamically consistent phase-field model of Reference 29 with an ideal ternary eutectic system, is used.

As a first step of the comparison, the applied phase-field model and the simulation setup are briefly presented. Then, the analytical approaches for two-dimensional[13,14,15] and three-dimensional[13] ternary eutectic directional solidification are discussed. In the derivation of the analytical approaches from CPN2011 and HU1999, different assumptions are made. The newly derived approach uses the assumptions of equal undercoolings from Reference 15 to calculate the average front undercooling in a 3D pattern. The comparison of both approaches allows to investigate the validity of the different assumptions.

The two-dimensional lamellar arrangement \(\alpha -\beta -\alpha -\gamma \) is compared with the analytical approaches from CPN2011 to validate the model by recapitulating the study of Reference 15, and also using the analytical approach from HU1999.

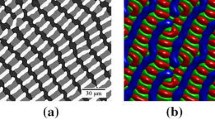
After the validation of the model, an extensive three-dimensional phase-field study of a chain-like pattern, which is also referred to as brick-like structure[4,36,37,38] is conducted. An experimental example of a brick-like structure is depicted in Figure 1, showing a cross section of the ternary eutectic system \(\mathrm {Al}\)-\(\mathrm {Ag}\)-\(\mathrm {Cu}\). The undercoolings obtained from the simulations are compared with the analytical approaches of HU1999 and the newly derived approach.

Finally, the results are summarized, and the conclusions are drawn.

Fig. 1
figure 1

Experimental micrograph of directionally solidified ternary eutectic \(\mathrm {Al}\)-\(\mathrm {Ag}\)-\(\mathrm {Cu}\), provided by A. Dennstedt at the German Aerospace Center (DLR), Cologne. The micrograph is obtained from a cross section parallel to the solidification front of an experiment with a velocity of \(0.08 \, {\mu m}/{s}\) and a temperature gradient of \(2.2 \, {K}/{mm}\). The three solid phases form a chain-like (brick-like) pattern of two phases, embedded in a matrix phase

Full size image

Methods

Phase-Field Model

For the simulations, a thermodynamically consistent phase-field model,[29,32,33] based on the Allen-Cahn approach, is applied. In the case of three-phase ternary eutectic directional solidification, the coupled evolution equations for the \(N=4\) phase-fields \(\phi _{\hat{\alpha }}\) in Eq. [1] as well as the \(K=3\) chemical potentials in the vector \(\varvec{\mu }=(\mu _A, \mu _B, \mu _C)^T\) in Eq. [2] are solved numerically, together with an expression for the evolution of the analytic temperature T in Eq. [3]. The evolution equations of the chemical potentials in Eq. [2] are derived from Fick‘s laws to ensure mass conservation. The set of evolution equations is written as

$$\begin{aligned}&\tau \epsilon \frac{\partial {\phi _{\hat{\alpha }}}}{\partial t} =\quad \underbrace{ -\epsilon T \left( \frac{\partial a(\varvec{\phi },\nabla \varvec{\phi })}{\partial \phi _{\hat{\alpha }}} - \nabla \cdot \frac{\partial a(\varvec{\phi },\nabla \varvec{\phi })}{\partial \nabla \phi _{\hat{\alpha }}} \right) -\frac{1}{\epsilon } T \frac{\partial {\omega (\varvec{\phi })}}{\partial \phi _{\hat{\alpha }}} - \sum ^N_{\hat{\beta }=1} \left( \psi _{\hat{\beta }}(\varvec{\mu },T) \frac{\partial {h_{\hat{\beta }}}(\varvec{\phi })}{\partial \phi _{\hat{\alpha }}} \right) }_{:=rhs_{\hat{\gamma }}} - \Lambda , \end{aligned}$$
(1)
$$\begin{aligned}& \frac{\partial {\varvec{\mu }}}{\partial t} = \left[ \sum _{\hat{\alpha }=1}^N h_{\hat{\alpha }}(\varvec{\phi }) \left( \frac{\partial \varvec{c}_{\hat{\alpha }}(\varvec{\mu }, T)}{\partial \varvec{\mu }} \right) \right] ^{-1} \Biggl ( \nabla \cdot {} \Big (\varvec{M}(\varvec{\phi },\varvec{\mu },T)\nabla {\varvec{\mu }} - \varvec{J}_{at}(\varvec{\phi },\varvec{\mu },T) \Big )\\ \nonumber & \qquad \qquad - \sum _{\hat{\alpha }=1}^N \varvec{c}_{\hat{\alpha }}(\varvec{\mu },T) \frac{\partial h_{\hat{\alpha }}(\varvec{\phi })}{\partial t} - \sum _{\hat{\alpha }=1}^N h_{\hat{\alpha }}(\varvec{\phi }) \left( \frac{\partial \varvec{c}_{\hat{\alpha }}(\varvec{\mu }, T)}{\partial T} \right) \frac{\partial {T}}{\partial t} \Biggr ), \end{aligned}$$
(2)
$$ \frac{\partial {T}}{\partial t} = \quad \frac{ \partial }{\partial t} \left( T_0 + G(z - vt)\right) = -Gv.$$
(3)

In Eq. [1], the parameter \(\tau \) is related to the kinetics of the interfaces, and \(\epsilon \) is related to its thickness. To model the shape of the diffuse interfaces, the gradient energy density a and the potential energy \(\omega \) are applied. As driving forces for the phase transition, the differences between the grand potentials \(\psi _{\hat{\beta }}\), which are calculated from the Gibbs energies, are used. The driving forces in the interface are interpolated with the polynomial function \(h_{\hat{\beta }}\). The usage of the Lagrange multiplier \(\Lambda =\frac{1}{N}\sum ^N_{\hat{\gamma }=1} rhs_{\hat{\gamma }}\) is introduced in the model to fulfill the constraint \(\sum ^N_{\hat{\alpha }=1} {\partial \phi _{\hat{\alpha }}}/{\partial t}=0\) for \(\phi _{\hat{\alpha }} \in \,[0,1]\,\). In Eq. [2], the matrix \(\varvec{M}\) is the mobility of the K chemical potentials, and \(\varvec{c}_{\hat{\alpha }}(\varvec{\mu }, T)\) is the concentration vector. The effect of the artificially enlarged interface[33,39,40] is balanced by the anti-trapping current vector \(\varvec{J}_{at}\). The evolution of the analytic temperature gradient in Eq. [3] is described with the initial base temperature \(T_0\), the applied gradient G, and the velocity v in the growth direction z.

The model is implemented as a combined solution of the Pace3D package[41] and the massive parallel framework waLBerla Footnote 1.[42,43] A detailed description of the model is given in Reference 29, and the discretization with finite differences is presented in Reference 44.

Simulation Setup

For the simulative investigations of the directional solidification process, an ideal ternary eutectic system is used. The characteristics of the system allow to study the influence of the growth velocity and the lamellar arrangement on the average front undercooling unaffected by unequal phase fractions and differing physical properties, like the interface energies. The ideal ternary eutectic is defined by equal phase fractions of the three solid phases, equal concentrations of the components in the melt, equal surface energies, and equal diffusion coefficients. For the thermodynamic definition, the Gibbs energies of the solid phases are equally distributed on the concentration simplex around the Gibbs energy of the liquid phase, which is located in the center of the simplex. The Gibbs energies are modeled as paraboloids[45] with equal slopes. The values of the used parameters are given in Reference 28.

To study the directional solidification, a simulation setting, which is schematically depicted in Figure 2, is applied. Starting from a defined cuboid initial structure, three phases solidify in a coupled growth mode from the melt and form different patterns in sections perpendicular to the growth direction. The plane parallel to the growth front is called base size in accordance with Reference 29. The lamellar spacings of the three solid phases are systematically varied and evaluated in the base plane as the distance between periodically continued arrangements.[8] Perpendicular to the growth direction, periodic boundary conditions are applied. For constant conditions, the undercooling below the ternary eutectic temperature converges during growth, and is calculated from the computed mean temperatures at the solidification front. The solidification front is defined as the isosurface, where the order parameter of the liquid phase equals 0.5. The growth velocity of the solidification front is controlled by the pulling speed of an analytic temperature gradient. To study the influences of the growth velocity and of the lamellar arrangements on the average front undercooling and on the arising patterns, the three velocities \(v_1=0.035\), \(v_2=0.071\) , and \(v_3=0.141\) in cells per time step are considered. In this study, all simulations were run at least 1 million time steps to ensure stable growth and converged average front temperatures.

Fig. 2
figure 2

Schematic illustration of the simulation setup to study the directional solidification of the ternary eutectic system. The plane called base size, in accordance with Ref. [29], is highlighted in red (Color figure online)

Full size image

Discussion of the Jackson–Hunt-Type Analytical Approach

In the following two analytical approaches, which are both in the line of Jackson and Hunt,[8] for the calculation of the average front undercooling in three-phase ternary eutectics, depending on the lamellar spacings, and the growth velocity are discussed and compared. In addition, based on these approaches, a new formulation for a three-dimensional chain-like pattern is proposed.

The first approach HU1999 is derived by Himemiya[14] as well as Himemiya and Umeda.[13] In their study, analytic solutions for the two-dimensional pattern \(\alpha \)-\(\beta \)-\(\alpha \)-\(\gamma \) and for a chain-like pattern as well as for a hexagonal pattern in 3D are derived. The second approach CPN2011 of Choudhury et al.[15] describes a generalized form for the calculation of arbitrary lamellar arrangements in 2D systems.

The undercooling \(\Delta T\) is defined as the difference between the temperature at the solidification front \(T_{front}\) and the temperature of the ternary eutectic point \(T_E\). According to the Gibbs–Thomson equation, \(\Delta T\) consists of the solutal undercooling \(\Delta T_{solutal}\), the curvature-based undercooling \(\Delta T_{curvature}\), and the kinetic undercooling \(\Delta T_{kinetic}\). According to Reference 8, \(\Delta T_{kinetic}\) can be neglected for the diffusion-controlled solidification of metals. To calculate the concentration fields in the liquid, a Fourier series approach is applied in both derivations.

In HU1999, it is assumed that the concentrations and the phase fractions of the developing microstructure are equal to those at \(T_E\). Thus, all Fourier coefficients, including the zeroth, are calculated by inserting the approach into the Stefan condition. As the phases solidify at a temperature below \(T_E\), the authors in CPN2011 argue that the concentrations of the solids differ from the equilibrium concentrations at the ternary eutectic temperature and therefore the phase fractions differ as well. The determination of the real phase fractions, depending on the solidification conditions, requires a self-consistent calculation with a high computational effort[15] Therefore, the zeroth Fourier coefficients are treated as unknowns, similar to the Jackson–Hunt approach,[8] and are solved in the calculation of the average front undercooling.

For the generalization of the lamellar arrangements in 2D, CPN2011 applies weighted averages in the case of more lamellae than involved solid phases to calculate the average concentration and the average curvature.

To determine the average front undercoolings \(\Delta T^{\xi }\) for each of the solid phases \(\xi \) with a constant velocity, two different procedures are applied.

In HU1999, the undercoolings consisting of \(\Delta T_{solutal}\) and \(\Delta T_{curvature}\) are rearranged as expressions of the form

$$\begin{aligned} \Delta T^{\xi } = A^{\xi } v \lambda _1 + B^{\xi }\frac{1}{\lambda _1}\quad \forall \,\xi \,. \end{aligned}$$
(4)

The functions \(A^{\xi }\) and \( B^{\xi }\) in Eq. [4] summarize the expressions of \(\Delta T_{solutal}^{\xi }\) and \(\Delta T_{curvature}^{\xi }\) from HU1999. In 2D, \(A^{\xi }\) and \( B^{\xi }\) depend on the lamellar spacing \(\lambda _1\), and in 3D, they depend on the two spacings \(\lambda _1\) and \(\lambda _2\).

By averaging the three undercoolings \(\Delta T^{\xi }\), the total front undercooling for two- and three-dimensional growth is determined as

$$\begin{aligned} \Delta T = \frac{3 }{\displaystyle \sum _{\xi =1}^3 \frac{1}{A^{\xi }}} v \lambda _1 + \frac{ \displaystyle \sum _{\xi =1}^3 \frac{ B^{\xi }}{A^{\xi }} }{ \displaystyle \sum _{\xi =1}^3 \frac{1}{A^{\xi }} } \frac{1}{\lambda _1}\,. \end{aligned}$$
(5)

CPN2011 is using a different procedure to calculate the average front undercooling. Due to treating the zeroth Fourier coefficients as unknowns (\(A_0\), \(B_0\), and\(C_0\) of the three components), the formulations for the average front undercooling of each of the solid phases can be rearranged as

$$\begin{aligned} \Delta T^{\alpha } = \hat{a}^{\alpha }(B_0,C_0) + \hat{A}^{\alpha }(\lambda _1) v \lambda _1 + \hat{B}^{\alpha }(\lambda _1)\frac{1}{\lambda _1} \end{aligned}$$
(6)
$$\begin{aligned} \Delta T^{\beta } = \hat{a}^{\beta }(A_0,C_0) + \hat{A}^{\beta }(\lambda _1) v \lambda _1 + \hat{B}^{\beta }(\lambda _1) \frac{1}{\lambda _1} \end{aligned}$$
(7)
$$\begin{aligned} \Delta T^{\gamma } = \hat{a}^{\gamma }(A_0,B_0) + \hat{A}^{\gamma }(\lambda _1) v \lambda _1 + \hat{B}^{\gamma }(\lambda _1) \frac{1}{\lambda _1}\,. \end{aligned}$$
(8)

The functions \(\hat{a}^{\xi }\), \(\hat{A}^{\xi }\), and \(\hat{B}^{\xi }\) summarize the expressions of \(\Delta T_{solutal}^{\xi }\) and \(\Delta T_{curvature}^{\xi }\) from CPN2011.

By means of the relation \(A_0+B_0+C_0 =0\) from the Stefan condition and assuming equal undercoolings for all solid phases \(\Delta T = \Delta T^{\alpha } = \Delta T^{\beta } = \Delta T^{\gamma }\), the set of equations can be solved, and the total average front undercooling can be calculated. As shown in Reference 46 and mentioned in CPN2011, the assumption of equal undercoolings is quite accurate for systems with similar phase fractions of the solid phases. However, for asymmetric systems in 2D, with unequal phase fractions or 3D structures, this assumption is inaccurate. In the current study, an ideal system with equal phase fractions is employed for the simulation studies.

In summary, it can be said that different undercoolings for the solid phases are determined in HU1999; however, due to the calculation of the zeroth Fourier coefficients, the concentrations are equal to the ones at \(T_E\). In contrast, the concentrations of the three solid phases at the growth front can be different from the values at \(T_E\), according to CPN2011. This requires equal undercoolings for all phases to close the equation system.

In addition to HU1999, we present an extension to calculate the undercoolings for the chain-like pattern in the following, which is based on HU1999, and is in the line of CPN2011. The extension provides a further analytical expression to calculate the undercooling for chain-like patterns with equal \(\Delta T\). The concentration fields in the melt and the curvatures of the solidification front are calculated according to HU1999. However, the zeroth Fourier coefficients (\(A_0\), \(B_0\), and \(C_0\)) are treated as unknowns, similar to CPN2011. By applying the relation \(A_0+B_0+C_0 =0\), and by assuming equal undercoolings for all solid phases, the total average front undercooling is calculated. This approach, which is labeled as HU\(_{\text {equal}\,\Delta T}\) in the following, allows to compare the effect of the different assumptions to calculate the average front undercooling.

Parameters for the Analytical Approaches

The parameters to calculate the undercooling from the analytical approaches in Sections II–E and III are described in Reference 28. The slopes of the liquidus planes, the equilibrium phase fractions, and the equilibrium concentrations in the phases are calculated from the Gibbs energies. The contact angles in equilibrium at triple and quadruple points are calculated with Young’s law from the interface energies. The Gibbs–Thomson coefficients \(\Gamma ^{\xi }\) are determined according to References 12 and 47 as

$$\begin{aligned} \Gamma ^{\xi } = \frac{\sigma ^{\xi \; liq} \sqrt{\sum _{i=1}^{2} m_i^{\xi \; liq}}}{\sqrt{\sum _{j=1}^{2} \left( \sum _{i=1}^{2} \frac{\partial ^2 g^{\xi }}{\partial c_i^{\xi } \partial c_j^{\xi }} (c_i^{\xi } - c_i^{liq}) \right) ^2 }}{,} \end{aligned}$$
(9)

with the Gibbs energy \(g^{\xi }\) of the solid phase \(\xi \) and the interface energies \(\sigma ^{\xi \; liq}\) between the phase \(\xi \) and the melt liq. The parameters \(m_i^{\xi \; liq}\) denote the slopes of the liquidus planes, and \(c_i^{liq}\) and \(c_i^{\xi }\) are the equilibrium concentrations of the chemical elements in the phases.

Validation of the Model with Simulations of the Stacking Sequence \(\alpha -\beta -\alpha -\gamma \)

In this section, the undercooling in the simulations for the stacking sequence \(\alpha -\beta -\alpha -\gamma \), with three different velocities, and with systematically varied lamellar spacings, are studied. The results of the 2D phase-field simulations are quantitatively compared with the analytical approaches of HU1999 and CPN2011. The comparison with CPN2011 recapitulates the investigations from Reference 15, conducted with the free energy model of Reference 17, to validate the applied phase-field model based on the grand potential approach. In the applied grand potential model, no excess energy does occur in the interface, which is in contrast to Reference 15, as discussed in Reference 33.

The investigated lamellar arrangement of the form \(\alpha -\beta -\alpha -\gamma \) is depicted in the inlet of Figure 3. This kind of stacking sequence is reported from experimental cross sections of the ternary eutectic systems \(\mathrm {Al}\)-\(\mathrm {Ag}\)-\(\mathrm {Cu}\)[6] and \(\mathrm {In}\)-\(\mathrm {Bi}\)-\(\mathrm {Sn}.\)[21,48] The width of the \(\alpha \) lamella is half the width of the \(\beta \) and the \(\gamma \) lamellae, respectively. As expected, different growth modes (oscillation, stable growth, and overgrowth) can be distinguished in the simulations, depending on the lamellar spacing. For the velocity \(v_2\), one of the \(\alpha \) lamellae is overgrown for \(\lambda \le 50\) cells. For \(\lambda \ge 55\) cells, stable lamellar growth occurs, and for a lamellar spacing larger than 75 cells, the width of the lamellae starts to oscillate. This is in accordance with the results in Reference 15.

The average front undercoolings of the 2D simulations over the lamellar spacing without overgrowth are depicted in Figure 3, with black marks. The behavior of the undercooling values shows the well-known trend of the Jackson–Hunt theory,[8] described by the relation

$$\begin{aligned} \Delta T=A v \lambda + \frac{B}{\lambda }\, , \end{aligned}$$
(10)

with a minimum undercooling at the operating point \(\lambda _{JH}\), and with the material-specific constants A and B.

In Figure 3, the analytical results from CPN2011 and HU1999 are plotted as solid blue and green lines, respectively.

The results from HU1999 predict a slightly larger undercooling than the results from CPN2011, but the operating points \(\lambda _{JH}\) differ by a maximum of 2.18 cells, for all three velocities. Compared with CPN2011, the maximum deviation of the undercooling between the simulations and the analytical results from HU1999 is \( 10.2\,\text {\rm pct} \) at \(\lambda =60\) for the velocity \(v_3\), and \(8.5 \,\text {\rm pct}\) at \(\lambda =100\) also for the velocity \(v_3\). The simulation results lie between both analytical curves for the considered lamellar spacings. For the velocity \(v_2\), the difference in \(\lambda _{JH}\) is \(3.7 \,\text {\rm pct}\) for CPN2011 and \(5.7 \,\text {\rm pct}\) for HU1999.

A good accordance between the simulations and the analytical approaches is found for the velocities \(v_1\) and \(v_2\).

For the velocity \(v_3\), which is four times higher than \(v_1\), the differences are larger. This behavior is also observed in Reference 15 and can be explained by the larger deviation from the thermodynamic equilibrium, and by the inherent assumptions used in the analytical derivations, like a planar solidification front, as reported in References 12 and 16. An analytical derivation, combined with a phase-field study that evaluates the influence of curved interfaces, is in preparation.[49]

In addition, an extension of the 2D simulations to 3D is conducted by expanding the two-dimensional setting to a quadratic base size in the third dimension. In Figure 3, the results of the 3D simulations without overgrowth are displayed as red marks. As expected, the deviation is in the order of the machine epsilon.

Fig. 3
figure 3

Average front undercooling over the lamellar spacing for the arrangement \(\alpha -\beta -\alpha -\gamma \) and three different velocities \(v_1\), \(v_2\) , and \(v_3\). The results from 2D and 3D simulations are drawn with black and red symbols, respectively. The analytical results from CPN2011[15] are drawn as blue curves, and the analytical results from HU1999[13] are displayed as green curves (Color figure online)

Full size image

The investigation with the stacking sequence \(\alpha -\beta -\alpha -\gamma \) shows a good accordance between the simulations and the analytical results. This demonstrates the capability of the model, based on the grand potential approach to quantitatively reproduce the undercoolings predicted from analytical results.

Results of 3D Simulations with Chain-Like Structures

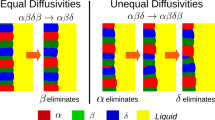
In the following, the undercooling of an inherently three-dimensional phase ordering, the chain-like structure, is investigated and compared with the analytical solutions of HU1999 and HU\(_{\text {equal}\,\Delta T}\). From CPN2011, no analytical solutions for three-dimensional patterns are reported, and therefore HU\(_{\text {equal}\,\Delta T}\) is derived. Chain-like patterns as exemplarily illustrated in Figure 1 are observed for example in experiments of the ternary eutectic system \(\mathrm {Al}\)-\(\mathrm {Ag}\)-\(\mathrm {Cu}.\)[4,36,37,38,38] In this pattern, chain links of the phases \(\beta \) and \(\gamma \) are embedded in an \(\alpha \) matrix.

The setting for the 3D phase-field studies is plotted in Figure 2 and in the inlet of Figure 4. To investigate this pattern, two lamellar spacings have to be considered: \(\lambda _1\) is defined perpendicular to the chain direction, and \(\lambda _2\) is defined in the chain direction.

Influence of the Growth Velocity in a Quadratic Base Size

In the first simulation series for the chain-like pattern, a quadratic base size is used with \(\lambda =\lambda _1=\lambda _2\), which is varied from \(30\times 30\) to \(100 \times 100\) cells with a step size of 5 cells. With this series, the influences of the growth velocity and the lamellar spacing on the undercooling are studied.

The undercooling over the lamellar spacing \(\lambda \) of the simulations with a retaining chain-like pattern, for the velocities \(v_1\), \(v_2\) and \(v_3\), is plotted in Figure 4 with red points. The results confirm the Jackson–Hunt-like behavior of Eq. [10], with an operating point \(\lambda _{JH}\). Besides the simulation results, the analytical predictions from HU1999 and HU\(_{\text {equal}\,\Delta T}\) are plotted in green and blue for the three velocities, respectively.

Both analytical approaches show a similar behavior for the considered velocities and the lamellar spacings. For the investigated parameters, combinations of velocity and lamellar spacings exist, where the approach with equal undercoolings (HU\(_{\text {equal}\,\Delta T}\)) predicts higher undercoolings than HU1999. This is in contrast to the studied two-dimensional \(\alpha -\beta -\alpha -\gamma \) stacking sequence.

For both analytical approaches, the operating points \(\lambda _{JH}\) differ from each other by a maximum of 3.7 cells for all three velocities. For the investigated spacings, the maximum deviation in the undercooling between the analytic curves is \(12.6\,\text {\rm pct}\) for \(v_1\) and \(\lambda =90\) referred to HU1999.

The undercoolings in Figure 4 record a good accordance between the simulations and the analytical results for different velocities and lamellar spacings for the considered 3D pattern. The comparison with HU1999 shows that the computed analytical undercoolings at the operating points differ by a maximum of \(16.3\,\text {\rm pct}\) for the velocity \(v_1\). However, for low velocities, the relative deviation becomes larger due to smaller absolute undercoolings. In the case of HU\(_{\text {equal}\,\Delta T}\), the maximum deviation at the \(\lambda _{JH}\)’s of the simulations is measured for the velocity \(v_3\) with \(7.5\,\text {\rm pct}\) referred to HU\(_{\text {equal}\,\Delta T}\). Despite the reported relative maximum deviation, the simulations and the analytical approaches follow the same trends.

Fig. 4
figure 4

Average front undercooling over the lamellar spacing for chain-like patterns with a quadratic base size for the three different velocities \(v_1\), \(v_2\) and \(v_3\). The results from 3D simulation are shown with red marks. The analytical results from HU1999[13] are depicted as green curves, and the results from HU\(_{\text {equal}\,\Delta T}\) are drawn in blue (Color figure online)

Full size image

For the arising microstructures, a behavior similar to the two-dimensional validation case is observed. With an increase of the lamellar spacings, the final microstructure evolves into different patterns, as shown in the equally scaled micrographs with different base sizes in Figure 5. First, the rods rearrange to non-chain-like structures, then a stable growth of the predicted pattern occurs. By further increasing the spacing, the phase widths start to oscillate, transition patterns occur, and finally multiple chain-like structures form.

The rearrangement of the pattern is accompanied by a decrease of the average front undercooling, which is in accordance with the results in Reference 25 for a binary eutectic and with the results in Reference 28, for a ternary eutectic hexagonal pattern. As expected, the average front undercoolings for the switched chain-like patterns are equal to the corresponding simulations with the half base size and without a pattern switch. This is reflected in the average front undercoolings for the base sizes \(110\times 110\) and \(120\times 120\), which are equal to the undercoolings of the simulations with the base sizes \(55\times 55\) and \(60\times 60\), respectively.

Fig. 5
figure 5

Average front undercoolings of the simulations for the velocity \(v_2\) with quadratic base sizes as well as a selection of occurring microstructures at different domain sizes

Full size image

Influence of Unequal Lamellar Spacings

In the next study, the influence of unequal lamellar spacings on evolving chain-like patterns for \(\lambda _1 \ne \lambda _2\) and on the average front undercooling is investigated.

In Figures 6(a) and (b), the undercoolings for the velocities \(v_1\), \(v_2\) and \(v_3\), calculated from the analytical approaches of HU1999 and HU\(_{\text {equal}\,\Delta T}\), are, respectively, plotted as red, green, and blue hyperplanes, depending on both lamellar spacings.

For all velocities, the planes follow a Jackson–Hunt-type behavior of Eq. [10] for \(\lambda _1\) with a constant \(\lambda _2\) and for \(\lambda _2\) with a constant \(\lambda _1\), respectively. All hyperplanes show global minima in the undercoolings, similar to the undercoolings at \(\lambda _{JH}\) in the previous studies. These minima on the planes and their projections on the bottom planes of the 3D plots are highlighted with colored marks corresponding to the planes. The ratios of \(\lambda _1\) and \(\lambda _2\), for the three minima, follow the relationship \({\lambda _2}/{\lambda _1}=1.138\) for HU1999, and \({\lambda _2}/{\lambda _1}=0.705\) for HU\(_{\text {equal}\,\Delta T}\), indicated by the black lines in the bottom planes in Figure 6.

Fig. 6
figure 6

Calculated undercooling \(\Delta T\), depending on the spacings \(\lambda _1\) and \(\lambda _2\), for the velocities \(v_1\), \(v_2\) and \(v_3\) in red, green, and blue, according to HU1999 in (a) and HU\(_{\text {equal}\,\Delta T}\) in (b). The global minima and the projections on the bottom planes are highlighted in the corresponding colors (Color figure online)

Full size image

For a comparison with the analytical approaches, a phase-field study with a systematic variation of \(\lambda _1\) and \(\lambda _2\) is conducted for the velocity \(v_2\). For this study, \(\lambda _1\) as well as \(\lambda _2\) are varied from 40 to 100 cells in steps of 5 cells. Each of the 169 three-dimensional simulations is computed with 360 CPUs for up to 120 minutes.

Different forms of chain-like structures occur in the simulations. Depending on the lamellar spacings, various patterns, such as stable growth, oscillation of the phase widths or a change of the phase arrangement, is observed. The different growth modes of the simulations, depending on \(\lambda _1\) and \(\lambda _2\), are outlined in a morphology classification diagram in Figure 7. Regions with stable growth are marked with green triangles. The area without pattern change, but with an oscillation of the phase widths, is depicted with red circles. Two regions are outlined with blue squares, in which the initial chain-like pattern changes. The behavior of the simulations differs in the \(\lambda _1\)- and \(\lambda _2\)-direction. The blue area, with a pattern change in the region \(90\le \lambda _1 \le 100\) and \(60\le \lambda _2 \le 80\), evolves through the interplay of the degrees of freedom for oscillation and limitations through diffusion and interface energies. Beside the mentioned areas, selected cross sections after 1 million time steps are placed around the \(\lambda _1\)-\(\lambda _2\) diagram in Figure 7 to illustrate the arising patterns. Especially for the simulations in the upper right corner oscillations occur, which lead to temporally different phase fractions. However, the average phase fractions remain constant for the whole simulation with one third for each solid phase in consistency with the lever rule.

Fig. 7
figure 7

Morphology diagram with different growth modes, depending on the spacings \(\lambda _1\) and \(\lambda _2\). The cross sections refer to evolution states after 1 million time steps and illustrate the different kinds of arising patterns

Full size image

The undercoolings \(\Delta T\), related to the velocity \(v_2\) of the simulations without pattern change, and the analytical approaches are plotted in Figure 8 over both lamellar spacings \(\lambda _1\) and \(\lambda _2\). The analytical results are inserted as translucent green and blue planes, and the simulation results are depicted as red points. The simulations show the same trends as the analytical approaches. In the bottom plane of the 3D plot, the direction of the sections for \(\lambda _1=const\) and \(\lambda _2=const\) is marked. In the lower parts of Figure 8, the undercoolings for these sections are plotted as marks for the simulations, depending on the respective lamellar spacings. For the simulations, both diagrams show the Jackson–Hunt-type behavior of Eq. [10] for \(\lambda _1\) with \(\lambda _2=const\) as well as for \(\lambda _2\) with \(\lambda _1=const\), respectively. The undercoolings for \(\lambda _1=\lambda _2\) are already displayed in Figure 4.

Similar to the analytical approaches in Figure 6, a global minimum of the undercoolings occurs in the simulated chain-like pattern for a variation of both lamellar spacings. The minimum undercooling point is located at approximately \(\lambda _1=50\) and \(\lambda _2=50\), resulting in a ratio of \({\lambda _2}/{\lambda _1}=1.0\) for the simulation series. The operating point of the simulations differ by 8.1 cells from the analytic of HU1999 and 15.5 cells from HU\(_{\text {equal}\,\Delta T}\) in euclidean metric. The simulated undercoolings referred to the analytic result have a deviation of \(2.1 \,\text {\rm pct}\) for HU1999 and of \(1.3\,\text {\rm pct}\) for HU\(_{\text {equal}\,\Delta T}\). In total, the maximum differences in the undercooling, which refer to the analytic values of HU1999, are \(3.4 \,\text {\rm pct}\) for the lamellar spacings \(\lambda _1=50\) and \(\lambda _2=100\), and for the analytic values of HU\(_{\text {equal}\,\Delta T}\), the maximum deviations are \(9.1\,\text {\rm pct}\) for the lamellar spacings \(\lambda _1=100\) and \(\lambda _2=40\).

Fig. 8
figure 8

Average front undercooling over the lamellar spacings \(\lambda _1\) and \(\lambda _2\) for a chain-like pattern. The results from 3D simulations are shown with red points. The analytical results from HU1999[13] are incorporated as a green plane, and the results from HU\(_{\text {equal}\,\Delta T}\) are incorporated as a blue plane. Below, results from selected sections for constant values of \(\lambda _1\) and \(\lambda _2\) are presented (Color figure online)

Full size image

Conclusion

In this study, the influence of the lamellar spacings on the arising patterns and on the average front undercooling during the directional solidification of an ideal ternary eutectic system is investigated with phase-field simulations.

For the validation of the phase-field model, based on a grand potential approach, the lamellar spacing is systematically varied for three different velocities and a lamellar arrangement \(\alpha -\beta -\alpha -\gamma \) in 2D and 3D simulations. The results show a good accordance with the analytical approaches from Himemiya and Umeda[13] (HU1999) and Choudhury et al.[15] (CPN2011).

In extensive three-dimensional phase-field studies, the inherently three-dimensional chain-like structure is investigated. The 3D simulation results are quantitatively compared with the analytical results from HU1999 and with a newly derived approach, HU\(_{\text {equal}\,\Delta T}\), based on Reference 13 with the assumption of equal undercoolings following.[15]

From the investigations, we draw our five main conclusions: (i) The used phase-field model,[29] based on a grand potential approach, is capable to correctly reproduce the undercooling–spacing–velocity relation in quantitative manner, for the considered ideal ternary eutectic system. (ii) The results indicate that a predefined chain-like pattern is favorable from an energetic point of view. The pattern remains stable for various values of \(\lambda _1\) and \(\lambda _2\). Even if a pattern change occurs, rearranged chain-like structures evolve. (iii) For the undercoolings of the chain-like patterns, a Jackson–Hunt-type behavior is observed in direction of both lamellar spacings for the analytics and the phase-field simulations. (iv) The occurrence of a global minimum in the undercooling for certain values of \(\lambda _1\) and \(\lambda _2\) as operating points is found both with analytical approaches as well as with the simulations. For the analytical approaches, the global minima follow lines through the origin, with different slopes in the \(\lambda _1\)-\(\lambda _2\) space for the considered velocities. The operating point for the simulations is located between both investigated analytical approaches. (v) The analytical approaches of HU1999 and HU\(_{\text {equal}\,\Delta T}\), based on different assumptions for the calculation of the average front undercoolings, show similar trends. This indicates that for the considered system, the assumptions of both analytical approaches are only partly fulfilled. Both approaches represent different idealized scenarios. The pattern formation in the considered ternary eutectic system seems to evolve from a mixture of both scenarios.

In summary, by applying 3D phase-field simulations and analytical approaches, we demonstrate that the Jackson–Hunt relationship for quasi-two-dimensional binary eutectic directional solidification[8] is also valid for three-dimensional ternary eutectics. Based on the accordance established in 2D and 3D, the phase-field model is validated and can be employed to predict the undercooling–spacing–velocity relationship for complex pattern arrangements commonly occurring in experimental micrographs.