Introduction

Reservoirs alter the spatial and temporal distribution of runoff to serve multiple functions, such as flood control, water resources allocation, hydropower generation, navigation and recreation, which play an important role in promoting social and economic development (Chang et al. 2017). The conventional practice of reservoir operation mainly focuses on the maximization of social-economic benefits while ignoring the downstream ecosystem requirements, and serious damaging the structure and function of river ecosystems (Xia et al. 2008). The goal with maximizing satisfaction rate of downstream ecological flow is to minimize the ecological lack water volume in hydropower generation, which requires enough water discharge. At the same time, maximum power generation is the basic requirement of hydropower station (Hu et al. 2019), which mainly focuses on more water volume for power generation in flood season and high water level in non-flood season (Zhang et al. 2013). However, the high water level in the non-flood season will lead to a decrease in outflow. Ecological goals and power generation goals are contradictory and difficult to optimize at the same time. Therefore, the multi-objective operation (MOO) is becoming an important optimization problem.

At present, many researchers solve the MOO problem using evolutionary and metaheuristic algorithms, such as genetic algorithm (GA) (Chen et al. 2016; Dai et al. 2016; Liu et al. 2019), artificial bee colony (ABC) (Choong et al. 2017), shuffling frog leaping algorithm (SFLA) (Yang et al. 2018), shark machine learning algorithm (SMLA) (Allawi et al. 2018) and harmony search (HS) (Bashiri-Atrabi et al. 2015). The bat algorithm (BA) is a new metaheuristic algorithm based on the echolocation features of microbats (Yang 2010). The applications of BA demonstrated that it was easy to implement and can deal with highly nonlinear problems efficiently (Yang 2010; Yang and Gandomi 2012). Case studies included micro-grid operation management (Bahmani-Firouzi and Azizipanah-Abarghooee 2014), interconnected power system (Sathya and Mohamed Thameem Ansari 2015) and dam-reservoir operation (Ethteram et al. 2018), and others. Original versions of bat algorithm have been frequently modified or hybridized to improve performance. To improve the convergence rate and precision of bat algorithm, Xie et al. (2013) put forward an improved bat algorithm based on differential operator and Levy flights trajectory (DLBA). The results showed that the proposed DLBA is feasible and effective. Mirjalili et al. (2013) proposed a binary bat algorithm (BBA), which has artificial bats navigating and hunting in binary search spaces by changing their positions. They calculated dispersion relation of photonic crystal waveguide, and compared the BA with binary particle swarm optimization (BPSO) and genetic algorithm (GA). They recommended applying the BBA to different practical application. The hybrid self-adaptive bat algorithm (HSABA) was proposed by combined bat algorithm with different evolution (DE) in literature (Fister et al. 2014). They compared this algorithm with some algorithms, and concluded that the HSABA performs better than other comparison algorithms. However, there are some limitation in BA and proposed algorithms: (1) the initial population randomly generated in BA may be highly repetitive and concentrated in a limited space, which will lead to the decrease of population diversity. (2) The rapid change of loudness A may cause BA to trap into local optima. (3) The most popular penalty method for dealing with equality constraints of reservoir operation problem is difficult to satisfy complex multi-objective scheduling of cascade reservoirs.

In this paper, to realize win–win goal of economic benefits and ecological benefits of cascade reservoirs, a multi-objective operation model is established to consider power generation and different ecological flow requirements. The new method named the Montana Method with seasonal variation is proposed to calculated different ecological flows. Moreover, to solve the multi-objective operation model, an improved chaotic bat algorithm (ICBA) is proposed in this paper. The main improvements of the proposed ICBA method are as follows: (1) Chaos is a common non-linear phenomenon with certainty, ergodicity and the stochastic property (Alatas and Akin 2009). Recently, chaotic sequences have been adopted instead of random sequences. Somewhat good results have been shown in many applications (Aydin et al. 2010; Wong et al. 2005). To improve the population diversity, the population initialization based on chaos theory was adopted. (2) The pulse emission rate was generated based on Sinusoidal map and varied to a chaotic number between 0 and 1. (3) The self-adaptive loudness update mechanism was designed to control the convergence speed according to the iterations process. (4) The constraint handling method with constraint transformation was used when solve the MOO problem.

The rest of the paper is organized as follows. The mathematical modeling of the MOO problem is introduced in “Mathematical modeling of the MOO problem”. The standard Bat Algorithm is described in “Overview of standard bat algorithm”. “Improved chaotic bat algorithm (ICBA)” presents the proposed improved chaotic bat algorithm (ICBA) for solving the MOO problem in detail. “Case study” reports the application in Qingjiang River and discusses the application results. Finally, “Conclusions” outlines the conclusions of this work.

Mathematical modeling of the MOO problem

Objective function

In this paper, multi-objective operation mainly considers economic benefits and ecological benefits, which are reflected in the total power generation of cascade power stations and the downstream ecological flow requirement. Therefore, the mathematical modeling of the multi-objective operation need meet two objective functions:

  1. ①

    Maximizing power generation:

    $$ \max f_{1} { = }\max \sum\limits_{i = 1}^{I} {\sum\limits_{k = 1}^{K} {N_{i,k} \times t_{i,k} } } , $$
    (1)
    $$ N_{i,k} { = }P_{i} \times Q_{i,k}^{{{\text{LEC}}}} \times \overline{H}_{i,k} , $$
    (2)

    where \(f_{1}\)(kWh) is the total power generation of cascade reservoirs during the scheduling period; I is the number of reservoirs; K is the number of periods; \(N_{i,k}\) is the power output of ith reservoir at the kth period (kW); \(t_{i,k}\) is the operational time of the ith reservoir at the kth period (h); \(P_{i}\) is the synthetic output coefficient of ith reservoir; \(Q_{i,k}^{{{\text{LEC}}}}\) is the generation flow of ith reservoir at the kth period (m3/s); \(\overline{H}_{i,k}\) is the average water head of ith reservoir at the kth period (m).

  2. ②

    Maximizing satisfaction rate of downstream ecological flow:

    $$ \max f_{2} { = }\max \sum\limits_{i = 1}^{I} {\alpha_{i} \sum\limits_{k = 1}^{K} {\beta_{k} \times G_{i,k} } } , $$
    (3)
    $$ G_{i,k} = \left\{ \begin{gathered} \frac{{Q_{i,k}^{{{\text{OUT}}}} }}{{Q_{i,k}^{{{\text{DE}}}} }} \times 100\% \;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \;{\text{if}}{\kern 1pt} Q_{i,k}^{{{\text{OUT}}}} < Q_{i,k}^{{{\text{DE}}}} \hfill \\ 100\% \;\;\;\;\;{\kern 1pt} {\kern 1pt} \;\;{\kern 1pt} {\kern 1pt} \,\,\,\,\,\,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \,\,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{if}}{\kern 1pt} {\kern 1pt} Q_{i,k}^{{{\text{OUT}}}} \ge Q_{i,k}^{{{\text{DE}}}} \hfill \\ \end{gathered} \right., $$
    (4)

    where \(f_{2}\) is the total satisfaction rate of downstream ecological flow during the scheduling period; I is the number of reservoirs; K is the number of periods; \(\alpha_{i}\) is the weight coefficient assigned to ith reservoir, \(\sum\nolimits_{i = 1}^{I} {\alpha_{i} } = 1\); \(\beta_{k}\) is the weight coefficient assigned to kth period, \(\sum\nolimits_{k = 1}^{K} {\beta_{k} } = 1\); \(G_{i,k}\) is the satisfaction rate of downstream ecological flow of ith reservoir at the kth period; \(Q_{i,k}^{{{\text{OUT}}}}\) is the outflow of ith reservoir at the kth period (m3/s); \(Q_{i,k}^{{{\text{DE}}}}\) is downstream ecological flow of ith reservoir at the kth period (m3/s).

Two optimization objectives are competitive with each other, and it is generally impossible to obtain optimal solution at the same time. The magnitude order of two objective functions is different. Therefore, this paper adopts the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) method (Srdjevic et al. 2004) to transform the multi-objective function into a single-objective function, so that the optimization results can be as close as possible to their respective ideal points. The converted objective function is given as follows:

$$ f(f_{1} ,f_{2} ) = \min \sqrt {\left( {\frac{{f_{1}^{\max } - f}}{{f_{1}^{\max } }}} \right)^{2} + \left( {\frac{{f_{2}^{\max } - f}}{{f_{2}^{\max } }}} \right)^{2} } , $$
(5)

where \(f(f_{1} ,f_{2} )\) is holistic objective that contains both power generation objectives and ecological objectives; \(f_{1}^{\max }\) is the maximum total power generation of cascade reservoirs when the objective function ① is considered only; \(f_{2}^{\max }\) is the maximum total satisfaction rate of downstream ecological flow when the objective function ② is considered only.

Constraints

Objective functions are subject to following constraints:

  1. ①

    Reservoir storage continuity constraint:

    $$ {\text{SV}}_{i,k} = {\text{SV}}_{i,k - 1} + (Q_{i,k}^{{{\text{IN}}}} - Q_{i,k}^{{{\text{OUT}}}} ) \times t_{i,k} , $$
    (6)

    where \({\text{SV}}_{i,k}\) and \({\text{SV}}_{i,k - 1}\) are reservoir storage of ith reservoir at the kth and (k-1)th period, respectively (m3); \(Q_{i,k}^{{{\text{IN}}}}\) and \(Q_{i,k}^{{{\text{OUT}}}}\) are inflow and outflow of ith reservoir at the kth period, respectively (m3/s).

  2. ②

    Reservoir water level constraint:

    $$ Z_{i,k}^{{{\text{min}}}} \le Z_{i,k} \le Z_{i,k}^{\max } , $$
    (7)

    where \(Z_{i,k}\) is the reservoir water level of ith reservoir at the kth period (m); \(Z_{i,k}^{{{\text{min}}}}\) and \(Z_{i,k}^{\max }\) are minimum and maximum reservoir water level of ith reservoir at the kth period, respectively (m).

  3. ③

    Reservoir release constraint:

    $$ Q_{i,k}^{{\text{OUT,min}}} \le Q_{i,k}^{{{\text{OUT}}}} \le Q_{i,k}^{{{\text{OUT}},\max }} , $$
    (8)

    where \(Q_{i,k}^{{\text{OUT,min}}}\) and \(Q_{i,k}^{{\text{OUT,max}}}\) are minimum and maximum reservoir outflow of ith reservoir at the kth period, respectively (m3/s).

  4. ④

    Power generation constraint:

    $$ N_{i,k}^{{{\text{min}}}} \le N_{i,k} \le N_{i,k}^{\max } , $$
    (9)

    where \(N_{i,k}^{{{\text{min}}}}\) and \(N_{i,k}^{\max }\) are minimum and maximum reservoir power output of ith reservoir at the kth period, respectively (kW).

  5. ⑤

    Reservoir storage constraint:

    $$ {\text{SV}}_{i,k}^{{{\text{min}}}} \le SV_{i,k} \le SV_{i,k}^{\max } , $$
    (10)

    where \({\text{SV}}_{i,k}^{{{\text{min}}}}\) and \(SV_{i,k}^{\max }\) are minimum and maximum reservoir storage of ith reservoir at the kth period, respectively (m3).

Downstream ecological flow acquisition

There are more than 200 methodologies for calculating environmental flow. They could be classified into hydrological, hydraulic rating, habitat simulation and holistic methodologies. Hydrological methods constituted the highest proportion of methodologies recorded (Tharme 2003), with the Montana Method (Tennant 1976) being the most popular. Grading standard of the condition of river ecosystem in Montana Method is shown in Table 1.

Table 1 Grading standard of the condition of river ecosystem in Montana Method
Full size table

The downstream ecological flow at the kth period can be obtained according to the base flow standard recommended by Montana Method:

$$ \left\{ \begin{gathered} \Phi_{i,k}^{\min } { = }Q_{i}^{{{\text{avg}}}} \theta_{i,k}^{\min } \hfill \\ \Phi_{i,k}^{{{\text{sui}}}} { = }Q_{i}^{{{\text{avg}}}} \theta_{i,k}^{{{\text{sui}}}} \hfill \\ \Phi_{i,k}^{{{\text{ide}}}} { = }Q_{i}^{{{\text{avg}}}} \theta_{i,k}^{{{\text{ide}}}} \hfill \\ \end{gathered} \right., $$
(11)

where \(\Phi_{i,k}^{\min }\),\(\Phi_{i,k}^{{{\text{sui}}}}\) and \(\Phi_{i,k}^{{{\text{ide}}}}\) are minimum, suitable and ideal downstream ecological flow of ith reservoir at the kth period obtained by Montana Method, respectively; \(Q_{i}^{{{\text{avg}}}}\) is the average annual downstream flow of ith reservoir; \(\theta_{i,k}^{\min }\),\(\theta_{i,k}^{{{\text{sui}}}}\) and \(\theta_{i,k}^{{{\text{ide}}}}\) are requirement index of minimum, suitable and ideal downstream ecological flow of ith reservoir at the kth period, respectively. Based on base flow regimes in Table 1, assuming that the \(\theta_{i,k}^{\min }\), \(\theta_{i,k}^{{{\text{sui}}}}\) and \(\theta_{i,k}^{{{\text{ide}}}}\) are 10%, 30% and 65% in October to March, and 30%, 50% and 75% in April to September, respectively.

The original Montana Method used the average annual flow as reference. The calculation results are susceptible to extreme flow (extreme wet or extreme dry) events. Montana Method focuses on the flow inter-annual change of flow, weakening the gap between river flow in wet season and dry season. If the original Montana Method is used to calculate the ideal downstream ecological flow in this paper, the ideal downstream ecological flow may be much higher than average flow in some dry months. When the river flow season changes greatly in 1 year, the river flow may not be able meet suitable and ideal ecological flow requirements in many months. It is more necessary to consider seasonal changes of rivers and select more realistic ecological flow at this time. Therefore, the Montana Method with seasonal variation is presented in this paper. The specific expression is given as follows.

$$ \left\{ \begin{gathered} Q_{i,k}^{{{\text{DE}},\min }} { = }\lambda_{1}^{\min } \Phi_{i,k}^{\min } + \lambda_{2}^{\min } \xi_{i,k} \Phi_{i,k}^{\min } \hfill \\ Q_{i,k}^{{\text{DE,sui}}} { = }\lambda_{1}^{{{\text{sui}}}} \Phi_{i,k}^{{{\text{sui}}}} + \lambda_{2}^{{{\text{sui}}}} \xi_{i,k} \Phi_{i,k}^{{{\text{sui}}}} \hfill \\ Q_{i,k}^{{\text{DE,ide}}} { = }\lambda_{1}^{{{\text{ide}}}} \Phi_{i,k}^{{{\text{ide}}}} + \lambda_{2}^{{{\text{ide}}}} \xi_{i,k} \Phi_{i,k}^{{{\text{ide}}}} \hfill \\ \end{gathered} \right., $$
(12)
$$ \xi_{i,k} = \frac{{Q_{i,k}^{{{\text{avg}}}} }}{{Q_{i}^{{{\text{avg}}}} }}, $$
(13)

where \(Q_{i,k}^{{{\text{DE}},\min }}\), \(Q_{i,k}^{{\text{DE,sui}}}\) and \(Q_{i,k}^{{\text{DE,ide}}}\) are minimum, suitable and ideal downstream ecological flow when considering seasonal changes of ith reservoir at the kth period, respectively; \(\Phi_{i,k}^{\min }\), \(\Phi_{i,k}^{{{\text{sui}}}}\) and \(\Phi_{i,k}^{{{\text{ide}}}}\) are minimum, suitable and ideal downstream ecological flow of ith reservoir at the kth period obtained by Montana Method, respectively; \(\lambda_{1}\) and \(\lambda_{2}\) are weight coefficient, \(\lambda_{1} + \lambda_{2} = 1\); \(\lambda_{1}^{\min }\) and \(\lambda_{2}^{\min }\) are assumed as 0.7 and 0.3, respectively; \(\lambda_{1}^{{{\text{sui}}}}\) and \(\lambda_{2}^{{{\text{sui}}}}\) are assumed as 0.5 and 0.5, respectively; \(\lambda_{1}^{{{\text{ide}}}}\) and \(\lambda_{2}^{{{\text{ide}}}}\) are assumed as 0.3 and 0.7, respectively; \(Q_{i,k}^{{{\text{avg}}}}\) is the average downstream flow of ith reservoir at the kth period; \(Q_{i}^{{{\text{avg}}}}\) is the average annual downstream flow of ith reservoir.

Overview of standard bat algorithm

The bat algorithm is a new heuristic algorithm based on the echolocation behavior of microbats. To simplify and facilitate application, the algorithm adopts following idealized rules:

  1. ①

    All bats apply echolocation to sense distance, and they always "know" the difference between prey and obstacles in some magical way.

  2. ②

    Bats fly randomly with speed V and a fixed frequency Fmin to search for prey at position X, varying frequency F and loudness A. They can automatically accommodate the frequency and adjust pulse emission rate r according to their proximity to the target.

  3. ③

    Assume the loudness changing from maximum to minimum.

In the BA, position and speed update can be obtained from Eqs. (15) and (16).

$$ F_{j} = F_{\min } + \left( {F_{\max } - F_{\min } } \right) \times \beta , $$
(14)
$$ V_{j}^{g} = V_{j}^{g - 1} + \left( {X_{j}^{{g{ - }1}} - X_{*} } \right) \times F_{j} , $$
(15)
$$ X_{j}^{g} = X_{j}^{g - 1} + V_{j}^{g} , $$
(16)

where j is the number of bats; g is the iteration number; \(F_{j} \in \left[ {F_{\min } ,F_{\max } } \right]\) is frequency; \(\beta \in \left[ {0,1} \right]\) is a random vector drawn from a uniform distribution; \(V_{j}^{g}\) is the speed of jth bat in gth generation; \(X_{j}^{g}\) is the position of jth bat in gth generation; \(X_{*}\) is the current global best location.

If \({\text{rand}} \,1 > r_{j}^{g}\), bat walks around the current best solution to complete local search according to Eq. (17). If \({\text{rand}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2 < A_{j}^{g} \& f\left( {X_{{j,{\text{new}}}}^{g} } \right) < f\left( {x_{*} } \right)\), accept new solution \(X_{{j,{\text{new}}}}^{g}\). Then, reduce \(A_{j}^{g}\) and increase \(r_{j}^{g}\) according to Eqs. (18) and (19):

$$ X_{{j,{\text{new}}}}^{g} = X_{j}^{g} + \varepsilon \times \overline{{A^{g} }} , $$
(17)
$$ A_{j}^{g + 1} = \alpha \times A_{j}^{g} , $$
(18)
$$ r_{j}^{g + 1} = r_{j}^{1} \times \left[ {1 - \exp ( - \gamma \times g)} \right], $$
(19)

where \(\varepsilon \in \left[ {0,1} \right]\) is a random number; \(X_{{j,{\text{new}}}}^{g}\) is the new position of jth bat in gth generation after local search; \(\overline{{A^{g} }}\) is the mean loudness of all bats in gth generation; \(A_{j}^{g}\) is the loudness of jth bat in gth generation; \(r_{j}^{g}\) is the pulse emission rate of jth bat in gth generation; \(\alpha\) and \(\gamma\) are constants. For any \( 0 < \alpha < 1\) and \(\gamma > 0\):

$$ A_{j}^{g} \to 0,{\kern 1pt} \;\;\;\;r_{j}^{g} \to r_{j}^{1} ,{\kern 1pt} {\kern 1pt} \;\;\;{\text{as}}\;\;g \to \infty . $$
(20)

Improved chaotic bat algorithm (ICBA)

Assuming that the D-dimensional real space is the search space of optimization problem, the algorithm is a generation population \(R^{g} = \left\{ {X_{1}^{g} ,X_{2}^{g} , \ldots ,X_{i}^{g} , \ldots ,X_{{{\text{NP}}}}^{g} } \right\}\) composed of NP D-dimensional real parameter vectors \(X_{j}^{g} = \left\{ {x_{j,1}^{g} ,x_{j,2}^{g} , \ldots ,x_{j,d}^{g} \ldots ,x_{j,D}^{g} } \right\}\). Where j is the number of individuals in the population, \(j = 1,2, \ldots ,{\text{NP}}\); g is the iteration number, \(g = 1, \ldots ,g_{\max }\). Based on the introduction of standard BA in previous section, we will explain how to combine the bat algorithm with chaotic theory in this section.

The population initialization based on chaos theory

The diversity and distribution of the initial population can influence final optimal solutions of the algorithm. As other evolutionary algorithms, initial population is usually generated randomly, which may lead to problems such as the repeated solutions occupying memory space and the concentration of initial solution in a certain interval. Generating random sequences with a long period and good uniformity is very important for heuristic optimization. Its quality determines the reduction of storage and computation time to achieve a desired accuracy. Chaos is a deterministic, random-like process found in non-linear, dynamical system, which is non-period, non-con verging and bounded. The nature of chaos is apparently random and unpredictable and it also possesses an element of regularity. In this paper, the initial population is generated based on chaos principle, which could enhance diversity and uniformity of the population distribution (Alatas et al. 2009). Here the Logistic Map is selected. Its equation is as follows:

$$ x_{d}^{q + 1} { = }\mu x_{d}^{q} \left( {1 - x_{d}^{q} } \right) \, d{ = 1,2} \ldots ,D{\kern 1pt} {\kern 1pt} ; \, q{ = 1,2} \ldots ,q_{\max } { ,} $$
(21)

where \(x_{d}^{q}\) is a chaotic variable, \(x_{d}^{1} \notin \left\{ {0.25,0.5,0.75} \right\}\); \(q\) is the iteration number;\(\mu\) is the control parameter. When \(\mu\) = 4, Eq. (21) is chaotic state.

Generate D different initial values within interval \(\left( {0,1} \right)\), and then generate D chaotic sequences with different trajectories by iteration using Eq. (21). For example, when \(\mu\) = 4, \(x_{d}^{1}\) = 0.7, and \(q_{\max }\) = 100, Logistic sequences diagram is shown in Fig. 1a.

Fig. 1
figure 1

Chaotic value distributions during 100 iterations

Full size image

Convert chaotic variables \(x_{d}^{q}\) to value interval of the decision variables [\(Z_{d}^{{{\text{min}}}}\),\(Z_{d}^{\max }\)], and the individual j is expressed as \(Z_{j} = \left\{ {Z_{j,1} ,Z_{j,2} , \cdots ,Z_{j,d} \cdots ,Z_{j,D} } \right\}\):

$$ Z_{j,d} { = }Z_{d}^{{{\text{min}}}} { + }\left( {Z_{d}^{\max } - Z_{d}^{{{\text{min}}}} } \right) \cdot x_{d}^{q} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = q, $$
(22)

where \(Z_{d}^{\max }\) and \(Z_{d}^{{{\text{min}}}}\) are the upper and lower limitations of the dth decision variable, respectively; \(Z_{j,d}\) is the value of the jth bat in dth dimension.

The pulse emission rate based on chaos theory

In the standard BA, pulse emission rate is monotonically decreased in the iterations progress. However, better results have been reported when the \(r_{j}\) has been varied chaotically. In literature (Gandomi and Yang 2014), thirteen different chaotic sequences were tried to tune \(r_{j}\). The best results is the CBA-IV with Sinusoidal sequences. Therefore, pulse emission rate \(r_{j}\) is generated based on Sinusoidal map and varied to a chaotic number between 0 and 1 in this paper. Its equation is as follows:

$$ x_{j}^{g + 1} { = }\mu \left( {x_{j}^{g} } \right)^{2} \sin \left( {\pi x_{j}^{g} } \right) \, g{ = 1,2} \ldots ,g_{\max } {,} $$
(23)

where \(x_{j}^{g}\) is a chaotic variable; \(g\) is the iteration number;\(\mu\) is the control parameter. When \(\mu\) = 2.3 and \(x_{j}^{1}\) = 0.7, it can be simplified to \(x_{j}^{g + 1} { = }\sin \left( {\pi x_{j}^{g} } \right)\), where \(g{ = 1,2} \ldots ,g_{\max }\).

Generate NP different initial values within interval \(\left( {0,1} \right)\), and then generate NP chaotic sequences with different trajectories by iteration using Eq. (23). Finally, assign chaotic variables to pulse emission rate \(r_{j}^{g}\). For example, when \(\mu\) = 2.3, \(x_{j}^{1}\) = 0.7, and \(g_{\max }\) = 100, Sinusoidal sequences diagram is shown in Fig. 1b.

Self-adaptive loudness update mechanism

In standard bat algorithm, both the local search operation and the condition of accepting optimal solutions are related to loudness. Therefore, the value of loudness directly affects the local search range and optimization results of the algorithm. In standard bat algorithm, the attenuation coefficient of loudness \(\alpha\) is a constant, which can largely determine the convergence speed of the algorithm. If the loudness reduces too fast, the convergence speed of the algorithm can be improved, but the algorithm may fall into the local optimal solution. Therefore, the self-adaptive loudness update mechanism is designed in this paper, which controls the convergence speed according to the iterations process. Now we have:

$$ A_{j}^{g + 1} = \left\{ \begin{gathered} \alpha A_{j}^{g} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha A_{j}^{g} {\kern 1pt} {\kern 1pt} \ge \frac{{A_{\max } }}{2} \hfill \\ \frac{{A_{\max } }}{2} - \frac{{\left( {\frac{{A_{\max } }}{2} - A_{\min } } \right)*\left( {g - g^{A} } \right)}}{{g_{\max } }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha A_{j}^{g} {\kern 1pt} {\kern 1pt} < \frac{{A_{\max } }}{2}{\kern 1pt} {\kern 1pt} \hfill \\ \end{gathered} \right., $$
(24)

where j is the number of bats; g is the iteration number; \(\alpha\) is the attenuation coefficient of loudness; \(A_{j}^{g}\) is the loudness of jth bat in gth generation; \(A_{\min }\) and \(A_{\max }\) are minimum and maximum loudness, respectively; \(g^{A}\) is the maximum number of iterations that satisfies \(\alpha A_{j}^{g} {\kern 1pt} \ge \frac{{A_{\max } }}{2}\); \(g_{\max }\) is the maximum iteration.

Set \(A_{\max } = 1\), \(A_{\min } = 0\) according to the reference (Yang 2010). It is assumed that better solutions can be found in each generation, and the loudness \(A_{j}^{g}\) in each generation needs to be updated. The comparison of the \(A_{j}^{g}\) between ICBA and BA is shown in Fig. 2.

Fig. 2
figure 2

Comparison of the loudness between ICBA and BA

Full size image

Loudness \(A_{j}^{g}\) is the search range of local search. As seen in Fig. 2, the change of loudness \(A_{j}^{g}\) in ICBA is slower than that in BA when \(\alpha\) changes. Therefore, compared to the BA, the search range of local search in ICBA is less influenced by the value of \(\alpha\). Moreover, the condition for accepting new solutions in BA and ICBA is \({\text{rand}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2 < A_{j}^{g} \& f\left( {X_{{j,{\text{new}}}}^{g} } \right) < f\left( {x_{*} } \right)\), the greater opportunity to accept better solutions can be achieved by using the proposed ICBA over BA, which demonstrates the superiority of the ICBA algorithm.

Constraint handling method

This section mainly focus on how to handle the reservoir water level constraint (7), reservoir release constraint (8) and power output constraint (9) when the proposed ICBA algorithm is applied to solve MOO problem. The way of constraint handling determines whether a reasonable optimal solution can be found for reservoir operation. At present, the penalty method is most popular strategy for dealing with equality constraints of reservoir operation problem. However, this strategy is difficult to satisfy complex multi-objective scheduling of cascade reservoirs, so the constraint handling method with constraint transformation (Lu et al. 2011) is used in this paper.

The reservoir release constraint (8) and power output constraint (9) are converted to constraint corridor of water level in the constraint handling method with constraint transformation. Flow-water level corridor [\(Z_{Q(i,t)}^{\min }\),\(Z_{Q(i,t)}^{\max }\)] and output-water level corridor [\(Z_{N(i,t)}^{\min }\),\(Z_{N(i,t)}^{\max }\)] can be obtained respectively. Then, combining the water level corridor with reservoir water level constraint [\(Z_{i,t}^{\min }\),\(Z_{i,t}^{\max }\)] in formula (7), feasible water level range of the reservoir can be obtained by taking intersection. In addition, the intersection is empty if there is a conflict between constraints. At this time, reservoir water level constraint will have priority.

The implementation of ICBA for MOO problem

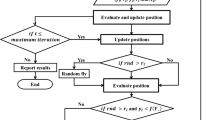
The flowchart of the improved chaotic bat algorithm (ICBA) for MOO problem is presented in Fig. 3.

Fig. 3
figure 3

The flowchart of ICBA for MOO problem

Full size image

Case study

Study area and scenarios setting

The Qingjiang River is one of the main tributary of Yangtze River. The 423 km long Qingjiang River has a catchment area of 1.7 × 103 km2. Along the Qingjiang River, a three-step cascade reservoir (Shuibuya, Geheyan, and Gaobazhou) has been constructed from upstream to downstream (Guo et al. 2018). The characteristic of these three reservoirs and main parameters of power stations are given in Table 2. Figure 4 shows the location of cascade reservoirs in the Qingjiang River. The downstream ecological flow results are listed in Table 3.

Table 2 Characteristic water level of cascade reservoirs and main parameters of power stations
Full size table
Fig. 4
figure 4

Location of cascade reservoirs in the Qingjiang River

Full size image
Table 3 Downstream ecological flow of cascade reservoirs m3/s
Full size table

According to the requirements of power generation and downstream ecological flow, four different scheduling scenarios are carried out in this paper.

Scenario 1: Power generation operation for cascade reservoirs is conducted. The downstream ecological flow requirement is not considered as the optimization goal. However, the satisfaction rates of minimum, suitable and ideal downstream ecological flow are calculated based on the outflow results of power generation operation.

Scenario 2: Cascade reservoirs are focused on the power generation and minimum downstream ecological flow requirement.

Scenario 3: Cascade reservoirs are focused on the power generation and suitable downstream ecological flow requirement.

Scenario 4: Cascade reservoirs are focused on the power generation and ideal downstream ecological flow requirement.

Basic data and parameter setting

According to the runoff data of the Qingjiang River basin from 1971 to 2005 year, the typical representatives of 1996 year, 2005 year, 1986 year and 2001 year are selected as the wet, normal, dry and extreme dry years, respectively. Using algorithms to solve scheduling model, water level of each reservoir is encoded, and the jth individual in the population can be expressed as Zj = {z1j,1,…, z1j,K; z2j,1,…, z2j,K; z3j,1,…, z3j,K}. Where z1j,k(k = 1,2,…,K) is water level of the Shuibuya Reservoir; z2j,k(k = 1,2,…,K) is water level of the Geheyan Reservoir; z3j,k(k = 1,2,…,K) is water level of the Gaobazhou Reservoir.

To verify the effectiveness of ICBA in the application of multi-objective scheduling, ICBA is compared with other algorithms, including chaotic genetic algorithm (CGA), chaotic particle swarm optimization (CPSO), chaotic differential evolution (CDE) and standard bat algorithm (BA). CGA mimics the process of natural evolution and generates new generations by selection, crossover, and mutation. CDE also produces new generations by selection, crossover, and mutation. However, the mutation of CDE is carried out on the basis of two paternal individuals, while the mutation in CGA is generated randomly. CPSO is based on the migration and clustering behavior of birds. In the optimization process, particles calculate their next flight direction and speed according to the optimal position of the whole particle swarm, its own optimal position in previous generations and the current position. BA is a heuristic algorithm based on the echolocation behavior of microbats. Bats search for global optimal solution by varying frequency and adjust pulse emission rate. In ICBA, the updating of pulse emission rate is based on chaos theory. The self-adaptive loudness update mechanism is designed to control the convergence speed according to the iterations process.

The initial population is generated based on chaos principle (Eq. 21) in the ICBA, CGA, CPSO and CDE. The population size \({\text{NP}} = 200\) and the maximum iteration of algorithm \(g_{\max } = 100\) are set for each algorithm. For ICBA, the maximum iteration of chaos operator \(q_{\max } = 200\) in the population initialization; the frequency F is varied from 0 to 1; the loudness A is decreased from 1 to 0; the \(\alpha = \gamma = 0.9\)(Yang 2010). For CGA, the maximum iteration of chaos operator \(q_{\max } = 200\) in the population initialization; the crossover and mutation operators are 1 and 0.01, respectively (Wang and Guo 2013). For CPSO, the maximum iteration of chaos operator \(q_{\max } = 200\) in the population initialization; the inertial constant is 0.3; the cognitive constant is 1; the social constant is 1 (Wang and Guo 2013). For CDE, the maximum iteration of chaos operator \(q_{\max } = 200\) in the population initialization; the crossover and mutation operators are 0.5 and 0.5, respectively (Wang and Guo 2013). For BA, the frequency F is varied from 0 to 1; the loudness A is decreased from 1 to 0; the \(\alpha = \gamma = 0.9\) (Yang 2010). We defined the scheduling period is one year, and the period length is one month. During flood season from June to July every year, the reservoir water level should be controlled below the flood control level.

Average annual operation results

Runoff datum from 1971 to 2005 year is selected to calculate average annual operation results. Table 4 shows average annual power generation results of cascade reservoirs in Qingjiang River under different scenarios calculated by the proposed ICBA algorithm. The downstream ecological flow satisfaction rate results of Shuibuya Reservoir, Geheyan Reservoir and Gaobazhou Reservoir are presented in Table 5. To verify the effectiveness of ICBA in the application of MOO problem, ICBA is compared with several other algorithms, including CGA, CPSO, CDE and BA. Average annual power generation and the satisfaction rate of downstream ecological flow under scenarios 2, 3 and 4 are analyzed. The specific results are shown in Table 6.

Table 4 Average annual power generation under different scenarios × 108 kWh
Full size table
Table 5 Satisfaction rate of different downstream ecological flow requirements
Full size table
Table 6 Comparison results of ICBA and other algorithms
Full size table

From Table 5, when considering requirements of minimum and suitable downstream ecological flow, the downstream ecological flow satisfaction rate of scenario 1, 2 and 3 are 100%, which can completely meet the minimum and suitable downstream ecological flow requirements. In Table 4, average annual power generation under these three scheduling scenarios is the same, among which Shuibuya reservoir has the largest average annual power generation (37.356 × 108 kWh).

As can be seen from Tables 4 and 5, when considering ideal downstream ecological flow requirement, the scenario 4 can increase the overall satisfaction rate of ecological flow by 1.772% compared to the scenario 1, while decreasing the average annual power generation by about 0.1 × 108 kWh. The ecological flow satisfaction rate of Geheyan increases the largest, from 97.496 to 99.743%. Compared to the scenario 1, the scenario 4 proposed in this paper can improve the satisfaction rate of ideal downstream ecological flow requirement, and has little influence on the average annual power generation.

As showed in Table 6, when using the average annual flow as the reservoir inflow, the overall satisfaction rate of downstream ecological flow are higher than 96%. Moreover, in Table 6, CPSO, CDE, BA and ICBA can fully meet the minimum (scenario 1) and suitable (scenario 2) downstream ecological flow requirement of three reservoirs. The total average annual power generation generated by BA is greater than that of CGA, CPSO and CDE. When considering the minimum and suitable downstream ecological flow requirements, the total average annual power generation of ICBA is 0.623 × 108 kWh and 0.644 × 108 kWh higher than that of BA, respectively. When considering the ideal ecological flow requirement, the overall ecological flow satisfaction rate obtained by ICBA is the highest (98.860%) and slightly higher than that of BA (98.851%).

Therefore, the above results fully prove that the MOO problem can be solved by the ICBA. Compared to other algorithms, the ICBA method proposed in this paper can get better results.

Typical hydrological year operation results

It can be seen from foregoing analysis that average annual operation schemes of cascade reservoirs in Qingjiang River can meet the minimum and suitable downstream ecological flow requirements. Therefore, reservoir scheduling schemes in different typical hydrological years are designed in terms of meeting the ideal downstream ecological flow requirement (scenario 4). Meanwhile the ecological conditions of dry year and extreme dry year are analyzed in this section.

Analysis of power generation and ecological satisfaction rate in typical hydrological year

The operation results of scenario 1 and scenario 4 are compared and analyzed in Table 7. Due to limited space, taking Shuibuya Reservoir and Geheyan Reservoir as examples, reservoir operation processes are shown in Fig. 5.

Table 7 Operation results under scenario 1 and scenario 4 in different hydrological years
Full size table
Fig. 5
figure 5

Reservoirs operation processes under scenario 1 and scenario 4 in different hydrological year

Full size image

In Table 7, when considering the ideal downstream ecological flow requirement, the overall satisfaction rate of downstream ecological flow of scenario 4 in wet year are 100%, which can completely meet the requirement of ideal downstream ecological flow. The overall satisfaction rates of downstream ecological flow in two scenarios can reach more than 93% and 83% in normal year and dry year, respectively. Moreover, as can be seen from Table 7, the annual power generation in extreme dry year is the least. Compared to the scenario 1, the scenario 4 can increase the overall satisfaction rate of downstream ecological flow by about 2.903% while decreasing the annual power generation by about 0.515 × 108 kWh in extreme dry year.

With detailed operation results of two reservoirs displayed in Fig. 5, the feasibility of the proposed ICBA is verified by testing the constraint violation conditions of the two schemes selected. It can be seen that inflows of Shuibuya Reservoir are the same, while inflows of Geheyan Reservoir are different under two schemes in Fig. 5. That is because Shuibuya Reservoir is the first reservoir of Qingjiang cascade reservoirs, which is located in the upper reaches of Geheyan Reservoir. The release of Shuibuya Reservoir will affect inflow of Geheyan Reservoir. Moreover, the inflow of reservoirs during the flood season (from June to July) is the largest in the whole year in Fig. 5. Therefore, the water level of reservoirs needs to be controlled below the flood control level.

Analysis of ecological status in downstream control sections in dry year and extreme dry year

Based on results of reservoir discharge simulated in “Analysis of power generation and ecological satisfaction rate in typical hydrological year” under dry and extreme dry years, we analyzed downstream ecological status according to the grading standard of river ecosystem condition obtained by Montana Method in Table 1. The specific analysis results are shown in Tables 8, 9 and 10.

Table 8 Downstream ecological status of Shuibuya Reservoir in dry year and extreme dry year
Full size table
Table 9 Downstream ecological status of Geheyan Reservoir in dry year and extreme dry year
Full size table
Table 10 Downstream ecological status of Gaobazhou Reservoir in dry year and extreme dry year
Full size table

It can be seen that the ecological status in dry year are generally better than those in extreme dry year in Tables 8, 9 and 10. Meanwhile, the satisfaction rate of downstream ecological flow can basically reach more than 20% of average annual flow in dry year, which is a good ecological condition.

The less inflow of Shuibuya Reservoir in January leads to fair or degrading ecological condition in extreme dry year. When entering flood control period in June and July, the reservoir water level should be controlled below the flood control level. Moreover, the inflow is relatively large at this time, and the satisfaction rate of downstream ecological flow can reach more than 70% of average annual flow, which are in the optimal range. From August to October is the storage period of reservoirs, and discharge decreases lead to gradual deterioration of downstream ecological condition. November and December are low water period of reservoirs, and the ecological condition is worse. In extreme dry year, inflow of reservoirs is the lowest in December. The satisfaction rate of downstream ecological flow of three reservoirs is less than 10% of average annual flow, resulting in serious ecological degradation.

Conclusions

In this paper, an improved chaotic bat algorithm (ICBA) has been established to handle the MOO problem. The ICBA is applied to the MOO problem of the Qingjiang cascade reservoirs in southern China. The results show that the minimum (scenario 2) and suitable (scenario 3) downstream ecological flow requirements can be satisfied, when the average annual flow is used as the reservoir inflow. When considering the ideal downstream ecological flow requirement, the overall satisfaction rate of downstream ecological flow can reach more than 90% in wet year and normal year. Compared to the scenario 1, the scenario 4 proposed in this paper can improve the satisfaction rate of ideal downstream ecological flow requirement, and has little influence on the annual power generation. In December of extreme dry year, the satisfaction rate of downstream ecological flow of cascade reservoirs is lower than 10% of average annual flow, resulting in serious ecological degradation.

The case study is implemented to verify the validity and feasibility of the ICBA method. The results indicate that compared to other several algorithms, the ICBA method proposed in this paper can significantly improve both power generation and satisfaction rate of downstream ecological flow, which provides a new approach for solving the MOO problem. However, the MOO of cascade reservoirs is very complex. The more ecological issues, such as sediment deposition and water quality of cascade reservoirs, need to be considered in detailed in the further.