Introduction

Background

Water resource managers intend to control available water resources to optimize benefit so that the available water resources are enough when critical conditions happen such as during drought periods (Bou-Zeid and El-Fadel 2002; Galelli et al. 2014; Bozorg-Hadad et al. 2014a, b). Considering the limitations of existing optimization algorithms, water resource decision-makers face a serious challenge when optimizing reservoir operation (Ramesh et al. 2013; Fallah-Mehdipour 2011; Bozorg-Hadad et al. 2008a, b). Thus, decision-makers search for efficient optimization algorithms for achieving optimal reservoir operation with high reliability (Bozorg-Hadad et al. 2009; Noory et al. 2012). Optimal operation of water resources reservoirs by optimization models is the appropriate way for better management, planning and operating available water systems (Bozorg-Hadad et al. 2014a, b; Jothiprakash and Shanthi 2006; Yang 2010). Currently, decision-makers apply mathematical models or software for providing proper decisions, such as determination of water release or reservoir storage, to accomplish optimal operation (Zhao et al. 2014; Bozorg-Hadad et al. 2014a, b). Considering reservoir constraints and the stochastic behavior of reservoir inflow pattern, the major challenge for these models is the ability to attain the optimal operation rule in adequate computation time. It is important for decision-makers to optimize water release pattern, minimize irrigation deficit, hydropower deficit and adequately meet downstream demands (Fallah-Mehdipour et al. 2012a, b; Taghian et al. 2013; Shokri et al. 2013; Mousavi et al. 2005). A variety of mathematical methods, such as dynamic programming, nonlinear programming, and linear programming, have been for reservoir operation. Although these methods lead to proper reservoir operation, several limitations have been experienced when applying them. For example, the use of a nonlinear and non-convex objective function makes optimization inefficient and sometimes non-convergent. Dynamic programming requires a relatively long computational time to converge if the reservoir has several decision and state variables.

Recently, meta-heuristic algorithms have found numerous applications in engineering optimization and water resource management. Reddy (2006) found that the ant colony method for reservoir operation satisfactorily supplied water demands downstream of a dam. Using the honey bee mating method for reservoir optimization, Afshar et al. (2007) were able to meet downstream demands well. Applying this method for multipurpose reservoir operation, Bozorg-Hadad et al. (2008a, b) showed it converged to the global solution well. Chang and Cheng (2009) found that the genetic algorithm supplied the different demands for a multiobejctive problem well. Fallah-Mehdipour et al. (2012b) showed that for reservoir operation the genetic programming method obtained the global solution in less computational time than did the genetic algorithm. For reservoir operation, Zhang et al. (2012) found that the guide particle swarm algorithm had a high-reliability index for water supply. Garousi et al. (2016) were able to meet downstream demands well by the firefly algorithm for reservoir operation. Thus, the above-mentioned studies show that meta-heuristic algorithms have satisfactorily performed in water resource management. One of the powerful algorithms in engineering optimization is the bat algorithm (Yang 2010) which acts based on position and sound of bats. The bats use echolocation ability for finding a prey. Yang (2010) found global optimum solutions well by applying the bat algorithm for benchmark functions. Reddy and Manoj (2012) applied the bat algorithm for finding the optimum capacitor placement to reduce loss of energy. For energy optimization, Niknam et al. (2013) showed the bat algorithm led to better distribution and management of power energy than did the genetic algorithm.

The objective of this study is to investigate the Bat Algorithm (BA) as an optimization algorithm for dam and reservoir operation based on different orders of rule curves. The algorithm is evaluated for two different case studies in Iran, one designed for supplying irrigation demands while the other is designed for hydropower generation. In most studies, a linear decision rule for water release is considered and the released water is computed based on inflow and reservoir storage (Bozorg-Hadad et al. 2008a, b, 2009, 2014a, b). The mathematical model of decision rule is considered, based on simple equations which do not lead to optimum reservoir operation; but different kinds of nonlinear decision rules can generate better simulation of a reservoir system. Thus, this paper employs nonlinear equations for reservoir operation.

The current paper uses nonlinear decision rules for reservoir operation. Different evaluation indices, such as reliability, vulnerability, and index reliability for comparing different performances of different rule curves, are examined. The first case study is related to minimizing irrigation deficits for three different order rule curves. The second case study is Karoun 4 dam which is designed to produce hydropower. Hence, the proposed optimization model is applied to increase hydropower generation by proper water release policy.

Problem statement

Dam and reservoir operation optimization is highly nonlinear and multimodal with noise, which makes the search for global optimal solution difficult. It is, therefore, important to find an algorithm that can lead to an optimal solution efficiently. The bat algorithm and bat intelligence algorithm are such algorithms.

1–4 reasons for modeling by bat algorithm

In recent years, various evolutionary algorithms such as genetic algorithm, particle swarm, and other evolutionary algorithms have been introduced to solve optimization problems. These algorithms have advantages and disadvantages. For instance, the genetic algorithm gets trapped by local optimization and finds local optima instead of global optimum (Ehteram et al. 2018). The particle swarm algorithm has an early convergence in solving some problems that cause immature answers instead of the main answer (Karami et al. 2018). Some of the evolutionary algorithms are slow in convergence and achieving the optimum answer. Also, it is difficult to determine the initial random parameters in other algorithms (Ehteram et al. 2017a). Two important features in the evolutionary algorithms are exploration and exploitation capabilities. The exploration capability shows the ability of the algorithm to search freely without considering any achievements during the search process. In contrast, the exploitation is called the algorithm’s attention to its achievements during the search process. Obviously, the more the exploration capability is in a search algorithm, the more random and unpredictable behavior can be seen for the algorithm (Ehteram et al. 2017b). On the contrary, enhancing the exploitation in an algorithm causes this algorithm to be more accountable and more cautious.

The bat algorithm is an evolutionary algorithm, has a simpler process in determining the initial parameters of the method, has an advantage over other algorithms by setting the correct value of the parameters, and has the ability to balance the exploration and exploitation capabilities (Yang 2010). In addition, the algorithm has a faster convergence rate than genetic, particle swarm, and ant algorithms (Yang 2010). Also, with the ability of local searching, it clearly identifies the range of main answers. Furthermore, the process of determining the parameters is simpler than other evolutionary algorithms.

This study considers optimization of the operation of Aydougmoush and Karun 4 dams reservoirs. These were selected for the importance of generating electricity and providing irrigation needs. Karun 4 dam is a key dam for power supply in Iran. The optimal way of releasing water and providing adequate storage behind the dam is an important issue. Therefore, the values of water release are defined as unknown values or candidates for solution by the algorithm.

Methodology

Bats are mammals which have a wing and produce intense pulses which return from the surroundings. Each bat provides 10–20 numbers of pulses per second and the frequency domain is between 25 and 100 kHz. When the bats are close to the prey, the number of pulses is about 200. Bats generate loud sounds so that the returning sounds and receiving of returning sounds direct bats to the best place for finding food (Merritt 2010). Bats continuously emit echolocation signals (Yovel et al. 2008) and identify their surroundings and locate preys by analyzing the returning echoes in the auditory system. Bats use the echolocation to identify the difference between obstacle and preys. It is these abilities of bats that have inspired the development of bat algorithm (BA) and bat intelligence algorithm (BIA) for solving optimization problems such as dam and reservoir operation.

For simplification, the bat algorithm makes certain assumptions:

  1. 1.

    All bats use the echolocation ability for the identification of prey and obstacle. The pulses returning from the surroundings help bats identify obstacles from preys.

  2. 2.

    Bats fly randomly with velocity \({v_{\text{i}}}\), constant frequency fmin, wavelength and loudness A0 at position xi.

  3. 3.

    The loudness changes from a large positive value (Amax) to a small positive value (Amin).

  4. 4.

    The frequency changes between fmin and fmax corresponding to the wavelength which changes between \({\lambda _{\hbox{min} }}\) and \({\lambda _{\hbox{max} }}\). The frequency can be modified based on each problem.

  5. 5.

    The generated sounds for the bats have a specific pulse rate so that the maximum value for the pulsation rate is 1 and the minimum value for the pulsation rate is 0 and the pulsation rate can be updated in each iteration.

The velocity, position, and frequency can be updated based on the following equations:

$${f_{\text{l}}}={f_{\hbox{min} }}+\left( {{f_{\hbox{max} }} - {f_{\hbox{min} }}} \right)\beta ,$$
(1)
$${v_{\text{l}}}\left( t \right)=\left[ {{y_{\text{l}}}\left( {t - 1} \right) - {Y_*}} \right] \times {f_{\text{l}}}\left( t \right),$$
(2)
$${y_{\text{l}}}\left( t \right)={y_{\text{l}}}\left( {t - 1} \right)+{v_{\text{l}}}\left( t \right),$$
(3)

where \(\beta\) is a random vector between 0 and 1, \({v_{\text{l}}}\left( t \right)\) is velocity at time step t, \({y_{\text{l}}}\left( {t - 1} \right)\) is position at time t − 1 and \({Y_ * }\) is the best position among other positions for the bat algorithm.

The updating procedure for the bat algorithm is similar to the particle swarm optimization (PSO) because the pace and range of the movement of bats are controlled by fl as in PSO.

Next, the local search is defined based on a random walk as:

$$y\left( t \right)=y\left( {t - 1} \right)+\varepsilon A\left( t \right),$$
(4)

where A is the loudness at time step t and \(\varepsilon\) is a random value between − 1 and 1. The loudness (A) and pulse rate should be updated for each iteration. When bats find their prey, the loudness decreases, but the pulse rate increases for each bat. The pulsation rate is updated as:

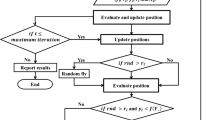
$$r_{{\text{l}}}^{{t+1}}=r_{{\text{l}}}^{0}\left[ {1 - \exp \left( { - \gamma t} \right)} \right]A_{{\text{l}}}^{{t+1}}=\alpha A_{{\text{l}}}^{t},$$
(5)

where \(\alpha ,\gamma\) are constant parameters, \(A_{{\text{l}}}^{t} \to 0,\quad r_{{\text{l}}}^{t} \to r_{{\text{l}}}^{0}\) when \(0<\alpha <1,\quad \gamma>0\) and \(\alpha\) parameter is similar to the cooling factor in the simulated annealing alorithm. Figure 1 shows the bat algorithm.

Fig. 1
figure 1

Bat algorithm

Full size image

Bat algorithm for reservoir operation

The bat algorithm has random parameters, such as frequency with unit Hz and sound height pulse with unit dB. For both dams, the water release is considered as the decision variable which is based on the amount of water released from the dam in such a way that the defined objectives at the downstream are satisfied. For example, irrigation needs for the Aydougmoush dam, and the hydropower needs for the Karun 4 dam will have to be met. The purpose of this study is to accurately determine the values of water release, which can be used to generate electricity and meet other needs. Since the bat algorithm and other evolutionary algorithms require an initial population, the water release values are considered as the initial population in the algorithm. The bat algorithm cycle must be completed once to determine the true and accurate amounts of water release. The purpose of this cycle is to determine the best values of water release after the initial guess of these values as the initial population. The water release values are entered into the algorithm as the initial location of the bat and the initial population.

The algorithm determines the best location of the bats or water release values, using Eq. 4 for which it is required to obtain the speed from Eq. 3. There is a random frequency parameter in Eq. 3, whose value must be determined from Eq. 2. After these steps, the bat algorithm updates the location of bats based on the local search and exploration capability using Eq. 5. This requires the sound loudness parameter the value of which is initially the best value reported in Yang (2010). Then, based on sensitivity analysis as shown in in Table 1, the exact values are obtained. In this procedure, considering the presence of several random parameters whose initial values are obtained based on the initial guess or the literature, the value of a variable parameter and the values of the rest of the parameters are kept constant. Then, the changes of the objective function are checked based on the changes in the parameter value, and whenever the objective function has the best value (for example, in a minimization problem when the objective function has its lowest value), the random parameter is considered to have its best value. To determine that the water release values have their best values and are optimal, the objective function is calculated, and in the case that it does not have the best value, the pulse rate increases according to Eq. 6 and the volume of the sound is reduced. The decision variable for the simplification in the computation process and thus, the initial water release values are inserted into the bat algorithm based on the initial population. Then, the reservoir storage using the continuity equation is computed, based on the initial values of released water. Then, the released water values and reservoir storage values are compared with the specified constraints and if the constraints are not satisfied, then penalties are added to the objective function. Then, the objective function is computed for each population. This procces is repeated for all operational periods. Then, the bat algorithm, shown in Fig. 1, is applied to all populations until the number of iteration reaches the maximum iteration. Then, the algorithm finishes and the optimal values of released water are obtained.

Table 1 (a) Characteristic for Aydoughmoush dam, (b) characteristic for Karun 4 dam, and (c) sensitivity analysis
Full size table

Case studies

General description of the case study

The reservoir of Karun 4 dam is located on the Karun River. This dam is the largest double-arched concrete dam and the fifth high dam and the source of hydropower in the world. The objectives of Karun 4 dam are the following:

  1. 1.

    Hydropower generation of 2000 MW annually.

  2. 2.

    Controlling surface waters of the area.

  3. 3.

    Controlling seasonal floods.

It is important to release water from the dam that the annual supply of hydropower and other desired objectives are met optimally. Therefore, the amount of water released in the dam is a decision variable and is unknown. The water release values are determined from Eqs. 10, 11, and 12. The unknown coefficients in the equations must be determined by the bat algorithm according to the objective function and the specified constraints, and then the amount of water release is determined. Therefore, the main issue is the release method so that the deficiencies are minimized and the objective function is defined based on the difference between requirements and the release of water.

The Ayudoghmous dam is selected as the second case study. Aydoghmoush dam is located in East Azarbaijan Province, Iran. The purpose of the dam is to provide irrigation for 15,000 hectares of agricultural land. The maximum, average, and minimum requirements for the demand volume are equal to \(39.57 \times {10^6}\frac{{{{\text{m}}^3}}}{{{\text{month}}}}\), \(12.12 \times {10^6}\frac{{{{\text{m}}^3}}}{{{\text{month}}}}\), and 0, respectively. Therefore, water should be released in such a way that the reservoir storage is not less than the minimum value, and the downstream water requirements are met. The amount of water drainage from the dam for supplying the downstream needs is considered as a decision variable and thus, this value can be calculated based on optimization by the bat algorithm.

Aydoughmoush dam

The Aydoughmoush dam is located in the eastern part of Azarbaijan province, Iran. This dam supplies the irrigation demands of \(15 \times {10^3}\) ha. The inflow to this reservoir is \(228 \times {10^3}{\text{m}}\), and the maximum and minimum storage are \(145.7 \times {10^3}\) and \(8.9 \times {10^3}{{\text{m}}^3}\), respectively. The period of 10 years (1991–2000) was selected for the case study. Figure 2a shows inflow and details of the study. There are extensive gardening and agriculture practices in this area that need water supply. Also, there are several drought periods that should be considered in reservoir operation.

Fig. 2
figure 2figure 2

a Inflow to the reservoir, b location of case study, c Karoun basin, and d mathematical model for reservoir operation

Full size image

The objective function is the minimization of irrigation deficit:

$${\text{MinimizeOF}}=\sum\limits_{{t=1}}^{T} {{{\left( {\frac{{{D_t} - {R_t}}}{{{D_{\partial \hbox{max} }}}}} \right)}^2}} ,$$
(8)

where Dt is the demand water (MCM), Rt is the released water (MCM), and \({D_{\hbox{max} }}\) is the maximum demand (MCM).

The continuity equation is defined as:

$${S_{t+1}}={S_t}+{I_t} - {R_t} - S{P_t} - Los{s_t},$$
(9)

where \({S_t}\) is the reservoir storage at time t, \({I_t}\) is the inflow at time t; SPt is the overflow at time t; and Loss is the reservoir losses at time t.

The released water is computed based on the linear and nonlinear equations as:

$${R_t}={a_i}+b{1_i}{S_t}+c{1_i}{I_t},$$
(10)
$${R_t}={a_i}+b{1_i}S_{t}^{1}+b2S_{t}^{2}+C{1_i}I_{t}^{1}+C{2_i}I_{t}^{2},$$
(11)
$${R_t}={a_i}+b{1_i}S_{t}^{1}+b{2_i}S_{t}^{2}+b{3_i}S_{t}^{3}+c{1_i}I_{t}^{1}+c{2_i}I_{t}^{2}+c{3_i}I_{t}^{3},$$
(12)

where a, b and c for a released value are known as decision variables and are computed by optimization. Equations 10, 11 and 12 show the first-, second- and third-order rule curves.

The loss and overflow are computed as follows:

$$\begin{gathered} {\text{Los}}{{\text{s}}_t}={A_t} \times {\text{E}}{{\text{V}}_t} \hfill \\ {\text{S}}{{\text{P}}_t}=\left[ \begin{gathered} 0 \leftarrow {\text{if}}\left( {{S_t}} \right) \leq {S_{\hbox{max} }} \hfill \\ {S_{\hbox{max} }} - {S_t} \leftarrow if\left( {{S_t}} \right) \geq {S_{\hbox{max} }} \hfill \\ \end{gathered} \right], \hfill \\ \end{gathered}$$
(13)

where At = the area of the reservoir lake, EV the evaporation depth (mm), and Smax the maximum storage.

Also, there are some constraints for reservoir optimization:

$$\begin{gathered} 0 \leq {R_t} \leq {D_t} \hfill \\ {S_{\hbox{min} }} \leq {S_t} \leq {S_{\hbox{max} }}. \hfill \\ \end{gathered}$$
(14)

If the constraints are not satisfied, the following equations are considered as penalty functions:

$${P_{1,t}}=\left[ \begin{gathered} 0 \leftarrow {\text{if}}\left( {{S_{t+1}}} \right)>{S_{\hbox{min} }} \hfill \\ \frac{{{{\left( {{S_{\hbox{min} }} - {S_{t+1}}} \right)}^2}}}{{{S_{\hbox{min} }}}} \leftarrow {\text{otherwise}} \hfill \\ \end{gathered} \right],$$
(15)
$${P_{2t}}=\left[ \begin{gathered} 0 \leftarrow {\text{if}}\left( {{S_{t+1}}<{S_{\hbox{max} }}} \right) \hfill \\ \frac{{{{\left( {{S_{t+1}} - {S_{\hbox{max} }}} \right)}^2}}}{{{S_{\hbox{max} }}}} \leftarrow {\text{otherwise}} \hfill \\ \end{gathered} \right],$$
(16)
$${P_3}=\left[ \begin{gathered} 0 \leftarrow {\text{if}}\left( {{R_t}} \right)<{D_t} \hfill \\ \frac{{{{\left( {{R_t} - {D_t}} \right)}^2}}}{{{D_{\hbox{max} }}}} \hfill \\ \end{gathered} \right],$$
(17)

where, P1, P2 and P3 are known as penalty functions. These penalty functions are added to the objective function.

Karoun 4 dam

The bat algorithm is evaluated for generating an optimal policy for reservoir operation for power generated by the downstream power plant based on three rule curves for water release. The Karoun 4 dam is 180 km southwest of Sharkord and the Karun River has the highest discharge of all Iranian rivers. The dam reservoir is operated for power generation for many industrial centers in this region. Hydropower station is near the dam and can produce 2107 MW power annually. Also, the maximum water release is \(450 \times {10^3}\frac{{{{\text{m}}^3}}}{{{\text{month}}}}\). The maximum generated power for powerhouse is \(1000 \times {10^6}{\text{w}}\). The Karin 4 dam is shown in Fig. 2c. The objective function for minimizing power deficit is expressed as:

$${\text{Minimize}}\left( {{\text{OF}}} \right)=\frac{1}{T}\left[ {\sum\limits_{{t=1}}^{T} {{{\left( {1 - \frac{{{P_t}}}{{{\text{PPC}}}}} \right)}^2}} } \right],$$
(18)

where OF the objective function; Pt the power generated; and PPC the total installed capacity for the powerhouse.

The power generated is computed as:

$${P_t}=\frac{{\gamma ^{\prime} \times \eta \times \Delta H \times {\text{Dis}}\;{{\operatorname{Re} }_t}}}{{{{10}^6} \times n}},$$
(19)

where \(\gamma ^{\prime}\) the specific weight water; \(\eta\) the efficiency of the power plant; \(\Delta H\) the difference of between water level in the downstream and upstream areas; DISRet the water released from the powerhouse; and n: a coefficient for evaluation of powerhouse performance.

The quantity \(\Delta H\) is computed as:

$$\Delta {H_t}=\left( {\frac{{{H_t}+{H_{t+1}}}}{2}} \right) - {\text{TR}},$$
(20)

where Ht the water level at the beginning of the period; and Ht+1 the water level at the end of the period.

Equations 9, 10, 11, 12 and 13 are used again. Also, another constraint is considered as:

$$0 \leq {P_t} \leq {\text{PPC,}}$$
(21)

where Pt the power generated.

Thus, if the above equation is not satisfied, the following penalty function is considered:

$${P_t}=\left[ \begin{gathered} 0 \leftarrow i{\text{f}}\left( {{P_t}<{\text{PPC}}} \right) \hfill \\ \frac{{{P_t} - {\text{PPC}}}}{{{\text{PPC}}}} \leftarrow {\text{otherwise}} \hfill \\ \end{gathered} \right].$$
(22)

Thus, if the equation was not satisfied, the penalty function (Eqs. 15, 16 and 22) would be used and added to the objective function.

Concepts in reservoir equations

Water release Water release is considered as the decision variable, i.e., a variable whose value is obtained from the algorithm and shows the amount of water drainage from the dam to meet the downstream needs (Al-aqeeli et al. 2015).

Loss Each reservoir faces losses. For example, evapotranspiration from the reservoir surface can be one of the reasons for the loss in water level and reservoir storage. The loss is obtained from the product of the surface of the reservoir and the depth of evaporation (“Aydoughmoush dam”, Eq. 13) (Al-aqeeli et al. 2016).

Overflow In case of excess water exceeding the reservoir storage, the additional amount flows out through the dam spillway, which is called overflow. After applying the algorithm each time, the amount of water is compared to the current storage.

Reservoir operation by bat algorithm

The optimal operation of reservoirs based on the bat algorithm involves the following steps:

  1. 4.

    The initial parameters of the method, such as the loudness of sound, pulse, and frequency, are entered into the algorithm as the initial guess and then sensitivity analysis is performed.

  2. 5.

    With the values of water release as the initial population and the decision variable, their best values are obtained by the algorithm, which are then introduced into the algorithm as the initial location of the bats.

  3. 6.

    There is a constraint for each case. For example, in light of constraints 13 and 14 for the Aydoghmoush dam, the values of water release should be compared with the maximum and the minimum water releases. Also, according to the continuity equation, there is an relationship between reservoir storage at the new time and a prior period, based on which the storage amount is calculated. If the water release values and storage in the permitted range are not satisfied, penalties such as Eqs. 15–17 and Eq. 22 are considered.

  4. 7.

    There is an objective function for each reservoir. For example, an objective in relation to a reservoir is to minimize irrigation deficit and in another reservoir, it is to minimize hydropower deficit. If there are penalty functions based on the previous stage, they are added to the objective function.

  5. 8.

    The location of the bats or the initial water release values should be updated for the algorithm’s next repetition, based on Eqs. 1–3.

  6. 9.

    The ability the algorithm to obtain the global solution is evaluated using Eq. 5, and if the algorithm is trapped in a local optimum, a new answer is generated.

  7. 10.

    The repeat counts are compared with the maximum repeat. In the case of being equal, the algorithm is complete, otherwise we return to the beginning of the algorithm.

Performance measures

Different indices are used for evaluation of the bat algorithm for different rule curves:

First case study

  1. 1.

    Volumetric reliability This index considers the ratio of released water to total demand in the operation period (Ehteram et al. 2017a).

    $${\alpha _{\text{V}}}=\frac{{\sum\nolimits_{{i=1}}^{N} {\sum\nolimits_{{t=1}}^{T} R } }}{{\sum\nolimits_{{i=1}}^{N} {\sum\nolimits_{{i=1}}^{T} D } }},$$
    (23)

    where R the released water; D the demand; and \({\alpha _{\text{V}}}\) the volumetric reliability

  2. 2.

    Vulnerability index This index shows the maximum intensity of failure during the operation period (Ehteram et al. 2017a).

    $$\lambda =\mathop{\text{Max}}\limits_{{i=1}}^{N}\left( {\mathop{\text{Max}}\limits_{{i=1}}^{T}\left( {\frac{{{D_t} - {R_t}}}{{{D_t}}}} \right)} \right),$$
    (24)

    where \(\lambda\) is the vulnerability index.

  3. 3.

    Resiliency index This index shows the way of existence of a system from a failure during the operation period.

    $${\gamma _i}=\frac{{{f_{{\text{si}}}}}}{{{F_i}}},$$
    (25)

    where \(\gamma\) the resiliency index; \({f_{{\text{si}}}}\) the number of failures series; and Fi the number of failure series. Reliability index This index shows the percentage of the generated hydropower to the capacity of power plant.

    $$R=\frac{{\sum\nolimits_{{t=1}}^{T} {\left[ {\left( {{P_t}|{P_t}<{\text{PPC}}} \right) \vee \left( {{\text{PPC}}|{P_t} \geq {\text{PPC}}} \right)} \right]} }}{{T \cdot {\text{PPC}}}},$$
    (26)

    where \(\sum\nolimits_{{t=1}}^{T} {\left[ {\left( {{P_t}|{P_t}<{\text{PPC}}} \right) \vee \left( {{\text{PPC}}|{P_t} \geq {\text{PPC}}} \right)} \right]}\) shows the generated hydropower and \(T \cdot {\text{PPC}}\) illustrates the maximum generation power.

    Resiliency index This index indicates the ability of system for escaping from failure (Ehteram et al. 2017b):

    $$\operatorname{Re} =\frac{{N_{{t=1}}^{{T - 1}}\left( {{P_t}<{\text{PPC}}|{P_{t+1}} \geq {\text{PPC}}} \right)}}{{N_{{t=1}}^{T}\left( {{P_t}<{\text{PPC}}} \right)}},$$
    (27)

    where \(N_{{t=1}}^{{T - 1}}\left( {{P_t}<{\text{PPC}}|{P_{t+1}} \geq {\text{PPC}}} \right)\) shows the number of periods in which the system can exit from a failure and \(N_{{t=1}}^{T}\left( {{P_t}<{\text{PPC}}} \right)\) shows the total deficit power.

    Vulnerability index This index shows the value of deficit during operation periods (Ehteram et al. 2017a).

    $$V=\frac{{\sum\nolimits_{{t=1}}^{T} {\left[ {\left( {{\text{PPC}} - {P_t}|{P_t}<{\text{PPC}}} \right) \cup \left( {0|{P_t} \geq {\text{PPC}}} \right)} \right]} }}{T},$$
    (28)

    where term \(\left( {{\text{PPC}} - {P_t}|{P_t}<{\text{PPC}}} \right) \cup \left( {0|{P_t} \geq {\text{PPC}}} \right)\) identifies the total deficit in a particular period.

Evaluation of bat algorithm in reservoir operation

Different indexes, introduced by Hashimoto et al. (1982), are used to evaluate water releases by the bat algorithm and its ability to properly exploit the reservoir. The system efficiency in supplying downstream needs based on the amount of abandoned water relative to need, which is known as the Reliability Index, is calculated. Such an index for Karun 4 dam represents the percentage of electricity generated to the maximum produced electricity during the period of operation. Higher percentage of the index represents a better performance of the algorithm. Another indicator is the Vulnerability Index which indicates the maximum failure ratio during the operation period. For the Karun 4 reservoir, this index shows the average failure rate. Another indicator is the Resiliency Index. This index indicates that if the system is faced with deficit or failure in some periods, how fast does the system switch from failure or the deficit period. For instance, if a 12-month operation period fails in four periods, the failure sequence affects the system performance. In other words, four consecutive failures have a different effect than the case that in each period, failure is followed by a non-failure period.

Results and discussion

The bat algorithm with three different rule curves was been applied to both case studies and the three performance indicators were calculated for each case.

Aydoughmoush dam

Table 1 shows the sensibility analysis for the bat algorithm for the first-, second- and third-order rule curves. It can be noted that the best population size for first-, second- and third-order rule curves was 60, 60 and 40, respectively. The maximum frequency (fmax) for first-, second- and third-order rule curves was 5, 5 and 3, respectively. The minimum loudness (A0) for first-, second- and third–order rule curves was 0.20, 0.10 and 0.10, respectively.

Table 2 shows results based on ten different random executions for the algorithm for Aydoughmoush Dam. Results were compared to the global solution with Lingo software (version. 11) which uses nonlinear programming. The minimal average solution was attained with the third-order rule curve as compared with the first- and second-order rule curves. The percentage of reduction of the average solution was equal to 6.3 and 16% as compared with the first- and second-order rule curves, respectively. The variation coefficient for the third rule curve was 50 and 70% of the resultant values attained using the first-order rule curve and the second-order rule curve, respectively. Also, the global solution based on Lingo software and nonlinear programming for the first-, second- and third-order rule curves was 1.77, 1.92, and 2.14 and as a result, the average solutions for first-, second- and third-order rule curves were 99, 98 and 98% of the global solution. Thus, the bat algorithm had the proper solution for different order rule curves, but the third-order rule curve had the least objective function and variation coefficient.

Table 2 Results for Aydoughmoush dam
Full size table

Table 3 shows the three performance indicators for the first-, second- and third-order curves. The reliability index for the third-order rule curve was 98%, and it was 4 and 2% more than for the first- and second-order rule curves. In other words, the bat algorithm with the third-order rule curve matched the demand pattern for irrigation water use efficiently. In addition, it can be shown that the resiliency index for the third-order rule curve was 45% which outperformed the other order rule curves. On the other hand, the third-order rule curve procedure efficiently improved the first- and second-order rule curve procedures by 7–4%, respectively. Also, the third-order rule curve had the lowest value of vulnerability among other two methods. Such performance for the resilience index indicates that the proposed optimization model could overcome the deficit effectively.

Table 3 Different indices for Aydoughmoush dam
Full size table

Figure 3 shows the convergence of three rule curves, and third rule curve had converged to the least objective function for the same number of iterations (Fig. 3b). Also, the maximum, minimum and average solutions converged to each other well. The released water for different months of operation, in Fig. 3c, shows that the third-order rule curve had supplied demands better than did two other rule curves. The water release from the reservoir and the demand pattern for irrigation strongly matched which means that the optimization algorithm minimized the deficit. Finally, Fig. 3d shows that the storage pattern was more stable within the range of maximum and minimum storages of the reservoir.

Fig. 3
figure 3

Simulation results for a convergence way, b maximum, minimum and average solution for third-order rule curve, c released water, and d storage value

Full size image

Table 4 shows the optimal monthly coefficient for third rule curve equation computed by the bat algorithm because the third-order rule curve had the best performance. Each coefficient was a decision variable for computation of released water based on the third-order rule curve. When the coefficient value was relatively small, the effect of that term on the released water was negligible. The value of b3 for January was small. Thus, the term b3S3 was negligible. The values of b1, b2 were also negligible. The value of released water for January was less dependent on the reservoir storage. These coefficients showed the importance of different terms which affected released water volume.

Table 4 Optimal monthly parameters for third rule curve (Aydoughmoush dam)
Full size table

Karoun 4 dam

Table 5 shows sensibility analysis and the best values of random parameters by the bat algorithm for Karoun 4 reservoir. Minimizing the hydropower deficit can be achieved when the objective function value for each parameter reaches the minimal value. This value was considered as the optimal random parameter. The best size of population for the first-, second- and third-order rule curves was 60, 60 and 40, respectively. The best value of maximum frequency for the first-, second- and third-order rule curves was 3, 3 and 5, respectively. The minimum frequency for the first-, second- and third-order rule curves was 1, 1 and 2, respectively.

Table 5 Sensibility analysis for Karoun 4 reservoir
Full size table

Table 6 shows ten random results for three kinds of rule curve. Results show that the average solution for the three rule curves was close to a global solution. The Lingo software based on nonlinear programming method computed the global solution. The average solution of the third-order rule curve was less than of the other two rule curves, and the coefficient variation of the third-order rule curve was 5.33 and 3.66 smaller than first-order and second-order rule curves, respectively.

Table 6 10 Random results for Karoun 4 reservoir
Full size table

Figure 4 shows the convergence versus the iteration number for the three rule curves. The bat algorithm with the third-order rule curve converged to the minimum value faster than the other rule curves. .

Fig. 4
figure 4

Convergence for different methods for Karoun 4 reservoir

Full size image

Figure 5 shows that the generated power for the released water for the third-order rule curve was more than for the first-order rule curve and second-order rule curve. Table 7 shows different indices for the three rule curves. The reliability index and the resiliency index had the highest percent and the vulnerability index had the smallest value for third-order rule curve. Table 8 shows the coefficients for the third-order rule curve. For example, the values of c1 and c2 and c3 for April were small and thus, the inflow volume was less important in the computation of released water and reservoir storage played an important role for this month. One of the reasons is related to less inflow for this month. The values of b1 and b2 and b3 for May were negligible, and as a result, the released water volume was less dependent on the reservoir storage for this month. Also, the value of each coefficient for each rule curve was a decision variable and was computed by the optimization algorithm.

Fig. 5
figure 5

Simulation results for a released water, and b generated power

Full size image
Table 7 Different indices for Karoun 4 reservoir
Full size table
Table 8 Optimal value for determination of coefficients of rule curve
Full size table

Conclusions

This study investigates the potential of utilizing the Bat algorithm with the rule curve method to identify an optimal reservoir operation policy. The BA algorithm was evaluated for two case studies, namely, Aydoghmush dam and Karoun 4 dam. The algorithms successfully achieved the targeted objective function which was minimizing the deficit in irrigation and hydropower generation for Aydoghmush dam and Karoun 4 dam, respectively. For both case studies, the bat algorithm with the third-order rule curve achieved a global solution close to the one attained by Lingo software. To evaluate the performance of the algorithm, reliability index, resiliency index, and vulnerability index were determined for both case studies with simulation for 10 years of operation. Results showed that the bat algorithm with third-order rule curve achieved the highest value for the reliability and resilience indexes and the lowest value for the vulnerability index for both case studies. Therefore, it can be concluded that the bat algorithm with the third-order rule curve performed better than the other order’s rule curves in deriving the optimal operating policy for reservoir operation.