1 Introduction

Although a systematic approach for water resources planning is not limited to mathematical modeling, but these models can effectively reveal the internal relations and interactions between the elements of a water resources system. Moreover, use of mathematical models allows estimation of physical and economic consequences of various operation policies for water storage and transfer structures. The main goal for reservoir operation is to supply water for the demands in a way that the lowest deficits occur during the operation period. This issue becomes more complicated in drought periods or arid regions. Mathematical simulation and optimization models are useful tools to deal with this problem (Singh and Panda 2013).

As one of the common policies for reservoirs operation is the hedging policy which aims to ration the reservoir’s storage for meeting the downstream demands. In this field, Klemes (1977) introduced a series of hedging rules for designing reservoirs. He noticed that not only hedging optimization requires a non-linear convex objective function but also the possibility of drought occurrence should be considered. Neelakantan and Pundarikanthan (1999) pointed to some reservoir operation rules including standard operating policy, linear decision rules and hedging rules. They used a neural network based simulation-optimization model to select the operation policy for a reservoir in condition of water deficit in India and found the hedging rules as a suitable allocation policy. Draper and Lund (2004) stated that the hedging rules for reservoir storage result an acceptable level of water deficit over a long period of operation. In other words, instead of releasing water equal to the demand amount in condition that the reservoir does not have adequate storage which results in crisis in months with low reservoir inflow and high demands, the outflow is rationed from several months beforehand to reduce the deficit intensity during the drought months. Tu et al. (2008) optimized hedging rules for reservoir operations. They reevaluated and updated the existing hedging rules to incorporate changes that have taken place in the reservoir system, as well as the demand characteristics. Dariane and Karami (2014) combined artificial neural networks, hedging rules and a heuristic algorithm to optimize operation of the reservoirs system in Tehran. Taghian et al. (2014) optimized conventional rule curves coupled with hedging rules for reservoir operation. Huang et al. (2016) analyzed optimal hedging rules for operation of a dual-purpose reservoir based on economic and multi-level environmental objectives and achievement of a balance between environmental and downstream water supply purposes. Spiliotis et al. (2016) optimized a reservoir operation in Spain by using the hedging rules and the particle swarm optimization algorithm. Kranthi and Srinivasan (2018) introduced generalized two-point linear hedging rules for operation of a reservoir which are identified based on two possibilities for the initial and ending water storages. Shenava and Shourian (2018) used a novel optimization-simulation approach for optimal reservoir operation with water supply enhancement and flood mitigation objectives.

Recently, Bat Algorithm (BA) which acts based on position and sound of bats is applied in engineering optimization problems as an efficient metaheuristic method. The bats use echolocation ability for finding a prey. Yang (2010) found global optimum solutions well by applying the bat algorithm for benchmark functions. Reddy and Manoj (2012) applied the bat algorithm for finding the optimum capacitor placement to reduce loss of energy. For energy optimization, Niknam et al. (2013) showed the bat algorithm led to better distribution and management of power energy than did the genetic algorithm. Ethteram et al. 2018) incorporated BA with different ordered rule curves for dam-reservoir operation. Ahmadianfar et al. (2016) optimized multireservoir operation by hybridizing bat algorithm and differential evolution. Zarei et al. (2019) optimized reservoir operation using bat and particle swarm algorithm and game theory based on optimal water allocation among consumers. Yaseen et al. (2019) applied a hybrid bat-swarm algorithm for optimizing dam and reservoir operation.

In the present study, application of the hedging policy for optimal operation of the Zhaveh Dam in Iran using the bat algorithm is investigated. Zhaveh Dam is one of the most important dams to be constructed in west of Iran. The height of the dam and operation of the reservoir due to its downstream users are some of the challenging subjects. Therefore, optimum operation of the reservoir is assessed in this study. Three hedging-based rules are defined for the reservoir operation and the water supply deficit is minimized as the objective function. For further investigation, the hedging policy is compared with the standard operating policy as a common reservoir operation policy.

2 Methodology

2.1 Reservoir Operation Policy

A reservoir operation policy is a decision support tool that provides guidance for reservoir operations to meet the requirements of various users (Rittima 2009). In general, it is widely known in the following forms:

2.1.1 Standard Operating Policy

A standard operating policy (SOP) is the simplest and most often-used reservoir policy that releases, if possible, only the demand required in each period, and does not preserve water for future requirements. If sufficient water is not available to meet demand, the reservoir is emptied. If there is excess water, the reservoir will fill and then spill the excess water as shown in Fig. 1. Thus, standard operating policy is the optimal operating policy with the objective to minimize the total deficit over the time horizon (Neelakantan and Pundarikanthan 1999).

Fig. 1
figure 1

Standard operating policy

Full size image

2.1.2 Hedging Policy

The concept of a hedging policy has been formulated since the 1980s and has been further emphasized in water resources planning and management up to the present. A hedging policy attempts to retain existing water storage for use in later periods. In principle, some water is stored, even when there is enough water for target demand in the present period. The common forms of hedging are described in the following manners (Draper and Lund 2004):

  1. (1)

    One-point hedging; release begins at the origin in Fig. 2 and increases linearly until it intersects with the target level of release.

  2. (2)

    Two-point hedging; a linear hedging rule begins from a first point occurring somewhere up from the origin in the shortage portion of the standard operation policy, to a second point occurring where the hedging slope intersects the target release.

  3. (3)

    Three-point hedging; an intermediate point is specified in the above rule, introducing two linear portions to the hedging portion of the overall release rule.

  4. (4)

    Continuous hedging; the slope of the hedging portion of the rule can vary continuously.

  5. (5)

    Zone-based hedging; hedging quantities are discrete proportions of release targets for different zonal levels of water availability.

Fig. 2
figure 2

Types of hedging rule for reservoir operation

Full size image

2.2 Bat Algorithm

Bats, the only winged mammals, can determine their locations while flying using sound emission and reception, which is called echolocation. Most bats are insectivores and use a type of sonar, called echolocation, to detect prey, avoid obstacles, and locate their roosting crevices in the dark. Bats emit sound pulses while flying and listen to their echoes from surrounding objects to assess their own location and those of the echoing objects. Each pulse has a constant frequency and lasts a few thousandths of a second. About 10 to 20 sounds are emitted every second with the rate of emission up to approximately 200 pulses per second when they fly near their prey while hunting. As the speed of sound in air is typically v = 340 m/s, the wave length (λ) of the ultrasonic sound bursts with a constant frequency (f) and is given by:

$$ \uplambda =\frac{v}{f} $$
(1)

In simulations, we have to use virtual bats. We have to define the rules how their positions xi and velocities vi in a d-dimensional search space are updated. The new solutions \( {x}_i^t \) and velocities \( {v}_i^t \) at time step t are given by (Yang 2010):

$$ {f}_i={f}_{min}+\left({f}_{max}-{f}_{min}\right)\beta $$
(2)
$$ {v}_i^t={v}_i^{t-1}+\left({x}_i^t-{x}_{\ast}\right){f}_i $$
(3)
$$ {x}_i^t={x}_i^{t-1}+{v}_i^t $$
(4)

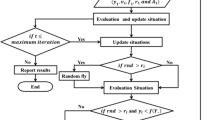
where β ∈ [0, 1] is a random vector drawn from a uniform distribution. Here x∗ is the current global best location (solution) which is located after comparing all the solutions among all the n bats. As the product λifi is the velocity increment, we can use fi (or λi) to adjust the velocity change while fixing the other factor‚ λi (or fi), depending on the type of the problem of interest. In our implementation, we will use fmin = 0 and fmax = 1, depending on the domain size of the problem of interest. Initially, each bat is randomly assigned a frequency which is drawn uniformly from [fmin, fmax]. For the local search part, once a solution is selected among the current best solutions, a new solution for each bat is generated locally using random walk (Bozorg-Haddad et al. 2014). In Fig. 3, the flowchart of the bat algorithm is shown.

Fig. 3
figure 3

Bat algorithm

Full size image

3 Case Study

The Zhaveh Reservoir is located on the Sirvan River in west of Iran. The maximum storage capacity of the reservoir is 169 million cubic meters (MCM). In Fig. 4, location of the Zhaveh Dam in the Sirvan River Basin is shown.

Fig. 4
figure 4

Location of the Zhaveh Dam in the Sirvan River Basin, Iran

Full size image

Average discharge of the Sirvan River at the dam site is 0.26 cubic meters per second (m3/s) which produces an average annual inflow of 8.11 MCM to the reservoir. In Fig. 5, the time series of the monthly inflows to the Zhaveh reservoir and the downstream demands are plotted. The reservoir’s maximum and minimum storages are 169 and 27 MCM, respectively.

Fig. 5
figure 5

Time series of the monthly inflows and downstream demand of the Zhaveh Dam

Full size image

4 Formulation of the Problem

For optimal reservoir operation, the goal is to determine the reservoir releases in a way that the objective function which here is the deficit of water supply for the demands is minimized. According to hedging rule curve, the decision variables are Kp values (the gradient of the release curve) which through determination of them, the amounts of releases are known. By obtaining the releases, the objective function’s value which is the deficit of water supply is then calculated for each set of the produced decision variables. The set of Kp’s which result the minimum objective function is used by the bat algorithm for generating the new values for the decision variables and this procedure is repeated until one of the convergence criteria defined for the algorithm is met. These criteria are repeating of the best solution in 25 successive iterations after iteration no. 100 or reaching to maximum number of searching iterations which is defined equal to 300 here. In Fig. 6, the workflow of the BA-hedging rule process is presented.

Fig. 6
figure 6

Workflow of the BA-hedging rule process for optimal reservoir operation

Full size image

The objective function is to minimize the water supply deficit. The decision variables are Kp values (hedging coefficients) which produce the reservoir releases according to Eq. 8. The deficit which is to be minimized as the objective function is defined in Eq. 5.

$$ Def={\sum}_{t=1}^T{\left(\frac{D(t)-R(t)}{D(t)}\right)}^2 $$
(5)

In Eq. 5, D(t) is the monthly demand, R(t) is the reservoir’s monthly release and T is the number of operation time steps. R(t)'s are unknown and the reservoir operation goal is to release water in a way that Def is minimized. The continuity constraint for the reservoir storages should be satisfied as in Eq. 6:

$$ S\left(t+1\right)=S(t)+I(t)-R(t)-E(t)- Sp(t) $$
(6)

where S(t) is the reservoir’s storage in beginning of month t and I(t), E(t) and Sp(t) are the inflow, evaporation and spill in month t, respectively. The reservoir’s storage should be in the feasible domain as shown in Eq. 7:

$$ {S}_{min}\le S(t)\le {S}_{max} $$
(7)

where Smin and Smax are the reservoir’s minimum and maximum storage capacities. If through Eq. 6, S(t) finds a value out of the feasible domain then it is restricted to the corresponding boundary and R(t) is decreased or Sp(t) is increased accordingly. Monthly reservoir releases are determined by the hedging relation as shown in Eq. 8.

$$ R(t)=\left(\frac{1}{K_p}\right)\ast \left(S(t)+I(t)\right) $$
(8)

where Kp is the hedging rule curve gradient coefficient. By defining Kp, other variables are determined. Therefore, Kp’s are introduced as the BA’s decision variables and finding their optimum values is the purpose of using the optimization algorithm. In this research, three scenarios for the reservoir operation rules are defined. In the first scenario, a constant Kp is considered for all months. In the second state, Kp’s have 12 values varying in different months of a year but are the same in 20 years of the reservoir operation. So, the problem has 12 decision variables in this state. And in the third scenario, Kp’s are relaxed to vary in all 240 months of the operation period which faces the problem with 240 decision variables. Therefore, in these three states, the reservoir operation rule curve finds more degree of freedom to search for the optimum solution in the search space of the problem. In Table 1, the differences between three scenarios defined for the reservoir operation are stated.

Table 1 Hedging rule-based reservoir operation optimization scenarios
Full size table

By defining the decision variables and the rules and coding the optimization procedure, the BA-hedging rule based reservoir operation model is executed in three above scenarios and the optimum answers are obtained. For further investigation, the hedging rules results are assessed through solving the problem by a non-linear program which is able to find the global optimum. Also the hedging rule policy is compared with the standard operating policy (SOP) to investigate the cons and pros of this method.

5 Results and Discussion

By execution of the BA-hedging rule model, the optimum values for the decision variables of the problem which are Kp’s in the defined scenarios, are obtained. The optimization procedure is run at least five times in each state for reassurance of convergence of the bat algorithm to the global optimum. The results obtained by the model in various executions are close to each other indicating the consistency of the algorithm. In Fig. 7, the convergence trend of the best objective function obtained by the bat algorithm in three defined scenarios is shown.

Fig. 7
figure 7

Convergence trend of the best objective function in hedging rules scenarios

Full size image

According to the results, the optimum values for the objective function are 105.3 for the first scenario, 102.8 for the second state and 80.5 for the third scenario. This states that by increase of the degree of freedom for the optimization algorithm, it is able to find a better solution in terms of the objective function. In other words, the hedging model performs more successfully in determining reservoir releases when a larger number of variables are employed by the bat algorithm. The objective function declines from the first to the third scenario with increases in the number of hedging coefficients (indicating the higher efficiency of the third scenario comparing the other two). The optimum values for the decision variable in the first and second scenario are reported in Table 2. Also, these values are presented in Fig. 8 for the third scenario.

Table 2 Optimum values for Kp in the first and second scenarios
Full size table
Fig. 8
figure 8

Optimum values obtained for Kp in scenario 3

Full size image

In Fig. 9, time series of the optimum reservoir releases in three scenarios of hedging rule-based operation are shown.

Fig. 9
figure 9

Time series of the Zhaveh reservoir’s optimum releases in hedging rules scenarios

Full size image

As seen in Fig. 9, the reservoir releases are almost close in scenarios 1 and 2 but they vary differently in scenario 3 where the optimization algorithm is allowed to select an optimum value for the release in each month of the operation period. In Fig. 10, the average monthly deficits for the reservoir downstream demands are shown.

Fig. 10
figure 10

Average monthly deficits for the reservoir demands in hedging rules scenarios

Full size image

According to Fig. 10, the average annual deficits for the Zhaveh reservoir downstream demands are 155.5, 154 and 73.5 MCM in scenarios 1, 2 and 3, respectively. The average annual deficit is 1% lower in the second scenario comparing the first state while it is 52% lower in the third scenario compared to scenario 2. This indicates that by increasing the dimension of the optimization problem from 12 (scenario 2) to 240 (scenario 3), the average annual deficit for the reservoir downstream demands is decreased more than 50%.

It is seen that the first scenario does not perform well for a 20-year operation period which includes wet and dry months because it employs a single rule, while the second scenario performs better where the hedging coefficients vary in the months of a year leading to better solution. The third scenario outperforms the other states because it is able to vary all monthly reservoir releases to find the best solution.

5.1 Assessment of the Results

In order to check the optimality of the solutions obtained by the bat algorithm, the hedging rule-based reservoir operation relations is coded in LINGO software and the problem is solved by the nonlinear programming used by LINGO. The main feature of a nonlinear programming method is its ability to find the global optimum of an optimization problem. The problem is nonlinear here because of the hedging relation (Eq. 8). So, by comparison of the results of these two methods, the optimality of the solutions obtained by the metaheuristic algorithm is assessed. The optimum reservoir releases are determined by modeling the hedging rule-based operation method in LINGO. In Fig. 11, monthly time series of the Zhaveh reservoir releases obtained by BA are compared with the NLP results in the second scenario.

Fig. 11
figure 11

Comparison of the optimum reservoir releases obtained by BA and NLP

Full size image

Figure 11 indicates that the bat algorithm has an acceptable ability to find the optimum solutions of the problem because the two curves match each other in most of time steps of the operation period. Moreover, the optimum value of the objective function obtained by NLP is 102.5 comparing the value of 102.8 obtained by BA which states the closeness of the solution found by BA to the global optimum of the problem. Also, in the first scenario, the optimum objective function obtained by the NLP method is 105.3 which is the same as the BA’s solution. In scenario 3 with 240 decision variables, the best objective function of 80.2 is found by NLP which is enough close to the bat algorithm’s solution which is 80.5.

5.2 Comparison of the Hedging Policy and the Standard Operation Policy

The standard operation policy (SOP) is a common method for analyzing the ability of a reservoir for satisfying the downstream demands. In SOP, the volume of releasing water at each time step is assumed to be equal to the demand amount in that step. If the reservoir is not able to supply the demand completely, it provides a portion of the demand as much as possible. In this policy, the total amount of deficit is minimized but the intensities of the deficits are usually high. For further analysis of the hedging rule-based reservoir operation results, the standard operation policy rules are modeled and the results are compared in this section. In SOP, the reservoir release is determined using Eq. 9.

$$ {R}_t=\left\{\begin{array}{c}{D}_t\kern1.25em if\kern1em {D}_t\le {S}_t\\ {}{S}_t\kern1.25em if\kern0.75em {D}_t>{S}_t\end{array}\right. $$
(9)

In fact, the main difference between the hedging policy and SOP is that the hedging coefficient (Kp) in SOP has a constant value of one and does not vary based on the reservoir’s storage during the operation period. By simulating the standard operation policy rule for the Zhaveh reservoir, the amounts of water supply and deficit for meeting the downstream demands are calculated. In Fig. 12, time series of the deficits in SOP and three scenarios of hedging rules are compared. In Fig. 13, the average monthly deficits in these states are shown.

Fig. 12
figure 12

Time series of the deficits for the Zhaveh reservoir’s demands in hedging rule-based and standard operation policies

Full size image
Fig. 13
figure 13

Average monthly deficits for the reservoir demands in hedging rule-based and standard operation policies

Full size image

By applying the hedging policy for the Zhaveh reservoir operation, the deficits are lowered comparing the SOP state, specially in scenario 3 where the model has more ability to adapt the releases with the hydrologic condition of the reservoir. By the hedging policy, a volume of water is stored in the reservoir in wet months when the storage is high which aids to supply the demands in the dry periods. In condition of using the optimum hedging policy, the probability of occurrence of intensive water shortages is reduced and the ability of the reservoir for supplying water at the threshold level is increased due to a foresight view which the optimization gives to the model. As seen in Fig. 12, the deficits in the standard operation policy are much larger compared to the hedging scenarios specially during the last months of the operation period which the inflows to the reservoir are lower due to the drought. This is because that the BA-hedging rule-based reservoir operation supplies a portion of the demands in the earlier months and tries to decrease the total deficits according to the defined objective function. This conclusion is consistent with the results obtained by Sheibani and Shourian (2019) where the optimum reliability for supplying agricultural demand downstream of a reservoir using an explicit method with an economic objective function is determined.

6 Concluding Remarks

Optimal reservoir operation involves diverse aspects for which a single optimum solution rarely exists, and there are usually a number of answers based on the purpose of the defined problem. In the present study, optimum operation of the Zhaveh reservoir in west of Iran using the hedging policy and the bat algorithm is determined. Three scenarios for optimizing the hedging coefficients are defined to minimize the deficit of water supply for the downstream demands. Results show that as the flexibility of the hedging rules increases, the total deficit decreases. Optimality of the results obtained by the bat algorithm is assessed through solving the problem with a nonlinear programming procedure which is able to find the global optimum. Closeness of the results showed the ability of BA to solve the real word engineering optimization problems.

For further investigation, the BA-hedging policy is compared with the standard operation policy (SOP) to show the efficiency of the optimization when combined to the reservoir operation rules. Results show that although the optimal hedging policy caused more failures than SOP in meeting the demands during the operation period but the intensities of the deficits are much lower. This could be named as an important feature for the hedging rule-based reservoir operation.