Introduction

In the past decades, soil nailing, which is developed on the base of New Austrian Tunneling Method (NATM) and can improve the soil shear strength significantly through steels or other high strength strip materials, has been proved a versatile and cost effective technique in reinforcing soil or soft rock slope (Martin 1997). However, whether a soil nail reinforced slope is available and economic or not depends to a considerable extent on the design method and criterion. The current design methods are usually sorted into criterion based on factor of safety and criterion based on the permanent displacement. The proper design of slope reinforced by structures makes colossal demands on the in-depth theoretical research, which in turn causes more and more attention to be paid by an increasing population of scientists.

The traditional concept for evaluating stability of slopes is minimum factor of safety. If the factor of safety is less than 1.0, the slope is often considered to be unsafe. Thus, assuming the factor of safety equate 1.0, it is usually convenient to obtain the maximum yield acceleration. At present, theoretical methods of evaluating slope stability based on factor of safety could be approximately categorized into three groups: finite element method, limit equilibrium method as well as limit analysis method. The finite element method is certainly an appreciative and comprehensive approach to investigate the performance of soil nail reinforced slope (Yang and Drumm 2000; Ng and Lee 2002; Cheuk et al. 2005; Zhou et al. 2009). However, its fulfillment is usually too highly skilled to many engineers and it usually requires accurate measurement of the properties of component materials which are often difficult to achieve. Referring to the limit equilibrium method, although it is easily understood and popular with engineers, its solution cannot be regarded as rigorous in a strict mechanical sense due to the arbitrary assumptions associated with interslice forces (Patra and Basudhr 2005; Nouri et al. 2006).

In addition, limit analysis method has grown increasingly important for slope stability design. Juran et al. (1990) presented a kinematical limit analysis design approach that provided a rational estimate of maximum tension and shear forces mobilized in reinforcements, while it did not take account of the action of seismic loading. However, the earth having earthquake occurred frequently in recent years, such as the 2008 Wenchuan earthquake, the 2010 Chile earthquake and the 2011 Tōhoku earthquake, has made colossal demands on the design of structured slope in which the seismic effects must be included (Derek 2005; Topal and Akin 2009). Thus, the limit analysis considering the seismic loading was further proposed. Chang et al. (1984) adopted the pseudo-static method of upper bound limit analysis and Newmark’s analytical procedure to determine the critical state and soil displacements of natural slopes. Ausilio et al. (2000, 2001) further extended the framework of the pseudo-static approach to the slopes reinforced with geosynthetics or piles. Furthermore, Michalowski and You (2000) based on the kinematical approach of limit analysis, investigated the seismic effects and soil displacements of slopes reinforced by geotechnical structures, but a shallow slip mechanism is assumed in advance. Giri and Sengupta (2009) proposed an analytical method based on the kinematic theorem of limit analysis to investigate the stability of reinforced slope under the seismic loading and compared the results with finite element solution. Nevertheless, they did not investigate the influences on critical yield acceleration from various characteristic parameters.

As is well known, design based on pseudo-static factor of safety analysis is generally considered as conservative, since even when the safety factor drops below one the slope could experience only a finite displacement rather than a complete failure. Hence, it is usually expensive for large value of yield seismic acceleration, while the design procedure based on permanent displacement is a proper choice (Ausilio et al. 2000, 2001).

Thus, in present paper, a kinematic theorem of limit analysis is proposed to investigate the critical seismic yield acceleration coefficient and the permanent displacement of soil nail reinforced slope. The log-spiral failure mechanism is considered and the analytical expressions are determined. Many numerical computations are carried out to investigate the influences on the critical seismic yield acceleration coefficient from various factors including cohesion and frictional angle of soil, cut slope ratio as well as characteristic parameters of soil nail.

Kinematic approach of limit analysis

The kinematic approach of limit analysis, which is based on the plasticity upper bound theory, has been widely adopted to investigate the problem of soil stability (Chen 1975). In fact, the upper bound theorem can be established directly if the following assumptions are made:

  1. 1.

    Soil is a perfect plastic material. This implies that the stress point cannot move outside the yield surface, so the stress rate vector must be tangential to the yield surface whenever plastic strain rates are occurring;

  2. 2.

    Yield function of the soil is convex in the stress space and the plastic strain rates are derivable from the yield function through the flow rule. Hence, it follows from the flow rule and the perfect plastic property assumption mentioned above, which gives \( \dot{\sigma }_{ij} \dot{\varepsilon }_{ij} = 0 \), where \( \dot{\sigma }_{ij} \) and \( \dot{\varepsilon }_{ij} \) are stress rate and plastic strain rate, respectively;

  3. 3.

    Geometry changes are insignificant at the limit load, which implies the virtual work principle can be applied.

Application of the kinematic theorem requires equating the rate of work done by tractions and body forces to the internal energy dissipation rate. Any assumed strain rate field, which is governed by the normality rule, is compatible with the velocities at the boundary of the failure soil mass. The work rate equation can be expressed as following:

$$ \int\limits_{V} {\sigma_{ij} } \dot{\varepsilon }_{ij} dV = \int\limits_{S} {F_{i} } \dot{v}_{i} ds + \int\limits_{V} {X_{i} } v_{i} dV \quad i,j = 1,2,3 $$
(1)

where \( X_{i} \) = body forces; F i = traction; v i = kinematically admissible velocity field; \(\dot{\varepsilon}_{ij}^{{}}\) = strain rate field compatible with v i ; \( \sigma_{ij}^{{}} \) = stress field relating to \( X_{i} \) and T i ; S and V are, respectively, the loaded boundary and volume of the sliding soil mass. In this paper, the kinematic approach is employed to calculate the critical seismic yield acceleration coefficient of soil nail reinforced slope.

Log-spiral failure mechanism

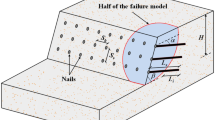
In the failure mode shown in Fig. 1, the reinforced soil mass above the failure surface rotates as a rigid body about the centre of rotation with angular velocity and the log-spiral failure surface can be described by the following equation:

$$ r = r_{0} e^{{\left( {\theta - \theta_{0} } \right)tg\varphi }} $$
(2)

where r 0 = radius of the log-spiral with respect to angle θ 0; φ = angle of soil shearing resistance and r and θ are the radius and angle of any point of the log-spiral. The assumed failure surface can be completely specified by the following three variables: the height of slope H, the angles θ 0 as well as θ h . Following Ausilio (2000), the rate of work due to soil weight and inertial force takes the form

$$ \dot{W} = \dot{\omega }r_{0}^{3} \gamma [f_{1} - f_{2} - f_{3} ] + k_{h} \dot{\omega }r_{0}^{3} \gamma \left( {f_{4} - f_{5} - f_{6} } \right) $$
(3)

where \( k_{h} \) = seismic coefficient; γ = soil unit weight; and the functions f 1 − f 6 depend on the angle of θ 0, θ h , φ and β. Expressions for f 1 − f 6 can be found in several works (Ausilio et al. 2000, 2001; Michalowski and You 2000). These expressions can be expressed as:

$$ f_{1} = {\frac{{\left\{ {\left( {3tg\varphi \cos \theta_{h} + \sin \theta_{h} } \right)\exp \left[ {3\left( {\theta_{h} - \theta_{0} } \right)tg\varphi } \right] - 3tg\varphi \cos \theta {}_{0} - \sin \theta_{0} } \right\}}}{{3\left( {1 + 9tg^{2} \varphi } \right)}}} $$
$$ f_{2} = \frac{1}{6}{\frac{L}{{r_{0} }}}\left( {2\cos \theta_{0} - {\frac{L}{{r_{0} }}}} \right)\sin \theta_{0} $$
$$ f_{3} = \frac{1}{6}\exp \left[ {\left( {\theta_{h} - \theta_{0} } \right)tg\varphi } \right]\left[ {\sin \left( {\theta_{h} - \theta_{0} } \right) - {\frac{L}{{r_{0} }}}\sin \theta_{h} } \right]\left\{ {\cos \theta_{0} - {\frac{L}{{r_{0} }}} + \cos \theta_{h} \exp \left[ {\left( {\theta_{h} - \theta_{0} } \right)tg\varphi } \right]} \right\} $$
$$ {\frac{L}{{r_{0} }}} = {\frac{{\sin \left( {\theta_{h} - \theta_{0} } \right)}}{{\sin \theta_{h} }}} - {\frac{{\sin \left( {\theta_{h} + \beta } \right)}}{{\sin \theta_{h} \sin \beta }}}\left\{ {\sin \theta_{h} \exp \left[ {\left( {\theta_{h} - \theta_{0} } \right)tg\varphi } \right] - \sin \theta_{0} } \right\} $$
$$ f_{4} = {\frac{{\left\{ {\left( {3tg\varphi \sin \theta_{h} - \cos \theta_{h} } \right)\exp \left[ {3\left( {\theta_{h} - \theta_{0} } \right)tg\varphi } \right] - 3tg\varphi \sin \theta {}_{0} + \cos \theta_{0} } \right\}}}{{3\left( {1 + 9tg^{2} \varphi } \right)}}} $$
$$ f_{5} = \frac{1}{3}{\frac{L}{{r_{0} }}}\sin^{2} \theta_{0} $$
$$ f_{6} = \frac{1}{6}\exp \left[ {\left( {\theta_{h} - \theta_{0} } \right)tg\varphi } \right]\left[ {\sin \left( {\theta_{h} - \theta_{0} } \right) - {\frac{L}{{r_{0} }}}\sin \theta_{h} } \right]\left\{ {\sin \theta_{0} + \sin \theta_{h} \exp \left[ {\left( {\theta_{h} - \theta_{0} } \right)tg\varphi } \right]} \right\} $$
Fig. 1
figure 1

Log-spiral failure mechanism of soil nail reinforced slope

Full size image

The energy dissipation rate during rotational failure due to soil nail can be expressed as

$$ \dot{D}_{1} = r_{0} \omega \sum\limits_{i = 1}^{n} {T_{i} } e^{{\left( {\theta_{i} - \theta_{0} } \right)tg\varphi }} \sin (\theta_{i} - \alpha ) $$
(4)

where z i = depth of layer measured downwards from the top of the slope; n = number of the reinforcement layers; α = the incline angle of soil nail; T i = force of the ith layer per unit width, which is usually written as:

$$ T_{i} = \pi d_{i} L_{i} \left[ \tau \right] $$
(5)

where d i = diameter of the ith soil nail; L i = length of the ith soil nail; \( \left[ \tau \right] \) = bond strength between soil nail and surrounding soil. θ i can be shown as:

$$ z_{i} = {\frac{1}{1 + tg\alpha ctg\beta }}\left\{ {Htg\alpha ctg\beta + r_{0} \left[ {e^{{\left( {\theta_{i} - \theta_{0} } \right)tg\varphi }} \left( {\sin \theta_{i} - \cos \theta_{i} tg\alpha } \right) + e^{{\left( {\theta_{h} - \theta_{0} } \right)tg\varphi }} \cos \theta_{h} tg\alpha - \sin \theta_{0} } \right]} \right\} $$
(6)

The energy dissipation rate during rotation failure along the sliding surface can be written as

$$ \dot{D}_{2} = {\frac{{cr_{0}^{2} \omega }}{2tg\varphi }}\left[ {e^{{2\left( {\theta_{h} - \theta_{0} } \right)tg\varphi }} - 1} \right] $$
(7)

By equating the rate of external work to the energy dissipation, we have

$$ \dot{W} = \dot{D}_{1} + \dot{D}_{2} $$
(8)

And substituting the expressions \( \dot{W} \), \( \dot{D}_{1} \) and \( \dot{D}_{2} \) into (8) yields

$$ \omega r_{o}^{3} \rho g[(f_{1} - f_{2} - f_{3} ) + k_{h} (f_{4} - f_{5} - f_{6} )] = r_{0} \omega \sum\limits_{i = 1}^{n} {T_{i} } e^{{\left( {\theta_{i} - \theta_{0} } \right)tg\varphi }} \sin (\theta_{i} - \alpha ) + {\frac{{cr_{0}^{2} \omega }}{2tg\varphi }}\left[ {e^{{2\left( {\theta_{0} - \theta_{h} } \right)tg\varphi }} - 1} \right] $$
(9)

where:

$$ {\frac{H}{{r_{0} }}} = a $$
(10)
$$ a = e^{{\left( {\theta_{h} - \theta_{0} } \right)tg\varphi }} \sin \theta_{h} - \sin \theta_{0} $$
(11)

Equation (9) can be reduced as

$$ H^{2} \gamma [(f_{1} - f_{2} - f_{3} ) + k_{h} (f_{4} - f_{5} - f_{6} )] = a^{2} \sum\limits_{i = 1}^{n} {T_{i} } e^{{\left( {\theta_{i} - \theta_{0} } \right)tg\varphi }} \sin (\theta_{i} - \alpha ) + {\frac{caH}{2tg\varphi }}\left[ {e^{{2\left( {\theta_{\text{h}} - \theta_{0} } \right)tg\varphi }} - 1} \right] $$
(12)

The kinematic theorem can be applied to give the upper-bound solution for the seismic yield acceleration coefficient of the log-spiral failure mechanism:

$$ k_{y} = {\frac{{a^{2} \sum_{i = 1}^{n} {T_{i} } e^{{\left( {\theta_{i} - \theta_{0} } \right)tg\varphi }} \sin (\theta_{i} - \alpha ) + {\frac{caH}{2tg\varphi }}\left[ {e^{{2\left( {\theta_{h} - \theta_{0} } \right)tg\varphi }} - 1} \right] - H^{2} \gamma (f_{1} - f_{2} - f_{3} )}}{{H^{2} \gamma (f_{4} - f_{5} - f_{6} )}}} $$
(13)

The seismic yield acceleration coefficient is defined as the horizontal ground acceleration in the downhill direction and requires to be brought the safety factor with respect to slope failure to one. However, it is assumed that the seismic acceleration coefficient in the uphill direction is sufficiently large as failure in that direction will not occur. The critical seismic yield acceleration coefficient is obtained by minimizing \( k_{y} \) with respect to θ 0 and θ h . This means taking the first derivatives of k y and equating them to zero,

$$ \left. {\begin{array}{*{20}c} {{\frac{{\partial k_{y} }}{{\partial \theta_{0} }}} = 0} \\ {{\frac{{\partial k_{y} }}{{\partial \theta_{h} }}} = 0} \\ \end{array} } \right\} $$
(14)

Thus, for a slope with the values of height \( {H} \) and unit weight γ known, we can employ the sequential quadratic programming to optimize the object function with respect to θ 0 and θ h to get a least upper bound for the seismic acceleration coefficient of the soil nail reinforced slope.

Assessment of permanent displacement

The permanent displacement is usually conducted using the sliding block method originally proposed by Newmark (1965). According to this method, the potential failure soil mass is treated as a rigid block on an inclined plane, which moves in the downhill direction whenever ground acceleration exceeds yield acceleration of slope. The earthquake-induced displacement can be obtained by integrating twice the equation of motion,

$$ \ddot{x} = sign(k_{h} (t) - k_{yc} )g{\frac{\cos (\phi - \theta )}{\cos \phi }} $$
(15)

where \( \ddot{x} \) = acceleration of the sliding block relation to the slip surface; k h (t)g = ground acceleration time-history; k y g = yield acceleration that is usually assumed to be constant with time; g = gravity acceleration; θ = angle that the inclined plane makes with the horizontal; sign represents signal function.

In the case of the rotational failure mechanism, it is more appropriate to express the equation of motion in terms of the angular rotation of the failure mass relative to the stable soil. The following equation can be derived:

$$ \ddot{\omega } = sign(k_{h} (t) - k_{yc} )g\gamma r_{0}^{3} (f_{4} - f_{5} - f_{6} )/(Wl^{2} ) $$
(16)

where W and l are expressed as:

$$ W = {\frac{{\gamma r_{0}^{2} }}{2}}\left\{ {{\frac{{\exp [2(\theta_{h} - \theta_{0} )\tan \varphi ] - 1}}{2\tan \varphi }} - {\frac{L}{{r_{0} }}}\sin \theta_{0} - \frac{H}{{r_{0}}}\frac{{\sin (\theta_{h} + \beta )}}{\sin \beta }\exp [(\theta_{h} - \theta_{0} )\tan \varphi ]} \right\} $$
(17)
$$ l = \sqrt {[\gamma r_{0}^{3} (f_{1} - f_{2} - f_{3} )]^{2} + \gamma r_{0}^{3} (f_{4} - f_{5} - f_{6} )]^{2} } /W $$
(18)

Results and discussion

As shown in Fig. 2, a rotational log-spiral failure mechanism is considered. In this paper, a series of calculations are carried out to illustrate the influences of various factors on the stability of a nail-reinforced slope. In order to show the influences of various factors in figures visually, only one variable varies with H ranging from 6 to 20 m in each situation while the other variables are kept constant. Without loss of generality, the following parameters are used when they are kept constant: H in  = 1 m; β = 45∘; α = 10∘; φ = 32∘; c = 25 kPa; [τ] = 50 kPa; γ = 19.5 kN/m3; d = 100 mm; L i  = 10 m (Fig. 2). As a matter of fact, modifications of value of those constants don’t change the tendency of the influences of various factors, although it has some influences on value of critical seismic yield acceleration coefficient. In the following sections, the critical seismic yield acceleration coefficient of the soil nail reinforced slope is calculated based on Eqs. (13) and (14) while the permanent displacement is calculated based on Eq. (16).

Fig. 2
figure 2

Soil nail reinforced slope stability problem

Full size image

Effect of friction angle and cohesion of soil on the critical seismic yield acceleration coefficient

In this section, we have investigated the influences of friction angle φ and cohesion c of soil on the critical seismic yield acceleration coefficient k yc . Figure 3 shows the influences of φ on the variation of k yc with different height H of slope. It is clearly demonstrated in Fig. 3 that both φ and H have significant effects on the k yc of the soil nail reinforced slope. First, Fig. 3 shows that k yc decreases with increasing H. This is consistent with the truth in reality that the higher of the slope, the more possible of failure. Actually, it will be found that, for all situations considered in this manuscript, k yc always decreases with the increase of H. Second, it is obviously shown in Fig. 3 that k yc increases with the increase of φ. The resistance capability of soil increases with the increase of φ. Hence, the increase of φ means larger k yc is required to cause the slope to collapse. In addition, Fig. 4 shows the influences of c on the variation of k yc with different height H of slope. It is seen that k yc varies significantly with soil cohesion c. With the increase of c, k yc increases obviously. Similar to the influences of friction angle φ, soil cohesion c has an equivalent effects on the strength of soil as well as k yc .

Fig. 3
figure 3

Critical seismic yield acceleration coefficient versus internal friction angle of soil with different height of slope

Full size image
Fig. 4
figure 4

Critical seismic yield acceleration coefficient versus cohesion of soil with different height of slope

Full size image

Effect of cut slope ratio on the critical seismic yield acceleration coefficient

In the slope engineering, if site conditions permitting, it is important available manner to design milder slope ratio in condition of the stability of slope. Thus, in order to investigate the influences of cut slope ratio, under other parameters remaining unchanged, the variations of k yc with H are studied with five kinds of cut slope ratio (1:0.5, 1:0.75, 1: 1, 1:1.25, 1:1.5). The results are shown in Fig. 5. It is seen that k yc varies significantly for different cut slope ratio. In the same value of H, as cut slope ratio increases, k yc decreases. In the same value of cut slope ratio, as H reduces, k yc increases. In addition, in the case of different height of slope, the sensitivity of k yc for cut slope ratio was significantly different. For H = 6 m, when the cut slope ratio reduces from H:D = 2 to H:D = 0.67, k yc only increases from 0.75 to 0.84. However, for H = 20 m, when cut slope ratio reduce from H:D = 2 to H:D = 0.67, k yc increases from 0.16 to 0.43.

Fig. 5
figure 5

Critical seismic yield acceleration coefficient versus slope ratio with different height of slope

Full size image

Effect of characteristic parameters of soil nail on the critical seismic yield acceleration coefficient

The characteristic parameters of soil nail also have significant effects on the critical seismic yield acceleration coefficient of soil nail reinforced slope. The results are shown in Figs. 6, 7, 8 and 9. From Fig. 6, as the length of soil nail L increases, k yc increases. Figure 7 shows the effects of bond strength of soil nail [τ] on k yc . It is seen that k yc increases with the increasing [τ]. In addition, Fig. 8 shows the influences of space distance of soil nail H in on k yc . It is found that k yc decreases significantly with the increase of H in . Nevertheless, it is demonstrated that, as seen in Fig. 9, the effect of incline angle of soil nail α on k yc is insignificant for different height of slope.

Fig. 6
figure 6

Critical seismic yield acceleration coefficient versus length of soil nail with different height of slope

Full size image
Fig. 7
figure 7

Critical seismic yield acceleration coefficient versus bond strength of soil nail with different height of slope

Full size image
Fig. 8
figure 8

Critical seismic yield acceleration coefficient versus space of soil nail with different height of slope

Full size image
Fig. 9
figure 9

Critical seismic yield acceleration coefficient versus incline angle of soil nail with different height of slope

Full size image

Permanent displacement of soil nail reinforced slope

In spite of critical seismic yield acceleration coefficient, permanent displacement evaluation becomes increasingly important to design of slope engineering. In order to obtain the value of permanent displacement, we compute the time integrations of Eq. (16) twice and get:

$$ \Updelta \omega = \int\limits_{0}^{t} {\int\limits_{0}^{t} {sign(k_{h} (t) - k_{yc} )g\gamma r_{0}^{3} (f_{4} - f_{5} - f_{6} )/(Wl^{2} )dtdt} } $$
(19)

As a matter of fact, once the input curves of k h (t) are gained, the solution of Eq. (19) becomes easy. For example, an earthquake is characterized with actual seismic acceleration coefficient k h  = 1 and with standing shock time t = 0.5 s. Similar to calculations shown in Fig. 3, the influences of φ on the rotational angle increment of slopes with various slope heights are investigated with the other parameters kept constant. The rotational angle increment versus internal friction angle of soil with different height of slope is shown in Fig. 10. It is demonstrated that the rotational angle increment increases with increasing H and decreases with increasing φ. Generating from above computation procedure, predicting permanent displacement of slope structures subjected to seismic loading from Eq. (19) is an available way to instruct the design of reinforced slope.

Fig. 10
figure 10

Permanent displacement increment versus internal friction angle of soil with different height of slope

Full size image

Conclusion

This paper attempts to analyze the critical seismic yield acceleration coefficient and permanent displacement of soil nail reinforced slope under earthquake loading with the upper bound theorem of limit analysis. A set of equations are derived and a series of parametric studies are carried out. Based on the results of parametric studies, the following conclusions are drawn:

  1. 1.

    The soil cohesion and frictional angle have a significant effect on the critical seismic yield acceleration coefficient of soil nail reinforced slope. The critical seismic yield acceleration coefficient increases with increasing soil frictional angle and soil cohesion.

  2. 2.

    The cut slope ratio and height of slope play a significant role on the critical seismic yield acceleration coefficient of soil nail reinforced slope. The critical seismic yield acceleration coefficient increases with the increase of cut slope ratio, while it decreases as the height of slope increases.

  3. 3.

    The characteristic parameters of soil nail have important influences on the critical seismic yield acceleration coefficient. The critical seismic yield acceleration coefficient increases with increasing length and bond strength of soil nail as well as decreasing space distance of soil nail while the effects of the incline angle of soil nail on the critical seismic yield acceleration coefficient is insignificant for different height slope.

  4. 4.

    The permanent displacement of soil nail reinforced slope has been derived and an example has been carried out. The results suggest that the permanent displacement prediction is consistent with the computation based factor of safety.