1 Introduction

In recent years, demand in large structures which have several basement floors was increased. Generally, such structures require deep excavations, which their stabilization is a challenging issue in geotechnical engineering problems. One of the most common methods for stabilizing such excavations is soil nailing. High construction speed, simultaneous excavation phases, easy access to drilling machines, and appropriate costs are the main reasons for the popularity of this method. In this method, it is necessary to obtain an optimal pattern of the nails, which requires an overall system stability analysis.

Most available methods for the analysis of the soil nail walls are based on the limit equilibrium method. In the framework of this method, Mittal (Mittal 2006) proposed that increasing the internal friction angle and cohesion of the soil results in improving the stability of the soil nail walls. Also, Meenal et al. (Meenal et al. 2009) proposed a method for quasi-static analysis of oblique nail walls.

Using the limit equilibrium method for stability analysis of geotechnical structures may lead to misleading results since it is unclear whether the obtained results correspond precisely to the failure state or are slightly different (smaller or larger) from the exact failure load. This limitation will be eliminated by using the limit analysis method. The safety factor obtained by using this method is the upper/lower bound of the exact safety factor. There exist some essential studies based on this method in the literature (Meenal et al. 2009; Chen and Liu 1990; Michalowski 1998; Giri and Sengupta 2009; He et al. 2012; Yang et al. 2020).

The experimental method was also used by researchers for analyzing soil nail walls. Zhou et al. (Zhou et al. 2009) conducted some actual scale tests for investigating the stability of soil nail walls. Moradi et al. (Moradi et al. 2020) performed four centrifuge tests to investigate the effect of convex corners on the deformation of soil-nailed walls. They evaluated the wall behavior according to the layout of nails. Also, the results of several pullout tests were used by Sharma et al. (Sharma et al. 2020) to investigate the behavior of helical nails in dry cohesionless soils under static and seismic conditions. They proposed a pullout capacity equation which can be used for stability analysis of helical soil-nailed walls. Jaya and Joy (Jaya and Joy 2013) and Rawat et al. (Rawat et al. 2013) used both laboratory tests and numerical methods for determining the safety factor of soil nail walls. In addition to the mentioned method, the application of numerical methods for stability analysis of soil nail walls becomes very common in recent years. Some of the essential works on this basis can be found in the literature (Giri and Sengupta 2010; Zhou and Yin 2008; Clarke et al. 2013; Babu et al. 2007).

Due to the difficulties in preparing laboratory models of soil nail walls, as well as the high sensitivity of the numerical methods to the input parameters, analytical methods generally provide a simple framework for determining the safety factor of soil nail walls. The importance and simplicity of such methods are crucial in the early stages of engineering project studies.

In the present paper, using the upper bound method of limit analysis, an equation for the safety factor of soil nail walls was developed, which can be used in both static and seismic conditions. The Mohr–Coulomb failure criterion was used for the soil, and the effects of the surcharge and inclined ground surface at the top of the wall were incorporated into the upper bound formulation.

2 The Basics of the Upper Bound Method of Limit Analysis

Dealing with the stability problems requires solving the stress equilibrium equations along with satisfying the compatibility conditions, simultaneously, which is too difficult even in simple problems. In the upper bound method, this procedure can be performed more simply by ignoring the stress equilibrium conditions. According to the upper bound method, in a kinematically admissible failure mechanism, the load obtained by equating the external work and the internal dissipated energy is not less than the actual failure load. Therefore:

$$ {\int}_V{\sigma}_{ij}{\dot{\varepsilon}}_{ij} dV\ge {\int}_s{T}_i{v}_i ds+{\int}_V{X}_i{v}_i dV $$
(1)

where σij and \( {\dot{\varepsilon}}_{ij} \) are the stress and strain tensors in any admissible velocity field, Ti is any surface traction applied to the failure mechanism, s is the admissible velocity field, Xi is the body force, V is the volume of the failure mechanism, and vi is the velocity along each discontinuity line. The upper bound limit analysis involves the solution of Eq. 1, which results in finding the optimal solution among the numerous acceptable answers.

3 Determination of the Safety Factor Using the Upper Bound Method

3.1 Selection of the Failure Mechanism

Two types of failure mechanisms were commonly used in the stability analysis of excavations, which include the multi-wedge translational failure mechanism and the rotational failure mechanism. The existing researches show that the rotational failure mechanism results in a more accurate safety factor (Zhou et al. 2009; Jaya and Joy 2013; Rawat et al. 2013; Giri and Sengupta 2010; Zhou and Yin 2008; Clarke et al. 2013; Babu et al. 2007). Therefore, it was used in this paper for obtaining the equation of the safety factor for soil nail walls subjected to static and seismic loadings, as shown in Fig. 1. This mechanism is capable of considering the inclination of the ground surface. Assuming that the failure surface is perpendicular to the ground surface, it can be proved that θ0 is equal to ϕ (Giri and Sengupta 2009).

Fig. 1
figure 1

The rotational failure mechanism considered in this study

Full size image

The equation of the logarithmic spiral failure line is as follows:

$$ {r}_h={r}_0{e}^{\left({\theta}_h-{\theta}_0\right)\tan \phi } $$
(2)

where r0 and rθ are the radiuses corresponding to the angles θ0 and θh, respectively, and ϕ is the soil internal friction angle. Based on the geometrical relations, the value of r0 can be obtained as follows (Mittal 2006):

$$ {r}_0=\frac{H\sin \lambda \cot \beta -H\cos \lambda }{e^{\left({\theta}_i-{\theta}_0\right)\tan \phi}\cos \lambda \sin {\theta}_h+{e}^{\left({\theta}_h-{\theta}_0\right)\tan \phi}\sin \lambda \cos {\theta}_h-\sin {\theta}_0\cos \lambda \cos {\theta}_0} $$
(3)

3.2 Calculation of the External Work

3.2.1 The External Work Due to the Weight of the Soil Mass

Based on Fig. 2, the general form of the external work performed by the weight of the moving soil mass, i.e., part abc, can be obtained as follows:

$$ W= M\omega $$
(4)
Fig. 2
figure 2

The moving soil mass

Full size image

where M is the moment due to the weight of the moving soil mass, and ω is the angular velocity. It is difficult to calculate the external work performed by the weight of the abc part directly. Therefore, it was calculated by using the principle of superposition as follows:

$$ {W}_{abc}={W}_{oab}-{W}_{ocb}-{W}_{oca} $$
(5)

where Wabc, Woab, Wocb, and Woca are the external works performed by the weight of the parts abc, oab, ocb, and oca, respectively.

Also, the effect of the earthquake on the soil mass was considered horizontal and vertical body forces applied to the center of gravity of the moving soil mass, which are equal to Fv = kvW and Fh = khW, respectively. kv and kh are the earthquake vertical and horizontal accelerations, respectively, and W is the weight of the moving soil mass (W = Wabc). Therefore, the general forms of the vertical and horizontal external works due to the soil mass are as follows, respectively:

$$ {W}_v=\left(1-{k}_v\right)\omega \gamma \kern0.1em {r}_0^3\left({f}_1-{f}_2-{f}_3\right) $$
(6)
$$ {W}_h={k}_h\omega \gamma \kern0.1em {r}_0^3\left({f}_4-{f}_5-{f}_6\right) $$
(7)

where the factors f1 to f6 are as follows:

$$ {f}_1=\frac{\left(3\tan \phi \cos {\theta}_h+\sin {\theta}_h\right)\kern0.1em {e}^{3\left({\theta}_h-{\theta}_0\right)\tan \phi }-2\sin {\theta}_0}{3\left(1+9{\tan}^2\phi \right)} $$
(8)
$$ {f}_2=\frac{1}{6}\cdot \frac{L}{r_0}\left(2\cos {\theta}_0-\frac{L}{r_0}\cos \lambda \right)\sin \left({\theta}_0+\lambda \right) $$
(9)
$$ {f}_3=\frac{1}{6}{e}^{\left({\theta}_h-{\theta}_0\right)\tan \phi}\left[\sin \left({\theta}_h-{\theta}_0\right)-\frac{L}{r_0}\sin \left({\theta}_h+\lambda \right)\right]\cdot \left[\cos {\theta}_0-\frac{L}{r_0}\cos \lambda +\cos \left({\theta}_h+\lambda \right){e}^{\left({\theta}_h-{\theta}_0\right)\tan \phi}\right] $$
(10)
$$ {f}_4=\frac{\left(3\tan \phi \sin {\theta}_h-\cos {\theta}_h\right){e}^{3\left({\theta}_h-{\theta}_0\right)\tan \phi }-3\tan \phi \sin {\theta}_0+\cos {\theta}_0}{3\left(1+9{\tan}^2\phi \right)} $$
(11)
$$ {f}_5=\frac{1}{3}\cdot \frac{L}{r_0}{\sin}^2\left({\theta}_0+\lambda \right) $$
(12)
$$ {f}_6=\frac{1}{6}{e}^{\left({\theta}_h-{\theta}_0\right)\tan \phi}\left[\sin \left({\theta}_h-{\theta}_0\right)-\frac{L}{r_0}\sin \left({\theta}_h+\lambda \right)\right]\cdot \left[\sin {\theta}_0+{e}^{\left({\theta}_h-{\theta}_0\right)\tan \phi}\sin {\theta}_h\right] $$
(13)

in which L is shown in Fig. 1, and its value can be obtained as follows:

$$ \frac{L}{r_0}=\frac{\sin \left({\theta}_h-{\theta}_0\right)}{\sin {\theta}_h}-\frac{\sin \left({\theta}_h+\beta \right)}{\sin {\theta}_h\sin \beta}\left[{e}^{\left({\theta}_h-{\theta}_0\right)\tan \phi}\sin {\theta}_h-\sin {\theta}_0\right] $$
(14)

3.2.2 The External Work Due to the Surcharge

As shown in Fig. 1, the surcharge q was applied to a length equal to L to the top of the wall. The external work due to the surcharge comprises the work due to itself and the work due to the effect of the earthquake on it. Therefore, the total vertical and horizontal works due to the surcharge are as follows, respectively:

$$ {W}_{qv}=\omega \kern0.1em qL\cos \lambda \left(1-{k}_v\right)\left({r}_0\cos {\theta}_0-\frac{L}{2}\cos \lambda \right) $$
(15)
$$ {W}_{qh}=\omega \kern0.1em qL\sin \lambda {k}_h\left({r}_0\cos {\theta}_0-\frac{L}{2}\cos \lambda \right) $$
(16)

3.2.3 The Total External Work

Summing the external works performed by different forces, the total external work in the whole mechanism can be calculated as follows:

$$ W={W}_v+{W}_h+{W}_{qv}+{W}_{qh} $$
(17)

3.3 Calculation of the Internal Energy Dissipation

3.3.1 The Energy Dissipation Due to the Soil Cohesion

Part of the energy dissipation in the failure mechanism is due to the soil cohesion which occurred along the velocity discontinuity lines and can be calculated as the summation of the multiplication of the soil cohesion by each discontinuity line length and by the velocity component along the discontinuity line. Therefore, the total energy dissipation along all velocity discontinuity lines is equal to:

$$ {D}_c={\int}_{\theta_0}^{\theta_h} cr\omega \cos \phi \frac{rd\theta}{\cos \phi }=\frac{cr_0^2\omega }{2\tan \phi}\left[{e}^{2\left({\theta}_h-{\theta}_0\right)\tan \phi }-1\right] $$
(18)

3.3.2 The Energy Dissipation Due to the Nails

The moment produced by the nail forces about the center of rotation of the failure surface, i.e., point O in Fig. 1, induces an energy dissipation that should be added to the total energy dissipation along the velocity discontinuity lines. According to Fig. 3, having each nail force and its vertical distance to the center of rotation, the moment produced by each nail force is equal to:

$$ M={T}_i{r}_i\sin \left({\theta}_i-\alpha \right) $$
(19)
Fig. 3
figure 3

The force of the nail and its arm to the rotation center

Full size image

where Ti is the nails force, ri is the length of the line extended from the center of rotation (point O) to the intersection point of each nail and the failure surface, θi is the angle between the line ri and the horizontal direction, and α is the angle of the nails with respect to the horizontal direction. Therefore, by obtaining ri from Eq. 2, the energy dissipation due to all nails was calculated as follows:

$$ {D}_n={r}_0\omega \sum \limits_{i=1}^n{T}_i{e}^{\left({\theta}_i-{\theta}_0\right)\tan \phi}\sin \left({\theta}_i-\alpha \right) $$
(20)

where n is the number of the nail layers at the wall height.

According to Fig. 4, the angle θi is a function of the vertical distance between the ith nail and the top of the wall, Zi. Therefore:

$$ {Z}_i={r}_i\sin {\theta}_i-{r}_0\sin {\theta}_0-\overline{ef}\sin \alpha $$
(21)
Fig. 4
figure 4

The nail length outside of the failure zone

Full size image

where \( e\overline{f} \) is the nail length in the failed soil volume and can be obtained as follows:

$$ \overline{ef}=\frac{r_i\cos {\theta}_i-{r}_h\cos {\theta}_h-\left(H-{Z}_i\right)\cot \beta }{\cos \alpha } $$
(22)

The nail force depends on the shear strength between the soil and the nail length outside the failure line, li, which can be calculated by subtracting Eq. 22 from the total length of each nail. Therefore, the nail force can be calculated as follows:

$$ {T}_i=\frac{q_u\pi {D}_{DH}{l}_i}{S_H} $$
(23)

where qu is the bond strength between the nails and the surrounding soil, DDH is the drillhole diameter, and SH is the horizontal spacing between the nails.

3.3.3 The Total Energy Dissipation

The total energy dissipation in the whole mechanism was obtained as follows:

$$ D={D}_c+{D}_n $$
(24)

3.4 The Factor of Safety

The upper bound method is based on the principle of virtual work, which states that the work of external forces applied to a failure mechanism is equal to the internal energy dissipated in the mechanism, i.e., W = D. The general form of the factor of safety, FS, is equal to the ratio of the resistant term, i.e., D, to the active term, i.e., W. Therefore, by replacing the relevant equations into the general form of the equation of the factor of safety, FS can be obtained as follows:

$$ {\displaystyle \begin{array}{c} FS=\left\{\frac{c{r}_0^2\omega }{2\tan \varphi}\left[{e}^{2\left({\theta}_h-{\theta}_0\right)\tan \varphi }-1\right]+{r}_0\omega \sum \limits_{i=1}^n{T}_i{e}^{\left({\theta}_i-{\theta}_0\right)\tan \varphi}\sin \left({\theta}_i-\alpha \right)\right\}/\left\{\left(1-{k}_v\right)\omega \gamma \kern0.1em {r}_0^3\left({f}_1-{f}_2-{f}_3\right)\right.\\ {}+{k}_h\omega \gamma \kern0.1em {r}_0^3\left({f}_4-{f}_5-{f}_6\right)+\omega \kern0.1em qL\cos \lambda \left(1-{k}_v\right)\left({r}_0\cos {\theta}_0-\frac{L}{2}\cos \lambda \right)\\ {}+\left.\omega \kern0.1em qL\sin \lambda {k}_h\left({r}_0\cos {\theta}_0-\frac{L}{2}\cos \lambda \right)\right\}\end{array}} $$
(25)

3.5 Optimization

The considered failure mechanism has two sets of known and unknown parameters. The known parameters include:

  1. 1.

    The soil parameters, including the friction angle (ϕ), cohesion (c), and the unit weight (γ).

  2. 2.

    The geometrical parameters of the nailed wall including the height (H), the angle of the wall to the horizontal direction (β), and the ground surface angle with respect to the horizon (λ).

  3. 3.

    The nail specifications including the length (Ln), the angle to the horizontal direction (α), the drillhole diameter (DDH), the horizontal and vertical spacings between the nails (SH and SV), the bond strength (qu), and the parameter Zi.

The unknown parameters should be determined using an optimization technique in a way that the best (lowest) possible value of the factor of safety can be achieved. The smallest factor of safety corresponds to the best failure surface that its location depends on θ0, θi, and θh. As already stated, θ0 is equal to the soil internal friction angle, which is a known parameter. Therefore, the unknowns of the problem are θi and θh, which should be optimized in order to obtain the least possible value for the safety factor. In the present study, the optimization was performed using the genetic algorithm provided in the MATLAB program. For the optimized mechanism to be kinematically admissible, the following constraints were taken into account:

$$ {\theta}_0<{\theta}_h<\frac{\pi }{2}+\phi $$
(26)
$$ {\theta}_0<{\theta}_1<\dots <{\theta}_h $$
(27)

Also, considering that the angle θi depends on the distance between the nail head and the ground surface (Zi), Eq. 21 was also considered one of the constraints of the problem.

4 Verification of the Results

4.1 Static Analysis

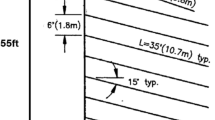
The factor of safety obtained from the formulation developed in the present paper was compared with the results of back-predicting the full-scale test conducted on a soil nail wall in 1986 for the French national research project, Clouterre (Plumelle et al. 1990). The cross-section of this wall is shown in Fig. 5. The angle between the nails and the horizontal direction was considered to be equal to 15°, and the horizontal and vertical spacing of the nails was considered equal to 1.15 and 1 m, respectively. The first and last rows of the nails are 16 mm in diameter and 6 m in length, while the rest of the nails are 40 mm in diameter and 8 m in length. Also, the cohesion, the internal friction angle, and the unit weight of the soil behind the wall were considered equal to 3 kPa, 38°, and 20 kN/m3, respectively.

Fig. 5
figure 5

Cross-section of the soil nail wall in the Clouterre project (Plumelle et al. 1990)

Full size image

Stability analysis of this wall in the static condition was performed using the Morgenstern–Price limit equilibrium method, which resulted in a factor of safety equal to 1.413 (Plumelle et al. 1990). The upper bound formulation presented in the current paper was also used for obtaining the safety factor, which resulted in FS = 1.418. Therefore, these two methods have good consistency with each other.

4.2 Seismic Analysis

Ghosh and Paul (Ghosh and Paul 2016) considered seismic analysis of soil nail walls under horizontal earthquake load. The specification of their models is H = 10 m, λ = 0°, q = 50 kPa, Ln = 7 m, SH = SV = 70 cm, c = 5 kPa, and kv = 0. Considering different values of the soil friction angle and various amounts of the horizontal earthquake accelerations, Table 1 presents the safety factor obtained by Ghosh and Paul (Ghosh and Paul 2016) and the method presented in the current paper. Good conformity between the results of these two methods can be seen.

Table 1 Comparison between the FS obtained from the present study and Ghosh and Paul (Ghosh and Paul 2016) method
Full size table

5 Sensitivity Analyses

To investigate the effect of different parameters on the safety factor of soil nail walls, a general sketch of the soil nail wall, as shown in Fig. 6, was considered. Three different magnitudes of H, including 5 m, 10 m, and 15 m, were taken into account. Extensive sensitivity analyses were performed, considering the parameters presented in Table 2. For investigating the effect of each parameter on the safety factor, a wide range was considered for most of the parameters, while a constant magnitude was considered for the rest of the parameters.

Fig. 6
figure 6

Examined model of the nailing trench

Full size image
Table 2 The parameters considered in the sensitivity analyses
Full size table

5.1 The Effect of Soil Internal Friction Angle

Figure 7 shows the variation of FS versus ϕ. As can be seen, FS increases by increasing the internal friction angle. Also, the rate of increment of the FS was increased for large values of ϕ. Increasing the horizontal acceleration of the earthquake (kh) and increasing the trench height (H) also decrease the safety factor.

Fig. 7
figure 7

Variation of FS versus ϕ, considering a H = 5 m, b H = 10 m, and c H = 15 m

Full size image

5.2 The Effect of Soil Cohesion

Figure 8 shows the variation of FS versus c. By increasing the cohesion from 5 to 45 kPa, the maximum increase in FS is equal to 22%, 19%, and 18% for the walls with H = 5 m, 10 m, and 15 m, respectively. Therefore, it can be concluded that increasing the height of the wall results in reducing the effect of cohesion on the safety factor. For each magnitude of c, increasing the earthquake horizontal acceleration results in reducing the safety factor.

Fig. 8
figure 8

Variation of FS versus c, considering a H = 5 m, b H = 10 m, and c H = 15 m

Full size image

5.3 The Effect of Surcharge

Given that many excavations are carried out next to the buildings or any other construction activities, it is essential to investigate the effect of surcharge loads on the safety factor of the nailed wall. Figure 9 shows the variation of FS versus q. According to the results, for all considered values of kh, increasing the surcharge results in decreasing the safety factor. As the surcharge increases, the rate of reduction of the safety factor decreases.

Fig. 9
figure 9

Variation of FS versus q, considering a H = 5 m, b H = 10 m, and c H = 15 m

Full size image

5.4 The Effect of Ground Surface Inclination

Figure 10 shows the variation of FS versus λ. The safety factor decreases with increasing the inclination of the ground surface. By increasing λ from zero to 35°, a maximum of 31%, 54%, and 29% reduction of the safety factor was observed for the walls with H = 5 m, 10 m, and 15 m, respectively.

Fig. 10
figure 10

Variation of FS versus λ, considering a H = 5 m, b H = 10 m, and c H = 15 m

Full size image

5.5 The Effect of Nail Length

Figure 11 shows the variation of FS versus Ln. The results show that the length of the nails has a considerable effect on the safety factor. In the case of H = 5 m, the safety factor of the case with Ln = 6 m is 2.64 times the case with Ln = 2 m. Also, for the case of H = 10 m, by increasing the nail length from 5 to 12 m, the maximum increase in the safety factor is about 94%. For a 15 m tall wall, by increasing the nail length from 10 to 20 m, the maximum increase in the safety factor is about 134%.

Fig. 11
figure 11

Variation of FS versus Ln, considering a H = 5 m, b H = 10 m, and c H = 15 m

Full size image

5.6 The Effect of Drillhole Diameter

Figure 12 shows the variation of FS versus DDH. As can be seen, for all considered values of kh, increasing the drillhole diameter has a significant effect on the safety factor, which is due to the increase in the resistance force produced by the bond strength. In the 5 m, 10 m, and 15 m tall walls, by increasing the drillhole diameter from 5 to 14 cm, the maximum increase in the safety factor is approximately equal to 204%, 71%, and 157%, respectively.

Fig. 12
figure 12

Variation of FS versus DDH, considering a H = 5 m, b H = 10 m, and c H = 15 m

Full size image

5.7 The Effect of Nail Inclination

Figure 13 shows the variation of FS versus α. It is clear that for all considered values of kh, the inclination of the nails to the horizontal direction has a small effect on the factor of safety. For the walls with H = 5 m, 10 m, and 15 m, the maximum reduction of the FS is equal to 9%, 12%, and 16%, respectively.

Fig. 13
figure 13

Variation of FS versus α, considering a H = 5 m, b H = 10 m, and c H = 15 m

Full size image

5.8 The Effect of Nail Horizontal Spacing

Figure 14 shows the effect of nail horizontal spacing on FS. As can be seen, by increasing the SH, the safety factor decreases. For the SH values approximately smaller than 1.5 m, the rate of reduction is more sensible than the rate of reduction of FS in the case of SH > 1.5 m. For the walls with H = 5 m, 10 m, and 15 m, by increasing SH from 0.5 to 2 m, the FS decreased about 45%, 43%, and 60%, respectively.

Fig. 14
figure 14

Variation of FS versus SH, considering a H = 5 m, b H = 10 m, and c H = 15 m

Full size image

5.9 The Effect of Nail Vertical Spacing

Figure 15 illustrates the variation of FS with SV. For all considered values of kh, FS decreases with increasing SV with an approximately linear rate. By increasing the nail vertical spacing from 1 to 2 m, the safety factor decreased about 54%, 38%, and 56% for the wall heights equal to H = 5 m, 10 m, and 15 m, respectively.

Fig. 15
figure 15

Variation of FS versus SV, considering a H = 5 m, b H = 10 m, and c H = 15 m

Full size image

5.10 The Effect of Nail Horizontal to Vertical Spacing Ratio

Assuming kh = 0.1, Fig. 16 illustrates the variation of FS with SH/SV ratio. It is clear that increasing the SH/SV ratio results in decreasing FS, but the rate of this reduction decreases with increasing the SH/SV ratio. For SH/SV smaller than 1.5, the rate of reduction of FS is more sensible than the cases of SH/SV > 1.5. For the walls with H = 5 m, 10 m, and 15 m, increasing SH/SV from 0.5 to 2 results in decreasing FS about 28%, 30%, and 37%, respectively.

Fig. 16
figure 16

Variation of FS versus SH/SV ratio

Full size image

5.11 The Effect of Earthquake Vertical Acceleration

The effect of earthquake vertical acceleration (kv) on the stability of soil nail walls was not investigated sufficiently by previous researchers. The upper bound formulation proposed in the present study has the capability of considering the earthquake vertical acceleration. As shown in Fig. 17, increasing kv results in decreasing FS, but its effect is less than the effect of the horizontal earthquake acceleration. In the walls with H = 5 m, 10 m, and 15 m, increasing kv from zero to 0.2 leads to decreasing the safety factor by 22%, 13%, and 15%, respectively.

Fig. 17
figure 17

Variation of FS versus kv, considering a H = 5 m, b H = 10 m, and c H = 15 m

Full size image

6 Conclusions

The safety factor of soil nail walls subjected to static and seismic loadings was studied. The main conclusions of the present paper are as follows:

  • Increasing the parameters like the soil cohesion, internal friction angle, the nail length, and the drillhole diameter results in increasing the factor of safety.

  • Increasing the parameters like the surcharge, the inclination of the nails and the ground surface, and the horizontal and vertical spacings of the nails results in decreasing the factor of safety.

  • Increasing the horizontal and vertical accelerations of earthquake results in decreasing the factor of safety.

  • The obtained results show that the effect of the horizontal acceleration of the earthquake on reducing the factor of safety is more paramount than the effect of the vertical acceleration of the earthquake.