1 Introduction

Distributed Generation (DG) systems are small-to-medium size (a few kilowatts to 50 MW) electricity generating units installed near the load centres (Prakash and Khatod 2016). The increased interest in integrating DGs across the distribution network is due to fossil fuel depletion, environmental concerns, promising DG technologies, cost reduction in transmission, reduced risk on investment and less installation time (Yammani et al. 2016; Dos Santos et al. 2022). Although the primary purpose of DG installation is power injection, its accommodation in the distribution network yields multiple benefits like reduced network power loss, enhanced voltage profile and stability, increased loadability, and decreased operational and investment costs (Yang et al. 2021). Notwithstanding the benefits, non-optimal DG accommodation attracts counterproductive results (Meena et al. 2017; Jha et al. 2020). Hence it is imperative to optimally locate and size the DG units in the distribution system.

DG accommodation problem is a complex multiobjective optimization problem involving multiple contravening objectives. It is customary to solve this problem by considering various technical objectives like reduction of network power loss (Singh et al. 2009; Hung and Mithulananthan 2013; Moradi et al. 2014; Gampa and Das 2015; Meena et al. 2018; Kashyap et al. 2022), minimization of node voltage deviation (Singh et al. 2009, 2020; Gampa and Das 2015; Leghari et al. 2021) and enhancement of voltage stability (Murty and Kumar 2015; Meena et al. 2018; Balu and Mukherjee 2020). Some studies (Shaaban et al. 2013; Gampa and Das 2015; Dixit et al. 2017; Tanwar and Khatod 2017; Arulraj and Kumarappan 2019; Kumar et al. 2020) also considered economic objectives for solving the DG accommodation problem. It is worth noting that DG optimal accommodation aiming only to improve the technical objectives may attract dearer DG investment costs. On the flip side, catering for the economic objectives alone may hamper the demanding technical performance parameters of the distribution network. Few researchers have addressed this issue by including both technical and economic objectives in the objective function for solving the DG accommodation problem. A cost factor index (Gampa and Das 2015) is taken as one of the minimization objectives to contain the DG investment cost. In (Dixit et al. 2017), the DG accommodation problem is addressed by considering DG investment cost and operation & maintenance costs. A cost index is framed in (Tanwar and Khatod 2017; Kumar et al. 2020), and a minimization index is developed to meet technical objectives. Recently in (Hassan et al. 2022) the installation cost of DG is considered as one of the objective for DG accommodation.

The studies addressing the economic objectives either consider the economic objectives alone (Shaaban et al. 2013; Dixit et al. 2017; Arulraj and Kumarappan 2019) or club them with some technical objectives (Gampa and Das 2015; Tanwar and Khatod 2017; Kumar et al. 2020; Hassan et al. 2022) to result in a single objective optimization function by assigning preference weights using the weighted-sum approach. The best solution obtained through the weighted-sum method depends on the selected preference weights. For a particular solution, these weights are fixed, and the solution may not be feasible if the decision-maker has a different preference. Further, inappropriate assignment of preference weights may result in a sub-optimal solution. Pareto optimality based multiobjective optimization enables simultaneous optimization of conflicting objectives (Nartu et al. 2019). This approach generates a set of solutions, and the decision-maker is free to select appropriate solution based on his preference. Hence, Pareto optimality based multiobjective optimization is a more promising approach to address the complex DG accommodation problem.

This study adopts a posteriori multiobjective optimization approach, and the technical and economic objectives are simultaneously optimized using Pareto optimality concept. Previous works that used the idea of Pareto optimality for the DG accommodation problem relied upon single objective optimizers. In (Nagaballi and Kale 2020), the authors suggested the merit of improved raven roosting optimization (IRRO) algorithm for simultaneously optimizing multiple objectives. A butterfly optimizer (BO) is used in (Thunuguntla and Injeti 2020) for optimal allocation of DGs for maximization of loadability and minimization of active power loss of the system. A monarch butterfly optimization (MBO) is applied (Singh et al. 2020) to cater multiple objectives for improving the distribution network performance. In (Ali et al. 2021), the authors highlighted the merit of an improved decomposition based evolutionary algorithm (I-DBEA) in solving the DG accommodation problem. The major drawback of using a single objective optimizer for generating the Pareto optimal solutions is the requirement of multiple runs to generate the Pareto optimal solutions.

To facilitate an effective a posteriori approach, the optimization algorithm selected should be capable of generating the Pareto optimal solutions in a single run (Rao et al. 2021). This requirement demands the use of a multiobjective optimizer which can handle multiple objectives simultaneously. Literature shows that the most popular multi-objective optimizer is non-dominated sorting genetic algorithm II (NSGA – II) (Deb et al. 2002). Although it is regarded as one of the strongest metaheuristic methods for solving multi-objective problems (Jafari and Rezvani 2021), several studies (Dilip et al. 2018; Kebriyaii et al. 2021; Li et al. 2022) report that multiobjective grey wolf optimizer (MOGWO) (Mirjalili et al. 2016) performs better than NSGA– II. Further in (Mirjalili et al. 2018) it can be seen that multiobjective grasshopper optimizer algorithm (MOGOA) gave better results compared with NSGA – II for multiple test suites. Hence, in this paper, MOGWO and MOGOA algorithms are employed for solving the multiobjective problem.

Optimizing the multiobjective DG accommodation problem using MOGWO and MOGOA yields non-dominated Pareto optimal solutions. In a posteriori approach, after generating these solutions, the task is to determine the best feasible solution. To find the best feasible solution, a robust multicriteria decision making (MCDM) method (Amiri et al. 2020), the technique for order of preference by similarity to ideal solution (TOPSIS) (Hwang et al. 1993), is employed. The fundamental idea of TOPSIS is rather straightforward. It originates from the concept of a displaced ideal point from which the best feasible solution has the shortest distance. It is a highly regarded, adopted and applied MCDM method due to its simplicity, ease of applicability and sound mathematical foundation (Chakraborty 2022). It has been extensively used in different fields such as energy (Yang and Deuse 2012), supply chain management (Tirkolaee et al. 2020, 2021), material selection (Chede et al. 2021) and manufacturing decision making (Parkan and Wu 1999). The best feasible solution selected through TOPSIS is subject to the preference given by the decision-maker for the objectives. Hence, multiple scenarios are created based on the decision-makers predisposition to the objectives of the study and the corresponding best feasible solutions are presented. The critical contributions of the paper are:

  1. (1)

    The traditional DG accommodation problem is extended by simultaneously optimizing conflicting technical and economic objectives using a posteriori approach.

  2. (2)

    The technical objectives include minimising reactive power loss, real power loss, voltage deviation and maximization of voltage stability index. The economic objectives include DG investment cost and DG operation and maintenance cost.

  3. (3)

    Maiden application of MOGWO and MOGOA to solve the multiobjective DG accommodation problem considering technical and economic objectives.

  4. (4)

    MCDM, through the TOPSIS approach, is employed for tracing the best feasible solution from the Pareto optimal solutions. Multiple solutions are presented based on the preference given to the objectives by the decision maker.

The remainder of the paper is organised as follows: The problem formulation is discussed in Sect. 2. The concept of a posteriori multiobjective optimization, Pareto optimality and TOPSIS are elaborated in Sect. 3. The multiobjective optimization algorithms are discussed in Sect. 4. The results and discussion are presented in Sect. 5. The conclusion is presented in Sect. 6.

2 Problem formulation

In this section, the technical and economic objectives that constitute the multiobjective optimization problem are formulated.

2.1 Technical objective function formulation

2.1.1 Minimization of real power loss and reactive power loss

In traditional centralized power systems, distribution networks contribute to substantial power loss. Optimal accommodation of DGs contributes significantly to the reduction of real power loss (\({P}_{T,loss})\) and reactive power loss (\({Q}_{T,loss})\). The \({P}_{T,loss}\) and \({Q}_{T,loss}\) of the whole network considered as minimization objectives can be expressed as given in Eqs. 1 and 3 (Balu and Mukherjee 2021). For a distribution network with \({n}_{b}\) branches, the expressions for branch real power loss \({(P}_{ij,loss}\)) and reactive power loss (\({Q}_{ij,loss})\) of the branch connecting buses \(i\) and \(j\) are shown in equations 2 and 4.

$${P}_{T,loss}= \sum_{i=1}^{{n}_{b}}{P}_{ij,loss}$$
(1)
$${P}_{ij,loss}= {R}_{ij}\times \left(\frac{{P}_{i}^{2}+{Q}_{i}^{2}}{{|{V}_{i}|}^{2}}\right)$$
(2)
$${Q}_{T,loss}= \sum_{i=1}^{{n}_{b}}{Q}_{ij,loss}$$
(3)
$${Q}_{ij,loss}= {X}_{ij}\times \left(\frac{{P}_{i}^{2}+{Q}_{i}^{2}}{{|{V}_{i}|}^{2}}\right)$$
(4)

where \({P}_{i}\) and \({Q}_{i}\) are real and reactive power flows from bus \(i,\) respectively, \({R}_{ij}\) and \({X}_{ij}\) are the resistance and reactance of branch connecting buses \(i\) and \(j,\) respectively, \({V}_{i}\) is the voltage at bus \(i\).

2.1.2 Minimization of voltage deviation

The voltage deviation of the nodes of the network is an indicator of the voltage quality of the distribution network. Therefore the utilities are concerned with maintaining the node voltage within permissible limits. The node voltage deviation of the \(i\)th bus in a \(n\) bus network is the difference between the reference voltage (\({V}_{ref}\)) and the \(i\)th bus voltage (\({V}_{i}\)). Total node voltage deviation (\(TVD\)) of the distribution network can be expressed as (Nagaballi and Kale 2020):

$$TVD= \sum_{i=1}^{n}({|{V}_{ref}-{V}_{i}|}^{2})$$
(5)

2.1.3 Maximization of the voltage stability index

A stability index (\(SI)\) is suggested in (Murty and Kumar 2015) to ascertain the probability of voltage collapse at a particular node. The node with the lowest value of \(SI\) is most vulnerable for voltage collapse. The \(SI\) of the node \(j\) in a \(n\) bus network is given in Eq. 6 and a maximization objective, total voltage stability index (\(TVSI)\) for the network is framed as shown in Eq. 7.

$${SI}_{j}= {|{V}_{i}|}^{4}-4{\left[{P}_{i}{X}_{ij}- {Q}_{i}{R}_{ij}\right]}^{2}-4\left[{P}_{i}{R}_{ij}+ {Q}_{i}{X}_{ij}\right]{|{V}_{i}|}^{2}$$
(6)
$$TVSI= \sum_{j=1}^{n}{SI}_{j}$$
(7)

2.1.4 Technical objective function

The technical objectives, viz. \({P}_{loss}\), \({Q}_{loss}\), \(TVD\) and \(TVSI\) are combined using weight factors to form a technical objective function (\(TOF),\) as shown in Eq. 8, giving equal priority to all the objectives. \({\sigma }_{i}\) being the weight factor of \({i}^{th}\) objective, the minimization objective \(TOF\) is treated as one of the two objectives of the multiobjective optimization problem.

$$TOF=\left({\sigma }_{1}* {P}_{T,loss}\right)+\left({\sigma }_{2}*{Q}_{T,loss}\right)+\left({\sigma }_{3}* TVD\right)+\left({\sigma }_{4}* \frac{1}{TVSI}\right)$$
(8)

where \(\sum_{i=1}^{4}{\sigma }_{i}=1.0\) and \({\sigma }_{i} \in [\mathrm{0,1}]\)

2.1.5 Constraints

The below-listed constraints (9) – (11) are related to the node voltage limits, real power balance and sizing limits of DG (Bagheri et al. 2020), respectively. Where \({V}_{min}\) and \({V}_{max}\) represent the minimum and maximum permissible node voltages.\({V}_{j}\) is the volatge of bus \(j\). \({P}_{s}\) is the real power supplied by the source station. \({P}_{DGT}\) is the total real power supplied by the DGs. \({P}_{D}\) is the real power demand on the network. \({P}_{DG}^{i}\) is the rating of \(i\) th DG. \({P}_{DG, min}^{i}\) and \({P}_{DG, max}^{i}\) are the minimum and maximum size limits of \(i\) th DG. \({n}_{g}\) is the number of optimally allocated DGs in the network.

The following constraints are imposed on the \(TOF\) presented in Eq. 8

$$|{V}_{min}| \le \left|{V}_{j}\right|\le |{V}_{max}|$$
(9)
$${P}_{s}+{P}_{DGT}= {P}_{D}+{P}_{T,loss}$$
(10)
$$P_{DG, min}^{i} \le P_{DG}^{i} \le P_{DG, max}^{i} \,\,\,i = 1,2 \ldots n_{g}$$
(11)

2.2 Economic objective function formulation

The second objective for multiobjective optimization is DG cost minimization. For this purpose, an economic objective function (\(EOF)\) is formulated. The total installation cost of DG is a function of the type, size and number of DG units to be installed in the distribution system. The \(EOF\) framed (Nagaballi and Kale 2020) involves the DG investment cost (\({DG}_{cost, inv}\)) and the DG maintenance and operation cost (\({DG}_{cost, m\&o}\)). \({DG}_{rated}^{i}\) being the rated capacity (MW) of optimally allocated DG at \({i}^{th}\) bus and \({n}_{g}\) being the number of optimally allocated DGs in the network, the \({DG}_{cost, inv}\) and \({DG}_{cost, m\&o}\) expressions for a palnning period of \({n}_{yr}\) in years are shown in the below equations.

$${DG}_{cost, inv}= \sum_{i=1}^{{n}_{g}}({DG}_{rated}^{i} \times {C}_{{inv}_{i}})$$
(12)
$${DG}_{cost, m\&o}= \sum_{i=1}^{{n}_{g}}{(P}_{DG}^{i} \times {C}_{m\&o} \times T) \times \sum_{k=1}^{{n}_{yr}}{\left(\frac{1+Infr}{1+Intr}\right)}^{k}$$
(13)

where \({C}_{{inv}_{i}}\) denotes the \({i}^{th}\) bus DG investment cost (\(\$/\) MW), \({P}_{DG}^{i}\) represents the DG generated active power (MW) at \({i}^{th}\) bus, \({C}_{m\&o}\) is the operation and maintenance cost (\(\$/\) MW), T denotes the number of hours in one year (8760 h), \(Infr\) denotes the inflation rate, and \(Intr\) indicates the interest rate. The \(EOF\) is mathematically expressed as shown below:

$$EOF= {DG}_{cost, inv}+ {DG}_{cost, m\&o}$$
(14)

3 Multiobjective optimization

The concept of multiobjective optimization facilitates the optimization of multiple conflicting objectives simultaneously. A generalised formulation of \(n\)-dimensional multiobjective problem is given as per the following equations:

$$Minimize: F\left(\overrightarrow{x}\right)=\{{f}_{1}\left(\overrightarrow{x}\right), {f}_{2}\left(\overrightarrow{x}\right),\dots ..,{f}_{n}\left(\overrightarrow{x}\right)\}$$
(15)
$$Subject\; to:$$
$${g}_{i}\left(\overrightarrow{x}\right)\ge 0, i=\mathrm{1,2},\dots .,p$$
(16)
$${h}_{i}\left(\overrightarrow{x}\right)\ge 0, i=\mathrm{1,2},\dots .,q$$
(17)
$${Lb}_{i}\le \left({x}_{i}\right)\le {Ub}_{i}, i=\mathrm{1,2},\dots .,m$$
(18)

where \(x\) is the \(m\)-dimesnional control variable vector, \({g}_{i}\left(x\right)\) and \({h}_{i}\left(x\right)\) denote the equality and inequality constraints, respectively. \({Ub}_{i}\) and \({Lb}_{i}\) represent the upper and lower bounds of the control variable.

3.1 Pareto optimal method

Pareto optimality is a keystone concept in multiobjective optimization. The goodness of a solution in a multiobjective optimization problem is determined by Pareto dominance. Mathematically for a minimization problem, Pareto dominance, often termed as Pareto optimality, is formulated as,

$$Minimize \left[{y}_{1}\left(c\right),{y}_{2}\left(c\right), \dots .{y}_{k}(c)\right]$$
(19)

such that \(c \in C\), where \(k\ge 2\) and \(C\) denotes the set of all acceptable solutions. A solution \({c}_{1}\) is said to dominate solution \({c}_{2}\) if and only if the following conditions are fulfilled.

  1. (1)

    \({y}_{i}\left({c}_{1}\right)\le {y}_{i}\left({c}_{2}\right)\) in all dimensions \(i\in \{1, 2,\dots , k\}\) and

  2. (2)

    \({y}_{j}\left({c}_{1}\right)< {y}_{i}\left({c}_{2}\right)\) for at least in one dimension \(j\in \{1, 2,\dots , k\}\)

Solution \({c}_{1}\) doesn't dominate \({c}_{1}\) if any one of the aforementioned conditions is violated.

3.2 A posteriori approach of multiobjective optimization

Multiobjective optimization problems are handled in two approaches (Mirjalili et al. 2018): a priori and a posteriori. In the a priori approach multiobjective problem is converted into a single objective problem by employing preference weights before the optimization process. The decision-maker decides the preference weight values based on the preference given to each objective. Inappropriate selection of preference weights by the decision-maker may result in a sub-optimal solution. Further, the summation of objectives results in circumventing the solutions lying in the concave region of the Pareto front; consequently, the obtained solution may not be the best optimal solution for the weights chosen.

In a posteriori approach, the multiobjective formulation is preserved, and all the objectives are optimized simultaneously. The decision making is involved after the optimization process. This approach demands a multiobjective optimization algorithm, and the Pareto optimal solution set can be obtained in one run. Because of the apparent shortcomings of the a priori approach, a posteriori approach is adopted to solve the multiobjective optimization problem. From the Pareto optimal set, the decision-maker is free to select the best feasible solution based on his preference for the objectives.

3.3 TOPSIS for ranking of solutions

In this study, the best feasible solution from the Pareto optimal solutions is found using the TOPSIS approach. TOPSIS is a popular MCDM technique based on the premise that the best solution is the solution that is closest to the ideal positive solution and farthest to the ideal negative solution. TOPSIS allows ranking the alternatives based on an index that suggests the distance of each alternative from the ideal solution. TOPSIS involves the following steps (Mathew et al. 2020):

Step I: Construct a decision matrix \(X\) = (\({x}_{ai})\) of order \(n\times m\), comprising Pareto optimal solutions, where \(a\) = 1, 2,….,\(n\) represents different alternatives and \(i\) = 1,2,…,\(m\) represent the criteria.

Step II: Normalize each element of the decision matrix using the below equation to result in a normalized decision matrix.

$$r_{ai} = \frac{{x_{ai} }}{{\sqrt {\mathop \sum \nolimits_{a = 1}^{n} x_{ai}^{2} } }},\,a = 1,2,.....,n\,\,\,{\text{and}}\,\,i = 1,2,.....,m$$
(20)

Step III: Convert the normalized decision matrix into a weighted matrix, the weighted decision scores \({u}_{ai}\) can be calculated as.

$$u_{ai} = \beta_{i} \times r_{ai} ,a = 1,2,.....,n\,\,\,{\text{and}}\,\,i = 1,2,.....,m$$
(21)

where \({\beta }_{i}\) is the weight of \({i}^{th}\) criterion and \(\sum_{i}^{m}{\beta }_{i}=1\)

Step IV: Determine the ideal positive point \({U}_{a}^{+}\) and ideal negative point \({U}_{a}^{-}\) for each criterion where,

$$U_{a}^{ + } = \left\{ {\begin{array}{*{20}l} {max \left( {{\text{u}}_{{{\text{ai}}}} } \right) \forall a,\; {\text{for}}\, {\text{the}}\, {\text{benfit}}\, {\text{criterion}}} \\ {min \left( {{\text{u}}_{{{\text{ai}}}} } \right) \forall a,\; {\text{for}}\, {\text{the}}\, {\text{cost}}\, {\text{criterion}}} \\ \end{array} } \right.$$
(22)
$$U_{a}^{ - } = \left\{ {\begin{array}{*{20}l} {min \left( {{\text{u}}_{{{\text{ai}}}} } \right) \forall a,\; {\text{for}}\, {\text{the benfit}}\, {\text{criterion}}} \\ {max \left( {{\text{u}}_{{{\text{ai}}}} } \right) \forall a,\; {\text{for}}\, {\text{the}}\, {\text{cost}}\, {\text{criterion}}} \\ \end{array} } \right.$$
(23)

Step V: For each criterion, find the Euclidean distances \({d}_{a}^{+}\) and \({d}_{a}^{-}\) from \({U}_{a}^{+}\) and \({U}_{a}^{-}\) each alternative by using

$${d}_{a}^{+}=\sqrt{\sum_{a=1}^{m}{\left({u}_{ai}-{U}_{a}^{+}\right)}^{2}}$$
(24)
$${d}_{a}^{-}=\sqrt{\sum_{a=1}^{m}{\left({u}_{ai}-{U}_{a}^{-}\right)}^{2}}$$
(25)

Step VI: For ranking the alternatives, compute the closeness ratio of each alternative as mentioned below:

$${C}^{a}= \frac{{d}_{a}^{-}}{{d}_{a}^{+}+{d}_{a}^{-}}$$
(26)

The alternatives representing the Pareto optimal solutions are ranked according to their closeness ratio. The best feasible solution is the one that has the highest value of closeness ratio. The rank of the solution may change if \({\beta }_{i}\) i.e. the weight assigned to the criterion in step III is changed.

4 Multiobjective optimization algorithms

In this section, the MOGOA and MOGWO techniques used for solving the conflicting objectives \(TOF\) and \(EOF\) are described. The time complexity of both MOGOA and MOGWO algorithms is \(O(M{N}^{2})\) where \(M\) is the number of objectives and \(N\) is the number of individuals in the population.

4.1 MOGWO

The Grey wolf optimizer (GWO) algorithm was proposed by Mirjalili et al. (Mirjalili et al. 2014). This algorithm emulates the hunting strategy and pack leadership of the grey wolves. A typical grey wolf pack comprises of four hierarchical levels, namely alpha (α), beta (β), delta (δ), and omega (ω), as shown in Fig. 3. The α wolves are the most dominant ones, and ω wolves are the least dominant ones. The hunting strategy of these wolves comprises searching, encircling, harassing and attacking the prey. The encircling behaviour is mathematically represented as:

$$\overrightarrow {D} = \left| {\overrightarrow {C } \cdot \overrightarrow {Xp} \left( t \right) - \vec{X}\left( t \right)} \right|$$
(27)
$$\vec{X} \left( {t + 1} \right) = \overrightarrow {Xp} \left( t \right) - \vec{A} \cdot \vec{D}$$
(28)

Here \(\overrightarrow{X}\left(t\right)\) and \(\overrightarrow{Xp} \left(t\right)\) denote the position vectors of grey wolf and prey respectively for the tth iteration. \(\overrightarrow{A}\) and \(\overrightarrow{C}\) are the coefficient vectors which are evaluated from equations given below

$$\vec{A} = 2 \vec{a} \cdot \overrightarrow {{r_{1} }} - \vec{a}$$
(29)
$$\vec{C} = 2 \cdot \overrightarrow {{r_{2} }}$$
(30)

The elements of the vector \(\overrightarrow{a}\) are decreased linearly from 2 to 0 as the iterations progress, and r1, r2 represent random vectors in [0, 1]. It is observed that the coefficient vectors \(\overrightarrow{A}\) and \(\overrightarrow{C}\) have the capacity to control exploration and exploitation. |A|> 1 diverges the grey wolves from the location of the prey, thereby assisting exploration. The coefficient vector \(\overrightarrow{C}\) also assists exploration, it takes random values in [0,2]. The random values of \(\overrightarrow{C}\) either emphasize (C > 1) or deemphasize (C < 1) the effect of prey in determining the distance.

The pack hierarchy of grey wolves is modelled by considering the best solution as α. Consequently, the next best solution as β and the third best solution as δ. All the other solutions are treated as ω wolves. The best three solutions attained so far are preserved, and the other search agents are forced to modify their positions as per the positions of α, β, and δ using the following formulas.

$$\overrightarrow {{D_{\alpha } }} = \left| {\overrightarrow {{C_{1} }} \cdot \overrightarrow {{X_{\alpha } }} - \vec{X}} \right|$$
(31)
$$\overrightarrow {{D_{\beta } }} = \left| {\overrightarrow {{C_{2} }} \cdot \overrightarrow {{X_{\beta } }} - \vec{X}} \right|$$
(32)
$$\overrightarrow {{D_{\delta } }} = \left| {\overrightarrow {{C_{3} }} \cdot \overrightarrow {{X_{\delta } }} - \vec{X}} \right|$$
(33)
$$\overrightarrow {{X_{1} }} = \overrightarrow {{X_{\alpha } }} - \overrightarrow {{A_{1} }} \cdot \left( {\overrightarrow {{D_{\alpha } }} } \right)$$
(34)
$$\overrightarrow {{X_{2} }} = \overrightarrow {{X_{\beta } }} - \overrightarrow {{A_{2} }} \cdot \left( {\overrightarrow {{D_{\beta } }} } \right)$$
(35)
$$\overrightarrow {{X_{3} }} = \overrightarrow {{X_{\delta } }} - \overrightarrow {{A_{3} }} \cdot \left( {\overrightarrow {{D_{\delta } }} } \right)$$
(36)
$$\overrightarrow{X} \left(t+1\right)= \frac{\overrightarrow{{X}_{1}}+ \overrightarrow{{X}_{2} }+ \overrightarrow{{X}_{3}}}{3}$$
(37)

In the multiobjective version of GWO, two new components are integrated. The first component is an archive, a repository to store the Pareto optimal solutions. The second component is a leader identification mechanism that enables to identify α, β and δ solutions from the archive. The leader identification mechanism uses a probability as given in Eq. 38, favouring selection from least crowded search spaces and a roulette wheel mechanism to identify the best solutions. \(K\) being a constant number whose value is greater than one and \({n}_{i}\) being the number of Pareto optimal solutions in \({i}^{th}\) segment, the probability is given as:

$$\rho_{i} = {\raise0.7ex\hbox{$K$} \!\mathord{\left/ {\vphantom {K {n_{i} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${n_{i} }$}}$$
(38)

4.2 MOGOA

The grasshopper optimization (GOA) is a swarm intelligence-bases nature inspired algorithm imitating the swarming tendency of grasshoppers (Saremi et al. 2017). Within the swarm, the position of the grasshoppers indicates a potential solution for the given problem to be optimized. The position model of the \({p}^{th}\) grasshopper is as follows:

$${X}_{p}= {{\mu }_{1}S}_{p}+ {\mu }_{2}{G}_{p}+{{\mu }_{3}W}_{p}$$
(39)

Here \({X}_{p}\) indicates the position of \(p{\text{th}}\) grasshopper, \({S}_{p}\) denotes the social component, \({G}_{p}\) denotes the gravity component, and the component \({W}_{p}\) indicates the advection due to wind. To simulate the random nature of grasshoppers \({\mu }_{1}\), \({\mu }_{2}\) and \({\mu }_{3}\) are introduced, where \({\mu }_{1}\), \({\mu }_{2}\) and \({\mu }_{3}\) are random numbers in [0,1]. \(Z\) being the number of grasshoppers, the social component is formulated as:

$${S}_{p}= \sum_{q=1, q\ne p}^{Z}s({d}_{pq})\widehat{{d}_{pq}}$$
(40)
$${d}_{pq}=|{x}_{q}-{x}_{p}|$$
(41)
$$\widehat{{d}_{pq}}=\frac{{x}_{q}-{x}_{p}}{{d}_{pq}}$$
(42)
$$s\left(r\right)=f{e}^{\frac{-r}{l}}- {e}^{-r}$$
(43)

where \({d}_{pq}\) which denotes the distance between \(p{\text{th}}\) and \(q{\text{th}}\) grasshoppers, function \(s\) indicates the firmness of social interaction, \(f\) and \(l\) denote the attraction strength and length of the attractive scale, respectively. The components \(G\) and \(W\) are calculated as:

$${G}_{p}= -g\widehat{{e}_{g}}$$
(44)
$${W}_{p}= u\widehat{{e}_{w}}$$
(45)

where \(\widehat{{e}_{g}}\) and \(g\) represent the unit vector towards the centre of the earth and gravitational constant. The \(\widehat{{e}_{w}}\) and \(u\) are the unit vector in the direction of the wind and drift constant, respectively. Finally, the grasshopper position for \({k}^{th}\) dimension can be updated by the following expression.

$${X}_{p}^{k}=c\left(\sum_{q=1, q\ne p}^{Z}c\frac{{Ub}_{k}-{Lb}_{k}}{2}s(|{x}_{q}^{k}-{x}_{p}^{k}|)\frac{{x}_{q}-{x}_{p}}{{d}_{pq}}\right)+\widehat{{\mathrm{T}}_{d}}$$
(46)
$$c= {c}_{max}- I\mathrm{t }\frac{{c}_{max}-{c}_{min}}{{I\mathrm{t}}_{max}}$$
(47)

where \({Ub}_{n}\) and \({Lb}_{n}\) represent the upper and lower bounds of \({k}^{th}\) dimension, \(\widehat{{\mathrm{T}}_{d}}\) represents the best solution found so far. The term \(c\) reins the grasshopper agents to favour exploitation as the number of iterations increases.

In the MOGOA (Mirjalili et al. 2018), the concept of Pareto dominance is employed, and the resulting Pareto optimal solutions are accumulated in an archive. A target solution selected from the archive should take into consideration the diversity of the solutions in the archive. For this purpose, a metric corresponding to the number of adjacent solutions in the vicinity of each archived solution is calculated. Based on this, the probability of a solution becoming the potential target is found. If \({n}_{i}\) is the number of solutions in the neighbourhood of \({i}^{th}\) solution, the probability is expressed as:

$$\rho_{i} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {n_{i} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${n_{i} }$}}$$
(48)

5 Results and discussion

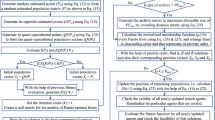
The multiobjective DG accommodation problem by simultaneously optimizing \(TOF\) and \(EOF\) is solved using MOGWO and MOGOA. The proposed approach is tested on 33 bus test system and 69 bus test system. Two case studies are conducted pertaining to the test systems. The criterion weights (\({\beta }_{1}\) for \(TOF\) and \({\beta }_{2}\) for \(EOF\)) given to each objective at the TOPSIS stage III are varied based on the preference given to objectives, and the best feasible solution in each scenario is presented. This approach provides multiple solutions, and the utilities can select an appropriate solution based on their preference for the objectives. The flowchart of the proposed multiobjective procedure with TOPSIS is depicted in Fig. 1. The considered scenarios in each case are:

Fig. 1
figure 1

Flow chart of proposed multiobjective approach with TOPSIS

Full size image

Scenario 1: Relatively higher weightage to \(EOF\) (\({\beta }_{1}=0.2\) and \({\beta }_{2}=0.8\)).

Scenario 2: Equal weightage to \(TOF\) and \(EOF\) (\({\beta }_{1}=0.5\) and \({\beta }_{2}=0.5\)).

Scenario 3: Relatively higher weightage to \(TOF\) (\({\beta }_{1}=0.8\) and \({\beta }_{2}=0.2\)).

5.1 Case studies

The 33 bus distribution network (case 1) caters for a total load of 3.7 MW and 2.3 MVAR (Hamouda and Zehar 2006). The 69 bus network (case 2) caters for a total load of 3.80 MW and 2.69 MVAR. The \({P}_{T,loss}\) and \({Q}_{T,loss}\) of the network estimated by performing power flow analysis are 211 kW and 143.04 kVAR  for case 1 and 224.92 kW and 102.19 kVAR for case 2 respectively. The resulting Pareto optimal fronts for the 33 bus test system are depicted in Fig. 2. The results obtained for different scenarios of case 1 are presented in Table 1. The \(TOF\) and \(EOF\) obtained through MOGWO for the best feasible solution are 0.6073 and 2.5508, 0.5488 and 3.2248, 0.4568 and 5.0789 for scenario 1, scenario 2 and scenario 3 respectively. In the case of MOGOA, the \(TOF\) and \(EOF\) for the best feasible solution are 0.5804 and 2.7508, 0.5416 and 3.2736, 0.4662 and 4.7864 for scenario 1, scenario 2 and scenario 3 respectively. After the optimal DG accommodation, it was observed that the \({P}_{T,loss}\) and \({Q}_{T,loss}\) reduced considerably. Further, an enhancement in the voltage profile and voltage stability of the network can be observed through the improvement of \(TVD\) and \(TVSI\) values after optimal DG accommodation. The voltage profiles for case 1 are shown in Fig. 3. The resulting Pareto fronts for case 2 are depicted in Fig. 4. The results obtained for different scenarios of case 2 are presented in Table 2. The voltage profiles for case 2 are shown in Fig. 5. Table 3 shows the comparative analysis with multiobjective particle swarm optimization (MOPSO) technique and NSGA – II giving equal weights to the objectives. Comparing the results, it can be inferred that the best values of \(TOF\) and \(EOF\) are provided by MOGOA and MOGWO respectively for case 1 and MOGWO and MOGOA respectively for case 2.

Fig. 2
figure 2

Pareto optimal fronts under various scenarios for 33 bus system

Full size image
Table 1 Results of 33 bus test system under different scenarios
Full size table
Fig. 3
figure 3

Voltage profile of the 33 bus system under various scenarios

Full size image
Fig. 4
figure 4

Pareto optimal fronts under various scenarios for 69 bus system

Full size image
Table 2 Results of 69 bus test system under different scenarios
Full size table
Fig. 5
figure 5

Voltage profile of the 69 bus system under various scenarios

Full size image
Table 3 Comparison of proposed method with existing methods
Full size table

5.2 Discussion

From the results obtained in the aforementioned case studies, it can be inferred that optimal DG accommodation can enhance the performance of the distribution network by minimizing the losses and improving the voltage profile Fig. 4. The probability of voltage collapse also shrinks after accommodating DGs. It can also be observed that the best feasible solutions obtained from the algorithms MOGWO and MOGOA are different. In case 1, the minimum value of \(TOF\) obtained is 0.4568 p.u. in scenario 3 by MOGWO, and the minimum value of \(EOF\) obtained is 2.5508 million $ in scenario 1 by MOGWO. In case 2, the minimum value of \(TOF\) obtained is 0.427 p.u. in scenario 3 by MOGWO, and the minimum value of \(EOF\) obtained is 2.5508 million $ in scenario 1 by MOGOA Fig. 5.

In case 2 scenario 1, the MOGOA algorithm outperformed the MOGWO in both objectives simultaneously. Except for case 2 scenario 1, neither of the algorithms topped in both objectives simultaneously. This kind of outcome may be attributed to the conflicting nature of the objectives (Kahourzade et al. 2015). Hence, the superiority of any one of the algorithms cannot be ascertained from the results. In both case studies, in scenario 1 where the decision-maker favours the \(EOF\), the DG penetration is relatively less, and hence the \(EOF\) values are better than scenario 2 and scenario 3. Whereas in scenario 3 where the decision-maker favours the \(TOF\), the DG penetration is relatively high and hence the \(TOF\) values are better than scenario 1 and scenario 2.

To provide more practical and managerial insights to the distribution company, the criteria weight (\({\beta }_{i}\)) is varied, and its effects on real power loss and DG cost are investigated. The summary of results for the MOGWO algorithm in both cases are given in Table 4. Figure 6 depicts the changes in real power loss reduction and DG cost by varying the criteria weights \({\beta }_{1}\) and \({\beta }_{2}\). According to the results obtained, it is found that in case 1 the DG cost for obtaining 50% real power loss reduction is 4.0502 million $, whereas in case 2, for obtaining 59% power loss reduction, the cost incurred is 4.9308 million $. A maximum reduction of 63.51% in real power loss can be achieved in case 1 when the distribution company can bear a DG cost of 8.3863 million $. In case 2, the maximum reduction can be up to 68.64%, while the DG cost can go up to 8.7331 million $. By analyzing these results, the distribution company can make an informed decision regarding the optimal DG accommodation in distribution networks.

Table 4 Impact of criteria weight on real power loss reduction and DG cost
Full size table
Fig. 6
figure 6

Variations in real power loss reduction and DG cost for different values of \({\beta }_{i}\)

Full size image

6 Conclusion

The optimal DG accommodation problem was addressed in this study by taking into account competing technological and economic objectives. A posteriori approach was adopted, and the multiobjective nature of the problem was maintained during the optimization process. MOGWO and MOGOA algorithms were used to solve the multiobjective DG accommodation problem, and the Pareto optimal solutions are generated. Three different scenarios were considered at the decision-making stage based on the decision-makers bias towards the objectives. The decision-making process was facilitated by TOPSIS, and multiple optimal solutions were presented to cater to diversity in preferences for the objectives. The approach was tested on 33 bus and 69 bus test systems. Results indicated that as the DG penetration in the network increased, the performance of the distribution network in terms of technical parameters improved. At the same time, the DG cost became dearer. Given the conflicting nature of the objectives, neither of the two algorithms outperformed simultaneously for both objectives. This study should help the distribution network planners and utilities plan the distribution systems along with DGs to derive technical benefits offered by optimally allocated DGs while giving due regard to the costs involved. This study can be extended by considering different load models and renewable DGs in the future. Furthermore, the problem may be solved with NSGA – III algorithm, and a comparative analysis can be performed.