1 Introduction

Frequency control is recognized as a basic concept in power systems to guarantee a safe performance in different situations. As known, reliable frequency performance hinges on equilibrium between generated and consumed active powers (Kundur 1994). In other words, any variations in active power can lead to frequency deviations (Shekari et al. 2016a, b). On the other hand, there are some other situations that can deteriorate frequency performance. Variation of different parameters in automatic generation control (AGC) process can be identified as such uncertainties ahead of successful performance of the established controllers. In order to model a generation unit in AGC structure, three components are needed: turbine, governor, and kinetic energy of the generator. In this regard, the main structure of AGC consists of two frequency control loops including primary and supplementary loops. As the primary frequency control loop, the governor contributes in frequency regulation. This is while; the primary loop is limited and it may lose its validity in sudden and severe variations of active power equilibrium. To fill in this technical gap, a supplementary frequency loop known as load frequency control (LFC) is further included in AGC structure (Bevrani 2009). In this process, a proportional-integral (PI) controller is used as the supplementary controller in general.

The design procedure of PI controller in LFC structure has attracted a lot of attentions among the researchers. A contemporary review on the application of optimization methods for tuning of PI controller gains is addressed in (Kalavani et al. 2017). In this context, some research studies have contributed to design of efficient PI controllers by applying robust methods (Mohamed et al. 2011; Yazdizadeh et al. 2012; Bevrani et al. 2004). Reference (Mohamed et al. 2011) has employed a model predictive control (MPC) technique to design a robust PI controller. In (Yazdizadeh et al. 2012), a robust multi-variable PI differential (PID) controller is applied to the LFC structure to attenuate frequency deviations. Moreover, in (Bevrani et al. 2004), the H∞ approach in combination of iterative linear matrix inequality (ILMI) is used to regulate the parameters of PI controller. An observer based robust integral sliding mode load frequency control for wind-integrated power systems is proposed in (Cui et al. 2017). As well, a dynamic gain-tuning control strategy is designed for AGC in power systems by (Xu et al. 2016). Applying robust techniques in design process of PI controller has some limitations due to complex mathematical basic of these approaches and also existence of different uncertainties. In this area, the Kharitonov theorem (Habibi et al. 2013), as an explicit robust method can be applied to the LFC structure for robust tuning of PI parameters. The Kharitonov theorem strengthens the PI controller against the uncertainties in the parameters of power system. In LFC design process, robust methods are merely apt to consider uncertainties in parameters of the system or load changes. Although linearization of initial nonlinear model accommodates the uncertainties in system parameters, these controllers fail in responding to load changing conditions, concurrently. In order to tackle this challenge, a fuzzy logic controller as an intelligent approach is supplemented to the PI controller which performs an online tuning of the parameters. In contradiction to the traditional and classic approaches, intelligent methods are directly established based on the measurements, long-term experience, and experts/operators knowledge. Moreover, the basic functionality of the fuzzy logic-based LFC is to improve the dynamic frequency performance during sudden load changes. The fuzzy logic has been used by different researchers to obtain particular advantageous in the LFC structure (Indulkar and Raj 1995; Khezri et al. 2016; Jawad and Fadel 1999; Hassan et al. 2014). An overview of fuzzy logic contribution to efficient LFC in multi-area power systems is provided by (Indulkar and Raj 1995). The fuzzy approach is used for fine-tuning of classic PI controller in (Khezri et al. 2016). Additionally, a gain scheduling of PI controller based on fuzzy logic is applied in (Jawad and Fadel 1999) to attain performance improvements in LFC structure. An adaptive fuzzy logic with approximation control scheme has been developed for frequency control of a power system in (Hassan et al. 2014).

Based on the aforementioned points, this article provokes a two-stage robust-intelligent control strategy for PI controller to enhance the frequency performance of the proposed LFC. At the first stage, the parameters of PI controller are adjusted based on a robust technique. In this context, Kharitonov theorem is applied to the LFC structure for offline tuning of the PI parameters against the deviations of turbine and governor time constants. However, a weak performance is still noticed against the uncertainties in load changes. Consequently, at the second stage, a fuzzy logic is triggered following the initial tuning of PI controller. In other words, an adaptive online gain tuning is achieved making the proposed controller an intelligent one against the load changes. Such a design concept ends in a robust and intelligent controller against different uncertainties in the LFC structure. Actually, two types of uncertainties including time constant and load condition are handled in the proposed control model. The time constant uncertainty in the turbine and governor are included in the mathematical model of Kharitonov theorem to design robust controller. In this step, the interval of deviation is specified by a valid reference. The other type of uncertainty, mentioned as load changes in the system, is considered in the process of the fuzzy logic controller design. Deviation in load condition of system cannot be specified because of frequent changes in loads. Therefore, a fuzzy logic based controller can be suitable for handling such uncertainty. Extensive numerical studies are conducted to assess performance of the proposed approach. The obtained results reveal a reliable frequency performance against the power system uncertainties.

The remainder of this paper is organized as follows. The LFC model and its different components are demonstrated and mathematically described in Sect. 2. The basic principles of Kharitonov theorem and its efficiency in gain tuning of PI controllers is illustrated in Sect. 3. In the following, Sect. 4 addresses the fuzzy logic-based control strategy for online tuning of PI controller gain values. Section 5 interrogates different simulation studies within which a complete discussion is provided for each of the investigated cases. Eventually, Sect. 6 concludes the manuscript.

2 LFC model and its components

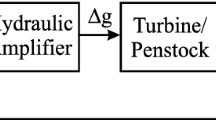
Stability analysis of power systems is aligned with high-order, nonlinear, and time varying features in modeling notions. However, in frequency stability investigation of power system, \(\omega\) (generator rotor speed) and its variations are considered. Although neglecting the fast dynamics of power systems leads to model reduction of power system, it puts forward some uncertainty issues ahead of the proposed controller. In this study, the investigated power system consists of a non-reheat steam generator with two frequency control loops. Figure 1 illustrates the investigated test system.

Fig. 1
figure 1

Investigated test system

Full size image

As depicted, the power system model for LFC structure consists of differential blocks which respectively illustrate the rotating mass of synchronous generator, turbine and governor models, and also the secondary frequency controller. In this figure, H is the inertia constant, D is the load damping coefficient, T t is the turbine time constant, T g is the governor time constant, \(K(s)\) is the supplementary frequency controller, R is the speed droop characteristic of governor and \(\Delta {P_L}\) demonstrates the load changes. Table 1 illustrates the detailed data in regard of the investigated system.

Table 1 Detailed data about the considered system
Full size table

The rotating mass block represents the relationship between the mismatched powers where the frequency deviation is as follows.

$$\Delta {P_m}(s) - \Delta {P_L}(s)=2Hs\Delta f(s)+D\Delta f(s),$$
(1)

here \(\Delta {P_m}\) is the mechanical power change of generator and \(\Delta f\) represents the resultant frequency deviation. The frequency deviation due to load changes or parameters uncertainties should be curbed based on two control loops in the LFC structure. As clarified, the secondary frequency controller, \(K(s),\) is often a PI controller being represented as follows.

$$K(s)={K_P}+\frac{{{K_I}{\text{ }}}}{s},$$
(2)

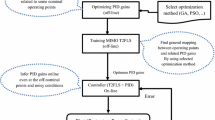
where K P and K I indicate the proportional and integral gain values. Generally, classic control methods or trial-and-error approaches are deployed to adjust these controllers. However, these methods could deteriorate the performance of these controllers against the sudden and severe disturbances. In fact, the parameters of classic PI controller are adjusted for nominal operating point and there is not efficient robustness against the parameter uncertainties and load changes. To tackle this challenge, a two-stage robust-intelligent approach is elaborated in this study. In the first stage, the parameters of the PI controller are adjusted in an offline manner based on Kharitonov theorem which provides a robust response against the uncertainties of parameters. Afterwards, in the second stage, fuzzy logic approach is used for online tuning of PI parameters suppressing the load changing transients. Figure 2 illustrates the proposed two-stage control layout. As demonstrated, the fuzzy logic and Kharitonov theorem operate in a parallel manner.

Fig. 2
figure 2

The parallel two-stage structure of controller

Full size image

3 Kharitonov theorem and its application to LFC

3.1 Kharitonov theorem: the basic principles

As a robust control approach, Kharitonov theorem is applied to regulate the controller gain values against the uncertainties in power system parameters. In fact, the Kharitonov theorem analyzes the stability robustness of polynomials with the perturbed coefficients. In this context, the Kharitonov theorem performs based on the characteristic polynomial of the main system by considering a closed-loop structure. To evaluate the system stability, Kharitonov theorem uses Routh–Hurwitz criteria. As known, the Routh–Hurwitz criteria can be used to check the system stability when the coefficients of characteristic polynomial are known. However, when the physical parameters of the system are not identified accurately or the coefficients are merely known within specific ranges, the Kharitonov theorem provides a test of stability for the interval polynomial. Mathematically speaking, the characteristic polynomial of linear systems can be considered as follows.

$$Q(S,P)={P_0}+{P_1}S+ \cdots +{P_{n - 1}}{S^{n - 1}}+{P_n}{S^n}$$
(3)
$${P_i}=\left[ {P_{i}^{ - },P_{i}^{+}} \right],i=0,1, \ldots ,n - 1,n,$$
(4)

where \({P_i}\) is a parameter of the system that can be fixed or changed in determined intervals. \(P_{i}^{+}\) and \(P_{i}^{ - }\) are the maximum and minimum bounds of the parameters. As can be deduced from (4), it is almost impossible to check all the uncertain parameters in the characteristic equation. Accordingly, the Kharitonov theorem evaluates stability of the whole system by investigating the Routh–Hurwitz criteria for four equations related to the main characteristic polynomial. These four equations can be mathematically described as follows.

$$\left\{ \begin{gathered} {K_1}(S)={P_0}^{ - }+{P_1}^{ - }S+{P_2}^{+}{S^2}+{P_3}^{+}{S^3}+{P_4}^{ - }{S^4}+ \cdots \hfill \\ {K_2}(S)={P_0}^{ - }+{P_1}^{+}S+{P_2}^{+}{S^2}+{P_3}^{ - }{S^3}+{P_4}^{ - }{S^4}+ \cdots \hfill \\ {K_3}(S)={P_0}^{+}+{P_1}^{ - }S+{P_2}^{ - }{S^2}+{P_3}^{+}{S^3}+{P_4}^{+}{S^4}+ \cdots \hfill \\ {K_4}(S)={P_0}^{+}+{P_1}^{+}S+{P_2}^{ - }{S^2}+{P_3}^{ - }{S^3}+{P_4}^{+}{S^4}+ \cdots \hfill \\ \end{gathered} \right.$$
(5)

The Routh–Hurwitz criterion determines the condition that instigates the system instability; also, it can determine the condition for making the system stable following any unstable condition. To simplify the calculations in Kharitonov theorem, there are some lemmas for polynomials with orders lower than 5th, which can simplify (5). For instance, in 3th order characteristic polynomials, if \(P_{0}^{ - }\rangle 0,\) it would be sufficient to merely check the Routh–Hurwitz criteria in \({K_4}(s).\) Also, for 4th order characteristic polynomial, the Kharitonov theorem is reduced to check the stability of \({K_1}(s)\) and \({K_4}(s).\) This is while; for 5th order polynomial, the stability of \({K_1}(s),\) \({K_3}(s),\) and \({K_4}(s)\) is examined. In general, the Kharitonov theorem provides an efficient, easy, and powerful tool for robust adjustment of practical controllers (Barmish 1994).

3.2 Applying Kharitonov theorem to LFC system

As mentioned, in order to apply the Kharitonov theorem to the LFC system, the main closed-loop characteristic polynomial of the investigated system (see Fig. 1) should be known. For this purpose, Fig. 3 illustrates the closed-loop system by considering the controller and the main system.

Fig. 3
figure 3

The closed-loop system with the established controller

Full size image

In this figure, \(G(s)\) represents the considered LFC structure and \(K(s)\) is the secondary PI controller. Thus, the general transfer function of the LFC system can be represented as follows.

$$P(s)=K(s) \cdot G(s) = \frac{{N(s)}}{{D(s)}},$$
(6)

where \(N(s)\) and \(D(s)\) demonstrate the nominator and denominator of the transfer function, respectively. In (7), \(D(s)\) illustrates the characteristic polynomial of the system which is involved in Kharitonov theorem. Considering the PI controller parameters and the transfer functions in Fig. 1, \(D(s)\) can be obtained as follows.

$$\begin{aligned} &D(s)=Q(s,a)={a_0}+{a_1}s+{a_2}{s^2}+{a_3}{s^3}+{a_4}{s^4} \hfill \\ & {a_0}={K_I} \times R \hfill \\ &{a_1}={K_P} \times R+D \times R+1 \hfill \\& {a_2}=2 \times R \times H+R \times D \times \left( {{T_g}+{T_t}} \right) \hfill \\& {a_3}=2 \times R \times H \times \left( {{T_g}+{T_t}} \right)+R \times D \times {T_g} \times {T_t} \hfill \\& {a_4}=2 \times R \times H \times {T_g} \times {T_t}, \hfill \\ \end{aligned}$$
(7)

where \({a_0},{a_1},{a_2},{a_3}\) and \({a_4}\) represent the parameters of the characteristic polynomial. It should be mentioned that in this process, the load change is considered as zero. As given in (7), the closed-loop system is a 4th order polynomial; therefore, it is sufficient to investigate the Routh–Hurwitz criteria for the following two polynomials.

$$\left\{ \begin{gathered} {K_1}(S)={P_0}^{ - }+{P_1}^{ - }S+{P_2}^{+}{S^2}+{P_3}^{+}{S^3}+{P_4}^{ - }{S^4}+ \cdots \hfill \\ {K_4}(S)={P_0}^{+}+{P_1}^{+}S+{P_2}^{ - }{S^2}+{P_3}^{ - }{S^3}+{P_4}^{+}{S^4}+ \cdots \hfill \\ \end{gathered} \right.$$
(8)

By obtaining the main closed-loop characteristic polynomial, the uncertain parameters should be identified in the system. In this paper, the turbine and governor time constants are selected as uncertain parameters. The deviation intervals of such parameters in non-reheat steam generators are as follows (Kundur 1994).

$$\begin{gathered} 0.025 \leq {T_g} \leq 0.15 \hfill \\ 0.4 \leq {T_t} \leq 11. \hfill \\ \end{gathered}$$
(9)

By assuming the above intervals, the closed-loop system coefficients (7) are bounded as follows.

$$\begin{gathered} \left[ {a_{2}^{+},a_{2}^{ - }} \right]=\left[ {1.00185,{\text{ }}0.519225} \right] \hfill \\ \left[ {a_{3}^{+},a_{3}^{ - }} \right]=\left[ {5.65040,{\text{ }}0.213000} \right] \hfill \\ \left[ {a_{4}^{+},a_{4}^{ - }} \right]=\left[ {0.82520,{\text{ }}0.005000} \right]. \hfill \\ \end{gathered}$$
(10)

By implementing the Kharitonov approach, the PI controller parameters are illustrated in Fig. 4.

Fig. 4
figure 4

PI controller parameters obtained based on Kharitonov theorem

Full size image

According to Kharitonov theorem, the design process is correct if the zero exclusion criteria are satisfied in Kharitonov rectangles (Fu 1999). Considering the frequency deviation between \(0 \leq \omega \leq 50kHz\), Kharitonov rectangles can be calculated by the following vertices.

$${K_1}(s),{K_2}(s),{K_3}(s),{K_4}(s),s=j\omega .$$
(11)

The basic geometry associated with the zero exclusion condition is illustrated in Fig. 5. Based on the zero exclusion condition, the closed-loop system is robustly stable if and only if, the rectangle plots do not include the origin of plane. This issue is clearly confirmed in Fig. 5.

Fig. 5
figure 5

a Motion of Kharitonov rectangles for \(0 \leq \omega \leq 50kHz\) and b a magnified view around origin

Full size image

As can be seen, the expected design process of PI controller based on Kharitonov theorem is accomplished in a satisfactory manner. As a consequence, the first stage of the proposed approach provides a robust controller against the parameters uncertainties.

The Kharitonov theorem is employed for a one-area one-machine power system. For such simple system, there are complexities in the mathematical model. Also, in this system, containing only one generator, there are only two uncertain parameters. In the case of multi-machine power systems, the established mathematical model seems rather complex which necessitates further and exact simplification techniques. As well, the application of heuristic methods could be considered in parallel with the proposed method. This issue will be investigated as a possible future research topic. The complexities in mathematical fundamentals of Kharitonov theorem make it rather a difficult notion in multi-area or multi-input multi-output (MIMO) systems. Alternatively, each area could be considered alone and Kharitonov theorem can be applied at each area, individually. This approach is not technically justified in today’s interconnected power systems. Alternatively, in MIMO systems, the combinatorial application of Kharitonov theorem with heuristic approaches seems to be an effective approach (Toulabi et al. 2014).

4 Intelligent fuzzy logic-based online tuning of LFC

Due to nonlinear and complex nature of the power systems, the design process of robust controllers encounters technical flaws against the uncertainties and limitations in system operating conditions (Bevrani and Hiyama 2011). In this regard, as mentioned earlier, the Kharitonov theorem is applied to the LFC structure which affords a robust response against the uncertainties in turbine and governor time constants. However, the load changing effects are excluded. Basically, the fuzzy logic is independent than the mathematical model of the investigated system. Recently, fuzzy logic has infiltrated in various aspects of power systems (Mokryani et al. 2013; Vaccaro and Zobaa 2011; Khezri et al. 2017). Also, it can be utilized as an online approach in complicated systems to adapt and coordinate the controllers (Khezri and Bevrani 2015). This study makes benefit of fuzzy logic to contribute to an intelligent controller in an online manner. Specifically speaking, the fuzzy logic is triggered following the robust controller obtained in the preceding section. This approach makes the PI controller an adaptive and intelligent one which accommodates the load changes accurately. To demonstrate the best response in online control actions, the primary gains of PI controller should be regulated by a robust method, as the case of the previous stage.

In the design procedure of fuzzy logic controller, four main steps should be accomplished as follows: fuzzification, fuzzy rule base, inference engine, and defuzzification. The first step, known as fuzzification, is to convert the crisp values into corresponding fuzzy values through proper membership functions. In this paper, the frequency deviation and its derivative are selected as input signals. As an indispensible task, appropriate input signals should be allocated in feeding the proposed fuzzy logic controller. As stated earlier, in a LFC problem, the frequency deviation signal represents a suitable input variable representing the performance features of the system. The frequency deviation of the system varies proportionally to the load fluctuations and generating unit conditions. In this regard, the derivative of frequency deviation is selected as the other input signal for better considering large deviations related to the load condition of the system. On the other hand, the defuzzification step has a similar function; however in defuzzification step fuzzy quantities are converted into crisp values through the output membership functions. Figure 6 illustrates the considered membership functions in fuzzification and defuzzification steps. The linguistic variables specify the quality of control process since they directly model the system characteristics through the expert’s knowledge. In this research, the membership functions corresponding to the input variables are arranged as Negative (N), Zero (Z), and Positive (P). Also, the membership functions of the output variables are arranged as Negative Large (NL), Negative Small (NS), Zero (Z), Positive small (PS), and Positive Large (PL). It should be mentioned that all membership functions are considered as triangular ones (Khezri et al. 2016).

Fig. 6
figure 6

Fuzzy membership functions for inputs and outputs variables

Full size image

What is more, optimization algorithms such as genetic algorithm can be applied in optimizing the range of membership functions in the established fuzzy controller. In future research studies, this issue could contribute to further improvements regarding the established controller performance.

As noted, the established fuzzy controller has two output signals which regulate the proportional and integral gain values. The inputs and outputs are connected by suitable fuzzy rules. All the possible compositions of inputs to define the appropriate output signals should be defined in this step. Originally, the fuzzy rule basis stands out as the heart of fuzzy logic. The control duties for the fuzzy online tuner are determined by the established rules. To make a proper rule base system for the controller, a look-up table is necessary. The determined fuzzy rules are gathered in Table 2. The inference engine uses a set of linguistic statements in form of IF-THEN phrases to convert the input signals into the output signals. In this research, the Mamdani inference engine is utilized for the proposed fuzzy online tuner Mamdani (1974). The fuzzy rules in the design process are extracted based on the expert’s knowledge about the system performance. Such data can be obtained by studying the dynamics of the investigated system and recording its response in different scenarios.

Table 2 Fuzzy rules
Full size table

5 Simulation results and discussions

In numerical validations, performance of a classic PI (CPI) controller is investigated in two scenarios of combined load disturbance and deviation of governor and turbine time constants. As well, in the third scenario, the transient and tracking performance of the embedded controller is assessed. After that, performance of the proposed Kharitonov-based controller is investigated in these scenarios. Eventually, the proposed fuzzy approach is explored on gain tuning of the LFC and settling down the frequency deviations. All the three cases are examined on the established power system shown in Fig. 1. The parameters of the considered test system could be accessed in (Bevrani 2009).

5.1 Performance of the classic PI (CPI) controller

At the first case, performance of the CPI controller is investigated. Considering the first scenario, the time constants of governor and turbine are considered at their maximum values. Then, 0.1 p.u. load step is further included. Frequency performance of the investigated system is illustrated in Fig. 7. The load disturbance is occurred at t = 5 s. As demonstrated, the power system experiences frequency instability following the simulated disturbance. Moreover, another scenario containing the minimum value of governor and turbine time constants along with 0.1 p.u. load step is included to show the inability of CPI controller. The frequency instability of the system is evidently seen in response to this disturbance (Fig. 8).

Fig. 7
figure 7

Frequency response of the system in the first scenario: CPI controller

Full size image
Fig. 8
figure 8

Frequency response of the system in the second scenario: CPI controller

Full size image

5.2 Performance of the Kharitonov-based PI controller

The gain values of PI controller based on Kharitonov approach have been shown in Fig. 3. In this section, the proportional and integral gains are selected as follows: K P  = −0.325 and K I  = 0.002. By applying these parameters in PI controller, performance of the Kharitonov-based controller is demonstrated in Fig. 9, recorded for scenario 1. As can be seen, the frequency stability is maintained through the Kharitonov approach in the LFC system. Performance of the Kharitonov-based controller for the second scenario is shown in Fig. 10. As illustrated, for both scenarios, the frequency stability is maintained sufficiently. However, steady-state error is seen in the frequency response. This is so due to neglecting the load changes in the design procedure of this controller.

Fig. 9
figure 9

Frequency response of the system in the first scenario: Kharitonov-based controller

Full size image
Fig. 10
figure 10

Frequency response of the system in the second scenario: Kharitonov-based controller

Full size image

As described earlier, the third scenario is considered to investigate the transient and tracking performance of the Kharitonov-based controller. To this end, random load disturbances shown in Fig. 11 are applied to test the tracking performance of the proposed Kharitonov-based controller. Results are demonstrated in Fig. 12. As can be seen, the proposed controller fails in suitable responding against the load disturbances and it cannot guarantee a stable performance. Thus, improper response of the Kharitonov-based LFC is revealed in load-changing conditions.

Fig. 11
figure 11

Random load disturbance in the third scenario

Full size image
Fig. 12
figure 12

Frequency response of the system in the third scenario: Kharitonov-based controller

Full size image

5.3 Performance of the fuzzy-based online PI controller

As clarified, at the second stage of the proposed approach, the fuzzy controller operates as an approach to retune the PI parameters against the load changes. As depicted, the fuzzy controller accepts the frequency deviation and its derivative as the input signals and updates the proportional and integral gain values. In other words, this controller adapts the PI parameters against the load changes. Figure 13 illustrates the frequency performance, proportional gain deviation, and integral gain deviation following the first scenario. As can be seen, subfigure (a) demonstrates that the fuzzy-based online tuning approach provokes a superior performance in regard of frequency stabilization with the least amount of steady state error. As well, the variations of proportional and integral gain values are shown in sub-figures (b) and (c), respectively.

Fig. 13
figure 13

The proposed fuzzy online controller in first scenario, a frequency performance, b proportional gain variations, and c integral gain variations

Full size image

Moreover, Fig. 14 illustrates performance of the proposed fuzzy controller in the second scenario. As can be seen, the intelligent adjustment of controller gains contributes to the least frequency deviations. In this way, Fig. 14a demonstrates that the frequency deviations are settled and the steady state error is curbed around zero. To do so, the proportional and the integral parameters are adaptively changed following the disturbance. See Fig. 14b, c for more details.

Fig. 14
figure 14

The proposed fuzzy online controller in second scenario, a frequency performance, b proportional gain variations, and c integral gain variations

Full size image

In the third scenario, the tracking performance of the proposed fuzzy controller is evaluated regarding the successive load changes. Results are demonstrated in Fig. 15. As illustrated, the fuzzy-based controller reveals a satisfactory performance against the load variations and effectively settles down the frequency deviations. This controller adopts the proportional and integral controllers in an online manner as seen in Fig. 15b, c. Suitable gain adjustments are performed against the online load variations to stabilize the whole system. These remarks confirm outperformance of the proposed fuzzy based controller following the initial adjustments performed based on the Kharitonov theorem. Accordingly, a reliable frequency response is attained for both the system parameters and load changing uncertainties.

Fig. 15
figure 15

The proposed fuzzy online controller in third scenario, a frequency performance, b proportional gain variations, and c integral gain variations

Full size image

6 Conclusion

This study intended to assess performance of a robust and intelligent method in a parallel structure for an efficient LFC structure against the uncertainties in parameters and load changes. The proposed controller was implemented in two stages. At the first stage, the Kharitonov theorem yielded an initial robust solution for the proportional and integral gain values pursuing the Routh–Hurwitz criterion. The simulation results approved well performance of this controller against the CPI controller facing with uncertainties in control parameters. The main shortcoming of the established Kharitonov-based controller was revealed as its inability in handling the uncertainties in load variations. Accordingly, at the second stage, an online fuzzy-based fine tuning approach was proposed to intelligently tune the gain values in the LFC structure. The outperformance of the proposed two-stage controller was certified in attaining a satisfactory frequency response in the investigated test system.