1 Introduction

Since Einstein developed general relativity in (1915), various attempts with different motivations have been carried out to generalize it [1]. Some of these motivations come from observations and inconsistencies between general relativity and observational data, which include the evolution of the Universe in very early time [2,3,4], late-time accelerated expansion [5,6,7,8], and singularity problem [9,10,11]. On the other hand, some inconsistencies between general relativity and quantum mechanics encourage people to modify general relativity by adding terms including Ricci scalar and its derivatives [12]. Moreover, from the string theory viewpoint as a robust modern theory in modern physics, Einstein’s gravity is only an effective low-energy theory that will receive higher-order corrections that become important as the energy scale increases [13].

Einstein himself introduced one of the original modified theories by adding a term including the cosmological constant [14]. It is confirmed general relativity field equations include the cosmological constant well fixed with observations [15, 16]. However, this model suffers from two coincidence and fine-tuning problems [17,18,19]. Eddington proposed another interesting alternative to general relativity in 1924 [20]. Following him, the Brans–Dicke theory [21] and the Einstein–Cartan theory [22] are two other alternative theories. However, after discovering dark energy and dark matter as two mysterious components, extending general relativity motivates many people to explore different plausible candidates for these new components.

The main modified gravity theories are focused on generalizing the gravitational Lagrangian through space–time curvature \(R\) including \(f(R)\) gravity [23,24,25,26]\(f(R,T)\). See [27,28,29,30,31,32] to review other alternative theories in general relativity and their applications. However, like other candidates, one could present the modified theories by generalizing the form of the matter Lagrangian in a nonlinear way such as adding energy–momentum squared term \({T}_{\mu \nu }{T}^{\mu \nu }\) [33]. These theories are more radical than other forms of fluid stress, like bulk viscosity or scalar fields. Considering this specific theory shows how the emergent Universe allows an expanding thermal history without the big-bang singularity for the spatially flat Universe [33]. Also, its black hole solution in the presence of the electromagnetic field and some aspects of the evolution of the Universe are investigated, respectively, in [33, 34].

Here, we attempt to reconsider the evolution of the cosmos through this modified gravity theory. In the following of this study, in Sec. II, we have derived the field equation of \(R-2\Lambda +\alpha {T}_{\mu \nu }{T}^{\mu \nu }\) gravity in the metric formalism. We also have shown how the interpretation of the cosmological constant gives different field equations. Consequently, in Sects. 3–5, the evolution of the Universe for three different interpretations of the dark energy field is considered. The conclusion comes in Sect. 6.

Throughout this paper, we adopt the Planck units, i.e., \(c=\hslash =G=1\) while reducing Planck mass \({M}_{P}^{2}={\left(8\pi \right)}^{-1}\).

2 Energy–momentum squared gravity

In the presence of a cosmological constant, the action of energy–momentum squared gravity is given by [33]

$$ S = \frac{1}{2\kappa }\int \sqrt { - g} \left[ {R - 2\Lambda - \alpha T_{\mu \nu } T^{\mu \nu } } \right]{\text{d}}^{4} x + \int \sqrt { - g} {\mathcal{L}}_{m} \,{\text{d}}^{4} x $$
(1)

in which \(\kappa =8\pi \), \(\alpha \) is the arbitrary constant of the model with mass dimension \({[M]}^{-6}\), \(g\) is the determinant of the metric \({g}_{\mu \nu }\), \({\mathcal{L}}_{m}\) presents matter Lagrangian, \(\Lambda \) denotes cosmological constant, and \({T}_{\mu \nu }{T}^{\mu \nu }\) is a self-contracting term of the energy–momentum tensor. Due to adding energy–momentum squared term to action, in an early Universe with high energy density, action (1) is different from the standard general relativity, while by going to lower energies, this deviation has to disappear. The action (1) can be rewritten as follows

$$ S = \int \sqrt { - g} \left[ {\frac{R - 2\Lambda }{{2\kappa }} + {\mathcal{L}}_{m,e} } \right]{\text{d}}^{4} x,\quad {\mathcal{L}}_{m,e} = {\mathcal{L}}_{m} - \frac{{\alpha T_{\mu \nu } T^{\mu \nu } }}{2\kappa } $$
(2)

Variation of action (1) with respect to metric gives a modified gravity field

$$ R_{\mu \nu } - \frac{1}{2}g_{\mu \nu } R + \Lambda g_{\mu \nu } = \kappa T_{\mu \nu }^{e} $$
(3)

where we have defined effective energy–momentum tensor

$$ T_{\mu \nu }^{e} = T_{\mu \nu } + \frac{2\alpha }{\kappa }\left( {{\Theta }_{\mu \nu } + T_{\mu }^{\sigma } T_{\nu \sigma } - \frac{1}{4}T_{\alpha \beta } T^{\alpha \beta } g_{\mu \nu } } \right) $$
(4)

for

$$ {\Theta }_{\mu \nu } = - {\mathcal{L}}_{m} \left( {T_{\mu \nu } - \frac{1}{2}Tg_{\mu \nu } } \right) - \frac{1}{2}TT_{\mu \nu } - 2T^{\alpha \beta } \frac{{\partial^{2} {\mathcal{L}}_{m} }}{{\partial g^{\mu \nu } \partial g^{\alpha \beta } }} $$
(5)

Obviously, for \(\alpha = 0\), the field Eq. (3) recasts to the usual Einstein field equations in the presence of cosmological constant \(\Lambda \). Moreover, Eq. (4) presents further degrees of freedom in energy–momentum squared gravity that can be formally dealt with under the standard of perfect fluids. One could assume here that \({\mathcal{L}}_{m}\) is free of derivatives of the metric components. By considering the perfect fluid, we have

$$ T_{\mu \nu } = \left( {\rho + p} \right)u_{\mu } u_{\nu } + pg_{\mu \nu } , $$
(6)

Consequently, the energy–momentum squared term is

$$ T_{\mu \nu } T^{\mu \nu } = \rho^{2} + 3p^{2} $$
(7)

where \(\rho\), \(p,\) and \(u_{\mu }\) denote the energy density, the pressure, and the co-moving four-velocity satisfying the condition \(u_{\mu } u^{\nu } = - 1\), respectively. Following [33, 35], by setting Lagrangian \({\mathcal{L}}_{m} = p\), the last term on the right-hand side of Eq. (5) cancels. As discussed in [33], the interpretation of the cosmological constant gives two general scenarios. In the first case, \({\Lambda }\) is considered the geometrical parameter and is written on the left-hand side of the Einstein equations. In this case, the field equation is given by

$$ G_{\mu \nu } + {\Lambda }g_{\mu \nu } = \kappa \left( {\left( {\rho + p} \right)u_{\mu } u_{\nu } + pg_{\mu \nu } } \right) - \alpha \left( {\frac{1}{2}\left( {\rho^{2} + 3p^{2} } \right)g_{\mu \nu } + \left( {\rho + p} \right)\left( {\rho + 3p} \right)u_{\mu } u_{\nu } } \right) $$
(8)

where \(G_{\mu \nu } = R_{\mu \nu } - \frac{1}{2}g_{\mu \nu } R\) is the Einstein tensor. The right-hand side of Eq. (8) illustrates that we no longer deal with a standard perfect fluid. It indicates the whole budget of energy–momentum squared terms does not come from standard matter fields only and comes from the non-Einsteinian part of the gravitational interaction [35]. On the other hand, the cosmological constant can be a part of the matter action. In this case, the total energy–momentum tensor is given by

$$ T_{\mu \nu }^{t} = T_{\mu \nu } + T_{\mu \nu }^{{\Lambda }} $$
(9)

Consequently, the field Eq. (3) can be written as [33]

$$ R_{\mu \nu } - \frac{1}{2}g_{\mu \nu } R + {\Lambda }g_{\mu \nu } = \kappa T_{\mu \nu }^{e} + {\Phi }_{\mu \nu } $$
(10)

in which

$$ \begin{aligned} {\Phi }_{\mu \nu } & = 2\alpha \left( {{\tilde{\Theta }}_{\mu \nu } + \tilde{T}^{\alpha \beta } \frac{{\delta T_{\alpha \beta } }}{{\delta g^{\mu \nu } }} + T^{\alpha \beta } \frac{{\delta \tilde{T}_{\alpha \beta } }}{{\delta g^{\mu \nu } }} + \tilde{T}_{\mu \sigma } T_{\nu }^{\sigma } + T_{\mu }^{\sigma } \tilde{T}_{\sigma \nu } } \right. \\ & \quad + \tilde{T}_{\mu \sigma } \tilde{T}_{\nu \varrho } g^{\varrho \sigma } - \frac{1}{4}g_{\mu \nu } \left( {\tilde{T}_{\alpha \beta } \tilde{T}^{\alpha \beta } + 2\tilde{T}_{\alpha \beta } \tilde{T}^{\alpha \beta } } \right) \\ \end{aligned} $$
(11)

where over tilde presents a parameter related to the cosmological constant. As shown in [33], \({\Phi }_{\mu \nu }\) does not vanish in general interpretation and thus in this case field equations are more complicated than the case in which \(\Lambda \) is interpreted as the geometrical parameter. The field Eqs. (8) and (10) give two general dark energy models. Equation (8) obtains pure cosmological constant dark energy with some deviations in the evolution of matter field, while field Eq. (10) yields dark energy as matter field includes two parts, cosmological constant and terms arise from energy–momentum squared part. However, one can assume the third scenario in which dark energy comes from a mix of two previous scenarios in which dark energy includes a geometrical part, cosmological constant, and the energy–momentum squared term as matter part. This scenario presents dark energy as a geo-matter field. Hence, the last scenario is same field equation given in (8), while the energy–momentum squared term is investigated as matter part of dark energy, not matter field. These scenarios are summarized as

$$ G_{\mu \nu } + \underbrace {{{\Lambda }g_{\mu \nu } }}_{{{\text{D}}.{\text{E}}.}} = \underbrace {{\kappa T_{\mu \nu } + \alpha \psi \left( {T_{\mu \nu } T^{\mu \nu } } \right)}}_{{{\text{Matter}}}} $$
(12)
$$ G_{\mu \nu } = \underbrace {{\kappa T_{\mu \nu } }}_{{{\text{Matter}}}} + \underbrace {{\alpha {\Upsilon }\left( {T_{\mu \nu } T^{\mu \nu } } \right) - {\Lambda }g_{\mu \nu } }}_{{{\text{D}}.{\text{E}}.}} $$
(13)
$$ G_{\mu \nu } + \underbrace {{{\Lambda }g_{\mu \nu } }}_{{{\text{D}}.{\text{E}}.}} = \underbrace {{\kappa T_{\mu \nu } }}_{{{\text{Matter}}}} + \underbrace {{\alpha \psi \left( {T_{\mu \nu } T^{\mu \nu } } \right)}}_{{{\text{D}}.{\text{E}}.}} $$
(14)

where \(\psi \) and \(\Upsilon \) are extra terms in field Eqs. (8) and (10). Equations (12)–(14) present these three plausible scenarios for dark energy. In Eq. (12), extra terms from the energy–momentum squared term are investigated as matter fields, while the cosmological constant stays on the left-hand side as the geometrical term. Field Eq. (13) presents the second scenario in which the cosmological constant is located on the right-hand side as part of the matter field. In this scenario, we assume dark energy arises from the cosmological constant and energy–momentum squared term which satisfies Eq. (10). The last scenario illustrates dark energy as the geometrical-matter mixed field, and cosmological constant plays the geometrical role of dark energy, while terms from energy–momentum squared part are matter sector of dark energy. In Sects. 3–5, these scenarios are studied.

3 Geometrical viewpoint

In this section, we review the model in which cosmological constant is considered as the geometrical property of gravity field and so extra terms in Eq. (8) are part of the matter component. Furthermore, in order to study the evolution of the cosmos, we suppose the Universe is homogenous and isotropic space–time and described through the metric of the Friedmann–Robertson–Walker

$$ {\text{d}}s^{2} = - {\text{d}}t^{2} + a^{2} \left( {\frac{{{\text{d}}r^{2} }}{{1 - kr^{2} }} + r^{2} {\text{d}}\theta^{2} + r^{2} \sin^{2} \theta \,{\text{d}}\phi^{2} } \right) $$
(15)

where \(k = 1, 0,\) and \(- 1\) is corresponding to the closed, flat, and open Universe, respectively, and the \(a = a\left( t \right)\) is the scale factor. Although Wang et al. [36] have proposed cosmological model independent to spatial curvature in which evolution of Universe can extract from other values of \(k\), following the recent observations and cosmological constant model, the Universe is flat spatially, and so we set \(k = 0\) [37]. Using metric (15) in field Eq. (8) gives the following modified Friedmann equations

$$ 3H^{2} = \kappa \rho + \Lambda - \frac{\alpha }{2}\left( {\rho^{2} + 3p^{2} + 8\rho p} \right) $$
(16)
$$ 3\frac{{\ddot{a}}}{a} = - \frac{\kappa }{2}\left( {\rho + 3p} \right) + \Lambda + \alpha \left( {\rho^{2} + 3p^{2} + 2\rho p} \right) $$
(17)

where \(H = \dot{a}/a\) is Hubble parameter. From conservation law, the continuity equation becomes

$$ \kappa \left( {\dot{\rho } + 3H\left( {\rho + p} \right)} \right) - \alpha \left( {\rho \dot{\rho } + 3p\dot{p} + 4\dot{\rho }p + 4\rho \dot{p} + 3H\left( {\rho^{2} + 3p^{2} + 4\rho p} \right)} \right) = 0 $$
(18)

For simplicity, we assume that the matter field behaves such as barotropic fluid in which \(p = \omega \rho\). Rewriting Eq. (18) gives,

$$ \dot{\rho } + 3H\left( {1 + \omega } \right)\rho - \tilde{\alpha }\left[ {\zeta \rho \dot{\rho } + 3\xi H\rho^{2} } \right] = 0 $$
(19)

where \(\tilde{\alpha } = \alpha /\kappa\) and we define

$$ \zeta \equiv 1 + 8\omega + 3\omega^{2} $$
(20)
$$ \xi \equiv 1 + 4\omega + 3\omega^{2} $$
(21)

These two defined parameters are reduced to \(1\) in the absence of radiation component, while matter supposed as dust field. However, we keep \(\omega \) in these parameters to find general form of energy density of matter. The differential Eq. (19) has no exact solution. Assuming \(|\alpha |\ll 1\), we can solve Eq. (19) using a perturbative method up to the arbitrary order and consider a solution as

$$\rho ={\rho }_{0}+\delta {\rho }_{1}+\cdots $$
(22)

where \({\rho }_{0}\) is the solution without squared terms and correction \(\delta {\rho }_{1}\) satisfies the following differential equation,

$$\delta {\dot{\rho }}_{1}+3H\left(1+\omega \right)\delta {\rho }_{1}-\widetilde{\alpha }\left[\zeta {\rho }_{0}{\dot{\rho }}_{0}+3\xi H{\rho }_{0}^{2}\right]=0$$
(23)

Applying the perturbative method obtains,

$$\rho ={c}_{1}{a}^{-3\left(1+\omega \right)}\left(1+\widetilde{\alpha }{c}_{1}\left(\zeta -\frac{\xi }{1+\omega }\right){a}^{-3\left(1+\omega \right)}\right)$$
(24)

where \({c}_{1}\) is an integration constant. Observations demonstrate that matter, baryonic and dark matter, and dark energy components play a key role in the evolution of the Universe in late time [37]. Thus, by ignoring radiation energy density in the whole of this study, Eq. (24) presents the evolution of matter and we set \({c}_{1}={\rho }_{m0}\). With aid of the definition of fractional energy density

$${\Omega }_{m}\equiv \frac{\kappa \rho }{3{H}^{2}}$$
(25)

for the current Universe, \(a\left({t}_{0}\right)=1\), we get

$${\Omega }_{m0}=\frac{\kappa {\rho }_{m0}}{3{H}_{0}^{2}}\left(1+\widetilde{\alpha }{\rho }_{m0}\left(\zeta -\frac{\xi }{1+\omega }\right)\right)$$
(26)

Moreover, the first Friedmann Eq. (16) recasts to

$$1={\Omega }_{m0}+{\Omega }_{\Lambda }-\frac{\widetilde{\alpha }}{2}\zeta {\Omega }_{m0}^{2}$$
(27)

To find constraints on this model, we use observational data, \({\Omega }_{m0}\approx 0.32\), \({\Omega }_{\Lambda }\approx 0.68,\) and \({H}_{0}\approx 67.4\) [37]. Solving Eqs. (26) and (27) for \(\widetilde{\alpha }\) and \(\omega \) yields

$$ \alpha = \kappa \tilde{\alpha } \approx - 3.97 \times 10^{ - 6} ,\quad \omega = 0 $$
(28)

It shows that energy–momentum squared gravity does not disturb the standard cosmic evolution in late time for geometrical interpretation of the cosmological constant scenario. However, analyzing this scenario and using the cosmological data may give some deviations in cosmological parameters during matter-dominated era [33,34,35]. In order to show this, we have plotted the behavior of the effective equation of the state \({\omega }_{e}\) in Fig. 1 for \(\omega =0\).

Fig. 1
figure 1

The evolution of the effective equation of state of the model (red curved), compared with \(\mathrm{\Lambda CDM}\) theory (blue curved) versus redshift for the same initial conditions

Full size image
$${\omega }_{e}=-1-\frac{2\dot{H}}{3{H}^{3}}$$
(29)

As shown, the deviation of the effective equation of state of the model is not too large with respect to its corresponding parameter in the \(\mathrm{\Lambda CDM}\) model; its error is around \(\sim 6\%\) in \(z\approx 4\).

4 \({\varvec{\Lambda}}\) as matter sector

In this section, the second scenario in which the cosmological constant behaves as part of the matter field is investigated. Thus, as shown in [33] and Sect. 2, this interpretation of cosmological constant satisfies field Eq. (10) for \({\Phi }_{\mu \nu }\ne 0\). Therefore, Friedmann equations for the such scenario are given by

$$3{H}^{2}=\kappa \rho +\Lambda -\frac{\alpha }{2}\left({\rho }^{2}+3{p}^{2}+8\rho p\right)+\frac{\alpha\Lambda }{2}\left(3\rho -p+\frac{2\Lambda }{\kappa }\right)$$
(30)
$$3\frac{\ddot{a}}{a}=-\frac{\kappa }{2}\left(\rho +3p\right)+\Lambda +\alpha \left({\rho }^{2}+3{p}^{2}+2\rho p\right)-\frac{2\alpha\Lambda }{\kappa }\left(2p-\frac{\Lambda }{\kappa }\right)$$
(31)

In this case, since the cosmological constant is treated as part of the matter field, we assume dark energy includes two parts, the cosmological constant and terms that arise from the energy–momentum squared part, see Eq. (13). As a result, the effective energy density and pressure of dark energy becomes, respectively

$${\rho }_{X}=\Lambda -\frac{\alpha }{2}\left({\rho }^{2}+3{p}^{2}+8\rho p\right)+\frac{\alpha\Lambda }{2}\left(3\rho -p+\frac{2\Lambda }{\kappa }\right)$$
(32)
$${p}_{X}=-\Lambda -\frac{\alpha }{2}\left({\rho }^{2}+3{p}^{2}\right)-\frac{\alpha\Lambda }{2}\left(\rho -3p+\frac{2\Lambda }{\kappa }\right)$$
(33)

Obviously, for \(\alpha =0\), we get \({\omega }_{X}=-1\) and so this model coincides with \(\mathrm{\Lambda CDM}\) theory. With the same process and using barotropic fluid assumption \(p=\omega \rho \), Eqs. (32) and (33) become

$${\rho }_{X}^{[e]}=\Lambda -\frac{\alpha }{2}\zeta {\rho }^{2}+\frac{\alpha\Lambda }{2}\left(\left(3-\omega \right)\rho +\frac{2\Lambda }{\kappa }\right)$$
(34)
$${p}_{X}^{[e]}=-\Lambda -\frac{\alpha }{2}\left(\xi -4\omega \right){\rho }^{2}-\frac{\alpha\Lambda }{2}\left(\left(1-3\omega \right)\rho +\frac{2\Lambda }{\kappa }\right)$$
(35)

where \({\rho }_{X}^{[e]}\) and \({p}_{X}^{[e]}\) denote effective energy density and pressure of dark energy, respectively. The equation of the state of dark energy becomes

$${\omega }_{X}=-1+\frac{2\kappa \rho \left(1+\omega \right)\left(\left(3\omega +1\right)\rho -\Lambda \right)}{\left(\zeta {\rho }^{2}+\Lambda \rho \left(\omega -3\right)\right)\kappa -2{\Lambda }^{2}-2\kappa\Lambda /\alpha }$$
(36)

Using \({\omega }_{X0}=-1\) and solving Eqs. (30) and (36) for the current Universe give two plausible constraint sets on the constant \(\alpha \) and cosmological constant:

$$ {\Lambda } = 3H_{0}^{2} \left( {1 - {\Omega }_{m0} } \right),\quad \alpha = 0. $$
(37)
$$ {\Lambda } = \frac{{3H_{0}^{2} {\Omega }_{m0} }}{\kappa }\left( {1 + 3\omega } \right),\quad \alpha = - \left( {\frac{\kappa }{{3{\Omega }_{m0} H_{0} }}} \right)^{2} \frac{{\left( {{\Omega }_{m0} \left( {1 + 3\omega } \right) - \kappa \left( {1 - {\Omega }_{m0} } \right)} \right)}}{{\kappa \left( {1 - 3\omega^{2} } \right) + \left( {1 + 3\omega } \right)^{2} }} $$
(38)

In the first case, canceling out the energy–momentum squared term gives \(\mathrm{\Lambda CDM}\) model and so it presents no new dark energy theory.

Substituting the second set of constraints (38) into the equation of state (36) and using current observational data reveal to have accelerated expansion in late time, the equation of state of matter must be small, \(0\le \omega <2\times {10}^{-2}\). As result, Eq. (36), the coupling constant of energy–momentum squared gravity, and cosmological constant become, respectively

$${\omega }_{X}=-1+\frac{2\kappa \rho \left(\rho -\Lambda \right)}{\left(\zeta {\rho }^{2}-3\Lambda \rho \right)\kappa -2{\Lambda }^{2}-2\kappa\Lambda /\alpha }$$
(39)
$$\alpha =-{\left(\frac{\kappa }{3{\Omega }_{m0}{H}_{0}}\right)}^{2}\frac{\left({\Omega }_{m0}-\kappa \left({1-\Omega }_{m0}\right)\right)}{\kappa +1}$$
(40)
$$\Lambda =\frac{3{H}_{0}^{2}{\Omega }_{m0}}{\kappa }$$
(41)

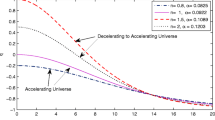
where we set \(\omega =0\). Comparing Eq. (41) with its corresponding value in the \(\mathrm{\Lambda CDM}\) model shows the second set of constraints (38) coincides with the cosmological constant theory for \({\Omega }_{m0}\approx 0.96\). Thus, the second case (38) behaves such as \(\mathrm{\Lambda CDM}\) theory during pick of the matter-dominated era, only. In Fig. 2, the behavior of the equation of state of dark energy for this case is plotted. For high redshift, it behaves like matter component when \({\omega }_{X}\to 1,\) while in current time it is about \(\sim -1\) and in near future it goes to \(\approx -0.52\) for \(z\approx -0.43\). However, its value grows up and treats such as cosmological constant at \(z=-1\), again. It indicates dark energy keeps its negative pressure in the evolution of the Universe as main cosmic component.

Fig. 2
figure 2

Evolution of equation of state of dark energy versus redshift for the second scenario. We set \(\omega =0\)

Full size image

However, this scenario gives no valuable model. To show this, by using the definition of deceleration parameter and using Eqs. (32) and (33), we get

$$q=-1-\frac{\dot{H}}{{H}^{2}}=-1-\frac{3\rho \kappa \left(1+\omega \right)\left(\kappa -\left(\left(1+3\omega \right)\rho -\Lambda \right)\alpha \right)}{\left(\zeta {\rho }^{2}+\kappa \rho\Lambda \left(\omega -3\right)-2{\Lambda }^{2}\right)\alpha -2\rho {\kappa }^{2}-2\kappa\Lambda }$$
(42)

For small values of \(\omega \), the deceleration parameter becomes

$$q=-1-\frac{3\rho \kappa \left(\kappa -\left(\rho -\Lambda \right)\alpha \right)}{\left(\zeta {\rho }^{2}-3\kappa \rho\Lambda -2{\Lambda }^{2}\right)\alpha -2\rho {\kappa }^{2}-2\kappa\Lambda }$$
(43)

Although plotting Eq. (43) gives a transition point \({z}_{T}\approx 0.58\) which satisfies observations [38], for high redshifts \(q\to 2\) and so it does not give well matter structure formation during a matter-dominated era [39, 40]. Moreover, this case is not stable classically. To show that, we study perturbation effects in classical stability theory wherein the squared speed of the sound \({\upsilon }_{s}^{2}=\partial {p}_{X}/\partial {\rho }_{X}\) should be positive and \({\upsilon }_{s}^{2}\le 1\). The computing of this parameter gives negative \({\upsilon }_{s}^{2}\) for \(z<1.3\). Moreover, \({\upsilon }_{s}^{2}>1\) for \(0\le z\le 1.94\) which shows causality broken in this interval of redshift (Fig. 3).

Fig. 3
figure 3

Deceleration parameter as a function of redshift for \(\omega =0\)

Full size image

In the short conclusion, assuming cosmological constant as part of matter field gives valuable evolution of the Universe only for \(\alpha =0\). In other words, by assuming the second scenario, Eq. (13), when \(\alpha \ne 0\), the model is not stable classically and gives no valuable matter structure formation in high redshifts (Fig. 4).

Fig. 4
figure 4

Squared speed of sound for this scenario versus redshift. We set \(\omega =0\)

Full size image

5 Dark energy as a geometrical-matter field component

As the last possible scenario, one can assume that dark energy fluid is a geometrical-matter field in which cosmological constant built geometrical part and terms arise from a squared part of the action (1) constructed matter sector. As result, one can use same Eqs. (16)–(18) for this scenario when effective energy density of dark energy becomes (we set \(p=\omega \rho \)),

$${\rho }_{X}^{[e]}=\Lambda -\frac{\alpha \zeta }{2}{\rho }^{2}$$
(44)

where the energy density of matter field calculated through perturbative method and given by Eq. (24). By ignoring effects of radiation in late-time evolution and assuming matter as pressureless field, \(\omega =0\), the energy density (24) shrinks to standard energy density of matter,

$$\rho ={\rho }_{m0}{a}^{-3}$$
(45)

As result, Friedmann equations for a flat Universe become

$$3{H}^{2}=\kappa \rho +\Lambda -\frac{\alpha }{2}{\rho }^{2}$$
(46)
$$3\frac{\ddot{a}}{a}=-\frac{\kappa }{2}\rho +\Lambda +\alpha {\rho }^{2}$$
(47)

Thus, the effective energy density and pressure of dark energy in this scenario are given by, respectively

$${\rho }_{X}^{[e]}=\Lambda -\frac{\alpha }{2}{\rho }^{2}$$
(48)
$${p}_{X}^{[e]}=-\Lambda -\frac{\alpha }{2}{\rho }^{2}$$
(49)

To develop this scenario in the absence of radiation, it is worthwhile to define the following fractional energy density of different terms of the model as

$$ {\Omega }_{{\Lambda }} \equiv \frac{{\Lambda }}{{3H^{2} }},\quad {\Omega }_{m} \equiv \frac{\kappa \rho }{{3H^{2} }},\quad {\Omega }_{\psi } \equiv \frac{{\alpha \rho^{2} }}{{6H^{2} }} . $$
(50)

As result, the fractional energy density of dark energy becomes

$${\Omega }_{X}={\Omega }_{\Lambda }-{\Omega }_{\psi }$$
(51)

By using e-number \(x=\mathrm{ln}(a)\), evolution of \({\Omega }_{X}\) becomes

$${\Omega }_{X}^{\mathrm{^{\prime}}}+3\left(2{\Omega }_{\psi }{-\Omega }_{m}\right){\Omega }_{X}-6{\Omega }_{\psi }=0$$
(52)

where we use

$${\Omega }_{m}^{^{\prime}}+3{\Omega }_{m}\left(1+2{\Omega }_{\psi }-{\Omega }_{m}\right)=0$$
(53)
$${\Omega }_{\psi }^{^{\prime}}+3{\Omega }_{\psi }\left(2-{\Omega }_{m}+2{\Omega }_{\psi }\right)=0$$
(54)

The prime denotes derivative with respect to \(x\). Equation (52) presents evolution of dark energy component in the last possible scenario. For late-time Universe in which energy density of matter vanished, \({\Omega }_{m}\to 0\), the energy density of matter sector of dark energy goes to zero, \({\Omega }_{\psi }\to 0\), and thus, \({\Omega }_{X}=\mathrm{const}.\)

In order to find observational constraints on the model, solving Eqs. (53) and (54) gives

$$ {\Omega }_{\psi } = \frac{{c_{2} }}{{c_{3} e^{6x} + 6e^{3x} - c_{2} }},\quad {\Omega }_{m} = \frac{{ - 6e^{ - 3x} }}{{c_{2} e^{ - 6x} - 6e^{ - 3x} + c_{3} }} $$
(55)

where \(c_{2}\) and \(c_{3}\) are constants. Using Eqs. (46), (50), and (55) for the current Universe, we find

$$ c_{2} = \frac{{c_{3} {\Omega }_{m0} + 6\left( {{\Omega }_{m0} - 1} \right)}}{{{\Omega }_{m0} }},\quad {\Omega }_{{\Lambda }} = \frac{{c_{3} {\Omega }_{m0} }}{6} $$
(56)

The deceleration parameter for this model becomes,

$$q=-\frac{\ddot{a}a}{{\dot{a}}^{2}}=\frac{1}{2}\left(1-\frac{3\left(\Lambda +\frac{\mathrm{\alpha }}{2}{\rho }^{2}\right)}{\kappa \rho +\Lambda -\frac{\alpha }{2}{\rho }^{2}}\right)$$
(57)

which for \(\alpha \to 0\), it coincides with the \(\Lambda \)CDM model. The evolution of the deceleration parameter is plotted in Fig. 5. It indicates the model is not in conflict with the \(\Lambda \)CDM model.

Fig. 5
figure 5

Deceleration parameter versus redshift for \(\varepsilon =0.05\) (red curve), \(\varepsilon =0.1\) (green curve), \(\varepsilon =0.2\) (purple curve) compared with \(\Lambda \)CDM model (blue curve)

Full size image

Using Eqs. (48) and (49), the equation of state of dark energy is given by

$${\omega }_{X}=-1-\frac{2{\Omega }_{\psi }}{1-{\Omega }_{m}}=-1+\frac{12-2\left({c}_{3}+6\right){\Omega }_{m0}}{{c}_{3}{\Omega }_{m0}{e}^{6x}-\left(6+{c}_{3}\right){\Omega }_{m0}+6}$$
(58)

where Eq. (55) are used. As result, for \({c}_{3}=-6+6/{\Omega }_{m0}\), model coincides with \(\Lambda \)CDM theory. This value of \({c}_{3}\) cancels out \({\Omega }_{\psi }\) which implies \(\alpha =0\). Hence, \({c}_{3}\ne -6+6/{\Omega }_{m0}\) gives some deviations from \(\Lambda \)CDM theory in which the energy–momentum squared part is preserved, \(\alpha \ne 0\). Consequently, it indicates the equation of state of dark energy in late time must be opposite to \(-1\) which supports by some independent observations [41,42,43]. In follows, we assume \({c}_{3}=-6+\varepsilon +6/{\Omega }_{m0}\) in which \(\varepsilon \) is depending on coupling constant \(\alpha \),

$$\varepsilon =\frac{9\alpha {\Omega }_{m0}{H}_{0}^{2}}{{\kappa }^{2}}$$
(59)

which gives \(\alpha \approx 48\times {10}^{-3}\varepsilon \). In Fig. 6, we have plotted the evolution of the equation of the state of dark energy in the last scenario (14) for some positive values of \(\varepsilon \) as a function of redshift. As shown, the model for \(\varepsilon =0\) gives \(\Lambda \)CDM theory, while for \(\varepsilon \ne 0\), the model presents quintessence dark energy which behaves like matter in high redshift values, \({\omega }_{X}=1,\) and treats such as a cosmological constant in near future.

Fig. 6
figure 6

The equation of state of dark energy as a function of redshift for \(\varepsilon =0.1\) (red curve), \(\varepsilon =0.2\) (green curve), \(\varepsilon =0.3\) (purple curve) compared with \(\Lambda \)CDM model (blue curve)

Full size image

As discussed, the equation of state of this model behaves like matter in past, and thus, at an earlier time the matter component is greater than in the best fits of the standard cosmological model. Accordingly, it is necessary to explore structure formation to see whether this dark energy would affect the growth rate of density perturbation or not. We investigate structure formation by modifying CAMB module [44]. As the first step, we have studied the angular spectrum of the CMB spectrum in Fig. 7. As shown, our model coincides with the ΛCDM model with small errors. The largest difference in the CMB TT spectrum between our model and the ΛCDM model is about \(\sim 18\%\) for \(\varepsilon =0.05\) at \(\mathcal{l}\approx 875\).

Fig. 7
figure 7

The theoretical CMB TT spectrum (dashed red curve), compared with the \(\Lambda \)CDM model (solid black curve) for \(\varepsilon =0.05\)

Full size image

Considering the CMB spectrum indicates dark energy in our model has no effective influence on structure formation when it behaves as matter during the matter-dominated era. Investigating the linear matter power spectrum confirms these results in which the model satisfies observational data (Fig. 8). The errors in the linear matter power spectrum for \(z=0\) are around \(\approx 0.85\%\) for \(k=5.5\times {10}^{-2}\).

Fig. 8
figure 8

The linear matter power spectrum of the model (dashed red curves) compared with observational data (solid black curves) for \(\varepsilon =0.05\)

Full size image

Furthermore, investigating the squared speed of the sound \({\upsilon }_{s}^{2}=\partial {p}_{X}/\partial {\rho }_{X}\) demonstrates model preserves causality, \({\upsilon }_{s}^{2}=1\), and thus, model is stable, classically.

6 Remarks

The exploring accelerated expansion of the late-time Universe needs to introduce a new mysterious component, called dark energy. The origin of this cosmic component is not clear, and thus, people with different approaches attempt to find a well-fixed dark energy model with observations. In this context, alternative theories in general relativity are considered one robust tool. In this study, we try to rebuild dark energy by reconsidering the new modified gravity theory in which the energy–momentum squared term is added to the usual Einstein-Hilbert action in the presence of a cosmological constant. As shown in Ref. [33], unlike Einstein’s field equation, the interpretation of the cosmological constant plays a key role. If it is suggested as the geometrical effect of space–time, one could keep it on the left-hand side and thus extra terms arise from energy–momentum squared term only effects on matter evolution. In such a model, dark energy is given by a cosmological constant. However, if we assume that the cosmological constant plays a part in the matter field, one finds out the additional term on the right-hand side of the field equation which it is depending on the cosmological constant and coupling constant \(\alpha \). In other words, dark energy can be assumed as a non-Einsteinian matter source including cosmological constant and energy–momentum squared terms. As result, these two interpretations of cosmological constant give two different field equations. In the first case, the cosmological constant presents dark energy as a geometrical component, while in the second case, dark energy includes the cosmological constant and its coupling with energy–momentum squared terms and plays as a non-familiar matter field. However, we can propose another case in which dark energy arises from geometrical effects, the cosmological constant, and matter field effects, terms from the energy–momentum squared part. In this study, we have investigated these three scenarios for dark energy. As discussed, the first model gives a pure cosmological constant model for dark energy, while we have some deviations in the evolution of matter. Although the second scenario obtains well dark energy model, this theory suffers from stability and structure formation during a matter-dominated era when \(\alpha \ne 0\) and so energy–momentum squared term preserved. The last case, geo-matter dark energy, gives a good candidate in which the model deviates so small from the \(\mathrm{\Lambda CDM}\) model. In this scenario, dark energy behaves like quintessence field. Since dark energy depends on matter field, coincidence problem is alleviated. Furthermore, in this case, the fine tuning is avoided, because dark energy is not associated only with \(\Lambda \), but with the energy density of squared matter field, \(\propto {\rho }^{2}\).