Thermal shock problem in porous orthotropic medium with three-phase-lag model

Abstract

The present article deals with the thermal shock response in homogeneous orthotropic medium under the purview of three-phase-lag model in the presence of voids. The normal mode analysis is used to obtain a vector matrix differential equation which is then solved by eigenvalue approach. In order to illustrate the analytical developments, the numerical solution is carried out and the results for stress, displacement and temperature are presented graphically. Comparison of stress, displacement and temperature for different thermoelastic models such as Lord–Shulman (LS) and Green–Naghdi-III (GN-III) is observed, and it is noticed that the value of all parameters is maximum for the LS model and minimum for the GN-III model.

1 Introduction

The theory of elastic materials with voids developed by Nunziato and Cowin [1] and Cowin and Nunziato [2] is one of the generalizations of the classical theory of elasticity which deals with the elastic materials consisting of small pores (voids). This new theory has applications in investigating geophysical, biological and synthetic porous materials. This theory can also be extended and applied in viscoelastic, micropolar and thermoelastic materials. Iesan [3] proposed a theory for thermoelastic materials with voids and Iesan [4] represented a theory of initially stressed thermoelastic materials with voids. Ciarletta and Scarpetta [5] proved uniqueness, reciprocity and variational theorems for generalized thermoelastic theory for non-simple materials with voids.

The generalized thermoelasticity theories have been developed with the aim of removing the paradox of infinite speed of heat propagation inherent in the classical coupled dynamical thermoelasticity theory. Lord and Shulman [6] first modified Fourier’s law by introducing the term representing the thermal relaxation time. The heat equation associated with this theory is a hyperbolic type, and it eliminates the paradox of infinite speed of propagation. The following Green and Lindsay [7] developed a more general theory of thermoelasticity by introducing two relaxation times. Later, Green and Naghdi [8,9,10] developed three models for generalized thermoelasticity of homogeneous isotropic materials which are known as models I, II, III. Detailed information regarding these theories can be found in [11, 12].The next generalization to the thermoelasticity is known as the dual-phase-lag model developed by Tzou [13]. Tzou [13] introduced two-phase lags to both the heat flux vector and the temperature gradient and considered as constitutive equation to describe the lagging behavior in the heat conduction in solids. Roychoudhuri [14] has established a generalized mathematical model of coupled thermoelasticity theory that includes three-phase lags in the heat flux vector, the temperature gradient and the thermal displacement gradient. The three-phase-lag model is very much useful in the problems of nuclear boiling, exothermic catalytic reactions, phonon–electron interactions, phonon-scattering, etc.

Baksi et al. [15] proposed magneto-thermoelastic problem with thermal relaxation and heat sources in three-dimensional infinite rotating elastic medium. Said [16] considered the influence of gravity on generalized magneto-thermoelastic medium for the three-phase-lag model. Othman et al. [17] considered the effect of magnetic field on generalized thermoelastic medium with two temperatures under the three-phase-lag model. Kalkal and Deswal [18] examined the effects of phase lags on three-dimensional wave propagation with temperature-dependent properties. El-Karamany and Ezzat [19] studied three-phase-lag linear micropolar thermoelasticity theory. Othman and Said [20] investigated a two-dimensional problem of magneto-thermoelasticity in fiber reinforced medium with three-phase-lag theory. Biswas et al. [21] discussed Rayleigh surface wave propagation in orthotropic thermoelastic solids with the three-phase-lag model. Abo-Dahab and Biswas [22] considered the effect of rotation on Rayleigh waves in magneto-thermoelastic transversely isotropic medium with thermal relaxation times. Biswas and Mukhopadhyay [23] employed the eigenfunction expansion method to analyze thermal shock behavior in magneto-thermoelastic orthotropic medium under three theories. El-Attar et al. [24] discussed phase-lag Green–Naghdi theory without energy dissipation for electro-thermoelasticity including heat sources. El-Karamany and Ezzat [25] considered fractional phase-lag Green–Naghdi thermoelasticity theories. Ezzat and El-Bary [26] proposed the unified GN model of thermoelasticity with the fractional order of heat transfer. Ezzat and El-Bary [27] considered electromagneto-thermoelastic interaction in thermoelastic solid with a cylindrical cavity. Ezzat and El-Bary [28] studied fractional magneto-thermoelasticity with Green–Naghdi theory. El-Karamany and Ezzat [29] discussed two-temperature Green–Naghdi theory of type-III in linear thermoelastic anisotropic solid. El-Karamany and Ezzat [30] considered thermoelastic problem with Green–Naghdi theory, and Ezzat et al. [31] studied fractional Fourier law with three-phase lag of thermoelasticity.

In this article, thermal shock response in orthotropic medium in the presence of voids is investigated. The problem is treated in the context of the three-phase-lag model of thermoelasticity. A vector matrix differential equation is formed by employing normal mode analysis which is then solved by eigenvalue approach. In order to illustrate the theoretical developments, the numerical results of stress, displacement and temperature for Lord–Shulman (LS), Green–Naghdi type-III (GN-III) and three-phase-lag (TPL) model are presented graphically.

2 Formulation of the problem

Let us consider a plane strain problem parallel to $xz$ plane of orthotropic thermoelastic medium. The body is initially at rest, and the surface $z = 0$ is assumed to be traction free. The surface of the half-space is subjected to a time-dependent thermal shock.

2.1 Basic equations

The basic governing equations of motion with the three-phase-lag thermoelastic model in anisotropic medium in the presence of voids are as follows:

• (a) Constitutive equations:

  $$ \sigma_{ij} = c_{ijkl} e_{kl} + B_{ij} \phi - \beta_{ij} T $$

  (1)
  $$ \rho ST_{0} = \rho C_{v} T + \beta_{ij} T_{0} e_{ij} + bT_{0} \phi $$

  (2)

• (b) Equation of motion:

  $$ \sigma_{ij,j} = \rho \ddot{u}_{i} $$

  (3)

• (c) Energy equation:

  $$ \rho \dot{S}T_{0} = - q_{i,i} $$

  (4)

• (d) Modified Fourier law with three-phase lags:

  $$ \left( {1 + \tau_{q} \frac{\partial }{\partial t} + \frac{{\tau_{q}^{2} }}{2}\frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\dot{q}_{i} = - \left[ {K_{ij} \left( {1 + \tau_{T} \frac{\partial }{\partial t}} \right)\dot{T}_{,j} + K_{ij}^{*} \left( {1 + \tau_{\nu } \frac{\partial }{\partial t}} \right)T_{,j} } \right] $$

  (5)

• (e) Balance of equilibrated forces:

  $$ A_{ij} \phi ,_{ij} - B_{ij} e_{ij} - \varsigma \phi + bT = \rho \chi \ddot{\phi } $$

  (6)

where $T$ is the temperature above reference temperature, $T_{0}$ is the reference uniform temperature of the body chosen such that $\left| {\frac{T}{{T_{0} }}} \right|$ $\ll 1$, $\rho$ is the mass density, $q_{i}$ are the components of the heat flux vector, $K_{ij}$ are the components of the thermal conductivity tensor, $K_{ij}^{*}$ are the material constant characteristic of the theory, $C_{v}$ is the specific heat at the constant strain, $c_{ijkl}$ are elastic constants, $\sigma_{ij}$ are the components of the stress tensor, $u_{i}$ are the components of the displacement vector, $e_{ij}$ are the components of the strain tensor, $S$ is the entropy per unit mass, $\beta_{ij}$ are the thermal moduli, $\tau_{q}$, $\tau_{T}$ and $\tau_{\nu }$ are the phase lags of heat flux, temperature gradient and thermal displacement gradient, respectively, where $0 \le \tau_{T} \le \tau_{q}$ and $t$ denotes time, $\phi$ is the void volume fraction field, $b$ is the measure of diffusion effects, $A_{ij} ,B_{ij}$ and $\varsigma$ are void parameters and $\chi$ is the equilibrated inertia. The comma notation is used for spatial derivatives.

We assume that the material parameters satisfy the inequality $0 \le \tau_{\nu } < \tau_{T} < \tau_{q}$ (Roychoudhuri [14]).

The displacement components have the following form:

$$ u = u(x,z,t),v = 0,w = w(x,z,t) $$

(7)

The stress–displacement–temperature relations (in the presence of voids) are given as

$$ \sigma_{xx} = c_{11} u_{,x} + c_{13} w_{,z} + B_{1} \phi - \beta_{1} T $$

(8)

$$ \sigma_{zz} = c_{13} u_{,x} + c_{33} w_{,z} + B_{3} \phi - \beta_{3} T $$

(9)

$$ \sigma_{xz} = c_{55} \left( {u_{,z} + w_{,x} } \right) $$

(10)

where $\sigma_{xx} ,\sigma_{zz} ,\sigma_{xz}$ are the stress components, $c_{ij}$ are the elastic constants, $\beta_{1}$ and $\beta_{3}$ are the thermal moduli.

The equations of motion are

$$ \sigma_{xx,x} + \sigma_{xz,z} = \rho \ddot{u} $$

(11)

$$ \sigma_{xz,x} + \sigma_{zz,z} = \rho \ddot{w} $$

(12)

The basic governing equations in porous orthotropic medium with the three-phase-lag model reduce to the following equations:

$$ c_{11} u_{,xx} + c_{55} u_{,zz} + \left( {c_{13} + c_{55} } \right)w_{,xz} + B_{1} \phi_{,x} - \beta_{1} T_{,x} = \rho \ddot{u} $$

(13)

$$ \left( {c_{13} + c_{55} } \right)u_{,xz} + c_{55} w_{,xx} + c_{33} w_{,zz} + B_{3} \phi_{,z} - \beta_{3} T_{,z} = \rho \ddot{w} $$

(14)

$$ \left( {A_{1} \phi_{,xx} + A_{3} \phi_{,zz} } \right) - \left( {B_{1} u_{,x} + B_{3} w_{,z} } \right) - \varsigma \phi + bT = \rho \chi \ddot{\phi } $$

(15)

$$ K_{1} \left( {1 + \tau_{T} \frac{\partial }{\partial t}} \right)\dot{T}_{,xx} + K_{3} \left( {1 + \tau_{T} \frac{\partial }{\partial t}} \right)\dot{T}_{,zz} + K_{1}^{*} \left( {1 + \tau_{\nu } \frac{\partial }{\partial t}} \right)T_{,xx} + K_{3}^{*} \left( {1 + \tau_{\nu } \frac{\partial }{\partial t}} \right)T_{,zz} = \left( {1 + \tau_{q} \frac{\partial }{\partial t} + \frac{{\tau_{q}^{2} }}{2}\frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\left( {\rho C_{v} \ddot{T} + \beta_{1} T_{0} \ddot{u}_{,x} + \beta_{3} T_{0} \ddot{w}_{,z} + bT_{0} \ddot{\phi }} \right). $$

(16)

2.2 Boundary conditions

The mechanical and thermal boundary conditions at the thermally stress-free surface $z = 0$ are

• (a) Thermal conditions:

  $$ T = F(t)H\left( {a - \left| x \right|} \right) $$

  (17)

  where $H$ is the Heaviside function.

• (b) Vanishing of the normal stress component:

  $$ \sigma_{zz} = 0 $$

  (18)

• (c) Vanishing of the tangential stress component:

  $$ \sigma_{xz} = 0 $$

  (19)

• (d) Condition on void volume fraction field:

  $$ \phi_{,z} = 0. $$

  (20)

3 Solution of the problem

We take the solutions of Eqs. (13)–(16) in the following form:

$$ \left( {u,w,\phi ,T} \right)\left( {x,z,t} \right) = \left( {\bar{u},\bar{w},\bar{\phi },\bar{T}} \right)\left( z \right)\exp \left[ {ik\left( {x - ct} \right)} \right] $$

(21)

where $k$ is wave number and $c$ is the phase velocity.

Using Eq. (21) in Eqs. (13), (14), (15) and (16), we obtain

$$ c_{55} \frac{{{\text{d}}^{2} \bar{u}}}{{{\text{d}}z^{2} }} + \left( {\rho k^{2} c^{2} - c_{11} k^{2} } \right)\bar{u} + \left( {c_{13} + c_{55} } \right)ik\frac{{{\text{d}}\bar{w}}}{{{\text{d}}z}} + ikB_{1} \bar{\phi } - ik\beta_{1} \bar{T} = 0 $$

(22)

$$ c_{33} \frac{{{\text{d}}^{2} \bar{w}}}{{{\text{d}}z^{2} }} + \left( {\rho k^{2} c^{2} - c_{55} k^{2} } \right)\bar{w} + \left( {c_{13} + c_{55} } \right)ik\frac{{{\text{d}}\bar{u}}}{{{\text{d}}z}} + B_{3} \frac{{{\text{d}}\bar{\phi }}}{{{\text{d}}z}} - \beta_{3} \frac{{{\text{d}}\bar{T}}}{{{\text{d}}z}} = 0 $$

(23)

$$ A_{3} \frac{{{\text{d}}^{2} \bar{\phi }}}{{{\text{d}}z^{2} }} + \left( {\rho \chi k^{2} c^{2} - k^{2} A_{1} - \varsigma } \right)\bar{\phi } - ikB_{1} \bar{u} - B_{3} \frac{{{\text{d}}\bar{w}}}{{{\text{d}}z}} + b\bar{T} = 0 $$

(24)

$$ \left( {K_{3}^{*} \tau_{2} - ikc\tau_{1} K_{3} } \right)\frac{{{\text{d}}^{2} \bar{T}}}{{{\text{d}}z^{2} }} + \left( {ik^{3} cK_{1} \tau_{1} + \rho C_{v} k^{2} c^{2} - K_{1}^{*} \tau_{2} k^{2} } \right)\bar{T} + \beta_{1} T_{0} ik^{3} c^{2} \bar{u} + \beta_{3} T_{0} k^{2} c^{2} \frac{{{\text{d}}\bar{w}}}{{{\text{d}}z}} + bT_{0} k^{2} c^{2} \bar{\phi } = 0 $$

(25)

in which$\tau_{1} = \frac{{1 - ikc\tau_{T} }}{{1 - ikc\tau_{q} - \frac{{k^{2} c^{2} }}{2}\tau_{q}^{2} }},$ $\tau_{2} = \frac{{1 - ikc\tau_{\nu } }}{{1 - ikc\tau_{q} - \frac{{k^{2} c^{2} }}{2}\tau_{q}^{2} }}$, $u,w,\phi$ and $T$ must be bounded at infinity to satisfy the regularity condition at infinity. So we assume that $u,w,\phi$ and $T$ as well as their derivatives vanish at infinity.

3.1 Formulation of vector matrix differential equation

Equations (22)–(25) can be written in the form of a vector matrix differential equation as follows:

$$ \frac{{{\text{d}}\tilde{V}}}{{{\text{d}}z}} = \tilde{A}\tilde{V} $$

(26)

where $\tilde{V} = \left[ {\bar{u},\bar{w},\bar{\phi },\bar{T},\frac{{{\text{d}}\bar{u}}}{{{\text{d}}z}},\frac{{{\text{d}}\bar{w}}}{{{\text{d}}z}},\frac{{{\text{d}}\bar{\phi }}}{{{\text{d}}z}},\frac{{{\text{d}}\bar{T}}}{{{\text{d}}z}}} \right]^{T}$and matrix $\tilde{A}$ is given by $\tilde{A} = \left( {\begin{array}{*{20}c} {\tilde{0}} & {\tilde{I}} \\ {\tilde{P}} & {\tilde{Q}} \\ \end{array} } \right)$with $\tilde{0} = \left( {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right),$$\tilde{I} = \left( {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right),$$\tilde{P} = \left( {\begin{array}{*{20}c} {a_{51} } & 0 & {a_{53} } & {a_{54} } \\ 0 & {a_{62} } & 0 & 0 \\ {a_{71} } & 0 & {a_{73} } & {a_{74} } \\ {a_{81} } & 0 & {a_{83} } & {a_{84} } \\ \end{array} } \right),$$\tilde{Q} = \left( {\begin{array}{*{20}c} 0 & {a_{56} } & 0 & 0 \\ {a_{65} } & 0 & {a_{67} } & {a_{68} } \\ 0 & {a_{76} } & 0 & 0 \\ 0 & {a_{86} } & 0 & 0 \\ \end{array} } \right)$in which

$$ \begin{aligned} a_{51} & = \frac{{\left( {c_{11} - \rho c^{2} } \right)k^{2} }}{{c_{55} }},\quad a_{53} = \frac{{ - ikB_{1} }}{{c_{55} }},\quad a_{54} = \frac{{ik\beta_{1} }}{{c_{55} }},\quad a_{56} = \frac{{ - ik\left( {c_{13} + c_{55} } \right)}}{{c_{55} }},\quad a_{62} = \frac{{\left( {c_{55} - \rho c^{2} } \right)k^{2} }}{{c_{33} }}, \\ a_{65} & = \frac{{ - ik\left( {c_{13} + c_{55} } \right)}}{{c_{33} }},\quad a_{67} = \frac{{ - B_{3} }}{{c_{33} }},\quad a_{68} = \frac{{\beta_{3} }}{{c_{33} }},\quad a_{71} = \frac{{ikB_{1} }}{{A_{3} }},\quad a_{73} = \frac{{k^{2} A_{1} + \zeta - \rho \chi k^{2} c^{2} }}{{A_{3} }},\quad a_{74} = \frac{ - b}{{A_{3} }},\quad a_{76} = \frac{{B_{3} }}{{A_{3} }}, \\ a_{81} & = \frac{{ - \beta_{1} T_{0} ik^{3} c^{2} }}{{\left( {K_{3}^{*} \tau_{2} - ikc\tau_{1} K_{3} } \right)}},\quad a_{83} = \frac{{ - bT_{0} k^{2} c^{2} }}{{\left( {K_{3}^{*} \tau_{2} - ikc\tau_{1} K_{3} } \right)}},\quad a_{84} = \frac{{ - \left( {ikcK_{1} \tau_{1} + \rho C_{v} c^{2} - K_{1}^{*} \tau_{2} } \right)k^{2} }}{{\left( {K_{3}^{*} \tau_{2} - ikc\tau_{1} K_{3} } \right)}},\quad a_{86} = \frac{{ - \beta_{3} T_{0} k^{2} c^{2} }}{{\left( {K_{3}^{*} \tau_{2} - ikc\tau_{1} K_{3} } \right)}}. \\ \end{aligned} $$

3.2 Solution of vector matrix differential equation

For the solution of Eq. (26), we follow the method of eigenvalue approach (Das et al. [32]).

The characteristic equation of matrix $\tilde{A}$ is given by

$$ \lambda^{8} - B_{1} \lambda^{6} + B_{2} \lambda^{4} + B_{3} \lambda^{2} + B_{4} = 0 $$

(27)

where

$$ B_{1} = \left( {a_{51} + a_{62} + a_{73} + a_{84} + a_{67} a_{76} + a_{68} a_{86} + a_{56} a_{65} } \right) $$

$$ B_{2} = a_{73} a_{84} - a_{74} a_{83} + a_{56} a_{71} + a_{51} a_{84} + a_{54} a_{81} + a_{62} a_{84} + q_{62} a_{73} - a_{51} a_{73} - a_{71} a_{53} - a_{51} a_{62} + a_{54} a_{65} a_{86} - a_{67} a_{74} a_{86} + a_{67} a_{84} a_{76} + a_{56} a_{65} a_{84} + a_{56} a_{65} a_{73} - a_{53} a_{65} a_{76} + a_{68} a_{73} a_{86} - a_{68} a_{76} a_{83} - a_{51} a_{67} a_{76} - a_{51} a_{68} a_{86} + a_{56} a_{68} a_{81} $$

$$ \begin{aligned} B_{3} & = - \,a_{53} a_{65} \left( {a_{74} a_{86} - a_{76} a_{84} } \right) + a_{54} a_{65} \left( {a_{73} a_{86} - a_{83} a_{76} } \right) + a_{56} a_{65} \left( {a_{73} a_{84} - a_{83} a_{74} } \right) \\ & \quad - \,a_{51} a_{67} \left( {a_{74} a_{86} - a_{76} a_{84} } \right) + a_{54} a_{67} \left( {a_{71} a_{86} - a_{81} a_{76} } \right) - a_{56} a_{67} \left( {a_{71} a_{84} - a_{74} a_{81} } \right) \\ & \quad - \,a_{68} \left( {a_{73} a_{86} - a_{76} a_{83} } \right) - a_{53} a_{68} \left( {a_{71} a_{86} - a_{76} a_{81} } \right) - a_{56} a_{68} \left( {a_{71} a_{83} - a_{73} a_{81} } \right) - a_{51} \left( {a_{73} a_{84} - a_{74} a_{83} } \right) \\ & \quad - \,a_{53} \left( {a_{71} a_{84} - a_{74} a_{81} } \right) - a_{54} \left( {a_{71} a_{83} - a_{73} a_{81} } \right) \\ & \quad + \,a_{57} a_{62} a_{84} - a_{51} a_{62} a_{73} + a_{53} a_{62} a_{71} - a_{57} a_{81} a_{62} - a_{62} \left( {a_{73} a_{84} - a_{83} a_{74} } \right) \\ \end{aligned} $$

$$ B_{4} = a_{51} a_{62} \left( {a_{73} a_{84} - a_{83} a_{74} } \right) - a_{53} a_{62} \left( {a_{73} a_{84} - a_{81} a_{74} } \right) + a_{62} a_{84} \left( {a_{71} a_{83} - a_{73} a_{81} } \right) $$

The roots of the characteristic Eq. (27) which are also the eigenvalues of the matrix $\tilde{A}$ are of the form $\lambda = \pm \lambda_{1} ,$ $\lambda = \pm \lambda_{2} ,$ $\lambda = \pm \lambda_{3}$ and $\lambda = \pm \lambda_{4}$

The right and left eigenvectors $\vec{X}$ and $\vec{Y}$ of the matrix $\tilde{A}$ corresponding to the eigenvalue $\lambda$ can be taken as follows:

$$ \vec{X} = \left[ {x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} ,x_{6} ,x_{7} ,x_{8} } \right]^{T} $$

$$ \vec{Y} = \left[ {y_{1} ,y_{2} ,y_{3} ,y_{4} ,y_{5} ,y_{6} ,y_{7} ,y_{8} } \right] $$

where

$$ x_{1} = \left( {a_{53} a_{68} - \lambda a_{54} a_{67} } \right)\left[ {\left( {a_{62} - \lambda^{2} } \right)a_{74} - \lambda^{2} a_{68} a_{76} } \right] - \left[ {\lambda a_{67} a_{74} - \lambda a_{68} \left( {a_{73} - \lambda^{2} } \right)} \right]\left[ {\lambda^{2} a_{68} a_{56} - a_{54} \left( {a_{62} - \lambda^{2} } \right)} \right] $$

$$ x_{2} = \left[ {\lambda a_{67} a_{74} - \lambda a_{68} \left( {a_{73} - \lambda^{2} } \right)} \right]\left[ {\lambda a_{68} \left( {a_{51} - \lambda^{2} } \right) - \lambda a_{54} a_{65} } \right] - \lambda^{2} \left( {a_{65} a_{74} - a_{68} a_{71} } \right)\left( {a_{53} a_{68} - a_{54} a_{67} } \right) $$

$$ x_{3} = \left[ {\lambda^{2} a_{52} a_{68} - a_{54} \left( {a_{62} - \lambda^{2} } \right)} \right]\left[ {\lambda a_{65} a_{74} - \lambda a_{63} a_{71} } \right] - \left[ {\left( {a_{62} - \lambda^{2} } \right)a_{74} - \lambda^{2} a_{76} a_{68} } \right]\left[ {\lambda a_{68} \left( {a_{51} - \lambda^{2} } \right) - \lambda a_{54} a_{65} } \right] $$

$$ x_{4} = \lambda a_{68} \left( {a_{51} - \lambda^{2} } \right)\left[ {\left( {a_{73} - \lambda^{2} } \right)\left( {a_{62} - \lambda^{2} } \right) - \lambda^{2} a_{67} a_{76} } \right] + \lambda^{2} a_{56} a_{68} \left[ {\lambda a_{67} a_{71} - \lambda a_{65} \left( {a_{73} - \lambda^{2} } \right)} \right] + \lambda a_{53} a_{68} \left[ {\lambda^{2} a_{76} a_{65} - a_{71} \left( {a_{62} - \lambda^{2} } \right)} \right] $$

$$ x_{5} = \lambda x_{1} ,\quad x_{6} = \lambda x_{2} ,\quad x_{7} = \lambda x_{3} ,\quad x_{8} = \lambda x_{4} $$

and

$$ y_{1} = \lambda^{2} a_{62}^{2} \left[ {\left( {a_{84} - \lambda^{2} } \right)\left( {a_{73} - \lambda^{2} } \right) - a_{74} a_{83} } \right]\left[ {\lambda^{2} a_{51} a_{62} a_{65} a_{83} - \lambda^{2} a_{62} a_{81} \left( {a_{53} a_{65} - \lambda^{2} a_{67} } \right)} \right] - \lambda^{2} a_{62}^{2} \left[ {a_{71} a_{83} - a_{81} \left( {a_{73} - \lambda^{2} } \right)} \right]\left[ {\lambda^{2} \left( {a_{53} a_{65} + \lambda^{2} a_{67} } \right)\left( {a_{84} a_{62} - \lambda^{2} a_{62} } \right) - \lambda^{2} a_{62} a_{83} \left( {a_{54} a_{65} - \lambda^{2} a_{68} } \right)} \right], $$

$$ y_{2} = \lambda^{2} a_{62}^{2} \left[ {a_{71} a_{83} - a_{81} \left( {a_{73} - \lambda^{2} } \right)} \right]\left[ {\lambda a_{53} a_{62} \left( {a_{84} a_{62} - \lambda^{2} a_{62} } \right) - \lambda a_{62}^{2} a_{83} a_{54} } \right] - \lambda^{2} a_{62}^{2} \left[ {\left( {a_{84} - \lambda^{2} } \right)\left( {a_{73} - \lambda^{2} } \right) - a_{74} a_{83} } \right]\left[ {\lambda a_{62}^{2} a_{83} \left( {a_{51} - \lambda^{2} } \right) - \lambda a_{62}^{2} a_{53} a_{81} } \right] $$

$$ y_{3} = \lambda^{2} \left( {a_{56} a_{83} - a_{53} a_{86} } \right)\left( {a_{54} a_{67} - a_{53} a_{68} } \right) - \lambda^{2} \left[ {a_{56} a_{67} - a_{53} \left( {a_{62} - \lambda^{2} } \right)} \right]\left[ {a_{54} a_{83} - a_{53} \left( {a_{84} - \lambda^{2} } \right)} \right] - \lambda a_{67} \left[ {a_{86} \left( {a_{73} - \lambda^{2} } \right) - a_{83} a_{76} } \right]\left[ {\left( {a_{84} - \lambda^{2} } \right)a_{53} - a_{54} a_{83} } \right] + \lambda^{2} a_{67} \left( {a_{53} a_{86} - a_{83} a_{56} } \right)\left[ {\left( {a_{73} - \lambda^{2} } \right)\left( {a_{84} - \lambda^{2} } \right) - a_{74} a_{83} } \right] $$

$$ y_{4} = \lambda \left[ {\lambda^{2} a_{56} a_{67} - a_{53} \left( {a_{62} - \lambda^{2} } \right)} \right]\left[ {a_{54} \left( {a_{73} - \lambda^{2} } \right) - a_{53} a_{74} } \right] - \lambda^{3} \left( {a_{54} a_{67} - a_{53} a_{68} } \right)\left[ {a_{56} \left( {a_{73} - \lambda^{2} } \right) - a_{53} a_{76} } \right] - \lambda a_{68} \left[ {a_{86} \left( {a_{73} - \lambda^{2} } \right) - a_{83} a_{76} } \right]\left[ {a_{53} \left( {a_{84} - \lambda^{2} } \right) - a_{54} a_{83} } \right] + \lambda^{2} a_{68} \left( {a_{53} a_{86} - a_{83} a_{56} } \right)\left[ {\left( {a_{73} - \lambda^{2} } \right)\left( {a_{84} - \lambda^{2} } \right) - a_{74} a_{83} } \right] $$

$$ y_{5} = \left[ {\left( {a_{73} - \lambda^{2} } \right)\left( {a_{84} - \lambda^{2} } \right) - a_{74} a_{83} } \right]\left[ {\lambda^{2} a_{67} a_{86} - a_{83} \left( {a_{62} - \lambda^{2} } \right)} \right] - \lambda^{2} \left[ {a_{86} \left( {a_{73} - \lambda^{2} } \right) - a_{83} a_{76} } \right]\left[ {a_{67} \left( {a_{84} - \lambda^{2} } \right) - a_{68} a_{83} } \right] $$

$$ y_{6} = \lambda \left[ {a_{86} \left( {a_{73} - \lambda^{2} } \right) - a_{83} a_{76} } \right]\left[ {\left( {a_{84} - \lambda^{2} } \right)a_{53} - a_{54} a_{83} } \right] - \lambda \left( {a_{53} a_{86} - a_{83} a_{56} } \right)\left[ {\left( {a_{73} - \lambda^{2} } \right)\left( {a_{84} - \lambda^{2} } \right) - a_{74} a_{83} } \right] $$

$$ y_{7} = \lambda^{2} \left( {a_{56} a_{83} - a_{53} a_{86} } \right)\left( {a_{54} a_{67} - a_{53} a_{68} } \right) - \lambda^{2} \left[ {a_{56} a_{67} - a_{53} \left( {a_{62} - \lambda^{2} } \right)} \right]\left[ {a_{54} a_{83} - a_{53} \left( {a_{84} - \lambda^{2} } \right)} \right] $$

$$ y_{8} = \left[ {\lambda^{2} a_{56} a_{67} - a_{53} \left( {a_{62} - \lambda^{2} } \right)} \right]\left[ {a_{54} \left( {a_{73} - \lambda^{2} } \right) - a_{53} a_{74} } \right] - \lambda^{2} \left( {a_{54} a_{67} - a_{53} a_{68} } \right)\left[ {a_{56} \left( {a_{73} - \lambda^{2} } \right) - a_{53} a_{76} } \right] $$

For further reference, we use the following notations:$X_{1} = \left[ X \right]_{{\lambda = \lambda_{1} }} ,$ $X_{2} = \left[ X \right]_{{\lambda = - \lambda_{1} }} ,$ $X_{3} = \left[ X \right]_{{\lambda = \lambda_{2} }} ,$ $X_{4} = \left[ X \right]_{{\lambda = - \lambda_{2} }} ,$ $X_{5} = \left[ X \right]_{{\lambda = \lambda_{3} }} ,$ $X_{6} = \left[ X \right]_{{\lambda = - \lambda_{3} }} ,$ $X_{7} = \left[ X \right]_{{\lambda = \lambda_{4} }} ,$

$$ X_{8} = \left[ X \right]_{{\lambda = - \lambda_{4} }} $$

and $Y_{1} = \left[ Y \right]_{{\lambda = \lambda_{1} }} ,$ $Y_{2} = \left[ Y \right]_{{\lambda = - \lambda_{1} }} ,$ $Y_{3} = \left[ Y \right]_{{\lambda = \lambda_{2} }} ,$ $Y_{4} = \left[ Y \right]_{{\lambda = - \lambda_{2} }} ,$ $Y_{5} = \left[ Y \right]_{{\lambda = \lambda_{3} }} ,$ $Y_{6} = \left[ Y \right]_{{\lambda = - \lambda_{3} }} ,$ $Y_{7} = \left[ Y \right]_{{\lambda = \lambda_{4} }} ,$

$$ Y_{8} = \left[ Y \right]_{{\lambda = - \lambda_{4} }} $$

Assuming the regularity condition at infinity, the solution of Eq. (26) can be written as

$$ \vec{V} = A_{1} X_{2} \exp \left( { - \lambda_{1} z} \right) + A_{2} X_{4} \exp \left( { - \lambda_{2} z} \right) + A_{3} X_{6} \exp \left( { - \lambda_{3} z} \right) + A_{4} X_{8} \exp \left( { - \lambda_{4} z} \right) $$

(28)

Now we obtain

$$ \bar{u} = \sum\limits_{n = 1}^{4} {\left\{ {\left( {a_{53} a_{68} - \lambda_{n} a_{54} a_{67} } \right)\left[ {\left( {a_{62} - \lambda_{n}^{2} } \right)a_{74} - \lambda_{n}^{2} a_{68} a_{76} } \right] - \left[ {\lambda_{n} a_{67} a_{74} - \lambda_{n} a_{68} \left( {a_{73} - \lambda_{n}^{2} } \right)} \right]\left[ {\lambda_{n}^{2} a_{68} a_{56} - a_{54} \left( {a_{62} - \lambda_{n}^{2} } \right)} \right]} \right\}} \exp \left( { - \lambda_{n} z} \right), $$

(29)

$$ \bar{w} = \sum\limits_{n = 1}^{4} {\left\{ {\left[ {\lambda_{n} a_{67} a_{74} - \lambda_{n} a_{68} \left( {a_{73} - \lambda_{n}^{2} } \right)} \right]\left[ {\lambda_{n} a_{68} \left( {a_{51} - \lambda_{n}^{2} } \right) - \lambda_{n} a_{54} a_{65} } \right] - \lambda_{n}^{2} \left( {a_{65} a_{74} - a_{68} a_{71} } \right)\left( {a_{53} a_{68} - a_{54} a_{67} } \right)} \right\}} \exp \left( { - \lambda_{n} z} \right), $$

(30)

$$ \bar{\phi } = \sum\limits_{n = 1}^{4} {\left\{ {\left[ {\lambda_{n}^{2} a_{52} a_{68} - a_{54} \left( {a_{62} - \lambda_{n}^{2} } \right)} \right]\left[ {\lambda_{n} a_{65} a_{74} - \lambda_{n} a_{63} a_{71} } \right] - \left[ {\left( {a_{62} - \lambda_{n}^{2} } \right)a_{74} - \lambda_{n}^{2} a_{76} a_{68} } \right]\left[ {\lambda_{n} a_{68} \left( {a_{51} - \lambda_{n}^{2} } \right) - \lambda_{n} a_{54} a_{65} } \right]} \right\}} \exp \left( { - \lambda_{n} z} \right), $$

(31)

$$ \bar{T} = \sum\limits_{n = 1}^{4} {\left\{ {\lambda_{n} a_{68} \left( {a_{51} - \lambda_{n}^{2} } \right)\left[ {\left( {a_{73} - \lambda_{n}^{2} } \right)\left( {a_{62} - \lambda_{n}^{2} } \right) - \lambda_{n}^{2} a_{67} a_{76} } \right] + \lambda_{n}^{2} a_{56} a_{68} \left[ {\lambda_{n} a_{67} a_{71} - \lambda_{n} a_{65} \left( {a_{73} - \lambda_{n}^{2} } \right)} \right] + \lambda_{n} a_{53} a_{68} \left[ {\lambda_{n}^{2} a_{76} a_{65} - a_{71} \left( {a_{62} - \lambda_{n}^{2} } \right)} \right]} \right\}} \exp \left( { - \lambda_{n} z} \right) $$

(32)

Hence, we get

$$ u = \sum\limits_{n = 1}^{4} {b_{n} } A_{n} \exp \left[ { - \lambda_{n} z + ik\left( {x - ct} \right)} \right] $$

$$ w = \sum\limits_{n = 1}^{4} {d_{n} } A_{n} \exp \left[ { - \lambda_{n} z + ik\left( {x - ct} \right)} \right] $$

(33)

$$ \phi = \sum\limits_{n = 1}^{4} {f_{n} } A_{n} \exp \left[ { - \lambda_{n} z + ik\left( {x - ct} \right)} \right] $$

$$ T = \sum\limits_{n = 1}^{4} {g_{n} } A_{n} \exp \left[ { - \lambda_{n} z + ik\left( {x - ct} \right)} \right] $$

where

$$ b_{n} = \left( {a_{53} a_{68} - \lambda_{n} a_{54} a_{67} } \right)\left[ {\left( {a_{62} - \lambda_{n}^{2} } \right)a_{74} - \lambda_{n}^{2} a_{68} a_{76} } \right] - \left[ {\lambda_{n} a_{67} a_{74} - \lambda_{n} a_{68} \left( {a_{73} - \lambda_{n}^{2} } \right)} \right]\left[ {\lambda_{n}^{2} a_{68} a_{56} - a_{54} \left( {a_{62} - \lambda_{n}^{2} } \right)} \right] $$

$$ d_{n} = \left[ {\lambda_{n} a_{67} a_{74} - \lambda_{n} a_{68} \left( {a_{73} - \lambda_{n}^{2} } \right)} \right]\left[ {\lambda_{n} a_{68} \left( {a_{51} - \lambda_{n}^{2} } \right) - \lambda_{n} a_{54} a_{65} } \right] - \lambda_{n}^{2} \left( {a_{65} a_{74} - a_{68} a_{71} } \right)\left( {a_{53} a_{68} - a_{54} a_{67} } \right) $$

$$ f_{n} = \left[ {\lambda_{n}^{2} a_{52} a_{68} - a_{54} \left( {a_{62} - \lambda_{n}^{2} } \right)} \right]\left[ {\lambda_{n} a_{65} a_{74} - \lambda_{n} a_{63} a_{71} } \right] - \left[ {\left( {a_{62} - \lambda_{n}^{2} } \right)a_{74} - \lambda_{n}^{2} a_{76} a_{68} } \right]\left[ {\lambda_{n} a_{68} \left( {a_{51} - \lambda_{n}^{2} } \right) - \lambda_{n} a_{54} a_{65} } \right] $$

$$ g_{n} = \lambda_{n} a_{68} \left( {a_{51} - \lambda_{n}^{2} } \right)\left[ {\left( {a_{73} - \lambda_{n}^{2} } \right)\left( {a_{62} - \lambda_{n}^{2} } \right) - \lambda_{n}^{2} a_{67} a_{76} } \right] + \lambda_{n}^{2} a_{56} a_{68} \left[ {\lambda_{n} a_{67} a_{71} - \lambda_{n} a_{65} \left( {a_{73} - \lambda_{n}^{2} } \right)} \right] + \lambda_{n} a_{53} a_{68} \left[ {\lambda_{n}^{2} a_{76} a_{65} - a_{71} \left( {a_{62} - \lambda_{n}^{2} } \right)} \right] $$

Now we derive the stress components as follows:

$$ \sigma_{xx} = \sum\limits_{n = 1}^{4} {\left( {ikc_{11} b_{n} - c_{13} \lambda_{n} d_{n} - \beta_{1} g_{n} + B_{1} f_{n} } \right)} A_{n} \exp \left[ { - \lambda_{n} z + ik\left( {x - ct} \right)} \right] $$

$$ \sigma_{zz} = \sum\limits_{n = 1}^{4} {\left( {ikc_{13} b_{n} - c_{33} \lambda_{n} d_{n} - \beta_{3} g_{n} + B_{3} f_{n} } \right)A_{n} } \exp \left[ { - \lambda_{n} z + ik\left( {x - ct} \right)} \right] $$

$$ \sigma_{xz} = \sum\limits_{n = 1}^{4} {c_{55} \left( {ikd_{n} - \lambda_{n} b_{n} } \right)} A_{n} \exp \left[ { - \lambda_{n} z + ik\left( {x - ct} \right)} \right] $$

4 Application

Using the boundary conditions (17), (18), (19) and (20), we obtain the following system of four equations in $A_{1} ,A_{2} ,A_{3} ,A_{4} :$

$$ \sum\limits_{n = 1}^{4} {g_{n} } A_{n} = F_{1} \left( {x,t} \right) $$

(34)

$$ \sum\limits_{n = 1}^{4} {\left( {ikc_{13} b_{n} - c_{33} \lambda_{n} d_{n} - \beta_{3} g_{n} + B_{3} f_{n} } \right)} A_{n} = 0 $$

(35)

$$ \sum\limits_{n = 1}^{4} {c_{55} \left( {ikd_{n} - \lambda_{n} b_{n} } \right)} A_{n} = 0 $$

(36)

$$ \sum\limits_{n = 1}^{4} {f_{n} \lambda_{n} } A_{n} = 0 $$

(37)

where $F_{1} \left( {x,t} \right) = F\left( t \right)H\left( {a - \left| x \right|} \right)\exp \left[ { - ik\left( {x - ct} \right)} \right]$Solving the above four equations, we obtain the arbitrary constants $A_{1} ,A_{2} ,A_{3} ,A_{4} .$

We obtain the constants as follows: $A_{1} = \frac{{D_{1} }}{\Delta },$ $A_{2} = \frac{{D_{2} }}{\Delta },$ $A_{3} = \frac{{D_{3} }}{\Delta },$ $A_{4} = \frac{{D_{4} }}{\Delta }$ in which

$$ \begin{aligned} \Delta & = g_{1} \left[ {N_{2} \left( {P_{3} Q_{4} - P_{4} Q_{3} } \right) - N_{3} \left( {P_{2} Q_{4} - P_{4} Q_{2} } \right) + N_{4} \left( {P_{2} Q_{3} - P_{3} Q_{2} } \right)} \right] \\ & \quad - \,g_{2} \left[ {N_{1} \left( {P_{3} Q_{4} - P_{4} Q_{3} } \right) - N_{3} \left( {P_{1} Q_{4} - P_{4} Q_{1} } \right) + N_{4} \left( {P_{1} Q_{3} - P_{3} Q_{1} } \right)} \right] \\ & \quad + \,g_{3} \left[ {N_{1} \left( {P_{2} Q_{4} - P_{4} Q_{2} } \right) - N_{2} \left( {P_{1} Q_{4} - P_{4} Q_{1} } \right) + N_{4} \left( {P_{1} Q_{2} - P_{2} Q_{1} } \right)} \right] \\ & \quad - \,g_{4} \left[ {N_{1} \left( {P_{2} Q_{3} - P_{3} Q_{2} } \right) - N_{2} \left( {P_{1} Q_{3} - P_{3} Q_{1} } \right) + N_{3} \left( {P_{1} Q_{2} - P_{2} Q_{1} } \right)} \right] \\ \end{aligned} $$

$$ D_{1} = F_{1} \left[ {N_{2} \left( {P_{3} Q_{4} - P_{4} Q_{3} } \right) - N_{3} \left( {P_{2} Q_{4} - P_{4} Q_{2} } \right) + N_{4} \left( {P_{2} Q_{3} - P_{3} Q_{2} } \right)} \right] $$

$$ D_{2} = - F_{1} \left[ {N_{1} \left( {P_{3} Q_{4} - P_{4} Q_{3} } \right) - N_{3} \left( {P_{1} Q_{4} - P_{4} Q_{1} } \right) + N_{4} \left( {P_{1} Q_{3} - P_{3} Q_{1} } \right)} \right] $$

$$ D_{3} = F_{1} \left[ {N_{1} \left( {P_{2} Q_{4} - P_{4} Q_{2} } \right) - N_{2} \left( {P_{1} Q_{4} - P_{4} Q_{1} } \right) + N_{4} \left( {P_{1} Q_{2} - P_{2} Q_{1} } \right)} \right] $$

$$ D_{4} = - F_{1} \left[ {N_{1} \left( {P_{2} Q_{3} - P_{3} Q_{2} } \right) - N_{2} \left( {P_{1} Q_{3} - P_{3} Q_{1} } \right) + N_{3} \left( {P_{1} Q_{2} - P_{2} Q_{1} } \right)} \right] $$

where $N_{n} = \left( {ikc_{13} b_{n} - c_{33} \lambda_{n} d_{n} - \beta_{3} g_{n} + B_{3} f_{n} } \right),$ $P_{n} = c_{55} \left( {ikd_{n} - \lambda_{n} b_{n} } \right),$ $Q_{n} = f_{n} \lambda_{n} .$

5 Particular cases

We obtain the following different results in orthotropic medium:

• (a) The problem falls into the theory of classical coupled thermoelasticity (C T) when we put $\tau_{\nu } = \tau_{q} = \tau_{T} = 0$ and $K_{i}^{*} = 0(i = 1,3)$.

• (b) When we put $\tau_{\nu } = \tau_{T} = 0$, $\tau_{q}^{2} = 0$ and $K_{i}^{*} = 0(i = 1,3),\tau_{q} \ne 0$, the problem falls into the theory of the Lord–Shulman model .

• (c) Equation (16) falls into the theory of GN model type-III when we put $\tau_{\nu } = \tau_{q} = \tau_{T} = 0.$

• (d) If we put $K_{i}^{*} = 0$ ($i = 1,3)$ in Eq. (16), then the problem falls into the theory of the dual-phase-lag model.

The problem reduces to the case of without voids if we take $b = \varsigma = A_{1} = A_{3} = B_{1} = B_{3} = 0$, and the results agree with Biswas and Mukhopadhyay [23].

6 Numerical results and discussion

For numerical computations, we take the following values of the relevant parameters for zinc material as follows:

$$ \begin{aligned} c_{11} & = 16.28 \times 10^{10} {\text{Nm}}^{ - 2} ,\quad c_{13} = 5.08 \times 10^{10} {\text{Nm}}^{ - 2} ,\quad c_{33} = 6.27 \times 10^{10} {\text{Nm}}^{ - 2} ,\quad c_{55} = 7.70 \times 10^{10} {\text{Nm}}^{ - 2} , \\ \beta_{1} & = 5.75 \times 10^{6} {\text{Nm}}^{ - 2} {\text{K}}^{ - 1} ,\quad \beta_{3} = 5.17 \times 10^{6} {\text{Nm}}^{ - 2} {\text{K}}^{ - 1} ,\quad K_{1} = 124{\text{Wm}}^{ - 1} {\text{K}}^{ - 1} ,\quad K_{3} = 124{\text{Wm}}^{ - 1} {\text{K}}^{ - 1} ,\\ K_{1}^{*} & = 42{\text{Wm}}^{ - 1} {\text{K}}^{ - 1} {\text{s}}^{ - 1 `} ,\quad K_{3}^{*} = 42{\text{Wm}}^{ - 1} {\text{K}}^{ - 1} {\text{s}}^{ - 1 `} ,\quad \rho = 7.14 \times 10^{3} {\text{Kgm}}^{ - 3} ,\quad C_{v} = 390{\text{JKg}}^{ - 1} {\text{K}}^{ - 1} ,T_{0} = 296{\text{K}} .\\ \end{aligned} $$

The void parameters are given as follows: $b = 1.2384 \times 10^{6} {\text{N/m}}^{ 2} {\text{K}} ,$ $\chi = 0.05655 \times 10^{ - 15} {\text{m}}^{ 2} ,$ $\varsigma = 0.19603 \times 10^{10} {\text{N/m}}^{ 2} ,$ $A_{1} = 14.798 \times 10^{ - 5} {\text{N}},$ $A_{3} = 10.9174 \times 10^{ - 5} {\text{N,}}$ $B_{1} = 10.52849 \times 10^{10} {\text{N/m}}^{ 2} ,$ $B_{3} = 0.41 \times 10^{10} {\text{N/m}}^{ 2} .$

For the three-phase-lag model, the heat conduction law is stable (Quintanilla and Racke [33]) if

$$ \frac{{2K_{i} \tau_{T} }}{{\tau_{q} }} > \tau_{\nu }^{*} > K_{i}^{*} \tau_{q} $$

where $\tau_{\nu }^{*} = K_{i}^{*} \tau_{\nu } + K_{i}$ and $i = 1,3$.

We have assumed the values of three-phase-lag parameters in this article in the way that they have satisfied the above condition, and hence, for numerical computation we have taken $\tau_{q} = 2 \times 10^{ - 7} {\text{s}},$ $\tau_{T} = 1.5 \times 10^{ - 7} {\text{s}},$ $\tau_{v} = 1 \times 10^{ - 8} {\text{s}}.$

In Fig. 1, stress $\left( {\sigma_{xx} } \right)$ with respect to $z$ is presented graphically for the fixed value of time. Stress for the LS model is maximum, and stress for the GN-III model is minimum. Stress decreases in the presence of voids, and stress decreases with the increase in distance.

Fig. 1

Comparison of $\sigma_{xx}$ with respect to $z$

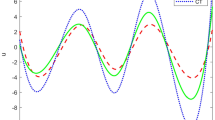
In Fig. 2, it is observed that the absolute value of horizontal displacement $\left( u \right)$ decreases with the increase of $z$. The absolute value of horizontal displacement for the LS model is maximum, and displacement for the GN-III model is minimum. Horizontal displacement decreases in the presence of voids.

Fig. 2

Comparison of $u$ with respect to $z$

It is noticed in Fig. 3 that vertical displacement $\left( w \right)$ decreases with the increase of $z$. Vertical displacement for the LS model is maximum, and displacement for the GN-III model is minimum. Vertical displacement decreases in the presence of voids.

Fig. 3

Comparison of $w$ with respect to $z$

It is found in Fig. 4 that the absolute value of temperature decreases with the increase of $z$. The absolute value of the temperature for the LS model is maximum, and temperature for the GN-III model is minimum.

Fig. 4

Comparison of $T$ with respect to $z$

In Fig. 5, it is observed that the absolute value of horizontal displacement $\left( u \right)$ decreases with the increase of $t$. The absolute value of horizontal displacement for the LS model is maximum, and displacement for the GN-III model is minimum. Horizontal displacement decreases in the presence of voids.

Fig. 5

Comparison of $u$ with respect to $t$

It is noticed in Fig. 6 that vertical displacement $\left( w \right)$ decreases with the increase of $z$. Vertical displacement for the LS model is maximum, and displacement for the GN-III model is minimum. Vertical displacement decreases in the presence of voids.

Fig. 6

Comparison of $w$ with respect to $t$

It is shown in Fig. 7 that the absolute value of the temperature decreases with the increase of $t$. The absolute value of the temperature for the LS model is maximum, and temperature for the GN-III model is minimum. Temperature for the TPL model lies between the temperatures for other two models.

Fig. 7

Comparison of $T$ with respect to $t$

7 Conclusion

In this article, thermal shock response in porous orthotropic medium is investigated in the context of the three-phase-lag model of thermoelasticity. The comparison of three generalized thermoelastic models in case of stress, displacements and temperature is presented graphically. From the theoretical and numerical discussion, the following concluding remarks can be drawn:

• (a) All considered parameters decrease in the presence of voids.

• (b) All parameters decrease with the increase in distance and time.

• (c) The value of all parameters for the LS model is maximum and minimum for the GN-III model.

• (d) There is significant difference in the considered parameters for different models.

• (e) The present problem is the most general one as other problems with different thermoelastic models can be obtained as special cases from it.