1 Introduction

Nonlinear evolution equations (NLEEs) are used to express various complex phenomena arising in different fields of nonlinear physical sciences, such as; mathematical physical, biological sciences, chemical processes and so on. Recently, various analytical approaches have been developed to seek the solutions of different kinds of NLEEs, such as; the Q-function scheme and trial solution approach [1], the Hirota method [2], the Pffafian method [3], the homogeneous balance method [4], the improved tan\((\phi /2)\)-expansion method [5], the extended \((G{'}/G)\)-expansion method [6], the extended tanh-function method [7], the sine-Gordon expansion method [8,9,10,11], the homotopy analysis method [12], the homotopy perturbation method [13], the jacobi elliptic function method [14], the simple equation method [15], the modified simple equation method [16], the improved Bernoulli sub-equation function method [17], the first integral method [18, 19], the modified f Fan sub-equation method [20], the simplified Hirotas method [21], and many other mathematical approaches [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46].

However, the purpose of this study is to use the modified exp \((-\phi (\eta ))\)-expansion function method (MEFM) [47] to investigate the solutions of the coupled nonlinear Maccari’s system given by [48]

$$\begin{aligned} \left\{ \begin{array}{l} iQ_{t}+Q_{xx}+RQ=0, \\ iS_{t}+S_{xx}+RS=0,\\ iN_{t}+N_{xx}+RN=0,\\ R_{t}+R_{y}+(|Q+S+N|^{2})_{x}=0. \end{array} \right. \end{aligned}$$
(1)

The coupled Maccari’s system is a complex nonlinear model which describes the dynamics of isolated waves, confined in a small part of space, in various fields such as hydrodynamic, plasma physics and nonlinear optics [48, 49].

Various computational approaches have been used to search for the solutions of different kinds of the coupled nonlinear Maccari’s system, this includes; the new extension of the \((G{'}/G)\)-expansion method [50], the first integral method [19], the improved \((G{'}/G)\)-expansion method [51], the tanh method [52], the Kudryashov method [53], the He’s semi-inverse variational principle [54], the mapping method and Lie symmetry analysis [55] etc.

2 The MEFM

In this section, the analysis of the MEFM is presented.

Consider the following general form of nonlinear partial differential equation:

$$\begin{aligned} P(u, u_{x}, u_{x}u^{2}, u_{xx}, u_{xxt}, \ldots )=0. \end{aligned}$$
(2)

Step 1 Utilizing the wave transformation

$$\begin{aligned} f(x, t)=F(\eta ),\quad \eta =v(x-kt), \end{aligned}$$
(3)

Equation (2) reduces to the following nonlinear ordinary differential equation (NODE):

$$\begin{aligned} Q(F, F^{2}, FF{'}, F{''}, \ldots )=0. \end{aligned}$$
(4)

Step 2 Supposing that the solutions of Eq. (4) take the following form:

$$\begin{aligned} F(\eta )=\frac{\sum _{i=0}^{\delta }A_{i} \left[ e^{-\phi (\eta )}\right] ^{i}}{\sum _{j=0}^{\phi }B_{j}\left[ e^{-\phi (\eta )}\right] ^{j}}= \frac{A_{0}+A_{1}e^{-\phi }+\cdots + A_{\delta }e^{-\delta \phi }}{B_{0}+B_{1}e^{-\phi }+\cdots + B_{\phi }e^{-\sigma \phi }}, \end{aligned}$$
(5)

where \(A_{i}, B_{j}, (0\le i\le \delta , 0\le j\le \sigma )\) are constants to be obtained later, such that \(A_{\delta }\ne o\), \(B_{\sigma }\ne o\), and \(\phi =\phi (\eta )\) solves the following equation:

$$\begin{aligned} \phi {'}(\eta )=e^{-\phi (\eta )}+\rho e^{\phi (\eta )}+\lambda . \end{aligned}$$
(6)

Equation (6) has the set of solutions as follows [56,57,58]:

Family 1

If \(\rho \ne 0\), \(\lambda ^{2}-4\rho >0\),

$$\begin{aligned} \phi (\eta )=ln\left( \frac{-\sqrt{\lambda ^{2}-4\rho }}{2\rho }tanh\left( \frac{\sqrt{\lambda ^{2}-4\rho }}{2}(\eta +\epsilon )\right) -\frac{\lambda }{2\rho }\right) . \end{aligned}$$
(7)

Family 2

If \(\rho \ne 0\), \(\lambda ^{2}-4\rho <0\),

$$\begin{aligned} \phi (\eta )=ln\left( \frac{\sqrt{-\lambda ^{2}+4\rho }}{2\rho }tan\left( \frac{\sqrt{-\lambda ^{2}+4\rho }}{2}(\eta +\epsilon )\right) -\frac{\lambda }{2\rho }\right) . \end{aligned}$$
(8)

Family 3

If \(\rho =0\), \(\lambda \ne 0\) and \(\lambda ^{2}-4\rho >0\),

$$\begin{aligned} \phi (\eta )=-ln\left( \frac{\lambda }{e^{\lambda (\eta +\epsilon )}-1}\right) . \end{aligned}$$
(9)

Family 4

If \(\rho \ne 0\), \(\lambda \ne 0\) and \(\lambda ^{2}-4\rho =0\),

$$\begin{aligned} \phi (\eta )=ln\left( -\frac{2\lambda (\eta +\epsilon )+4}{\lambda ^{2}(\eta +\epsilon )}\right) . \end{aligned}$$
(10)

Family 5

If \(\rho =0\), \(\lambda =0\) and \(\lambda ^{2}-4\rho =0\),

$$\begin{aligned} \phi (\eta )=ln(\eta +\epsilon ), \end{aligned}$$
(11)

where \(A_{i}, B_{j}, (0\le i\le \delta , 0\le j\le \sigma )\), \(\epsilon , \lambda , \rho \) are coefficients to be obtained later, and \(\sigma \), \(\delta \) are positive integers which can be obtained by using the balancing principle.

Step 3 Substituting Eq. (5), its derivatives and Eq. (6) into Eq. (4), yields an equation in \(e^{-\phi (\eta )}\). We collect a set of algebraic equations from that equation by summing all the coefficients of \(e^{-\phi (\eta )}\) of the same power and equating each summation to zero. To get the values of the parameters involved in the equation, we simply the set of algebraic equations with aid of the Wolfram Mathematica package. Substituting the obtained values of the coefficients and one of Eqs. (7–11) into Eq. (5), produces new solutions to (2).

3 Theoretical calculation

In this section, the MEFM [47] is used to find the waves solutions to Eq. (1).

To carry Eq. (1) into a single NODE, the following assumptions are made:

$$\begin{aligned} \begin{array}{cccl} Q(x,y,t)=f(x,y,t)e^{\psi } \\ S(x,y,t)=g(x,y,t)e^{\psi }\\ N(x,y,t)=h(x,y,t)e^{\psi } \end{array} \end{aligned}$$
(12)

where \(\psi =i(kx+\alpha y+\beta t+\kappa )\), \(k,\;\alpha \), \(\beta \), \(\kappa \) are nonzero constants, and \(i=\sqrt{-1}\).

Substituting Eq. (12) into Eq. (1), yields

$$\begin{aligned} \left\{ \begin{array}{l} i(f_{t}+2kf_{x})+f_{xx}-(\lambda +k^{2})f+fR=0, \\ i(g_{t}+2kg_{x})+g_{xx}-(\lambda +k^{2})g+gR=0,\\ i(h_{t}+2kh_{x})+h_{xx}-(\lambda +k^{2})h+hR=0,\\ R_{t}+R_{y}+((f+g+h)^{2})_{x}=0. \end{array} \right. \end{aligned}$$
(13)

Utilizing the wave transformation; \(f=F(\eta )\), \(g=G(\eta )\), \(h=H(\eta )\), \(R=R(\eta )\), \(\eta =x+y-2kt\) on Eq. (13), gives

$$\begin{aligned} \left\{ \begin{array}{lr} F{''}-(\lambda +k^{2})F+FR=0, \\ G{''}-(\lambda +k^{2})G+GR=0,\\ H{''}-(\lambda +k^{2})H+HR=0,\\ (1-2k)\frac{\partial R}{\partial \eta }+\frac{\partial (F+G+H)^{2}}{\partial \eta }=0. \end{array} \right. \end{aligned}$$
(14)

Integrating the fourth part of Eq. (14), yields

$$\begin{aligned} R=-\frac{1}{(1-2k)}(F+G+H)^{2}. \end{aligned}$$
(15)

Substituting Eq. (15) into the remaining three parts of Eq. (14), yields

$$\begin{aligned} \left\{ \begin{array}{l} F{''}-(\lambda +k^{2})F-\frac{1}{(1-2k)}(F+G+H)^{2}F=0, \\ G{''}-(\lambda +k^{2})G-\frac{1}{(1-2k)}(F+G+H)^{2}G=0,\\ H{''}-(\lambda +k^{2})H-\frac{1}{(1-2k)}(F+G+H)^{2}H=0. \end{array} \right. \end{aligned}$$
(16)

We carry Eq. (16) into a single NODE in F by setting

$$\begin{aligned} G=aF, \quad H=bF, \end{aligned}$$
(17)

where a, b are arbitrary constants,

$$\begin{aligned} (1-2k)F{''}-(1-2k)(\lambda +k^{2})F-(1+a+b)^{2}F^{3}=0. \end{aligned}$$
(18)

Balancing \(F{''}\) and \(F^{3}\) in Eq. (18), gives the following relation:

$$\begin{aligned} \delta =\sigma +1, \end{aligned}$$
(19)

choosing \(\sigma =1\), yields \(\delta =2\).

Utilizing \(\sigma =1\) and \(\delta =2\) along with Eq. (5), gives

$$\begin{aligned} F(\eta )=\frac{A_{0}+A_{1}e^{-\phi (\eta )}+A_{2}e^{-2\phi (\eta )}}{B_{0}+B_{1}e^{-\phi (\eta )}}. \end{aligned}$$
(20)

Inserting Eq. (20) and it’s second derivative into Eq. (18), yields a polynomial in \(e^{-\phi (\eta )}\). We collect a set of algebraic equations from this equation and simplify the set of equations with aid of the Wolfram Mathematica package to find the values of the parameters involved in the equation. For each set, substituting the obtained values of the parameters into Eq. (20), gives the solutions to Eq. (1).

Set 1

$$\begin{aligned} A_{1}&= {} \frac{A_{0}(2B_{0}-\lambda B_{1})}{\lambda B_{0}-2\mu B_{1}}, \quad A_{2}=0, a=-\frac{1}{2A_{0}^{2}(2B_{0}-\lambda B_{1})^{3}}\left( 2A_{0}^{2}(1+b)(2B_{0}-\lambda B_{1})^{3}\right. \\&\quad \left. +\sqrt{2}(\lambda B_{0}-2\mu B_{1})^{3}\sqrt{\frac{\left( 1+\sqrt{2}\sqrt{4\mu -2\beta -\lambda ^{2}}(\lambda B_{1}-2B_{0})^{6}A_{0}^{2}\right) }{(\lambda B_{0}-2\mu B_{1})^{4}}}\right) ,\quad k=-\sqrt{2\mu -\beta -\frac{\lambda ^{2}}{2}}. \end{aligned}$$

Solutions 1.1

When \(\rho \ne 0\), \(\lambda ^{2}-4\rho >0\), we have

$$\begin{aligned}f_{1}(x, y, t)&=\frac{1}{\left( (\lambda B_{0}-2\mu B_{1})\left( -2\mu B_{1}+B_{0}\left( \lambda +\sqrt{\lambda ^{2}-4\mu }\; tanh[\Psi _{1}(\xi )]\right) \right) \right) }\nonumber \\&\quad \left( A_{0}\left( -2\mu B_{1}\sqrt{\lambda ^{2}-4\mu }\;tanh[\Psi _{1}(\xi )]+ B_{0}\left( \lambda ^{2}-4\mu +\lambda \sqrt{\lambda ^{2}-4\mu }\; tan[\Psi _{1}(\xi )]\right) \right) \right) , \end{aligned}$$
(21)
$$\begin{aligned}&g_{1}(x, y, t)=af_{1}(x, y, t), \end{aligned}$$
(22)
$$\begin{aligned}&h_{1}(x, y, t)=bf_{1}(x, y, t), \end{aligned}$$
(23)
$$\begin{aligned}&Q_{1}(x, y, t)=f_{1}(x, y, t)e^{i\left( -\sqrt{2\mu -\beta -\frac{\lambda ^{2}}{2}}\;x+\alpha y+\beta t+\kappa \right) }, \end{aligned}$$
(24)
$$\begin{aligned}&S_{1}(x, y, t)=af_{1}(x, y, t)e^{i\left( -\sqrt{2\mu -\beta -\frac{\lambda ^{2}}{2}}\;x+\alpha y+\beta t+\kappa \right) }, \end{aligned}$$
(25)
$$\begin{aligned}&N_{1}(x, y, t)=bf_{1}(x, y, t)e^{i\left( -\sqrt{2\mu -\beta -\frac{\lambda ^{2}}{2}}\;x+\alpha y+\beta t+\kappa \right) }, \end{aligned}$$
(26)
$$\begin{aligned}&R_{1}(x, y, t)=-\frac{f_{1}^{2}(x, y, t)}{1+2\sqrt{2\mu -\beta -\frac{\lambda ^{2}}{2}}}(1+a+b)^{2}, \end{aligned}$$
(27)

where \(\Psi _{1}(\xi )=\frac{1}{2}\sqrt{\lambda ^{2}-4\mu }(\epsilon +\xi )\), \(\xi =x+y-2kt\).

Set 2

$$\begin{aligned} A_{0}=\frac{i\sqrt{2k-1}\lambda B_{0}}{\sqrt{2}(1+a+b)},\quad A_{1}=\frac{i\sqrt{2(2k-1)}(2B_{0}+\lambda B_{1})}{2(1+a+b)},\quad A_{2}=\frac{i\sqrt{2(2k-1)}B_{1}}{1+a+b},\quad \beta =2\mu -k^{2}-\frac{\lambda ^{2}}{2}, \end{aligned}$$

Solutions 2.1

When \(\rho \ne 0\), \(\lambda ^{2}-4\rho >0\), we have

$$\begin{aligned} f_{2}(x, y, t)= {} \frac{i\sqrt{2k-1}\left( \lambda ^{2}-4\mu +\lambda \sqrt{\lambda ^{2}-4\mu }\;tanh[\Psi _{2}(\xi )]\right) }{\sqrt{2}(1+a+b)\left( \lambda +\sqrt{\lambda ^{2}-4\mu }\; tanh[\Psi _{2}(\xi )]\right) }, \end{aligned}$$
(28)
$$\begin{aligned} g_{2}(x, y, t)= {} af_{2}(x, y, t),\end{aligned}$$
(29)
$$\begin{aligned} h_{2}(x, y, t)= {} bf_{2}(x, y, t), \end{aligned}$$
(30)
$$\begin{aligned} Q_{2}(x, y, t)= {} f_{2}(x, y, t)e^{i(kx+\alpha y+\beta t+\kappa )}, \end{aligned}$$
(31)
$$\begin{aligned} S_{2}(x, y, t)= {} af_{2}(x, y, t)e^{i(x+\alpha y+\beta t+\kappa )}, \end{aligned}$$
(32)
$$\begin{aligned} N_{2}(x, y, t)= {} bf_{2}(x, y, t)e^{i(kx+\alpha y+\beta t+\kappa )}, \end{aligned}$$
(33)
$$\begin{aligned} R_{2}(x, y, t)= {} -\frac{f_{2}(x, y, t)}{1-2k}(1+a+b), \end{aligned}$$
(34)

where \(\Psi _{2}(\xi )=\frac{1}{2}\sqrt{\lambda ^{2}-4\mu }(\epsilon +\xi )\), \(\xi =x+y-2kt\).

Solutions 2.2

When \(\rho \ne 0\), \(\lambda ^{2}-4\rho <0\), we have

$$\begin{aligned} f_{3}(x, y, t)= {} \frac{i\sqrt{2k-1} \left( \lambda ^{2}-4\mu -\lambda \sqrt{4\mu -\lambda ^{2}} \;tan[\Psi _{3}(\xi )]\right) }{\sqrt{2}(1+a+b) \left( \lambda -\sqrt{4\mu -\lambda ^{2}}\;tan[\Psi _{3}(\xi )]\right) }, \end{aligned}$$
(35)
$$\begin{aligned} g_{3}(x, y, t)= {} af_{3}(x, y, t), \end{aligned}$$
(36)
$$\begin{aligned} h_{3}(x, y, t)= {} bf_{3}(x, y, t), \end{aligned}$$
(37)
$$\begin{aligned} Q_{3}(x, y, t)= {} f_{3}(x, y, t)e^{i(kx+\alpha y+\beta t+\kappa )}, \end{aligned}$$
(38)
$$\begin{aligned} S_{3}(x, y, t)= {} af_{3}(x, y, t)e^{i(x+\alpha y+\beta t+\kappa )}, \end{aligned}$$
(39)
$$\begin{aligned} N_{3}(x, y, t)= {} bf_{3}(x, y, t)e^{i(kx+\alpha y+\beta t+\kappa )}, \end{aligned}$$
(40)
$$\begin{aligned} R_{3}(x, y, t)= {} -\frac{f_{3}(x, y, t)}{1-2k}(1+a+b), \end{aligned}$$
(41)

where \(\Psi _{3}(\xi )=\frac{1}{2}\sqrt{4\mu -\lambda ^{2}}(\epsilon +\xi )\), \(\xi =x+y-2kt\).

Solutions 2.3

When \(\rho =0\), \(\lambda \ne 0\) and \(\lambda ^{2}-4\rho >0\), we have

$$\begin{aligned} f_{4}(x, y, t)= {} \frac{i\sqrt{2k-1}\; coth[\Psi _{4}(\xi )]}{\sqrt{2}(1+a+b)}, \end{aligned}$$
(42)
$$\begin{aligned} g_{4}(x, y, t)= {} af_{4}(x, y, t), \end{aligned}$$
(43)
$$\begin{aligned} h_{4}(x, y, t)= {} bf_{4}(x, y, t), \end{aligned}$$
(44)
$$\begin{aligned} Q_{4}(x, y, t)= {} f_{4}(x, y, t)e^{i(kx+\alpha y+\beta t+\kappa )}, \end{aligned}$$
(45)
$$\begin{aligned} S_{4}(x, y, t)= {} af_{4}(x, y, t)e^{i(x+\alpha y+\beta t+\kappa )}, \end{aligned}$$
(46)
$$\begin{aligned} N_{4}(x, y, t)= {} bf_{4}(x, y, t)e^{i(kx+\alpha y+\beta t+\kappa )}, \end{aligned}$$
(47)
$$\begin{aligned} R_{4}(x, y, t)= {} -\frac{f_{4}(x, y, t)}{1-2k}(1+a+b), \end{aligned}$$
(48)

where \(\Psi _{4}(\xi )=\frac{1}{2}\lambda (\epsilon +\xi )\), \(\xi =x+y-2kt\).

4 Results and discussion

In this section, we discuss the results to Eq. (1) obtained by using the available techniques in the literature and the reported results in this study. Baskonus et al. [48] have applied the sine-Gordon expansion method to this model and obtained some complex hyperbolic function solutions. Rostatny et al. [19] have employed the first integral method to seek the solutions of Eq. (1) and some complex hyperbolic and exponential function solutions were obtained. In this study, by using the MEFM, we successfully constructed some new soliton, singular periodic waves and singular soliton solutions to Eq. (1). When we compare our results with the results reported in Baskonus et al. [48] and Rostatny et al. [19], we observed that all the results obtained in this study by using the modified exp \((-\phi (\eta ))\)-expansion function method are newly constructed solutions with some similar structure to the results obtained by Baskonus et al. [48] and Rostatny et al. [19]. It shows that the modified exp \((-\phi (\eta ))\)-expansion function approach gives an efficient and reliable mathematical tool for obtaining variety of solutions to various nonlinear evolution equations.

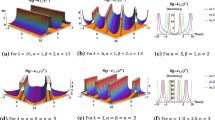
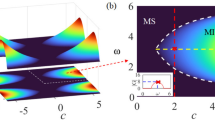
It can be seen that; solutions (24)–(27) and (31)–(34) are soliton solutions, solutions (38)–(41) are singular periodic wave solutions and solutions (45)–(48) are singular soliton solutions. A soliton is a localized wave of translation that arises from a balance between nonlinear and dispersive effects, the singular periodic waves is a solitary wave with discontinuous derivatives whose wave propagates in a periodic pattern and the singular soliton solutions is a solitary wave with discontinuous derivatives; examples of such solitary waves include compactions, which have finite (compact) support, and peakons, whose peaks have a discontinuous first derivative [59, 60]. The perspective view of the soliton (34) can be seen in the 3D graphs which are depicted in Figs. 1, 2, 3 and 4, respectively. The perspective view of the singular periodic wave solutions (38) and (41) can be seen in the 3D graphs which are depicted in Figs. 5 and 6, respectively. The perspective view of the singular soliton solutions (45) and (48) can be seen in the 3D graphs which are depicted in Figs. 7 and 8, respectively. The propagation pattern of the wave along the x-axes for each solution can be seen through the 2D graphs in Figs. 1, 2, 3, 4, 5, 6, 7 and 8. The contour plot is an alternative of the 3D graph where the fixed value of t is considered. The contour plots in Figs. 9 and 10 illustrate the stable propagation of the exact soliton solutions. The contour plots in Fig. 11 illustrate the unstable propagation of the exact singular periodic wave solutions. The contour plots in Fig. 12, also illustrate the unstable propagation of the exact singular soliton solutions. The jumps in discontinuities can be observed in the (a) parts of Figs. 11 and 12.

Fig. 1
figure 1

The 3D and 2D graphs of Eq. (24) under \(\lambda =3\), \(\alpha =2\), \(\mu =2\), \(\beta =-1.5\), \(\kappa =1.5\), \(B_{0}=1\), \(B_{1}=3\), \(A_{0}=5\), \(\epsilon =4\), \(t=1.5\), \(-10<x<10\), \(-5<y<5\) and \(y=1.6\) for 2D

Full size image
Fig. 2
figure 2

The 3D and 2D graphs of Eq. (27) under \(b=3.5\), \(\lambda =3\), \(\alpha =2\), \(\mu =2\), \(\beta =-1.5\), \(\kappa =1.5\), \(B_{0}=1\), \(B_{1}=3\), \(A_{0}=5\), \(\epsilon =4\), \(t=1.5\), \(-10<x<10\), \(-5<y<5\) and \(y=0.6\) for 2D

Full size image
Fig. 3
figure 3

The 3D and 2D graphs of Eq. (31) under \(a=2.5\), \(b=3.5\), \(\beta =\kappa =1.5\), \(k=3\), \(\lambda =2\), \(\alpha =2\), \(\mu =0.002\), \(\epsilon =4\), \(t=1.5\), \(-5<x<5\), \(-4<y<4\) and \(y=0.6\) for 2D

Full size image
Fig. 4
figure 4

The 3D and 2D graphs of Eq. (34) under \(k=0.05\), \(\lambda =2\), \(\alpha =0.24\), \(\mu =0.02\), \(\beta =a=b=\kappa =0.5\), \(\epsilon =0.65\), \(t=1.5\), \(-4<x<4\), \(-5<y<5\) and \(y=0.6\) for 2D

Full size image
Fig. 5
figure 5

The 3D and 2D graphs of Eq. (38) under \(a=2.5\), \(b=3.5\), \(k=3\), \(\lambda =1.5\), \(\alpha =2\), \(\mu =2\), \(\beta =1.5\), \(\kappa =1.5\), \(\epsilon =4\), \(t=1.5\), \(-10<x<10\), \(-2<y<2\) and \(y=1.6\) for 2D

Full size image
Fig. 6
figure 6

The 3D and 2D graphs of Eq. (41) under \(a=2.5\), \(b=3.5\), \(k=3\), \(\lambda =1.5\), \(\alpha =2\), \(\mu =2\), \(\beta =1.5\), \(\kappa =1.5\), \(\epsilon =4\), \(t=1.5\), \(-5<x<5\), \(-2<y<2\) and \(y=1.6\) for 2D

Full size image
Fig. 7
figure 7

The 3D and 2D graphs of Eq. (46) under \(a=2.5\), \(b=3.5\), \(k=3\), \(\lambda =1.5\), \(\alpha =2\), \(\beta =1.5\), \(\kappa =1.5\), \(\epsilon =4\), \(t=1.5\), \(-3<x<3\), \(-2<y<2\) and \(y=0.6\) for 2D

Full size image
Fig. 8
figure 8

The 3D and 2D graphs of Eq. (48) under \(a=2.5\), \(b=0.35\), \(k=3\), \(\lambda =1.5\), \(\alpha =2\), \(\mu =2\), \(\beta =1.5\), \(\kappa =1.5\), \(\epsilon =4\), \(t=1.5\), \(-13<x<13\), \(-13<y<13\) and \(y=1.6\) for 2D

Full size image
Fig. 9
figure 9

The contour plots of (a) Eq. (24) and (b) Eq. (27)

Full size image
Fig. 10
figure 10

The contour plots of (a) Eq. (31) and (b) Eq. (34)

Full size image
Fig. 11
figure 11

The contour plots of (a) Eq. (38) and (b) Eq. (41)

Full size image
Fig. 12
figure 12

The contour plots of (a) Eq. (42) and (b) Eq. (48)

Full size image

5 Conclusions

In this study, the modified exp \((-\phi (\eta ))\)-expansion function approach is utilized acquiring some travelling wave solutions to the nonlinear Maccari’s system. We successfully constructed some soliton, singular soliton and singular periodic wave solutions. All the obtained solutions verified the considered model in this study. We also present the 2D, 3D graphs and the contour plots to some of the obtained solutions in this study. From the reported results, it shows that the MEFM is easy and manageable in finding varieties of travelling wave solutions to complex nonlinear models. All the computations in this paper are carried out with help of the Wolfram Mathematica software. To the best of our knowledge, the application of MEFM to the considered model in this article has not been submitted to the literature beforehand.