1 Introduction

Beside the deadly infectious disease known as Ebola hemorrhagic fever, there is another one called Lassa hemorrhagic fever [3]. This disease is classified under the arenaviridae virus family. The first outbreaks of the disease have been observed in the following countries including: Nigeria, Liberia, Sierra Leone, and Central Africa Republic. However, it was first described in 1969 in the town of Lassa, in Borno State, Nigeria [1]. The main host of the Lassa virus is the Natal multimammate mouse, an animal homegrown in most of sub-Saharan Africa; this animal is presented in Fig. 1. The contamination in human characteristically takes place by disclosure to animal excrement all the way through the respiratory or gastrointestinal tracts. Mouthful of air of tiny particle of infective material is understood to be the mainly noteworthy way of exposure. It is also likely to get hold of the infection through broken skin or mucous membrane that directly exposed to infective material [2].

Fig. 1
figure 1

Mastomys natalensis, the natural reservoir of the Lassa fever virus

Full size image

A study has revealed that about 15–20 % of the hospitalized Lassa fever patients will die from the disease. However, during epidemics, mortality can climb as high as 50 % [4]. The mortality rate is greater than 80 % when it occurs in pregnant women during their third trimester; fetal death also occurs in nearly all those cases [4]. The aim of this paper is to provide a clear description of the spread, infection, and death of the populations of the pregnant.

Mathematical tools have always been used for the description of many physical problems; for instance to approximate the speed done by an object for a given distance and time done, we used the idea of the rate of change. All these models use the basic idea of derivative. However, it has been recognized in the recent decade that it is rather better to use derivative that has a new parameter that the classical version of Newtonian derivative. These derivatives with new parameters are referred to fractional order derivative. Even if these fractional derivatives have been intensively used with success to describe real-world problems, there are fundamental problems that we face when using these derivative, for example, what could be the Caputo/Riemann–Liouville fractional derivative of a product of functions? Will we obtain a formula similar to that of chain when dealing with composition of function? Recently, a new derivative called the beta-derivative was proposed [5], and this derivative is the modified version of the one proposed in [6]. This derivative is not perhaps a fractional derivative but has a fractional order. This derivative satisfies several properties that were as limitation for the fractional derivatives and has been used to model some biological problems [6, 7]. The derivative under consideration here is given as

$${}_{0}^{A} D_{x}^{\beta } \left( {f(x)} \right) = \mathop {\lim }\limits_{\varepsilon \to 0} \frac{{f\left( {x + \varepsilon \left( {x + \frac{1}{\varGamma \left( \beta \right)}} \right)^{1 - \beta } } \right) - f(x)}}{\varepsilon }$$
(1)

for all \(x \ge a, \beta \in (0,1]\). Then if the limit of the above exists, f is said to be \(\beta\)-differentiable.

Theorem 1 [5]

Assuming that, f is differential and \(\beta\) -differentiable on the opened interval \((a, b)\) , then

$${}_{0}^{A} D_{x}^{\beta } \left( {f(x)} \right) = \left( {x + \frac{1}{\varGamma \left( \beta \right)}} \right)^{1 - \beta } \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right) - f(x)}}{h}.$$
(2)

Definition 1 [5]

Let \(f:[a,\text{ }\infty ) \to {\mathbb{R}}\) is given function, then we propose that the integral of order \(\beta\)-integral of \(f\) is

$${}_{a}^{A} I_{x}^{\beta } \left( {f(x)} \right) = \int \limits_{a}^{x} \left( {t + \frac{1}{\varGamma \left( \beta \right)}} \right)^{\beta - 1} f(t){\text{d}}t.$$
(3)

The above operator is the inverse operator of the proposed beta-derivative, and is called the Atangana beta integral [5].

2 Mathematical formulation of the problems

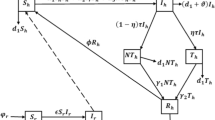
Let \(N\) be a total number of adult women in a given country, \(S\) be the susceptible population of pregnant women, R be the recovery population of pregnant women, I the infected population of pregnant women, D the population of pregnant women dying in that country. We shall assume that women are being pregnant at the rate \(b\), they are susceptible at a rate \(a\), they are infected at a rate \(c\), they infected women are dying at a rate \(f\) and recovery at the rate \(h\). We assume that they die with natural death or other disease at a rate \(l\). Then the mathematical formula underpinning the change in time of the susceptible population within the scope of beta-derivative is given as

$${}_{0}^{A} D_{t}^{\beta } S\left( t \right) = - cS\left( t \right)I\left( t \right) + bN - lN + fR(t) + hS\left( t \right) - lS(t)$$
(4)

The above equation is obtained because \(c\) is the rate of infectious, pregnant women from recovery population turn out to be vulnerable again at the rate \(h\), a proportion of adult women will be pregnant at a rate \(b\), and finally the number of pregnant women that die due to natural death and other diseases at the rate \(l\). The change of infected populations can be expressed with the following linear ordinary differential equation

$${}_{0}^{A} D_{t}^{\beta } I\left( t \right) = cS\left( t \right)I\left( t \right) - (f + h)I(t) - hS(t)$$
(5)

The physical explanation underpinning the above equation is that, since, the total number of pregnant women removed from susceptible group can be mathematically expressed as \(cS\left( t \right)I\left( t \right)\). However, due to the introduction of medication, a number of pregnant women will be recovered at a rate of \(h\), and a number of pregnant women will die at a rate \(f\). The change in time of the recovery population is given by

$${}_{0}^{A} D_{t}^{\beta } R\left( t \right) = hI\left( t \right) - fR(t)$$
(6)

Finally, we can expressed the change in time of the population of the death as

$${}_{0}^{A} D_{t}^{\beta } D\left( t \right) = fI\left( t \right) + lN - bN$$
(7)

Therefore, the description of the spread and consequences associate can be underpinned by the following set of mathematical formula

$$\left\{ {\begin{array}{*{20}l} {{}_{0}^{A} D_{t}^{\beta } S\left( t \right) = - cS\left( t \right)I\left( t \right) + bN - lN + fR\left( t \right) - lS\left( t \right) + hS(t)} \hfill \\ {{}_{0}^{A} D_{t}^{\beta } I\left( t \right) = cS\left( t \right)I\left( t \right) - \left( {f + h} \right)I\left( t \right) - hS(t)} \hfill \\ {{}_{0}^{A} D_{t}^{\beta } R\left( t \right) = hI\left( t \right) - fR\left( t \right) } \hfill \\ {{}_{0}^{A} D_{t}^{\beta } D(t) = fI\left( t \right) + lN - bN + lS(t)} \hfill \\ \end{array} } \right.$$
(8)

We shall test the validity and also a possible mathematical analysis of the above system of equations and this will be done in the next section.

3 Analysis and rationality of the system

One of the important parts of this modeling is to check the rationality of the proposed system. This usually consists of assuring that the sum of the equations in the system is equal to zero. Thus adding together equation in the system, we obtain the following

$${}_{0}^{A} D_{t}^{\beta } S\left( t \right) + {}_{0}^{A} D_{t}^{\beta } R\left( t \right) + {}_{0}^{A} D_{t}^{\beta } I\left( t \right) + {}_{0}^{A} D_{t}^{\beta } D\left( t \right) = 0$$
(9)

Now using the linearity of the beta-derivative, we have

$${}_{0}^{A} D_{t}^{\beta } \left\{ {S\left( t \right) + R\left( t \right) + I\left( t \right) + D(t)} \right\} = 0$$

Now applying the inverse operator of \({}_{0}^{A} D_{t}^{\beta }\) given in Definition (1), we obtain

$$S\left( t \right) + R\left( t \right) + I\left( t \right) + D\left( t \right) = {\text{constance}} = N$$

We shall now check the steady-state solutions and the eigenvalues associate

3.1 Disease control

To find the endemic equilibrium points, we assume that the system is time independent such that using the one of the properties of the beta-derivative we have:

$$\left\{ {\begin{array}{*{20}l} {0 = - c\bar{S}\bar{I} + bN - lN + f\bar{R} + h\bar{S} - l\bar{S}} \hfill \\ {0 = c\bar{S}\bar{I} - \left( {f + h} \right)\bar{I} - h\bar{S}} \hfill \\ {0 = h\bar{I} - f\bar{R}} \hfill \\ \end{array} } \right.$$
(10)

By solving the last two equations of the system, we obtain

$$\bar{R} = \frac{{h\bar{I}}}{f},\quad \bar{S} = \frac{(f + h)}{{c\bar{I} - h}}\bar{I}$$
(11)

Now replacing the above solutions into the first equation of the system, we obtain

$$\begin{aligned} & A\bar{I}^{2} + B\bar{I} + C = 0 \\ & C = - h\left( {b - l} \right)N, \quad B = \left( {h + c - l} \right)f + cN\left( {b - l} \right) + h(c - l), \quad A = hc \\ \end{aligned}$$
(12)

Thus the solution of the above equation are given as

$$\bar{I}_{ \mp } = \frac{{ - B \mp \sqrt {B^{2} + 4Chc} }}{2A}$$
(13)

We consider only the positive solution and obtain the endemic equilibrium points.

$$\bar{I} = \frac{{\sqrt {B^{2} + 4Chc} }}{2A} - \frac{B}{2A} = \frac{B}{2A}\left( {\frac{{\sqrt {B^{2} + 4Chc} }}{B} - 1} \right) = \frac{B}{2A}\left( {R_{0} - 1} \right)$$

The disease-free equilibrium points are given as

$$\left( {\frac{b - l}{l},0,0} \right)$$
(14)

One the most important concerns when modeling an infectious disease is to determine its ability to invade a population. The basic reproductive number \(R_{0}\) is a measure of the prospective for the disease spread in a target population and is inarguably one of the principal and precious ideas that mathematical accepted wisdom has brought to epidemic theory [8]. This measurement presents the average number of secondary cases generated by an infected individual if introduced into a susceptible population with no invulnerability to the disease in the absence of interventions to control the infection. If \(1 < R_{0}\) then on average, an infected individual produces less than one newly infected individual over the course of his infectious period. In this case, the infection may die out in the long run. Contrary if \(R_{0} > 0\), then each infected individual produces, on average, more than one new infection, and the infection will be able to spread in a population. It is worth noting that a large value of \(R_{0}\) may indicate the possibility of a major epidemic. In our case, the reproductive number is given as

$$R_{0} = \frac{{\sqrt {B^{2} + 4Chc} }}{B}$$
(15)

Accordingly, if B is negative, then \(R_{0} < 1\) and the disease-free equilibrium is stable and the endemic equilibrium points are unstable. If B is positive and \(Chc\) is positive, then \(R_{0} > 1\) the disease-free equilibrium is unstable and the endemic stable. Another way is to find the equation of eigenvalues and check their sign.

4 Derivation of special solution

One of the key aspects of modeling is perhaps the simulation or the prediction of the physical problem using the mathematical formula. In order to achieve this, we solve the proposed mathematical formula numerically or analytically. Whether it is numerically or analytically, when we are dealing with nonlinear equations, the problem become more demanding. There are quite few methods in the literature dealing with nonlinear equations [9–11]. In this paper, we shall make use of the Laplace transform [13–15] and the idea of an imbedding parameter to propose a special solution for Eq. (8). We shall present some useful tools for Laplace transform.

Definition 2

The Laplace transform is a widely used integral transform with many applications in physics and engineering. The Laplace transform of the function f is defined as follows

$${\mathcal{L}}\left( {f\left( x \right)} \right)\left( s \right) = \int \limits_{0}^{\infty } e^{ - sx} f(x){\text{d}}x$$
(16)

Some useful tools are given as follows

$$\begin{aligned} {\mathcal{L}}\left( {I\left( f \right)} \right) & = {\mathcal{L}}\left( {\int \limits_{0}^{x} f\left( \tau \right){\text{d}}\tau } \right)\left( s \right) = \frac{1}{s}{\mathcal{L}}\left( {f\left( x \right)} \right)(s) \\ {\mathcal{L}}\left( {I^{2} \left( f \right)} \right) & = {\mathcal{L}}\left( {\int \limits_{0}^{x} \int \limits_{0}^{{x_{1} }} f\left( \tau \right){\text{d}}\tau {\text{d}}x_{1} } \right)\left( s \right) = \frac{1}{{s^{2} }}{\mathcal{L}}\left( {f\left( x \right)} \right)(s) \\ \end{aligned}$$
(17)

Now using the recursive method, we arrive at the following

$${\mathcal{L}}\left( {I^{n} \left( f \right)} \right) = = \frac{1}{{s^{n} }}{\mathcal{L}}\left( {f\left( x \right)} \right)(s)$$
(18)

From the above equation, we can obtain the following

$${\mathcal{L}}\left( {I^{n} \left( f \right)} \right) = \frac{1}{{s^{n} }}{\mathcal{L}}\left( {f\left( x \right)} \right)\left( s \right) \Rightarrow I^{n} \left( f \right) = {\mathcal{L}}^{ - 1} \left( {\frac{1}{{s^{n} }}{\mathcal{L}}\left( {f\left( x \right)} \right)\left( s \right)} \right)$$
(19)

It is well known from the convolution theorem of Laplace transform that,

$${\mathcal{L}}\left( {f \times g\left( x \right)} \right)\left( s \right) = {\mathcal{L}}\left( {f\left( x \right)} \right)\left( s \right) \cdot {\mathcal{L}}\left( {g\left( x \right)} \right)\left( s \right)$$
(20)

We finally consider the following one

$${\mathcal{L}}\left( {\partial_{t}^{n} f(t)} \right) = s^{n} {\mathcal{L}}\left( {f(t)} \right) - \mathop \sum \limits_{k = 1}^{n} s^{k - 1} f^{{\left( {n - k} \right)}} (0)$$
(21)

However, it is possible to use directly the Laplace transform for this case due to the nature of the beta-derivative. We shall therefore introduce a novel operator called Atangana transform.

Definition 3

Let f be a function such that for any \(0 < \beta \le n\), the Laplace transform of \(\left( {t + \frac{1}{\varGamma \left( \beta \right)}} \right)^{\beta - 1} f(t)\) exists, then the Atangana transform of f is defined as

$${\mathcal{L}}_{\beta } \left( {f\left( t \right)} \right)\left( s \right) = \int \limits_{0}^{\infty } \left( {t + \frac{1}{\varGamma \left( \beta \right)}} \right)^{\beta - n} f(t)e^{ - st} {\text{d}}t$$
(22)

We shall present some properties of the Atangana transform operator

  1. 1.

    \({\mathcal{L}}_{\beta } \left( {af\left( t \right) + bg(t)} \right)\left( s \right) = a{\mathcal{L}}_{\beta } \left( {f\left( t \right)} \right)\left( s \right) + b{\mathcal{L}}_{\beta } \left( {g\left( t \right)} \right)\left( s \right)\)

  2. 2.

    If a function \(f\) is n-time differentiable, then

    $${\mathcal{L}}_{\beta } \left( {{}_{0}^{A} D_{t}^{\beta } f\left( t \right)} \right)\left( s \right) = s^{n} {\mathcal{L}}\left( {f(t)} \right) - \mathop \sum \limits_{k = 1}^{n} s^{k - 1} f^{{\left( {n - k} \right)}} (0)$$
  3. 3.

    \({\mathcal{L}}_{\beta } \left( {\left( {t + \frac{1}{\varGamma \left( \beta \right)}} \right)^{n - \beta } f\left( t \right)} \right)\left( s \right) = {\mathcal{L}}\left( {f(t)} \right)(s)\)

Proof

  1. 1.

    The first property is very easy to prove since

    $${\mathcal{L}}_{\beta } \left( {af\left( t \right) + bg(t)} \right)\left( s \right) = \int \limits_{0}^{\infty } \left( {t + \frac{1}{\varGamma \left( \beta \right)}} \right)^{\beta - n} \left( {af\left( t \right) + bg(t)} \right)e^{ - st} {\text{d}}t$$
    (23)
    $$\begin{aligned} & \int \limits_{0}^{\infty } \left( {t + \frac{1}{\varGamma \left( \beta \right)}} \right)^{\beta - n} \left( {af\left( t \right) + bg(t)} \right)e^{ - st} {\text{d}}t \\ & \quad = a\int \limits_{0}^{\infty } \left( {t + \frac{1}{\varGamma \left( \beta \right)}} \right)^{\beta - n} f(t)e^{ - st} {\text{d}}t + b\int \limits_{0}^{\infty } \left( {t + \frac{1}{\varGamma \left( \beta \right)}} \right)^{\beta - n} g(t)e^{ - st} {\text{d}}t \\ & \quad = a{\mathcal{L}}_{\beta } \left( {f\left( t \right)} \right)\left( s \right) + b{\mathcal{L}}_{\beta } \left( {g\left( t \right)} \right)\left( s \right) \\ \end{aligned}$$
  2. 2.

    For the second property, we have the following

    $${\mathcal{L}}_{\beta } \left( {{}_{0}^{A} D_{t}^{\beta } f\left( t \right)} \right)\left( s \right) = \int \limits_{0}^{\infty } \left( {t + \frac{1}{\varGamma \left( \beta \right)}} \right)^{\beta - n} {}_{0}^{A} D_{t}^{\beta } f(t)e^{ - st} {\text{d}}t$$
    (24)

Now since f is n-time differentiable, the, it beta-derivative is given as follow

$${}_{0}^{A} D_{t}^{\beta } f\left( t \right) = \left( {t + \frac{1}{\varGamma \left( \beta \right)}} \right)^{n - \beta } \mathop {\lim }\limits_{h \to 0} \frac{{f^{(n - 1)} \left( {t + h} \right) - f^{(n - 1)} (t)}}{h}$$

Then, Eq. (24) can be rewriting as

$${\mathcal{L}}_{\beta } \left( {{}_{0}^{A} D_{t}^{\beta } f\left( t \right)} \right)\left( s \right) = \int \limits_{0}^{\infty } \left( {t + \frac{1}{\varGamma \left( \beta \right)}} \right)^{\beta - n} \left\{ {\left( {t + \frac{1}{\varGamma \left( \beta \right)}} \right)^{n - \beta } \mathop {\lim }\limits_{h \to 0} \frac{{f^{(n - 1)} \left( {t + h} \right) - f^{(n - 1)} (t)}}{h}} \right\}e^{ - st} {\text{d}}t$$

After simplification, we obtain the following expression

$${\mathcal{L}}_{\beta } \left( {{}_{0}^{A} D_{t}^{\beta } f\left( t \right)} \right)\left( s \right) = \int \limits_{0}^{\infty } \left\{ {\mathop {\lim }\limits_{h \to 0} \frac{{f^{(n - 1)} \left( {t + h} \right) - f^{(n - 1)} (t)}}{h}} \right\}e^{ - st} {\text{d}}t$$

After using the Laplace property Eq. (21) above expression give us

$${\mathcal{L}}_{\beta } \left( {{}_{0}^{A} D_{t}^{\beta } f\left( t \right)} \right)\left( s \right) = s^{n} {\mathcal{L}}\left( {f(t)} \right) - \mathop \sum \limits_{k = 1}^{n} s^{k - 1} f^{{\left( {n - k} \right)}} (0)$$

4.1 The special solution

Now making use of the above operator, on both sides of Eq. (8), we obtain

$$\left\{ {\begin{array}{*{20}l} {S\left( s \right) = \frac{S(0)}{s} + \frac{1}{s}{\mathcal{L}}_{\beta } \left\{ { - cS\left( t \right)I\left( t \right) + bN - lN + fR\left( t \right) - lS\left( t \right) + hS\left( t \right)} \right\}(s)} \hfill \\ {I\left( s \right) = \frac{I(0)}{s} + \frac{1}{s}{\mathcal{L}}_{\beta } \left\{ {cS\left( t \right)I\left( t \right) - \left( {f + h} \right)I\left( t \right) - hS\left( t \right)} \right\}(s)} \hfill \\ {R\left( s \right) = \frac{R(0)}{s} + \frac{1}{s}{\mathcal{L}}_{\beta } \left\{ {hI\left( t \right) - fR\left( t \right) } \right\}(s) } \hfill \\ {D\left( s \right) = \frac{D\left( 0 \right)}{s} + \frac{1}{s}{\mathcal{L}}_{\beta } \left\{ {fI\left( t \right) + lN - bN + lS\left( t \right)} \right\}(s)} \hfill \\ \end{array} } \right.$$
(25)

Thus applying the inverse Laplace operator on both sides of the above, we obtain

$$\left\{ {\begin{array}{*{20}l} {S\left( t \right) = S(0) + {\mathcal{L}}^{ - 1} \left\{ {\frac{1}{s}{\mathcal{L}}_{\beta } \left\{ { - cS\left( t \right)I\left( t \right) + bN - lN + fR\left( t \right) - lS\left( t \right) + hS\left( t \right)} \right\}(s)} \right\}} \hfill \\ {I\left( t \right) = I(0) + {\mathcal{L}}^{ - 1} \left\{ {\frac{1}{s}{\mathcal{L}}_{\beta } \left\{ {cS\left( t \right)I\left( t \right) - \left( {f + h} \right)I\left( t \right) - hS\left( t \right)} \right\}(s)} \right\}} \hfill \\ {R\left( t \right) = R(0) + {\mathcal{L}}^{ - 1} \left\{ {\frac{1}{s}{\mathcal{L}}_{\beta } \left\{ {hI\left( t \right) - fR\left( t \right) } \right\}(s)} \right\} } \hfill \\ {D\left( t \right) = D(0) + {\mathcal{L}}^{ - 1} \left\{ {\frac{1}{s}{\mathcal{L}}_{\beta } \left\{ {fI\left( t \right) + lN - bN + lS\left( t \right)} \right\}(s)} \right\}} \hfill \\ \end{array} } \right.$$
(26)

The iterative method of (26) can now be employed to put frontward the main recursive formula connecting the Lagrange multiplier as

$$\left\{ {\begin{array}{*{20}c} {S_{0} \left( t \right) = S(0)} \\ {I_{0} \left( t \right) = I(0)} \\ {R_{0} \left( t \right) = R(0) } \\ {D_{0} \left( t \right) = D(0)} \\ \end{array} } \right.$$
(27)
$$\left\{ {\begin{array}{*{20}l} {S_{n + 1} \left( t \right) = S_{n} (t) + {\mathcal{L}}^{ - 1} \left\{ {\frac{1}{s}{\mathcal{L}}_{\beta } \left\{ { - cS_{n} \left( t \right)I_{n} \left( t \right) + bN - lN + fR_{n} \left( t \right) - lS_{n} \left( t \right) + hS_{n} \left( t \right)} \right\}\left( s \right)} \right\}\left( t \right)} \hfill \\ {I_{n + 1} \left( t \right) = I_{n} (t) + {\mathcal{L}}^{ - 1} \left\{ {\frac{1}{s}{\mathcal{L}}_{\beta } \left\{ {cS_{n} \left( t \right)I_{n} \left( t \right) - \left( {f + h} \right)I_{n} \left( t \right) - hS_{n} \left( t \right)} \right\}(s)} \right\}\left( t \right)} \hfill \\ {R_{n + 1} \left( t \right) = R_{n} (t) + {\mathcal{L}}^{ - 1} \left\{ {\frac{1}{s}{\mathcal{L}}_{\beta } \left\{ {hI_{n} \left( t \right) - fR_{n} \left( t \right) } \right\}(s)} \right\} \left( t \right) } \hfill \\ {D_{n + 1} \left( t \right) = D_{n} (t) + {\mathcal{L}}^{ - 1} \left\{ {\frac{1}{s}{\mathcal{L}}_{\beta } \left\{ {fI_{n} \left( t \right) + lN - bN + lS_{n} \left( t \right)} \right\}(s)} \right\} \left( t \right) } \hfill \\ \end{array} } \right.$$

The special solution of this equation is therefore given as

$$\left\{ {\begin{array}{*{20}c} {\mathop {\lim }\limits_{n \to \infty } S_{n} \left( t \right) = S(t)} \\ {\mathop {\lim }\limits_{n \to \infty } I_{n} \left( t \right) = I(t)} \\ {\mathop {\lim }\limits_{n \to \infty } R_{n} \left( t \right) = R(t) } \\ {\mathop {\lim }\limits_{n \to \infty } D_{n} \left( t \right) = D(t)} \\ \end{array} } \right.$$
(28)

4.2 Stability and uniqueness analysis

The efficiency of the used method can only be expressed via the stability and the convergence analysis. Therefore, we present in this section the stability analysis of the used method for solving the novel system Eq. (8). To achieve this, we consider the following operator

$$E\left( {S,I,R,D} \right) = \left\{ {\begin{array}{*{20}c} {{}_{0}^{A} D_{t}^{\beta } S\left( t \right)} \\ {{}_{0}^{A} D_{t}^{\beta } I\left( t \right)} \\ {{}_{0}^{A} D_{t}^{\beta } R\left( t \right) } \\ {{}_{0}^{A} D_{t}^{\beta } D(t) } \\ \end{array} } \right. = \left\{ {\begin{array}{*{20}l} { - cS\left( t \right)I\left( t \right) + bN - lN + fR\left( t \right) - lS\left( t \right) + hS(t)} \hfill \\ {cS\left( t \right)I\left( t \right) - \left( {f + h} \right)I\left( t \right) - hS(t)} \hfill \\ {hI\left( t \right) - fR\left( t \right)} \hfill \\ {fI\left( t \right) + lN - bN + lS(t) } \hfill \\ \end{array} } \right.$$
(29)

Theorem 1

Let us think about the above operator \(E\) and think about the initial condition for the system of Eqs. ( 8 ), then the method used leads to a special solution of system Eq. ( 8 )

Proof

To achieve this, we shall think about the following \(Z -\) sub-Hilbert space of the Hilbert space \(H = L^{2} \left( {\left( {0,T} \right)} \right)\) [12] that can be defined as the set of those functions the following space

$$P:\left( {0 ,T} \right) \to {\mathbb{R}}, Z = \left\{ {u,v\left| {\int \limits_{0}^{t} \left( {\tau + \frac{1}{\varGamma \left( \beta \right)}} \right)^{\beta - 1} } \right.uv{\text{d}}\tau < \infty } \right\}$$

We agreeably undertake that the differential operators are limited under the \(L^{2}\) norms. Exploiting the description of the operator, \(E\) we ensure the succeeding

$$E\left( {S,I,R,D} \right) - E\left( {S_{1} ,I_{1} ,R_{1} ,D_{1} } \right) = \left\{ {\begin{array}{*{20}l} {cS_{1} I_{1} - cSI + f\left( {R - R_{1} } \right) - l\left( {S - S_{1} } \right) + h\left( {S - S_{1} } \right)} \hfill \\ { - cS_{1} I_{1} + cSI - \left( {f + h} \right)\left( {I - I_{1} } \right) - h\left( {S - S_{1} } \right)} \hfill \\ {h\left( {I - I_{1} } \right) - f\left( {R - R_{1} } \right) } \hfill \\ {f\left( {I - I_{1} } \right) + l\left( {S - S_{1} } \right) } \hfill \\ \end{array} } \right.$$
(30)

We shall evaluate next the beta inner product of \(G = A\left( {E\left( {S,I,R,D} \right) - E\left( {S_{1} ,I_{1} ,R_{1} ,D_{1} } \right), \left( {S - S_{1} ,I - I_{1} ,R - R_{1} ,D - D_{1} } \right)} \right)\) where the beta inner product is defined as [7]

Definition 4

Let f and g be two functions defined on \([0, b].\) Assuming that \(fg\) is beta integrable, the beta inner product is defined as

$$A(f,g) = \int \limits_{0}^{b} \left( {t + \frac{1}{\varGamma \left( \beta \right)}} \right)^{\beta - 1} f(t)\overline{g(t)} {\text{d}}t$$
(31)

Remark

We can notice that if b is a finite number, then the beta inner product can be bounded by the inner product as follow

$$A\left( {f,g} \right) = \int \limits_{0}^{b} \left( {t + \frac{1}{\varGamma \left( \beta \right)}} \right)^{\beta - 1} f\left( t \right)\overline{g(t)} {\text{d}}t \le c_{\beta } \int \limits_{0}^{b} f(t)\overline{g(t)} {\text{d}}t$$
(32)
$$c_{\beta } = \left( {b + \frac{1}{\varGamma \left( \beta \right)}} \right)^{\beta - 1}$$

Therefore using the above remark, we obtain the following

$$\begin{aligned} G & = A\left( {E\left( {S,I,R,D} \right) - E\left( {S_{1} ,I_{1} ,R_{1} ,D_{1} } \right), \left( {S - S_{1} ,I - I_{1} ,R - R_{1} ,D - D_{1} } \right)} \right) \\ & \le c_{\beta } \left( {E\left( {S,I,R,D} \right) - E\left( {S_{1} ,I_{1} ,R_{1} ,D_{1} } \right), \left( {S - S_{1} ,I - I_{1} ,R - R_{1} ,D - D_{1} } \right)} \right) \\ \end{aligned}$$
(33)

Our next concern now is to evaluate the inner product

$$\begin{aligned} & \left( {E\left( {S,I,R,D} \right) - E\left( {S_{1} ,I_{1} ,R_{1} ,D_{1} } \right), \left( {S - S_{1} ,I - I_{1} ,R - R_{1} ,D - D_{1} } \right)} \right) \\ & \quad = \left\{ {\begin{array}{*{20}l} {\left( {cS_{1} I_{1} - cSI + f\left( {R - R_{1} } \right) - l\left( {S - S_{1} } \right) + h\left( {S - S_{1} } \right),\left( {S - S_{1} } \right) } \right)} \hfill \\ {\left( { - cS_{1} I_{1} + cSI - \left( {f + h} \right)\left( {I - I_{1} } \right) - h\left( {S - S_{1} } \right),\left( {I - I_{1} } \right)} \right)} \hfill \\ {\left( {h\left( {I - I_{1} } \right) - f\left( {R - R_{1} } \right),\left( {R - R_{1} } \right)} \right) } \hfill \\ {\left( {f\left( {I - I_{1} } \right) + l\left( {S - S_{1} } \right),\left( {D - D_{1} } \right)} \right) } \hfill \\ \end{array} } \right. \\ \end{aligned}$$
(34)

We shall examine case by case

$$\begin{aligned} & \left( {cS_{1} I_{1} - cSI + f\left( {R - R_{1} } \right) - l\left( {S - S_{1} } \right) + h\left( {S - S_{1} } \right),\left( {S - S_{1} } \right) } \right) \\ & \quad \le \left\| {S - S_{1} } \right\|\left\{ {f\left\| {\left( {R - R_{1} } \right)} \right\| + \left( {l - h} \right)\left\| {S_{1} - S} \right\| + c\left\| {S_{1} I_{1} - cSI} \right\|} \right\} \\ \end{aligned}$$
(35)

However, due to the physical problem under investigation, all the representative are bounded, implied, we can find some positive parameters \(O_{1} , O_{2} ,O_{3} ,\) such that

$$\left\| {\left( {R - R_{1} } \right)} \right\| \le O_{1} , \left\| {S_{1} - S} \right\| \le O_{2} \;{\text{and}}\;\left\| { S_{1} I_{1} - cSI} \right\| \le O_{3}$$

Thus replacing the above inequalities in (35) to obtain

$$\begin{aligned} & \left( {cS_{1} I_{1} - cSI + f\left( {R - R_{1} } \right) - l\left( {S - S_{1} } \right) + h\left( {S - S_{1} } \right),\left( {S - S_{1} } \right) } \right) \\ & \quad \le \left\| {S - S_{1} } \right\|\left\{ {fO_{1} + \left( {l - h} \right)O_{2} + cO_{3} } \right\} = p_{1} \left\| {S - S_{1} } \right\| \\ \end{aligned}$$
(36)

Using the same footsteps, we obtain the following

$$\begin{aligned} & \left( { - cS_{1} I_{1} + cSI - \left( {f + h} \right)\left( {I - I_{1} } \right) - h\left( {S - S_{1} } \right),\left( {I - I_{1} } \right)} \right) \le p_{2} \left\| {(I - I_{1} )} \right\| \\ & \quad \left( {h\left( {I - I_{1} } \right) - f\left( {R - R_{1} } \right),\left( {R - R_{1} } \right)} \right) \le p_{3} \left\| {R - R_{1} } \right\| \\ & \quad \left( {f\left( {I - I_{1} } \right) + l\left( {S - S_{1} } \right),\left( {D - D_{1} } \right)} \right) \le p_{4} \left\| {D - D_{1} } \right\| \\ \end{aligned}$$
(37)

Thus replacing the above inequalities (37), (36) and (35) into (34) to obtain

$$\left( {E\left( {S,I,R,D} \right) - E\left( {S_{1} ,I_{1} ,R_{1} ,D_{1} } \right), \left( {S - S_{1} ,I - I_{1} ,R - R_{1} ,D - D_{1} } \right)} \right) \le \left\{ {\begin{array}{*{20}l} {p_{1} \left\| {S - S_{1} } \right\|} \hfill \\ {p_{2} \left\| {\left( {I - I_{1} } \right)} \right\|} \hfill \\ {p_{3} \left\| {R - R_{1} } \right\|} \hfill \\ {p_{4} \left\| {D - D_{1} } \right\|} \hfill \\ \end{array} } \right.$$
(38)

Thus, Eq. (32) becomes

$$G \le c_{\beta } \left\{ {\begin{array}{*{20}l} {p_{1} \left\| {S - S_{1} } \right\|} \hfill \\ {p_{2} \left\| {\left( {I - I_{1} } \right)} \right\|} \hfill \\ {p_{3} \left\| {R - R_{1} } \right\|} \hfill \\ {p_{4} \left\| {D - D_{1} } \right\|} \hfill \\ \end{array} } \right.$$
(39)

Following the same line of ideas, we can find a positive vector \(F(f_{1} ,f_{2} ,f_{3} ,f_{4} )\) such that for all vector \(V\left( {V_{1} ,V_{2} ,V_{3} ,V_{4} } \right) \in H\)

$$G \le c_{\beta } \left\{ {\begin{array}{*{20}c} {f_{1} \left\| {S - S_{1} } \right\|\left\| {V_{1} } \right\|} \\ {f_{2} \left\| {\left( {I - I_{1} } \right)} \right\|\left\| {V_{2} } \right\|} \\ {f_{3} \left\| {R - R_{1} } \right\|\left\| {V_{3} } \right\|} \\ {f_{4} \left\| {D - D_{1} } \right\|\left\| {V_{4} } \right\|} \\ \end{array} } \right.$$
(40)

Putting together (40) and (39) completes the proof of Theorem 1.

Theorem 2

Taking into account the initial conditions of Eq. ( 8 ), there is only one unique special solution for Eq. ( 8 ) while using the new variational iteration method.

Proof

Assuming that \(I\) is the exact solution of system (8), let \(T\) and \(T_{1}\) be two difference special solutions of system and converge to \(I \ne 0\) for some large number \(n\) and \(m\) (2) while using the homotopy method, then using Theorem 1, we have the following inequality

$$\begin{aligned} & \left( {E\left( {u,v,w,s,z} \right) - E\left( {u_{1} ,v_{1} ,w_{1} ,s_{1} ,z_{1} } \right), \left( {w_{1} ,w_{2} ,w_{3} ,w_{4} ,w_{5} } \right)} \right) \le c_{\beta } F\left\| {T - T_{1} } \right\|\left\| I \right\| \\ & \quad F\left\| {T - T_{1} } \right\|\left\| I \right\| \le c_{\beta } F\left\| {T - I + I - T} \right\|\left\| I \right\| \\ \end{aligned}$$

Employing the triangular inequality, we arrive at the succeeding

$$F\left\| {T - T_{1} } \right\|\left\| I \right\| \le c_{\beta } F\left\{ {\left\| {I - T_{1} } \right\| + \left\| {T - I} \right\|} \right\}\left\| I \right\|$$
(41)

Nevertheless, subsequently \(T\) and \(T_{1}\) convergence to W for large number \(n\) and \(m\), then we can find a small positive parameter \(\varepsilon\), such that:

$$\left\| {I - T_{1} } \right\| < \frac{\varepsilon }{{2c_{\beta } P\left\| I \right\|}},\quad {\text{for}}\;n$$
$$\left\| {T - I} \right\| < \frac{\varepsilon }{{2c_{\beta } P\left\| I \right\|}},\quad {\text{for}}\;m$$

Now consider \(M = { \hbox{max} }(n, m)\), then

$$F\left\| {T - T_{1} } \right\|\left\| I \right\| \le c_{\beta } F\left\{ {\left\| {I - T_{1} } \right\| + \left\| {T - I} \right\|} \right\}\left\| I \right\| < \frac{\varepsilon }{{2Fc_{\beta } \left\| I \right\|}} + \frac{\varepsilon }{{2Fc_{\beta } \left\| I \right\|}} = \varepsilon \;{\text{for}}\;M$$

Nonetheless using the topology knowledge, we have that

$$F\left\| {T - T_{1} } \right\|\left\| I \right\| = 0$$

Since \(I \ne 0\) and \(F \ne 0\), then \(\left\| {T - T_{1} } \right\| = 0\) implying \(T = T_{1}\). This shows the uniqueness of the special solution.

5 Numerical applications

It is important to give an instruction to the computer to generate the iteratively the special solution. To achieve this, we shall give the following code that will be used to derive the special solution of system (2)

$${\text{Input}}:\left\{ {\begin{array}{*{20}c} {S_{0} \left( t \right) = S(0)} \\ {I_{0} \left( t \right) = I(0)} \\ {R_{0} \left( t \right) = R(0) } \\ {D_{0} \left( t \right) = D(0)} \\ \end{array} } \right.\;{\text{as}}\;{\text{preliminary}}\;{\text{input}},$$

  • i—number terms in the rough calculation

  • \({\text{Output}}:\left\{ {\begin{array}{*{20}c} {S_{Ap} \left( t \right)} \\ {I_{Ap} \left( t \right)} \\ {R_{Ap} \left( t \right) } \\ {D_{Ap} \left( t \right)} \\ \end{array} } \right., \;{\text{the}}\;{\text{approximate}}\;{\text{solution}}\)

  • Step 1: Put

    $$\left\{ {\begin{array}{*{20}l} {S_{0} (t) = S(0)} \hfill \\ {I_{0} (t) = I (0)} \hfill \\ {R_{0} (t) = R (0)} \hfill \\ {D_{0} (t) = D(0)} \hfill \\ \end{array} } \right.\;{\text{and}}\;\left\{ {\begin{array}{*{20}l} {S_{Ap} (t)} \hfill \\ {I_{Ap} (t)} \hfill \\ {R_{Ap} (t)} \hfill \\ {D_{Ap} (t)} \hfill \\ \end{array} } \right. = \left\{ {\begin{array}{*{20}l} {S_{Ap} (t)} \hfill \\ {I_{Ap} (t)} \hfill \\ {E_{Ap} (t)} \hfill \\ {D_{Ap} (t)} \hfill \\ \end{array} } \right.$$

  • Step 2: for i = 1 to n–1 do step 3, step 4 and step 5

    $$\left\{ {\begin{array}{*{20}l} {S_{n + 1} \left( t \right) = S_{n} (t) + {\mathcal{L}}^{ - 1} \left\{ {\frac{1}{s}{\mathcal{L}}_{\beta } \left\{ { - cS_{n} \left( t \right)I_{n} \left( t \right) + bN - lN + fR_{n} \left( t \right) - lS_{n} \left( t \right) + hS_{n} \left( t \right)} \right\}\left( s \right)} \right\}\left( t \right)} \hfill \\ {I_{n + 1} \left( t \right) = I_{n} (t) + {\mathcal{L}}^{ - 1} \left\{ {\frac{1}{s}{\mathcal{L}}_{\beta } \left\{ {cS_{n} \left( t \right)I_{n} \left( t \right) - \left( {f + h} \right)I_{n} \left( t \right) - hS_{n} \left( t \right)} \right\}(s)} \right\}\left( t \right)} \hfill \\ {R_{n + 1} \left( t \right) = R_{n} (t) + {\mathcal{L}}^{ - 1} \left\{ {\frac{1}{s}{\mathcal{L}}_{\beta } \left\{ {hI_{n} \left( t \right) - fR_{n} \left( t \right) } \right\}(s)} \right\} \left( t \right) } \hfill \\ {D_{n + 1} \left( t \right) = D_{n} (t) + {\mathcal{L}}^{ - 1} \left\{ {\frac{1}{s}{\mathcal{L}}_{\beta } \left\{ {fI_{n} \left( t \right) + lN - bN + lS_{n} \left( t \right)} \right\}(s)} \right\} \left( t \right) } \hfill \\ \end{array} } \right.$$

  • Step 3: compute

    $$\left\{ {\begin{array}{*{20}c} {\beta_{{1\left( {n + 1} \right)}} \left( t \right) = \beta_{1\left( n \right)} \left( t \right) + S_{Ap} (t) } \\ {\beta_{{2\left( {n + 1} \right)}} \left( t \right) = \beta_{2\left( n \right)} \left( t \right) + I_{Ap} \left( t \right) } \\ {\beta_{{3\left( {n + 1} \right)}} \left( t \right) = \beta_{3\left( n \right)} \left( t \right) + R_{Ap} \left( t \right) } \\ {\beta_{{4\left( {n + 1} \right)}} \left( t \right) = \beta_{4\left( n \right)} \left( t \right) + D_{Ap} \left( t \right) } \\ {} \\ \end{array} } \right.$$

  • Step 4: compute

    $$\left\{ {\begin{array}{*{20}l} {S_{{Ap}} (t)} \hfill \\ {I_{{Ap}} (t)} \hfill \\ {R_{{Ap}} (t)} \hfill \\ {D_{{Ap}} (t)} \hfill \\ \end{array} } \right. = \left\{ {\begin{array}{*{20}l} {S_{{Ap}} (t) + \beta _{{1\left( {n + 1} \right)}} \left( t \right)} \hfill \\ {I_{{Ap}} \left( t \right) + \beta _{{2\left( {n + 1} \right)}} \left( t \right)} \hfill \\ {R_{{Ap}} \left( t \right) + \beta _{{3\left( {n + 1} \right)}} \left( t \right)} \hfill \\ {D_{{Ap}} \left( t \right) + \beta _{{4\left( {n + 1} \right)}} \left( t \right)} \hfill \\ \end{array} } \right.$$

    Stop.

The overhead procedure shall be employed to yield the numerical replication of the physical problem under investigation (Table 1).

Table 1 Theoretical values used for simulation
Full size table

The parameters in table one are used to predict the following Figs. 2, 3, 4, 5, and 6 for different values of β.

Fig. 2
figure 2

Prediction for β = 1

Full size image
Fig. 3
figure 3

Prediction for β = 0.85

Full size image
Fig. 4
figure 4

Prediction for β = 0.65

Full size image
Fig. 5
figure 5

Prediction for β = 0.45

Full size image
Fig. 6
figure 6

Prediction for β = 0.25

Full size image

6 Conclusion

In the recent decade, many deadly diseases have revealed their existence in many countries around the world. In particular, in Africa, we have faced severe destruction of human kind by strange disease classified as hemorrhagic fever, for instance Ebola that started in Zaire in 1975, and then in Sierra Leone, Nigeria, Guinea, and Liberia in 2014. Beside this one, another one called Lassa was observed for the first time 1969 in town of Lassa, in Borno state Nigeria. The outbreaks of the disease have been observed in Nigeria, Liberia, Sierra Leone, Guinea, and the Central Africa Republic. However, this hemorrhagic fever is more fatal for pregnant women, with the mortality rate of about 80 %. Since mathematical tools have been always used to model approximately some observed physical problems, we have constructed a set of mathematical equations describing the spread of this disease amount in pregnant women. We achieved this by employing the novel derivative called beta-derivative. We studied the steady state and also find the reproductive number. We proposed a novel operator called the Atangana transform and used it to solve iteratively the set of equations. We presented in detail the stability and uniqueness analysis of this method for solving the set of equations. We used some theoretical parameters to show the numerical simulations.