Solution approach to multi-objective linear fractional programming problem using parametric functions

Abstract

In this paper, an iterative technique based on the use of parametric functions is proposed to obtain the best preferred optimal solution of a multi-objective linear fractional programming problem. The decision maker ascertains own desired tolerance values for the objectives as termination constants and imposes them on each iteratively computed objective functions in terms of termination conditions. Each fractional objective is transformed into non-fractional parametric function using certain initial values of parameters. The parametric values are iteratively computed and $\epsilon$-constraint method is used to obtain the pareto (weakly) optimal solutions in each step. The computations get terminated when all the termination conditions are satisfied at a pareto optimal solution of an iterative step. A numerical example is discussed at the end to illustrate the proposed method and fuzzy max–min operator method is applied to validate the obtained results.

1 Introduction

Mathematical modelling of numerous existent problems of human society engenders several objectives which are conflicted as well as inter-related to each other. Many times, they exist in fractional or rational form of two other functions and need simultaneous optimization under a common set of constraints. If the numerators and denominators of the fractional objectives with constraints are all affine functions (i.e, linear plus constants) , such modelled optimization problems are interpreted as multi-objective linear fractional programming problems. Several mathematical optimization problems comprise fractional objectives to be optimized which are frequently encountered [21] in many real life situations like profit/cost, inventory/sale, output/employee, risk-assets/capital, debt/equity etc. Linear Fractional programming problem which was developed by Hungarian mathematician B.Martos in 1960, has wide range of application in various important fields such as economics, finance, science, engineering, business, management, information theory, marine transportation, water resourses, health care, corporate planning and so forth. Multi-objective FPP has attracted considerable research interest since recent few years and several methods have been proposed in this context for determination of the optimal solutions. Usually multi-objective optimization problem does not contain single feasible solution which can optimize all the objectives absolutely and simultaneously. Therefore the concept of pareto optimal solution otherwise called non-inferior or non-dominated solution was developed by Vilfredo Pareto which improves (i.e, minimizes or maximizes) atleast one objective function without degrading (i.e, maximizes or minimizes) other objectives in case of multi-objective optimization (i.e, minimization or maximization) problems. Various methods have been developed to generate pareto optimal solutions from which the best preferred optimal solution is determined by the DM to satisfy all the objectives. Charnes and Cooper [7] developed a transformation technique in 1960 to linearize the fractional objectives with an additional variable. Bitran and Novaes [3] proposed a method which is widely used to solve FPP. Tantawy [22] used conjugate gradient method to solve LFPP. WOLF [25] used parametric linear programming to solve nonlinear FPP. Pal and Sen [20] proposed goal programming method to solve interval valued MOLFPP. Costa [10] derived an algorithm to solve MOLFPP which goes on dividing the non-dominated region to search the maximum value of weighted sum of the objectives. Valipour et al. [24] developed a method to solve MOLFPP which is an extension of Dinkelbach’s parametric approach [13] to solve LFPP. Borza et al. [4] used parametric approach to solve a single objective LFPP with interval coefficients in the objective function. Almogy and Levin [1] used parametric technique to solve a problem with the objective defined as sum of fractional functions. Miettinen [16] illustrates many methods to solve muti-objective optimization problems.

Zhixia and Fengqi [26] developed a parametric algorithm to solve mixed integer linear and nonlinear fractional programming problems by transforming it into equivalent parametric formulation. Das et al. [12] proposed a model to solve fuzzy LFPP by formulating an equivalent tri-objective LFPP. Osman et al. [19] developed an interactive approach to solve multi-level MOLFPP with fuzzy parameters. Chinnadurai and Muthukumar [8] proposed a method to derive $(\alpha , r)$-optimal solutions of a fuzzy LFPP. Chakrobarty and Gupta [5] proposed fuzzy approach to solve MOLFPP by formulating its equivalent linear programming whereas Chang [6] proposed a goal programming approach to solve fuzzy MOLFPP. Liu [15] developed a method to derive fuzzy objective values of a geometric programming with fuzzy parameters. Ojha and Biswal [18] proposed $\epsilon$-constraint method to derive pareto optimal solutions of a multi-objective geometric programming problem. Toksari [23] developed Taylor series approach to solve fuzzy MOLFPP by linearizing fuzzy membership functions but Dangwal [11] applied first order Taylor series to linearize fractional objective functions to solve a MOLFPP.

In this present work we have proposed a method to solve a multi-objective linear fractional programming problem using the concept of parametric functions and $\epsilon$-constraint method together. It converts the LFPP to suitable non-fractional problem using certain parameters to find a set of non-inferior solutions through iterative computations. Termination conditions are imposed on all the objectives by the DM to determine the best preferred optimal solution at which a certain level of satisficing optimality is attained by all the objective functions.

The organization of the paper is as follows: following introduction, a brief explanation of multi-objective optimization problem and existence of it’s optimal solution are presented in Sect. 2 whereas the use of $\epsilon$-constraint method is discussed in Sect. 3. Fuzzy programming to solve multi-objective optimization problem using membership functions is briefly discussed in Sect. 4. Some proposed theorems with proofs are incorporated in Sect. 5 regarding parametric approach to MOLFPP. Section 6 describes the proposed solution procedure. An example is discussed in Sect. 6.1 for illustration of the proposed method and finally, some conclusions are incorporated in Sect. 7.

2 Multi-objective optimization problem (MOOP)

In multi-objective optimization problem, several objective functions are optimized simultaneously with respect to a common set of constraints. Usually there does not exist single optimal solution which optimizes all the objectives together with their respective best satisfactory level. In such cases, a set of pareto optimal solutions are generated using an appropriate method available in literature and the best preferred (compromise) optimal solution that satisfies all the objectives with the best possibility, is determined by the decision maker (DM) comparing the objective values in accordance to own desire on priority basis or the requirement of the system. A multi-objective optimization problem [14, 16] can be mathematically stated as:

$$\begin{aligned}&\min f(x)=(f_1(x),f_2(x),\ldots ,f_k(x))\nonumber \\&\quad {\hbox {subject to}}\nonumber \\&\quad x\in \varOmega \nonumber \\&\quad {\hbox {where}}\, x\in {\mathbb {R}}^n\,{\hbox {and}}\, f_i:{\mathbb {R}}^n \rightarrow {\mathbb {R}}, i=1,2\ldots , k \end{aligned}$$

(1)

$\varOmega$ is the set of constraints, considered as a non-empty compact feasible region. A multi-objective optimization problem is otherwise called as a multi-criterion optimization or vector optimization problem whereas a pareto optimal solution is otherwise called as non-inferior or non-dominated or efficient solution.

Definition 1

$x^* \in \varOmega$ is a pareto optimal solution of the MOOP (1) if there does not exist another feasible solution ${\bar{x}} \in \varOmega$ such that $f_i({\bar{x}}) \le f_i(x^*) ~\forall ~ i$  and  $f_j({\bar{x}}) < f_j(x^*)$ for at least one j.

Definition 2

$x^* \in \varOmega$ is a weakly pareto optimal solution of the MOOP (1) if there does not exist another feasible solution ${\bar{x}} \in \varOmega$ such that $f_i({\bar{x}}) < f_i(x^*) ~\forall ~ i$.

Definition 3

Trade-off or Pareto front is a part of the objective feasible region which consists of the objective values evaluated at the pareto optimal solutions of the MOOP.

Definition 4

Ideal objective vector has the co-ordinates which are obtained by evaluating the values of the objectives at their respective individual minimal points.

Definition 5

Nadir objective vector has the co-ordinates which are the respective worst objective values when the set of solutions is restricted to the trade-off.

3 $\epsilon$-Constraint method

The $\epsilon$-constraint method [9, 16, 17] was proposed by Haimes et al. for obtaining pareto (weakly) optimal solutions of a MOOP. It is a preference based method that generates the non-inferior solutions by optimizing one objective function as the best prioritized one and converting the remaining objective functions as the constraints along with their respective goals which alternate in the range of their best and worst values. In other words, it minimizes one objective function and simultaneously maintains the maximum acceptability level for other objective functions. It is applicable for both convex as well as concave feasible region. The $\epsilon$-constraint method is mathematically defined as:

$$\begin{aligned}&\min f_s(x),~ s \in \{1,2,\ldots ,k\}\nonumber \\&\quad {\hbox {subject to}}\nonumber \\&\quad f_i(x)\le \epsilon _i, ~i=1,2,\ldots ,s-1,s+1,\ldots ,k.\nonumber \\&\quad x\in \varOmega ,\nonumber \\&\quad {\hbox {where}} \,\epsilon _i^L\le \epsilon _i\le \epsilon _i^U \end{aligned}$$

(2)

$\epsilon _i^L,~\epsilon _i^U$ are the respective best and worst values of the objective function $f_i(x)$. Substituting different values of $\epsilon _i$ lying in the range $[\epsilon _i^L,\epsilon _i^U]$ and solving its corresponding above formulated optimization problem, a set of optimal solutions can be generated which are considered as the pareto optimal solutions of the MOOP from which DM determines the best preferred optimal solution by comparing the objective values.

4 Fuzzy programming

To tackle numerous real world problems comprising uncertainty and vagueness in complexity of data, Zadeh developed fuzzy set theory in 1965 that transforms imprecise information into precise mathematical form. The concept of Bellman and Zadeh [2] was extended and implemented by Zimmermann [27] to form a mathematical modelling based on fuzzy concept to solve various multi-objective optimization problems using max–min operator method. Each fuzzy set is associated with a membership function whose domain and range are the set of decision variables and [0,1] respectively. An appropriate membership function is selected to determine the optimal solution. According to Zimmermanns fuzzy technique, best preferred optimal solution of a MOOP can be obtained by using the following steps.

Step 1 Determine the best and worst values i.e., the aspired $(f_i^{min})$ and acceptable $(f_i^{max})$ values respectively for each objective function $f_i(x),~i=1,\ldots ,k$ satisfying $f_i^{min} \le f_i(x) \le f_i^{max}$, for $x \in \varOmega$.

Step 2 Define following linear fuzzy membership function $\mu _i(x)$ for each objective function $f_i(x)$ to derive the best preferred optimal solution of the MOOP as:

$$\begin{aligned} \mu _i(x)= {\left\{ \begin{array}{ll} 1 ,&\quad{}f_i(x)\le f_i^{min}\\ \displaystyle \frac{f_i^{max}-f_i(x)}{f_i^{max}-f_i^{min}},&\quad{} f_i^{min}\le f_i(x) \le f_i^{max} \\ 0,&\quad{}f_i(x) \ge f_i^{max} \end{array}\right. } \end{aligned}$$

(3)

Fig. 1

Membership function defined for minimization problem

The geometrical interpretation of the linear fuzzy membership function for a minimization problem is represented in Fig. 1.

Step 3 Construct the following crisp model to obtain the optimal solution as follows:

$$\begin{aligned}&{\hbox{Max}} \{\min \limits _{1\le i \le k}\mu _i(x)\}\nonumber \\&\quad {\hbox {subject to}}\nonumber \\&\quad x \in ~\varOmega \end{aligned}$$

(4)

Step 4 The above crisp model can be transformed into an equivalent mathematical programming problem as follows:

$$\begin{aligned}&{\hbox{Max}} \beta \nonumber \\&\quad {\hbox {subject to}} \nonumber \\&\quad \mu _i(x)=\displaystyle \frac{f_i^{max}-f_i(x)}{f_i^{max}-f_i^{min}} \ge \beta , ~i=1,2,\ldots ,k \nonumber \\&\quad x \in ~\varOmega \end{aligned}$$

(5)

where ‘$\beta$’ is an auxiliary variable assumed as the value of $\min \nolimits _{1\le i \le k}\mu _i(x)$ . The constraints $\mu _i(x) \ge \beta$ can be replaced by $f_i(x)+\beta (f_i^{max}-f_i^{min})\le f_i^{max}, ~i=1,2,\ldots ,k$ for simplicity.

Step 5 Solve the above maximization problem to obtain the best preferred optimal solution of the MOOP and evaluate the optimal objective values at this solution.

5 Parametric approach to solve FPP

Consider the following single objective fractional programming and parametric non-fractional programming problems respectively.

$$\begin{aligned}&Problem-I : \min \limits _{x\in \varOmega } ~\frac{f(x)}{g(x)} \end{aligned}$$

(6)

$$\begin{aligned}&Problem-II : \min \limits _{x\in \varOmega } ~\{f(x)-\gamma g(x) \} \end{aligned}$$

(7)

where $\gamma$ is a parameter and $\varOmega$ is the non-empty compact feasible region in which both f and g are continuous affine functions with $g(x)>0, ~\forall ~x \in \varOmega$.

Theorem 1

[21]  $x^*$ is optimal solution of Problem-I iff$\min \nolimits _{x\in \varOmega } \{f(x)-\gamma ^* g(x) \}=0$ where$\gamma ^*=\frac{f(x^*)}{g(x^*)}$.

Consider the following multi-objective fractional programming and parametric linear programming problems respectively.

$$\begin{aligned} Problem-III : \min \limits _{x\in \varOmega } \frac{f_i(x)}{g_i(x)},~ i=1,2,\ldots ,k \end{aligned}$$

(8)

$$\begin{aligned} Problem-IV : \min \limits _{x\in \varOmega } \{f_i(x)-\gamma _i^* g_i(x) \},~ i=1,2,\ldots ,k \end{aligned}$$

(9)

Assume that  $g_i(x)>0, \forall ~x\in \varOmega$ and $\gamma _i^*=\frac{f_i(x^*)}{g_i(x^*)}$, where $x^*\in \varOmega$

Remark 1

$x^*$ is pareto optimal solution of Problem-IV if for each $x\in \varOmega$, $f_i(x)-\gamma _i^* g_i(x)=0 ~\forall ~i$ or $f_j(x)-\gamma _j^* g_j(x) >0$ for at least one $j \in \{1,2,\ldots ,k\}$.

Using the above Remark 1 and Theorem 1 due to Dinkelbach, the following results are achieved.

Theorem 2

$x^*$ is pareto optimal solution of Problem-III iff $x^*$ is pareto optimal solution of Problem-IV.

Proof

Consider the following notations for convenience of the proof. $G_i(x)=\frac{f_i(x)}{g_i(x)}$ and $F_i(x)=\{f_i(x)-\gamma _i^* g_i(x)\}$ for $i=1,2,\ldots ,k.$

Let $x^*$ is a pareto optimal solution of the Problem-III.

Suppose on contrary, $x^*$ is not pareto optimal for Problem-IV.

i.e, by definition $\exists ~~{\bar{x}}\in \varOmega$ such that, $F_i({\bar{x}})\le F_i(x^*)~~ \forall ~i=1,2,\ldots ,k$ and $F_j({\bar{x}}) < F_j(x^*)$ for at least one $j\in \{1,2,\ldots ,k\}$.

i.e, $f_i({\bar{x}})-\gamma _i^* g_i({\bar{x}}) \le f_i(x^*)-\gamma _i^* g_i(x^*)~~\forall ~~i$ and $f_j({\bar{x}})-\gamma _j^* g_j({\bar{x}}) < f_j(x^*)-\gamma _j^* g_j(x^*)$ for at least one j.

Since $\gamma _i^*=\frac{f_i(x^*)}{g_i(x^*)}$, we have $f_i(x^*)-\gamma _i^* g_i(x^*)=0$.

i.e, $f_i({\bar{x}})-\gamma _i^* g_i({\bar{x}}) \le 0$ and $f_j({\bar{x}})-\gamma _j^* g_j({\bar{x}}) < 0$ for at least one j.

i.e, $\frac{f_i({\bar{x}})}{g_i({\bar{x}})} \le \frac{f_i(x^*)}{g_i(x^*)} ~~\forall ~i$ and $\frac{f_j({\bar{x}})}{g_j({\bar{x}})} < \frac{f_j(x^*)}{g_j(x^*)}$ for at least one j.

It contradicts the pareto optimality of $x^*$ for the Problem-III. Thus, $x^*$ is pareto optimal solution for Problem-IV.

Conversely, let $x^*$ is pareto optimal for Problem-IV.

Suppose on contrary, $x^*$ is not pareto optimal for Problem-III.

i.e, $\exists ~~ {\bar{x}} \in \varOmega$ such that,

$$\begin{aligned} G_i({\bar{x}}) \le G_i(x^*)~~\forall ~~i{\hbox { and }}G_j({\bar{x}}) < G_j(x^*)\, {\hbox {for at least one}}\, j. \end{aligned}$$

On simplifying we get,

$$\begin{aligned} f_i({\bar{x}})-\gamma _i^* g_i({\bar{x}}) \le 0 {\hbox { and }} f_j({\bar{x}})-\gamma _j^* g_j({\bar{x}}) < 0 \,{\hbox {for at least one }} j. \end{aligned}$$

i.e, $F_i({\bar{x}}) \le 0~~\forall ~i$ and $F_j({\bar{x}}) < 0$ for at least one j.

But,

$$\begin{aligned} F_i(x^*)=f_i(x^*)-\gamma _i^* g_i(x^*)=0 {\hbox { as }} \gamma _i^*=\frac{f_i(x^*)}{g_i(x^*)} \end{aligned}$$

So,

$$\begin{aligned} F_i({\bar{x}}) \le F_i(x^*)~~\forall ~i \,\mathrm{and}\, F_j({\bar{x}}) < F_j(x^*) \,{\hbox {for at least one }} j. \end{aligned}$$

It contradicts the pareto optimality of $x^*$ for Problem-IV. Thus, $x^*$ is pareto optimal solution of Problem-III. $\square$

Theorem 3

The pareto optimal solutions of Problem-IV are also pareto optimal of Problem-III if $x^*$ is pareto optimal of Problem-IV.

Proof

Let ${\bar{x}}$ be a pareto optimal solution of Problem-IV.

i.e, by definition $\exists$  no $x\in \varOmega$ such that,

$f_i(x)-\gamma _i^* g_i(x) \le f_i({\bar{x}})-\gamma _i^* g_i({\bar{x}}) ~\forall ~i$ and $f_j(x)-\gamma _j^* g_j(x) < f_j({\bar{x}})-\gamma _j^* g_j({\bar{x}})$ for at least one j.

In other words for each $x\in \varOmega$,

$$\begin{aligned} f_i(x)-\gamma _i^* g_i(x) = f_i({\bar{x}})-\gamma _i^* g_i({\bar{x}}) ~\forall ~i{\hbox { or }}f_j(x)-\gamma _j^* g_j(x) > f_j({\bar{x}})-\gamma _j^* g_j({\bar{x}}) {\hbox { for at least one }} j. \end{aligned}$$

i.e, for $x=x^*$ we have,

$$\begin{aligned} f_i(x^*)-\gamma _i^* g_i(x^*) = f_i({\bar{x}})-\gamma _i^* g_i({\bar{x}}) ~\forall ~i{\hbox { or }}f_j(x^*)-\gamma _j^* g_j(x^*) > f_j({\bar{x}})-\gamma _j^* g_j({\bar{x}}) {\hbox { for at least one }} j. \end{aligned}$$

Since $\gamma _i^*=\frac{f_i(x^*)}{g_i(x^*)}$,

$$\begin{aligned} f_i({\bar{x}})-\gamma _i^* g_i({\bar{x}})= & {} 0 ~\forall ~i{\hbox { or }} f_j({\bar{x}})-\gamma _j^* g_j({\bar{x}})<0 {\hbox { for at least one }} j.\nonumber \\ i.e,~~\frac{f_i({\bar{x}})}{g_i({\bar{x}})}= & {} \frac{f_i(x^*)}{g_i(x^*)}~~ \forall ~~i ~~or~~ \frac{f_j({\bar{x}})}{g_j({\bar{x}})} < \frac{f_j(x^*)}{g_j(x^*)} ~~for ~at ~least ~one ~j \end{aligned}$$

(10)

By Theorem 2, $x^*$ is pareto optimal for Problem-III as it is pareto optimal for Problem-IV.

i.e, for each $x\in \varOmega$

$$\begin{aligned} \frac{f_i(x^*)}{g_i(x^*)}=\frac{f_i(x)}{g_i(x)}~ ~\forall ~~i ~~or ~~\frac{f_j(x^*)}{g_j(x^*)} < \frac{f_j(x)}{g_j(x)} ~~for~ at ~least ~one~ j. \end{aligned}$$

(11)

Combining (10) and (11),  for each $x\in \varOmega$$\frac{f_i({\bar{x}})}{g_i({\bar{x}})}=\frac{f_i(x)}{g_i(x)}~ \forall ~i$ or $\frac{f_j({\bar{x}}}{g_j({\bar{x}})} < \frac{f_j(x)}{g_j(x)}$ for at least one j.

So ${\bar{x}}$ is pareto optimal of Problem-III.    $\square$

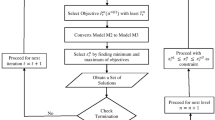
6 Proposed method to solve MOLFPP

General form of a multi-objective LFPP is defined as:

$$\begin{aligned}&{\mathbf{Problem}}\text{-}{\mathbf{P:}}\, \min \,f(x)=(f_1(x),f_2(x),\ldots ,f_k(x))\nonumber \\&\quad\quad\quad\quad {\hbox {subject to}}\nonumber \\&\quad \varOmega =\{x\in {\mathbb {R}}^n\arrowvert Ax(\le , =, \ge )b, x\ge 0\}\nonumber \\&\quad {\hbox {where, }}f_i(x)=\frac{\sum \nolimits _{j=1}^n c_{ij}x_j+\alpha _i}{\sum \nolimits _{j=1}^n d_{ij}x_j+\beta _i},~ i=1,2,\ldots ,k \nonumber \\&\quad c_{ij},~ d_{ij}, ~\alpha _i, ~\beta _i ~\in {\mathbb {R}}, ~b\in {\mathbb {R}}^m, ~A\in {\mathbb {R}}^{m\times n} \end{aligned}$$

(12)

In order to solve the above MOLFPP, we consider the following procedure using both parametric approach and $\epsilon$-constraint method.

Assume that, $f_i(x)=\frac{\sum \nolimits _{j=1}^n c_{ij}x_j+\alpha _i}{\sum \nolimits _{j=1}^n d_{ij}x_j+\beta _i}=\gamma _i^{(t)}$,  $i=1,2,\ldots ,k$ where ‘t’ denotes the iteration or step number of the proposed iterative method and $\gamma ^{(t)}=(\gamma _1^{(t)},\gamma _2^{(t)},\ldots ,\gamma _k^{(t)})$ denotes the vector of parameters assigned to the vector of objective functions $f(x)=(f_1(x),f_2(x),\ldots ,f_k(x))$.

Let, $F_i(\gamma ^{(t)})=(\sum \nolimits _{j=1}^n c_{ij}x_j+\alpha _i)-\gamma _i^{(t)}(\sum \nolimits _{j=1}^n d_{ij}x_j+\beta _i)$. Consider the following multi-objective parametric non-fractional programming problem as:

$$\begin{aligned}&\mathbf{Problem- }{\mathbf {P_1}}:~\min F_i(\gamma ^{(t)})=\sum \limits _{j=1}^n (c_{ij}-\gamma _i^{(t)}d_{ij})x_j+(\alpha _i-\gamma _i^{(t)}\beta _i)\nonumber \\&\quad\quad\quad\quad {\hbox {subject to}}\nonumber \\&\quad\quad\quad\quad x \in \varOmega \end{aligned}$$

(13)

Using $\epsilon$-constraint method, Problem-$P_1$ is transformed into the following single objective optimization problem as:

$$\begin{aligned}&\min \,F_s(\gamma ^{(t)})\nonumber \\&\quad {\hbox {subject to}}\nonumber \\&\quad F_i(\gamma ^{(t)}) \le \epsilon _i,~ i=1,2,\ldots ,s-1,s+1,\ldots ,k, ~x \in \varOmega \end{aligned}$$

(14)

This Problem-P$_1$ can be formulated in more generalized form as:

$$\begin{aligned}&\mathbf{Problem- }{\mathbf {P_2}}:~\min \sum \limits _{j=1}^n (c_{sj}-\gamma _s^{(t)}d_{sj})x_j+(\alpha _s-\gamma _s^{(t)}\beta _s) \nonumber \\&\quad {\hbox {subject to}} \nonumber \\&\quad \sum \limits _{j=1}^n (c_{ij}-\gamma _i^{(t)}d_{ij})x_j+(\alpha _i-\gamma _i^{(t)}\beta _i) \le \epsilon _i \in [\epsilon _i^L, \epsilon _i^U], i=1,2,\ldots ,s-1,s+1,\ldots ,k \nonumber \\&\quad Ax(\le ,=,\ge )b, ~x\ge 0 \end{aligned}$$

(15)

Construct the following pay-off Table 1 to obtain the best values $\epsilon _i^L$ and relative worst values $\epsilon _i^U$ of the objectives $F_i(\gamma ^{(t)})$.

Table 1 Pay-off table for objective functions of Problem-$P_1$

From the Table 1, evaluate $\epsilon _i^L$ and $\epsilon _i^U$ as : $\epsilon _i^L=\min \{F_i(X_l^*)|l=1,2,\ldots ,k\}=F_i(X_i^*)$ and $\epsilon _i^U=$ max$\{F_i(X_l^*)|l=1,2,\ldots ,k\},~ i=1,2,\ldots ,k$, where $X_l^*$$(l=1,2,\ldots ,k)$ are the individual optimal solution of the objectives $F_l(\gamma ^{(t)})$ obtained by minimizing them individually over the set of constraints $\varOmega$. $(\epsilon _1^L, \epsilon _2^L,\ldots ,\epsilon _k^L)$ and $(\epsilon _1^U, \epsilon _2^U,\ldots ,\epsilon _k^U)$ are the ideal and nadir objective vectors of Problem-$P_1$ respectively. Following assumptions are undertaken to obtain the pareto optimal solutions of Problem-P.

Assumptions

• Initialize the vector of parameters as $\gamma ^{(1)}=(\gamma _1^{(1)},\gamma _2^{(1)},\ldots ,\gamma _k^{(1)})$ which is equated to the vector of objective functions f(x) of Problem-P. where $\gamma _i^{(1)}=\frac{\sum \nolimits _{j=1}^n c_{ij}x_j^{(0)}+\alpha _i}{\sum \nolimits _{j=1}^n d_{ij}x_j^{(0)}+\beta _i}$,  $X^{(0)}=\sum \nolimits _{i=1}^{k}w_iX_i=(x_j^{(0)}|j=1,2,\ldots ,n)$,  $\sum \nolimits _{i=1}^{k}w_i=1$, $w_i>0$ and $X_i$ are the individual minimal solutions of the objectives $f_i(x)$ of Problem-P which can be obtained by using Charns and Cooper variable transformation technique [7]. Almost equal weights ‘$w_i$’ are used to obtain $X^{(0)}$ as the initial feasible solution.

• Define termination conditions of the proposed iterative procedure which are imposed on each objective functions of Problem-$P_1$ at the iterative steps where $\gamma ^{(t)}$ changes from one to another step. Termination conditions : $|F_i(\gamma ^{(t)})|\le T_i, i=1,2\ldots k$ where, $T_i > 0$ are the termination constants and considered as tolerance values acceptable by the objectives ‘$f_i(x)$’ to obtain the best compromise/preferred solution. The values of ‘$T_i$’ are predefined by the decision maker (DM) for each objective functions and usually their values are taken closer to zero.

The following steps are executed from the initial step (t $=$ 1) till reaching the desired optimal solution at which termination conditions are satisfied.

Step-t Let $\gamma ^{(t)}$ be the vector of parameters at t-th step.

• Substitute the values of the parameters $\gamma _i^{(t)}$ in Problem-$P_1$.

• The objective function $F_i(\gamma ^{(t)})$ of Problem-$P_1$ which has least value of termination constant ‘$T_i$’ i.e., tolerance, is considered as the objective function $F_s(\gamma ^{(t)})$.

• Formulate Problem-$P_2$ and substitute different values of $\epsilon _i \in [\epsilon _i^L, \epsilon _i^U]$ such that either one of the following two cases occurs.

  • 1. $\epsilon _i \in [-T_i, T_i]$ for satisfying the termination conditions $|F_i(\gamma ^{(t)})|$$\le T_i$  as $F_i(\gamma ^{(t)}) \approx \epsilon _i$ occurs oftenly for $i=1,2,\ldots ,s-1,s+1,\ldots ,k$.

  • 2. If $[-T_i, T_i]$ and $[\epsilon _i^L, \epsilon _i^U]$ are disjoint, choose $\epsilon _i \in [\epsilon _i^L, \epsilon _i^U]$ only.

• Solve Problem-$P_2$ for different $\epsilon _i$ to generate a set of pareto optimal solutions.

• Test the aforesaid termination conditions $|F_i(\gamma ^{(t)})|\le T_i, i=1,2\ldots k$ at each pareto optimal solution for each objective function $F_i(\gamma ^{(t)})$ of Problem-$P_1$.

• If the pareto optimal solution $X^{(t^*)}=(x_1^{(t^*)},x_2^{(t^*)}\ldots .x_n^{(t^*)})$ obtained above satisfies all the termination conditions then stop the procedure and this solution is considered as the required best preferred optimal solution.

• Otherwise at each pareto optimal solution, find $\sum \nolimits _i \{|F_i(\gamma ^{(t)})|-T_i\}$ for those values of $i\in \{1,2,\ldots k\}$ at which termination condition is violated i.e., $|F_i(\gamma ^{(t)})|-T_i >0$. Determine the pareto optimal solution $X^{(t)}=(x_1^{(t)},x_2^{(t)}\ldots x_n^{(t)})$ as the compromise solution of t-th step at which the total violation in satisfying the termination conditions i.e., $\sum \nolimits _i \{|F_i(\gamma ^{(t)})|-T_i\}$ has minimum value then go to the next step-(t+1).

Step-(t+1)

• Compute $\gamma _i^{(t+1)}=\frac{\sum \nolimits _{j=1}^n c_{ij}x_j^{(t)}+\alpha _i}{\sum \nolimits _{j=1}^n d_{ij}x_j^{(t)}+\beta _i}$  for i=1,2...k, where $X^{(t)}=(x_j^{(t)})=(x_1^{(t)},x_2^{(t)}\ldots x_n^{(t)})$ is obtained in the previous step-t as the compromise solution.

• Solve Problem-$P_2$ as in Step-t by substituting $\gamma ^{(t+1)}=(\gamma _i^{(t+1)}:i=1,2\ldots k)$ in place of $\gamma ^{(t)}=(\gamma _i^{(t)}:i=1,2\ldots k)$ and different values of ‘$\epsilon _i$’ to generate another set of pareto optimal solutions of Problem-$P_2$ and check the termination conditions again.

Repeat the procedure until unless a pareto optimal solution is obtained satisfying all the termination conditions imposed on the objectives by the DM. Otherwise redefine the values of termination constants ‘$T_i$’. By Theorem 3, the pareto optimal solutions of Problem-$P_2$ are also pareto optimal of Problem-P as $X^{(t)}$ (using which $\gamma ^{(t)}$ is computed) is pareto optimal for Problem-$P_2$. The solution so obtained is considered as the best preferred optimal solution of Problem-P.

6.1 Convergence analysis

The following dicussions are incorporated regarding the convergency of the above interpreted method which seeks a best compromise solution starting from an initial solution and moving to another compromise solution in the feasible region of Problem-$P_2$. The feasible region in each step changes with the change of ‘$\epsilon _i$’ in the constraints. It is clear that the possibility of satisfying the termination conditions in step-$(t+1)$ is more than that of due to the preceeding step-t beacuse of the selection procedure followed to determine the compromise solution in each step. Since a minimization problem is considered here, the objective values evaluated at the compromise solution of step-t are usually greater than that of due to step-$(t+1)$ i.e., $f_i(X^{(t)}) \ge f_i(X^{(t+1)})$ which ensures convergency of the method as $\gamma _i^{(t)}=f_i(X^{(t-1)})$ are decreasing functions and also bounded due to $\epsilon _i^L \le f_i(x) \le \epsilon _i^U$.

Fuzzy programming as discussed in Sect. 4 is also applied to solve the MOLFPP for ensuring the feasibility of the proposed method by comparing the obtained results.

7 Numerical example

Consider the following multi-objective linear fractional programming problem.

$$\begin{aligned}&\min \displaystyle \left\{ f_1(x)=\frac{-x_1+3x_2+2}{x_1+2x_2+1},~~ f_2(x)=\frac{5x_1+2x_2+2}{2x_1+3x_2+1} \right\} \\&\quad {\hbox {subject to}}\\&\quad {\mathbf{\varOmega }}= {\left\{ \begin{array}{ll} 2x_1+x_2\le 4\\ 3x_1-2x_2\le 5\\ x_1+2x_2\le 3 \\ x_1+3x_2\ge 2\\ x_1, x_2 \ge 0\\ \end{array}\right. } \end{aligned}$$

Solution due to proposed method Using Charnes and Cooper variable transformation technique, it is obtained that $X_1$$=(1.7272, 0.0910)$ and $X_2=(0, 1.5)$ are the individual optimal solutions of the objectives $f_1(x)$ and $f_2(x)$ respectively. The range of best and worst values of the objectives are determined using pay-off Table 1 as:

$$\begin{aligned}&0.1875 \le f_1(x) \le 1.6250\\&0.9091 \le f_2(x) \le 2.2884 \end{aligned}$$

Assigning equal weights i.e, $w_1=w_2=0.5$, the initial solution of the proposed iterative method is obtained as $X^{(0)}=w_1X_1+w_2X_2=(0.8636, 0.7955)$. So the initial vector of parameters is obtained as:

$$\begin{aligned} \gamma ^{(1)}=(\gamma _1^{(1)}, \gamma _2^{(1)})=\left( f_1(X^{(0)}), f_2(X^{(0)})\right) =(1.0198, 1.5466). \end{aligned}$$

The fractional objectives can be parametrically linearized as:

$$\begin{aligned} F_1(\gamma ^{(t)})= & {} (-x_1+3x_2+2)-\gamma _1^{(t)}(x_1+2x_2+1)\\ F_2(\gamma ^{(t)})= & {} (5x_1+2x_2+2)-\gamma _2^{(t)}(2x_1+3x_2+1) \end{aligned}$$

Termination constants for the two objectives are defined as $(T_1, T_2)=(0.02, 0.03).$

Step 1 Using the proposed method, find $x=(x_1, x_2)$ to minimize,

$$\begin{aligned}&F_1(\gamma ^{(1)})=-\,2.0198x_1+0.9604x_2+0.9802\\&F_2(\gamma ^{(1)})=1.9068x_1-2.6398x_2+0.4534\\&\quad {\hbox {subject to }}x \in {\mathbf {\varOmega }} \end{aligned}$$

It is observed that $\min \nolimits _{x \in {\mathbf {\varOmega }}} F_1(\gamma ^{(1)})$ and $\min \nolimits _{x \in {\mathbf {\varOmega }}} F_2(\gamma ^{(1)})$ occur at (1.8571, 0.2857) and (0, 1.5) respectively.

Using pay-off Table 1, $[\epsilon _2^L, \epsilon _2^U]$ is computed as [-3.5063, 3.2403]. As $T_1 < T_2$, using $\epsilon$-constraint method the above problem is formulated as:

$$\begin{aligned}&\min \,F_1(\gamma ^{(1)})\\&\quad {\hbox {subject to}}\\&\quad F_2(\gamma ^{(1)}) \le \epsilon _2\\&\quad x \in {\mathbf {\varOmega }} \end{aligned}$$

Since $[-T_2, T_2] \subseteq [\epsilon _2^L, \epsilon _2^U]$, the problem is stated as:

$$\begin{aligned}&\min F_1(\gamma ^{(1)})=-2.0198x_1+0.9604x_2+0.9802\\&\quad {\hbox {subject to}}\\&\quad F_2(\gamma ^{(1)})=1.9068x_1-2.6398x_2+0.4534 \le \epsilon _2\\&\quad x \in {\mathbf {\varOmega }},\\&\quad {\hbox {where}}\, \epsilon _2 \in [-T_2, T_2]=[-0.03, 0.03] \end{aligned}$$

Substituting different values of $\epsilon _2$, the following set of pareto optimal solutions are generated in Table 2.

Table 2 Pareto optimal solutions of step-1

It is observed that at each pareto optimal solution obtained in the above table, $F_2(\gamma ^{(1)}) \approx \epsilon _2$  and  $|F_2(\gamma ^{(1)})| \le T_2$ but $|F_1(\gamma ^{(1)})| >T_1$ . As termination condition is only violated by $F_1(\gamma ^{(1)})$, according to the proposed method, min $\sum \nolimits _{i \in \{1, 2\}} \{|F_i(\gamma ^{(1)})|-T_i\}$=min {$|F_1(\gamma ^{(1)})|-T_1$} and it occurs at the pareto optimal solution $X^{(1)}=(1.0774, 0.9613)$. Thus, $X^{(1)}$ is considered as the compromise solution of step-1.

Step 2 The new vector of parameters is computed as $\gamma ^{(2)}=(\gamma _1^{(2)}, \gamma _2^{(2)})=(0.9516, 1.5417)$. The problem to be solved is formulated as:

Find $x=(x_1, x_2)$ so as to minimize,

$$\begin{aligned}&F_1(\gamma ^{(2)})=(-x_1+3x_2+2)-\gamma _1^{(2)}(x_1+2x_2+1)= -\,1.9516x_1+1.0968x_2+1.0484\\&\quad F_2(\gamma ^{(2)})=(5x_1+2x_2+2)-\gamma _2^{(2)}(2x_1+3x_2+1)=1.9166x_1-2.6251x_2+0.4583\\&\quad {\hbox {subject to }}x \in {\mathbf {\varOmega }} \end{aligned}$$

It is observed that $\min \nolimits _{x \in {\mathbf {\varOmega }}} F_1(\gamma ^{(2)})$ and $\min \nolimits _{x \in {\mathbf {\varOmega }}} F_2(\gamma ^{(2)})$ occur at (1.8571, 0.2857) and (0, 1.5) respectively. Using pay-off Table 1, $[\epsilon _2^L, \epsilon _2^U]$ is computed as [-3.4794, 3.2676]. Since $[-T_2, T_2] \subseteq [\epsilon _2^L, \epsilon _2^U]$, using $\epsilon$-constraint method the above problem is formulated as:

$$\begin{aligned}&min F_1(\gamma ^{(2)})=-\,1.9516x_1+1.0968x_2+1.0484\\&\quad {\hbox {subject to}}\\&\quad F_2(\gamma ^{(2)})=1.9166x_1-2.6251x_2+0.4583 \le \epsilon _2 and x \in {\mathbf {\varOmega }}\\&\quad {\hbox {where, }}\epsilon _2 \in [-T_2, T_2]=[-0.03, 0.03] \end{aligned}$$

Substituting different values of $\epsilon _2$, the following set of pareto optimal solutions are generated in Table 3.

Table 3 Pareto optimal solutions of step-2

It is observed that at each solution obtained in Table 3, $F_2(\gamma ^{(2)}) \approx \epsilon _2$ and $F_i(\gamma ^{(2)}) > 0$ for at least one $i\in \{1,2\}$, so all these are pareto optimal for Problem-P by Theorem 3 . However, the termination conditions $|F_i(\gamma ^{(2)})| \le T_i$, $i=(1,2)$  are not satisfied at (1.0682, 0.9659) and (1.0868, 0.9566). As the rest pareto optimal solutions satisfy all the termination conditions, the decision maker (DM) chooses one of them as the best preferred optimal solution. The set of objective values evaluated at the solutions of Table 3 satisfying termination conditions, are:

$$\begin{aligned} \{ \left( f_1(x), f_2(x)\right) \}= \{(0.9561, 1.5378),(0.9558, 1.5387), (0.9535, 1.5401), (0.9522, 1.5412), (0.9509, 1.5423), (0.9496, 1.5434), (0.9483, 1.5445), (0.9471, 1.5455)\}. \end{aligned}$$

Solution due to fuzzy programming The aspired and acceptable values i.e., the obtained best and worst values of the objectives are:

$$\begin{aligned} f_1^{min}= & {} 0.1875 \le f_1(x) \le 1.6250=f_1^{max}\\ f_2^{min}= & {} 0.9091 \le f_2(x) \le 2.2884=f_2^{max} \end{aligned}$$

Thus constructing the membership functions as discussed in Sect. 4, the crisp model is formulated as follows:

$$\begin{aligned}&\max~~\beta \\&\quad {\hbox {subject to}}\\&\quad 2.625x_1+0.25x_2-1.4375\beta (x_1+2x_2+1)\ge 0.375\\&\quad 0.4232x_1-4.8652x_2+1.3793\beta (2x_1+3x_2+1)\le 0.2884\\&\quad 2x_1+x_2\le 4,~ 3x_1-2x_2\le 5\\&\quad x_1+2x_2\le 3,~ x_1+3x_2\ge 2x_1, x_2 \ge 0 \end{aligned}$$

The best preferred optimal solution is obtained as $x=(1.1664, 0.9168)$ by solving the above problem due to fuzzy programming and the corresponding optimal objective values are $(f_1(x), f_2(x))=(0.8960, 1.5889)$.

Remark 2

The optimal objective values of $\left( f_1(x), f_2(x)\right)$ obtained due to the proposed method are:

$$\begin{aligned} \{ \left( f_1(x), f_2(x)\right) \}=\{(0.9561, 1.5378),(0.9558, 1.5387), (0.9535, 1.5401), (0.9522, 1.5412), (0.9509, 1.5423), (0.9496, 1.5434), (0.9483, 1.5445), (0.9471, 1.5455)\} \end{aligned}$$

whereas $(f_1(x), f_2(x))=(0.8960, 1.5889)$ is obtained using fuzzy method.

The following Fig. 2 is drawn as a comparative study using some objective values obtained due to proposed method(P.M.) and the fuzzy method(F.M.), where P.M.$i~(i=1,2,3,4,5)$ represents the objective values, (0.9471, 1.5455), (0.9483, 1.5445), (0.9496, 1.5434), (0.9509, 1.5423), (0.9522, 1.5412) respectively and F.M. represents the objective value (0.8960, 1.5889).

Fig. 2

Comparative study on the objective values

It is observed that the optimal objective values $\left( f_1(x), f_2(x)\right)$ obtained due to the proposed method are considerably closer and comparable to that of due to fuzzy method and lie within the predetermined range of best and worst values i.e., $[f_i^{min}, f_i^{max}]$ which justifies the feasibility of the proposed method.

8 Conclusion

In this paper, parametric approach transforms fractional objectives into non-fractional form using a vector of parameters. The values of the parameters are changed from one to another step in order to generate a new set of pareto optimal solutions using $\epsilon$-constraint method which converts multi-objective into single objective optimization problem. Until, unless the termination conditions defined by the DM are satisfied at a pareto optimal solution, the iterative procedure continues. The solution obtained due to the proposed method is compared with the existing fuzzy programming method which verifies the effectiveness of its performance. The computational works in the numerical example are carried out using the softwares LINGO and MATLAB.