Keywords

1 Introduction

Fractional programming belongs to the class of mathematical programming and deals with the optimization of a function existing in the form of ratio of two linear or nonlinear functions. Some common and practical instances of objectives belonging to the category of fractional programming are profit/cost, cost/time, output/employee, inventory/sale, risk assets/capital, debt/equity, and so forth. A linear fractional programming problem (LFPP) developed by Martos [1] optimizes an objective function (existing in form of ratio of two affine functions, i.e., linear plus constant) subject to a set of linear constraints as

$$ \begin{aligned} & \hbox{max} \frac{{\sum\nolimits_{j = 1}^{n} c_{j} x_{j} + \alpha }}{{\sum\nolimits_{j = 1}^{n} d_{j} x_{j} + \beta }} \\ & {\text{subject to}} \\ \end{aligned} $$

\( x \in \Omega \), i.e., a set of linear constraints.

In numerous real-world decision-making situations, several fractional objectives are encountered which need to be optimized simultaneously restricted within a common set of constraints. Such mathematically modeled optimization problems are well known as multi-objective fractional programming or ratio optimization problem. Research activities in this field has been considerably accelerated since a few years because of its wide range of application in numerous important fields like engineering, economics, information theory, finance, management science, marine transportation, water resources, corporate planning, and so forth.

Charnes and Cooper [2] proposed a variable transformation technique to solve an LFPP with an additional constraint and a variable. Stancu-Minasian [3] discussed various methods and theoretical concepts on fractional programming. Costa [4] proposed an algorithm to solve MOLFPP which goes on dividing the no-dominated region to find the maximum value of the weighted sum of the objectives. Mishra [5] used weighting method to solve a bi-level LFPP. Toksar [6] proposed an approach to solve a fuzzy MOLFPP where membership functions are linearized using Taylor series expansion. Ojha and Ota [7] used a hybrid method to solve a multi-objective geometric programming problem. Valipour et al. [8] proposed parametric approach with weighting sum method to solve a MOLFPP. Ojha and Biswal [9] used \( \epsilon \)-Constraint method to produce a set of Pareto optimal solutions. [10–12] discussed basic concepts and many methods of solution to a multi-objective optimization problem.

This paper is organized as follows: Sect. 2 interprets basics of multi-objective optimization and some techniques for its solution. The concept of fuzzy programming with details of fuzzy max–min operator method is discussed in Sect 3. Section 4 describes the proposed method to solve a MOLFPP. A numerical example with its solution and some remarks are incorporated in Sects. 5 and 6 contains the concluding part.

2 Multi-objective Optimization Problem

A multi-objective optimization problem (MOOP) can be mathematically stated as follows:

$$ \begin{aligned} \hbox{max} \,f & (x) = \left( {f_{1} (x),f_{2} (x), \ldots ,f_{k} (x)} \right) \\ & \quad {\text{subject}}\,{\text{to}}\quad x \in \Omega \\ \end{aligned} $$
(1)

where \( \Omega \) is the nonempty compact feasible region. Usually, a single optimal solution does not exist to satisfy all the objectives simultaneously with their best individual optimality level which generates the concept of Pareto optimal solutions.

Definition

(See [ 11 ]) \( x^{*} \in \Omega \) is a Pareto optimal solution of MOOP (1) if there does not exist another feasible solution \( \bar{x} \in \Omega \) such that \( f_{i} (\bar{x}) \le f_{i} \left( {x^{*} } \right) \forall i \) and \( f_{j} (\bar{x}) < f_{j} \left( {x^{*} } \right) \) for at least one j.

A set of Pareto optimal solutions comprising the most preferred optimal (best compromise) solution that satisfies all the objective functions with best possibility, can be generated using an appropriate method.

2.1 Weighting Sum Method

In this method [10, 11] nonnegative and normalized weights are assigned to all the objectives with smaller or bigger values regarding their importance at the DM as bigger and smaller weights represent greater and lesser importance of the objective, respectively. Finally, their weighted sum is optimized on the constraint feasible region to generate a set of Pareto optimal solutions by varying the weights. In other words, it scalarizes a vector optimization that converts a multi-objective to single-objective optimization problem. Mathematically, it can be stated for the MOOP (1) as

$$ \begin{aligned} & \hbox{max} \sum\limits_{i = 1}^{k} w_{i} f_{i} (x) \\ {\text{subject to}}\quad & x \in \Omega ,\quad w_{i} \ge 0, \quad \sum\limits_{i = 1}^{k} w_{i} = 1 \\ \end{aligned} $$
(2)

Convexity of the feasible region guarantees Pareto optimality of the solution generated due to this method whereas concavity does not.

2.2 ϵ-Constraint Method

This method [10, 11, 13] is based on preference which considers an objective as the best prioritized one and converts the rest objectives with their goals as constraints, i.e., it maximizes an objective and simultaneously maintains minimum acceptability level for other objective functions. Mathematically, it can be stated as

$$ \begin{aligned} \hbox{max} \,f_{s} & (x),\quad s \in \{ 1,2, \ldots ,k\} \\ & {\text{subject}}\,{\text{to}} \\ f_{i} (x) \ge \varepsilon_{i} ,\quad & i = 1,2, \ldots ,s - 1,\quad s + 1, \ldots ,k \\ x \in \Omega ,\quad & \varepsilon_{i}^{L} \le \varepsilon_{i} \le \varepsilon_{i}^{U} \\ \end{aligned} $$
(3)

where \( f_{s} (x) \) is the best prioritized function and \( \epsilon_{i}^{L} \), \( \epsilon_{i}^{U} \) are, respectively, the relative minimum, maximum values of the objective \( f_{i} (x) \) with respect to other objectives. Substituting different values of \( \epsilon_{i} \in \left[\epsilon_{i}^{L} , \epsilon_{i}^{U} \right] \), a set of Pareto optimal solutions of (1) can be generated by solving (3).

2.3 Hybrid Method

This method [10] considers both priority of objective functions by assigning weights ‘\( w_{i} \)’ and achievement of minimum aspired objective values by the DM simultaneously. Mathematically, it can be stated as

$$ \begin{aligned} \hbox{max} & \sum\limits_{i = 1}^{k} w_{i} f_{i} (x) \\ & {\text{subject to}} \\ f_{i} (x) \ge \bar{f}_{i} ,\quad & x \in \Omega \,i = 1,2, \ldots ,k \\ \end{aligned} $$
(4)

where \( \bar{f}_{i} \) is the aspired value for the objective \( f_{i} (x) \).

3 Fuzzy Programming

Zadeh developed fuzzy set theory in 1965 that transforms imprecise information into precise mathematical form. Zimmermann [14] proposed fuzzy max–min operator method to solve various multi-objective optimization problems which is based on the concept of Bellman and Zadeh [15]. Each fuzzy set is associated with a membership function whose domain and range are the set of decision variables and [0, 1], respectively. An appropriate membership function is selected to determine the optimal solution. According to Zimmermanns fuzzy technique, best preferred optimal solution of a MOOP can be obtained using the following steps:

  1. Step-1:

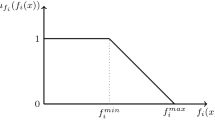
    Determine the best and worst values, i.e., the aspired \( \left( {f_{i}^{\hbox{max} } } \right) \) and acceptable \( \left( {f_{i}^{\hbox{min} } } \right) \) values, respectively, for each objective function \( f_{i} (x), i = 1, \ldots ,k \) satisfying \( f_{i}^{\hbox{min} } \le f_{i} (x) \le f_{i}^{\hbox{max} } \), for \( x \in \Omega \).

  2. Step-2:

    Define following linear fuzzy membership function \( \mu_{i} (x) \) for each objective function \( f_{i} (x) \) to derive the best preferred optimal solution of the MOOP as

    $$ \mu_{i} (x) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {f_{i} (x) \le f_{i}^{\hbox{min} } } \hfill \\ {\frac{{f_{i} (x) - f_{i}^{\hbox{min} } }}{{f_{i}^{\hbox{max} } - f_{i}^{\hbox{min} } }},} \hfill & {f_{i}^{\hbox{min} } \le f_{i} (x) \le f_{i}^{\hbox{max} } } \hfill \\ {1,} \hfill & {f_{i} (x) \ge f_{i}^{\hbox{max} } } \hfill \\ \end{array} } \right. $$
    (5)
  3. Step-3:

    Construct the following crisp model to obtain the optimal solution as follows:

    $$ \begin{aligned} {\text{Max}} & \left\{ {\mathop {\hbox{min} }\limits_{1 \le i \le k} \mu_{i} (x)} \right\} \\ & {\text{subject to}} \\ & x \in \Omega \\ \end{aligned} $$
    (6)
  4. Step-4:

    The above crisp model can be transformed into an equivalent mathematical programming problem as follows:

    $$ \begin{aligned} & {\text{Max}}\,\beta \\ & {\text{subjectto}} \\ \mu_{i} (x) = & \frac{{f_{i} (x) - f_{i}^{\hbox{min} } }}{{f_{i}^{\hbox{max} } - f_{i}^{\hbox{min} } }} \ge \beta , \quad i = 1,2, \ldots ,k \\ & x \in \Omega \\ \end{aligned} $$
    (7)

    where ‘\( \beta \)’ is an auxiliary variable assumed as the value of \( \mathop {\hbox{min} }\limits_{1 \le i \le k} \,\mu_{i} (x) \). The constraints \( \mu_{i} (x) \ge \beta \) can be replaced by \( f_{i} (x) - \beta \left( {f_{i}^{\hbox{max} } - f_{i}^{\hbox{min} } } \right) \ge f_{i}^{\hbox{min} } , i = 1,2, \ldots ,k \) for simplicity.

  5. Step-5:

    Solve the above maximization problem to obtain the best preferred optimal solution of the MOOP and evaluate the optimal objective values at this solution.

4 Proposed Method to Solve MOLFPP

A MOLFPP can be mathematically formulated as

$$ \begin{aligned} \hbox{max} \,f_{i} (x) & = \frac{{\sum\nolimits_{j = 1}^{n} {N_{ij} x_{j} + \alpha_{i} } }}{{\sum\nolimits_{j = 1}^{n} {D_{ij} x_{j} + \beta_{i} } }} \\ & {\text{subject}}\,{\text{to}} \\ x \in \Omega = & \left\{ {x \in R^{n} |Ax( \le , = , \ge )b,x \ge 0} \right\} \\ {\text{where}}\quad x = \left( {x_{j} } \right) \in R^{n} , & \,N_{ij} , \,D_{ij} , \alpha_{i} , \beta_{i} \in R, b = \left( {b_{t} } \right) \in R^{m} \\ A = \left( {a_{tj} } \right) & \in R^{m \times n} ,\quad t = 1,2, \ldots ,m \\ {\text{Assume that}},\sum\limits_{j = 1}^{n} {D_{ij} x_{j} } & \, + \,\beta_{i} > 0\quad {\text{for}}\,{\text{each}}\quad x \in \Omega \quad {\text{and}}\quad i = 1,2, \ldots ,k \\ \end{aligned} $$
(8)

Solution approach

Maximize the fractional objective function \( f_{i} (x) \) for each ‘\( i \)’ separately on the feasible region of constraints \( \Omega \) to obtain their individual optimal solutions.

$$ \begin{aligned} \hbox{max} \, & \frac{{\sum\nolimits_{j = 1}^{n} N_{ij} x_{j} + \alpha_{i} }}{{\sum\nolimits_{j = 1}^{n} D_{ij} x_{j} + \beta_{i} }} \\ {\text{subject}}\,{\text{to}}\,\sum\limits_{j = 1}^{n} a_{t} jx_{j} & ( \le , = , \ge )b_{t} ,\quad t = 1,2, \ldots ,m \,\, {\text{and}} \,\, x_{j} \ge 0 \\ \end{aligned} $$

Variable transformation technique [2] can be applied to obtain individual optimal solutions for each fractional objectives. For the \( k \)th objective function \( f_{k} (x) \), this technique is mathematically interpreted as

$$ \begin{aligned} \hbox{max} & \sum\limits_{j = 1}^{n} N_{kj} y_{j} + \alpha_{k} z \\ & {\text{subject to}} \\ \sum\limits_{j = 1}^{n} & D_{kj} y_{j} + \beta_{k} z = 1 \\ \sum\limits_{j = 1}^{n} & a_{tj} y_{j} ( \le , = , \ge )b_{t} \\ y_{j} & \ge 0, z > 0 \\ \end{aligned} $$
(9)

If \( \left( {y_{j} ,z} \right) \) is the optimal solution of (5) then \( \left( {x_{j} } \right) = \left( {\frac{{y_{j} }}{z}} \right) \) is considered as the individual optimal solution of the \( k \)th objective function \( f_{k} (x) \).

Let \( X_{1}^{*} ,X_{2}^{*} , \ldots ,X_{k}^{*} \) be the individual optimal solutions of the objective functions \( f_{1} (x),f_{2} (x), \ldots ,f_{k} (x) \), respectively, where \( X_{i}^{*} = \left( {x_{i}^{(j)*}, j = 1,2, \ldots ,n} \right), i = 1,2, \ldots ,k. \)

Evaluate relative minimum and maximum objective values, i.e., \( \epsilon_{i}^{L} \) and \( \epsilon_{i}^{U} \), respectively, for the \( i \)th objective function as

$$ \begin{aligned} \varepsilon_{i}^{L} & = \mathop {\hbox{min} }\limits_{1 \le j \le k} f_{i} \left( {X_{j}^{*} } \right) \\ \varepsilon_{i}^{U} & = \mathop {\hbox{max} }\limits_{1 \le j \le k} f_{i} \left( {X_{j}^{*} } \right) = f_{i} \left( {X_{i}^{*} } \right) \\ \end{aligned} $$

Approximate each fractional objective function \( f_{i} (x) \) by its first-order Taylor’s series expansion evaluated at its individual optimal solution \( X_{i}^{*} \) as

$$ f_{i} (x) \approx f_{i} (X_{i}^{*} ) + \sum\limits_{j = 1}^{n} \left( {x_{j} - x_{i}^{(j)*} } \right)\frac{{\partial f_{i} \left( {X_{i}^{*} } \right)}}{{\partial x_{j} }},\quad {\text{for}}\quad i = 1,2, \ldots ,k $$

As each fractional objective functions get transformed into nonfractional linear functions, the MOLFPP is converted into a single-objective linear programming problem (SOLPP) using the Hybrid method, i.e., the combination of both weighting sum and \( \epsilon \)-constraint methods can be mathematically formulated as

$$ \begin{aligned} \hbox{max} \sum\limits_{i = 1}^{k} w_{i} & \left[ {f_{i} \pi \left( {X_{i}^{*} } \right) + \sum\limits_{j = 1}^{n} \left( {x_{j} - x_{i}^{(j)*} } \right)\frac{{\partial f_{i} \left( {X_{i}^{*} } \right)}}{{\partial x_{j} }}} \right] \\ & {\text{subject}}\,{\text{to}} \\ f_{i} \left( {X_{i}^{*} } \right) + \sum\limits_{j = 1}^{n} & \left( {x_{j} - x_{i}^{(j)*} } \right)\frac{{\partial f_{i} \left( {X_{i}^{*} } \right)}}{{\partial x_{j} }} \ge \varepsilon_{i} , \quad i = 1,2, \ldots ,k \\ \sum\limits_{j = 1}^{n} a_{t} jx_{j} & ( \le , = , \ge )b_{t} ,\quad t = 1,2, \ldots ,m \\ x_{j} \ge 0,\quad w_{i} > = & 0,\quad \sum\limits_{i = 1}^{k} {w_{i} = 1,} \quad \varepsilon_{i} \in \left[ {\varepsilon_{i}^{L} ,\varepsilon_{i}^{U} } \right] \\ \end{aligned} $$
(10)

Substituting different values of \( \epsilon_{i} \), i.e., minimum aspired objective values to be achieved by the objectives \( f_{i} (x) \) for different weights \( w_{i} \), a set of Pareto optimal solutions can be generated by solving the above problem (7) from which the DM can choose the most preferred optimal solution by comparing the objective values.

5 Numerical Example

Consider the following multi-objective linear fractional programming problem:

$$ \begin{aligned} \hbox{max} \,f_{1} (x) & = \frac{{2x_{1} + 3x_{2} - 4x_{3} + 3}}{{x_{1} + x_{2} + 2x_{3} + 1}} \\ f_{2} (x) & = \frac{{5x_{1} - 2x_{2} + x_{3} + 1}}{{2x_{1} + 3x_{2} + x_{3} + 2}} \\ & {\text{subject}}\,{\text{to}} \\ \Omega & = \left\{ {\begin{array}{*{20}l} {x_{1} + x_{2} + x_{3} \ge 1} \hfill \\ {3x_{1} - x_{2} - 2x_{3} \le 2} \hfill \\ {2x_{1} + x_{2} + 3x_{3} \le 5} \hfill \\ {x_{1} ,x_{2} ,x_{3} \ge 0} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

Individual optimal solutions of the objectives are obtained as

$$ \begin{aligned} \mathop {\hbox{max} }\limits_{x \in \Omega } f_{1} (x) & = 3\quad {\text{at}}\quad X_{1}^{*} = (0,1,0) \\ \mathop {\hbox{max} }\limits_{x \in \Omega } f_{2} (x) & = 1.5072\quad {\text{at}}\quad X_{2}^{*} = (1.2308,0,0.8462) \\ \end{aligned} $$

Using the criteria of the proposed method, relative minimum and maximum values of the objectives are obtained as

$$ \epsilon_{1} \in [\epsilon_{1}^{L} ,\epsilon_{1}^{U} ] = [ - 1.8464,3]\quad{\text{and}}\quad\epsilon_{2} \in [\epsilon_{2}^{L} ,\epsilon_{2}^{U} ] = [ - 0.1010,1.5072] $$

Fractional objectives are approximated by linear functions as

$$ \begin{aligned} & f_{1} (x) \approx - 0.5x_{1} - 5x_{3} + 3 \\ & f_{2} (x) \approx 0.3741x_{1} - 1.2287x_{2} - 0.0956x_{3} + 1.1277 \\ \end{aligned} $$

The multi-objective LFPP is transformed into the following single-objective LPP using the proposed method as

$$ \max \left( { - 0.5w_{1} + 0.3741w_{2} } \right)x_{1} - 1.2287w_{2} x_{2} + \left( { - 5w_{1} - 0.0956w_{2} } \right)x_{3} + \left( {3w_{1} + 1.1277w_{2} } \right) $$

subject to

$$ \begin{array}{c} - 0.5x_{1} - 5x_{3} + 3 \ge \varepsilon_{1} \\ 0.3741x_{1} - 1.2287x_{2} - 0.0956x_{3} + 1.1277 \ge \varepsilon_{2} \\ x_{1} + x_{2} + x_{3} \ge 1, \quad 3x_{1} - x_{2} - 2x_{3} \le 2,\quad 2x_{1} + x_{2} + 3x_{3} \le 5 \\ x_{1} , x_{2} ,x_{3} \ge 0 \\ w_1+w_2=1, \,w_1, w_2\ge 0,\,\epsilon_1^L \le \epsilon_1 \le \epsilon_1^U, \,\epsilon_2^L \le \epsilon_2 \le \epsilon_2^U \end{array} $$

Substituting different weights ‘\( w_{i} \)’ on priority basis of objectives and aspired objective values \( \epsilon_{i} \), a set of Pareto optimal solutions \( \left( {x_{1}^{*} ,x_{2}^{*} ,x_{3}^{*} } \right) \) are generated in the following Table 1 by solving the above problem.

Table 1 Pareto optimal solutions of the MOLFPP
Full size table

5.1 Result Due to Fuzzy Method

The relative minimum and maximum values of the objectives are the worst (acceptable) and best (aspired) values, respectively, i.e.,

$$ \begin{aligned} - 1.8464 & = \epsilon_{1}^{L} = f_{1}^{ \hbox{min} } \le f_{1} (x) \le f_{1}^{ \hbox{max} } = \epsilon_{1}^{U} = 3 \\ - 0.1010 & = \epsilon_{2}^{L} = f_{2}^{ \hbox{min} } \le f_{2} (x) \le f_{2}^{ \hbox{max} } = \epsilon_{2}^{U} = 1.5072 \\ \end{aligned} $$

For approximated linear objectives Since fractional objectives are approximated by linear objectives, constructing the linear membership functions as defined in Sect. 3 (step-2) and solving the corresponding optimization problem due to fuzzy max–min operator method as defined in Sect. 3 (step-4), the best preferred optimal solution is obtained as \( x^{*} = \left( {x_{1}^{*} ,x_{2}^{*} ,x_{3}^{*} } \right) = (0.7718,0.1411,0.0871) \). The values of the given fractional objective functions at this solution are \( f_{1} \left( {x^{*} } \right) = 2.2130 \) and \( f_{2} \left( {x^{*} } \right) = 1.1504 \).

For given fractional objectives Constructing membership functions with the given fractional objectives and solving the corresponding crisp model as defined in Sect. 3, the best preferred optimal solution is obtained as \( x^{*} = \left( {x_{1}^{*} ,x_{2}^{*} ,x_{3}^{*} } \right) = (0.7790,0.1052,0.1159) \). The values of the given fractional objective functions at this solution are \( f_{1} \left( {x^{*} } \right) = 2.0842 \) and \( f_{2} \left( {x^{*} } \right) = 1.2033 \).

Remark 1

Ascertaining the weights ‘\( w_{i} \)’ and changing the aspired objective values ‘\( \epsilon_{i} \)’ in the range \( \left[\epsilon_{i}^{L} ,\epsilon_{i}^{U} \right] \), a set of Pareto optimal solutions \( (x_{1}^{*} ,x_{2}^{*} ,x_{3}^{*} ) \) are generated which are same for the weights \( (1,0),(0.8,0.2) \) and \( (0.2,0.8),(0,1) \). \( f_{1}^{*} \) and \( f_{2}^{*} \) are the values of the fractional objectives evaluated at \( \left( {x_{1}^{*} ,x_{2}^{*} ,x_{3}^{*} } \right) \). Since, fractional objectives are approximated by linear functions, \( f_{i}^{*} \,{\succcurlyeq}\,\epsilon_{i} (i = 1,2) \) are satisfied where ‘\( { \succcurlyeq } \)’ represents “greater than or approximately equal to.” As \( f_{i}^{*} \in \left[\epsilon_{i}^{L},\epsilon_{i}^{U}\right] \) for each \( \left( {x_{1}^{*} ,x_{2}^{*} ,x_{3}^{*} } \right) \), it shows the correctness of the proposed method. DM can choose one Pareto optimal solution from Table 1 as the most preferred optimal solution on priority basis as required in the practical decision-making situation. If DM is still unsatisfied, more Pareto optimal solutions \( \left( {x_{1}^{*} ,x_{2}^{*} ,x_{3}^{*} } \right) \) can be generated by substituting more aspired objective values ‘\( \epsilon_{i} \)’ within the specified range \( \left[\epsilon_{i}^{L},\epsilon_{i}^{U}\right] \).

Remark 2

The highlighted objective values in Table 1 obtained due to the proposed method are considerably closer to the objective values obtained due to fuzzy max–min operator method using both cases of fractional and approximated linear objective functions. Besides this, using the proposed method DM obtains a set of solutions to choose the best preferred optimal solution as per the requirement of the system but in case of fuzzy, there is no choice to choose. It justifies the use of the proposed method.

6 Conclusions

This paper comprises conversion of fractional objectives into linear functions using Taylor’s series approximation and a hybrid method that combines the ideas “priority of objectives” and “achievement of possible aspired objective values” of both weighting sum and \( \epsilon \)-constraint methods, is implemented to generate a set of Pareto optimal solutions of a MOLFPP. As the proposed method offers numerous options to DM, we can select one solution as the most preferred optimal solution. “LINGO” and “MATLAB” softwares are used for computational works in the numerical example. Comparison of the results so obtained with existing fuzzy max–min operator method ensures the effectiveness of the proposed method.