Intuitionistic single-valued neutrosophic hypergraphs

Abstract

The concept of neutrosophic sets can be utilized as a mathematical tool to deal with imprecise and unspecified information. It is more convenient to apply single-valued neutrosophic sets rather than neutrosophic sets. In this paper, we discuss the concepts of intuitionistic single-valued neutrosophic hypergraphs and dual intuitionistic single-valued neutrosophic hypergraphs. We discuss the notion of $(\eta , \phi , \psi )$-level hypergraphs, tempered intuitionistic single-valued neutrosophic hypergraphs and transversal of intuitionistic single-valued neutrosophic hypergraphs. We also describe an application of intuitionistic single-valued neutrosophic hypergraphs in clustering problem.

1 Background

As a generalization of the classical set theory, fuzzy set theory was introduced by Zadeh [36] in 1965 to solve problems with uncertainties. At present, in modeling and controlling unsure systems in industry, society and nature, fuzzy sets and fuzzy logic are playing a vital role. In decision making, they can be used as powerful mathematical tools which facilitate for approximate reasoning. They play a significant role in complex phenomena which is not easily described by classical mathematics. In 1986, Atanassov [7] illustrated the extension of fuzzy sets by adding a new component, called, intuitionistic fuzzy sets. The intuitionistic fuzzy sets have essentially higher describing possibilities than fuzzy sets. The idea of intuitionistic fuzzy set is more meaningful as well as inventive due to the presence of degree of truth, degree of false and the hesitation margin. The hesitation margin of intuitionistic fuzzy set is its indeterminacy value by default. In 1998, Smarandache [24] submitted the idea of neutrosophic set (NS) by combining the non-standard analysis, a tricomponent logic/set/probability theory and philosophy. “It is a branch of philosophy which studies the origin, nature and scope of neutralities as well as their interactions with different ideational spectra” [25]. A NS has three components: truth membership, indeterminacy membership and falsity membership, in which each membership value is a real standard or non-standard subset of the nonstandard unit interval $]0-, 1+[$ ([23, 24]). To apply NSs in real-life problems more conveniently, the single-valued neutrosophic set (SVNS) was introduced for the first time by Smarandache in 1998 in his book: F. Smarandache, Neutrosophy/Neutrosophic probability, set and logic. A SVNS is a generalization of intuitionistic fuzzy sets [7]. In SVNS three components are not dependent and their values are contained in the standard unit interval [0, 1]. SVNSs have been a new hot research topic and many researchers have addressed this issue. Majumdar and Samanta [18] studied similarity and entropy of SVNSs. Ye [29, 31] proposed correlation coefficients of SVNSs, and applied it to single-valued neutrosophic decision-making problems. To simplify neutrosophic sets, Ye [32] proposed a multicriteria decision-making method using aggregation operators. Being motivated from the idea of NSs, Bhowmik and Pal [10, 11] defined the notion of intuitionistic neutrosophic set in 2009.

Fuzzy graphs were narrated by Rosenfeld [22] in 1975. After that in 1987, some remarks on fuzzy graphs were represented by Bhattacharya [9]. He showed that all the concepts of crisp graph theory do not have similarities in fuzzy graph theory. Kaufmann [15] introduced the notion of fuzzy hypergraphs and Chen [13] defined the interval-valued fuzzy hypergraphs. Generalization and redefinition of fuzzy hypergraphs were discussed by Lee-Kwang and Keon-Myung [16]. They also described some applications to show that the decomposition of data in clustering problem can be done by using the strength of an edge. Parvathi et al. [21] established the notion of intuitionistic fuzzy hypergraph. Later, Akram and Dudek extended this idea and studied its various properties in [1]. They also represented various applications of intuitionistic fuzzy hypergraphs such as radio coverage network and clustering problem. Single-valued neutrosophic minimum spanning tree and its clustering method were studied by Ye [30]. The same author gave many clustering algorithms based on different methods, including similarity measures, netting method and distance based similarity measures [33,34,35]. Yang et al. [28] discussed single-valued neutrosophic relations. Dhavaseelan et al. [14] defined strong neutrosophic graphs. Broumi et al. [12] portrayed single-valued neutrosophic graphs. Akram and Shahzadi [2] introduced the notion of neutrosophic soft graphs with applications. Akram [4] introduced the notion of single-valued neutrosophic planar graphs. Akram et al. [3] also introduced the single-valued neutrosophic hypergraphs. Representation of graphs using intuitionistic neutrosophic soft sets was discussed in [6]. Akram and Shahzadi [5] studied properties of single-valued neutrosophic graphs by level graphs. They also highlighted some flaws in the definitions of Broumi et al. [12]. In this article, we propose the concept of intuitionistic single-valued neutrosophic hypergraphs (ISVNHGs) and dual intuitionistic single-valued neutrosophic hypergraphs. We discuss the concepts of $(\eta , \phi , \psi )$-level hypergraphs, tempered intuitionistic single-valued neutrosophic hypergraphs and transversal intuitionistic single-valued neutrosophic hypergraphs. We also describe an application of intuitionistic single-valued neutrosophic hypergraphs in clustering problem.

2 Intuitionistic single-valued neutrosophic hypergraphs

Definition 2.1

[24] A neutrosophic set N in universe U is defined by a truth membership function $T_{N}: U\rightarrow [0^-, 1^+]$, indeterminacy membership function $I_{N}: U\rightarrow [0^-, 1^+]$ and a falsity membership function $F_{N}: U\rightarrow [0^-, 1^+]$, with no condition on the sum of $T_{N}(u)$, $I_{N}(u)$ and $F_{N}(u)$ for all $u\in U$.

Definition 2.2

[26] Let U be a set of universe. A single-valued neutrosophic set is characterized by truth-value, indeterminacy-value and falsity-value, i.e., $S=\{T_S(u), I_S(u), F_S(u):u\in U\}$ where $T_S(u), I_S(u), F_S(u):U\rightarrow [0,1]$ and $0\le T_S(u)+I_S(u)+F_S(u)\le 3$.

Definition 2.3

[17] Let U be a fixed set. A generalized intuitionistic fuzzy set (GIFS) I of U is an object having the form I = $\{(u,\mu _I(u), \nu _I(u))|u\in U\}$, where the functions $\mu _I(u):\rightarrow [0,1]$ and $\nu _I(u):\rightarrow [0,1]$ define the degree of membership and degree of nonmembership of an element $u\in U$, respectively, such that

$$\begin{aligned} \min \{\mu _I(u), \nu _I(u)\}\le 0.5,\hbox { for all }u\in U. \end{aligned}$$

This condition is called the generalized intuitionistic condition (GIC).

Being motivated from this definition, Bhowmik and Pal [10] gave the idea of an intuitionistic single-valued neutrosophic set and discussed its certain properties.

Definition 2.4

[10, 11] An intuitionistic single-valued neutrosophic (ISVN) set on a universal set V can be stated as a set having the form $A=\{T_A(u), I_A(u), F_A(u):u\in V\}$, where

$$\begin{aligned}&\min \{T_A(u), I_A(u)\}\le 0.5,\\&\min \{F_A(u), I_A(u)\}\le 0.5,\\&\min \{T_A(u), F_A(u)\}\le 0.5, \end{aligned}$$

and $0\le T_A(u)+I_A(u)+F_A(u)\le 2$.

Definition 2.5

The support set of an ISVNS $A=\{(v, T_A(v), I_A(v), F_A(v)): v \in V \}$ is defined as $supp(A)=\{v|T_A(v)\ne 0$ and $I_A(v)\ne 0$ and $F_A(v)\ne 0\}$.

The support set of an ISVNS is a crisp set.

Definition 2.6

The height of an ISVNS $A=\{(v, T_A(v), I_A(v), F_A(v)):v \in V \}$ is defined as h(A) = ($\max \limits _{v\in V} T_A(v)$, $\max \limits _{v\in V} I_A(v)$, $\min \limits _{v\in V} F_A(v))$. An ISVNS A is called normal if there is an element v in A such that $T_A(v)=1, I_A(v)=1, F_A(v)=0$.

Definition 2.7

Let $A=\{(v, T_A(v), I_A(v), F_A(v)): v \in V \}$ be an ISVNS on V. Let $\eta , \phi , \psi \in [0, 1]$ such that $\eta +\phi +\psi \le 2$, then the $(\eta , \phi , \psi )$-level set of A is defined as $A_{(\eta , \phi , \psi )}=\{v:T_A(v) \ge \eta , I_A(v)\ge \phi , F_A(v)\le \psi \}$. Note that $(\eta , \phi , \psi )$-level set is a crisp set.

Example 2.1

Let $X=\{b_1, b_2, b_3, b_4\}$ be a set. We define an ISVN set on X as $A=\{(b_1, 0.5, 0.4, 0.3), (b_2, 0.4, 0.3, 0.3 ), (b_3, 0.2, 0.3, 0.1), (b_4, 0.9, 0.5, 0.3)\}$. By direct calculations, we have $supp(A)=\{b_1, b_2, b_3, b_4\}$, $h(A)=(0.9, 0.5, 0.1)$. Take $(\eta , \phi , \psi )=(0.5, 0.2, 0.3)\in [0, 1]$. By direct calculations, (0.5, 0.2, 0.3)-level set is $A_{(0.5, 0.2, 0.3)}=\{b_1, b_4\}$.

We first define intuitionistic single-valued neutrosophic graph.

Definition 2.8

An intuitionistic single-valued neutrosophic (ISVN) graph with underlying set U is a pair $\mathbb {H}=(\mathbf {C,D})$, such that:

• 1. The degree of truth-membership, degree of indeterminacy-membership and falsity-membership of the element $x_i\in U$, are denoted by the mappings $T_C:U\rightarrow [0,1]$, $I_C:U\rightarrow [0, 1]$ and $F_C:U\rightarrow [0, 1]$, respectively, where

  $$\begin{aligned} \min \{T_C(x_i), F_C(x_i)\}\le 0.5, \min \{T_C(x_i), I_C(x_i)\}\le 0.5, \min \{F_C(x_i), I_C(x_i)\}\le 0.5, \end{aligned}$$

  for all $x_i \in U$, $i=1, 2, 3, \ldots , m,$ with the condition

  $$\begin{aligned} 0 \le T_C(x_i)+F_C(x_i)+I_C(x_i)\le 2. \end{aligned}$$

• 2. The mappings $T_D:D \subseteq U \times U \rightarrow [0, 1]$, $I_D:D\subseteq U \times U \rightarrow [0, 1]$ and $F_D:D \subseteq U \times U \rightarrow [0, 1]$ are defined by

  $$\begin{aligned} T_D(x_ix_j)\le \min \{T_C(x_i), T_C(x_j)\}, I_D(x_ix_j)\le \min \{I_C(x_i), I_C(x_j)\}, F_D(x_ix_j)\le \max \{F_C(x_i), F_C(x_j)\}, \end{aligned}$$

  denote the degree of truth-membership, indeterminacy-membership and falsity-membership of the edge $x_ix_j\in D$, respectively, where

  $$\begin{aligned} \min \{T_D(x_ix_j), I_D(x_ix_j)\}\le 0.5, \min \{T_D(x_ix_j), F_D(x_ix_j)\}\le 0.5, \min \{F_D(x_ix_j), I_D(x_ix_j)\}\le 0.5, \end{aligned}$$

  for all $x_ix_j\in D$, $i=1, 2, 3, \ldots , m$, $j=1, 2, 3,\ldots ,m$, with the condition

  $$\begin{aligned} 0\le T_D(x_ix_j)+F_D(x_ix_j)+I_D(x_ix_j)\le 2. \end{aligned}$$

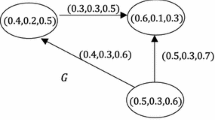
We call $\mathbf C$ an ISVN vertex set, $\mathbf D$ an ISVN edge set. $\mathbf D$ is called a symmetric ISVN relation on $\mathbf C$. We consider an intuitionistic single-valued neutrosophic graph as shown in (Fig. 1).

Fig. 1

Intuitionistic single-valued neutrosophic graph

We now define an intuitionistic single-valued neutrosophic hypergraph (ISVNHG).

Definition 2.9

Let $C = \{c_1, c_2,\ldots , c_m\}$ be a finite set of vertices and $D = \{D_1, D_2,\ldots , D_m\}$ a finite family of non-trivial ISVN subsets of vertex set C such that

$$\begin{aligned} C = \bigcup \limits _{i} supp(D_i), i = 1, 2, 3, \ldots , \hbox {m}, \end{aligned}$$

where the edges $D_i$ are ISVN subsets of C, $D_i = \{(v_j , T_{D_i}(v_j), I_{D_i} (vj ), F_{D_i}(v_j ))\}$, $D_i \ne \phi$, for $i = 1, 2, 3, \ldots ,m,$ and

$$\begin{aligned}&\min \{T_{D_i}(v_j), I_{D_i}(v_j)\}\le 0.5,\\&\min \{F_{D_i}(v_j), I_{D_i}(v_j)\}\le 0.5,\\&\min \{T_{D_i}(v_j), F_{D_i}(v_j)\}\le 0.5,\\ \end{aligned}$$

with the condition

$$\begin{aligned} 0\le T_{D_i}(v_j)+F_{D_i}(v_j)+I_{D_j}(v_j)\le 2. \end{aligned}$$

Then the ordered pair $\mathcal {G} = (C, D)$ is an ISVNHG on C, D is the family of ISVN hyperedges of $\mathcal {G}$ and C is the crisp vertex set of $\mathcal {G}$.

Example 2.2

Consider an ISVNHG $\mathcal {G} = (C, D)$ as shown in Fig. 2, such that $C = \{c_1, c_2, c_3, c_4\}$ and $D = \{D_1, D_2, D_3\}$, which is represented by the following incidence matrix:

$N_\mathcal {G}$	$D_1$	$D_2$	$D_3$
$c_1$	(0.5, 0.4, 0.3)	(0.5, 0.4, 0.3)	(0, 0, 0)
$c_2$	(0.2, 0.3, 0.4)	(0, 0, 0)	(0, 0, 0)
$c_3$	(0, 0, 0)	(0, 0, 0)	(0.3, 0.4, 0.5)
$c_4$	(0, 0, 0)	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)

Fig. 2

Intuitionistic single-valued neutrosophic hypergraph

Definition 2.10

In an ISVNHG, two vertices $c_1$ and $c_2$ are said to be adjacent if there is a hyperedge $D_i\in D$ which contains both $c_1$ and $c_2$, i.e., $c_1$, $c_2\in supp(D_i )$.

Two hyperedges $D_i$ and $D_j$ are called adjacent edges if they have non-empty intersection, i.e., $supp(D_i)\bigcap supp(D_j)\ne \emptyset$, $i\ne j$. The number of elements in C, i.e., |C| is called the order and |D| is called the size of an ISVN hypergraph.

An ISVNHG is said to be n-uniform if $supp(D_i)=n$ for each $D_i\in D$.

Definition 2.11

The height of an ISVNHG $\mathcal {G}=(C, D)$ is defined as $h(\mathcal {G})=\bigvee \{h(D_i)|D_i\in D\}$.

Definition 2.12

Consider an ISVNHG $\mathcal {G}=(C, D),$ the cardinality of an ISVN hyperedge is the sum of truth-membership, indeterminacy-membership and falsity-membership values of the vertices connected to a hyperedge, it is denoted by $|D_i|$. The degree of an ISVN hyperedge, $D_i\in D$ is its cardinality, i.e., $d_{\mathcal {G}}(D_i) = |D_i|$. The rank of an ISVNHG is the maximum cardinality of any hyperedge in $\mathcal {G}$, i.e., $\max \limits _{D_i\in D}d_\mathcal {G}(D_i)$ and anti rank is the minimum cardinality of any hyperedge in $\mathcal {G}$, i.e., $\min \limits _{D_i\in D}d_\mathcal {G}(D_i)$.

Remark 2.1

• 1. If an ISVNHG $\mathcal {G}=(C, D)$ is simple, then $(\eta , \phi , \psi )$-level hypergraph $\mathcal {G}_{(\eta , \phi , \psi )}$ may or may not be simple. Also, it is possible $D_{i(\eta , \phi , \psi )}=D_{j(\eta , \phi , \psi )}$ for $D_i \ne D_j$, where $D_i, D_j \in D$ are any two ISVN hyperedges.

• 2. An ISVNHG $\mathcal {G}=(C, D)$ is an ISVN graph (with loops) if and only if $\mathcal {G}$ is elementary, support simple and every hyperedge has two (or one) element support.

• 3. The families of crisp hypergraphs (sets) which are formed by the $(\eta , \phi , \psi )$-levels of ISVNHGs have an important relationship in common with each other. Let $\mathbf U$ and $\mathbf V$ be two families of hypergraphs such that for every set U in $\mathbf U$ there is atleast one set V belonging to $\mathbf V$ which is superset of U. We can say that $\mathbf V$ absorbs $\mathbf U$ and symbolically we represent this relation between $\mathbf U$ and $\mathbf V$ as $\mathbf U \sqsubseteq \mathbf Y$. It is possible that $\mathbf V$ absorbs $\mathbf U$ while $\mathbf U \bigcap \mathbf V$ = $\emptyset$, also we have $\mathbf U \subseteq \mathbf V$ implies $\mathbf U \sqsubseteq \mathbf V$, but the converse may be false generally. If $\mathbf U \sqsubseteq \mathbf V$ and $\mathbf U \ne \mathbf V$, then $\mathbf U \sqsubset \mathbf V$.

Definition 2.13

Let $\mathcal {G}$ = (C, D) be an ISVNHG such that $h(\mathcal {G})$ = (u, v, w). Let $\mathcal {G}_{(u_i, v_i, w_i)}$ = $\left( C_ {(u_i, v_i, w_i)}, D_{(u_i, v_i, w_i)}\right)$ be the $(u_i, v_i, w_i)$-level hypergraphs of $\mathcal {G}$. The sequence of real numbers ${(u_1, v_1, w_1), (u_2, v_2, w_2), \ldots , (r_n, v_n, w_n)}, 0< u_n< u_{n+1}<, \ldots ,< u_1 = u, 0< v_n< v_{n+1}<, \ldots , < v_1 = v,$ and $w_n> w_{n+1}>, \ldots ,>, w_1 = w > 0$, which satisfies the properties:

• 1. if $u_{i+1}< u'< u_i, v_{i+1}< v'< v_i, w_{i+1}> w' > w_i(w_i< w' < w_{i+1})$, then $D_{(u',v',w')}$ $=D_{(u_i,v_i,w_i)}$,

• 2. $D_{(u_i,v_i,w_i)} \sqsubseteq D_{(u_{i+1},v_{i+1},w_{i+1})}$,

is fundamental sequence of ISVNHG $\mathcal {G}$, denoted by $FS(\mathcal {G})$, the set of $(u_i, v_i, w_i)$-level hypergraphs $\{\mathcal {G}_{(u_1, v_1, w_1)}, \mathcal {G}_{(u_2, v_2, w_2)}, \ldots , \mathcal {G}_{(u_n, v_n, w_n)}\}$ is known as core hypergraphs of ISVNHG $\mathcal {G}$, and is denoted by $C(\mathcal {G})$.

Definition 2.14

An ISVNHG $\mathcal {G}=(C, D)$ is simple if $D_1, D_2 \in D$ and $T_{D_1}(v_j)\le T_{D_2}(v_j)$, $F_{D_1}(v_j) \ge F_{D_2}(v_j)$, $I_{D_1}(v_j)\le I_{D_2}(v_j)$ imply $T_{D_1}(v_j)= T_{D_2}(v_j)$, $F_{D_1}(v_j)= F_{D_2}(v_j)$, $I_{D_1}(v_j)= I_{D_2}(v_j)$, $j=1, 2, 3, \ldots , m.$

Definition 2.15

Let $\mathcal {G}=(C, D)$ be an ISVNHG with $FS(\mathcal {G})$ = $\{(u_1, v_1, w_1), (u_2, v_2, w_2), \ldots , (u_m, v_m, w_m)\}$ and $u_{m+1} = 0, v_{m+1} = 0, w_{m+1} = 0$. $\mathcal {G}$ is sectionally elementary if for every edge $D_i \in D$ and each $(u_i, v_i, w_i) \in FS(\mathcal {G})$, $D_{i(u_i,v_i,w_i)} = D_{i(u, v, w)}$ for all $(u, v, w)\in ((u_{i+1}, v_{i+1}, w_{i+1}), (u_i, v_i, w_i)]$.

Definition 2.16

Let $\mathcal {G}_1=(C_1, D_1)$ and $\mathcal {G}_1^*=(C_1^*, D_1^*)$ be ISVNHGs and $D_1^*\subseteq D_1$ then $\mathcal {G}_1^*=(C_1^*, D_1^*)$ is called a partial ISVNHG of $\mathcal {G}_1$, denoted by, $\mathcal {G}_1^*\subseteq \mathcal {G}_1$. If $\mathcal {G}_1^*$ is a partial ISVNHG of $\mathcal {G}_1$ and $D_1^*\subset D_1$, then we write $\mathcal {G}_1^*\subset \mathcal {G}_1$.

Definition 2.17

An ISVNHG $\mathcal {G}=(C, D)$ is elementary whose hyperedges are elementary. An ISVNS $I=(T_I, I_I, F_I)$ is elementary if I is single-valued on supp(I).

Example 2.3

Consider the ISVNHG $\mathcal {G}=(C, D)$, where $C=\{c_1, c_2, c_3, c_4\}$ and $D=\{D_1, D_2, D_3, D_4, D_5\}$. Then the corresponding incidence is given as follows:

$I_\mathcal {G}$	$D_1$	$D_2$	$D_3$	$D_4$	$D_5$
$c_1$	(0.7, 0.5, 0.5)	(0.9, 0.5, 0.1)	(0, 0, 0)	(0, 0 ,0)	(0, 0, 0)
$c_2$	(0.7, 0.5, 0.5)	(0.9, 0.5, 0.1)	(0.9, 0.5, 0.1)	(0.7, 0.5, 0.5)	(0, 0, 0)
$c_3$	(0, 0, 0)	(0, 0, 0)	(0.9, 0.5, 0.1)	(0.7, 0.5, 0.5)	(0.4, 0.3, 0.3)
$c_4$	(0, 0, 0)	(0.4, 0.3, 0.3)	(0, 0, 0)	(0.4, 0.3, 0.3)	(0.4, 0.3, 0.3)

Here $h(\mathcal {G})$ = (0.9, 0.5, 0.1). By calculating the $(u_i, v_i, w_i)$-level hypergraphs of $\mathcal {G}$ we have

$$\begin{aligned} D_{(0.9, 0.5, 0.1)}=\{\{c_1, c_2\}, \{c_2, c_3\}\}=D_{(0.7, 0.5, 0.5)}=\tilde{D_1}. \end{aligned}$$

$D_{(0.4, 0.3, 0.3)}=\{\{c_1, c_2, c_4\}, \{c_2, c_3\}, \{c_3, c_4\}\}=\tilde{D_2}$. $\mathcal {G}$ is not simple ISVNHG and not support simple. Further, $D_{(0.9, 0.5, 0.1)}\ne D_{(0.4, 0.3, 0.3)}$ and $D_{(0.9, 0.5, 0.1)}\sqsubseteq D_{(0.4, 0.3, 0.3)}$. So, the fundamental sequence is $FS(\mathcal {G})$ = $\{(u_1, v_1, w_1)=(0.9, 0.5, 0.1), (u_2, v_2, w_2)=(0.4, 0.3, 0.3)\}$ and the set of core hypergraphs is $C(\mathcal {G})$ = $\{\mathcal {G}_{(0.9, 0.5, 0.1)}=(V_1, \tilde{D_1}), \mathcal {G}_{(0.4, 0.3, 0.3)}=(C_2, \tilde{D_2})\}$. $\mathcal {G}$ is not sectionally elementary as $D_{1(u, v, w)} \ne D_{1(0.9, 0.5, 0.1)}$ for $(u, v, w)=(0.7, 0.5, 0.5)$.

The partial ISVN hypergraphs, $\mathcal {G}^*=(C^*, D^*)$, where $D^*=\{D_2, D_3, D_5\}$ is simple, $\mathcal {G}^{**}=(C^{**}, D^{**}),$ where $D^{**}=\{D_1, D_5, D_3\}$ is elementary, $\mathcal {G}^{***}=(C^{***}, D^{***}),$ where $D^{***}=\{D_2, D_3, D_5\}$ is sectionally elementary.

Definition 2.18

An ordered ISVNHG is an ISVN hypergraph in which $C(\mathcal {G})$ is ordered, i.e., if $C(\mathcal {G})$ = $\{\mathcal {G}_{(l_1, m_1, n_1)}, \mathcal {G}_{(l_2, m_2, n_2)}, \ldots , \mathcal {G}_{(l_n, m_n, n_n)}\}$, then $\mathcal {G}_{(l_1, m_1, n_1)} \subseteq \mathcal {G}_{(l_2, m_2, n_2)}\subseteq ,\ldots , \subseteq \mathcal {G}_{(l_n, m_n, n_n)}$. If $C(\mathcal {G})$ is ordered and if whenever $D^*\in D^*_{j+1} \setminus D_j$, then $D^*\nsubseteq C^*_j$ then ISVNHG $\mathcal {G}$ is simply ordered.

Definition 2.19

The strength of a hyperedge $D_j$, denoted by $\eta (D_j)$, is defined as

$$\begin{aligned} \eta (D_j)=(\min (T_{D_j}(v)), \min (I_{D_j}(v)), \max (F_{D_j}(v))), \end{aligned}$$

for every $T_{D_j}(v)>0, F_{D_j}(v)>0, I_{D_j}(v)>0$.

Example 2.4

In the above example, the strength of each hyperedge is $\eta (D_1)=(0.7, 0.5, 0.5), \eta (D_2)=(0.4, 0.3, 0.3), \eta (D_3)=(0.9, 0.5, 0.1), \eta (D_4)=(0.4, 0.3, 0.5), \eta (D_5)=(0.4, 0.3, 0.3)$. Thus, $D_3$ is the stronger edge than $D_1, D_2, D_4, D_5$.

We now define the $D^T$ tempered ISVNHG as follows:

Definition 2.20

An ISVNHG $\mathcal {G}=(C, D)$ is called a $D^T$ tempered ISVNHG if there is a crisp hypergraph $\mathcal {G}'=(C, D')$ and ISVNS $D^T$ is defined on C, where $T_{D^T}:C\longrightarrow (0, 1]$, $F_{D^T}:C\longrightarrow (0, 1]$ and $I_{D^T}:C\longrightarrow (0, 1]$ with the condition

$$\begin{aligned}&\min \{T_{D^T}(v), I_{D^T}(v)\}\le 0.5,\\&\min \{F_{D^T}(v), I_{D^T}(v)\}\le 0.5,\\&\min \{T_{D^T}(v), F_{D^T}(v)\}\le 0.5,\\ \end{aligned}$$

such that $D=\{C_D|D\in D'\},$ where

$$\begin{aligned} T_{C_D}(x)= & {} \left\{ \begin{array}{ll} \min \{T_{D^T}(y) | y\in D\}, &{}\quad \mathrm{if}\quad x\in D; \\ 0 , &{}\quad \mathrm{otherwise}. \end{array} \right. \\ I_{C_D}(x)= & {} \left\{ \begin{array}{ll} \min \{ I_{D^T}(y) | y \in D\} , &{}\quad \mathrm{if}\quad x\in D; \\ 0 , &{}\quad otherwise. \end{array} \right. \\ F_{C_D}(x)= & {} \left\{ \begin{array}{ll } \max \{F_{D^T}(y) | y \in D\} , &{}\quad \mathrm{if}\quad x\in D; \\ 0 , &{}\quad \mathrm{otherwise}. \end{array} \right. \end{aligned}$$

We will denote the $D^T$ tempered ISVNHG of $\mathcal {G}'=(C, D')$ and ISVNS $D^T$ by $D^T \boxtimes \mathcal {G}'$.

Theorem 2.1

An ISVNHG $\mathcal {G} = (C, D)$ is a $D^T$ tempered ISVNHG of $\mathcal {G}'$ if and only if $\mathcal {G}$ is elementary, support simple and simply ordered.

Proof

Consider $\mathcal {G}$ = (C, D) is a $D^T$ tempered ISVN hypergraph of $\mathcal {G}'$. Clearly, $\mathcal {G}$ is elementary and support simple. We will prove that $\mathcal {G}$ is simply ordered. Let $C(\mathcal {G})=\{ \mathcal {G}_{(l_1, m_1, n_1)}= (C_1,D'_1), \mathcal {G}_{(l_2, m_2, n_2)}=(C_2, D'_2), \ldots , \mathcal {G}_{(l_n,m_n,n_n)} = (C_n, D'_{n} )\}$. Since $\mathcal {G}$ is elementary, then $\mathcal {G}$ is ordered. Suppose there is $D\in D'_{j+1}\setminus D'_{j}$ and $d\in D$ such that $T_{D}(d) = l_{j+1}, I_{D}(d)=m_{j+1}$, and $F_{D}(d)=n_{j+1}$. Since $T_D(d) = l_{j+1}< l_j, I_{D}(d) = m_{j+1} < m_j$, and $F_{D}(d) = n_{j+1} > n_i$, it follows that $d\notin C_j$ and $D \nsubseteq C_j$, hence $\mathcal {G}$ is simply ordered.

Conversaly, suppose that $\mathcal {G}$ is elementary, support simple and simply ordered. For $C(\mathcal {G})=\{ \mathcal {G}_{(l_1, m_1, n_1)}= (C_1,D'_1), \mathcal {G}_{(l_2, m_2, n_2)}=(C_2, D'_2), \ldots , \mathcal {G}_{(l_n,m_n,m_n)} = (C_n, D'_{n} )\}$, the fundamental sequence is $FS(\mathcal {G})$ = $\{(l_1, m_1, n_1), (l_2, m_2, n_2), \ldots , (l_n, m_n, n_n)\}$ with $0<l_n<l_{n-1}<, \ldots ,<l_1,0<m_n<m_{n-1}<, \ldots , <m_1, n_n>n_{n-1}>,\ldots ,>n_1>0.$ $\mathcal {G}_{(l_n, m_n, n_n)}$ = $(C_n, D'_n)$ and ISVN set $D^T$ on $C_n$ is defined as

$$\begin{aligned} T_{D^T}(d)= & {} \left\{ \begin{array}{ll} l_1, &{}\quad if d\in C_1;\\ l_j, &{}\quad if d\in C_j\setminus C_{j-1}, j=2, 3, \ldots , n. \end{array} \right. \\ I_{D^T}(d)= & {} \left\{ \begin{array}{ll} m_1, &{}\quad if d\in C_1;\\ m_j, &{}\quad if d\in C_j\setminus C_{j-1}, j=2, 3, \ldots , n. \end{array} \right. \\ F_{D^T}(d)= & {} \left\{ \begin{array}{ll} n_1, &{}\quad if d\in C_1;\\ n_j, &{}\quad if d\in C_j\setminus C_{j-1}, j=2, 3, \ldots , n. \end{array} \right. \end{aligned}$$

Now we prove that D = $\{C_D|D\in D'_n\}$, where

$$\begin{aligned} T_{C_D}(a)= & {} \left\{ \begin{array}{ll} \wedge \{T_{D^T}(y|y\in D)\}, &{}\quad \mathrm{if}\quad a\in D; \\ 0 , &{}\quad \mathrm{otherwise}. \end{array} \right. \\ I_{C_D}(a)= & {} \left\{ \begin{array}{ll} \wedge \{I_{D^T}(y|y\in D)\}, &{}\quad \mathrm{if}\quad a\in D; \\ 0 , &{}\quad \mathrm{otherwise}. \end{array} \right. \\ F_{C_D}(a)= & {} \left\{ \begin{array}{ll} \wedge \{F_{D^T}(y|y\in D)\}, &{}\quad \mathrm{if}\quad a\in D; \\ 0 , &{}\quad \mathrm{otherwise}. \end{array} \right. \end{aligned}$$

Let $D\in D'_n$. As $\mathcal {G}$ is elementary and support simple then there is a unique ISVN hyperedge $D_i$ in D having support $D\in D'_n$. We will show that $D^T$ tempered ISVN hypergraph $\mathcal {G} = (C, D)$ is determined by the crisp graph $\mathcal {G}'_n=(C, D'_n)$, i.e., $C_{D\in D'_n}=D_i$, $i=1, 2, 3, \ldots , n$.

Since all ISVN hyperedges are elementary and $\mathcal {G}$ is support simple, then distinct edges have different supports, i.e., $h(D_i)$ is equal to some member $(l_i, m_i, n_i)$ of $FS(\mathcal {G})$. As a consequence, $D\subseteq C_j$ and if $j>1$, then $D\in D'_{j}\setminus D'_{j-1}$, $T_D(d)\ge l_i, I_D(d)\ge m_i$, and $F_D(d)\le n_i$ for some $d\in D.$ Since $D\subseteq C_j$, we claim that $T_{D^T}(d)=l_i, I_{D^T}(d)= m_i, F_{D^T} (d) = n_i$ for some $d\in D$, if not then $T_{D^T}(d)\ge l_{i-1}, I_{D^T }(d)\ge m_{i-1}, F_{D^T}(d)\le n_{i-1}$ for all $d\in D$ implies $D \subseteq C_{i-1}$ and because $\mathcal {G}$ is simply ordered, $D\in D'_i\setminus D'_{i-1}$, then $D\nsubseteq C_{i-1}$, which is a contradiction. Thus $C_D = D_i$, $i = 1, 2, \ldots ,m,$ by the definition of $C_D$.$\square$

Proposition 2.1

Let $\mathcal {G} = (C, D)$ be a simply ordered ISVN hypergraph and $FS(\mathcal {G}) = \{(l_1, m_1, n_1), (l_2, m_2, n_2), \ldots , (l_n, m_n, n_n)\}$. For a crisp hypergraph $\mathcal {G}_{(l_n,m_n,n_n)}$, there is a partial ISVNS hypergraph $\mathcal {G}^*= (C, D^*)$ of $\mathcal {G} = (C, D)$ such that following hold:

• 1. $\mathcal {G}^*$ is a $D^T$ tempered ISVN hypergraph of $\mathcal {G}_{(l_n, m_n, n_n)}$,

• 2. $FS(\mathcal {G}^*)$ = $FS(\mathcal {G})$ and $C(\mathcal {G}^*) = C(\mathcal {G})$.

Proof

Since $\mathcal {G}$ is simply ordered, $\mathcal {G}$ is an elementary ISVNS hypergraph. We take the partial ISVN hypergraph $\mathcal {G}^*=(C, D^*)$ of $\mathcal {G}=(C, D)$ by removing all those edges of D which are properly contained in another edge, where $D^*= \{D_i\in D |$ if $D_i\subseteq D_j$ and $D_j\in D$, then $D_i=D_j\}$. Since $\mathcal {G}_{(l_n, m_n, n_n)}$ is simple and its all edges are elementary, if any hyperedge in $\mathcal {G}$ is subset of another hyperedge then both edges have the same support. So $FS(\mathcal {G}^*)$ = $\mathcal {G}$ and $C(\mathcal {G}^*) = C(\mathcal {G})$. From the definition of $D^*$, $\mathcal {G}^*$is elementary, support simple. Thus by above Theorem $\mathcal {G}^*$ is a $D^T$ tempered ISVN hypergraph.$\square$

Example 2.5

Consider an ISVN hypergraph $\mathcal {G}=(C, D)$, where $C=\{p_1, p_2, p_3, p_4 \}$ and $D=\{Q_1, Q_2, Q_3\}$ and the incidence matrix of $\mathcal {G}$ is given as:

$I_\mathcal {G}$	$Q_1$	$Q_2$	$Q_3$
$p_1$	(0.1, 0.2, 0.6)	(0, 0, 0)	(0.3, 0.4, 0.6)
$p_2$	(0.1, 0.2, 0.6)	(0.1, 0.2, 0.3)	(0, 0, 0)
$p_3$	(0.1, 0.2, 0.6)	(0, 0, 0)	(0.3, 0.4, 0.6)
$p_4$	(0, 0, 0)	(0.1, 0.2, 0.3)	(0, 0, 0)

Let $D^T=\{(p_1, 0.3, 0.4, 0.5), (p_2, 0.1, 0.2, 0.3), (p_3, 0.5, 0.4, 0.6), (p_4, 0.4, 0.3, 0.3)\}$ be an ISVN subset defined on C.

Then, it can be seen that $T_{\{p_1, p_2, p_3\}}(p_1)=\min \{T_{D^T}(p_1), T_{D^T}(p_2), T_{D^T}(p_3)\}=0.1, I_{\{p_1, p_2, p_3\}}(p_1)=\min \{I_{D^T}(p_1), I_{D^T}(p_2), I_{D^T}(p_3)\}=0.2, F_{\{p_1, p_2, p_3\}}(p_1)=\max \{F_{D^T}(p_1), F_{D^T}(p_2), F_{D^T}(p_3)\}=0.6$ and $T_{\{p_1, p_2, p_3\}}(p_2)=\min \{T_{D^T}(p_1), T_{D^T}(p_2), T_{D^T}(p_3)\}=0.1, I_{\{p_1, p_2, p_3\}}(p_2)=\min \{I_{D^T}(p_1), I_{D^T}(p_2), I_{D^T}(p_3)\}=0.2, F_{\{p_1, p_2, p_3\}}(p_2)=\max \{F_{D^T}(p_1), F_{D^T}(p_2), F_{D^T}(p_3)\}=0.2$, and $T_{\{p_1, p_2, p_3\}}(p_3)= \min \{T_{D^T}(p_1), T_{D^T}(p_2), T_{D^T}(p_3)\}=0.1, I_{\{p_1, p_2, p_3\}}(p_3)=\min \{I_{D^T}(p_1), I_{D^T}(p_2), I_{D^T}(p_3)\}=0.2, F_{\{p_1, p_2, p_3\}}(p_3)=\max \{F_{D^T}(p_1), F_{D^T}(p_2), F_{D^T}(p_3)\} =0.6$, that is $C_{\{p_1, p_2, p_3\}}=D_1$. Also $C_{\{p_2, p_4\}}=D_2, C_{\{p_1, p_3\}}=D_3$. Thus $\mathcal {G}$ is $D^T$ tempered.

Definition 2.21

The dual of an ISVNHG $\mathcal {G} = (C, D)$ is an ISVNHG $\mathcal {G}^\star = (D,C),$ where $D = \{e_1, e_2,\ldots , e_n\}$ is set of vertices corresponding to $D_1, D_2, \ldots , D_n$, respectively and C = $\{C_1, C_2, \ldots , C_n\}$ set of hyperedges corresponding to $C_1, C_2, \ldots , C_n$, respectively.

Example 2.6

Consider an ISVNHG $\mathcal {D} = (C, D)$, where $C = \{q_1, q_2, q_3, q_4\}$ and $D = \{P_1, P_2, P_3\}$ is represented by the incidence matrix. The ISVNHG and its dual are shown in Figs. 3 and 4, respectively.

$M_\mathcal {D}$	$P_1$	$P_2$	$P_3$
$q_1$	(0.5, 0.4, 0.3)	(0.5, 0.4, 0.3)	(0, 0, 0)
$q_2$	(0.2, 0.3, 0.4)	(0, 0, 0)	(0, 0, 0)
$q_3$	(0, 0, 0)	(0, 0, 0)	(0.3, 0.4, 0.5)
$q_4$	(0, 0, 0)	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)

Fig. 3

ISVNHG

The dual of ISVNHG $\mathcal {D}$ is $\mathcal {D}^\star =(D, C)$ such that $D=\{p_1, p_2, p_3\}, C=\{Q_1, Q_2, Q_3, Q_4\}$, where

$$\begin{aligned} Q_1= & {} \{(p_1, 0.5, 0.4, 0.3), (p_2, 0.5, 0.4, 0.3), (p_3, 0, 0, 0)\},\\ Q_2= & {} \{(p_1, 0.2, 0.3, 0.4), (p_2, 0, 0, 0), (p_3, 0, 0, 0)\},\\ Q_3= & {} \{(p_1, 0, 0, 0), (p_2, 0, 0, 0), (p_3, 0.3, 0.4, 0.5)\},\\ Q_4= & {} \{(p_1, 0, 0, 0), (p_2, 0.5, 0.5, 0.5), (p_3, 0.5, 0.5, 0.5)\}. \end{aligned}$$

Fig. 4

Dual ISVNHG $\mathcal {D}^\star$

The incidence matrix of Dual ISVNHG is given as follows:

$I_{\mathcal {D}^\star }$	$Q_1$	$Q_2$	$Q_3$	$Q_4$
$p_1$	(0.5, 0.4, 0.3)	(0.2, 0.3, 0.4)	(0, 0, 0)	(0, 0, 0)
$p_2$	(0.5, 0.4, 0.3)	(0, 0, 0)	(0, 0, 0)	(0.5, 0.5, 0.5)
$p_3$	(0, 0, 0)	(0, 0, 0)	(0.3, 0.4, 0.5)	(0.5, 0.5, 0.5)

Theorem 2.2

If $\mathcal {G}$ is linear ISVNHG, then its dual ISVNHG $\mathcal {G}^*$ without isolated vertex is linear ISVNHG.

Proof

Let $\mathcal {G}$ be a linear ISVNHG. Suppose that $\mathcal {G}^*$ is not linear ISVNHG, then there must be two distinct ISVN hyperedges $C_i$ and $C_j$ of $\mathcal {G}^*$ having at least two vertices $e_1$ and $e_2$ in common. By defnition of dual ISVNHG, $v_i$ and $v_j$ belongs to $D_1$ and $D_2$ (the ISVN hyperedges of $\mathcal {G}$ corresponds to the vertices $e_1$, $e_2$ of $\mathcal {G}^*$, respectively) so $\mathcal {G}$ is not linear ISVNHG. A Contradiction to the statement that $\mathcal {G}$ is linear ISVNHG. Hence, dual $\mathcal {G}^*$ of a linear ISVNHG without isolated vertex is also linear ISVNHG.$\square$

Remark 2.2

$\mathcal {G}^*=(\mathcal {G})^t$, That is, incidence matrix of $\mathcal {G}^*$ is the transpose of the incidence matrix of $\mathcal {G}$. Also, the dual of a simple ISVNHG may or may not be simple.

Now, we define the ISVN transversal of an ISVN hypergraph.

Definition 2.22

Let $\mathcal {G}=(C, D)$ be an ISVNHG and $h(D_i)$ the height of ISVN hyperedge $D_i$. Then the ISVN transversal $\tau$ of $\mathcal {G}$ is defined as an ISVN subset defined on C such that $\tau _{h(D_i)} \cap D_{h(D_i)} \ne \emptyset$ for all $D_i \in D.$

If $\tau ' \subset \tau$ and $\tau '$ is not an ISVN transversal of $\mathcal {G}$ then $\tau$ is called the minimal transversal.

Here, we state the following propositions without proof.

Proposition 2.2

For an ISVN transversal of $\mathcal {G}=(C, D)$ , we have $h(\tau )\ge h(D_i)$ for all $D_i\in D$ , and for a minimal transversal of $\mathcal {G}$ , we have $h(\tau )=\vee \{D_i|D_i\in D\}=h(\mathcal {G}).$

Theorem 2.3

Let $\mathcal {G}$ be an ISVNHG and $Tr(\mathcal {G})$ be the family of minimal ISVN transversals of $\mathcal {G}$ then $Tr(\mathcal {G})\ne \emptyset$.

Example 2.7

Consider the ISVNHG $\mathcal {G}$ = (C, D), where C = $\{u_1, u_2, u_3\}$ and D = $\{d_1,d_2,d_3\}$, which is represented by the following incidence matrix:

$I_\mathcal {G}$	$d_1$	$d_2$	$d_3$
$u_1$	(0, 0, 0)	(0, 0, 0)	(0.4, 0.3, 0.2)
$u_2$	(0.9, 0.3, 0.1)	(0.4, 0.3, 0.2)	(0.4, 0.3, 0.2)
$u_3$	(0.4, 0.3, 0.2)	(0, 0, 0)	(0.4, 0.3, 0.2)

Clearly, $h(\mathcal {G})$ = (0.9, 0.3, 0.1), the ISVN transversals of $\mathcal {G}$ are $\tau _1(\mathcal {G})=\{(u_2, 0.9, 0.3, 0.1), (u_3, 0.4, 0.3, 0.2)\}$ and $\tau _2(\mathcal {G})=\{(u_2, 0.9, 0.3, 0.1)\}$. FS of $\mathcal {G}$ is $FS(\mathcal {G})$ = $\{(0.9, 0.3, 0.1), (0.4, 0.3, 0.2)\}$, $\tau _{1(0.9, 0.3, 0.1)}=\{u_2\}$ and $\tau _{1(0.4, 0.3, 0.2)}=\{u_2, u_3\}.$ $\tau _{2(0.9, 0.3, 0.1)}=\{u_2\}$ and $\tau _{2(0.4, 0.3, 0.2)}=\{u_2\}.$ $D_{(0.9, 0.3, 0.1)}=\{u_2\}$, $D_{(0.4, 0.3, 0.2)}=\{\{u_2, u_3\}, \{u_2\}, \{u_1, u_2, u_3\}\}$. The minimal transversal of $\mathcal {G}$ is $\tau _2(\mathcal {G})=\{(u_2, 0.9, 0.3, 0.1)\}$.

3 Clustering problem

Clustering (or cluster analysis) involves the task of classifying data points into clusters or classes in such a way that the objects in the same class or cluster are similar and the objects belonging to different clusters are not much similar. The identification of clusters can be done by means of similarity measures. The connectivity and distance can be taken as the similarity measures. Similarity measures are chosen according to the choice of data or the application. The purpose of graph clustering is to grouping the vertices into classes according to the properties of the graph. So that the edges having high similarity are in the same group. In statistical data analysis, clustering analysis serves as a strong and significant tool, which can be widely used in various fields, like pattern recognition, banking sector, microbiology, document classification and data mining, etc. In a computer cluster, a set of more than one connected computers work together. The benefit of such clustering of computers is that if any one computer of the cluster fails, another computer can manage the workload of failed computer.

Definition 3.1

Let W be a universal set. A collection of ISVN sets $\{A_1, A_2, A_3, \ldots , A_m\}$ is an ISVN partition if

• (i) $\bigcup \limits _{j}supp(A_j)=W$, $j=1,2,3,\ldots ,m$,

• (ii) $\sum \limits ^{m}_{j=1}T_{A_{j}}(x)$ = 1 for all $x\in W$,

• (iii) $\sum \limits ^{m}_{j=1} I_{A_{j}}(x)$ = 1 for all $x\in W$,

• (iv) there is at most one j for which $F_{A_{j}}(x)=0$ for all $x\in W$ (there is atmost one ISVNS for which $T_{A_{j}}(x)+I_{A_{j}}(x)+F_{A_{j}}(x)=2$ for all $x\in W$).

A family of ISVN subsets $\{A_1, A_2, A_3, \ldots , A_m\}$ is said to be an ISVN partition if it captivates the above conditions.

An ISVN matrix $(a_{ij})$ can be used to interpret an ISVN partition, where $a_{ij}$ indicates the truth value, indeterminacy value and falsity value of element $x_i$ in class j. We see that the incidence matrix in ISVNHG is as similar as this matrix. So that we can express an ISVN partition by an ISVNHG $\mathcal {G}$ = (W, D) such that

• (i) $W=\{x_1, x_2, x_3, \ldots \ , x_n\}$ is a set of elements, $i=1, 2, 3,\ldots , n$,

• (ii) $D=\{D_1, D_2, D_3,\ldots , D_m\}$ be a finite class of nontrivial ISVN sets,

• (iii) $\bigcup \limits _{k}supp(D_k)=W$, $k=1,2,3,\ldots ,n$,

• (iv) $\sum \limits ^{m}_{k=1}T_{A_{j}}(x)= 1$ for all $x\in W$,

• (v) $\sum \limits ^{m}_{k=1}I_{A_{j}}(x)= 1$ for all $x\in W$,

• (vi) there is at most one j for which $F_{A_{j}}(x)=0$ for all $x\in W$ (there is atmost one ISVNS such that $T_{A_{j}}(x)+I_{A_{j}}(x)+F_{A_{j}}(x)=2$ for all x).

It should be noted that the conditions (iv)–(vi) are combined with the ISVNHG for ISVN partition. Along with these three conditions, an ISVN covering can be represented as an ISVNHG. Naturally, $(\eta , \phi , \psi )$-level cut can be applied to ISVN partition.

Example 3.1

Let us suppose the clustering problem as an illustrative example of an ISVN partition on the visual image processing. We take the five objects which are restricted into two classes:tank and house. To cluster these five objects $a_1, a_2, a_3, a_3, a_4, a_5$ into $A_t$ (tank) and $B_h$ (house), an ISVN partition matrix is given in Table 1 below in the form of incidence matrix of an ISVNHG.

By applying $(\eta , \phi , \psi )$-cut to the hypergraph we attain a hypergraph $\mathcal {G}_{(\eta , \phi , \psi )}$ as given in Table 2 which is not an ISVNHG. We denote the edge in $\mathcal {G}_{(\eta , \phi , \psi )}$-cut hypergraph $\mathcal {G}_{(\eta , \phi , \psi )}$ as $D_{j(\eta , \phi , \psi )}$. This hypergraph $\mathcal {G}$ represents the covering because of condition:$(iv)\sum \limits ^{m}_{j=1}T_{A_{j}}(x)= 1$ for all $x\in W$,$(v)\sum \limits ^{m}_{j=1}I_{A_{j}}(x)= 1$ for all $x\in W$ and (vi)there is at most one j for which $F_{A_{j}}(x)=0$, is not always guaranteed.

Table 1 ISVN partition matrix

Table 2 Hypergraph $\mathcal {G}_{(0.60, 0.50, 0.04)}$

Dual of the above hypergraph is given in Table 3.

Table 3 Dual of hypergraph

The clarifications for $\tilde{\eta }(D_{j(\eta , \phi , \psi )})$ are:

• The elements having at least $\tilde{\eta }$ truth value, indeterminacy value and most falsity value are grouped as an edge in the partition hypergraph $H_{(\eta , \phi , \psi )}$.

• The strength of edge $\tilde{\eta }(D_{j(\eta , \phi , \psi )})$ in $H_{(\eta , \phi , \psi )}$ is $\tilde{\eta }$. Thus, cohesion or strength of a class in a partition can be measured by the strength of edge.

  As an example, the strength of classes $A_{t(0.60, 0.50, 0.04)}$ and $B_{h(0.60, 0.50, 0.04)}$ at $\eta =0.60$, $\phi =0.50$, $\psi =0.04$ are $\tilde{\eta }(A_{t(0.56, 0.50, 0.40)})=(0.96, 0.50, 0.04)$ and $\tilde{\eta }(B_{h(0.60, 0.50, 0.04)})=(0.70, 0.50, 0.04)$, respectively. Thus, we see that the class $\tilde{\eta }(A_{t(0.60, 0.50, 0.04)})$ is stronger than $\tilde{\eta }(B_{h(0.60, 0.50, 0.04)})$ because $\tilde{\eta }_{T}{(A_{t(0.60, 0.50, 0.04)})}>\tilde{\eta }_{T}{(B_{h(0.60, 0.50, 0.04)})}$. Taking into account the above analysis on the hypergraph $H_{(0.60, 0.50, 0.04)}$ and $H^*_{(0.60, 0.50, 0.04)}$, we have:

  • 1. The ISVN partition can be represented by ISVN hypergraph, visually. The $(\eta , \phi , \psi )$-cut hypergraph also represents the $(\eta , \phi , \psi )$-cut partition.

  • 2. The dual hypergraph $H^{*}_{(0.60, 0.50, 0.04)}$ represents those elements $W_i$, which can be classified into same class $D_{j(\eta , \phi , \psi )}$. For example, the edges $W_1, W_2, W_5$ of the dual hypergraph represent that the elements $a_1, a_2, a_5$ can be grouped into $A_t$ at level (0.60, 0.50, 0.04).

  • 3. In the ISVN partition, we have $\sum \limits ^{m}_{j=1}T_{A_{j}}(x)$ = 1, $\sum \limits ^{m}_{j=1}I_{A_{j}}(x)$ = 1 for all $x\in W$ and for all $x\in W$, there is at most one j such that $F_{A_j}(x)=0$ . If we take $(\eta , \phi , \psi )$-cut at level $(\eta \ge 0.5$ or $\phi \ge 0.5$ or $\psi \le 0.5)$, no element can be grouped into two classes at the same time. That is, if $\eta \ge 0.5$ or $\phi \ge 0.5$ or $\psi \le 0.5$, distinct elements are contained in distinct classes in $H_{(\eta , \phi , \psi )}$.

  • 4. At the $(\eta , \phi , \psi )=(0.60, 0.50, 0.04$) level, $\eta (A_{t(0.60, 0.50, 0.04)})$ is strongest class as its strength is highest, i.e., (0.96, 0.50, 0.04). It means that this class can be grouped independently from other parts. Thus the class $B_h$ can be removed from other classes and continue the clustering process. In this way, the elimination of weak classes from the others can allow us to decompose a clustering problem into smaller ones. Following this strategy, we can reduce data in clustering problem.

4 Conclusions

An intuitionistic neutrosophic set is an extension of an intuitionistic fuzzy set. In several areas of computer science research such as data mining, image distribution, clustering, image capturing and networking, various theoretical ideas of graphs as well as hypergraphs are applied. The models which are based on intuitionistic neutrosophic sets are more appropriate and well-suited as compare to traditional models. In this paper we have discussed intuitionistic single-valued neutrosophic hypergraphs. We also discussed an application of intuitionistic single-valued neutrosophic hypergraphs in clustering problem. We plan to widen our research of fuzzification to (1) Interval-valued neutrosophic graphs, (2) bipolar neutrosophic hypergraphs, (3) rough neutrosophic graphs and (4) application of intuitionistic neutrosophic graphs in decision support systems.