An approach to neutrosophic graph theory with applications

Abstract

Graph theory that can be used to describe the relationships among several individuals has numerous applications in diverse fields such as modern sciences and technology, database theory, data mining, neural networks, expert systems, cluster analysis, control theory, and image capturing. As a generalization of fuzzy set (FS) and intuitionistic fuzzy set (IFS), the concept of neutrosophic set is a more functional tool for handling indeterminate, inconsistent and uncertain information that exist in real life compared to FSs and IFSs. In this paper, we apply the graph theory to the single-valued neutrosophic sets and investigate a new kind of graph structure which is called single-valued neutrosophic graphs and is generalized the results concerning crisp graphs, fuzzy graphs and intuitionistic fuzzy graphs. Then we describe some of their theoretical properties, such as the Cartesian product, composition, union and join. By applying two different procedures to solve single-valued neutrosophic decision-making problems, a neutrosophic graph-based multicriteria decision-making model is developed to consider relationships among the multi-input arguments which cannot be handled well by means of the existing methods. Finally, two illustrative examples are given to demonstrate the applicability, feasibility, effectiveness and advantages of these two proposed approaches.

1 Introduction

To deal with vagueness and uncertainty in many real-life areas, Zadeh (1965) introduced fuzzy sets (FSs) which have been a great success in different disciplines including group decision, engineering, medical diagnosis, expert systems, and pattern recognition. Atanassov (1986) added in the definition of fuzzy set a new component which determines the degree of non-membership and introduced the concept of intuitionistic fuzzy set (IFS), which is a generalization of the notion of FS. However, the FSs and IFSs face certain limitations, as they fail to present an overall description of all of the information that is relevant to the studied problems. As a generalization of the FS (Zadeh 1965) and the IFS (Atanassov 1986), Smarandache (1999) investigated the neutrosophic set (NS) which is characterized by a truth-membership function, an indeterminacy-membership function, and a falsity-membership function. To easily use in technical applications of the NSs, Wang et al. (2010) introduced single-valued neutrosophic set (SVNS), in which its membership are real numbers. Then Wang et al. (2005) generalized SVNS to uncertain situations and introduced the interval neutrosophic set (INS). In the INS, the truth membership, indeterminacy membership and falsity membership are interval numbers. SVNS and INS are very useful for describing the indeterminate, imprecise, incomplete, and inconsistent information; they have received wide attention since their appearance in the different fields (Ye 2013, 2014a, b, c, d; Peng et al. 2014, 2016, 2015; Chi and Liu 2013; Liu et al. 2014; Liu and Wang 2014; Majumdar and Samanta 2014; Biswas et al. 2016; Pramanik et al. 2017; Broumi and Smarandache 2013a, b, 2014; Şahin and Küçük 2015; Şahin and Liu 2016; Şahin 2017; Şahin and Liu 2017).

Graph theory (Berge 1976; Diestel 2006) is a very convenient tool to describe the decision-making problems. Therefore, it has numerous applications to problems in computer science, electrical engineering, system analysis, operations research, economics, networking routing, and transportation. However, in many cases, some aspects of a graph-theoretic problem may be uncertain, vague and indeterminate. Kauffman (1973) proposed the definition of a fuzzy graph based on fuzzy relations. Rosenfeld (1975) introduced the fuzzy analogue of several basic graph-theoretic concepts and Bhattacharya (1987) gave some remarks on fuzzy graphs. Mordeson and Nair (1998) studied some operations on fuzzy graphs. Sunitha and Vijayakumar (2002) proposed the definition of complement of a fuzzy graph. Some researchers studied the fuzzy graphs from different perspective Mordeson and Peng (1994), Bhutani and Rosenfeld (2003), Bhutani and Battou (2003), Akram and Dudek (2012). Shannon and Atanassov (1994) introduced the concepts of intuitionistic fuzzy relation and intuitionistic fuzzy graph and investigated some of their properties. Parvathi et al. (2009) presented the intuitionistic fuzzy hypergraphs with properties. Parvathi et al. (2009) investigated some operations on intuitionistic fuzzy graphs. Akram and Dudek (2013), Akram and Davvaz (2012), Akram et al. (2012), Akram and Alshehri (2014) introduced many new concepts including intuitionistic fuzzy hypergraphs, strong intuitionistic fuzzy graphs, intuitionistic fuzzy cycles, intuitionistic fuzzy trees, intuitionistic fuzzy bridges, intuitionistic fuzzy cut vertices, intuitionistic fuzzy cycles and intuitionistic fuzzy trees and investigated some of their interesting properties.

Most of the multicriteria decision-making (MCDM) methods with single-valued neutrosophic information are to serve a kind of problems that there exist no relationships among criteria. However, these relationships should be taken into account in the actual applications. Therefore, it is necessary to pay attention to this issue. This paper applies the graph theory to SVNSs and develops a new methodology called the neutrosophic graph-based multicriteria decision making (NGMCDM) for solving the complex problems under single-valued neutrosophic environment. The desirable characteristic of the methodology is its capability to capture the relationships among the criteria which cannot be handled well by means of the existing methods. In order to do so, the rest of the paper is organized as follows: we first introduce the notion of single-valued neutrosophic graphs as a further generalization of fuzzy graphs and intuitionistic fuzzy graphs and investigate some of their important properties. Then we define the operations of Cartesian product, composition, union and join on single-valued neutrosophic graphs. Finally, a methodology with two procedures is developed based on the single-valued neutrosophic graph, and two numerical examples are presented to illustrate how to deal with the NGMCDM problem with single-valued neutrosophic information. Some corresponding conclusions are provided in the last section.

2 Preliminaries

In the subsection, we give some concepts related to NSs and SVNSs.

2.1 Neutrosophic set

Definition 1

(Smarandache 1999) Let X be a universe of discourse, then a neutrosophic set is defined as:

$$\begin{aligned} A=\left\{ {\langle x,T_A \left( x \right) ,I_A \left( x \right) , F_A \left( x \right) \rangle :x\in X} \right\} \end{aligned}$$

which is characterized by a truth-membership function $T_A :X\rightarrow {]} {0^{-},1^{+}} [$, an indeterminacy-membership function $I_A :X\rightarrow {]} {0^{-},1^{+}} {[}$ and a falsity-membership function $F_A :X\rightarrow {]} {0^{-},1^{+}} {[}$.

There is not restriction on the sum of $T_A \left( x \right)$, $I_A \left( x \right)$ and $F_A \left( x \right)$, so $0^{-}\le \sup T_A \left( x \right) +\sup I_A \left( x \right) +\sup F_A \left( x \right) \le 3^{+}$.

In the following, it will be used the representations $t_A \left( x \right)$, $\mathscr {i}_A \left( x \right)$ and $f_A \left( x \right)$ instead of $T_A \left( x \right)$, $I_A \left( x \right)$ and $F_A \left( x \right)$, respectively.

2.2 Single-valued neutrosophic sets

Definition 2

(Wang et al. 2010) A mapping $A=\left( {t_A ,{\mathscr {i}}_A ,f_A } \right) :X\rightarrow [0,1] \times [0,1] \times [0,1]$ is called a single-valued neutrosophic set in X if $t_A \left( x \right) +\mathscr {i}_A \left( x \right) +f_A \left( x \right) \le 3$ for all $x\in X$, where the mappings $t_A :X\rightarrow [0,1]$, $\mathscr {i}_A :X\rightarrow \left[ {0,1} \right]$ and $f_A :X\rightarrow \left[ {0,1} \right]$ represent the degree of truth membership (that is, $t_A \left( x \right) )$, the degree of indeterminacy membership (that is, $\mathscr {i}_A \left( x \right) )$ and the degree of falsity membership (that is, $f_A \left( x \right) )$, of x to A, respectively.

Definition 3

(Wang et al. 2010) Let $A=\langle t_A ,\mathscr {i}_A ,f_A \rangle$ and $B=\langle t_B ,\mathscr {i}_B ,f_B \rangle$ be two single-valued neutrosophic sets. Then,

• (1) $\left( {A \cap B} \right) \left( x \right) = \left\{ \langle x,\min \left( {t_A \left( x \right) ,t_B \left( x \right) } \right) , \max \left( \mathscr {i}_A \left( x \right) ,\right. \right.$$\left. \left. \mathscr {i}_A \left( x \right) \right) ,\max \left( {f_A \left( x \right) ,f_B \left( x \right) } \right) \rangle :x\in X \right\}$;

• (2) $\left( {A\cup B} \right) \left( x \right) = \left\{ \langle x, \max \left( {t_A \left( x \right) ,t_B \left( x \right) } \right) , \min \left( \mathscr {i}_A \left( x \right) ,\right. \right.$$\left. \left. \mathscr {i}_A \left( x \right) \right) ,\min \left( {f_A \left( x \right) ,f_B \left( x \right) } \right) \rangle :x\in X \right\}$.

A single-valued neutrosophic number (SVNN) is denoted by $\alpha =\langle t,\mathscr {i},f \rangle$ for convenience.

Definition 4

(Şahin and Liu 2016) Let $\alpha =t,\mathscr {i},f$ be a SVNN. Then its score function s can be defined by

$$\begin{aligned} s\left( \alpha \right) =\frac{1+t-2\mathscr {i}-f}{2} \end{aligned}$$

(1)

where $s\left( \alpha \right) \in \left[ {-1,1} \right]$. For two SVNNs $\alpha _1$ and $\alpha _2$, if $s\left( {\alpha _1 } \right) >s\left( {\alpha _2 } \right)$, then $\alpha _1 \succ \alpha _2$.

Definition 5

Let $\alpha _1 = \langle t_1 ,\mathscr {i}_1 ,f_1 \rangle$ and $\alpha _2 = \langle t_2 ,\mathscr {i}_2 ,f_2 \rangle$ be any two single-valued neutrosophic numbers, the Hamming distance between $\alpha _1$ and $\alpha _2$ is defined as follows

$$\begin{aligned} d\left( {\alpha _1 ,\alpha _2 } \right) =\frac{1}{3}\left( {\left| {t_1 -t_2 } \right| +\left| {\mathscr {i}_1 -\mathscr {i}_2 } \right| +\left| {f_1 -f_2 } \right| } \right) . \end{aligned}$$

(2)

Then a similarity measure between $\alpha _1$ and $\alpha _2$ can be defined as $S\left( {\alpha _1 ,\alpha _2 } \right) =1-d\left( {\alpha _1 ,\alpha _2 } \right)$.

Peng et al. (2016) defined some operations for SVNNs, which can be described as follows:

Definition 6

Let $\alpha _1 =\langle t_1 ,\mathscr {i}_1 ,f_1\rangle$ and $\alpha _2 =\langle t_2 ,\mathscr {i}_2 ,f_2 \rangle$ be any two single-valued neutrosophic numbers and $\lambda >0$, then the operational laws for SVNNs are defined as below.

• (1)
  $$\begin{aligned} \lambda \alpha _1 = \langle 1-\left( {1-t_1 } \right) ^{\lambda },\lambda \mathscr {i}_1 ,\lambda f_1\rangle \end{aligned}$$

  (3)
• (2)
  $$\begin{aligned} \alpha _1 \oplus \alpha _2 = \langle t_1 +t_2 -t_1 t_2 ,\mathscr {i}_1 \mathscr {i}_2 ,f_1 f_2 \rangle \end{aligned}$$

  (4)

2.3 Some definitions in graph theory

In this section, we give some basic concepts, which will be used in the next sections.

Definition 7

(Diestel 2006) A graph is an ordered pair $G^{*}=\left( {V,E} \right)$, where V is the set of vertices of $G^{*}$ and E is the set of edges of $G^{*}$.

Two vertices x and y in an undirected graph $G^{*}$ are said to be adjacent in $G^{*}$ if $\left\{ {x,y} \right\}$ is an edge of $G^{*}$. A simple graph is an undirected graph that has no loops and no more than one edge between any two different vertices. A complete graph is a simple graph in which every pair of distinct vertices is connected by an edge. A subgraph of a graph $G^{*}=\left( {V,E} \right)$ is a graph $H^{*}=\left( {W,F} \right)$, where $W \subseteq V$ and $F\subseteq E$.

Note that there are various ways to construct new graphs from existing graphs, such as Cartesian product, union, join, composition.

Definition 8

(Diestel 2006) Let $G_1^*=\left( {V_1 ,E_1 } \right)$ and $G_2^*=\left( {V_2 ,E_2 } \right)$ be two simple graphs. Then Cartesian product of graphs $G_1^*$ and $G_2^*$ is a graph defined by $G^{*}=G_1^*\times G_2^*=\left( {V,E} \right)$ with $V=V_1 \times V_2$ and $E=\left\{ {\left( {x,x_2 } \right) \left( {x,y_2 } \right) :x\in V_1 , x_2 y_2 \in E_2 } \right\} \cup \left\{ \left( {x_1 ,z} \right) \left( {y_1 ,z} \right) :\right.$$\left. z\in V_2 , x_1 y_1 \in E_1 \right\}$.

Definition 9

(Diestel 2006) Let $G_1^*=\left( {V_1 ,E_1 } \right)$ and $G_2^*=\left( {V_2 ,E_2 } \right)$ be two simple graphs. Then, the composition of graphs $G_1^*$ and $G_2^*$ is a graph defined by $G^{*}=G_1^*\left[ {G_2^*} \right] =\left( {V_1 \times V_2 ,E^{0}} \right)$, where $E^{0}=E\cup \left\{ \left( {x_1 ,x_2 } \right) \left( {y_1 ,y_2 } \right) :x_1 y_1 \right. \left. \in E_1 , x_2 \ne y_2 \right\}$ and E is defined as in $G_1^*\times G_2^*$. Note that $G_1^*\left[ {G_2^*} \right] \ne G_2^*\left[ {G_1^*} \right]$.

Definition 10

(Diestel 2006) Let $G_1^*=\left( {V_1 ,E_1 } \right)$ and $G_2^*=\left( {V_2 ,E_2 } \right)$ be two simple graphs. Then the join of graphs $G_1^*$ and $G_2^*$ is a simple graph defined by $G^{*}=G_1^*+G_2^*=\left( {V_1 \cup V_2 ,E_1 \cup E_2 \cup {E}'} \right)$, where ${E}'$ is the set of all edges joining the nodes of $V_1$ and $V_2$, and assume that $V_1 \cap V_2 \ne \emptyset$.

Definition 11

(Diestel 2006) Let $G_1^*=\left( {V_1 ,E_1 } \right)$ and $G_2^*=\left( {V_2 ,E_2 } \right)$ be two simple graphs. Then the union of two simple graphs $G_1^*$ and $G_2^*$ is a simple graph defined by $G^{*}=G_1^*\cup G_2^*=\left( {V_1 \cup V_2 ,E_1 \cup E_2 } \right)$.

3 Single-valued neutrosophic graphs

The concept of a neutrosophic relation can be defined as follows:

Definition 12

A single-valued neutrosophic relation R in a universe $X\times Y$ is a neutrosophic set of the form

$$\begin{aligned} R\left( {x,y} \right) =\left\{ \langle \left( {x,y} \right) ,t_R \left( {x,y} \right) ,\mathscr {i}_R \left( {x,y} \right) ,f_R \left( {x,y} \right) \rangle \right. \\ \left. : \left( {x,y} \right) \in X\times Y \right\} , \end{aligned}$$

where $t_R : X\times Y\rightarrow \left[ {0,1} \right]$, $\mathscr {i}_R : X\times Y\rightarrow \left[ {0,1} \right]$ and $f_R : X\times Y\rightarrow \left[ {0,1} \right]$. The neutrosophic relation satisfies the property $t_R \left( {x,y} \right) +\mathscr {i}_R \left( {x,y} \right) +f_R \left( {x,y} \right) \le 3$ for all $x,y\in X$.

Definition 13

$A= \langle t_A ,\mathscr {i}_A ,f_A \rangle$ and $B=\langle t_B ,\mathscr {i}_B ,f_B \rangle$ be single-valued neutrosophic sets on a set X. If $A=\langle t_A ,\mathscr {i}_A ,f_A \rangle$ is a single-valued neutrosophic relation on a set X, then $A=\langle t_A ,\mathscr {i}_A ,f_A \rangle$ is called a single-valued neutrosophic relation on $B=\langle t_B ,\mathscr {i}_B ,f_B\rangle$ if

$$\begin{aligned} t_A \left( {x,y} \right)\le & {} \min \left( {t_B \left( x \right) ,t_B \left( y \right) } \right) , \mathscr {i}_A \left( {x,y} \right) \\\ge & {} \max \left( {\mathscr {i}_B \left( x \right) ,\mathscr {i}_B \left( y \right) } \right) \hbox {and } f_A \left( {x,y} \right) \\\ge & {} \max \left( {f_B \left( x \right) ,f_B \left( y \right) } \right) \end{aligned}$$

for all $x,y\in X$. A single-valued neutrosophic relation A on X is called symmetric if $t_A \left( {x,y} \right) =t_A \left( {y,x} \right)$, $\mathscr {i}_A \left( {x,y} \right) =\mathscr {i}_A \left( {y,x} \right)$ and $f_A \left( {x,y} \right) =f_A \left( {y,x} \right)$.

Throughout this paper, $G^{*}$ will be a crisp graph, and G a single-valued neutrosophic graph. Moreover, we use the notation $``xy''$ for an element $``\left( {x,y} \right) ''$ of E.

Smarandache (2015) proposed a symbolic definition of neutrosophic graphs. However, we give the following definition to apply a neutrosophic graph to a decision-making problem.

Definition 14

A single-valued neutrosophic graph of a graph $G^{*}=\left( {V,E} \right)$ is a pair $G=\left( {A,B} \right)$, where $A= \langle t_A ,\mathscr {i}_A ,f_A \rangle$ is a single-valued neutrosophic set on V and $B=\langle t_B ,\mathscr {i}_B ,f_B \rangle$ is a single-valued neutrosophic relation on E such that

$$\begin{aligned} t_B \left( {xy} \right)\le & {} \min \left( {t_A \left( x \right) , t_A \left( y \right) } \right) ,\\ \mathscr {i}_B \left( {xy} \right)\ge & {} \max \left( {\mathscr {i}_A \left( x \right) ,\mathscr {i}_A \left( y \right) } \right) \\ f_B \left( {xy} \right)\ge & {} \max \left( {v_A \left( x \right) ,v_A \left( y \right) } \right) \end{aligned}$$

and $0\le t_B \left( {xy} \right) +\mathscr {i}_B \left( {xy} \right) +f_B \left( {xy} \right) \le 3$ for all $x,y\in V$.

Then, the A is the single-valued neutrosophic vertex set of G and B is the single-valued neutrosophic edge set of G, respectively. Moreover, $G=\left( {A,B} \right)$ is a strong single-valued neutrosophic graph if

$$\begin{aligned} t_B \left( {xy} \right)= & {} \min \left( {t_A \left( x \right) ,t_A \left( y \right) } \right) , \mathscr {i}_B \left( {xy} \right) \\= & {} \max \left( {\mathscr {i}_A \left( x \right) ,\mathscr {i}_A \left( y \right) } \right) ,f_B \left( {xy} \right) \\= & {} \max \left( {f_A \left( x \right) ,f_A \left( y \right) } \right) \end{aligned}$$

such that $0\le t_B \left( {xy} \right) +\mathscr {i}_B \left( {xy} \right) +f_B \left( {xy} \right) \le 3$ for all $xy\in E$.

Here, the triple $\left( {x,t_A \left( x \right) ,\mathscr {i}_A \left( x \right) ,f_A \left( x \right) } \right)$ denotes the degree of truth membership, the degree of indeterminacy membership and the degree of falsity membership of the vertex x. The triple $\left( {xy,t_B \left( {xy} \right) ,\mathscr {i}_B \left( {xy} \right) ,f_B \left( {xy} \right) } \right)$ describes the degree of truth membership, degree of indeterminacy membership and degree of falsity membership of the edge xy.

Thus, the single-valued neutrosophic graph $G=\left( {A,B} \right)$ reduces to an intuitionistic fuzzy graph (Parvathi et al. 2009) if $\mathscr {i}_A =\emptyset$ such that $0\le t_A +f_A \le 1$, and reduces a fuzzy graph (Rosenfeld 1975) if $\mathscr {i}_A =\emptyset$ and $f_A =\emptyset$.

Example 1

Consider a graph $G^{*}=\left( {V,E} \right)$ such that $V=\left\{ {a,b,c} \right\}$, $E=\left\{ {ab,bc,ac} \right\} \subseteq V\times V$. Let $A= \langle t_A ,\mathscr {i}_A ,f_A \rangle$ be a single-valued neutrosophic subset of V and $B=\langle t_B ,\mathscr {i}_B ,f_B \rangle$ be a single-valued neutrosophic relation on $E\subseteq V\times V$ defined by

$$\begin{aligned} A= & {} \left\langle \frac{a}{{0.5,0.3,0.6}},\frac{b}{{0.4,0.2,0.5}},\frac{c}{{0.6,0.1,0.3}}\right\rangle ,\\ B= & {} \left\langle \frac{{ab}}{{0.4,0.3,0.6}},\frac{{bc}}{{0.3,0.3,0.5}},\frac{{ac}}{{0.5,0.3,0.6}}\right\rangle \end{aligned}$$

Fig. 1

The single-valued neutrosophic graph G

After routine computations, it is easy to see that $G=\left( {A,B} \right)$ is a single-valued neutrosophic graph of $G^{*}$(see Fig. 1).

Next, we give some categorical properties of the single-valued neutrosophic graphs such as Cartesian product, composition, union and so on.

Suppose that $G_1 =\left( {A_1 ,B_1 } \right)$ and $G_2 =\left( {A_2 ,B_2 } \right)$ are two single-valued neutrosophic graphs of the graphs $G_1^*=\left( {V_1 ,E_1 } \right)$ and $G_2^*=\left( {V_2 ,E_2 } \right)$, where $A_1 =\langle t_{A_1 } ,\mathscr {i}_{A_1 } ,f_{A_1 } \rangle$ and $A_2 =\langle t_{A_2 } ,\mathscr {i}_{A_2 } ,f_{A_2 } \rangle$ are two single-valued neutrosophic subsets of $V_1$ and $V_2$, and $B_1 =\langle t_{B_1 } ,\mathscr {i}_{B_1 } ,f_{B_1 } \rangle$ and $B_2 =\langle t_{B_2 } ,\mathscr {i}_{B_2 } ,f_{B_2 } \rangle$ are single-valued neutrosophic subsets of $E_1$ and $E_2$, respectively.

Definition 15

Let $G_1$ and $G_2$ are two single-valued neutrosophic graphs. Then the Cartesian product of $G_1$ and $G_2$ denoted by $G_1 \times G_2 =\left( {A_1 \times A_2 ,B_1 \times B_2 } \right)$ is defined as:

• i.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {t_{A_1 }\! \times t_{A_2 } } \right) \left( {x_1 x_2 } \right) =\min \left( {t_{A_1 } \left( {x_1 } \right) ,t_{A_2 } \left( {x_2 } \right) } \right) } \\ {\left( {\mathscr {i}_{A_1 }\! \times \! \mathscr {i}_{A_2 } } \right) \left( {x_1 x_2 } \right) \!=\!\max \left( {\mathscr {i}_{A_1 } \left( {x_1 } \right) ,\!\mathscr {i}_{A_2 } \left( {x_2 } \right) } \right) } \\ {\left( {f_{A_1 } \times f_{A_2 } } \right) \left( {x_1 x_2 } \right) =\max \left( {f_{A_1 } \left( {x_1 } \right) ,f_{A_2 } \left( {x_2 } \right) } \right) } \\ \end{array} }} \right. \,\, \left( {\left( {x_1 x_2 } \right) \!\in \! V_1 \!\times \! V_2 \!=\!V} \right) , \end{aligned}$$
• ii.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {t_{B_1 } \times t_{B_2 } } \right) \left( {\left( {xx_2 } \right) \left( {xy_2 } \right) } \right) =\min \left( {t_{A_1 } \left( x \right) ,t_{B_2 } \left( {x_2 y_2 } \right) } \right) } \\ {\left( {\mathscr {i}_{B_1 }\!\! \times \! \mathscr {i}_{B_2 } } \right) \left( {\left( {xx_2 } \right) \left( {xy_2 } \right) } \right) \!\!=\!\max \left( {\mathscr {i}_{A_1 }\!\! \left( x \right) ,\mathscr {i}_{B_2 } \left( {x_2 y_2 } \right) } \right) } \\ {\left( {f_{B_1 } \!\times \! f_{B_2 } } \right) \left( {\left( {xx_2 } \right) \left( {xy_2 } \right) } \right) \!=\!\max \left( {f_{A_1 }\!\! \left( x \right) ,f_{B_2 } \left( {x_2 y_2 } \right) } \right) } \\ \end{array} }} \right. \left( {x\!\in \! V_1 , x_2 y_2\! \in \! E_2 } \right) \!, \end{aligned}$$
• iii.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {t_{B_1 } \times t_{B_2 } } \right) \left( {\left( {x_1 z} \right) \left( {y_1 z} \right) } \right) =\min \left( {t_{B_1 } \left( {x_1 y_1 } \right) ,t_{A_2 } \left( z \right) } \right) } \\ {\left( {\mathscr {i}_{B_1 }\! \!\times \! \mathscr {i}_{B_2 } } \right) \!\left( {\left( {x_1 z} \right) \left( {y_1 z} \right) } \right) \!=\!\max \left( {\mathscr {i}_{B_1 }\! \left( {x_1 y_1 } \right) ,\mathscr {i}_{A_2 }\! \left( z \right) } \right) } \\ {\left( {f_{B_1 }\! \!\times \!f_{B_2 } } \right) \left( {\left( {x_1 z} \right) \left( {y_1 z} \right) } \right) \!=\!\max \left( {f_{B_1 } \left( {x_1 y_1 } \right) ,f_{A_2 } \left( z \right) } \right) } \\ \end{array} }} \right. \left( {z\!\in \! V_2 , x_1 y_1 \!\in \! E_1 } \right) \!. \end{aligned}$$

Proposition 1

Let $G_1$ and $G_2$ be two single-valued neutrosophic graphs. Then $G_1 \times G_2$ is a single-valued neutrosophic graph.

Proof

Let $x\in V_1 , x_2 y_2 \in E_2$. Then we have

$$\begin{aligned}&\left( {t_{B_1 } \times t_{B_2 } } \right) \left( {\left( {xx_2 } \right) \left( {xy_2 } \right) } \right) \\&\quad =\min \left( {t_{A_1 } \left( x \right) ,t_{B_2 } \left( {x_2 y_2 } \right) } \right) \\&\quad \le \min \left( {t_{A_1 } \left( x \right) ,\min \left( {t_{A_2 } \left( {x_2 } \right) ,t_{A_2 } \left( {y_2 } \right) } \right) } \right) \\&\quad =\min \left( {\min \left( {t_{A_1 } \left( x \right) ,t_{A_2 } \left( {x_2 } \right) } \right) ,\min \left( {t_{A_1 } \left( x \right) ,t_{A_2 } \left( {y_2 } \right) } \right) } \right) \\&\quad =\min \left( {\left( {t_{A_1 } \times t_{A_2 } } \right) \left( {xx_2 } \right) ,\left( {t_{A_1 } \times t_{A_2 } } \right) \left( {xy_2 } \right) } \right) ,\\&\left( {\mathscr {i}_{B_1 } \times \mathscr {i}_{B_2 } } \right) \left( {\left( {xx_2 } \right) \left( {xy_2 } \right) } \right) \\&\quad =\max \left( {\mathscr {i}_{A_1 } \left( x \right) ,\mathscr {i}_{B_2 } \left( {x_2 y_2 } \right) } \right) \\&\quad \ge \max \left( {\mathscr {i}_{A_1 } \left( x \right) ,\max \left( {\mathscr {i}_{A_2 } \left( {x_2 } \right) ,\mathscr {i}_{A_2 } \left( {y_2 } \right) } \right) } \right) \\&\quad =\max \! \left( {\max \left( {\mathscr {i}_{A_1 }\! \left( x \right) \!,\mathscr {i}_{A_2 }\! \left( {x_2 } \right) } \right) \!,\max \left( {\mathscr {i}_{A_1 }\! \left( x \right) ,\mathscr {i}_{A_2 }\! \left( {y_2 } \right) } \right) } \right) \\&\quad =\max \left( {\left( {\mathscr {i}_{A_1 } \times \mathscr {i}_{A_2 } } \right) \left( {xx_2 } \right) ,\left( {\mathscr {i}_{A_1 } \times \mathscr {i}_{A_2 } } \right) \left( {xy_2 } \right) } \right) ,\\&\left( {f_{B_1 } \times f_{B_2 } } \right) \left( {\left( {xx_2 } \right) \left( {xy_2 } \right) } \right) \\&\quad =\max \left( {f_{A_1 } \left( x \right) ,f_{B_2 } \left( {x_2 y_2 } \right) } \right) \\&\quad \ge \max \left( {f_{A_1 } \left( x \right) ,\max \left( {f_{A_2 } \left( {x_2 } \right) ,\mathscr {i}_{A_2 } \left( {y_2 } \right) } \right) } \right) \\&\quad =\max \!\left( {\max \left( {f_{A_1 }\! \left( x \right) \!,f_{A_2 } \left( {x_2 } \right) } \right) \!,\max \left( {f_{A_1 }\! \left( x \right) ,f_{A_2 }\! \left( {y_2 } \right) } \right) } \right) \\&\quad =\max \left( {\left( {f_{A_1 } \times f_{A_2 } } \right) \left( {xx_2 } \right) ,\left( {f_{A_1 } \times f_{A_2 } } \right) \left( {xy_2 } \right) } \right) , \end{aligned}$$

Let $z\in V_2 , x_1 y_1 \in E_1$. Then we have

$$\begin{aligned}&\left( {t_{B_1 } \times t_{B_2 } } \right) \left( {\left( {x_1 z} \right) \left( {y_1 z} \right) } \right) \\&\quad =\min \left( {t_{B_1 } \left( {x_1 y_1 } \right) ,t_{A_2 } \left( z \right) } \right) \\&\quad \le \min \left( {\min \left( {t_{A_1 } \left( {x_1 } \right) ,t_{A_1 } \left( {y_1 } \right) } \right) ,t_{A_2 } \left( z \right) } \right) \\&\quad =\min \left( {\min \left( {t_{A_1 } \left( {x_1 } \right) ,t_{A_2 } \left( z \right) } \right) ,\min \left( {t_{A_1 } \left( {y_1 } \right) ,t_{A_2 } \left( z \right) } \right) } \right) \\&\quad =\min \left( {\left( {t_{A_1 } \times t_{A_2 } } \right) \left( {x_1 z} \right) ,\left( {t_{A_1 } \times t_{A_2 } } \right) \left( {y_1 z} \right) } \right) ,\\&\left( {\mathscr {i}_{B_1 } \times \mathscr {i}_{B_2 } } \right) \left( {\left( {x_1 z} \right) \left( {y_1 z} \right) } \right) \\&\quad =\max \left( {\mathscr {i}_{B_1 } \left( {x_1 y_1 } \right) ,\mathscr {i}_{A_2 } \left( z \right) } \right) \\&\quad \ge \max \left( {\max \left( {\mathscr {i}_{A_1 } \left( {x_1 } \right) ,\mathscr {i}_{A_1 } \left( {y_1 } \right) } \right) ,\mathscr {i}_{A_2 } \left( z \right) } \right) \\&\quad =\max \!\left( {\max \left( {\mathscr {i}_{A_1 }\! \left( {x_1 } \right) \!,\mathscr {i}_{A_2 }\! \left( z \right) } \right) ,\max \left( {\mathscr {i}_{A_1 } \left( {y_1 } \right) \!,\mathscr {i}_{A_2 }\! \left( z \right) } \right) } \right) \\&\quad =\max \left( {\left( {\mathscr {i}_{A_1 } \times \mathscr {i}_{A_2 } } \right) \left( {x_1 z} \right) ,\left( {\mathscr {i}_{A_1 } \times \mathscr {i}_{A_2 } } \right) \left( {y_1 z} \right) } \right) ,\\&\left( {{f_{{B_1}}} \times {f_{{B_2}}}} \right) \left( {\left( {{x_1}z} \right) \left( {{y_1}z} \right) } \right) = \max \left( {{f_{{B_1}}}\left( {{x_1}{y_1}} \right) ,{f_{{A_2}}}\left( z \right) } \right) \\&\quad \ge \max \left( {\max \left( {{f_{{A_1}}}\left( {{x_1}} \right) ,{f_{{A_1}}}\left( {{y_1}} \right) } \right) ,{f_{{A_2}}}\left( z \right) } \right) \\&\quad = \max \left( {\max \left( {{f_{{A_1}}}\left( {{x_1}} \right) ,{\mathscr {i}_f}\left( z \right) } \right) ,\max \left( {{f_{{A_1}}}\left( {{y_1}} \right) ,{f_{{A_2}}}\left( z \right) } \right) } \right) \\&\quad = \max \left( {\left( {{f_{{A_1}}} \times {f_{{A_2}}}} \right) \left( {{x_1}z} \right) ,\left( {{f_{{A_1}}} \times {f_{{A_2}}}} \right) \left( {{y_1}z} \right) } \right) . \end{aligned}$$

This completes the proof. $\square$

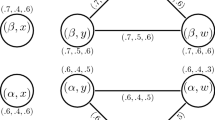
Example 2

Let $G_1^*=\left( {V_1 ,E_1 } \right)$ and $G_2^*=\left( {V_2 ,E_2 } \right)$ be two simple graphs such that $V_1 =\left\{ {a,b} \right\}$, $V_2 =\left\{ {c,d} \right\}$, $E_1 =\left\{ {ab} \right\}$ and $E_2 =\left\{ {cd} \right\}$. Consider two single-valued neutrosophic graphs $G_1 =\left( {A_1 ,B_1 } \right)$ and $G_2 =\left( {A_2 ,B_2 } \right)$, where

$$\begin{aligned} A_1= & {} \left\langle \frac{a}{\left( {0.4,0.3,0.5} \right) }, \frac{b}{\left( {0.5,0.2,0.4} \right) }\right\rangle ,\\ B_1= & {} \left\langle \frac{ab}{\left( {0.4,0.4,0.5} \right) }\right\rangle \\ A_2= & {} \left\langle \frac{c}{\left( {0.6,0.1,0.6} \right) }, \frac{d}{\left( {0.6,0.2,0.2} \right) }\right\rangle ,\\ B_2= & {} \left\langle \frac{cd}{\left( {0.5,0.3,0.6} \right) }\right\rangle \end{aligned}$$

Then we can construct the $G_1 \times G_2$ as follows.

After routine computations, it is easy to see that $G=G_1 \times G_2$ is a single-valued neutrosophic graph of $G^{*}$(see Fig. 2).

Fig. 2

The Cartesian product of $G_1$ and $G_2$

Definition 16

Let $G_1$ and $G_2$ be two single-valued neutrosophic graphs. Then the composition of two single-valued neutrosophic graphs $G_1$ and $G_2$ of $G_1^*$ and $G_2^*$ denoted by $G_1 \left[ {G_2 } \right] =\left( {A_1 \circ A_2 ,B_1 \circ B_2 } \right)$ is defined as:

• i.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {t_{A_1 } \circ t_{A_1 } } \right) \left( {x_1 x_2 } \right) =\min \left( {t_{A_1 } \left( {x_1 } \right) ,t_{A_2 } \left( {x_2 } \right) } \right) } \\ {\left( {\mathscr {i}_{A_1 } \circ \mathscr {i}_{A_1 } } \right) \left( {x_1 x_2 } \right) =\max \left( {\mathscr {i}_{A_1 } \left( {x_1 } \right) ,\mathscr {i}_{A_2 } \left( {x_2 } \right) } \right) } \\ {\left( {f_{A_1 } \circ f_{A_1 } } \right) \left( {x_1 x_2 } \right) =\max \left( {f_{A_1 } \left( {x_1 } \right) ,f_{A_2 } \left( {x_2 } \right) } \right) } \\ \end{array} }} \right. \left( {\left( {x_1 x_2 } \right) \in V} \right) , \end{aligned}$$
• ii.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {t_{B_1 } \circ t_{B_1 } } \right) \left( {\left( {xx_2 } \right) \left( {xy_2 } \right) } \right) =\min \left( {t_{A_1 } \left( x \right) ,t_{B_2 } \left( {x_2 y_2 } \right) } \right) } \\ {\left( {\mathscr {i}_{B_1 }\! \circ \! \mathscr {i}_{B_1 } } \right) \left( {\left( {xx_2 } \right) \left( {xy_2 } \right) } \right) \!=\!\max \left( {\mathscr {i}_{A_1 }\! \left( x \right) ,\!\mathscr {i}_{B_2 }\! \left( {x_2 y_2 } \right) } \right) } \\ {\left( {f_{B_1 } \circ f_{B_1 } } \right) \left( {\left( {xx_2 } \right) \left( {xy_2 } \right) } \right) \!=\!\max \left( {f_{A_1 }\! \left( x \right) ,f_{B_2 }\! \left( {x_2 y_2 } \right) } \right) } \\ \end{array} }} \right. \left( {x\!\in \! V_1 , x_2 y_2 \!\in \!E_2 } \right) \!, \end{aligned}$$
• iii.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {t_{B_1 } \circ t_{B_1 } } \right) \left( {\left( {x_1 z} \right) \left( {y_1 z} \right) } \right) =\min \left( {t_{B_1 } \left( {x_1 y_1 } \right) ,t_{A_2 } \left( z \right) } \right) } \\ {\left( {\mathscr {i}_{B_1 } \circ \mathscr {i}_{B_1 } } \right) \left( {\left( {x_1 z} \right) \left( {y_1 z} \right) } \right) \!=\!\max \left( {\mathscr {i}_{B_1 }\! \left( {x_1 y_1 } \right) ,\mathscr {i}_{A_2 }\! \left( z \right) } \right) } \\ {\left( {f_{B_1 }\! \circ f_{B_1 } } \right) \left( {\left( {x_1 z} \right) \left( {y_1 z} \right) } \right) \!=\!\max \left( {f_{B_1 } \left( {x_1 y_1 } \right) ,f_{A_2 } \left( z \right) } \right) } \\ \end{array} }} \right. \left( {z\!\in \! V_2 , x_1 y_1 \!\in \! E_1 } \right) \!, \end{aligned}$$
• iv.
  $$\begin{aligned} \left\{ {{\begin{array}{l} \left( {{t_{{B_1}}} \circ {t_{{B_1}}}} \right) \left( {\left( {{x_1}{x_2}} \right) \left( {{y_1}{y_2}} \right) } \right) \\ \quad = \min \left( {{t_{{A_2}}}\left( {{x_2}} \right) ,{t_{{A_2}}}\left( {{y_2}} \right) ,{t_{{B_1}}}\left( {{x_1}{y_1}} \right) } \right) \\ \left( {{\mathscr {i}_{{B_1}}} \circ {_{{B_1}}}} \right) \left( {\left( {{x_1}{x_2}} \right) \left( {{y_1}{y_2}} \right) } \right) \\ \quad = \max \left( {{\mathscr {i}_{{A_2}}}\left( {{x_2}} \right) ,{_{{A_2}}}\left( {{y_2}} \right) ,{\mathscr {i}_{{B_1}}}\left( {{x_1}{y_1}} \right) } \right) \\ \left( {{f_{{B_1}}} \circ {f_{{B_1}}}} \right) \left( {\left( {{x_1}{x_2}} \right) \left( {{y_1}{y_2}} \right) } \right) \\ \quad = \max \left( {{f_{{A_2}}}\left( {{x_2}} \right) ,{f_{{A_2}}}\left( {{y_2}} \right) ,{f_{{B_1}}}\left( {{x_1}{y_1}} \right) } \right) \end{array} }} \right. \left( {\left( {{x_1}{x_2}} \right) \left( {{y_1}{y_2}} \right) \in {E^0} - E} \right) , \end{aligned}$$

where $E^{0}=E\cup \left\{ {\left( {x_1 ,x_2 } \right) \left( {y_1 ,y_2 } \right) :x_1 y_1 \in E_1 , x_2 \ne y_2 } \right\}$.

Proposition 2

Let $G_1$ and $G_2$ be two single-valued neutrosophic graphs. Then $G_1 \left[ {G_2 } \right]$ is a single-valued neutrosophic graph.

Proof

Let $x\in V_1 , x_2 y_2 \in E_2$. Then we have

$$\begin{aligned}&\left( {t_{B_1 } \circ t_{B_2 } } \right) \left( {\left( {xx_2 } \right) \left( {xy_2 } \right) } \right) =\min \left( {t_{A_1 } \left( x \right) ,t_{B_2 } \left( {x_2 y_2 } \right) } \right) \\&\quad \le \min \left( {t_{A_1 } \left( x \right) ,\min \left( {t_{A_2 } \left( {x_2 } \right) ,t_{A_2 } \left( {y_2 } \right) } \right) } \right) \\&\quad =\min \left( {\min \left( {t_{A_1 } \left( x \right) ,t_{A_2 } \left( {x_2 } \right) } \right) ,\min \left( {t_{A_1 } \left( x \right) ,t_{A_2 } \left( {y_2 } \right) } \right) } \right) \\&\quad =\min \left( {\left( {t_{A_1 } \circ t_{A_2 } } \right) \left( {xx_2 } \right) ,\left( {t_{A_1 } \circ t_{A_2 } } \right) \left( {xy_2 } \right) } \right) ,\\&\left( {\mathscr {i}_{B_1 } \circ \mathscr {i}_{B_2 } } \right) \left( {\left( {xx_2 } \right) \left( {xy_2 } \right) } \right) =\max \left( {\mathscr {i}_{A_1 } \left( x \right) ,\mathscr {i}_{B_2 } \left( {x_2 y_2 } \right) } \right) \\&\quad \ge \max \left( {\mathscr {i}_{A_1 } \left( x \right) ,\max \left( {\mathscr {i}_{A_2 } \left( {x_2 } \right) ,\mathscr {i}_{A_2 } \left( {y_2 } \right) } \right) } \right) \\&\quad =\max \! \left( {\max \left( {\mathscr {i}_{A_1 }\! \left( x \right) ,\mathscr {i}_{A_2 }\! \left( {x_2 } \right) } \right) ,\max \left( {\mathscr {i}_{A_1 }\! \left( x \right) ,\mathscr {i}_{A_2 }\! \left( {y_2 } \right) } \right) } \right) \\&\quad =\max \left( {\left( {\mathscr {i}_{A_1 } \circ \mathscr {i}_{A_2 } } \right) \left( {xx_2 } \right) ,\left( {\mathscr {i}_{A_1 } \circ \mathscr {i}_{A_2 } } \right) \left( {xy_2 } \right) } \right) ,\\&\left( {f_{B_1 } \circ f_{B_2 } } \right) \left( {\left( {xx_2 } \right) \left( {xy_2 } \right) } \right) =\max \left( {f_{A_1 } \left( x \right) ,f_{B_2 } \left( {x_2 y_2 } \right) } \right) \\&\quad \ge \max \left( {f_{A_1 } \left( x \right) ,\max \left( {f_{A_2 } \left( {x_2 } \right) ,\mathscr {i}_{A_2 } \left( {y_2 } \right) } \right) } \right) \\&\quad =\max \!\left( {\max \left( {f_{A_1 }\! \left( x \right) ,f_{A_2 }\! \left( {x_2 } \right) } \right) \!,\max \left( {f_{A_1 }\! \left( x \right) \!,f_{A_2 }\! \left( {y_2 } \right) } \right) } \right) \\&\quad =\max \left( {\left( {f_{A_1 } \circ f_{A_2 } } \right) \left( {xx_2 } \right) ,\left( {f_{A_1 } \circ f_{A_2 } } \right) \left( {xy_2 } \right) } \right) ,\\ \end{aligned}$$

Let $z\in V_2 , x_1 y_1 \in E_1$. Then we have

$$\begin{aligned}&\left( {t_{B_1 } \circ t_{B_2 } } \right) \left( {\left( {x_1 z} \right) \left( {y_1 z} \right) } \right) =\min \left( {t_{B_1 } \left( {x_1 y_1 } \right) ,t_{A_2 } \left( z \right) } \right) \\&\quad \le \min \left( {\min \left( {t_{A_1 } \left( {x_1 } \right) ,t_{A_1 } \left( {y_1 } \right) } \right) ,t_{A_2 } \left( z \right) } \right) \\&\quad =\min \left( {\min \left( {t_{A_1 } \left( {x_1 } \right) ,t_{A_2 } \left( z \right) } \right) ,\min \left( {t_{A_1 } \left( {y_1 } \right) ,t_{A_2 } \left( z \right) } \right) } \right) \\&\quad =\min \left( {\left( {t_{A_1 } \circ t_{A_2 } } \right) \left( {x_1 z} \right) ,\left( {t_{A_1 } \circ t_{A_2 } } \right) \left( {y_1 z} \right) } \right) ,\\&\left( {\mathscr {i}_{B_1 } \circ \mathscr {i}_{B_2 } } \right) \left( {\left( {x_1 z} \right) \left( {y_1 z} \right) } \right) =\max \left( {\mathscr {i}_{B_1 } \left( {x_1 y_1 } \right) ,\mathscr {i}_{A_2 } \left( z \right) } \right) \\&\quad \ge \max \left( {\max \left( {\mathscr {i}_{A_1 } \left( {x_1 } \right) ,\mathscr {i}_{A_1 } \left( {y_1 } \right) } \right) ,\mathscr {i}_{A_2 } \left( z \right) } \right) \\&\quad =\max \left( {\max \!\left( {\mathscr {i}_{A_1 }\! \left( {x_1 } \right) ,\mathscr {i}_{A_2 }\! \left( z \right) } \right) \!,\max \left( {\mathscr {i}_{A_1 } \left( {y_1 } \right) ,\mathscr {i}_{A_2 } \left( z \right) } \right) } \right) \\&\quad =\max \left( {\left( {\mathscr {i}_{A_1 } \circ \mathscr {i}_{A_2 } } \right) \left( {x_1 z} \right) ,\left( {\mathscr {i}_{A_1 } \circ \mathscr {i}_{A_2 } } \right) \left( {y_1 z} \right) } \right) ,\\&\left( {f_{B_1 } \circ f_{B_2 } } \right) \left( {\left( {x_1 z} \right) \left( {y_1 z} \right) } \right) =\max \left( {f_{B_1 } \left( {x_1 y_1 } \right) ,f_{A_2 } \left( z \right) } \right) \\&\quad \ge \max \left( {\max \left( {f_{A_1 } \left( {x_1 } \right) ,f_{A_1 } \left( {y_1 } \right) } \right) ,f_{A_2 } \left( z \right) } \right) \\&\quad =\max \! \left( {\max \left( {f_{A_1 }\! \left( {x_1 } \right) \!,\mathscr {i}_f \left( z \right) } \right) ,\max \left( {f_{A_1 }\! \left( {y_1 } \right) \!,f_{A_2 } \left( z \right) } \right) } \right) \\&\quad =\max \left( {\left( {f_{A_1 } \circ f_{A_2 } } \right) \left( {x_1 z} \right) ,\left( {f_{A_1 } \circ f_{A_2 } } \right) \left( {y_1 z} \right) } \right) . \end{aligned}$$

Let $\left( {x_1 x_2 } \right) ,\left( {y_1 y_2 } \right) \in E^{0}-E$, so $x_1 y_1 \in E_1$, $x_2 \ne y_2$. Then it follows that

$$\begin{aligned}&\left( {t_{B_1 } \circ t_{B_2 } } \right) \left( {\left( {x_1 x_2 } \right) ,\left( {y_1 y_2 } \right) } \right) \\&\quad =\min \left( {t_{A_2 } \left( {x_2 } \right) ,t_{A_2 } \left( {y_2 } \right) ,t_{A_2 } \left( {x_1 y_1 } \right) } \right) \\&\quad \le \min \left( {t_{A_2 } \left( {x_2 } \right) ,t_{A_2 } \left( {y_2 } \right) ,\min \left( {t_{A_1 } \left( {x_1 } \right) ,t_{A_1 } \left( {y_1 } \right) } \right) } \right) \\&\quad =\min \left( {\min \left( {t_{A_1 }\! \left( {x_1 } \right) ,t_{A_2 }\! \left( {x_2 } \right) } \right) \!,\min \left( {t_{A_1 } \left( {y_1 } \right) ,t_{A_2 } \left( {y_2 } \right) } \right) } \right) \\&\quad =\min \left( {\left( {t_{A_1 } \circ t_{A_2 } } \right) \left( {x_1 x_2 } \right) ,\left( {t_{A_1 } \circ t_{A_2 } } \right) \left( {y_1 y_2 } \right) } \right) ,\\&\left( {\mathscr {i}_{B_1 } \circ \mathscr {i}_{B_2 } } \right) \left( {\left( {x_1 x_2 } \right) ,\left( {y_1 y_2 } \right) } \right) \\&\quad =\max \left( {\mathscr {i}_{A_2 } \left( {x_2 } \right) ,\mathscr {i}_{A_2 } \left( {y_2 } \right) ,\mathscr {i}_{A_2 } \left( {x_1 y_1 } \right) } \right) \\&\quad \ge \max \left( {\mathscr {i}_{A_2 } \left( {x_2 } \right) ,\mathscr {i}_{A_2 } \left( {y_2 } \right) ,\max \left( {\mathscr {i}_{A_1 } \left( {x_1 } \right) ,\mathscr {i}_{A_1 } \left( {y_1 } \right) } \right) } \right) \\&\quad =\max \left( {\max \left( {\mathscr {i}_{A_1 }\! \left( {x_1 } \right) \!,\mathscr {i}_{A_2 }\! \left( {x_2 } \right) } \right) \!,\max \left( {\mathscr {i}_{A_1 }\! \left( {y_1 } \right) \!,\mathscr {i}_{A_2 }\! \left( {y_2 } \right) } \right) } \right) \\&\quad =\max \left( {\left( {\mathscr {i}_{A_1 } \circ \mathscr {i}_{A_2 } } \right) \left( {x_1 x_2 } \right) ,\left( {\mathscr {i}_{A_1 } \circ \mathscr {i}_{A_2 } } \right) \left( {y_1 y_2 } \right) } \right) ,\\&\left( {f_{B_1 } \circ f_{B_2 } } \right) \left( {\left( {x_1 x_2 } \right) ,\left( {y_1 y_2 } \right) } \right) \\&\quad =\max \left( {f_{A_2 } \left( {x_2 } \right) ,f_{A_2 } \left( {y_2 } \right) ,f_{A_2 } \left( {x_1 y_1 } \right) } \right) \\&\quad \ge \max \left( {f_{A_2 } \left( {x_2 } \right) ,f_{A_2 } \left( {y_2 } \right) ,\max \left( {f_{A_1 } \left( {x_1 } \right) ,f_{A_1 } \left( {y_1 } \right) } \right) } \right) \\&\quad =\max \! \left( {\max \! \left( {f_{A_1 }\! \left( {x_1 } \right) \!,f_{A_2 }\! \left( {x_2 } \right) } \right) \!,\max \left( {f_{A_1 }\! \left( {y_1 }\! \right) \!,f_{A_2 }\! \left( {y_2 } \right) } \right) } \right) \\&\quad =\max \left( {\left( {f_{A_1 } \circ f_{A_2 } } \right) \left( {x_1 x_2 } \right) ,\left( {f_{A_1 } \circ f_{A_2 } } \right) \left( {y_1 y_2 } \right) } \right) . \end{aligned}$$

This completes the proof. $\square$

Example 3

Consider two single-valued neutrosophic graphs $G_1 =\left( {A_1 ,B_1 } \right)$ and $G_2 =\left( {A_2 ,B_2 } \right)$ given in Example 2 .

Then we can construct the $G_1 \circ G_2$ in Fig. 3.

Fig. 3

The composition product of $\hbox {G}_1$and$\hbox {G}_2$

Definition 17

Let $G_1$ and $G_2$ be two single-valued neutrosophic graphs. Then the union of single-valued neutrosophic graphs $G_1$ and $G_2$ of $G_1^*$ and $G_2^*$ denoted by $G=G_1 \cup G_2 =\left( {A_1 \cup A_2 ,B_1 \cup B_2 } \right)$ is defined as:

• i.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {t_{A_1 } \cup t_{A_2 } } \right) \left( x \right) =t_{A_1 } \left( x \right) \hbox { if } x\in V_1 \cap {\bar{V}}_2 } \\ {\left( {t_{A_1 } \cup t_{A_2 } } \right) \left( x \right) =t_{A_2 } \left( x \right) \hbox { if } x\in V_2 \cap {\bar{V}}_1 } \\ {\left( {t_{A_1 } \cup t_{A_2 } } \right) \left( x \right) =\max \left( {t_{A_1 } \left( {x_1 } \right) ,t_{A_2 } \left( {x_2 } \right) } \right) \hbox { if } x\in V_1 \cap V_2 } \\ \end{array} }} \right. \end{aligned}$$
• ii.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {\mathscr {i}_{A_1 } \cap \mathscr {i}_{A_2 } } \right) \left( x \right) =\mathscr {i}_{A_1 } \left( {x_1 } \right) \hbox { if } x\in V_1 \cap {\bar{V}}_2 } \\ {\left( {\mathscr {i}_{A_1 } \cap \mathscr {i}_{A_2 } } \right) \left( x \right) =\mathscr {i}_{A_2 } \left( {x_1 } \right) \hbox { if } x\in V_2 \cap {\bar{V}}_1 } \\ {\left( {\mathscr {i}_{A_1 } \cap \mathscr {i}_{A_2 } } \right) \left( x \right) =\min \left( {\mathscr {i}_{A_1 } \left( {x_1 } \right) ,\mathscr {i}_{A_2 } \left( {x_2 } \right) } \right) \hbox { if } x\in V_1 \cap V_2 } \\ \end{array} }} \right. \end{aligned}$$
• iii.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {f_{A_1 } \cap f_{A_2 } } \right) \left( x \right) =f_{A_1 } \left( {x_1 } \right) \hbox { if } x\in V_1 \cap {\bar{V}}_2 } \\ {\left( {f_{A_1 } \cap f_{A_2 } } \right) \left( x \right) =f_{A_2 } \left( {x_1 } \right) \hbox { if } x\in V_2 \cap {\bar{V}}_1 } \\ {\left( {f_{A_1 } \cap f_{A_2 } } \right) \left( x \right) =\min \left( {f_{A_1 } \left( {x_1 } \right) ,f_{A_2 } \left( {x_2 } \right) } \right) \hbox { if } x\in V_1 \cap V_2 } \\ \end{array} }} \right. \end{aligned}$$
• iv.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {t_{B_1 } \cup t_{B_2 } } \right) \left( {xy} \right) =t_{B_1 } \left( {xy} \right) \hbox { if } xy\in E_1 \cap {\bar{E}}_2 } \\ {\left( {t_{B_1 } \cup t_{B_2 } } \right) \left( {xy} \right) =t_{B_2 } \left( {xy} \right) \hbox { if } xy\in E_2 \cap {\bar{E}}_1 } \\ {\left( {t_{B_1 } \cup t_{B_2 } } \right) \left( {xy} \right) =\max \left( {t_{B_1 } \left( {xy} \right) ,t_{B_2 } \left( {xy} \right) } \right) \hbox { if } xy\in E_1 \cap E_2 } \\ \end{array} }} \right. \end{aligned}$$
• v.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {\mathscr {i}_{B_1 } \cap \mathscr {i}_{B_2 } } \right) \left( {xy} \right) =\mathscr {i}_{B_1 } \left( {xy} \right) \hbox { if } xy\in E_1 \cap {\bar{E}}_2 } \\ {\left( {\mathscr {i}_{B_1 } \cap \mathscr {i}_{B_2 } } \right) \left( {xy} \right) =\mathscr {i}_{B_2 } \left( {xy} \right) \hbox { if } xy\in E_2 \cap {\bar{E}}_1 } \\ {\left( {\mathscr {i}_{B_1 } \cap \mathscr {i}_{B_2 } } \right) \left( {xy} \right) =\min \left( {\mathscr {i}_{B_1 } \left( {x_1 } \right) ,\mathscr {i}_{B_2 } \left( {x_2 } \right) } \right) \hbox { if } xy\in E_1 \cap E_2 } \\ \end{array} }} \right. \end{aligned}$$
• vi.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {f_{B_1 } \cap f_{B_2 } } \right) \left( {xy} \right) =f_{B_1 } \left( {xy} \right) \hbox { if } xy\in E_1 \cap {\bar{E}}_2 } \\ {\left( {f_{B_1 } \cap f_{B_2 } } \right) \left( {xy} \right) =f_{B_2 } \left( {xy} \right) \hbox { if } xy\in E_2 \cap {\bar{E}}_1 } \\ {\left( {f_{B_1 } \cap f_{B_2 } } \right) \left( {xy} \right) =\min \left( {f_{B_1 } \left( {x_1 } \right) ,f_{B_2 } \left( {x_2 } \right) } \right) \hbox { if } xy\in E_1 \cap E_2 } \\ \end{array} }} \right. \end{aligned}$$

Fig. 4

The single-valued neutrosophic graph $G_{1}$

Example 4

Let $G_1^*=\left( {V_1 ,E_1 } \right)$ and $G_2^*=\left( {V_2 ,E_2 } \right)$ be two simple graphs such that $V_1 =\left\{ {a,b,c,d,f} \right\}$, $V_2 =\left\{ {a,b,c,e} \right\}$, $E_1 =\left\{ {ab,bc,cf,ad} \right\}$ and $E_2 =\left\{ {ab,bc,ce,be,ae} \right\}$ (see Figs.  4, 5). Consider two single-valued neutrosophic graphs $G_1 =\left( {A_1 ,B_1 } \right)$ and $G_2 =\left( {A_2 ,B_2 } \right)$, where

$$\begin{aligned} A_1= & {} \left\langle \frac{a}{\left( {0.5,0.3,0.2} \right) },\frac{b}{\left( {0.4,0.1,0.3} \right) },\frac{c}{\left( {0.2,0.4,0.5} \right) },\right. \\&\left. \frac{d}{\left( {0.3,0.2,0.2} \right) },\frac{f}{\left( {0.6,0.1,0.2} \right) },\right\rangle \\ B_1= & {} \left\langle \frac{ab}{\left( {0.4,0.3,0.3} \right) },\frac{bc}{\left( {0.2,0.4,0.5} \right) },\right. \\&\left. \frac{cf}{\left( {0.2,0.5,0.5} \right) },\frac{ad}{\left( {0.3,0.3,0.2} \right) }\right\rangle \\ A_2= & {} \left\langle \frac{a}{\left( {0.4,0.2,0.3} \right) },\frac{b}{\left( {0.5,0.3,0.2} \right) },\right. \\&\left. \frac{c}{\left( {0.6,0.4,0.4} \right) },\frac{e}{\left( {0.3,0.5,0.2} \right) },\right\rangle \\ B_2= & {} \left\langle \frac{ab}{\left( {0.4,0.3,0.3} \right) },\frac{bc}{\left( {0.5,0.4,0.4} \right) },\frac{ce}{\left( {0.3,0.5,0.4} \right) },\right. \\&\left. \frac{be}{\left( {0.3,0.5,0.2} \right) },\frac{ae}{\left( {0.3,0.5,0.3} \right) }\right\rangle \end{aligned}$$

Fig. 5

The single-valued neutrosophic graph $G_{2}$

Then we can construct the $G_1 \cup G_2$ in Fig. 6.

After routine computations, it is easy to see that $G=G_1 \cup G_2 =\left( {A_1 \cup A_2 ,B_1 \cup B_2 } \right)$ is a single-valued neutrosophic graph of $G_1^*\cup G_2^*$.

Proposition 3

Let $G_1$ and $G_2$ are two single-valued neutrosophic graphs. Then $G_1 \cup G_2$ is a single-valued neutrosophic graph.

Fig. 6

The union of $\hbox {G}_1$ and $\hbox {G}_2$

Proof

Let $xy\in E_1 \cap E_2$. Then

$$\begin{aligned}&\left( {{t_{{B_1}}} \cup {t_{{B_2}}}} \right) \left( {xy} \right) = \max \left( {{t_{{B_1}}}\left( {xy} \right) ,{t_{{B_2}}}\left( {xy} \right) } \right) \\&\quad \le \max \left( {\min \left( {{t_{{A_1}}}\left( x \right) ,{t_{{A_1}}}\left( y \right) } \right) ,\min \left( {{t_{{A_2}}}\left( x \right) ,{t_{{A_2}}}\left( y \right) } \right) } \right) \\&\quad = \min \left( {\max \left( {{t_{{A_1}}}\left( x \right) ,{t_{{A_2}}}\left( x \right) } \right) ,\max \left( {{t_{{A_1}}}\left( {{y_1}} \right) ,{t_{{A_2}}}\left( y \right) } \right) } \right) \\&\quad = \min \left( {\left( {{t_{{A_1}}} \cup {t_{{A_2}}}} \right) \left( x \right) ,\left( {{t_{{A_1}}} \cup {t_{{A_2}}}} \right) \left( y \right) } \right) ,\\&\left( {\mathscr {i}_{B_1 } \cup \mathscr {i}_{B_2 } } \right) \left( {xy} \right) =\min \left( {\mathscr {i}_{B_1 } \left( {xy} \right) ,\mathscr {i}_{B_2 } \left( {xy} \right) } \right) \\&\quad \ge \min \left( {\max \left( {\mathscr {i}_{A_1 } \left( x \right) ,\mathscr {i}_{A_1 } \left( y \right) } \right) ,\max \left( {\mathscr {i}_{A_2 } \left( x \right) ,\mathscr {i}_{A_2 } \left( y \right) } \right) } \right) \\&\quad =\max \left( {\min \left( {\mathscr {i}_{A_1 } \left( x \right) ,\mathscr {i}_{A_2 } \left( x \right) } \right) ,\min \left( {\mathscr {i}_{A_1 } \left( y \right) ,\mathscr {i}_{A_2 } \left( y \right) } \right) } \right) \\&\quad =\max \left( {\left( {\mathscr {i}_{A_1 } \cup \mathscr {i}_{A_2 } } \right) \left( x \right) ,\left( {\mathscr {i}_{A_1 } \cup \mathscr {i}_{A_2 } } \right) \left( y \right) } \right) ,\\&\left( {f_{B_1 } \cup f_{B_2 } } \right) \left( {xy} \right) =\min \left( {f_{B_1 } \left( {xy} \right) ,f_{B_2 } \left( {xy} \right) } \right) \\&\quad \ge \min \left( {\max \left( {f_{A_1 } \left( x \right) ,f_{A_1 } \left( y \right) } \right) ,\max \left( {f_{A_2 } \left( x \right) ,f_{A_2 } \left( y \right) } \right) } \right) \\&\quad =\max \left( {\min \left( {f_{A_1 } \left( x \right) ,f_{A_2 } \left( x \right) } \right) ,\min \left( {f_{A_1 } \left( y \right) ,f_{A_2 } \left( y \right) } \right) } \right) \\&\quad =\max \left( {\left( {f_{A_1 } \cup f_{A_2 } } \right) \left( x \right) ,\left( {f_{A_1 } \cup f_{A_2 } } \right) \left( y \right) } \right) , \end{aligned}$$

Similarly, let $xy\in E_1 \cap {\bar{E}}_2$. Then

$$\begin{aligned} \left( {t_{B_1 } \cup t_{B_2 } } \right) \left( {xy} \right)\le & {} \min \left( {\left( {t_{A_1 } \cup t_{A_2 } } \right) \left( x \right) ,\left( {t_{A_1 } \cup t_{A_2 } } \right) \left( y \right) } \right) ,\\ \left( {\mathscr {i}_{B_1 } \cup \mathscr {i}_{B_2 } } \right) \left( {xy} \right)\ge & {} \max \left( {\left( {\mathscr {i}_{A_1 } \cup \mathscr {i}_{A_2 } } \right) \left( x \right) ,\left( {\mathscr {i}_{A_1 } \cup \mathscr {i}_{A_2 } } \right) \left( y \right) } \right) ,\\ \left( {f_{B_1 } \cup f_{B_2 } } \right) \left( {xy} \right)\ge & {} \max \left( {\left( {f_{A_1 } \cup f_{A_2 } } \right) \left( x \right) ,\left( {f_{A_1 } \cup f_{A_2 } } \right) \left( y \right) } \right) , \end{aligned}$$

If $xy\in E_2 \cap {\bar{E}}_1$, it follows that

$$\begin{aligned} \left( {t_{B_1 } \cup t_{B_2 } } \right) \left( {xy} \right)\le & {} \min \left( {\left( {t_{A_1 } \cup t_{A_2 } } \right) \left( x \right) ,\left( {t_{A_1 } \cup t_{A_2 } } \right) \left( y \right) } \right) ,\\ \left( {\mathscr {i}_{B_1 } \cup \mathscr {i}_{B_2 } } \right) \left( {xy} \right)\ge & {} \max \left( {\left( {\mathscr {i}_{A_1 } \cup \mathscr {i}_{A_2 } } \right) \left( x \right) ,\left( {\mathscr {i}_{A_1 } \cup \mathscr {i}_{A_2 } } \right) \left( y \right) } \right) ,\\ \left( {f_{B_1 } \cup f_{B_2 } } \right) \left( {xy} \right)\ge & {} \max \left( {\left( {f_{A_1 }\! \cup f_{A_2 } } \right) \left( x \right) ,\left( {f_{A_1 }\! \cup f_{A_2 } } \right) \left( y \right) } \right) \!, \end{aligned}$$

This completes the proof. $\square$

Proposition 4

Let $\left\{ {G_i : i\in I} \right\}$ be a family of single-valued neutrosophic graphs with the underlying set V. Then $\cap \, G_i$ is a single-valued neutrosophic graph.

Proof

For any $x,y\in V$, we have that

$$\begin{aligned} \bigcap t_B \left( {xy} \right)= & {} \mathop {\inf }\limits _{i\in I} t_B \left( {xy} \right) \le \mathop {\inf }\limits _{i\in I} \min \left\{ {t_{A_i } \left( x \right) ,t_{A_i } \left( y \right) } \right\} \\= & {} \min \left\{ {\mathop {\inf }\limits _{i\in I} t_{A_i } \left( x \right) ,\mathop {\inf }\limits _{i\in I} t_{A_i } \left( y \right) } \right\} \\= & {} \min \left\{ {\cap \, t_{A_i } \left( x \right) ,\cap \,t_{A_i } \left( y \right) } \right\} ,\\ \bigcap \mathscr {i}_B \left( {xy} \right)= & {} \mathop {\sup }\limits _{i\in I} \mathscr {i}_B \left( {xy} \right) \ge \mathop {\sup }\limits _{i\in I} \max \left\{ {\mathscr {i}_{A_i } \left( x \right) ,\mathscr {i}_{A_i } \left( y \right) } \right\} \\= & {} \max \left\{ {\mathop {\sup }\limits _{i\in I} \mathscr {i}_{A_i } \left( x \right) ,\mathop {\sup }\limits _{i\in I} \mathscr {i}_{A_i } \left( y \right) } \right\} \\= & {} \max \left\{ {\cap \, \mathscr {i}_{A_i } \left( x \right) ,\cap \,\mathscr {i}_{A_i } \left( y \right) } \right\} \\ \bigcap f_B \left( {xy} \right)= & {} \mathop {\sup }\limits _{i\in I} f_B \left( {xy} \right) \ge \mathop {\sup }\limits _{i\in I} \max \left\{ {f_{A_i } \left( x \right) ,f_{A_i } \left( y \right) } \right\} \\= & {} \max \left\{ {\mathop {\sup }\limits _{i\in I} f_{A_i } \left( x \right) ,\mathop {\sup }\limits _{i\in I} f_{A_i } \left( y \right) } \right\} \\= & {} \max \left\{ {\cap \, f_{A_i } \left( x \right) ,\cap \, f_{A_i } \left( y \right) } \right\} \end{aligned}$$

Thus, $\cap \,G_i$ is a single-valued neutrosophic graph. $\square$

Definition 18

Let $G_1$ and $G_2$ be two single-valued neutrosophic graphs. Then the join of single-valued neutrosophic graphs $G_1$ and $G_2$ of the graphs $G_1^*$ and $G_2^*$ denoted by $G^{*}=G_1 +G_2 =\left( {A_1 +A_2 ,B_1 +B_2 } \right)$ is defined as:

• i.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {t_{A_1 } +t_{A_2 } } \right) \left( x \right) =\left( {t_{A_1 } \cup t_{A_2 } } \right) \left( x \right) } \\ {\left( {\mathscr {i}_{A_1 } +\mathscr {i}_{A_2 } } \right) \left( x \right) =\left( {\mathscr {i}_{A_1 } \cap \mathscr {i}_{A_2 } } \right) \left( x \right) } \\ {\left( {f_{A_1 } +f_{A_2 } } \right) \left( x \right) =\left( {f_{A_1 } \cap f_{A_2 } } \right) \left( x \right) \hbox { if } x\in V_1 \cup V_2 } \\ \end{array} }} \right. \end{aligned}$$
• ii.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {t_{B_1 } +t_{B_2 } } \right) \left( {xy} \right) =\left( {t_{B_1 } \cup t_{B_2 } } \right) \left( {xy} \right) =t_{B_1 } \left( {xy} \right) } \\ {\left( {\mathscr {i}_{B_1 } +\mathscr {i}_{B_2 } } \right) \left( {xy} \right) =\left( {\mathscr {i}_{B_1 } \cap \mathscr {i}_{B_2 } } \right) \left( {xy} \right) =\mathscr {i}_{B_1 } \left( {xy} \right) } \\ {\left( {f_{B_1 } +f_{B_2 } } \right) \left( {xy} \right) =\left( {f_{B_1 } \cap f_{B_2 } } \right) \left( {xy} \right) =f_{B_1 } \left( {xy} \right) \hbox { if } xy\in E_1 \cap E_2 } \\ \end{array} }} \right. \end{aligned}$$
• iii.
  $$\begin{aligned} \left\{ {{\begin{array}{l} {\left( {t_{B_1 } +t_{B_2 } } \right) \left( {xy} \right) =\max \left( {t_{A_1 } \left( x \right) ,t_{A_2 } \left( x \right) } \right) } \\ {\left( {\mathscr {i}_{B_1 } +\mathscr {i}_{B_2 } } \right) \left( {xy} \right) =\min \left( {\mathscr {i}_{A_1 } \left( x \right) ,\mathscr {i}_{A_2 } \left( x \right) } \right) } \\ {\left( {f_{B_1 }\! +\!f_{B_2 } } \right) \left( {xy} \right) =\min \left( {f_{A_1 } \left( x \right) ,f_{A_2 } \left( x \right) } \right) \hbox { If }xy\in \! {E}^{\prime }}\!, \\ \end{array} }} \right. \end{aligned}$$

where $E^{\prime }$ is the set of all edges joining the nodes of $V_1$ and $V_2$.

Proposition 5

Let $G_1$ and $G_2$ are two single-valued neutrosophic graphs. Then $G_1 +G_2$ is a single-valued neutrosophic graph.

Proof

It is carried out analogous manner to other propositions. $\square$

4 Neutrosophic graph-based multicriteria decision making (NGMCDM)

The single-valued neutrosophic set proposed by Wang et al. (2010) is characterized by the truth membership, the indeterminacy membership and the falsity membership independently, which is a powerful tool to deal with incomplete, indeterminate and inconsistent information. Recently, the single-valued neutrosophic sets have become an interesting research topic and attracted widely attentions. Therefore, the single-valued neutrosophic graph can well describe the uncertainly in real-life word. Here, we apply the graph theory to decision-making problems with single-valued neutrosophic information and then develop two new procedures.

Suppose that $P=\left\{ {p_1 ,p_2 ,\ldots ,p_m } \right\}$ is a set of alternatives, $B=\left\{ {\alpha _1 ,\alpha _2 ,\ldots ,\alpha _n } \right\}$ is the set of criteria, and $\omega =\left( {\omega _1 ,\omega _2 ,\ldots \omega _n } \right) ^{T}$ be the potential weighting vector of the criterion $\alpha _j \left( {j=1,2,\ldots ,n} \right)$, where $\omega _j \ge 0$, $j=1,2,\ldots ,n$, $\mathop \sum \limits _{j=1}^n \omega _j =1$. If the decision maker provide a single-valued neutrosophic value for the alternative $p_k \left( {k=1,2,\ldots ,m} \right)$ under the attribute $\alpha _j \left( {j=1,2,\ldots ,n} \right)$, it can be characterized by a single-valued neutrosophic number (SVNN) $d_{kj} =\left\{ {t_{kj} ,\mathscr {i}_{kj} ,f_{kj} } \right\} \quad \left( {j=1,2,\ldots ,n;k=1,2,\ldots ,m} \right)$. Assume that $D=\left[ {d_{kj} } \right] _{m\times n}$ is the decision matrix, where $d_{kj}$ is expressed by SVNN. If there exists a neutrosophic relation between two criteria $\alpha _i = \langle t_i ,\mathscr {i}_i ,f_i \rangle$ and $\alpha _j =\langle t_j ,\mathscr {i}_j ,f_j \rangle$, we denote the neutrosophic relation as $e_{ij} =\left\{ {t_{ij} ,\mathscr {i}_{ij} ,f_{ij} } \right\}$ with the properties $t_{ij} \le \min \left( {t_i ,t_j } \right)$, $\mathscr {i}_{ij} \ge \max \left( {\mathscr {i}_i ,\mathscr {i}_j } \right)$ and $f_{ij} \ge \max \left( {f_i ,f_j } \right) \left( {i,j=1,2,\ldots ,m} \right)$; otherwise, $e_{ij} = \langle 0,1,1 \rangle$.

On the basis of the developed graph structure, two procedures are developed to solve neutrosophic decision-making problems with single-valued neutrosophic information, which involve the following steps:

Procedure 1

• Step 1.Compute the influence coefficient between the criteria $\alpha _i$and $\alpha _j \quad \left( {i,j=1,2,\ldots ,n} \right)$in decision process by

  $$\begin{aligned} {\xi _{ij}} = \frac{{{t_{ij}} + \left( {1 - {\mathscr {i}_{ij}}} \right) \left( {1 - {f_{ij}}} \right) }}{3}, \end{aligned}$$

  (5)

  where $e_{ij} = \langle t_{ij} ,\mathscr {i}_{ij} ,f_{ij} \rangle$is the single-valued neutrosophic edge between the vertexes $\alpha _i$and $\alpha _j \left( i,j=1,2,\right.$$\left. \ldots ,n \right)$. We have $\xi _{ij} =1$and $\xi _{ij} =\xi _{ji}$, for $i=j$.

• Step 2.Obtain the overall criterion value of the alternative $p_k \left( {k=1,2,\ldots ,m} \right)$by

  $$\begin{aligned} {{\tilde{p}}_k} = \left\langle {{\tilde{t}}_k}, {{\tilde{\mathscr {i}}}_k},{{\tilde{f}}_k}\right\rangle = \left\langle \mathop \sum \limits _{j = 1}^n {\omega _j}\left( {\mathop \sum \limits _{s = 1}^n {\xi _{sj}}{d_{ks}}} \right) \right\rangle \end{aligned}$$

  (6)

  where $e_{sj} = \langle t_{sj} ,\mathscr {i}_{sj} ,f_{sj}\rangle$is clearly a SVNN and $\omega =\left( {\omega _1 ,\omega _2 ,\ldots \omega _n } \right) ^{T}$is the potential weighting vector of the criteria$\alpha _j \left( {j=1,2,\ldots ,n} \right)$, where $\omega _j \ge 0$, $j=1,2,\ldots ,n$, $\mathop \sum \nolimits _{j=1}^n \omega _j =1$.

• Step 3. Compute the score value of the alternative ${\tilde{p}}_k \left( {k=1,2,\ldots ,m} \right)$ by

  $$\begin{aligned} s\left( {{\tilde{p}}_k } \right) = \frac{1+{\tilde{t}}_k -2\tilde{\mathscr {i}}_k - {\tilde{f}}_k }{2} \end{aligned}$$

  (7)

• Step 4. Rank all the alternatives $p_k \left( {k=1,2,\ldots ,m} \right)$ and select the best one(s) in accordance with $s\left( {{\tilde{p}}_k } \right)$

• Step 5.End.

Procedure 2

Suppose that $p=\langle t_j ,\mathscr {i}_j ,f_j \rangle \left( {j=1,2,\ldots ,n} \right)$ is a decision solution. Here, the approach developed is based on the neutrosophic graph, and the similarity measure between SVNNs. Its advantage is that it can capture the relationships among multi-input arguments via the graph approach.

• Step 1. It is the same as step1 in Procedure1.

• Step 2.Obtain the associated weighted values of criterion $\alpha _j \left( {j=1,2,\ldots ,n} \right)$over other criteria by

  $$\begin{aligned} {\tilde{d}}_{kj} = \left\langle {{\tilde{t}}_{kj}},{{\tilde{\mathscr {i}}}_{kj}}, {{\tilde{f}}_{kj}}\right\rangle = \left\langle {\omega _j} \left( {\mathop \sum \limits _{s = 1}^n {\xi _{sj}}{d_{ks}}} \right) \right\rangle , \end{aligned}$$

  (8)

  where $e_{sj} =\langle t_{sj} ,\mathscr {i}_{sj} ,f_{sj} \rangle$is clearly a SVNN and $\omega =\left( {\omega _1 ,\omega _2 ,\ldots \omega _n } \right) ^{T}$is the potential weighting vector of the criterion $\alpha _j \left( {j=1,2,\ldots ,n} \right)$, where $\omega _j \ge 0$, $j=1,2,\ldots ,n$, $\mathop \sum \limits _{j=1}^n \omega _j =1$.

• Step 3. Use the similarity measure between the decision solution $p=\left\{ {\langle t_j ,\mathscr {i}_j ,f_j\rangle :j=1,2,\ldots ,n} \right\}$ and each alternative $p_k \left( {k=1,2,\ldots ,m} \right)$ as follows:

  $$\begin{aligned} S\left( {p,p_k } \right)= & {} 1-\frac{1}{3n}\mathop \sum \limits _{j=1}^n \left| {t_j -{\tilde{t}}_{kj} } \right| \nonumber \\&+\left| {\mathscr {i}_j -{\tilde{\mathscr {i}}}_{kj} } \right| +\left| {f_j -f_{kj} } \right| . \end{aligned}$$

  (9)

• Step 4.Determine the ranking order of all alternatives according to $S\left( {p,p_k } \right) \left( {k=1,2,\ldots ,m} \right)$.

• Step5.End.

5 Numerical example

In this section, an example for a NGMCDM problem with single-valued neutrosophic information are used to demonstrate the application of the proposed decision-making method.

Let us consider a decision-making problem adapted from Peng et al. (2016).

Example 5

Suppose that an investment company that wants to invest a sum of money in the best option. There is a panel with four possible alternatives in which to invest the money: (1) $p_1$ is a car company, (2) $p_2$ is a food company, (3) $p_3$ is a computer company, and (4) $p_4$ is an arms company. The investment company must make a decision according to the three criterions: (1) $\alpha _1$ is the risk analysis; (2) $\alpha _2$ is the growth analysis, and (3) $\alpha _3$ is the environmental impact analysis. Then, the weight vector of the criteria is given by ${\upomega }=\left( {0.35,0.25,0.40} \right)$. The four possible alternatives are to be evaluated under these three criterions and are presented in the form of single-valued neutrosophic information by decision maker according to three criterions $\alpha _j \left( {j=1,2,3} \right)$, and the evaluation information on the alternative $p_k \left( {k=1,2,3,4} \right)$ under the factors $\alpha _j \left( {j=1,2,3} \right)$ can be shown in the following single-valued neutrosophic decision matrix D:

$$\begin{aligned} D=\left[ {{\begin{array}{lll} \langle {0.4,0.2,0.3}\rangle &{} \langle {0.4,0.2,0.3} \rangle &{} \langle {0.2,0.2,0.5}\rangle \\ \langle {0.6,0.1,0.3}\rangle &{} \langle {0.6,0.1,0.2}\rangle &{} \langle {0.5,0.2,0.2}\rangle \\ \langle {0.3,0.2,0.3}\rangle &{} \langle {0.5,0.2,0.3}\rangle &{} \langle {0.5,0.3,0.2}\rangle \\ \langle {0.7,0.0,0.1} \rangle &{} \langle {0.6,0.1,0.2}\rangle &{} \langle {0.4,0.3,0.2}\rangle \\ \end{array} }} \right] \end{aligned}$$

Moreover, we assume that the relationships among the criteria $\alpha _{j}(j=1,2,3)$ can be described by a complete graph $G=(A,E)$, where $A=\{\alpha _{1}, \alpha _{2}, \alpha _{3}\}$ and $E=\{\alpha _{1} \alpha _{2}, \alpha _{1} \alpha _{3}, \alpha _{2} \alpha _{3}\}$ (see Fig. 7). By Eq. (5), we can obtain all influence coefficients to quantify the relationships among the criteria.

Suppose that the neutrosophic edges denoting the connection among the criteria is described as follows:

$$\begin{aligned} {e_{12}} = \langle {t_{12}},{\mathscr {i}_{12}},{f_{12}}\rangle = \langle 0.3,0.3,0.4\rangle \\ {e_{13}} = \langle {t_{13}},{\mathscr {i}_{13}},{f_{13}}\rangle = \langle 0.2,0.4,0.5\rangle \\ {e_{23}} = \langle {t_{23}},{\mathscr {i}_{23}},{f_{23}}\rangle = \langle 0.2,0.3,0.6\rangle . \end{aligned}$$

Fig. 7

The graph relationships among the criteria

Note that $G=\left( {A,E} \right)$ describes a single-valued neutrosophic graph according to the relationship among criteria for each alternatives

To get the best alternative(s), the following steps are involved:

• Step1. We apply only all computations in the alternative $p_1$. Others can be similarly proved.

  The influence coefficients between criteria $\alpha _j \left( {j\!=\!1,2,3} \right)$ were computed as follows:

  $$\begin{aligned} {\upxi }_{12}= & {} \frac{\hbox {t}_{12} +\left( {1-\mathscr {i}_{12} } \right) \left( {1-f_{12} } \right) }{3}\\= & {} \frac{0.3+\left( {1-0.3} \right) \left( {1-0.4} \right) }{3}=0.240,\\ {\upxi }_{13}= & {} \frac{\hbox {t}_{13} +\left( {1-\mathscr {i}_{13} } \right) \left( {1-f_{13} } \right) }{3}\\= & {} \frac{0.2+\left( {1-0.4} \right) \left( {1-0.5} \right) }{3}=0.166,\\ {\upxi }_{23}= & {} \frac{\hbox {t}_{23} +\left( {1-\mathscr {i}_{23} } \right) \left( {1-f_{23} } \right) }{3}\\= & {} \frac{0.2+\left( {1-0.3} \right) \left( {1-0.6} \right) }{3}=0.160. \end{aligned}$$

• Step 2. The overall criterion value of the alternative $p_1$ was obtained as follows:

  $$\begin{aligned} {\tilde{p}}_1= & {} {\upomega }_1 \times (\xi _{11} d_{11} +\xi _{21} d_{12} +\xi _{31} d_{13} )\\&+{\upomega }_2 \times (\xi _{12} d_{11} +\xi _{22} d_{12} +\xi _{32} d_{13} )\\&+{\upomega }_3 \times (\xi _{13} d_{11} +\xi _{23} d_{12} +\xi _{33} d_{13} )\\= & {} 0.35\times \left( \langle 0.4,0.2,0.3\rangle +0.240 \times \langle 0.4,0.2,0.3\rangle \right. \\&\left. +0.166\times \langle 0.2,0.2,0.5\rangle \right) \\&+0.25\times \left( 0.240\times \langle 0.4,0.2,0.3\rangle \right. \\&\left. +\langle 0.4,0.2,0.3\rangle +0.160\times \langle 0.2,0.2,0.5\rangle \right) \\&+0.40\times \left( 0.166\times \langle 0.4,0.2,0.3\rangle \right. \\&\left. +0.160\times \langle 0.4,0.2,0.3\rangle +\langle 0.2,0.2,0.5\rangle \right) \\= & {} \langle 0.4275,0.1098,0.2470\rangle \end{aligned}$$

  Similarly, ${\tilde{p}}_2 =\langle 0.6822,0.0599, 0.1098\rangle$, ${\tilde{p}}_3 =\langle 0.5466,$$0.1345, 0.1565\rangle$ and ${\tilde{p}}_4 =\langle 0.6966,0.000, 0.0789\rangle$.

• Step 3. The score value of ${\tilde{p}}_1$ was computed as follows:

  $$\begin{aligned} s\left( {{\tilde{p}}_1 } \right)= & {} \frac{1+{\tilde{t}}_1 -2{\tilde{\mathscr {i}}}_1 -{\tilde{f}}_1 }{2}\\= & {} \frac{1+0.4275-2\times 0.1098-0.2470}{2}=0.4804. \end{aligned}$$

  Similarly, it follows that $\hbox {s}\left( {\tilde{\alpha } _2 } \right) =0.7263,\hbox {s}\left( {{\tilde{p}}_3 } \right) =0.5607$ and $\hbox {s}\left( {{\tilde{p}}_4 } \right) =0.8088$.

• Step 4. Thus, we rank these alternatives as: $p_4 \succ p_2 \succ p_3 \succ p_1$.

Table 1 Characteristic values of the considered diseases

From the above numerical results, we say that the alternative $p_4$ is the ideal alternative in the decision-making problem. Note that the ranking is the same as Peng et al. (2016). Then, the above example shows that this kind of developed method is well suitable for single-valued neutrosophic information and is a useful technical that provides a different perspective than others for neutrosophic environment.

In the following example, we will also discuss the medical diagnosis problem in Ye (2015). Actually, this is also a pattern recognition problem.

Example 6

Assume that a set of diagnoses and a set of symptoms are given as follows, respectively

$$\begin{aligned} P= & {} \left\{ p_1 \left( {\hbox {viral fever}} \right) , p_2 \left( {\hbox {malaria}} \right) ,\right. \\&\left. p_3 \left( {\hbox {typhoid}} \right) , p_4 \left( {\hbox {gastritis}} \right) , p_5 \left( {\hbox {stenocardia}} \right) \right\} ,\\ R= & {} \left\{ r_1 \left( {\hbox {fever}} \right) , r_2 \left( {\hbox {headache}} \right) ,\right. \\&\left. r_3 \left( {\hbox {stomach pain}} \right) , r_4 \left( {\hbox {cough}} \right) ,r_5 \left( {\hbox {chest pain}} \right) \right\} . \end{aligned}$$

Suppose that the weight vector of symptoms is ${\upomega }=\left( {0.25,0.15,0.10,0.20,0.30} \right)$.

In addition, the performance values of the considered diseases are characterized by the form of SVNSs and this results are listed in Table 1.

A sample from a patient $\hbox {p}$ with all the symptoms is represented by the following SVN information:

$$\begin{aligned} p= & {} \left\{ \langle r_1 ,0.8,0.2,0.1\rangle ,\langle r_2 ,0.6,0.3,0.1\rangle ,\langle r_3 ,0.2,0.1,0.8\rangle ,\right. \\&\left. \langle r_4 ,0.6,0.5,0.1\rangle ,\langle r_5 ,0.1,0.4,0.6\rangle \right\} . \end{aligned}$$

Suppose that the neutrosophic edges denoting the connection among the symptoms (see Fig. 8) are described as follows:

$$\begin{aligned} {e_{12}} = \langle {t_{12}},{\mathscr {i}_{12}},{f_{12}}\rangle = \langle 0.1,0.6,0.8 \rangle \\ {e_{13}} = \langle {t_{13}},{\mathscr {i}_{13}},{f_{13}}\rangle = \langle 0.0,0.6,0.8 \rangle \\ {e_{14}} = \langle {t_{13}},{\mathscr {i}_{13}},{f_{13}}\rangle = \langle 0.1,0.7,0.9 \rangle \\ {e_{15}} = \langle {t_{13}},{\mathscr {i}_{13}},{f_{13}}\rangle = \langle 0.1,0.6,0.9 \rangle \\ {e_{23}} = \langle {t_{23}},{\mathscr {i}_{23}},{f_{23}}\rangle = \langle 0.0,0.5,0.9 \rangle \\ {e_{24}} = \langle {t_{13}},{\mathscr {i}_{13}},{f_{13}}\rangle = \langle 0.0,0.6,0.8 \rangle \\ {e_{25}} = \langle {t_{13}},{\mathscr {i}_{13}},{f_{13}}\rangle = \langle 0.0,0.4,0.9 \rangle \\ {e_{34}} = \langle {t_{13}},{\mathscr {i}_{13}},{f_{13}}\rangle = \langle 0.0,0.5,0.9 \rangle \\ {e_{35}} = \langle {t_{13}},{\mathscr {i}_{13}},{f_{13}}\rangle = \langle 0.0,0.3,0.9 \rangle \\ {e_{45}} = \langle {t_{13}},{\mathscr {i}_{13}},{f_{13}}\rangle = \langle 0.1,0.5,0.9 \rangle \end{aligned}$$

Fig. 8

The graph relationships among the criteria

The influence coefficients between symptoms are computed as follows:

$$\begin{aligned} {\upxi }_{12}= & {} \frac{\hbox {t}_{12} +\left( {1-\mathscr {i}_{12} } \right) \left( {1-f_{12} } \right) }{3}\\= & {} \frac{0.1+\left( {1-0.6} \right) \left( {1-0.8} \right) }{3}=0.060. \end{aligned}$$

Similarly,

$$\begin{aligned} {\upxi }_{13}= & {} 0.027,{\upxi }_{14} =0.043, {\upxi }_{15} =0.047, {\upxi }_{23} =0.017\\ {\upxi }_{24}= & {} 0.027,{\upxi }_{25} =0.020 {\upxi }_{34} =0.017,{\upxi }_{35} =0.023,\\ {\upxi }_{45}= & {} 0.050. \end{aligned}$$

Then the associated weighted values of diseases are obtained by

$$\begin{aligned} {\tilde{d}}_{kj} ={\upomega }_j \left( {\mathop \sum \limits _{s=1}^n \xi _{sj} d_{ks} } \right) , \end{aligned}$$

where ${\tilde{d}}_{kj} = \langle {\tilde{t}}_{kj} ,{\tilde{\mathscr {i}}}_{kj} ,{\tilde{f}}_{kj} \rangle$ is a SVNN. For example,

$$\begin{aligned} {\tilde{d}}_{11}= & {} {\upomega }_1 \times (\xi _{11} d_{11} +\xi _{12} d_{12}\\&+\xi _{13} d_{13} +\xi _{14} d_{14} +\xi _{15} d_{15} )\\= & {} 0.25\times \left( \langle 0.4,0.6,0.0 \rangle \right. \\&+0.060 \times \langle 0.6,0.3,0.1\rangle +0.027\times \langle 0.6,0.3,0.1\rangle \\&+0.043\times \langle 0.7,0.3,0.3\rangle +0.047\\&\left. \times \langle 0.4,0.4,0.5\rangle \right) =\langle 0.131,0.826,0.000\rangle . \end{aligned}$$

So, the results obtained are given in Table 2.

Table 2 The associated weighted values of diseases

By Eq. (8), the similarity measures between the ideal solution p and each diseases $p_k \left( {k=1,2,3,4,5} \right)$ are calculated as follows:

$$\begin{aligned} S\left( {p,p_1 } \right)= & {} 1-d\left( {p,p_1 } \right) =0.602,\\ S\left( {p,p_2 } \right)= & {} 1-d\left( {p,p_2 } \right) =0.609,\\ S\left( {p,p_3 } \right)= & {} 1-d\left( {p,p_3 } \right) =0.607,\\ S\left( {p,p_4 } \right)= & {} 1-d\left( {p,p_4 } \right) =0.631,\\ S\left( {p,p_5 } \right)= & {} 1-d\left( {p,p_5 } \right) =0.568. \end{aligned}$$

Then, the patient p can be assigned to the diagnosis $p_4 \left( {\hbox {gastritis}} \right)$ according to the recognition principle. The result is not the same as the one obtained in Ye (2015). The reason for this difference is that the developed method not only considers the relationships among the symptoms but also involves their weight information in the process. This can directly affect the decision process and change the final results. Therefore, the result obtained by Ye (2015) is not always reliable. Then the final result obtained by the proposed approach is more conclusive than one produced by Ye (2015), and it is evident that the proposed approach is accurate and reliable for solving the single-valued neutrosophic decision-making problems.

6 Conclusions

The single-valued neutrosophic sets are a generalization of Zadeh’s fuzzy set theory (Zadeh 1965) and Atanassov’s intuitionistic fuzzy set theory (Atanassov 1986). So, the single-valued neutrosophic models give more precision, flexibility and compatibility to the system as compare to the classic and fuzzy models. Moreover, graph theory has been applied widely in various areas of engineering, computer science, database theory, expert systems, neural networks, artificial intelligence, signal processing, pattern recognition, robotics, computer networks, and medical diagnosis. In this study, the information carried by the truth-membership degree, indeterminacy-membership degree and the falsity-membership degree in SVNSs was considered as a graph representation with the two elements, and the single-valued neutrosophic graphs with their properties were defined. Then, some technical operators to derive new graphs were discussed, which are the Cartesian product, composition, intersection, join, and union. Finally, considering the important of relationships among criteria in decision process, two new procedures based on the single-valued neutrosophic graph were developed to solve complex problems with the single-valued neutrosophic information. Finally, two numerical examples was presented to illustrate how to deal with the NGMCDM problems under single-valued neutrosophic environment.