Introduction

There are quite a few innovative concepts in optical solitons that have encapsulated the field of nonlinear optics [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. These ideas range from fiber Bragg gratings [5, 11] when chromatic dispersion runs low, highly dispersive optical solitons [7, 19], pure–cubic optical solitons [17], pure–quartic optical solitons [4], cubic–quartic (CQ) optical solitons [3, 6, 16], Kudryashov’s law of refractive index [9,10,11,12,13], generalized Kudryashov’s law of refractive index [8]. This paper is an infusion of two such concepts to formulate a model that is with CQ optical solitons modeled by generalized Kudryashov’s equation (GKE). In the past, CQ solitons with Kudryashov’s equation (KE) have been studied and its conservation laws have been reported as well [3]. This paper addresses CQ–GKE by the aid of three innovative integration schemes, and they are Riccati equation method, F-expansion scheme and the exp-expansion method. These algorithms retrieve bright, dark and singular soliton solutions as well as a couple of forms for combo optical solitons. The paper closes with a list of conserved quantities that are recovered. The details are enumerated in the rest of the paper, once the model is introduced with the inclusion of perturbation terms that are all of Hamiltonian type and appear with maximum intensity.

Governing model

The cubic–quartic generalized Kudryashov’s equation (CQ–GKE) with the perturbation terms is [3]:

$$\begin{aligned}&iq_{t}+iaq_{xxx}+bq_{xxxx}\nonumber \\&\qquad +\,\left( \frac{c_{1}}{\left| q\right| ^{4n}}\right. \nonumber \\&\left. \qquad +\,\frac{c_{2}}{\left| q\right| ^{3n}}+\frac{c_{3}}{\left| q\right| ^{2n}}\right. \nonumber \\&\left. \qquad +\,\frac{c_{4}}{\left| q\right| ^{n}} +c_{5}\left| q\right| ^{n}+c_{6}\left| q\right| ^{2n}\right. \nonumber \\&\left. \quad +\,c_{7}\left| q\right| ^{3n}+c_{8}\left| q\right| ^{4n}\right) q\nonumber \\&\quad = i\left[ \lambda \left( \left| q\right| ^{2m}q\right) _{x}+\theta \left( \left| q\right| ^{2m}\right) _{x}q+\mu \left| q\right| ^{2m}q_{x}\right] . \end{aligned}$$
(1)

In (1), the independent variables are spatial x and temporal t, while the dependent variable is \(q\left( x,t\right)\) that represents the complex valued wave profile. Next, a is the coefficient of third–order dispersion (3OD), b is the coefficient of fourth–order dispersion (4OD), and \(i=\sqrt{-1}\). The constants \(c_{j}\) for \(1\le j\le 8\) are the coefficient of nonlinearity effects. Then, \(\lambda\) represents self–steepening term, while \(\theta\) and \(\mu\) are the coefficients of higher–order dispersion and nonlinear dispersion. Finally, m represents maximum intensity and n is the power nonlinearity parameter which is in the range \(0<n<1/2.\) It must be noted that the parameter m is not unbounded. Its bounds are determined by Benjamin–Feir stability analysis and is a whole different project by itself which is on the bucket list for now.

Mathematical analysis

The starting point for decomposing the governing equation into real and imaginary parts is:

$$\begin{aligned} q(x,t)=U(\xi )\mathrm{e}^{i\varphi (x,t)} \end{aligned}$$
(2)

where

$$\begin{aligned} \xi =x-vt \end{aligned}$$
(3)

and v is the speed of the wave. From the phase component,

$$\begin{aligned} \varphi (x,t)=-\kappa x+\omega t+\zeta \end{aligned}$$
(4)

where \(\kappa\), \(\omega\), \(\zeta\) stand for the frequency, wave number and phase center, respectively. Insert (2) into (1). Real part yields

$$\begin{aligned}&bU^{\prime \prime \prime \prime }+3\kappa \left( a-2b{\kappa }\right) U^{\prime \prime }-\left( \omega +a{\kappa }^{3}-b{\kappa }^{4}\right) U\nonumber \\&\quad +\,c_{{ 1}}U^{1-4\,n}+c_{{2}}U^{1-3\,n}+c_{{3}}U^{1-2\,n} \nonumber \\&\quad +\,c_{{4}}U^{1-n}+c_{{5}}U^{1+n}+c_{{6}}U^{1+2\,n}+c_{{7}}U^{1+3\,n}\nonumber \\&\quad +\,c_{{8}}U^{1+4\,n}-\kappa \left( \mu +\lambda \right) U^{1+2\,m}=0, \end{aligned}$$
(5)

while imaginary part causes

$$\begin{aligned}&\left( a-4b\kappa \right) U^{\prime \prime \prime }+\left( 4b{\kappa }^{3}-3a {\kappa }^{2}-v\right) U^{\prime }\nonumber \\&\quad -\,\left( \lambda +\mu +2\theta m+2\lambda m\right) U^{\prime }U^{2\,m}=0 . \end{aligned}$$
(6)

Form Eq. (6), the constraint conditions are recovered as

$$\begin{aligned} a=4b\kappa \end{aligned}$$
(7)
$$\begin{aligned} \lambda +\mu +2\theta m+2\lambda m=0 \end{aligned}$$
(8)

and then the velocity is

$$\begin{aligned} v=-8b{\kappa }^{3} . \end{aligned}$$
(9)

So, the real part equation given by (5) turns into

$$\begin{aligned}&bU^{\prime \prime \prime \prime }+6b\kappa ^{2}U^{\prime \prime }\nonumber \\&\quad -\,\left( \omega +3b{\kappa }^{4}\right) U+c_{{1}}U^{1-4\,n}\nonumber \\&\quad +\,c_{{2}}U^{1-3\,n}+c_{{3} }U^{1-2\,n}+c_{{4}}U^{1-n} \nonumber \\&\quad +\,c_{{5}}U^{1+n}+c_{{6}}U^{1+2\,n}+c_{{7}}U^{1+3\,n}+c_{{8}}U^{1+4\,n}\nonumber \\&\quad -\,\kappa \left( \mu +\lambda \right) U^{1+2\,m}=0. \end{aligned}$$
(10)

By virtue of the transformation \(U=Q^{\frac{1}{n}}\), Eq. (10) changes to

$$\begin{aligned}&b\left( \begin{array}{c} \left( 1-n\right) \left( 1-2n\right) \left( 1-3n\right) \left( Q^{\prime }\right) ^{4}\\ +6n\left( 1-n\right) \left( 1-2n\right) Q\left( Q^{\prime }\right) ^{2}Q^{\prime \prime } \\ +3n^{2}\left( 1-n\right) Q^{2}\left( Q^{\prime \prime }\right) ^{2}\\ +4n^{2}\left( 1-n\right) Q^{2}Q^{\prime }Q^{\prime \prime \prime }+n^{3}Q^{3}Q^{\prime \prime \prime \prime } \end{array}\right) \nonumber \\&\quad +\,6b\kappa ^{2}n^{2}Q^{2}\left( \left( 1-n\right) \left( Q^{\prime }\right) ^{2}+nQQ^{\prime \prime }\right) \nonumber \\&\quad -\,n^{4}\left( \omega +3b{\kappa }^{4}\right) Q^{4}+c_{{1}}n^{4}+c_{{2}}n^{4}Q+c_{{3}}n^{4}Q^{2}\nonumber \\&\quad +\,c_{{4}}n^{4}Q^{3}+c_{{5}}n^{4}Q^{5}+c_{{6}}n^{4}Q^{6}+c_{{7}}n^{4}Q^{7}\nonumber \\&\quad +\,c_{{8}}n^{4}Q^{8}-n^{4}\kappa \left( \lambda +\mu \right) Q^{\frac{2m}{n}+4}=0 . \end{aligned}$$
(11)

The last equation will now be studied by three integration schemes in next subsections.

Application TO CQ–GKE

Riccati Equation Method

This methodology suggests the formal solution of Eq. (11) as

$$\begin{aligned} Q(\xi )=\sum _{i=0}^{N}A_{i}V^{i}(\xi ) \end{aligned}$$
(12)

where N is the balance number, \(A_{i}\) for \(0\le i\le N\) are constants, and the function \(V(\xi )\) holds

$$\begin{aligned} V^{\prime }(\xi )=S_{2}V^{2}\left( \xi \right) +S_{1}V\left( \xi \right) +S_{0},\ \ \ S_{2}\ne 0 \end{aligned}$$
(13)

with constants \(S_{2}\), \(S_{1}\) and \(S_{0}\). Also, it needs to be mentioned that Eq. (13) has the solutions as follows:

$$\begin{aligned} \begin{array}{ll} \displaystyle V\left( \xi \right) = -\frac{S_{1}}{2S_{2}}-\frac{\sqrt{\sigma }}{2S_{2}} \tanh \left( \frac{\sqrt{\sigma }}{2}\xi +\xi _{0}\right) , &{} \sigma>0,\\ \displaystyle V\left( \xi \right) = -\frac{S_{1}}{2S_{2}}-\frac{\sqrt{\sigma }}{2S_{2}} \coth \left( \frac{\sqrt{\sigma }}{2}\xi +\xi _{0}\right) , &{} \sigma >0,\\ \displaystyle V\left( \xi \right) = -\frac{S_{1}}{2S_{2}}+\frac{\sqrt{-\sigma }}{2S_{2}} \tan \left( \frac{\sqrt{-\sigma }}{2}\xi +\xi _{0}\right) , &{} \sigma<0,\\ \displaystyle V\left( \xi \right) = -\frac{S_{1}}{2S_{2}}-\frac{\sqrt{-\sigma }}{2S_{2}} \cot \left( \frac{\sqrt{-\sigma }}{2}\xi +\xi _{0}\right) , &{} \sigma <0,\\ \displaystyle V\left( \xi \right) = -\frac{S_{1}}{2S_{2}}-\frac{1}{S_{2}\xi +\xi _{0}}, &{} \sigma =0 \end{array} \end{aligned}$$
(14)

where \(\xi _{0}\) is a constant and \(\sigma =\) \(S_{1}^{2}-4S_{0}S_{2}\).

According to the balancing principle, the solution of Eq. (11) is

$$\begin{aligned} Q\left( \xi \right) =A_{0}+A_{1}V\left( \xi \right) . \end{aligned}$$
(15)

Then, putting (15) along with (13) into (11) yields

$$\begin{aligned} m=2n,\ \ \ c_{{1}}={\frac{b\left( {A_{{0}}}^{2}S_{{2}}-A_{{0}}A_{{1}}S_{{1}}+ {A_{{1}}}^{2}S_{{0}}\right) ^{4}\left( n-1\right) \left( 3\,n-1\right) \left( 2\,n-1\right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(16)
$$\begin{aligned} c_{{2}}=-{\frac{2b\left( 2\,A_{{0}}S_{{2}}-A_{{1}}S_{{1}}\right) \left( {A_{{ 0}}}^{2}S_{{2}}-A_{{0}}A_{{1}}S_{{1}}+{A_{{1}}}^{2}S_{{0}}\right) ^{3}\left( n-1\right) \left( 2\,n-1\right) \left( 3\,n-2\right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(17)
$$\begin{aligned} c_{{3}}={\frac{b\left( {A_{{0}}}^{2}S_{{2}}-A_{{0}}A_{{1}}S_{{1}}+{A_{{1}}} ^{2}S_{{0}}\right) ^{2}\left( n-1\right) \left( \begin{array}{l} 6\,{\kappa }^{2}{n}^{2}{A_{{1}}}^{2}+36\,{n}^{2}{A_{{0}}}^{2}{S_{{2}}} ^{2}-36\,{n}^{2}A_{{0}}A_{{1}}S_{{1}}S_{{2}} \\ +8\,{n}^{2}{A_{{1}}}^{2}S_{{0}}S_{{2}}+7\,{n}^{2}{A_{{1}}}^{2}{S_{{1}}} ^{2}-56\,n{A_{{0}}}^{2}{S_{{2}}}^{2} \\ +56\,nA_{{0}}A_{{1}}S_{{1}}S_{{2}}-8\,n{A_{{1}}}^{2}S_{{0}}S_{{2}}-12\,n{A_{{ 1}}}^{2}{S_{{1}}}^{2} \\ +28\,{A_{{0}}}^{2}{S_{{2}}}^{2}-28\,A_{{0}}A_{{1}}S_{{1}}S_{{2}}+4\,{A_{{1}}} ^{2}S_{{0}}S_{{2}}+6\,{A_{{1}}}^{2}{S_{{1}}}^{2} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(18)
$$\begin{aligned} c_{{4}}=-{\frac{b\left( 2\,A_{{0}}S_{{2}}-A_{{1}}S_{{1}}\right) \left( {A_{{0 }}}^{2}S_{{2}}-A_{{0}}A_{{1}}S_{{1}}+{A_{{1}}}^{2}S_{{0}}\right) \left( n-2\right) \left( \begin{array}{l} 6\,{\kappa }^{2}{n}^{2}{A_{{1}}}^{2}+12\,{n}^{2}{A_{{0}}}^{2}{S_{{2}}}^{2} \\ -12\,{n}^{2}A_{{0}}A_{{1}}S_{{1}}S_{{2}}+8\,{n}^{2}{A_{{1}}}^{2}S_{{0}}S_{{2} } \\ +{n}^{2}{A_{{1}}}^{2}{S_{{1}}}^{2}-14\,n{A_{{0}}}^{2}{S_{{2}}}^{2} \\ +14\,nA_{{0}}A_{{1}}S_{{1}}S_{{2}}-6\,n{A_{{1}}}^{2}S_{{0}}S_{{2}} \\ -2\,n{A_{{1}}}^{2}{S_{{1}}}^{2}+14\,{A_{{0}}}^{2}{S_{{2}}}^{2} \\ -14\,A_{{0}}A_{{1}}S_{{1}}S_{{2}}+6\,{A_{{1}}}^{2}S_{{0}}S_{{2}}+2\,{A_{{1}}} ^{2}{S_{{1}}}^{2} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(19)
$$\begin{aligned} c_{{5}}={\frac{bS_{{2}}\left( 2\,A_{{0}}S_{{2}}-A_{{1}}S_{{1}}\right) \left( n+2\right) \left( \begin{array}{l} 6\,{\kappa }^{2}{n}^{2}{A_{{1}}}^{2}+12\,{n}^{2}{A_{{0}}}^{2}{S_{{2}}} ^{2}-12\,{n}^{2}A_{{0}}A_{{1}}S_{{1}}S_{{2}} \\ +8\,{n}^{2}{A_{{1}}}^{2}S_{{0}}S_{{2}}+{n}^{2}{A_{{1}}}^{2}{S_{{1}}} ^{2}+14\,n{A_{{0}}}^{2}{S_{{2}}}^{2} \\ -14\,nA_{{0}}A_{{1}}S_{{1}}S_{{2}}+6\,n{A_{{1}}}^{2}S_{{0}}S_{{2}}+2\,n{A_{{1 }}}^{2}{S_{{1}}}^{2} \\ +14\,{A_{{0}}}^{2}{S_{{2}}}^{2}-14\,A_{{0}}A_{{1}}S_{{1}}S_{{2}}+6\,{A_{{1}}} ^{2}S_{{0}}S_{{2}}+2\,{A_{{1}}}^{2}{S_{{1}}}^{2} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(20)
$$\begin{aligned} c_{{6}}=-{\frac{b{S_{{2}}}^{2}\left( n+1\right) \left( \begin{array}{l} 6\,{\kappa }^{2}{n}^{2}{A_{{1}}}^{2}+36\,{n}^{2}{A_{{0}}}^{2}{S_{{2}}} ^{2}-36\,{n}^{2}A_{{0}}A_{{1}}S_{{1}}S_{{2}} \\ +8\,{n}^{2}{A_{{1}}}^{2}S_{{0}}S_{{2}}+7\,{n}^{2}{A_{{1}}}^{2}{S_{{1}}} ^{2}+56\,n{A_{{0}}}^{2}{S_{{2}}}^{2} \\ -56\,nA_{{0}}A_{{1}}S_{{1}}S_{{2}}+8\,n{A_{{1}}}^{2}S_{{0}}S_{{2}}+12\,n{A_{{ 1}}}^{2}{S_{{1}}}^{2} \\ +28\,{A_{{0}}}^{2}{S_{{2}}}^{2}-28\,A_{{0}}A_{{1}}S_{{1}}S_{{2}}+4\,{A_{{1}}} ^{2}S_{{0}}S_{{2}}+6\,{A_{{1}}}^{2}{S_{{1}}}^{2} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(21)
$$\begin{aligned} c_{{7}}={\frac{2b{S_{{2}}}^{3}\left( 3\,n+2\right) \left( 2\,n+1\right) \left( n+1\right) \left( 2\,A_{{0}}S_{{2}}-A_{{1}}S_{{1}}\right) }{{n}^{4}{ A_{{1}}}^{4}}} \end{aligned}$$
(22)
$$\begin{aligned} c_{{8}}=-{\frac{-\kappa \,\lambda \,{n}^{4}{A_{{1}}}^{4}-\kappa \,\mu \,{n} ^{4}{A_{{1}}}^{4}+6\,b{n}^{3}{S_{{2}}}^{4}+11\,b{n}^{2}{S_{{2}}}^{4}+6\,bn{ S_{{2}}}^{4}+b{S_{{2}}}^{4}}{{n}^{4}{A_{{1}}}^{4}} } \end{aligned}$$
(23)
$$\begin{aligned} \omega =-{\frac{b\left( \begin{array}{l} 3\,{\kappa }^{4}{n}^{4}{A_{{1}}}^{4}-36\,{\kappa }^{2}{n}^{2}{A_{{0}}}^{2}{ A_{{1}}}^{2}{S_{{2}}}^{2}+36\,{\kappa }^{2}{n}^{2}A_{{0}}{A_{{1}}}^{3}S_{{1} }S_{{2}} \\ -12\,{\kappa }^{2}{n}^{2}{A_{{1}}}^{4}S_{{0}}S_{{2}}-6\,{\kappa }^{2}{n}^{2}{ A_{{1}}}^{4}{S_{{1}}}^{2}-50\,{n}^{2}{A_{{0}}}^{4}{S_{{2}}}^{4} \\ +100\,{n}^{2}{A_{{0}}}^{3}A_{{1}}S_{{1}}{S_{{2}}}^{3}-60\,{n}^{2}{A_{{0}}} ^{2}{A_{{1}}}^{2}S_{{0}}{S_{{2}}}^{3}-60\,{n}^{2}{A_{{0}}}^{2}{A_{{1}}}^{2}{ S_{{1}}}^{2}{S_{{2}}}^{2} \\ +60\,{n}^{2}A_{{0}}{A_{{1}}}^{3}S_{{0}}S_{{1}}{S_{{2}}}^{2}+10\,{n}^{2}A_{{0} }{A_{{1}}}^{3}{S_{{1}}}^{3}S_{{2}}-10\,{n}^{2}{A_{{1}}}^{4}{S_{{0}}}^{2}{S_{{ 2}}}^{2} \\ -10\,{n}^{2}{A_{{1}}}^{4}S_{{0}}{S_{{1}}}^{2}S_{{2}}-70\,{A_{{0}}}^{4}{S_{{2} }}^{4}+140\,{A_{{0}}}^{3}A_{{1}}S_{{1}}{S_{{2}}}^{3} \\ -60\,{A_{{0}}}^{2}{A_{{1}}}^{2}S_{{0}}{S_{{2}}}^{3}-90\,{A_{{0}}}^{2}{A_{{1}} }^{2}{S_{{1}}}^{2}{S_{{2}}}^{2}+60\,A_{{0}}{A_{{1}}}^{3}S_{{0}}S_{{1}}{S_{{2} }}^{2} \\ +20\,A_{{0}}{A_{{1}}}^{3}{S_{{1}}}^{3}S_{{2}}-6\,{A_{{1}}}^{4}{S_{{0}}}^{2}{ S_{{2}}}^{2}-12\,{A_{{1}}}^{4}S_{{0}}{S_{{1}}}^{2}S_{{2}}-{A_{{1}}}^{4}{S_{{1 }}}^{4} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}}. \end{aligned}$$
(24)

Plugging (16)–(24) with (14) into (15), the following soliton solutions to CQ–GKE are secured:

Dark soliton is

$$\begin{aligned} q(x,t)&=\left( {{{A_{{0}}}}}-\frac{{{{A_{{1}}}}}S_{1}}{2S_{2}}-\frac{{{{A_{{1} }}}}\sqrt{S_{1}^{2}-4S_{0}S_{2}}}{2S_{2}}\tanh \right. \nonumber \\&\quad \left. \left[ \frac{\sqrt{ S_{1}^{2}-4S_{0}S_{2}}}{2}\left( x+8b{\kappa }^{3}t\right) \right] \right) ^{ \frac{1}{n}}\mathrm{e}^{i\left( -\kappa x+\omega t+\zeta \right) } \end{aligned}$$
(25)

with

$$\begin{aligned} S_{1}^{2}-4S_{0}S_{2}>0. \end{aligned}$$
(26)

Singular soliton is

$$\begin{aligned} q(x,t)&=\left( {{{A_{{0}}}}}-\frac{{{{A_{{1}}}}}S_{1}}{2S_{2}}-\frac{{{{A_{{1} }}}}\sqrt{S_{1}^{2}-4S_{0}S_{2}}}{2S_{2}}\coth \right. \nonumber \\&\left. \times \left[ \frac{\sqrt{ S_{1}^{2}-4S_{0}S_{2}}}{2}\left( x+8b{\kappa }^{3}t\right) \right] \right) ^{ \frac{1}{n}}\mathrm{e}^{i\left( -\kappa x+\omega t+\zeta \right) } \end{aligned}$$
(27)

with

$$\begin{aligned} S_{1}^{2}-4S_{0}S_{2}>0. \end{aligned}$$
(28)

F-Expansion procedure

This innovative integration algorithm assumes that the formal solution of Eq. (11) is structured as below:

$$\begin{aligned} Q\left( \xi \right) =\sum _{i=0}^{N}A_{i}F^{i}\left( \xi \right) \end{aligned}$$
(29)

where N is the balance number, \(A_{i}\) for \(0\le i\le N\) are constants, and the function \(F(\xi )\) satisfies

$$\begin{aligned} F^{\prime }\left( \xi \right) =\sqrt{PF^{4}\left( \xi \right) +QF^{2}\left( \xi \right) +R} \end{aligned}$$
(30)

with constants P, Q and R. Also, here, it should be noted that the solutions of Eq. (30) are:

Case

P

Q

R

\(F(\xi )\)

\(F(\xi ) \, (m\rightarrow 1)\)

\(F(\xi ) \, (m\rightarrow 0)\)

 

1

\(m^{2}\)

\(-(1+m^{2})\)

1

\({{\,\mathrm{sn}\,}}\xi\)

\(\tanh \xi\)

\(\sin \xi\)

(31)

2

1

\(-(1+m^{2})\)

\(m^{2}\)

\({{\,\mathrm{ns}\,}}\xi\)

\(\coth \xi\)

\(\csc \xi\)

3

\(1-m^{2}\)

\(2-m^{2}\)

1

\(\text {sc} \, \xi\)

\(\sinh \xi\)

\(\tan \xi\)

4

1

\(2-m^{2}\)

\(1-m^{2}\)

\({{\,\mathrm{cs}\,}}\xi\)

\({{\,\mathrm{csch}\,}}\xi\)

\(\cot \xi\)

5

\(-m^{2}\)

\(2m^{2}-1\)

\(1-m^{2}\)

\({{\,\mathrm{cn}\,}}\xi\)

\({{\,\mathrm{sech}\,}}\xi\)

\(\cos \xi\)

6

1

\(2m^{2}-1\)

\(-m^{2}\left( 1-m^{2}\right)\)

\({{\,\mathrm{ds}\,}}\xi\)

\({{\,\mathrm{csch}\,}}\xi\)

\(\csc \xi\)

7

\(1-m^{2}\)

\(2m^{2}-1\)

\(-m^{2}\)

\({{\,\mathrm{nc}\,}}\xi\)

\(\cosh \xi\)

\(\sec \xi\)

8

1

\(-(1+m^{2})\)

\(m^{2}\)

\({{\,\mathrm{ns}\,}}\xi\)

\(\coth \xi\)

\(\csc \xi\)

9

\(\frac{1}{4}\)

\(\frac{m^{2}-2}{2}\)

\(\frac{m^{2}}{4}\)

\({{\,\mathrm{ns}\,}}\xi \pm {{\,\mathrm{ds}\,}}\xi\)

\(\coth \xi \pm {{\,\mathrm{csch}\,}}\xi\)

\(2\csc \xi\)

10

\(\frac{m^{2}}{4}\)

\(\frac{m^{2}-2}{2}\)

\(\frac{m^{2}}{4}\)

\({{\,\mathrm{sn}\,}}\xi \pm i {{\,\mathrm{cn}\,}}\xi\)

\(\tanh \xi \pm i {{\,\mathrm{sech}\,}}\xi\)

\(\sin \xi \pm i \cos \xi\)

11

\(\frac{1}{4}\)

\(\frac{1-2m^{2}}{2}\)

\(\frac{1}{4}\)

\({{\,\mathrm{ns}\,}}\xi \pm {{\,\mathrm{cs}\,}}\xi\)

\(\coth \xi \pm {{\,\mathrm{csch}\,}}\xi\)

\(\csc \xi \pm \cot \xi\)

12

\(\frac{1-m^{2}}{4}\)

\(\frac{1+m^{2}}{2}\)

\(\frac{1-m^{2}}{4}\)

\({{\,\mathrm{nc}\,}}\xi \pm \text {sc} \, \xi\)

\(\cosh \xi \pm \sinh \xi\)

\(\sec \xi \pm \tan \xi\)

According to the balancing principle, the solution of Eq. (11) takes the form of

$$\begin{aligned} Q\left( \xi \right) =A_{0}+A_{1}F\left( \xi \right) . \end{aligned}$$
(32)

Plugging (32) with (30) into (11) leads to

$$\begin{aligned} m=2n,\ \ \ c_{{1}}={\frac{b\left( -1+n\right) \left( -1+3\,n\right) \left( -1+2\,n\right) \left( P{A_{{0}}}^{4}+Q{A_{{0}}}^{2}{A_{{1}}}^{2}+R{A_{{1}}} ^{4}\right) ^{2}}{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(33)
$$\begin{aligned} c_{{2}}=-{\frac{2bA_{{0}}\left( -1+n\right) \left( -1+2\,n\right) \left( 3\,n-2\right) \left( 2\,P{A_{{0}}}^{2}+Q{A_{{1}}}^{2}\right) \left( P{A_{{0}} }^{4}+Q{A_{{0}}}^{2}{A_{{1}}}^{2}+R{A_{{1}}}^{4}\right) }{{n}^{4}{A_{{1}}} ^{4}}} \end{aligned}$$
(34)
$$\begin{aligned} c_{{3}}={\frac{b\left( -1+n\right) \left( \begin{array}{l} 6\,P{\kappa }^{2}{n}^{2}{A_{{0}}}^{4}{A_{{1}}}^{2}+6\,Q{\kappa }^{2}{n}^{2}{ A_{{0}}}^{2}{A_{{1}}}^{4}+6\,R{\kappa }^{2}{n}^{2}{A_{{1}}}^{6} \\ +36\,{P}^{2}{n}^{2}{A_{{0}}}^{6}+40\,PQ{n}^{2}{A_{{0}}}^{4}{A_{{1}}} ^{2}+24\,PR{n}^{2}{A_{{0}}}^{2}{A_{{1}}}^{4} \\ +7\,{Q}^{2}{n}^{2}{A_{{0}}}^{2}{A_{{1}}}^{4}+4\,QR{n}^{2}{A_{{1}}}^{6}-56\,{P }^{2}n{A_{{0}}}^{6} \\ -60\,PQn{A_{{0}}}^{4}{A_{{1}}}^{2}-24\,PRn{A_{{0}}}^{2}{A_{{1}}}^{4}-12\,{Q} ^{2}n{A_{{0}}}^{2}{A_{{1}}}^{4} \\ -4\,QRn{A_{{1}}}^{6}+28\,{P}^{2}{A_{{0}}}^{6}+30\,PQ{A_{{0}}}^{4}{A_{{1}}} ^{2} \\ +12\,PR{A_{{0}}}^{2}{A_{{1}}}^{4}+6\,{Q}^{2}{A_{{0}}}^{2}{A_{{1}}}^{4}+2\,QR{ A_{{1}}}^{6} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(35)
$$\begin{aligned} c_{{4}}=-{\frac{bA_{{0}}\left( n-2\right) \left( \begin{array}{l} 12\,P{\kappa }^{2}{n}^{2}{A_{{0}}}^{2}{A_{{1}}}^{2}+6\,Q{\kappa }^{2}{n}^{2}{ A_{{1}}}^{4}+24\,{P}^{2}{n}^{2}{A_{{0}}}^{4} \\ +20\,PQ{n}^{2}{A_{{0}}}^{2}{A_{{1}}}^{2}+12\,PR{n}^{2}{A_{{1}}}^{4}+{Q}^{2}{n }^{2}{A_{{1}}}^{4} \\ -28\,{P}^{2}n{A_{{0}}}^{4}-20\,PQn{A_{{0}}}^{2}{A_{{1}}}^{2}-4\,PRn{A_{{1}}} ^{4} \\ -2\,{Q}^{2}n{A_{{1}}}^{4}+28\,{P}^{2}{A_{{0}}}^{4}+20\,PQ{A_{{0}}}^{2}{A_{{1} }}^{2} \\ +4\,PR{A_{{1}}}^{4}+2\,{Q}^{2}{A_{{1}}}^{4} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(36)
$$\begin{aligned} c_{{5}}={\frac{2A_{{0}}Pb\left( n+2\right) \left( \begin{array}{l} 6\,{\kappa }^{2}{n}^{2}{A_{{1}}}^{2}+12\,P{n}^{2}{A_{{0}}}^{2}+4\,Q{n}^{2}{ A_{{1}}}^{2} \\ +14\,Pn{A_{{0}}}^{2}+3\,Qn{A_{{1}}}^{2}+14\,P{A_{{0}}}^{2}+3\,Q{A_{{1}}}^{2} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(37)
$$\begin{aligned} c_{{6}}=-{\frac{2Pb\left( n+1\right) \left( \begin{array}{l} 3\,{\kappa }^{2}{n}^{2}{A_{{1}}}^{2}+18\,P{n}^{2}{A_{{0}}}^{2}+2\,Q{n}^{2}{ A_{{1}}}^{2} \\ +28\,Pn{A_{{0}}}^{2}+2\,Qn{A_{{1}}}^{2}+14\,P{A_{{0}}}^{2}+Q{A_{{1}}}^{2} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(38)
$$\begin{aligned} c_{{7}}={\frac{4b{P}^{2}A_{{0}}\left( 3\,n+2\right) \left( 2\,n+1\right) \left( n+1\right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(39)
$$\begin{aligned} c_{{8}}=-{\frac{-\kappa \,\lambda \,{n}^{4}{A_{{1}}}^{4}-\kappa \,\mu \,{n} ^{4}{A_{{1}}}^{4}+6\,b{n}^{3}{P}^{2}+11\,b{n}^{2}{P}^{2}+6\,bn{P}^{2}+{P} ^{2}b}{{n}^{4}{A_{{1}}}^{4}} } \end{aligned}$$
(40)
$$\begin{aligned} \omega ={\frac{b\left( \begin{array}{l} -3\,{\kappa }^{4}{n}^{4}{A_{{1}}}^{4}+36\,P{\kappa }^{2}{n}^{2}{A_{{0}}}^{2}{ A_{{1}}}^{2}+6\,Q{\kappa }^{2}{n}^{2}{A_{{1}}}^{4} \\ +50\,{P}^{2}{n}^{2}{A_{{0}}}^{4}+30\,PQ{n}^{2}{A_{{0}}}^{2}{A_{{1}}} ^{2}+10\,PR{n}^{2}{A_{{1}}}^{4} \\ +70\,{P}^{2}{A_{{0}}}^{4}+30\,PQ{A_{{0}}}^{2}{A_{{1}}}^{2}+2\,PR{A_{{1}}} ^{4}+{Q}^{2}{A_{{1}}}^{4} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}}. \end{aligned}$$
(41)

As a consequence, inserting (33)–(41) along with (31) into (32), soliton solutions to the model are revealed as:

Dark soliton is

$$\begin{aligned} q(x,t)=\left( A_{0}+A_{1}\tanh \left( x+8b{\kappa }^{3}t\right) \right) ^{ \frac{1}{n}} \mathrm{e}^{i\left( -\kappa x+\omega t+\zeta \right) } . \end{aligned}$$
(42)

Singular soliton is

$$\begin{aligned} q(x,t)=\left( A_{0}+A_{1}\coth \left( x+8b{\kappa }^{3}t\right) \right) ^{ \frac{1}{n}} \mathrm{e}^{i\left( -\kappa x+\omega t+\zeta \right) } . \end{aligned}$$
(43)

Bright soliton is

$$\begin{aligned} q(x,t)=\left( A_{0}+A_{1}{{\,\mathrm{sech}\,}}\left( x+8b{\kappa }^{3}t\right) \right) ^{\frac{1}{n}} \mathrm{e}^{i\left( -\kappa x+\omega t+\zeta \right) } . \end{aligned}$$
(44)

Singular soliton is

$$\begin{aligned} q(x,t)=\left( A_{0}+A_{1}{{\,\mathrm{csch}\,}}\left( x+8b{\kappa }^{3}t\right) \right) ^{\frac{1}{n}} \mathrm{e}^{i\left( -\kappa x+\omega t+\zeta \right) } . \end{aligned}$$
(45)

Combo singular soliton is

$$\begin{aligned} q(x,t)&=\left( A_{0}+A_{1}\left( \coth \left( x+8b{\kappa }^{3}t\right) \right. \right. \nonumber \\&\left. \left. \pm {{\,\mathrm{csch}\,}}\left( x+8b{\kappa }^{3}t\right) \right) \right) ^{\frac{1}{n} } \mathrm{e}^{i\left( -\kappa x+\omega t+\zeta \right) } . \end{aligned}$$
(46)

Exp-expansion method

The solution of Eq. (11) according to this form of integration norm is taken to be:

$$\begin{aligned} Q(\xi )=\sum _{i=0}^{N}A_{i}\left\{ \exp \left( -V(\xi )\right) \right\} ^{i} \end{aligned}$$
(47)

where N is the balance number, \(A_{i}\) for \(0\le i\le N\) are constants, and the function \(V(\xi )\) ensures

$$\begin{aligned} V^{\prime }(\xi )=\exp \left( -V(\xi )\right) +S\exp \left( V(\xi )\right) +R \end{aligned}$$
(48)

with constants S and R. Also, it should be remarked that Eq. (48) has the solutions

$$\begin{aligned} \begin{array}{lll} \displaystyle V\left( \xi \right) =\ln \left[ -\frac{R}{2S}-\frac{\sqrt{\sigma }}{2S} \tanh \left( \dfrac{\sqrt{\sigma }}{2}\left( \xi +\xi _{0}\right) \right) \right] , \\ S\ne 0, \sigma>0,\\ \displaystyle V\left( \xi \right) =\ln \left[ -\frac{R}{2S}-\frac{\sqrt{\sigma }}{2S} \coth \left( \dfrac{\sqrt{\sigma }}{2}\left( \xi +\xi _{0}\right) \right) \right] , \\ S\ne 0, \sigma >0,\\ \displaystyle V\left( \xi \right) =\ln \left[ -\frac{R}{2S}+\frac{\sqrt{-\sigma }}{2S} \tan \left( \dfrac{\sqrt{-\sigma }}{2}\left( \xi +\xi _{0}\right) \right) \right] , \\ S\ne 0, \sigma<0,\\ \displaystyle V\left( \xi \right) =\ln \left[ -\frac{R}{2S}-\frac{\sqrt{-\sigma }}{2S} \cot \left( \dfrac{\sqrt{-\sigma }}{2}\left( \xi +\xi _{0}\right) \right) \right] , \\ S\ne 0, \sigma <0 \end{array} \end{aligned}$$
(49)

where \(\xi _{0}\) constant and \(\sigma =R^{2}-4S\).

From the balancing principle, Eq. (11) has the solution form given by

$$\begin{aligned} Q\left( \xi \right) =A_{0}+A_{1}\exp \left( -V(\xi )\right) . \end{aligned}$$
(50)

Inserting (50) with (48) into (11), the following results are obtained:

$$\begin{aligned} m=2n,\ \ \ c_{{1}}={\frac{b\left( -1+n\right) \left( -1+3\,n\right) \left( -1+2\,n\right) \left( RA_{{0}}A_{{1}}-S{A_{{1}}}^{2}-{A_{{0}}}^{2}\right) ^{4}}{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(51)
$$\begin{aligned} c_{{2}}=-{\frac{2b\left( -1+n\right) \left( -1+2\,n\right) \left( 3\,n-2\right) \left( RA_{{1}}-2\,A_{{0}}\right) \left( RA_{{0}}A_{{1}}-S{A_{{ 1}}}^{2}-{A_{{0}}}^{2}\right) ^{3}}{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(52)
$$\begin{aligned} c_{{3}}={\frac{b\left( -1+n\right) \left( RA_{{0}}A_{{1}}-S{A_{{1}}}^{2}-{A_{ {0}}}^{2}\right) ^{2}\left( \begin{array}{l} 7\,{R}^{2}{n}^{2}{A_{{1}}}^{2}+6\,{\kappa }^{2}{n}^{2}{A_{{1}}}^{2}-12\,{R} ^{2}n{A_{{1}}}^{2} \\ -36\,R{n}^{2}A_{{0}}A_{{1}}+8\,S{n}^{2}{A_{{1}}}^{2}+6\,{R}^{2}{A_{{1}}}^{2} \\ +56\,RnA_{{0}}A_{{1}}-8\,Sn{A_{{1}}}^{2}+36\,{n}^{2}{A_{{0}}}^{2} \\ -28\,RA_{{0}}A_{{1}}+4\,S{A_{{1}}}^{2}-56\,n{A_{{0}}}^{2}+28\,{A_{{0}}}^{2} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(53)
$$\begin{aligned} c_{{4}}=-{\frac{b\left( n-2\right) \left( RA_{{1}}-2\,A_{{0}}\right) \left( RA_{{0}}A_{{1}}-S{A_{{1}}}^{2}-{A_{{0}}}^{2}\right) \left( \begin{array}{l} {R}^{2}{n}^{2}{A_{{1}}}^{2}+6\,{\kappa }^{2}{n}^{2}{A_{{1}}}^{2}-2\,{R}^{2}n{ A_{{1}}}^{2} \\ -12\,R{n}^{2}A_{{0}}A_{{1}}+8\,S{n}^{2}{A_{{1}}}^{2}+2\,{R}^{2}{A_{{1}}}^{2} \\ +14\,RnA_{{0}}A_{{1}}-6\,Sn{A_{{1}}}^{2}+12\,{n}^{2}{A_{{0}}}^{2} \\ -14\,RA_{{0}}A_{{1}}+6\,S{A_{{1}}}^{2}-14\,n{A_{{0}}}^{2}+14\,{A_{{0}}}^{2} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(54)
$$\begin{aligned} c_{{5}}=-{\frac{b\left( n+2\right) \left( RA_{{1}}-2\,A_{{0}}\right) \left( \begin{array}{l} {R}^{2}{n}^{2}{A_{{1}}}^{2}+6\,{\kappa }^{2}{n}^{2}{A_{{1}}}^{2}+2\,{R}^{2}n{ A_{{1}}}^{2} \\ -12\,R{n}^{2}A_{{0}}A_{{1}}+8\,S{n}^{2}{A_{{1}}}^{2}+2\,{R}^{2}{A_{{1}}}^{2} \\ -14\,RnA_{{0}}A_{{1}}+6\,Sn{A_{{1}}}^{2}+12\,{n}^{2}{A_{{0}}}^{2} \\ -14\,RA_{{0}}A_{{1}}+6\,S{A_{{1}}}^{2}+14\,n{A_{{0}}}^{2}+14\,{A_{{0}}}^{2} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(55)
$$\begin{aligned} c_{{6}}=-{\frac{b\left( n+1\right) \left( \begin{array}{l} 7\,{R}^{2}{n}^{2}{A_{{1}}}^{2}+6\,{\kappa }^{2}{n}^{2}{A_{{1}}}^{2}+12\,{R} ^{2}n{A_{{1}}}^{2} \\ -36\,R{n}^{2}A_{{0}}A_{{1}}+8\,S{n}^{2}{A_{{1}}}^{2}+6\,{R}^{2}{A_{{1}}}^{2} \\ -56\,RnA_{{0}}A_{{1}}+8\,Sn{A_{{1}}}^{2}+36\,{n}^{2}{A_{{0}}}^{2} \\ -28\,RA_{{0}}A_{{1}}+4\,S{A_{{1}}}^{2}+56\,n{A_{{0}}}^{2}+28\,{A_{{0}}}^{2} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(56)
$$\begin{aligned} c_{{7}}=-{\frac{2b\left( 3\,n+2\right) \left( 2\,n+1\right) \left( n+1\right) \left( RA_{{1}}-2\,A_{{0}}\right) }{{n}^{4}{A_{{1}}}^{4}}} \end{aligned}$$
(57)
$$\begin{aligned} c_{{8}}=-{\frac{-\kappa \,\lambda \,{n}^{4}{A_{{1}}}^{4}-\kappa \,\mu \,{n} ^{4}{A_{{1}}}^{4}+6\,b{n}^{3}+11\,b{n}^{2}+6\,bn+b}{{n}^{4}{A_{{1}}}^{4}} } \end{aligned}$$
(58)
$$\begin{aligned} \omega ={\frac{b\left( \begin{array}{l} -3\,{\kappa }^{4}{n}^{4}{A_{{1}}}^{4}+6\,{R}^{2}{\kappa }^{2}{n}^{2}{A_{{1}}} ^{4}-10\,{R}^{3}{n}^{2}A_{{0}}{A_{{1}}}^{3} \\ +10\,{R}^{2}S{n}^{2}{A_{{1}}}^{4}-36\,R{\kappa }^{2}{n}^{2}A_{{0}}{A_{{1}}} ^{3}+12\,S{\kappa }^{2}{n}^{2}{A_{{1}}}^{4} \\ +{R}^{4}{A_{{1}}}^{4}+60\,{R}^{2}{n}^{2}{A_{{0}}}^{2}{A_{{1}}}^{2}-60\,RS{n} ^{2}A_{{0}}{A_{{1}}}^{3} \\ +10\,{S}^{2}{n}^{2}{A_{{1}}}^{4}+36\,{\kappa }^{2}{n}^{2}{A_{{0}}}^{2}{A_{{1} }}^{2}-20\,{R}^{3}A_{{0}}{A_{{1}}}^{3} \\ +12\,{R}^{2}S{A_{{1}}}^{4}-100\,R{n}^{2}{A_{{0}}}^{3}A_{{1}}+60\,S{n}^{2}{A_{ {0}}}^{2}{A_{{1}}}^{2} \\ +90\,{R}^{2}{A_{{0}}}^{2}{A_{{1}}}^{2}-60\,RSA_{{0}}{A_{{1}}}^{3}+6\,{S}^{2}{ A_{{1}}}^{4} \\ +50\,{n}^{2}{A_{{0}}}^{4}-140\,R{A_{{0}}}^{3}A_{{1}}+60\,S{A_{{0}}}^{2}{A_{{1 }}}^{2}+70\,{A_{{0}}}^{4} \end{array} \right) }{{n}^{4}{A_{{1}}}^{4}}}. \end{aligned}$$
(59)

Plugging (51)–(59) along with (49) into (50), the solutions for (1) are discovered as:

Singular soliton is

$$\begin{aligned} q(x,t)=\left( {{{A_{{0}}-}}}\frac{{{{A_{{1}}}}}}{ \displaystyle \frac{{R}}{2S}+\frac{\sqrt{ R^{2}-4S}}{2S}\tanh \left[ \frac{\sqrt{R^{2}-4S}}{2}\left( x+8b{\kappa } ^{3}t\right) \right] }\right) ^{\frac{1}{n}}\mathrm{e}^{i\left( -\kappa x+\omega t+\zeta \right) } \end{aligned}$$
(60)

with

$$\begin{aligned} R^{2}-4S>0. \end{aligned}$$
(61)

Dark soliton is

$$\begin{aligned} q(x,t)=\left( {{{A_{{0}}-}}}\frac{{{{A_{{1}}}}}}{ \displaystyle \frac{{R}}{2S}+\frac{\sqrt{ R^{2}-4S}}{2S}\coth \left[ \frac{\sqrt{R^{2}-4S}}{2}\left( x+8b{\kappa } ^{3}t\right) \right] }\right) ^{\frac{1}{n}}\mathrm{e}^{i\left( -\kappa x+\omega t+\zeta \right) } \end{aligned}$$
(62)

with

$$\begin{aligned} R^{2}-4S>0. \end{aligned}$$
(63)

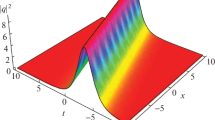
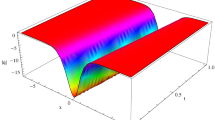
A surface plot of a bright soliton is given here (Fig. 1).

Fig. 1
figure 1

The plot of (44) setting all arbitrary parameters to unity except \(n=0,3\)

Full size image

Conservation laws

In the complex system (1) above, we let \(q=u+iw\) to obtain a system two pdes whose conserved flows \((T^t,T^x)\) are established employing the multiplier approach. It turns out that a single multiplier \(M=(-u,v)\) giving rise to the ‘power’ conserved density

$$\begin{aligned} T_1^t =\frac{1}{2} \left( u^2+v^2\right) \end{aligned}$$
(64)

so that a corresponding conserved density for (1) is

$$\begin{aligned} \mathcal{T}_1^t=|q|^2. \end{aligned}$$
(65)

Also, if \(\lambda =-\theta\), we have linear momentum and Hamiltonian conservation too. Then following conserved density, \(T_2^t\), for linear momentum is

$$\begin{aligned} T_2^t =-\frac{1}{2}u_{{x}}v_{{}}+\frac{1}{2}v_{{x}}u \end{aligned}$$
(66)

and the ‘momentum density’ for (1) is

$$\begin{aligned} \mathcal{T}_2^t=\mathcal{I}(q^*q_x). \end{aligned}$$
(67)

The conserved density corresponding to ‘Hamiltonian’, \(\mathcal{T}^t_3\), is rather lengthy and the calculation for the conserved quantity would be meaningless; we will not produce it here.

Noting that bright soliton solution to (1) is of the form:

$$\begin{aligned} q(x,t) = A {{\,\mathrm{sech}\,}}^{\frac{1}{n}} [B(x-vt)] \mathrm{e}^{i \left( - \kappa x + \omega t + \theta _0 \right) } \end{aligned}$$
(68)

where A is the amplitude and B is its inverse width, the two conserved quantities, power (P) and linear momentum (M), respectively, are

$$\begin{aligned} P = \int _{-\infty }^{\infty } \left| q \right| ^2 dx = \frac{A^2}{B} \frac{ \Gamma \left( \frac{1}{n} \right) \left( \frac{1}{2} \right) }{ \Gamma \left( \frac{1}{n} + \frac{1}{2} \right) } \end{aligned}$$
(69)

and

$$\begin{aligned} M = i \kappa \int _{-\infty }^{\infty } \left( qq_x^{*} - q^{*} q_x \right) dx = \frac{\kappa A^2}{B} \frac{ \Gamma \left( \frac{1}{n} \right) \left( \frac{1}{2} \right) }{ \Gamma \left( \frac{1}{n} + \frac{1}{2} \right) }. \end{aligned}$$
(70)

Conclusions

This paper obtained CQ optical soliton solutions to GKE by utilizing three forms of integration norms. A wide range of soliton solutions are secured. The conservation laws are finally identified for the model. These con laws will be of great value to probe into the model further along. One immediate area to extend this study is to consider soliton perturbation theory, both deterministic and stochastic. Thus, one can study soliton cooling effect and the effect of stochastic perturbation by addressing the corresponding Langevin equations. Another avenue of obvious extension is to take a look at the aspect of modeling CQ–GKE with Bragg gratings and in birefringent fibers as well as DWDM/UDWDM networking. Additional, and yet powerful, mathematical tools such as Lie symmetry and others are going to be implemented in future as applied earlier in several other areas of physics [21,22,23,24,25]. These would lead to several avenues of research. Such studies are under way, and the results are going to be visible sooner than later.