Introduction

The captivating theory and dynamics of optical solitons forms an engineering marvel in telecommunications industry [1,2,3,4,5,6,7,8,9,10]. There are several forms of self-phase modulation (SPM) structures that make this dynamics a reality. While several new models are being continuously proposed, abundant models have been lately introduced by Kudryashov [1, 3,4,5,6,7,8,9]. A couple of them have been recently labeled as Kudryashov’s law of refractive index and Kudryashov’s generalized law of refractive index. The current paper is another form of SPM that was proposed by Kudryashov and it was coined as arbitrary refractive index [8, 9]. Thus, the title of the manuscript is kept as such. This form of SPM is a combination of two or three types of previously studied laws. It linearly combines dual-power law and non-local nonlinearity but with any arbitrary exponent, odd or even, either way. This proposed law of nonlinear refractive index will be explored in today’s paper with the governing nonlinear Schrödinger’s equation (NLSE) that is going to be addressed in presence of chromatic dispersion (CD).

The paper will integrate NLSE using a few algorithms that will reveal soliton solutions to the model and thus will make the model a viable candidate for soliton transmission through optical fibers or other such form of equivalent waveguides. There is only one form of conservation law that is also recovered from this model and is exhibited at the end. The presence of the generalized form of non-local form of nonlinearity prevents the retrieval of additional forms of conservation law.

Three well-known powerful integration schemes are adopted in the paper to handle the model from its integrability perspective. These integration schemes implemented in the paper are Riccati equation method, F-expansion scheme and finally the trial equation algorithm. These methodologies collectively retrieved a full spectrum of single solitons and in addition F-expansion revealed a straddled singular soliton structure. The existence criteria for such solitons are also listed as their respective parameter constraints. Surface plots of bright and dark solitons are also included for visual illustration. The analytical details of these are discussed in the remainder of the paper after a quick intro to the governing model.

Governing model

The dimensionless form of NLSE Kudryashov’s form of arbitrary refractive index is [8]:

$$\begin{aligned} iq_{t}+aq_{xx}+\left\{ b_{1}\left| q\right| ^{n}+b_{2}\left| q\right| ^{2n}+b_{3}\left( \left| q\right| ^{n}\right) _{xx}\right\} q=0 \end{aligned}$$
(1)

where x represents spatial variable while t represents temporal variable. Then, \(q\left( x,t\right)\) is the complex-valued dependent variable and it stands for the soliton profile. Next, a is the coefficient of CD and \(i=\sqrt{-1}\). The constants \(b_{j}\) for \(1\le j\le 3\) are the coefficients of SPM and n is the power-law nonlinearity parameter.

Mathematical analysis

In order to locate soliton solutions, the following decomposition in phase-amplitude format is carried out:

$$\begin{aligned} q(x,t)=U(\zeta )e^{i\varphi (x,t)} \end{aligned}$$
(2)

where

$$\begin{aligned} \zeta =\eta \left( x-vt\right) \end{aligned}$$
(3)

and v is the soliton velocity. Next, from the phase component

$$\begin{aligned} \varphi (x,t)=-\kappa x+\omega t+\theta _{0} \end{aligned}$$
(4)

where \(\kappa\), \(\omega\) and \(\theta _{0}\) are, respectively, the frequency, wave number and phase constant. Substitute (2) into (1). Real part gives

$$\begin{aligned}&\left( {\omega +a{\kappa }^{2}}\right) {U-a{\eta }^{2}U^{\prime \prime }-{ \eta }^{2}nb_{{3}}U^{n}U^{\prime \prime }+{\eta }^{2}b_{{3}}n}\left( {1-{n}} \right) \\&\quad \times{\left( U^{\prime }\right) ^{2}U^{n-1}-b_{{1}}U^{n+1}-b_{{2} }U^{2\,n+1}=0} \end{aligned}$$
(5)

, while imaginary part leads to the speed of the soliton as

$$\begin{aligned} {v=-2a\kappa }. \end{aligned}$$
(6)

By the use of \(U=Q^{\frac{1}{n}}\), Eq. (5) changes to

$$\begin{aligned}&n^{2}\left( {\omega +a{\kappa }^{2}}\right) Q^{2}-a{\eta }^{2}\left( \left( 1-n\right) \left( Q^{\prime }\right) ^{2}+nQQ^{\prime \prime }\right) \\&\quad -{n} ^{2}{\eta }^{2}b_{{3}}Q^{2}Q^{\prime \prime }-n^{2}{b}_{1}Q^{3}{-n^{2}b}_{2}{ Q^{4}}=0. \end{aligned}$$
(7)

Application to NLSE

This section recovers soliton solutions to the model by the application of three algorithms that are detailed in the subsequent subsections.

Riccati equation method

This scheme assumes that Eq. (7) has the formal solution as

$$\begin{aligned} Q(\zeta )=\sum _{i=0}^{N}A_{i}V^{i}(\zeta ) \end{aligned}$$
(8)

where N is the balance number, \(A_{i}\) for \(0\le i\le N\) are constants and \(V(\zeta )\) ensures

$$\begin{aligned} V^{\prime }(\zeta )=S_{2}V^{2}\left( \zeta \right) +S_{1}V\left( \zeta \right) +S_{0},\quad S_{2}\ne 0 \end{aligned}$$
(9)

with constants \(S_{2}\), \(S_{1}\) and \(S_{0}\). Also, it should be noted that the solutions of Eq. (9) are:

$$\begin{aligned} \begin{array}{ll} V\left( \zeta \right) = -\frac{S_{1}}{2S_{2}}-\frac{\sqrt{\sigma }}{2S_{2}} \tanh \left( \frac{\sqrt{\sigma }}{2}\zeta +\zeta _{0}\right) , &{} \sigma>0, \\ V\left( \zeta \right) = -\frac{S_{1}}{2S_{2}}-\frac{\sqrt{\sigma }}{2S_{2}} \coth \left( \frac{\sqrt{\sigma }}{2}\zeta +\zeta _{0}\right) , &{} \sigma >0 \end{array} \end{aligned}$$
(10)

where \(\zeta _{0}\) is a constant and \(\sigma =\) \(S_{1}^{2}-4S_{0}S_{2}\).

From, the balancing principle, the solution (8) becomes

$$\begin{aligned} Q\left( \zeta \right) =A_{0}+A_{1}V\left( \zeta \right) +A_{2}V^{2}\left( \zeta \right) . \end{aligned}$$
(11)

Substituting (11) with (9) into (7) yields

$$\begin{aligned} A_{{0}} &= -{\frac{3b_{{3}}\left( a{\eta }^{2}{S_{{1}}}^{2}-{n}^{2}a{\kappa } ^{2}-{n}^{2}\omega \right) }{2ab_{{2}}}}, \\ A_{{1}} &=-{\frac{6{\eta }^{2}S_{{ 1}}S_{{2}}b_{{3}}}{b_{{2}}}}, \\A_{{2}}&=-{\frac{6{\eta }^{2}{S_{{2}}}^{2}b_{ {3}}}{b_{{2}}}}, \\ S_{{0}}& = {\frac{a{\eta }^{2}{S_{{1}}}^{2}-{n}^{2}a{\kappa }^{2}-{n} ^{2}\omega }{4{\eta }^{2}S_{{2}}a}}, \\ b_{{1}}&={\frac{-3\,a{\kappa }^{2}{n} ^{4}{b_{{3}}}^{2}-3\,{n}^{4}\omega \,{b_{{3}}}^{2}+{a}^{2}nb_{{2}}+2\,{a} ^{2}b_{{2}}}{3{n}^{2}ab_{{3}}}.} \end{aligned}$$
(12)

Plugging (12) along with (10) into (11), one recovers dark and singular solitons, respectively

$$\begin{aligned}q(x,t)&=\left( {\frac{3b_{{3}}{n}^{2}{\left( a{\kappa }^{2}+\omega \right) } }{2ab_{{2}}}}-{\frac{3b_{{3}}{n}^{2}{\left( a{\kappa }^{2}+\omega \right) }}{ 2ab_{{2}}}} \right. \\&\quad \times\left. \tanh ^{2}\left[ \sqrt{{\frac{{n}^{2}\left( a{\kappa }^{2}+\omega \right) }{4a}}}\left( x+2a\kappa t\right) \right] \right) ^{\frac{1}{n} }e^{i\left( -\kappa x+\omega t+\theta _{0}\right) } \end{aligned}$$
(13)

and

$$\begin{aligned} q(x,t)&=\left( {\frac{3b_{{3}}{n}^{2}{\left( a{\kappa }^{2}+\omega \right) } }{2ab_{{2}}}}-{\frac{3b_{{3}}{n}^{2}{\left( a{\kappa }^{2}+\omega \right) }}{ 2ab_{{2}}}} \right. \\&\quad \times\left. \coth ^{2}\left[ \sqrt{{\frac{{n}^{2}\left( a{\kappa }^{2}+\omega \right) }{4a}}}\left( x+2a\kappa t\right) \right] \right) ^{\frac{1}{n} }e^{i\left( -\kappa x+\omega t+\theta _{0}\right) } \end{aligned}$$
(14)

with

$$\begin{aligned} a\left( a{\kappa }^{2}+\omega \right) >0. \end{aligned}$$
(15)

F-expansion scheme

This methodology suggests that the formal solution of Eq. (7) is:

$$\begin{aligned} Q\left( \zeta \right) =\sum _{i=0}^{N}A_{i}F^{i}\left( \zeta \right) \end{aligned}$$
(16)

where N is the balance number, \(A_{i}\) for \(0\le i\le N\) are constants and the function \(F(\zeta )\) provides

$$\begin{aligned} F^{\prime }\left( \zeta \right) =\sqrt{PF^{4}\left( \zeta \right) +QF^{2}\left( \zeta \right) +R} \end{aligned}$$
(17)

with constants P, Q and R. Also, it needs to be mentioned that some solutions of Eq. (17) are listed as:

$$\begin{aligned}&F\left( \zeta \right) ={{\,\mathrm{sn}\,}}\zeta =\tanh \zeta ,\ \ P=m^{2},\ \ Q=-(1+m^{2}),\ \ R=1,\ \ m\rightarrow 1, \\&F\left( \zeta \right) ={{\,\mathrm{ns}\,}}\zeta =\coth \zeta ,\ \ P=1,\ \ Q=-(1+m^{2}),\ \ R=m^{2},\ \ m\rightarrow 1, \\&F\left( \zeta \right) ={{\,\mathrm{cn}\,}}\zeta ={{\,\mathrm{sech}\,}}\zeta ,\ \ P=-m^{2},\ \ Q=2m^{2}-1,\ \ R=1-m^{2},\ \ m\rightarrow 1, \\&F\left( \zeta \right) ={{\,\mathrm{ds}\,}}\zeta ={{\,\mathrm{csch}\,}}\zeta , \ \ P=1,\ \ Q=2m^{2}-1,\ \ R=-m^{2}\left( 1-m^{2}\right) ,\ \ m\rightarrow 1, \\&F\left( \zeta \right) ={{\,\mathrm{ns}\,}}\zeta \pm {{\,\mathrm{ds}\,}}\zeta =\coth \zeta \pm {{\,\mathrm{csch}\,}}\zeta ,\ \ P= \frac{1}{4},\ \ Q=\frac{m^{2}-2}{2},\ \ R=\frac{m^{2}}{4},\ \ m\rightarrow 1. \end{aligned}$$
(18)

With the help of the balancing principle, the solution of Eq. (7) reduces to

$$\begin{aligned} Q\left( \zeta \right) =A_{0}+A_{1}F\left( \zeta \right) +A_{2}F^{2}\left( \zeta \right) . \end{aligned}$$
(19)

Putting (19) with (17) into (7) leads to

$$\begin{aligned} P &= {\frac{{Q}^{2}}{4R}},\ \ \eta =\pm \,\sqrt{-{\frac{2n^{2}\left( a{ \kappa }^{2}+\omega \right) }{4Qa}}}, \\ A_{{0}}&={\frac{3\left( a{\kappa } ^{2}+\omega \right) {n}^{2}b_{{3}}}{2b_{{2}}a}},\quad A_{{1}}=0, \\ A_{{2}} &= {\frac{3{n}^{2}\left( a{\kappa }^{2}+\omega \right) Qb_{{3}}}{ 4aRb_{{2}}}}, \\ b_{{1}}&={\frac{-3\,a{\kappa }^{2}{n}^{4}{b_{{3}}}^{2}-3\,{n} ^{4}\omega \,{b_{{3}}}^{2}+{a}^{2}nb_{{2}}+2\,{a}^{2}b_{{2}}}{3a{n}^{2}b_{{3} }}.} \end{aligned}$$
(20)

Inserting (20) along with (18) into (19), one reveals the solutions to the governing model in the forms:

Dark soliton is

$$\begin{aligned} q(x,t)&=\left( {\frac{3\left( a{\kappa }^{2}+\omega \right) {n}^{2}b_{{3}}}{ 2b_{{2}}a}}-\frac{3\left( a{\kappa }^{2}+\omega \right) {n}^{2}b_{{3}}}{2b_{ {2}}a} \right. \\&\quad \left. \times \tanh ^{2}\left[ \sqrt{{\frac{n^{2}\left( a{\kappa }^{2}+\omega \right) }{4a}}}\left( x+{2a\kappa }\right) \right] \right) ^{\frac{1}{n} }e^{i\left( -\kappa x+\omega t+\theta _{0}\right) } \end{aligned}$$
(21)

singular soliton is

$$\begin{aligned} q(x,t)&=\left( {\frac{3\left( a{\kappa }^{2}+\omega \right) {n}^{2}b_{{3}}}{ 2b_{{2}}a}}-\frac{3\left( a{\kappa }^{2}+\omega \right) {n}^{2}b_{{3}}}{2b_{ {2}}a} \right. \\&\quad \left. \times \coth ^{2}\left[ \sqrt{{\frac{n^{2}\left( a{\kappa }^{2}+\omega \right) }{4a}}}\left( x+{2a\kappa }\right) \right] \right) ^{\frac{1}{n} }e^{i\left( -\kappa x+\omega t+\theta _{0}\right) } \end{aligned}$$
(22)

and combo singular solitons are

$$\begin{aligned}&q(x,t) \\&\quad= \left( \begin{array}{l} {\dfrac{3\left( a{\kappa }^{2}+\omega \right) {n}^{2}b_{{3}}}{2b_{{2}}a}}-{ \dfrac{3\left( a{\kappa }^{2}+\omega \right) {n}^{2}b_{{3}}}{2b_{{2}}a}} \\ \\ \times {\left( \mathrm {\coth }\left[ \sqrt{{\dfrac{n\left( a{\kappa } ^{2}+\omega \right) }{a}}}\left( x+{2a\kappa }\right) \right] \pm {{\,\mathrm{csch}\,}}\left[ \sqrt{{\dfrac{n\left( a{\kappa }^{2}+\omega \right) }{a}}}\left( x+{ 2a\kappa }\right) \right] \right) ^{2}} \end{array} \right) ^{\frac{1}{n}} \\ & \quad \times e^{i\left( -\kappa x+\omega t+\theta _{0}\right) } \end{aligned}$$
(23)

with

$$\begin{aligned} a\left( a{\kappa }^{2}+\omega \right) >0. \end{aligned}$$
(24)

Trial equation algorithm

According to this form of integration norm, the solution of Eq. (7) is adopted as

$$\begin{aligned} \left( Q^{\prime }\left( \zeta \right) \right) ^{2}=\sum _{i=0}^{N}A_{i}Q^{i}\left( \zeta \right) \end{aligned}$$
(25)

where N is the balance number, \(A_{i}\) for \(0\le i\le N\) are constants and \(Q\left( \zeta \right)\) is a function that needs to be determined later.

Utilizing the balancing principle gives

$$\begin{aligned} \left( Q^{\prime }\left( \zeta \right) \right) ^{2}=A_{0}+A_{1}Q\left( \zeta \right) +A_{2}Q^{2}\left( \zeta \right) +A_{3}Q^{3}\left( \zeta \right) . \end{aligned}$$
(26)

Then, plugging (26) into (7), one procures the results

$$\begin{aligned} A_{{0}} &= 0,\quad A_{{1}}=0,\quad A_{{2}}={\frac{{n}^{2}\left( a{\kappa } ^{2}+\omega \right) }{a{\eta }^{2}}},\quad A_{{3}}=-{\frac{2b_{{2}}}{3{\eta } ^{2}b_{{3}}}}, \\ b_{{1}} &= {\frac{-3\,a{\kappa }^{2}{n}^{4}{b_{{3}}}^{2}-3\,{n}^{4}\omega \,{ b_{{3}}}^{2}+{a}^{2}nb_{{2}}+2\,{a}^{2}b_{{2}}}{3a{n}^{2}b_{{3}}}.} \end{aligned}$$
(27)

Next, substituting the solution set (27) into (26) brings bout

$$\begin{aligned} \pm \left( \zeta -\zeta _{0}\right) =\int \frac{dQ}{\sqrt{\dfrac{{n}^{2}\left( a{ \kappa }^{2}+\omega \right) }{a{\eta }^{2}}Q^{2}-{\dfrac{2b_{{2}}}{3{\eta } ^{2}b_{{3}}}}Q^{3}}}. \end{aligned}$$
(28)

Consequently, integrating Eq. (28) with respect to Q, bright and singular solitons fall out as

$$\begin{aligned} q(x,t)&=\left( \dfrac{3b_{{3}}{n}^{2}\left( a{\kappa }^{2}+\omega \right) }{ 2ab_{{2}}} \right. \\&\quad \times\left. {{\,\mathrm{sech}\,}}^{2}\left[ \sqrt{\dfrac{{n}^{2}\left( a{\kappa } ^{2}+\omega \right) }{4a}}\left( x+{2a\kappa }\right) \right] \right) ^{ \frac{1}{n}}e^{i\left( -\kappa x+\omega t+\theta _{0}\right) } \end{aligned}$$
(29)

and

$$\begin{aligned} q(x,t)&=\left( -\dfrac{3b_{{3}}{n}^{2}\left( a{\kappa }^{2}+\omega \right) }{ 2ab_{{2}}} \right. \\ &\quad \left. \times{{\,\mathrm{csch}\,}}^{2}\left[ \sqrt{\dfrac{{n}^{2}\left( a{\kappa } ^{2}+\omega \right) }{4a}}\left( x+{2a\kappa }\right) \right] \right) ^{ \frac{1}{n}}e^{i\left( -\kappa x+\omega t+\theta _{0}\right) } \end{aligned}$$
(30)

with

$$\begin{aligned} a\left( a{\kappa }^{2}+\omega \right) >0. \end{aligned}$$
(31)

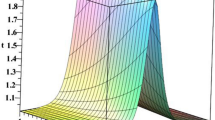
The following two surface plots represent bright and dark single solitons, respectively. The parameter values chosen are: \(a= -0.4,\ b_2= 0.3,\ b_3= -1,\ n= 1,\ \kappa = 2,\ \omega = 0.2\) (Figs. 1, 2).

Fig. 1
figure 1

Profile of dark soliton (13)

Full size image
Fig. 2
figure 2

Profile of bright soliton (29)

Full size image

Conservation law

Invariance of (1) under translation in time t and space x (\(\partial _t\) and \(\partial _x\)), (1) does not admit any Hamiltonian and linear momentum conservation unless \(b_3=0\). That is, the derivative of \(|q|^n\) with respect to x annihilates the conserved Hamiltonian/momentum densities. The notion of approximate conservation is still being developed and we may study these in the future with \(b_3\) relatively ‘small.’ Thus, the only conservation is the ‘power,’ with density \(|q|^2\). Noting that the bright 1-soliton solution to (1) is written as:

$$\begin{aligned} q(x,t) = A {{\,\mathrm{sech}\,}}^{\frac{2}{n}} [B(x-vt)] e^{i \left( - \kappa x + \omega t + \theta _0 \right) } \end{aligned}$$
(32)

where A is the amplitude and B is its inverse width, the power (P) of the soliton is:

$$\begin{aligned} P = \int _{-\infty }^{\infty } \left| q \right| ^2 dx = \frac{A^2}{B} \frac{ \Gamma \left( \frac{2}{n} \right) \left( \frac{1}{2} \right) }{ \Gamma \left( \frac{2}{n} + \frac{1}{2} \right) }. \end{aligned}$$
(33)

Conclusions

This work applies three mathematical algorithms to secure a range of soliton solutions to NLSE that carries arbitrary refractive index form for SPM as proposed by Kudryashov. A full spectrum of soliton solutions, including combo-singular type, has emerged from the scheme that are exhibited along with their existence criteria. The only conservation law that has been located is presented. This work therefore paves the pathway for further development in this regard. One avenue of research would be to address the current model with perturbation terms that would lead to the evolution of additional information. While the prospect of applying soliton perturbation theory no longer exists, because the model does not yield more than one conserved quantity, there are nevertheless additional avenues to venture. This would include application of semi-inverse variational principle and other algorithms to handle perturbation terms that are of Hamiltonian type [11,12,13,14,15,16, 16,17,18,19,20]. The research-rich crew members are thus preoccupied to disseminate these upcoming precious novel results of the model, due to Kudryashov, for gaining momentum, with full throttle, in the fields of quantum optics and telecommunications engineering.