A novel approach for secure compressive sensing of images using multiple chaotic maps

Abstract

In this paper, a novel approach for secure compressive sensing of images based on multiple one dimensional chaotic maps is proposed. The basic idea is to perform the random selection of a combination of two one dimensional chaotic maps to generate a random stream. One or more values from the random stream are used to generate each normal value in the random measurement matrix for compressive sensing. In the proposed approach, eight different one dimensional chaotic maps are used. For one measurement matrix generation, two of them are randomly selected based on a secret key. The number of iterations and the initial states of the chaotic maps are also decided by external secret keys. The chaotic output of iterations of the two selected chaotic maps are XORed to generate a new chaotic value so that the measurement matrix so generated can withstand known plaintext attack. The block-based compressive sensing (BCS) of images is adopted to validate the proposed system. Further enhancement in the security of the proposed system for BCS of images can be obtained by using different measurement matrices for different blocks of images. An algorithm for generating multiple measurement matrices is also presented in this work. It is experimentally proved that the proposed encryption system can maintain the robustness to noise of the compressive sensing system. The proposed robust encryption system is subjected to several forms of attacks and is proved to be resistant against all.

Introduction

The increasing demand in the multimedia data necessitates the use of efficient compression techniques for maintaining the huge traffic in the limited bandwidth environment. The newly developed compressive sensing system is a method in this direction, where the sampling rate is less than the Nyquist rate so that the achievable compression performance is better than the standard coding techniques. Compressive sensing (CS) is a mathematical framework meant for permitting signals to be sampled at sub-Nyquist rates (subrates) under certain conditions, by linear projection into a lower dimension than the original signal [11].

The basic theory of CS is investigated in [2, 6, 11, 12, 34]. Compressive sensing relies in the sparseness of the signal and gathers linear measurement y = ϕx of a sparse signal x, where size of y is a small fraction of samples needed for Nyquist sampling. The random measurement ensemble ϕ follows uniform uncertainty principle (UUP) [5] and gives equal importance to each measurement. This helps to provide unified decoder for compressive sensed coding schemes [8]. The receiver obtains the linear measurements y and reconstructs the signal by solving it as an optimization problem.

Over the last years, a number of image/video coding schemes based on compressive sensing were proposed. In [21], Han et al. proposed an image representation problem for visual sensor networks. Multi-scale wavelet based CS scheme was proposed by Deng et al. [7, 8]. In [40], different compressive sensing based surveillance video coding systems were proposed and compared by Venkatraman et al. Information theoretic approach for CS based image coding is presented in [20]. A compressive sensing based robust image transmission scheme for wireless channels was proposed by Gao et al. in [18]. The block-based CS (BCS) for 2D images was initially proposed by Gan [17] to reduce the large computational complexity and storage requirement of measurement matrices for large sized images. Smoothed projected Landweber (SPL) iterations were incorporated in the block-based compressive sensing reconstruction to enhance the reconstruction quality. The further enhancement in quality of the reconstructed images was obtained by using directional transforms (dual-tree DWT and contourlet transforms) [28] or multiscale variant of BCS-SPL [16].

To protect the private data from the unauthorized usage, perfect security is a mandatory requirement in the compressive sensing framework. A robust encryption system based on cryptographic key based selection of random measurement matrix was proposed by Orsdemir et al. [31]. Rachlin et al. showed that compressed sensing based encryption does not achieve Shannon’s definition of perfect secrecy, but can provide a computational guarantee of secrecy [33]. In another approach, Kumar et al. proposed an encryption system by performing the compressive measurements over an encrypted image [25]. A compression-combined digital image encryption method which is robust against consecutive packet loss and malicious shear attack was proposed by Huang et al., where one dimensional logistic mapping is used to generate chaotic sequences, which is regarded as the parameters of block Arnold transformation and the pseudorandom sequence for XOR operation [23]. In [27], Lu et al. proposed an image information encryption method based on compressive sensing and double random-phase encoding. Soman et al., proposed an encryption system by scrambling the compressed measurements using Arnold transform [37]. These approaches are either vulnerable to some forms of attack or offer high level of complexity. Moreover, most of the above mentioned approaches do not maintain the robustness to noise of the compressive sensing system.

The main motivation behind the proposed work is to design a less complicated encryption system with high level of security such that it maintains the robustness of the CS system. Multiple one dimensional chaotic maps based CS encryption technique can provide a highly secure system with low complexity. In the proposed approach, pairs of chaotic maps are considered and the pairs are randomly selected to generate random values. The chaotic output values of the selected pair are XORed to get new random value so that the newly generated random stream can withstand known plaintext attack. One or more uniform values from this random stream are used to generate each normal value in the random measurement matrix for performing the secure compressive sensing operation. It is proposed to use separate measurement matrices for different blocks of images in BCS to increase security of the proposed encryption system.

The remaining sections of this paper are organized as follows. Section “Basic principle of compressive sensing” deals with the basic principles of compressive sensing. Section “Proposed system: secure compressive sensing based on multiple chaotic maps” proposes a multiple chaotic map based encryption system for compressive sensing of images. The experimental analysis of the proposed system is given in section “Analysis of the proposed encryption system”. The paper concludes in section “Conclusion”.

Basic principle of compressive sensing

This section briefly explains the theory behind the compressive sensing, the different imaging techniques via compressive sensing and the different reconstruction techniques in BCS of images.

Compressive sensing

The compressed sensing framework is used to reduce the data acquisition and computational load at sensors, at the cost of increased computation at the intended receiver [11, 12]. Thus, the basic idea is to recover signal $\textbf{x}$ with length N from M samples such that M ≪ N with subsampling rate or subrate, being S = M/N. Even if, the number of unknowns $\textbf{x} \in R^{N}$ is larger than number of observations $\textbf{y} \in R^{M}$, it is possible to reconstruct $\textbf{x}$ from $\textbf{y}$, if $\textbf{x}$ is sufficiently sparse in some domain [11].

A real-valued, finite length, one dimensional signal $\textbf{x}$, represented as N ×1 column vector in R ^N, can be represented in terms of an orthonormal basis $\lbrace \psi_i\rbrace^N_{i=1}$ as follows.

$$ \textbf{x} = \sum^N_{i=1}s_i\psi _i = \psi \textbf{s} $$

(1)

where, $\textbf{x}$ and $\textbf{s}$ are the same signal representations in time/space domain and ψ domain respectively. $\textbf{s}$ is an N ×1 column vector of weighting coefficients, $s_i = \langle \textbf{x}, \psi _i \rangle$. But $\textbf{x}$ has sparsity such that $\textbf{x}$ can be represented as a linear combination of only K basis vectors [2]. In compressive sensing, instead of direct sampling $\textbf{x}$, a lower number of CS measurements are taken. Let the measurement matrix be ϕ = $\lbrace \phi_i\rbrace^N_{i=1}$ of order M ×N with M ≪ N. Then, the M linear samples $\textbf{y}$ can be represented as,

$$ \textbf{y} = \lbrace y_{i}\rbrace^M_{i=1} = \phi \textbf{x} = \lbrace \langle \textbf{x}, \phi _i \rangle \rbrace^M_{i=1} $$

(2)

Even if, $\textbf{y}$ is quantized as finite precision samples and added with some amount of noise in real-world, the signal can be reconstructed, maintaining the robustness to noise by solving it as a convex optimization problem under the condition that the measurement matrix ϕ satisfies uniform uncertainty principle (UUP) [5, 8].

$$\label{equ3} \text{min} \Vert \psi^{T} \tilde{x}\Vert_{l_1} s.t. \Vert \phi \psi^{T} \tilde{x} - y \Vert_{l_2} \leq \epsilon $$

(3)

for some tolerance ε > 0. For Θ = ϕψ ^T to be stable solution for this optimization problem, Θ should satisfy the restricted isometry property (RIP) [3]. The related condition for RIP is incoherence, which requires that the rows of ϕ cannot sparsely represent the columns of ψ [2]. Both the properties, RIP and incoherence can be achieved by selecting ϕ as a random matrix. A random matrix whose elements ϕ _ij are iid random variables from a Gaussian probability density function with mean zero and variance $\frac{1}{N}$ is able to satisfy these requirements [11]. Multiplying the sparse signal with random iid Gaussian matrix gives equal importance to each CS measurements. This feature makes the CS technique to have inherent error controlling capability [8]. The basic constrained optimization given in (3) is closely related to the unconstrained Lagrangian formulation, known as basic-pursuit denoising (BPDN) given by,

$$ \text{min} \Vert \psi^{T} \tilde{x}\Vert_{l_1} + \lambda \Vert \phi \psi^{T} \tilde{x} - y \Vert_{l_2} $$

(4)

where, the l ₁ driven sparsity against the l ₂ based measure of distortion is balanced by the Lagrangian multiplier λ [15]. The following subsection discusses the different imaging techniques via compressive sensing.

Imaging via compressive sensing

A number of architectures for the CS acquisition of images were proposed in the literature. Rice university proposed a single-pixel camera for CS based acquisition of images [12]. Neifeld et al. proposed some optical architectures for compressive imaging [30]. In another approach, Xiao et al. proposed a CMOS low data rate imaging approach by implementing compressed sensing [42]. An overview of different CS acquisition architectures are described in [13]. The single-pixel camera from Rice university for CS acquisition is given in Fig. 1.

Fig. 1

Block diagram of single-pixel pixel camera system for CS acquisition [38]

The CS based implementation of images is classified into straightforward approach and block-based approach. In straightforward approach, the 2D image is converted into a 1D vector and the compressive sensing procedure is performed on this 1D vector. Since there is a linear increase in the size of the measurement matrix with the increase in size of the image, the memory requirement to store the ϕ matrix and the computational complexity are very high for large images in the straightforward approach. In block-based compressive sensing (BCS) method, the image is divided into non-overlapping blocks and the compressive sensing operation is performed on the corresponding 1D vector of each block, where primary importance is given to the memory efficient measurement operator so that the drawbacks of straightforward approach for large sized images can be reduced.

Block-based compressive sensing for images

To alleviate the large memory requirement Gan proposed a method to divide the image into smaller blocks and to perform CS on smaller blocks independently. This method is known as block-based compressive sensing (BCS) [17]. In BCS scheme, the image is divided into blocks of size B ×B with respect to the size requirement of measurement matrix. Let $\textbf{x}_j$ be the 1D vector corresponding the j ^th block of image $\textbf{X}$. Then, the BCS output is given as,

$$ \textbf{y}_j = \phi_B \textbf{x}_j $$

(5)

Let the order of ϕ _B be $M_B \times B^2$, where $M_B = \lfloor\frac{M}{N}B^2\rfloor$. Then, the subrate of the image is given as, S = M _B /B ². The whole image measurement matrix can be represented as a block diagonal matrix given as follows,

$$ \phi = \begin{bmatrix} \phi_B & 0 & ... & 0\\ 0 & \phi_B & ... & 0\\ ... &... & ... & ...\\ 0&... &0 &\phi_B \end{bmatrix} $$

If block-by-block reconstruction is directly performed, it will create blocking artifacts on the reconstructed image. To improve the quality of the reconstructed image, several methods were proposed time to time. The following subsections deal with the BCS reconstruction methods to improve the reconstructed image quality.

BCS-TV based reconstruction

The total variation (TV) based CS reconstruction replaces the sparsity in the transform domain with the sparsity in the discretized gradient domain. It can provide smoothness in the reconstructed image [26]. This is due to the fact that it has the ability to suppress the high frequency artifacts produced by the direct block-by-block reconstruction of image. The optimization problem is reformulated as follows,

$$\label{equ6} \text{min} \Vert \textbf{X}\Vert_{TV} + \lambda \Vert \textbf{y} - \phi \textbf{x}\Vert_{l_2} $$

(6)

The total variation of the image is given as,

$$ \Vert \textbf{X}\Vert_{TV} = \sum\limits_{i,j} \sqrt{{(x_{i+1,j} - x_{i,j})}^2 + {(x_{i,j+1} - x_{i,j})}^2} $$

(7)

where, x _i,j represents the pixel value in the location (i,j).

The above minimization problem can be solved by using the second order cone programming, which is solvable by interior-point algorithms [4, 26]. In this method, the first step is to find an initial feasible solution from the received measurement vector $\textbf{y}$ and the generated ϕ matrix. The initial feasible solution represents a noisy version of the original image. Total variation of feasible solution is calculated from (6) and it is minimized through log-barrier iteration. At each log-barrier iteration, Newton’s method proceeds with the approximate solution at the last iteration as the initial guess. Applying Newton’s method at each iteration is still time consuming in a large-scale problem.

BCS with smoothed projected Landweber (BCS-SPL) reconstruction

The BCS-SPL is a iterative projection and thresholding based reconstruction method [22]. It starts from an initial approximation $\breve{x}$. The approximation in (i + 1)^th iteration is a specific instance of specific projected Landweber (PL) algorithm and is given as [28],

$$ \breve{\breve{x}}^{(i)} = \breve{x}^{(i)} + \frac{1}{\gamma}\psi \phi ^T (y - \phi \psi^{-1}\breve{x}^{(i)}), $$

(8)

$$ \breve{x}^{(i+1)} = \left\{ \begin{array}{l l} \breve{\breve{x}}^{(i)}, & \vert \breve{\breve{x}}^{(i)}\vert \geq \tau ^{(i)} \\ 0, & \text{else} \end{array} \right. $$

(9)

where, γ is the scaling factor and its value is chosen by finding the largest eigenvalue of ϕ ^T ϕ and τ ⁽ⁱ⁾ is the threshold value chosen appropriately at each iteration.

To improve the quality of reconstructed image Wiener filtering is incorporated into the basic PL framework [17] to provide smoothness in the reconstruction. The approximation of the image in the (i + 1)^th iteration is given as follows [15],

$$ x^{(i+1)} = \text{SPL}(x^{(i)}, y, \phi _B, \psi , \lambda) $$

$$ \hat{x}^{(i)} = \text{Wiener}(x^{(i)}) $$

for each block j

$$ \hat{\hat{x}}^{(i)}_j = \hat{x}^{(i)}_j + \phi ^T _B\big(y -\phi _B\hat{x}^{(i)}_j\big) $$

$$ \breve{\breve{x}}^{(i)} = \psi \hat{\hat{x}}^{(i)} $$

$$ \breve{x}^{(i)} = \text{Threshold}(\breve{\breve{x}}^{(i)},\lambda) $$

$$ \bar{x}^{(i)} = \psi^{-1}\breve{x}^{(i)} $$

for each block j

$$ x^{(i+1)}_j = \bar{x}^{(i)}_j + \phi ^T _B\big(y -\phi _B\bar{x}^{(i)}_j\big) $$

$$ D^{(i+1)} = \frac{1}{\sqrt{N}}\Vert x^{(i+1)} - \hat{\hat{x}}^{(i)}_j\Vert _2 $$

$$ \text{until} \vert D^{(i+1)} - D^{(i)}\vert < 10^{-4} $$

$$ x=x^{(i+1)} $$

where, Wiener(.) is pixelwise adaptive Wiener filtering operation and Threshold(.) is a thresholding operation. The initial value x ⁽⁰⁾ is given as,

$$ x^{(0)}= \phi ^T y $$

For BCS-SPL-DCT, ψ is selected as discrete cosine transform (DCT) and hard thresholding is used to select the value of τ. The universal threshold is the suitable candidate for such an application [10].

$$ \tau ^{(i)}=\lambda \sigma ^{(i)}\sqrt{2log K} $$

(10)

where, K is the number of transform coefficients and λ is a constant to manage the convergence. σ ⁽ⁱ⁾ can be estimated using the median estimator, which is given as,

$$ \sigma ^{(i)} = \dfrac{\text{median}\vert \breve{\breve{x}}^{(i)}\vert}{0.6745} $$

(11)

Since the hard thresholding is based on the fact that the transform coefficients are independent, the hard thresholding is not a suitable choice in DWT based BCS-SPL reconstruction techniques. Bivariate shrinkage function [36] gives superior performance than hard thresholding in DWT based BCS-SPL reconstruction methods. Thus, the threshold function in BCS-SPL-DWT is the MAP estimator and is given as,

$$ \text{Threshold}(\xi , \lambda) = \dfrac{\left( \sqrt{\xi ^2 + \xi ^2_p} - \lambda \frac{\sqrt{3\sigma ^{(i)}}}{\sigma _\xi}\right)_+}{\sqrt{\xi ^2 + \xi ^2_p}}.\xi $$

(12)

where the function,

$$ (g)_+ = \left\{ \begin{array}{l l} 0, & g < 0 \\ g, & \text{else} \end{array} \right. $$

ξ and ξ _p are the specific transform coefficient and its parent coefficient respectively. σ ⁽ⁱ⁾ is the median estimator applied to only first scale transform coefficients and λ is the convergence control factor. $\sigma _\xi^2$ is the marginal variance of coefficient ξ estimated in a local 3 ×3 neighbourhood surrounding of ξ [28]. Since the directional transforms, contourlet transform (CT) [9] and dual-tree discrete wavelet transform (DDWT) [24] show good directional sensitivity and shift invariance properties than DWT, Fowler et al. proposed that the BCS-SPL based on directional transforms (BCS-SPL-DDWT and BCS-SPL-CT) give better reconstruction quality than BCS-SPL-DCT and BCS-SPL-DWT [28].

Multiscale block-based compressive sampling

In [16], Fowler et al. proposed a multiscale variant of block based compressive sensing smoothed projected Landweber reconstruction (MS-BCS-SPL). In this approach, block-based compressive sampling is performed in each subband of wavelet transform of an image. The compressive sensed image in the MS-BCS-SPL based approach is given as,

$$ \textbf{y} = \phi '\Omega \textbf{x} $$

(13)

where, Ω represents the multiscale transform and ϕ′ is the multiscale block based measurement process. For L level of decomposition, ϕ′ consists of L different block based sampling operators. Let the DWT of the image be,

$$ \tilde{\textbf{x}} = \Omega \textbf{x} $$

(14)

Then, each subband s at a level l is divided into B _l ×B _l blocks and sampled with corresponding ϕ _l . Then, for 1 ≤ l ≤ L

$$ \textbf{y}_{l,s,j} = \phi _l\tilde{\textbf{x}}_{l,s,j} $$

(15)

where, $\tilde{\textbf{x}}_{l,s,j}$ represents the vector corresponding to the jth block of subband s at level l, with $s \in \lbrace H,V,D \rbrace$.

Since different levels of wavelet decomposition have different significance in the reconstruction, Fowler et al. proposed to use different subrate S _l at each level l, where the subrate for DWT baseband is taken as S ₀ = 1. The subrate for lth level is given as,

$$ S_l = W_lS' $$

(16)

under the condition that the overall subrate becomes,

$$ S=\dfrac{1}{4^L}S_0+\sum^L_{l=1}\dfrac{3}{4^{L-l+1}}W_lS' $$

(17)

For a given subrate S and level weights W _l , it is possible to find out the value of S′ to obtain the level subrate values S _l . This procedure may produce S _l  > 1. If S ₁ > 1, set S ₁ = 1 and modify the (19) as,

$$ S=\dfrac{1}{4^L}S_0+ \dfrac{3}{4^L}S_1+ \sum^L_{l=2}\dfrac{3}{4^{L-l+1}}W_lS' $$

(18)

and repeat this procedure to keep all S _l  ≤ 1. The level weights can be calculated as follows,

$$\label{eq19} W_l = 16^{L-l+1} $$

(19)

In MS-BCS-SPL reconstruction, Landweber step on each block of each subband in each decomposition level use different ϕ _l for current level l [15, 16]. Among all BCS approaches, the BCS-TV has the highest computational time than BCS-SPL and MS-BCS approaches.

The following section proposes a robust encryption system through compressive sensing, based on multiple one dimensional chaotic maps for generating the measurement matrix used in the compressive sensing paradigm.

Proposed system: secure compressive sensing based on multiple chaotic maps

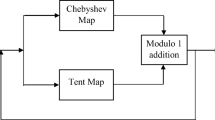
The chaotic maps have great importance in cryptography due to its sensitive dependence to the initial condition and system parameter, nonperiodicity, ergodicity and pseudorandom property [43]. Over the last years, a large number of discrete chaotic maps were proposed for cryptographic applications. In this paper, eight well known one dimensional discrete chaotic maps are chosen to develop an encryption system for compressive sensing applications. The selected one dimensional chaotic maps are logistic map, sine map, cubic map, tent map, Gao’s new chaotic map (GNCA), Singer map, piecewise linear chaotic map (PLCM) and Mehrab map. The selected chaotic maps, their mathematical representations and the system parameter values are listed in Table 1. A number is assigned to each chaotic map starting from ‘0’ to ‘7’, mentioned as chaotic index number (CIN) in the first column of Table 1. In all chaotic maps, the initial value and/or system parameter value are kept as secret to attain the secrecy.

Table 1 Selected one dimensional chaotic maps, the chaotic index number(CIN), mathematical expressions and parameter values

The one dimensional logistic map shows the exact chaotic behaviour only in the region μ ∈ [3.6,4) [19]. Even though, the logistic map provides high efficiency with simple design, it has smaller key space and lower security. Hence, Gao et al. proposed a new chaotic algorithm named as NCA [19]. It consists of two system parameters α and β. The typical parameter value of sine map is 0.99 [1]. The expressions for cubic map and tent map and the typical paremeter values are mentioned in [32]. In [39], it is mentioned that the the typical parameter values of Singer is in the interval (0.90, 1.08). The PLCM shows the chaotic behaviour on interval [0, 1) [41]. Mehrab map is a modified version of PLCM, which consists of two system parameters [14].

The main drawback with the chaotic maps is their vulnerability to known plaintext attack. To overcome this issue, in this paper, it is proposed to select any two chaotic maps from the chosen group of eight chaotic maps using a secret key. Combining the corresponding random values of these two chaotic maps will ensure that the security of the newly generated chaotic values is increased. The initial values of these two chaotic maps and the number of iterations are also determined by secret keys. The random array generated by the proposed approach is used as the random stream for generating the measurement matrix in the compressive sensing operation of images.

Secure measurement matrix generation

Four stages of encryption are proposed in this approach; one for chaotic maps selection, second for initial value of first chaotic map, third for initial value of second chaotic map and fourth for the number of iterations of the selected chaotic maps to get the required number of random values to form the random array. Four secret keys (32-bit each) are considered for this purpose. Thus, the total key size of the proposed measurement matrix generation is 128-bit. If we use hexadecimal representation for the key, total 32 characters are included in the key. Let Key be the external secret key to the user. Then, it can be represented as follows,

$$ Key =Key_1Key_2Key_3Key_4 $$

(20)

where, Key ₁, Key ₂, Key ₃ and Key ₄ represent the secret keys used for chaotic map pair selection, initial value of first chaotic map, initial value of second chaotic map and the number of iteration of the chaotic maps respectively. The key selection is based on the condition that Key ₁, Key ₂, Key ₃ and Key ₄ do not divide each other.

$$ Key_i \nmid Key_j; i \neq j $$

(21)

As mentioned earlier, a pairwise selection of chaotic maps are proposed in this paper. The eight chaotic maps are identified by chaotic index number (CIN) as mentioned in Table 1. By using CIN, the chaotic pair index number (CPIN) can be represented as follows,

$$ \text{CPIN} = \{mn\}_{m,n=0,1,...,7} $$

(22)

For example, if the random selection of CPIN using Key ₁ is 12, the selected chaotic maps will be sine map and cubic map respectively. Similarly, if CPIN is 55, both the selected chaotic maps will be tent map itself. For eight chaotic maps, 64 pairwise combinations are possible. CPIN for each pair is coming as the octal number repesentation starting from ‘00’ to ‘77’.

The random selection of pairwise chaotic maps based on Key ₁ can be implemented by using the following relation after converting the hexadecimal number Key ₁ into corresponding decimal representation $Key_1^d$.

$$ CP_1 = Key_1^d \text{mod} K $$

(23)

where, K represents the total number of pairwise combinations of chaotic maps (K = 64 in the proposed system). Converting CP ₁ to corresponding octal representation gives the chaotic pair $CP_1^c$.

The initial values of the chaotic maps in the selected pair is found by using the following mathematical expressions by converting Key ₂ and Key ₃ into corresponding decimal representations, say $Key_2^d$ and $Key_3^d$

$$ x^1(0) = \left( \dfrac{Key_2^d}{Key_1^d}\right) - \left \lfloor{ \dfrac{Key_2^d}{Key_1^d}}\right \rfloor $$

(24)

$$ x^2(0) = \left( \dfrac{Key_3^d}{Key_1^d}\right) - \left \lfloor{ \dfrac{Key_3^d}{Key_1^d}}\right \rfloor $$

(25)

where, x ¹(0) and x ²(0) represent the initial values of the first and second chaotic maps in the selected pair respectively. The required number of iterations N ¹ for the chaotic maps to form the random array of size N ¹ is found by using Key ₄ based on linear congruential generator (LCG) as follows,

$$ N^1 = Z_{1}=(aZ_0+c)\text{mod}L $$

(26)

In the proposed approach, it is chosen that $Z_0 = Key_4^d$, a = 5, c = 1 and L = 128, so that the maximum number iterations is 127.

$$ N^1 =\big(5Key_4^d+1\big)\text{mod}$$

(27)

Let the chaotic values produced by the first and second chosen chaotic maps and the generated chaotic values from these chaotic maps be $\textbf{x}^1$, $\textbf{x}^2$ and $\textbf{x}_r$ respectively. Then,

$$ \begin{array}{l} \textbf{x}^1 = \left( x^1(0), x^1(1), ...., x^1(N^1-1)\right) \\[4pt] \textbf{x}^2 = \left( x^2(0), x^2(1), ...., x^2(N^1-1)\right) \\[4pt] \textbf{x}_r = \left( x_r(0), x_r(1), ...., x_r(N^1-1)\right) \end{array} $$

where,

$$ x_r(j) = x^1(j)\oplus x^2(j) $$

(28)

One or more values from the generated random array $\textbf{x}_r$= $(x_r(0), x_r(1), ...., x_r(N^1-1))$ act as the random stream which is used to generate each normal value in the Gaussian random measurement matrix with mean zero and variance $\frac{1}{N}$.

$$ \phi_B \longleftarrow \dfrac{1}{N}\text{randn}\left(\textbf{x}_r, M, N \right) $$

(29)

where N and M represents the number of input samples and measured samples respectively in the CS operation.

Algorithm description of secure measurement matrix generation

The algorithm description of the proposed secure measurement matrix generation for compressive sensing operation using multiple chaotic maps is described below.

• 1. Generate the encryption key Key as a hexadecimal number, where

  $$ Key =Key_1Key_2Key_3Key_4 $$
  $$ s.t. Key_i \nmid Key_j; i \neq j $$

• 2. Select the chaotic pair CP ₁ using the decimal equivalent of Key ₁.

  $$ \begin{array}{l} CP_1 = Key_1^d \text{mod}\\ CP_1 \xrightarrow{\mbox{\small{octal}}} CP_1^c\\ CPIN_1 = CP_1^c \end{array} $$

• 3. Find the initial values of the selected chaotic maps using the decimal equivalents of Key ₁, Key ₂ and Key ₃ by using the following relations.

  $$ x^1(0) = \left( \dfrac{Key_2^d}{Key_1^d}\right) - \left \lfloor{ \dfrac{Key_2^d}{Key_1^d}}\right \rfloor $$
  $$ x^2(0) = \left( \dfrac{Key_3^d}{Key_1^d}\right) - \left \lfloor{ \dfrac{Key_3^d}{Key_1^d}}\right \rfloor $$

• 4. Find the number of iterations using Key ₄ based on the following relation,

  $$ N^1 =\big(5Key_4^d+1\big)\text{mod}$$

• 5. for j = 0: N ¹ − 1

  Generate the chaotic values for the first and second chaotic maps x ¹(j) and x ²(j) respectively to generate the the random value x _r (j).

  $$ x_r(j) = x^1(j\,)\oplus x^2(j\,) $$

• 6. Generate the M ×N Gaussian random measurement matrix using the N ¹ ×1 array $\textbf{x}_1^r$ as the random stream.

  $$ \phi_B \longleftarrow \dfrac{1}{N}\text{randn}\left(\textbf{x}_r, M, N \right) $$

The following subsection discusses the BCS technique of images using the secure measurement matrix.

BCS of images using single secure measurement matrix

By using multiple chaotic map based measurement matrix in compressive sensing techniques, sampling, compression and encryption can be achieved in a single step. The measurements y are a function of sensing matrix. The receiver has to know the information about the key used to generate the measurement matrix Key (128-bit) in order to formulate the optimization problem to reconstruct the signal. This section proposes a cryptographic key based random measurement matrix for block-based compressive sensing techniques.

Algorithm description

In BCS, the N ₁ ×N ₂ image is divided into n non-overlapping blocks of size B ×B. Fowler et al. proved experimentally that the suitable block size in the BCS approach is 32 ×32 [15]. The algorithm description of the single measurement based encryption of BCS techniques is given below.

• 1. Divide the 2D image $\textbf{X}$ of size N ₁ ×N ₂ into n blocks of size B ×B.

• 2. Rasterize the 2D blocks $\{\textbf{X}_i\}_{i = 1,...,n}$ into B ² ×1 vectors $\{\textbf{x}_i\}_{i = 1,...,n}$

  $$ \{\textbf{x}_i\}_{i = 1,...,n} = \text{Raster}(\{\textbf{X}_i\}_{i = 1,...,n}) $$

  where, Raster(.) represents the rasterization operator.

• 3. Generate a secure $M_B \times B^2$ measurement matrix ϕ _B based on a 128-bit key (Key), where $M_B = \lfloor\frac{M}{N}B^2\rfloor$.

  $$ \phi_B \longleftarrow \dfrac{1}{B^2}\text{randn}\left(\textbf{x}_r, M_B,B^2 \right) $$

• 4. Apply $M_B \times B^2$ measurement matrix ϕ _B on $\{\textbf{x}_i\}_{i = 1,...,n}$ to get the the measured vectors $\{\textbf{y}_i\}_{i = 1,...,n}$

  $$ \{\textbf{y}_i\}_{i = 1,...,n} = \phi _B \{\textbf{x}_i\}_{i = 1,...,n} $$

• 5. Apply the reconstruction algorithm to reconstruct the 1D vector representation of the image, where ϕ _B is generated using 128-bit decryption key (Key).

  $$ \begin{array}{lll} && \tilde{\{\textbf{x}_i\}}_{i = 1,...,n} \\ &&\quad = \text{CS\_Reconstruction}\left( \{\textbf{y}_i\}_{i = 1,...,n},\phi _B,\psi\right) \end{array} $$

• 6. Unrasterize the image from $\tilde{\{\textbf{x}_i\}}_{i = 1,...,n}$

  $$ \tilde{\{\textbf{X}\}_i}_{i = 1,...,n} = \text{Unraster}\big(\tilde{\{\textbf{x}_i\}}_{i = 1,...,n}\big) $$

• 7. Obtain the reconstructed image $\tilde{\textbf{X}}$ from $\tilde{\{\textbf{X}_i}\}_{i = 1,...,n}$

Here, the CS_Reconsruction(.) is the reconstruction operator used to reconstruct the CS measured images. TV, SPL or MS-BCS-SPL based BCS approaches can be applied in the proposed method.

Security

The total key size of the proposed encryption system is 128 bits. For image/compressive sensing application point of view, this produce a large key space of 2¹²⁸. Hence, performing Brute force attack is a tedius task in the proposed system. On an average 2¹²⁷ operations are required to be performed for the Brute force attack. Since two chaotic maps are chosen at random for random number of iterations and the random values of two maps are combined together, performing known plaintext attack is also a difficult task. However, if the information of a single block is available with the attacker, there is a chance of retrieving the complete image.

To avoid this possibility, it is proposed to use separate measurement matrix for different blocks of images in BCS of images. Thus, the modified system can provide high level of security with a marginal increase in computational complexity. The following section proposes a secure BCS of images based on multiple measurement matrices.

BCS of images using multiple secure measurement matrices

To generate multiple measurement matrices for multiple blocks of images, it is proposed to generate different random streams from the random pair of chaotic maps for each measurement matrix. It is based on the fact that from the known random stream it is difficult to find out the chaotic maps used due to the combining effect of these two chaotic maps. That means, CP ₁ is unknown for an attacker. In this paper, it is proposed to select the next CPIN based on the current CPIN and number of iterations based on the previous iteration number. The initial values of the newly selected chaotic maps are the final chaotic values of the previous chaotic maps.

Let CP _i be the selected chaotic pairs for the generation of i ^th measurement matrix. Then, the chaotic pair for the next measurement matrix is found by using LCG, which is given as,

$$ CP_{i+1} = \left( 5CP_i + 1\right) \text{mod} $$

(30)

Similarly, if N ⁱ represents the number of iterations of the chaotic maps for the i ^th measurement matrix, then the number of iterations of next chaotic maps for the next measurement matrix will be,

$$ N^{i+1} = \left( 5CP_iN_i + 1\right) \text{mod} $$

(31)

The remaining procedure for generating the measurement matrix is same as that explained in section “Algorithm description of secure measurement matrix generation”. The measurement matrix for jth block is given as,

$$ \phi_{Bj} \longleftarrow \dfrac{1}{B^2}\text{randn}\left(\textbf{x}_{rj}, M_B, B^2 \right) $$

Algorithm description of multiple measurement matrices based BCS of images

Assume that the N ₁ ×N ₂ image is divided into n non-overlapping blocks of size B ×B. Since there are ‘n’ blocks present in the original image, ‘n’ measurement matrices are required to perform the secure compressive sensing operation in the proposed system. The measurement matrix generation can be performed in parallel with the compressive sensing operation of individual blocks so that the effective time of operation can be reduced. Let ϕ _B1, ϕ _B2,...,ϕ _Bn be ‘n’ measurement matrices generated by the LFSR based secure system. Then the overall measurement matrix can be represented as a block diagonal matrix as given below,

$$ \phi = \begin{bmatrix} \phi_{B1} & 0 & ... & 0\\ 0 & \phi_{B2} & ... & 0\\ ... &... & ... & ...\\ 0&... &0 &\phi_{Bn} \end{bmatrix}$$

The algorithm description of the above mentioned encryption method is given below.

• 1. Divide the 2D image $\textbf{X}$ of size N ₁ ×N ₂ into ‘n’ blocks of size B ×B (Eg: 32 ×32).

• 2. Rasterize the 2D blocks $\{\textbf{X}_i\}_{i = 1,...,n}$ into B ² ×1 vectors $\{{\textbf{x}_i}\}_{i = 1,...,n}$

  $$ \{\textbf{x}_i\}_{i = 1,...,n} = \text{Raster}\left( \{\textbf{X}_i\}_{i = 1,...,n}\right) $$

  where, Raster(.) represents the rasterization operator.

• 3. For the ith block, generate the measurement matrix {ϕ _Bi } _{i = 1,...,n} using the proposed multiple chaotic map based approach mentioned in section “Algorithm description of secure measurement matrix generation” based on the encryption key Key, where, the chaotic maps used and the number of chaotic maps can be decided by the following relations.

  $$ CP_{i+1} = \left( 5CP_i + 1\right) \text{mod} $$
  $$ N^{i+1} = \left( 5CP_iN_i + 1\right) \text{mod} $$

• 4. Apply $M_{{\kern-1pt}B} {\kern-2pt}\times{\kern-3pt} B^2$ measurement matrix {ϕ _Bi } _{i =  1,...,n} on $\{\textbf{x}_i\}_{i = 1,...,n}$ to generate

  $$ \{{\textbf{y}_i}\}_{i = 1,...,n} = \{\phi _{Bi} {\textbf{x}_i}\}_{i = 1,...,n} $$

  where, the subrate $S=\frac{M_B}{B^2}$

• 5. Apply the reconstruction algorithm to reconstruct the 1D vector representation of the image, by generating the measurement matrices {ϕ _Bi } _{i = 1,...,n} based on multiple chaotic maps using the decryption key Key.

  $$ \{\tilde{{\textbf{x}_i}}\}{\kern-1pt} ={\kern-1pt} \text{CS\_Reconstruction}({\kern-.5pt}\{\textbf{y}_i\},\{\phi _{Bi}\},\psi{\kern-1pt}\}{\kern-.5pt})_{i = 1,...,n} $$

• 6. Unrasterize the image from $\{ \tilde{{\textbf{x}_i}}\}_{i = 1,...,n}$

  $$ \{\tilde{{\textbf{X}}_i}\}_{i = 1,...,n}) = \text{Unraster}( \{\tilde{{\textbf{x}_i}}\}_{i = 1,...,n}) $$

• 7. Obtain the reconstructed image $\tilde{{\textbf{X}}}$ from $\{\tilde{{\textbf{X}_i}}\}_{i = 1,...,n}$

Even though, the proposed multiple measurement matrix based encryption technique for BCS of images takes higher computational time than single measurement matrix based encryption technique, the complexity of both the proposed approaches are simple and can maintain the robustness of the compressive sensing system to noise.

Analysis of the proposed encryption system

The different BCS approaches for images are considered for evaluating the performance of the proposed encryption system. Both the single and the multiple measurement matrices based encryption methods are validated through BCS-TV, BCS-SPL-DCT, BCS-SPL-DWT, BCS-SPL-DDWT and MS-BCS-SPL techniques. Experimentally it is proved that the proposed system maintains the reconstruction quality and the robustness of these approaches with high level of security.

Experimental analysis of the proposed encryption system is performed on several images. For analysis standard images of size 512 ×512 divided into non-overlapping blocks of 32 ×32 are considered. Thus, each block can be converted into a column vector of 1024 ×1 and the total number of blocks for each image is 256. For multiple measurement matrix based encryption system, 256 measurement matrices are required. In MS-BCS-SPL, DWT transform with 3 decomposition levels is considered and each level is divided into 32 ×32 blocks. The proposed system is performed with different subrates, S = 0.1, 0.2, 0.3, 0.4 and 0.5 for various images. In hard thresholding, the convergence factor λ is chosen as 6 whereas in bivariate shrinkage the convergence factor λ is selected as 25.

Security analysis

The proposed encryption system is tested against various forms of attacks and proved to be resistant against the same. The main problem with the chaotic maps is its vulnerability to known plaintext attack. In the proposed system, the random selection of chaotic maps and combining their outputs make it capable of withstanding known plaintext attack.

Known plaintext attack

In the proposed system, instead of random selection of a single chaotic map, it is proposed to select a pair of chaotic maps based on a secret key. The number of iterations for these chaotic maps is also determined by another secret key. Thus, there is a randomization in the chaotic map selection from 64 combinations and number of random elements used for generating the measurement matrix. In the proposed approach, the randomly selected chaotic maps are run for random number iterations to form two sets of random arrays. The corresponding elements of these arrays are XORed to form new random array.

$$ x_r(j) = x^1(j)\oplus x^2(j) $$

Thus, the newly generated random array depends on initial values of both the selected chaotic maps. From the known random elements, it is very difficult to find out the chaotic maps used in this combination and corresponding initial values. Moreover, the process of finding out the random stream used for generating the measurement matrix becomes a tedious task.

If the plaintext-ciphertext pairs of a single block are available with the attacker, the only possible way to find out the measurement matrix used for that block will be the Brute force search approach. This rare chance of attack can be negated, if all blocks are measured with different measurement matrices. In the proposed approach, the chaotic maps for the next measurement matrix and the number iterations used for generating the random array to form the measurement matrix are based on the relations.

$$ CP_{i+1} = \left( 5CP_i + 1\right) \text{mod} $$

$$ N^{i+1} = \left( 5CP_iN_i + 1\right) \text{mod} $$

The chaotic pair selection is dependent on the previous chaotic pair selection. That is not known for the attacker. Moreover, the number of iterations depends on the previous number of iterations as well as the previous chaotic pair map number. Even though, the attacker has the knowledge about the number of iterations without knowing the previously used chaotic pair map number, he will not be able to find the number of iterations for the current pair of chaotic maps. Thus, the proposed encryption system can withstand known plaintext attack.

Cipher text-only attack

Cipher text-only attack (COA) or known ciphertext attack is an attack model for cryptanalysis where the attacker is assumed to have access only to a set of ciphertexts. The attack is completely successful if the corresponding plaintexts can be deduced, or even better, the key. Since the attacker has only minimum information about the message, the ciphertext only attack is much more difficult than known plaintext attack. In this case, the only possibility to retrieve plaintext is to make Brute force trials on both keys, which is very complex. Thus, a system, which is capable of resisting known plaintext attack can withstand against ciphertext only attack.

Brute force attack

In the proposed approach, the external secret key has a size of 128-bit. Thus, the key space for the proposed encryption system for BCS of images is 2¹²⁸. For image application, this accounts to very large key space. For successful Brute force attack, on an average (2¹²⁸/2) operations are required to retrieve the key used for encryption. Hence the security of the proposed encryption for BCS of images against Brute force attack is very high.

Reconstruction performance of the proposed encryption system

The quality analysis of reconstructed images of the proposed encryption system for BCS of images is performed. Various test images are considered for evaluating the performance of the proposed encryption system. Different BCS approaches like, BCS-TV, BCS-SPL-DCT, BCS-SPL-DWT, BCS-SPL-DDWT and MS-BCS-SPL are applied to these images to check the reconstruction quality, which is measured in terms of the peak signal to noise ratio (PSNR) value of the reconstructed images with the corresponding original images. The PSNR for an N ₁×N ₂ image can be calculated as,

$$ PSNR=10log_{10}\left(X_{\rm max}^{2}/MSE\right) $$

(32)

where, X _max is the maximum possible pixel value of the image. The MSE can be calculated as,

$$ MSE = \frac{1}{N_1N_2}\sum^{N_1}_{i=1}\sum^{N_2}_{j=1}\left(X\left(i,j\right)-Y\left(i,j\right)\right)^{2} $$

(33)

where X(i, j) and Y(i, j) represent corresponding pixel values of the original and reconstructed images respectively.

The rate can be calculated by using the following relation,

$$ \text{Rate} = \dfrac{M}{N}H_y $$

(34)

where, H _y is the entropy of the measured data y after quantization in bits per pixel, where the problem of unused quantisation values can be avoided by considering that these values occurred at once [35]. For single measurement matrix approach, DPCM is incorporated to get quantized BCS instead of only scalar quantization [29]. The PSNR and the rate at different subrates for the test images Lena, Goldhill and Barbara are given in Table 2. Comparable PSNR values as that of the results given in [15] are obtained from the proposed system, which shows that the proposed encryption system can maintain the quality level.

Table 2 Reconstruction performance of the proposed encryption system for 512×512 images

The rate-distortion characteristics of the Lena, Goldhill and Barbara images for different BCS reconstruction approaches are given in Fig. 2a–c. The reconstructed images under different reconstruction methods for ‘Peppers’ image at a subrate S = 0.2 are shown in Fig. 3a–e. The construction qualities in PSNR for Peppers image under different reconstruction methods are 31.41 dB (Fig. 3a), 31.11 dB (Fig. 3b), 31.72 dB (Fig. 3c), 32.09 dB (Fig. 3d) and 32.96 dB (Fig. 3e) for BCS-TV, BCS-SPL-DCT, BCS-SPL-DWT, BCS-SPL-DDWT and MS-BCS-SPL respectively.

Fig. 2

Rate distortion curves for the proposed encryption system (a) Lena, (b) Goldhill, (c) Barbara images

Fig. 3

Reconstruction using a BCS-TV (31.41 dB), b BCS- SPL-DCT (31.11 dB), c BCS-SPL-DWT (31.72 dB), d BCS-SPL-DDWT (32.09 dB), e MS-BCS-SPL (32.96 dB) for “Peppers” image at S = 0.2

Robustness to noise of the proposed system

In [4], it is mentioned that the compressive sensing paradigm provides perfect reconstruction in the presence of added noise in the real-application by solving it as an optimization problem. In the proposed encryption system, the key based generation of random measurement matrix maintain the robustness of the compressive sensing system. The empirical evaluation of the robustness can be performed by finding the characteristics between the PSNR and normalized noise perturbation power. The normalized noise perturbation power (nPERT _y ) on y is given as [31],

$$ nPERT_y = 10 log\frac{\Vert \tilde{y} - y\Vert^2}{\Vert y\Vert^2} $$

(35)

where, $\tilde{y}$ represents the noisy version of measurement vector. The robustness of the proposed system can be evaluated from normalized noise perturbation power versus PSNR characteristics.

Figure 4a shows the robustness characteristics of the proposed encryption method to noise for various standard images of size 512 ×512 at S = 0.2, where BCS-SPL-DDWT approach is adopted. From the characteristics, it can be understood that the proposed encryption system can maintain the robustness of the compressive sensing approach for any image. Even at − 20 dB of normalized noise perturbation power (nPERT _y ), the proposed encryption method for BCS-SPL approaches give good PSNR value. Thus, the proposed encryption system maintains robustness to noise as that of the ordinary compressive sensing system for BCS-SPL reconstruction approaches. Figure 4b represents the robustness characteristics to noise for Lena image for MS-BCS-SPL reconstruction approach. In general, the proposed encryption system maintains the robustness to noise in the compressive sensing framework at any subrate for any reconstruction approach.

Fig. 4

a Robustness characteristics to noise of the proposed encryption system for different images under BCS-SPL-DDWT reconstruction at S = 0.2, b Robustness characteristics to noise for MS-BCS-SPL reconstruction approach for Lena image

Conclusion

In this paper, a novel approach for secure compressive sensing of images is presented by generating random measurement matrix based on multiple chaotic maps so that the encryption system can maintain the robustness of the compressive sensing system to noise. For the generation of measurement matrix, eight one dimensional chaotic maps are chosen from which two are randomly selected based on a secret key. The number of iterations of these chaotic maps are also decided by an external key and the chaotic values obtained from these maps are combined together to form a new random array. To improve the security, key based decision of initial values of the chaotic maps are incorporated. The generated random stream is used to generate each normal value of the random measurement matrix. Since the chaotic values of two randomly selected chaotic maps are combined together, it is very difficult to mount a successful known plaintext attack. To improve the security further, it is proposed to use different measurement matrices for different blocks of images. The chaotic map selection and its number of iterations are determined by the previous chaotic maps and its number of iterations. The proposed encryption system is validated through different reconstruction approaches of BCS and it was found that it maintains the reconstruction quality and robustness of the compressive sensing with high level of security.