1 Introduction

The innovation in the field of imaging sensors, multimedia systems, optics, affordable storage systems and high-speed internet communication technologies is manifold. Consequently, a colossal amount of data is generated that must be processed and distributed. The major constraints in any multimedia communication systems are limited bandwidth and security. Data compression overcomes bandwidth limitations by reducing the amount of data to be transmitted and stored, whereas encryption thwarts security risks. In [31] the authors proposed a wavelet based scheme, that extracts and encodes only approximations of the image using fixed-point arithmetic, which considerably improved the lifetime of the sensors. In [32] only shift and add operations together with BinDCT is used to directly extract and encode the DC coefficient and the first three AC coefficients of an 8 × 8 image blocks. An efficient multimedia communication must provide rapid transmission, information security and prompt retrieval, which can be achieved by performing compression and encryption simultaneously.

Traditional encryption schemes like DES, AES etc. are not suitable for image encryption because of the inherent properties of digital images like bulk data capacity, redundancy and strong correlation among adjacent pixels. Chaos based cryptosystem is widely used due to the properties of chaotic systems like periodicity, sensitive dependence on initial conditions and pseudo-randomness. Zhou et al. [46] proposed a new chaotic system that generates three new one-dimensional chaotic maps by combining existing one-dimensional chaotic maps like the Logistic, Sine and Tent maps. They proved that the new chaotic system has larger chaotic range, excellent diffusion and confusion properties. The proposed scheme has a 4-round encryption structure that could resist brute force attack. A cryptosystem using chaos and permutation-substitution network was proposed by Belazi et al. [3]. A new one-dimensional chaotic map which outperforms the logistic map is first used to diffuse the plain image. The substitution operation is performed by using the s-boxes. A diffusion operation is also implemented using logistic map, thereby increasing the cryptographic strength. Finally, a permutation function is used to obtain an encrypted image, that can resist statistical attacks. In [12] a double image encryption scheme using logistic map and cellular automata is proposed. The keys for the encryption are generated by the convolution of the logistic maps. The least significant bits of the two images are first combined and then diffused using cellular automata. The performance of the proposed scheme and the randomness of the key are experimentally verified. In [8] a multiple image encryption using logistic map and Fractional Fourier Transform is proposed. The fractional order is used as the key in the encryption process. The performance analysis showed that the proposed scheme is highly secure and requires less bandwidth to transmit the encrypted data.

In general, the chaotic cryptosystem based on low dimensional maps are vulnerable to security threats. The low dimensional maps are simple in structure and their chaotic values can be predicted using chaotic signal estimation technologies. Hence higher dimensional chaotic maps or coupled chaotic systems are used in many recent chaos based encryption schemes. In [42] the 3D bit matrix of an image is permuted by using a coupled chaotic system, which is obtained by coupling the Chen system and 3D chaotic map. The permuted image is again diffused to obtain the cipher image. A 2D–Sine Logistic Modulation Map [14] based encryption was proposed by Hua et al. The two one-dimensional maps are combined to form a 2D map which is then used in the encryption of the image. In [3, 14, 42, 46] the chaos based encryption is performed in the pixel domain, whereas in [36] the encryption is performed in both pixel and wavelet domain. A 6D–hyperchotic system together with 2D–DWT is used to encrypt the image. The key for the encryption scheme depends on the image and the hyperchaotic system. A non-uniform cellular automata framework together with hyper-chaos is used for encryption in [29]. Security analysis and experimental results showed that the proposed method has a very large key space and is resistive against noise and other attacks. In many applications in addition to image encryption it also requires image copyright protection and content authentication. Therefore, in areas like military, medicine etc. data hiding techniques [18, 20] can be employed along with encryption to ensure privacy and secrecy of the transmitted images.

The proposed schemes discussed above performs only encryption of the plain image. For an efficient multimedia communication, it is necessary to perform compression and encryption concurrently. [35, 40, 48] presents various models that perform both compression and encryption thereby providing a secure and fast image transmission. Yuen et al. [40] introduced a chaos based joint image compression and encryption scheme using DCT and SHA-1. The SHA-1 algorithm uses the low frequency components and the secret key to generate a message digest which is then used to diffuse the high-frequency coefficients. Huffman code is used to compress the encrypted data. The algorithm exhibited both key and plain image sensitivity. In [48] an image encryption - compression algorithm based on hyper-chaos and Chinese remainder theorem was proposed. The plain image was first shuffled using a 2D hyper-chaotic system. The Chinese remainder theorem was used to diffuse and compress the image simultaneously. The proposed method could encrypt and compress the image with a given compression ratio. A wavelet transform and a cross-chaos map based image compression and encryption is proposed by Tong et al. [35]. The high-dimensional chaotic sequence generated by the proposed cross-chaotic map is used to scramble the image pixels and then substituted by the ciphertext feedback algorithm. The low frequency components of the wavelet transform are encrypted and the security analysis showed that the algorithm has high security, good encryption speed and compression.

Compressive Sensing (CS) [9] is a new sampling, reconstruction technique which can perform sampling and compression simultaneously. Compressive sensing is extensively used in wireless sensor networks and in many applications like image encryption [44], image data hiding [19], healthcare monitoring system [39], activity recognition [17] etc. Dimensionality reduction plays a vital role in extracting salient features from a high dimensional data set. In vision based motion tracking [7, 23] and classification [22] dimensionality reduction is used. For such applications compressive sensing can be employed to achieve dimensionality reduction. CS uses optimization technique to reconstruct the original signal from the linear measurements. The linear measurements are obtained by sampling the signal at significantly lower rate than the Nyquist rate. Optimization techniques are used to maximize the benefits and minimize the production cost in various application. For example, optimization techniques are used in activity recognition [24, 26, 28], water quality prediction [27], predicting political ideology using online behavior of individuals [33], future career path prediction [25] etc.

In the resource constrained environment, it is necessary to reduce the amount of data transmitted and reduce energy consumption. Also, data security is of great importance. In the traditional method of data transmission compression and encryption are done in two steps. The sender compresses the data and then encrypts the compressed data. The receiver decompresses the received data through the channel and then decrypts the decompressed data. Compressive sensing performs the compression and encryption simultaneously. The measurement matrix that is used to compressively sample the signal acts as the shared secret key between the sender and the receiver. Generally, a Gaussian random matrix is used as the measurement matrix. However, in such a scenario the overhead required to transmit and store the secret key is high. In this paper a chaos based compressive sensing is proposed that satisfies the above stringent requirements. Compared with the traditional compressive sensing, chaos based compressive sensing can reduce the overhead required to store and transmit the secret key. Only the parameter required to generate the chaotic sequence must be stored. In addition, the sensitivity of chaos improves the security of data transmission.

In [43] the authors review the different types of encryption models that can be implemented using CS. The paper elaborates the six-different framework for an image cryptosystem, that can be implemented by combining CS with optics and chaos. In compressive sensing, based encryption models the measurement matrix acts as the secret key that is shared between the sender and receiver. In [34] the authors showed that CS based image cryptosystem does not achieve Shannon’s definition of perfect secrecy but computational secrecy is accomplished. Even though the secret key i.e. the measurement matrix is not known to the eavesdropper, the recovery of the original signal is a NP-hard problem. Hence providing computational secrecy. Orsdemir et al. [30] analysed the encryption method based on compressive sensing and proved that the method is computationally secure. Cambareri et al. [4] quantified the security of CS based encryption against known-plaintext attack theoretically. They showed that there exist many encoding matrices that generate similar plaintext-ciphertext pair. Hence a brute-force attack to find the encoding matrix is inconclusive.

The security property of the low complexity multiclass encryption is analysed by Cambareri et al. in [5]. The authors first investigate theoretically the properties of the multiclass encryption scheme. The performance bounds on the recovery quality obtained by lower-class receivers with respect to high class ones are derived. They showed that asymptotic spherical secrecy i.e. weak form of secrecy, can be achieved. Cambareri et al. proved that compressive sensing with iid Gaussian encoding matrix has the property that no information can be inferred from the statistical properties of all its possible cipher text but its power. The implications of this property are the basic guarantee that a malicious eavesdropper intercepting the measurement vector will not be able to extract any information on the plain text except for its power. Fay [10] introduced Counter mode of operation in compressive sensing based encryption to achieve probabilistic encryption with security against chosen plaintext attacks. The inherent secrecy of the compressed measurements is solely responsible for the security of the proposed scheme. One secret key is used to encrypt multiple messages. Random binary matrices are generated by evaluating a pseudorandom function at different points by using the secret key, a counter and the matrix row index. Zhang et al. [41] analysed the problem of constructing a CS based symmetric cipher under the key reuse circumstance i.e. the cipher is resistant to common attacks even if a fixed measurement matrix is used multiple times.

Huang and Sakurai [15] proposed a compression combined digital image encryption method that is robust against consecutive packet loss and shear attack. A Gaussian measurement matrix was used to generate the reduced measurements and then the measurements are scrambled using an Arnold map. The scheme exhibited robustness, incoherence, low data volume, key sensitivity and resistance to brute force attack. Zhou et al. [44] introduced a key-controlled measurement matrix for performing hybrid image compression - encryption. They showed that the key-controlled measurement matrix reduces the complexity in the distribution and storage of key. The security of the scheme was verified against different attacks and also the method provided good compression performance. In [45] an image cryptosystem using chaos and compressive sensing, to achieve simultaneous compression-encryption is proposed. In [16] the authors proposed CS based encryption in a parallel computing environment. Since the measurements are linear, the cipher is vulnerable to chosen-plaintext attack. To thwart such attack, the paper proposed a block cipher structure consisting of scrambling, mixing, s-box and chaotic lattice xor. The technique increased compressibility and encryption speed because of the parallel encryption structure. Hu et al. [13] proposed an image coding scheme based on parallel compressive sensing framework. Each column of the two-dimensional image data is sampled in parallel. Since CS sampling is a linear process, security against chosen plaintext attack is achieved by employing a nonlinear chaotic sensing matrix and counter mode of operation. The energy information leakage is overcome by the implementation of a diffusion operation. In [19] a new separable data hiding in encrypted images by using CS and Discrete Fourier Transform (DFT) is proposed. After performing DFT, embedding of the secret image is done on the high frequency parts of real part and imaginary part of DFT. Iterative Reweighted Least Squares Optimization is used as the recovery algorithm of CS.

In this paper, a parallel compressive sensing framework is used to compressively sample the signal using an incoherence rotated chaotic matrix. A novel one-dimensional chaotic map is proposed and it is used in the generation of the measurement matrix. The generation of the chaotic matrix is controlled by a secret key which is dependent on the input image. Further encryption is achieved by performing confusion and diffusion operation using the chaotic sequence generated by the proposed map. The rest of the paper is organised as follows. Section 2 gives a brief introduction about compressive sensing. Section 3 elaborates the proposed chaotic map and analyses its chaotic behaviour. The incoherence rotated chaotic matrix structure and its generation is explained in Section 4. The proposed compression-encryption scheme is explained in Section 5. In Section 6, the experimental results and the performance of the proposed scheme are discussed. Finally, the conclusion is drawn in Section 6.

2 Preliminaries

2.1 Compressive sensing

Classical data acquisition states that, if a signal is sampled at Nyquist rate i.e. twice the maximum frequency it can be perfectly reconstructed. In multimedia applications the Nyquist rate can result in large amount of samples, which has to be compressed for storage and faster transmission.

Compressive Sensing [2] is a new paradigm that states that if a signal is compressible/sparse in some domain, then it can be perfectly reconstructed by sampling at a rate less than the Nyquist sampling rate. The fundamental requirements in compressive sensing are sparsity, measurement matrix and the reconstruction algorithm. Sparsity indicates that the signal has a concise representation in some basis ψ. If an image is sparse in a basis, it has few large coefficients that capture most of the information and all the other coefficients are small. Sparsity leads to efficient estimation, compression and dimensionality reduction. The image data is naturally sparse in some basis.

For a signal x with N real valued samples, its transform coefficients α is given by

$$ \alpha ={\psi}^Tx $$
(1)

where ψ is the orthogonal basis. Only a few large coefficients of α capture the principal information and all the other coefficients of α are close to zero. A linear measurement process is used to compute the measurements y by projecting x onto a measurement matrix φ. The measurement matrix is of size M⨯N and the measurements are computed as follows

$$ y=\varphi x=\varphi \psi \alpha =\varTheta \alpha $$
(2)

where Θ = φψ is the sensor matrix with size M⨯N.

The measurement matrix must guarantee the recovery of the signal from a small number (M < <N) of measurements y. Candes [6] presented the Restricted Isometry Property (RIP) as a sufficient condition on the sensing matrix to perform perfect recovery. A matrix φ satisfies the restricted isometry property if

$$ \left(1-{\delta}_k\right){\left\Vert f\right\Vert}_2^2\le {\left\Vert \varphi f\right\Vert}_2^2\le \left(1+{\delta}_k\right){\left\Vert f\right\Vert}_2^2 $$
(3)

holds for all vectors f Є Rn with sparsity k. In [1] Banderia et al. proved that the determination of RIP for a matrix is NP-hard. An alternative approach to perfect reconstruction is to ensure that the measurement matrix φ is incoherent with the basis ψ.

The signal x can be recovered from the measurements y by finding the sparsest solution

$$ \kern0.5em \min \kern0.5em {\left\Vert \alpha \right\Vert}_0\kern1em subject\kern1.5em to,\kern1em y=\varTheta \alpha $$
(4)

The commonly employed methods are Matching Pursuit (MP), Orthogonal Matching Pursuit (OMP), Smoothed l 0 (Sl 0) and so on. In this paper OMP [21] is used for reconstruction.

2.2 Security analysis of compressive sensing measurements

In this section security analysis of the compressive sensing measurements against different attacks are discussed. As CS sampling is a linear process it is prone to known/chosen-plaintext attacks. The Adversary model for the proposed scheme is that an eavesdropper has access to the encryption oracle. The eavesdropper also has access to known plaintext-ciphertext pair. From the captured data the eavesdropper tries to recover the secret key used by the encryption oracle. As proved by Rachlin and Baron [34], in CS recovering the original signal without the appropriate secret key (i.e. the measurement matrix) is equivalent to solving a NP-hard problem. In the proposed scheme a secret key shared between the sender and receiver is used as the seed to generate the measurement matrix φ. Since a data dependent key generation is used different symmetric keys are generated for different images. Therefore, a security breach will not reveal the other secret keys. Hence the adversary cannot estimate a fixed measurement matrix φ through known-plaintext attack. The eavesdropper will not be able to gather enough data to launch a known-plaintext attack as a new measurement matrix is generated for each plaintext.

The CS sampling process is vulnerable to energy leakage. In the proposed scheme a parallel CS sampling technique is used. The sparse transform coefficients of the plain image are measured column by column. Finally, a chaos based confusion-diffusion is employed to obtain the cipher image. The parallel CS sampling results in the preservation of energy information within each column. In [13] it is showed that chaos based diffusion operation results in uniform energy distribution over the entire image. Therefore, the proposed scheme mitigates the problem of energy information leakage.

In the proposed scheme a chaos based measurement matrix is used for simultaneous compression-encryption. The security of chaos based CS depends on the chaotic map’s sensitivity to the initial condition and the control parameters. In the case of the widely used Gaussian measurement matrix, it is easy for the eavesdropper to decrypt the data by using an intercepted approximate key. In chaos based measurement matrix construction even a small perturbation of the order of 10−15 to the secret key makes the decryption unsuccessful. Security against these perturbations are quantified in Section 4.6.

3 Proposed scheme

The proposed compression-encryption scheme involves key scheduling, Chaotic map generation, IRC measurement matrix construction, compressive sampling, permutation, quantization and diffusion.

3.1 Proposed chaotic map

Chaotic maps are dynamical systems with high sensitivity to initial conditions and control parameter. An arbitrary small change in the initial conditions leads to significant deviations. This sensitivity puts an effective limit on our ability to predict the behavior of chaotic systems over long periods of time. Chaos based encryption schemes employs the initial conditions as secret key for encryption. It is impossible to know the initial conditions exactly with infinite precision. Hence, chaos based encryption schemes can resist attacks from intruders. The chaotic maps can be classified into one-dimensional chaotic maps and high-dimensional chaotic maps. The one-dimensional chaotic maps usually contain one variable and a few parameters. The 1D–maps like Logistic, Sine and Tent maps have simple structures. The chaotic structure can be determined by using chaotic signal estimation technologies. Therefore, the encryption schemes based on these 1D maps are vulnerable to various cryptographic attacks. Hence higher dimensional chaotic maps are employed for encryption. Logistic map is simple in structure and it is widely used in image encryption. The logistic map has single control parameter μ L and is defined by the following equation

$$ {L}_{n+1}={\mu}_L\;{L}_n\;\left(1-{L}_n\right);\kern0.48em L\in \left[0,1\right],0\le {\mu}_L\le 4 $$
(5)

The Sine Map has single control parameter μ S and is defined as

$$ {S}_{n+1}={\mu}_S\;\sin\;\left(\pi \ast {S}_n\;\right);\kern0.36em S\in \left[0,1\right],0\le {\mu}_S\le 1 $$
(6)

The Tent Map is given by

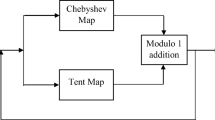
$$ {T}_{n+1}=1-{\mu}_T\ast \left|{T}_n-0.5\right|;T\in \left[0,1\right],0\le {\mu}_T\le 2 $$
(7)

In the 1D maps the next iteration value is obtained by a linear transform. Hence it can be predicted easily. Hence for chaos based cryptosystem the security can be enhanced by combining the existing 1D maps to form a one-dimensional or a higher dimensional chaotic map. Several new one-dimensional chaotic maps are proposed in literature. In this paper, a new 1D chaotic map is proposed by combining the Logistic, Sine and the Tent map. The chaotic behavior of the new map is verified by performing the bifurcation and Lyapunov exponent analysis. The proposed Sine-Tent-Logistic map (STL) is formed by performing fusion and cascading operations on the three 1D maps. The fusion operation generates new chaotic maps by mixing the dynamics of two seed maps in a nonlinear way. The cascading operation connects two 1D maps in series [47]. The new map is generated by first performing fusion operation on the two seed maps – Logistic and Tent map. Secondly, cascading operation is performed using the Sine map and the map generated in the first step. The structure for generating the proposed one-dimensional map is as shown in Fig. 1.

Fig. 1
figure 1

Structure of proposed chaotic map

Full size image

The Tent map exhibits highly chaotic behavior when the control parameter μ T  = 2, therefore in the first seed map the control parameter is taken as the constant value 2. The fusion operation combines the two seed maps – Tent, Logistic map in a non-linear way. The input Z n is simultaneously fed into the two seed maps and then the output of the two seed maps are added together. The cascading operation connects the Sine map and the fusion of the Tent, Logistic map in series to obtain Z n + 1. The proposed map is mathematically represented as

$$ {Z}_{n+1}=\left\{\begin{array}{l}\sin\;\left(\pi \left(\;\left(1-2\ast \left|{Z}_n-0.5\right|\;\right)+\left(\mu \ast {Z}_n\ast \left(1-{Z}_n\right)\right)\right)\right)-1,{Z}_n>1\\ {}\sin\;\left(\pi \left(\;\left(1-2\ast \left|{Z}_n-0.5\right|\;\right)+\left(\mu \ast {Z}_n\ast \left(1-{Z}_n\right)\right)\right)\right)+1,{Z}_n<0\end{array}\right.\kern0.36em ;{Z}_n\in \left(0,1\right),\mu >0 $$
(8)

where n = 0, 1, 2, ….

The chaotic behavior of the proposed map is evaluated using the Lyapunov exponent, Shannon entropy and bifurcation analysis. The performance of the proposed map is compared with that of the one-dimensional seed maps. The bifurcation diagrams of the seed maps and the proposed map are shown in Fig. 2. The bifurcation diagram is obtained by plotting the chaotic sequence generated for an initial value 0.2301. From Fig. 2, we can infer that the chaotic sequence generated by the proposed STL map is highly chaotic and uniformly distributed for μ ∈ (0, 4). The seed maps are not uniformly distributed, they are chaotic in certain intervals of μ. when the parameter μ L ϵ [3.86, 4], the logistic map exhibits good chaotic characters. The logistic map exhibits chaotic behavior when μ L  > 3 with intermittent intervals of stability called the periodic window. For 3.284 ≤ μ L ≤ 3.8415 the logistic map exhibits a stable 3-cycle [11]. As μ L moves further away from this periodic window, interspersed periods of chaos start appearing and fully chaotic behavior is once again achieved. For an initial value of x 0 = 0.2301, the bifurcation diagram of the logistic map in the interval [3.5, 4] is shown in Fig.2(a). From the figure, we can observe that for μ L  = 3.86 the logistic map exhibits a fully chaotic behavior.

Fig. 2
figure 2

Bifurcation diagram of (a) Logistic map, (b) Tent map, (c) Sine map, (d) Proposed Chaotic map

Full size image

Chaotic behavior of a map can be evaluated using the Lyapunov exponent. The Lyapunov Exponent (LE) is a measure of the sensitivity of the map to the initial condition i.e. an estimate of the amount of chaos in a system. If the Lyapunov exponent is negative then the system is stable. A positive LE quantify the exponential divergence from the initial condition. The greater the value of the maximum LE, greater the chaos in a system. The LE of the seed maps and the proposed maps are shown in Fig. 3. The LE of the proposed map is positive for all μ ∈ (0, 4). From Fig. 3(a), we can see that the logistic map is not chaotic for some values of μ. The comparison of the LE of the proposed map and the 1D map employed by Belazi et al. [3] is shown in Fig.3(b). The values of the initial parameter Z 0 and the control parameter μ of the chaotic map is used as the secret key in the encryption operation. For μ ∈ (0, 8) the map in [3] is chaotic in certain bands, whereas the proposed map is highly chaotic in the entire range. Hence, a larger key space can be obtained when using the proposed map thereby increasing the cryptographic strength of the algorithm. The Lyapunov exponent determines the overall predictability of the system. The Lyapunov exponents sharply discriminate between the different dynamics. A fixed point or stable periodic orbit will have all negative exponents, a LE of zero indicates that the system is in some sort of steady state mode and a positive LE indicates that the system is chaotic. Also, larger the Lyapunov exponent greater the chaos of the system. Table 1 shows the comparison between the LE values of the Logistic map, Proposed map and the map used in [3]. For a given initial value and control parameter the LE of different maps are computed and tabulated in Table 1. The sequence generated by the maps for the given parameters are chaotic, as indicated by the positive LE values in Table 1. Also, it is inferred that the LE obtained for the chaotic sequence generated using the proposed map is greater than the LE of the compared maps i.e. the sequence generated using the proposed map is more chaotic. Therefore, the proposed map is more suitable for measurement matrix construction.

Fig. 3
figure 3

Comparison of Lyapunov Exponent (LE)

Full size image
Table 1 Comparison of Lyapunov Exponent value for different Initial Parameter (IP) and Control Parameters (CP)
Full size table

For the exact recovery of signal from the reduced measurements, the measurement matrix must satisfy the Restricted Isometry Property. The measurement matrix constructed using elements drawn from distributions like Gaussian and Bernoulli satisfies the RIP condition with high probability. The drawback of these random distribution based measurement matrix construction is hardware implementation, the overhead to store and transmit the same. Yu et al. [38] employed chaotic sequence in the construction of the measurement matrix. They showed that the pseudorandom measurement matrix constructed using the chaotic sequence satisfied the RIP with overwhelming probability. The hardware implementation of the chaotic matrix can be realized easily and only the initial condition, the control parameter should be stored and transmitted. The experimental results verified that the performance of the chaotic measurement matrix is comparable to that of the commonly used Gaussian random matrix. Yu et al. showed that chaotic measurement matrix can be used in compressive sensing applications. The embedding of security in compressive sensing application can be achieved by using the initial conditions and the control parameter as the shared key between the sender and the receiver.

3.2 Generation of parameters of Chaotic map

The generation of the chaotic map is controlled by the initial parameter Z 0 and the control parameter μ. These two parameters are used as the shared secret key between the sender and receiver. The secret key is distributed through a secure channel. The plain image is used in the key generation process. A 256-bit secret key K is obtained using the SHA-256 hash function on the plain image. The 256-bit key is divided into eight subkeys of length 32-bits, such that

$$ K={k}_1,{k}_2,\cdots, {k}_8;\kern0.48em {k}_i=\left\{{k}_{i,0},{k}_{i,1},\cdots, {k}_{i,31}\right\} $$
(9)

where k i, j denotes the j th bit in the i th subkey.

The subkeys together with the secret keys Z ′ 0, μ′ is used to generate the initial conditions and the control parameters of the chaotic maps used in the encryption process.

$$ {\displaystyle \begin{array}{l}{Z}_{0k}=\left(k{Z}_0^{\prime }+{t}_{2k-1}\right) \operatorname {mod}1\\ {}{\mu}_k=\left(k{\mu}_0^{\prime }+{t}_{2k}\right) \operatorname {mod}\;8;k=1,2,3,4\end{array}} $$
(10)

where t i is the intermediate value. The intermediate values are computed using the subkeys k i as follows,

$$ {t}_i=\sum \limits_{j=1}^{32}{k}_{i,j}\ast \left(\frac{2^{32-j}}{2^{32}}\right);\kern0.48em i=1,2,\cdots 8 $$
(11)

By varying the keys Z ′ 0 and μ′ different secret keys can be generated for the same image. Hence it is difficult for an attacker to find the secret key. To thwart chosen plaintext attack, the reuse of measurement matrix should be avoided. By using the key controlled chaotic measurement matrix construction and input dependent key generation the chosen plaintext attack can be resisted by the proposed compression-encryption scheme.

3.3 Chaotic measurement matrix generation

The measurement matrix used for compressive sampling and reconstruction is constructed using the chaotic sequence generated by the proposed map. The measurement matrix construction is based on the Incoherence Rotated Chaotic (IRC) as proposed by Yao et al. [37]. They proved that the IRC measurement matrix satisfied RIP and has better performance than Gaussian matrix, Bernoulli matrix etc. The proposed map is used to generate a chaotic sequence Z. The chaotic sequence is then down sampled at sampling distance d = 10 and transformed to obtain a sequence r. The construction of the IRC matrix φ M × N is as follows,

  1. 1.

    A chaotic sequence of length N 0 + dN is generated using the proposed map, whose initial parameter is Z 0 and the control parameter is μ. The Initial N 0 = 1000 values of the chaotic sequence are neglected to remove the transient effect.

  2. 2.

    The chaotic sequence is sampled at a distance d and a transformed sequence is obtained using

$$ {r}_i=1-2{Z}_{N_0+ id},i=1,2,\cdots $$
(12)
  1. 3.

    The transformed sequence is then employed to construct a IRC matrix whose structure is given below.

$$ \varphi =\sqrt{\frac{1}{2M}}\kern0.28em \left[\begin{array}{ccccc}{r}_1& {r}_2& \cdots & {r}_{N-1}& {r}_N\\ {}\eta {r}_N& {r}_1& {r}_2& \cdots & {r}_{N-1}\\ {}\eta {r}_{N-1}& {\eta}^2{r}_n& {r}_1& \cdots & {r}_{N-2}\\ {}\eta {r}_{N-2}& {\eta}^2{r}_{N-1}& {\eta}^3{r}_N& \cdots & {r}_{N-3}\\ {}\vdots & \vdots & \vdots & \ddots & \vdots \\ {}\eta {r}_{N-M+2}& {\eta}^2{r}_{N-M+3}& {\eta}^3{r}_{N-M+4}& \cdots & {r}_{N-M+1}\end{array}\right] $$
(13)

where η is the incoherent coefficient and M is the number of measurements.

3.4 Proposed compression-encryption scheme

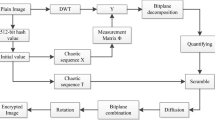
The overall schematic of the proposed scheme is shown in Fig. 4(a). The block diagram of the proposed compression-encryption scheme is given in Fig. 4(b).

Fig. 4
figure 4

(a) Flowchart of the proposed scheme (b) Block diagram of the proposed compression-encryption scheme

Full size image

The proposed scheme is as follows,

  1. 1.

    The SHA-256 hash function of the plain image is generated and a 256-bit secret key K is obtained. The secret key K and the parameters Z ′ 0, μ′ are used to generate the initial condition and the control parameters for the four chaotic maps used in the compression-encryption scheme as given in Section 3.2.

  2. 2.

    The plain image P of size N × N is transformed using the DWT to obtain the sparse coefficients matrix α whose size is same as that of the plain image.

  3. 3.

    The measurement matrix φ of size M × N is constructed using the chaotic sequence generated using the proposed STL map as given in Section 3.3. The number of measurements M = round (Sampling Ratio × N).

  4. 4.

    Each column (x i ) of the coefficient matrix α, of length N, is measured using parallel compressive sensing using the measurement matrix φ as given below,

$$ {y}_i=\varphi \kern0.28em {x}_i $$
(14)

where the size of x i is N × 1 and the measurement y i is of size M × 1. The measurement Y of the coefficient matrix α is represented as

$$ Y=\left[{y}_1,{y}_2,\cdots, {y}_N\right] $$
(15)
  1. 5.

    The measurement Y of size M × N is then mapped to the interval [0, 255] using

$$ {Y}_q= round\;\left(\frac{255\ast \left(Y-{Y}_{\mathrm{min}}\right)}{Y_{\mathrm{max}}-{Y}_{\mathrm{min}}}\right) $$
(16)

where Y min and Y max are the maximum and minimum values of the measurement Y. round(x) rounds the value of x to the nearest integer.

  1. 6.

    Block Scrambling: The mapped measurements Y q are then divided into blocks of size b 1 × b 2, where b 1 = M / gcd(M, N) and b 2 = N / gcd(M, N). The number of blocks b depends on the number of measurements M. The blocks are then scrambled using Arnold transform to obtain scrambled measurements Y 1. If the block index is (p, q), then the scrambled index of the block after Arnold transform is given by (p′, q′)

$$ \left[\begin{array}{c}{p}^{\prime}\\ {}{q}^{\prime}\end{array}\right]=\left[\begin{array}{c}1\\ {}1\end{array}\kern0.6em \begin{array}{c}1\\ {}2\end{array}\right]\kern0.24em \left[\begin{array}{c}p\\ {}q\end{array}\right]\operatorname{mod}\;\sqrt{b} $$
(17)

By performing l iterations of Arnold transform the security of the encryption can be greatly enhanced.

  1. 7.

    Row Scrambling: The scrambled measurements (Y 1) are then subjected to row scrambling using the STL map. A chaotic sequence of length 2M is generated. The first M elements of the sequence is neglected to remove the transient effect. Then the sequence of length M is sorted in ascending order to obtain the index sequence. The index sequence is then used to scramble the rows of Y 1 to obtain Y 2.

  2. 8.

    Column Scrambling: Column scrambling is applied on Y 2 using the proposed STL map. A chaotic sequence of length 2N is generated using the STL map. The first N elements of the sequence is neglected to remove the transient effect. Then the sequence of length N is sorted in ascending order to obtain the index sequence. The index sequence is then used to scramble the columns of Y 2 to obtain Y 3.

  3. 9.

    Diffusion: Y 3 is then rasterized to form a sequence (Y 4) of length MN × 1. The cipher image (C) is obtained by performing sequential xor operation between Y 4 and the integer sequence (int_seq) obtained from the chaotic sequence generated by the proposed map.

$$ {C}_i=\left\{\begin{array}{l}{Y}_4(i)\oplus \operatorname{int}\_ seq(i),\kern2.16em i=1\\ {}{Y}_4(i)\oplus \operatorname{int}\_ seq(i)\oplus {C}_{i-1},i=2,3,\cdots, MN\end{array}\right.\operatorname{} $$
(18)

where int_seq = ⌊mod (Z × 1014, 256)⌋ and the length of the sequence is MN × 1. ⌊x⌋ calculates the largest integer that is less than or equal to x.

The sequence C i is reshaped to obtain the cipher image of dimension M × N. The proposed compression-encryption algorithm is summarized in Table 2. At the receiver, the cipher image obtained is subjected to inverse operations which are performed in the reverse order. The shared secret key between the sender and receiver is used to generate the four-chaotic sequences, which are then used to descramble and reconstruct the original image. The OMP algorithm is used for the reconstruction of the transform coefficients and inverse DWT is applied to reconstruct the plain image.

Table 2 Summarized proposed compression-encryption Algorithm
Full size table

4 Experimental results and analysis

The test images are taken from USC-SIPI Miscellaneous image data set. The test images are resized to a size 256 × 256. The plain image is transformed using DWT to obtain the sparse transform coefficients. The DWT decomposition is achieved using the ‘Symlet4’ wavelet function. A four-level wavelet decomposition is used. The parameters of the chaotic maps used as the shared secret key are Z ′ 0 = 0.5489, μ′ = 4.0856. The IRC measurement matrix is constructed using the chaotic sequence and used to compressively sample the sparse transform coefficients. The chaotic sequence is down sampled using a sampling interval d = 10. The parameters used in the construction of IRC matrix are η = 0.85 and M, the number of measurements. The measurements are confused and diffused to obtain the cipher image. The proposed scheme was tested using five different test images. The OMP algorithm is used for the reconstruction operation. The plain image, cipher image, the reconstructed image and their corresponding histogram are as shown in Fig. 5.

Fig. 5
figure 5

(a) Plain Image, (b) Cipher image, (c) Reconstructed Image; Histogram of (d) Plain Image, (e) Cipher image, (f) Reconstructed Image

Full size image

4.1 PSNR and SSIM analysis

The proposed scheme compresses and encrypt the plain image simultaneously. The quality of the reconstructed image can be evaluated by computing the Peak Signal to Noise Ratio (PSNR) and the Structural Similarity Index (SSIM). Mathematically PSNR is defined by,

$$ PSNR=10\;\log \frac{255^2}{\left(1/{N}^2\right)\sum \limits_{i=1}^N\sum \limits_{j=1}^N{\left[P\left(i,j\right)-{P}^{\prime}\left(i,j\right)\right]}^2} $$
(19)

where P(i, j) is the plain image and P ′ (i, j) is the reconstructed image. The test image is of size N × N. Structural Similarity Index (SSIM) is used for measuring the similarity between plain image and reconstructed image. The SSIM is given by

$$ SSIM=\frac{\left(2\;{\mu}_P\;{\mu}_{P^{\prime }}+{C}_1\right)\;\left(2\;{\sigma}_{P{P}^{\prime }}+{C}_2\right)}{\left({\mu}_P^2+{\mu}_{P^{\prime}}^2+{C}_1\right)\;\left({\sigma}_P^2+{\sigma}_{P^{\prime}}^2+{C}_2\right)} $$
(20)

where C 1 = 0.01 × (28–1), C 2 = 0.01 × (28–1), μ P , μ P′ , σ P, σ P′ , σ PP′ are the mean, standard deviation and cross-covariance of the plain and reconstructed image respectively. The effectiveness of the IRC measurement matrix constructed using the proposed map is verified by comparing it to other measurement matrices. The measurement matrices used for comparison are the Gaussian matrix, Bernoulli matrix, Hadamard matrix and the IRC matrix constructed using the chaotic sequence generated by the logistic map. For the test image Peppers of size 256 × 256, the sampling ratio is varied and the PSNR is computed and tabulated in Table 3 for different measurement matrices. From Table 3, we can infer that the PSNR value is high for the proposed measurement matrix i.e. the quality of the reconstructed image is better for the measurement matrix constructed using the proposed map. The PSNR and SSIM of the test images Baboon, Boat, Lake, Man and Peppers are computed for different sampling ratio and tabulated in Table 4. The PSNR and SSIM values are compared with the schemes proposed in [13] and [45]. From Table 4, it is evident that the proposed scheme achieves high PSNR compared to other schemes. The average PSNR is approximately 8 dB higher than that obtained in [13] and approximately 6 dB higher than the scheme in [45]. From Table 3, we also infer that the reconstruction quality of the proposed scheme is better as the average SSIM value achieved using the proposed scheme is high. The SSIM of the proposed scheme is higher than [13], [45] by 43.22%, 77.29% respectively. In Fig. 6 the PSNR of different test images obtained using the proposed and the compared schemes are plotted. Fig.6 clearly shows that the PSNR values for the proposed scheme are higher for all five test images compared with that of [13] and [45].

Table 3 Comparison of PSNR of reconstructed peppers image for different measurement Matrix for varying sampling ratio
Full size table
Table 4 PSNR and SSIM analysis for different test images for sampling ratio = 0.5
Full size table
Fig. 6
figure 6

Comparison of PSNR

Full size image

4.2 Histogram analysis

Histogram graphically represent the distribution of the pixel intensities of a digital image. The histogram of the plain image is unique, which makes it vulnerable to statistical attacks. To thwart such attacks the histogram of the encrypted images must have uniform distribution and significantly different from the plain image. Fig. 7 shows the histogram of the test images and their corresponding cipher. The histogram of the ciphers is relatively uniform and different from the plain image. Hence the proposed technique is robust against statistical attacks.

Fig. 7
figure 7

(a) Test Images, (b) Histogram of Test images, (c) Histogram of Cipher images

Full size image

4.3 Correlation analysis

The digital images pixels are highly correlated. An encryption algorithm resistant to statistical attack must be able to break the correlation between the pixels given by

$$ {r}_{xy}=\frac{\operatorname{cov}\kern0.24em \left(x,y\right)}{\sqrt{D\;(x)\;D\;(y)}} $$
(21)

where \( \operatorname{cov}\;\left(x,y\right)=\frac{1}{P}\sum \limits_{i=1}^P\left[{x}_i-E\;(x)\right]\;\left[{y}_i-E\;(y)\right] \), \( D\;(x)=\frac{1}{P}\sum \limits_i^P{\left[{x}_i-E\;(x)\right]}^2 \), \( E\;(x)=\frac{1}{P}\sum \limits_{i=1}^P{x}_i \).

2000 pixels and their corresponding adjacent pixels along the horizontal, vertical and diagonal directions were randomly chosen for the correlation analysis. A correlation coefficient value of one represents a highly-correlated image which is susceptible to statistical attacks. So, for a cipher image the correlation coefficient must be close to zero. From the Table 5, we infer that in the proposed scheme, the correlation between adjacent pixels in the cipher image is negligible. Table 5 also shows that the correlation coefficient of the cipher is very negligible when compared with the plain image. In comparison to the correlation coefficient achieved by the algorithms [13] and [45], the proposed method is better in the horizontal direction and comparable with the other schemes in the vertical and diagonal direction. Fig. 8 shows the pictorial representation of the distribution of the pixels in plain and cipher images in the horizontal, vertical and diagonal direction for the test image Peppers.

Table 5 Comparison of correlation coefficient
Full size table
Fig. 8
figure 8

Scatter plot of the correlation coefficient for the test image Peppers (a) Plain image (b) Cipher image

Full size image

4.4 Entropy analysis

Entropy is used to measure the randomness of the image. The entropy of the image is given by,

$$ H(X)=-\sum \limits_{i=1}^{N\times N}\Pr \left({I}_i\right){\log}_2\Pr \left({I}_i\right) $$
(22)

where Pr(I i) is the probability of I i. For an image with 256 Grey levels the absolute maximum of entropy is 8 bits per pixel. The maximum entropy is obtained when the gray levels have equal probability of occurrence. Therefore, the maximum entropy is achieved when the histogram is flat. Hence for a cipher image, the entropy value should be close to 8. From Table 6, we can infer that the encrypted image has high randomness as the entropy of cipher is close to theoretical value of 8. The average entropy of the proposed scheme is 7.9941 which is better than the entropy of the scheme in [45] and equal to the average entropy in [13].

Table 6 Entropy analysis
Full size table

4.5 UACI and NPCR analysis

The one-bit pixel change can lead to considerably distinct cipher image. The sensitivity to this change is measured by the Number of Pixels Change Rate (NPCR) and by Unified Average Changing Intensity (UACI) computed using the expression given below

$$ NPCR=\frac{\sum_{i,j}D\;\left(i,j\right)}{M\times N}\times 100\% $$
(23)
$$ UACI=\frac{1}{M\times N}\frac{\sum_{i,j}\mid {C}_1\kern0.28em \left(i,j\right)-{C}_2\left(i,j\right)\kern0.14em \mid }{L}\times 100\% $$
(24)

C 1 (i, j) and C 2 (i, j) are the values of the pixels in the position (i, j) of the two ciphered-image C 1 and C 2 respectively; L is the number of gray levels. D (i, j) is determined based on the rule

$$ D\;\left(i,j\right)=\left\{\begin{array}{l}0,{C}_1\;\left(i,j\right)={C}_2\;\left(i,j\right)\\ {}1,\kern0.36em otherwise\end{array}\right. $$
(25)

For NPCR and UACI analysis, a pixel was chosen at random and the least significant bit of its binary representation was toggled to form the modified image. Using the ciphered version of the plain image (C 1) and the ciphered version of the modified image (C 2), values for NPCR and UACI were computed and tabulated in Table 7. The results shown in Table 7 indicates that the algorithm can resist differential attacks as the NPCR and UACI values are close to the theoretical values of 99.61% and 33.46% respectively. The average NPCR of the proposed scheme is better than the compared algorithms [13, 45]. From Table 7, we can infer that the average UACI value of proposed scheme is better than the other two schemes. Table 7 shows that the encryption scheme proposed in [45] has poor NPCR and UACI values as it does not employ diffusion operation.

Table 7 NPCR and UACI analysis
Full size table

4.6 Keyspace and key sensitivity analysis

To resist brute-force attack an encryption scheme must have a large key space. In the proposed scheme the key generation is dependent on the input image. The 256-bit hash code generated by implementing the SHA-256 algorithm on the input image. This hash code together with the keys Z′0, μ′ are shared between the sender and receiver using a secure channel. According to the IEEE floating point standard the data precision for the double values is 10−15. Therefore, the keyspace of the proposed scheme is given by 2256 × 1015 × 1015 which is approximately equal to 2356.The comparison between the key space of the proposed scheme and the schemes in [13] and [45] is shown in Table 8. The key space provided by the proposed scheme is very large when compared with the other algorithms, which indicates a very high security.

Table 8 Key space analysis
Full size table

For an efficient encryption scheme the security key should be highly sensitive. A small change in the security key should result in a totally different decrypted image. The cipher is decrypted using the same key as used in encryption and the reconstructed image is shown in Fig. 9(b). A small value Δ=10−15 is added to the correct keys (Z ′ 0, μ′) and the cipher image is decrypted. The reconstructed images with incorrect keys are shown in Fig. 9, which shows that the proposed scheme is highly sensitive to even a small change in the key.

Fig. 9
figure 9

(a) Original Image (b) Reconstructed Image with correct keys (c) Reconstructed Image with incorrect key Z ′ 0 (d) Reconstructed Image with incorrect key μ′

Full size image

4.7 Chosen-plaintext attack analysis

In chosen-plaintext attack the adversary has access to the encryption oracle and tries to gain information by encrypting arbitrary plaintext of his choice. In a CS based cryptosystem, the cipher text is vulnerable to chosen plaintext attack, as the measurement matrix (i.e. the secret key) can be retrieved by cryptanalysis. By choosing an identity matrix as plaintext the measurement matrix can be deduced as the compressive sensing measurements are linear. The chosen-plaintext attack can be thwarted by diffusing the linearity of the CS measurements. In the proposed scheme a permutation process is used to break the linearity. If a single permutation vector is used for multiple images, the encryption algorithm can be easily broken. By employing a plaintext dependent diffusion process chosen-plaintext attack can be prevented. In the proposed scheme a chaos based permutation process is utilized. A SHA-256 hash code of the plain image is generated which is used to generate the parameters of the chaotic system. The proposed chaotic system is then used to generate a chaotic sequence which is used to scramble the measurements. Block scrambling using Arnold transform followed by proposed chaotic map based row and column scrambling greatly increase the resistance to chosen-plaintext attack. Also, the proposed cryptosystem adopts xor based substitution function that chosen-plaintext attack the adversary has access to the encryption oracle and tries to gain information by encrypting arbitrary plaintext of his choice.

4.8 Maximum deviation analysis

The deviations in the pixel values between the plain image and cipher image is a measure of the quality of the encryption algorithm. Higher the deviation greater the strength of the encryption algorithm. The maximum deviation MD is computed as follows:

$$ MD=\frac{A0+ AN-1}{2}+\sum \limits_{i=1}^{L-2} Ai $$
(26)

where L is the number of gray levels and A i is the amplitude difference between the histogram of the plain image and the cipher image at index i. The cipher image is highly deviated from the plain image if the value of M D is higher. The Table 9 shows the maximum deviation of the proposed scheme in comparison to that of [13] and [45]. The average maximum deviation value is slightly less when compared with [13] and greater when compared with [45]. The average maximum deviation value of the proposed scheme is high enough to conceal statistical information from an intruder.

Table 9 Maximum deviation analysis
Full size table

4.9 Contrast analysis

Contrast of an image is defined as the difference between the maximum and the minimum pixel intensity in an image. The encrypted image has high contrast levels because of the randomness of the pixel intensity. Hence higher the contrast greater the encryption strength. The contrast is mathematically computed as:

$$ Contrast=\sum \limits_{i,j}{\left|i-j\right|}^2G\left(i,j\right) $$
(27)

where G(i, j) is the number of gray-level co-occurrence matrices. The contrast of the encrypted image obtained using the proposed scheme is high, when compared to other techniques. It indicates that the high randomness of the pixels in the cipher image. From Table 10, we can observe that the average contrast value of the proposed scheme is comparable to other schemes.

Table 10 Contrast analysis
Full size table

5 Conclusion

In this paper, a compression-encryption algorithm based on parallel compressive sensing and chaotic measurement matrix is proposed. The proposed chaotic map is used to construct an incoherence rotated measurement matrix. The experimental results demonstrated the effectiveness of the measurement matrix in reconstructing the image when compared with other measurement matrices. The increase in average PSNR is about 6–8 dB, when compared with other schemes. For enhancing security against chosen plain text attack, an input dependent key scheduling is employed. The keyspace of the proposed scheme is large enough to resist brute-force attacks. The histogram, entropy and correlation analysis shows that the proposed scheme can thwart statistical attacks. Simulation results verify that the proposed scheme is efficient as well as secure.