Analysis of Multi-delay and Piecewise Constant Delay Systems by Hybrid Functions Approximation

Abstract

In this paper, a new numerical method for solving multi-delay and piecewise constant delay systems is presented. The method is based upon hybrid functions approximation. The properties of hybrid functions consisting of block-pulse functions and Bernoulli polynomials are presented. The operational matrices of integration, product and delay are given. These matrices are then utilized to reduce the solution of multi-delay systems and the piecewise constant delay systems to the solution of algebraic equations. Illustrative examples are included to demonstrate the validity and applicability of the technique.

Introduction

Delays occur frequently in biological, chemical, electronic and transportation systems. Time-delay systems are therefore a very important class of systems whose control and optimization have been of interest to many investigators [1–4]. It is well known that it is difficult to analytically solve a delay system. Several numerical methods have been used to obtain an approximate solution for delay differential equations [5].

The available sets of orthogonal functions can be divided into three classes. The first class includes sets of piecewise constant basis functions (e.g., block-pulse, Haar, Walsh, etc.). The second class consists of sets of orthogonal polynomials (e.g., Chebyshev, Laguerre, Legendre, etc.). The third class is the set of sine–cosine functions in the Fourier series. Orthogonal functions have been used when dealing with various problems of the dynamical systems. The main advantage of using orthogonal functions is that they reduce the dynamical system problems to those of solving a system of algebraic equations. The approach is based on converting the underlying differential equation into an integral equation through integration, approximating various signals involved in the equation by truncated orthogonal functions, and using the operational matrix of integration $P$ to eliminate the integral operations. The matrix $P$ can be uniquely determined based on the particular orthogonal functions. Typical examples are given in [6–11].

Among piecewise constant basis functions, block-pulse functions are found to be very attractive, in view of their properties of simplicity and disjointedness. Bernoulli polynomials and Taylor series are not based on orthogonal functions, nevertheless, they possess the operational matrix of integration. However, since the integration of the cross product of two Taylor series vectors is given in terms of a Hilbert matrix [12], which are known to be ill conditioned, the applications of Taylor series are limited. Furthermore, the operational matrix $P$, in Bernoulli polynomials $\beta _m(t),\, m=0,1,2,\ldots ,$ where $0 \le t \le 1,$ has less errors than $P$ for Taylor series in $\frac{1}{2}\le t\le 1$ and $1<m<8$. This is because for $P$ in $\beta _m(t)$ we ignore the term $\frac{\beta _{m+1}(t)}{m+1}$ while for $P$ in Taylor series we ignore the term $\frac{t^{m+1}}{m+1}$.

For approximating an arbitrary time function the advantages of Bernoulli polynomials $\beta _m(t),$ over shifted Chebyshev polynomials $T_m(t)$, and shifted Legendre polynomials $L_m(t), \, m=0,1,2,\ldots$, where $0 \le t \le 1,$ are:

• (a) the operational matrix $P$, in Bernoulli polynomials has less errors than $P$ for shifted Chebyshev and shifted Legendre polynomials for $1<m<10$. This is because for $P$ in $T_m(t)$ we ignore the term $\frac{T_{m+1}(t)}{4(m+1)};$ and for $P$ in $L_m(t)$ we ignore the term $\frac{L_{m+1}(t)}{2(2m+1)};$

• (b) the Bernoulli polynomials have less terms than shifted Chebyshev polynomials and shifted Legendre polynomials. For example $\beta _6(t)$ has 5 terms, while $T_6(t)$ and $L_6(t)$ have 7 terms, and this difference will increase by increasing $m$. Hence for approximating an arbitrary function we use less CPU time by applying Bernoulli polynomials as compared to shifted Chebyshev and shifted Legendre polynomials;

• (c) the coefficient of individual terms in Bernoulli polynomials are smaller than the coefficient of individual terms in the shifted Chebyshev and shifted Legendre polynomials. Since the computational errors in the product are related to the coefficients of individual terms, the computational errors are less by using Bernoulli polynomials.

In recent years different types of hybrid functions have been shown to be mathematical power tools for discretization of selected problems [13–17]. In the present paper we introduce a new direct computational method to solve delay systems. The method consists of reducing the delay differential equations to a set of algebraic equations by first expanding the solution of delay differential equations as a hybrid function with unknown coefficients. These hybrid functions, which consist of block-pulse functions and Bernoulli polynomials, are introduced. The operational matrices of integration, product, and delay are given. These matrices are then used to evaluate the coefficients of the hybrid functions for the solution of the delay differential equations.

The outline of this paper is as follows: In “Properties of Hybrid Functions” section we introduce the basic properties of the hybrid functions of block-pulse and Bernoulli polynomials required for our subsequent development. Section “Problem Statement” is devoted to the problem statement. In “The Numerical Method” section we apply the proposed numerical method to approximate the multi-delay systems and piecewise constant delay systems. In “Discussion” section a discussion of the present method is given and in “Illustrative Examples” section we report our numerical findings and demonstrate the accuracy of the proposed numerical scheme by considering four numerical examples.

Properties of Hybrid Functions

Hybrid of Block-Pulse and Bernoulli Polynomials

Hybrid functions $b_{nm}(t),\, n=1,2,\ldots ,N,\,m=0,1,\ldots ,M$ are defined on the interval $[0,t_f)$ as

$$\begin{aligned} b_{nm}(t)=\left\{ \begin{array}{ll} \beta _m\left( \frac{N}{t_f}t-n+1\right) , \quad t\in \left[ \frac{n-1}{N}t_f,\frac{n}{N}t_f\right) ,\\ 0,\quad \mathrm{{otherwise}}, \end{array}\right. \end{aligned}$$

(1)

where $n$ and $m$ are the order of block-pulse functions and Bernoulli polynomials, respectively. In Eq. (1), $\beta _m(t),\,\ m=0,1,2,\ldots ,$ are the Bernoulli polynomials of order $m$, which can be defined by [18]

$$\begin{aligned} \beta _m(t)=\sum \limits _{k = 0}^{m}{\left( \begin{array}{l}m\\ k\end{array}\right) } \alpha _kt^{m-k}, \end{aligned}$$

where $\alpha _k,\quad k=0,1,\ldots ,m,$ are Bernoulli numbers. These numbers are a sequence of signed rational numbers, which arise in the series expansions of trigonometric functions [19] and can be defined by the identity

$$\begin{aligned} \frac{t}{e^t-1}=\sum \limits _{n = 0}^{\infty }\alpha _n\frac{t^n}{n!}. \end{aligned}$$

The first few Bernoulli numbers are

$$\begin{aligned} \alpha _0 = 1, \quad \alpha _1 = \frac{-1}{2}, \quad \alpha _2 = \frac{1}{6}, \quad \alpha _4 = \frac{-1}{30}, \end{aligned}$$

with $\alpha _{2k+1}=0,\, k=1,2,3,\ldots .$

The first few Bernoulli polynomials are

$$\begin{aligned} \beta _0 (t) = 1, \quad \beta _1 (t) = t-\frac{1}{2},\quad \beta _2 (t) = t^2 -t +\frac{1}{6}, \quad \beta _3 (t) = t^3 -\frac{3}{2}t^2+\frac{1}{2}t. \end{aligned}$$

According to [20], Bernoulli polynomials form a complete basis over the interval [0,1].

Function Approximation

Suppose that $H=L^{2}[0,1]$ and $\{b_{10}(t),b_{20}(t),\ldots ,b_{NM}(t)\}\subset H$ be the set of hybrid of block-pulse and Bernoulli polynomials and

$$\begin{aligned} Y&= \mathrm{{span}}\{b_{10}(t),b_{20}(t),\ldots ,b_{N0}(t),b_{11}(t),b_{21}(t),\ldots ,b_{N1}(t),\ldots ,b_{1M}(t),\\&\qquad \quad b_{2M}(t),\ldots ,b_{NM}(t)\}, \end{aligned}$$

and $f$ be an arbitrary element in $H$. Since $Y$ is a finite dimensional vector space, $f$ has the unique best approximation out of $Y$ such as $f_0\in Y,$ that is

$$\begin{aligned} \forall y\in Y, \quad ||f-f_0||\le ||f-y||. \end{aligned}$$

Since $f_0\in Y,$ there exist unique coefficients $c_{10},c_{20},\ldots ,c_{NM}$ such that

$$\begin{aligned} f\simeq f_0 = \sum \limits _{m= 0}^{M}\sum \limits _{n= 1}^{N} c_{nm} b_{nm}(t)=C^T B(t), \end{aligned}$$

(2)

where

$$\begin{aligned} B^T(t)&= \big [b_{10}(t),b_{20}(t),\ldots ,b_{N0}(t),b_{11}(t),b_{21}(t),\ldots ,b_{N1}(t),\ldots ,b_{1M}(t),\nonumber \\&b_{2M}(t),\ldots ,b_{NM}(t)\big ], \end{aligned}$$

(3)

and

$$\begin{aligned} C^T=\big [c_{10},c_{20},\ldots ,c_{N0},c_{11},c_{21},\ldots ,c_{N1},\ldots ,c_{1M},c_{2M},\ldots ,c_{NM}\big ]. \end{aligned}$$

(4)

Approximation Errors

In this section we obtain bounds for the error of best approximation in terms of Sobolev norms. This norm is defined in the interval $(a,b)$ for $\mu \ge 0$ by

$$\begin{aligned} ||f||_{H^\mu (a,b)}=\left( \sum \limits _{k=0}^{\mu }\int \limits _a^b|f^{(k)}(x)|^2dx\right) ^{\frac{1}{2}}=\left( \,\,\sum \limits _{k=0}^{\mu }||f^{(k)}||^2_{L^2(a,b)}\right) ^{\frac{1}{2}}, \end{aligned}$$

(5)

where $f^{(k)}$ denotes the $k$th derivative of $f$. The symbol $|f|_{H^{\mu ;M}(0,1)}$ which is introduced in [21] was defined by

$$\begin{aligned} |f|_{H^{\mu ;M}(0,1)}=\left( \sum \limits _{k=\mathrm{{min}}(\mu ,M+1)}^{\mu }||f^{(k)}||^2_{L^2(0,1)}\right) ^{\frac{1}{2}}. \end{aligned}$$

The seminorm [22] is

$$\begin{aligned} |f|_{H^{r;\mu ;M;N}(0,1)}=\left( \sum _{k=\mathrm{{min}}(\mu ,M+1)}^\mu N^{2r-2k}||u^{(k)}||^2_{L^2(0,1)}\right) ^{\frac{1}{2}}, \end{aligned}$$

where

$$\begin{aligned} |f|_{H^{r;\mu ;M;N}(0,1)}=N^{r-\mu }||f^{(\mu )}||_{L^2(0,1)}, \end{aligned}$$

(6)

$M\ge \mu -1,$ and if $N=1,\,|\cdot |_{H^{r;\mu ;M;N}}$ coincides with $|\cdot |_{H^{\mu ;M}}$ which was introduced in [21].

To state our main results, the following theorem and lemma will be required.

Theorem 1

Suppose that $f\in H^\mu (0,1)$ with $\mu \ge 0$. If $P_Mf=\sum _{m=0}^{M}c_m\beta _m$ is the best approximation of $f$ then

$$\begin{aligned} ||f-P_Mf||_{L^2(0,1)}\le cM^{-\mu }|f|_{H^{\mu ;M}(0,1)}, \end{aligned}$$

(7)

and for $1\le r\le \mu$,

$$\begin{aligned} ||f-P_Mf||_{H^r(0,1)}\le cM^{2r-\frac{1}{2}-\mu }|f|_{H^{\mu ;M}(0,1)}, \end{aligned}$$

(8)

where $c$ depends on $\mu$.

Proof

Let $f\in H^\mu (0,1)$ with $\mu \ge 0$ and $\sum _{m=0}^{M}\acute{c}_mL_m$ be the best approximation of $f$, which is constructed by using shifted Legendre polynomials $L_m,~m=0,\ldots ,M$ in the interval $[0,1]$. Then [21]

$$\begin{aligned} \bigg |\bigg |f-\sum _{m=0}^{M}\acute{c}_mL_m\bigg |\bigg |_{L^2(0,1)}\le cM^{-\mu }|f|_{H^{\mu ;M}(0,1)}, \end{aligned}$$

(9)

and for $1\le r\le \mu$,

$$\begin{aligned} \bigg |\bigg |f-\sum _{m=0}^{M}\acute{c}_mL_m\bigg |\bigg |_{H^r(0,1)}\le cM^{2r-\frac{1}{2}-\mu }|f|_{H^{\mu ;M}(0,1)}. \end{aligned}$$

(10)

Since the best approximation is unique [20], we have

$$\begin{aligned} \bigg |\bigg |f-\sum _{m=0}^{M}\acute{c}_mL_m\bigg |\bigg |_{L^2(0,1)}=\bigg |\bigg |f-P_Mf\bigg |\bigg |_{L^2(0,1)}, \quad \bigg |\bigg |f-\sum _{m=0}^{M}\acute{c}_mL_m\bigg |\bigg |_{H^r(0,1)}=\bigg |\bigg |f-P_Mf||_{H^r(0,1)}, \end{aligned}$$

(11)

and by using Eqs. (9–11) we can obtain Eqs. (7) and (8). $\square$

Lemma 1

For $n=1,2,\ldots ,N$ suppose $f_n:(\frac{n-1}{N},\frac{n}{N})\rightarrow R$ is a function in $H^\mu (\frac{n-1}{N},\frac{n}{N}).$ Consider the function $F_nf_n:(0,1)\rightarrow R$ such that $(F_nf_n)(x)=f_n(\frac{1}{N}(x+n-1))$ for all $x\in (0,1),$ then for $0\le l\le \mu ,$ we have

$$\begin{aligned} ||(F_nf_n)^{(l)}||_{L^2(0,1)}=N^{\frac{1}{2}-l}||f^{(l)}_n||_{L^2(\frac{n-1}{N},\frac{n}{N})}. \end{aligned}$$

Proof

For $0\le l\le \mu ,$ we have

$$\begin{aligned} ||(F_nf_n)^{(l)}||^2_{L^2(0,1)}&= \int \limits _0^1|(F_nf_n)^{(l)}(x)|^2dx=\int \limits _0^1\left| f^{(l)}_n\left( \frac{1}{N}(x+n-1)\right) \right| ^2dx\\&= \int \limits _{\frac{n-1}{N}}^{\frac{n}{N}}N^{-2l}|f^{(l)}_n(t)|^2Ndt=N^{1-2l}||f^{(l)}_n||^2_{L^2\left( \frac{n-1}{N},\frac{n}{N}\right) }, \end{aligned}$$

where for the third equality, we used the change of variable rule by setting $t=\frac{1}{N}(x+n-1)$.

$\square$

By using the following Theorem we can obtain error for the approximation function.

Theorem 2

Suppose $f\in H^\mu (0,1)$ with $\mu \ge 0$, then

$$\begin{aligned} ||f-P_M^Nf||_{L^2(0,1)}\le cM^{-\mu }|f|_{H^{0;\mu ;M;N}(0,1)}, \end{aligned}$$

(12)

and for $1\le r\le \mu$,

$$\begin{aligned} ||f-P_M^Nf||_{H^r(0,1)}\le cM^{2r-\frac{1}{2}-\mu }|f|_{H^{r;\mu ;M;N}(0,1)}. \end{aligned}$$

(13)

Proof

For $n=1,2,\ldots ,N$ we consider the function $f_n:(\frac{n-1}{N},\frac{n}{N})\rightarrow R$ such that $f_n(x)=f(x)$ for all $x\in (\frac{n-1}{N},\frac{n}{N})$. By using Lemma 1 and Eq. (7) we have

$$\begin{aligned} ||f\!-\!P_M^Nf||^2_{L^2(0,1)}&\!=\!&\sum \limits _{n=1}^{N}\bigg |\bigg |f_n-\sum \limits _{m\!=\!0}^{M}c_{nm}b_{nm}\bigg |\bigg |^2_{L^2(\frac{n-1}{N},\frac{n}{N})}\!=\!cN^{-1}\sum \limits _{n\!=\!1}^{N}\big |\big |F_nf_n-P_M(F_nf_n)\big |\big |^2_{L^2(0,1)}\\&\le cN^{-1}M^{-2\mu }\sum \limits _{n=1}^{N}\sum \limits _{k=\mathrm{{min}}(\mu ,M+1)}^{\mu }||(F_nf_n)^{(k)}||^2_{L^2(0,1)}\\&= cN^{-1}M^{-2\mu }\sum \limits _{k=\mathrm{{min}}(\mu ,M+1)}^{\mu }\sum \limits _{n=1}^{N}N^{1-2k}||f_n^{(k)}||^2_{L^2(\frac{n-1}{N},\frac{n}{N})}\\&= cM^{-2\mu }\sum \limits _{k=\mathrm{{min}}(\mu ,M+1)}^{\mu }N^{-2k}||f^{(k)}||^2_{L^2(0,1)}, \end{aligned}$$

Also, for $1\le r\le \mu ,$ by using Lemma 1 and Eq. (8) we have

$$\begin{aligned} ||f-P_M^Nf||^2_{H^r(0,1)}&= \sum _{n=1}^{N}\bigg |\bigg |f_n-\sum _{m=0}^{M}c_{nm}b_{nm}\bigg |\bigg |^2_{H^r\left( \frac{n-1}{N},\frac{n}{N}\right) }\\&= c\sum _{n=1}^{N}\sum _{p=0}^{r}N^{2p-1}||(F_nf_n)^{(p)}-(P_M(F_nf_n))^{(p)}||^2_{L^2(0,1)}\\&\le cN^{2r-1}M^{4r-1-2\mu }\sum _{n=1}^{N}\sum _{k=\mathrm{{min}}(\mu ,M+1)}^{\mu }||(F_nf_n)^{(k)}||^2_{L^2(0,1)}\\&= cN^{2r-1}M^{4r-1-2\mu }\sum _{k=\mathrm{{min}}(\mu ,M+1)}^{\mu }\sum _{n=1}^{N}N^{1-2k}||f_n^{(k)}||^2_{L^2\left( \frac{n-1}{N},\frac{n}{N}\right) }\\&= cM^{4r-1-2\mu }\sum _{k=\mathrm{{min}}(\mu ,M+1)}^{\mu }N^{2r-2k}||f^{(k)}||^2_{L^2(0,1)}. \end{aligned}$$

$\square$

Conclusion Suppose $f\in H^\mu (0,1)$ with $\mu \ge 0,$ and $M\ge \mu -1,$ then by using Eq. (6) and Theorem 2 we get

$$\begin{aligned} ||f-P_M^Nf||_{L^2(0,1)}\le cM^{-\mu }N^{-\mu }||f^{(\mu )}||_{L^2(0,1)}, \end{aligned}$$

(14)

and for $r\ge 1$,

$$\begin{aligned} ||f-P_M^Nf||_{H^r(0,1)}\le cM^{2r-\frac{1}{2}-\mu }N^{r-\mu }||f^{(\mu )}||_{L^2(0,1)}. \end{aligned}$$

(15)

This result shows that in the case $f$ is infinitely smooth, the rate of convergence of $P_M^Nf$ to $f$ is faster than $\frac{1}{N}$ to the power of $M+1-r$ and any power of $\frac{1}{M}$, which is superior to that for the classical spectral methods [21].

Operational Matrix of Integration and Product

The integration of the $B(t)$ defined in Eq. (3) is given by

$$\begin{aligned} \int \limits _{0}^{t}B(t')dt'\simeq PB(t), \end{aligned}$$

(16)

where $P$ is the $N(M+1)\times N(M+1)$ operational matrix of integration. The matrix $P$ for $t_{f}=1$ is given in [23] by

$$\begin{aligned} P=\frac{1}{N}\left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} P_0 &{} I&{}O &{} \ldots &{}O \\ \frac{-1}{2}\alpha _2I &{} O &{} \frac{1}{2}I &{}\ldots &{}O \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ \frac{-1}{M}\alpha _{M}I &{} O &{} O &{}\ldots &{}\frac{1}{M}I\\ \frac{-1}{M+1}\alpha _{M+1}I &{} O &{} O &{}\ldots &{}O\\ \end{array}} \right] , \end{aligned}$$

where $I$ and $O$ are $N\times N$ identity and zero matrices respectively, and

$$\begin{aligned} P_0=\left[ {\begin{array}{cccccc} -\alpha _1 &{} 1 &{} \ldots &{} 1 &{}1 \\ 0 &{} -\alpha _1 &{} \ldots &{} 1 &{}1 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} \ldots &{} -\alpha _1 &{}1\\ 0 &{} 0 &{}\ldots &{} 0 &{}-\alpha _1\\ \end{array}} \right] . \end{aligned}$$

It is seen that $P$ is more sparse than operational matrices of integration for the hybrid of block-pulse and Chebyshev polynomials [13], the hybrid of block-pulse and Legendre polynomials [14], and the hybrid of block-pulse and Taylor series [15].

The product of two hybrid functions with the vector $C$ is given by

$$\begin{aligned} B(t)B^T(t)C\simeq \tilde{C}B(t), \end{aligned}$$

(17)

where $\tilde{C}$ is a $N(M+1)\times N(M+1)$ product operational matrix which is given in [24].

The Operational Matrix of Multi-delay Systems

The delay function $B(t-\eta _j), j=1,2,\ldots ,r,$ is the shift of the function $B(t)$ defined in Eq. (3), along the time axis by $\eta _j$, where $\eta _1,\eta _2, \ldots , \eta _r$ are rational numbers in $(0,1)$. It is assumed that without loss of generality that $\eta _1<\eta _2< \cdots <\eta _r$. The general expression is given by

$$\begin{aligned} B(t-\eta _j)={D_j}B(t), \quad \ t>\eta _j, \quad 0<t<1, \end{aligned}$$

(18)

where $D_j$ is the operational matrix of delay of hybrid functions corresponding to $\eta _j$. To find $D_j$, for $j=1,2,\ldots ,r,$ we first choose $N$ in the following manner:

We define $w$ as the smallest positive integer number for which $w\eta _j\in Z$ for $j=1,2,\ldots ,r,$ where $Z$ is the set of all integer numbers. Next we choose $\lambda$ as the greatest common divisor of the integers $w\eta _j,\,j=1,2,\ldots ,r$. That is

$$\begin{aligned} \lambda =\mathrm{{g.c.d}}(w\eta _1,w\eta _2,\ldots ,w\eta _r). \end{aligned}$$

Let

$$\begin{aligned} N=\left\{ \begin{array}{ll} \frac{w}{\lambda }, &{}\quad \frac{w}{\lambda }\in Z,\\ \left[ \frac{w}{\lambda }\right] +1, &{}\quad \mathrm{{otherwise}}, \\ \end{array}\right. \end{aligned}$$

(19)

where $[\cdot ]$ denotes the greatest integer value. Thus we have different subintervals given by

$$\begin{aligned} \left[ 0,\frac{1}{N}\right) ,\,\left[ \frac{1}{N},\frac{2}{N}\right) ,\ldots ,\left[ \frac{N-1}{N},1\right) . \end{aligned}$$

With the aid of Eq. (1), it is noted that $b_{im}(t), m=0,1, \ldots , M,$ are non zero in the interval $[\frac{i-1}{N},\frac{i}{N})$. Thus $b_{im}(t-\eta _j)$ are non-zero in the $[\frac{i-1}{N}+\eta _j,\frac{i}{N}+\eta _j)$. If we expand $b_{im}(t-\eta _j)$ in terms of the element of $B(t)$ in Eq. (3), we have $b_{im}(t-\eta _j)=b_{\beta _{ij}m}(t)$ where $\beta _{ij}=[N\eta _j+i].$ Thus, if we expand $B(t-\eta _j)$ in terms of $B(t)$ we find $N(M+1)\times N(M+1)$ delay matrix $D_j$ as

$$\begin{aligned} {D_j}=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \psi _j &{} O &{} O &{} \cdots &{} O \\ O &{} \psi _j &{} O &{} \cdots &{} O \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ O &{} O &{} O &{} \psi _j &{} O \\ O &{} O &{} O &{} O &{} \psi _j \\ \end{array}\right] , \end{aligned}$$

where $O$ is $N\times N$ zero matrix, and $\psi _j$ is $N\times N$ matrix which is given by

$$\begin{aligned} \psi _j=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} \cdots &{} 1 &{} 0&{}\cdots &{}0 \\ 0 &{} 0 &{} \cdots &{} 0 &{} 1&{} \cdots &{}0 \\ \vdots &{} \vdots &{} \vdots &{} \cdots &{} \vdots &{}\vdots &{}\vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} 0&{}\cdots &{}1 \\ \vdots &{} \vdots &{} \vdots &{} \cdots &{} \vdots &{}\vdots &{}\vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} 0&{}0&{}0 \\ \end{array}\right] . \end{aligned}$$

It is noted that the first one in the first row is located at the $\beta _{1j}$ th column.

The Operational Matrix of Piecewise Constant Delay Systems

In this section we obtain the operational matrix of delay $Q$ for piecewise constant delay systems. The general expression is given by

$$\begin{aligned} B(t-a(t))=QB(t),\quad 0<t<1, \end{aligned}$$

(20)

where $a(t)$ is considered as follows:

$$\begin{aligned} a(t)=\left\{ \begin{array}{cc} \xi _1,&{}\quad 0\le t< T_1,\\ \xi _2,&{}\quad T_1\le t< T_2,\\ \vdots &{}\quad \vdots \\ \xi _s,&{}\quad T_{s-1}\le t< 1.\\ \end{array}\right. \end{aligned}$$

It is assumed that $\xi _1,\xi _2, \ldots , \xi _r$ are rational numbers in $[0,1)$, and $\xi _1<\xi _2< \cdots <\xi _r$. We first choose $N$ in the following manner: Let

$$\begin{aligned} K=\{i: \, \xi _i\ne 0\}, \end{aligned}$$

and define $\gamma$ as the smallest positive integer number for which

$$\begin{aligned} \gamma \xi _i\in Z,\quad \gamma T_j\in Z,\quad i\in K, \quad j=1,2,\ldots ,s-1. \end{aligned}$$

Next suppose $|K|=\alpha ,$ and choose $\delta$ as the greatest common divisor of the integers $\gamma \xi _i$ and $\gamma T_j,~i\in K,\,j=1,2,\ldots ,s-1.$ That is

$$\begin{aligned} \delta =\mathrm{{g.c.d}}(\gamma \xi _1,\gamma \xi _2,\ldots ,\gamma \xi _\alpha ,\gamma T_1,\gamma T_2,\ldots ,\gamma T_{s-1}). \end{aligned}$$

Let $h=\frac{\delta }{\gamma }$ and select $N$ to minimize the number of subintervals as

$$\begin{aligned} N=\left\{ \begin{array}{ll} \frac{1}{h}, &{}\quad \frac{1}{h}\in Z,\\ \left[ \frac{1}{h}\right] +1, &{}\quad \mathrm{{otherwise}}. \\ \end{array}\right. \end{aligned}$$

(21)

Thus we have different subintervals given by

$$\begin{aligned}{}[0,h),[h,2h),\ldots ,[(N-1)h,Nh). \end{aligned}$$

For these subintervals we can redefine $a(t)$ as

$a(t)=\xi _i$ for   $h\left( \,\,\sum \limits _{l=0}^{i-1}N_l\right) \le t<h\left( \,\,\sum \limits _{l=0}^{i}N_l\right) ,\quad i=1,2,\ldots ,s$,

where

$$\begin{aligned} N_0=0,\,\quad N_j=\frac{T_j-T_{j-1}}{h},\,\quad T_0=0,\, \quad T_s=1, \end{aligned}$$

clearly $\sum _{j=1}^{s}N_j=N$. Therefore the problem has been reduced to find the delay operational matrix for the following delay function:

$$\begin{aligned} B(t-a(t))=\left\{ \begin{array}{cc} B(t-v_1h),&{}\quad 0\le t< t_1,\\ B(t-v_2h),&{}\quad t_1\le t< t_2,\\ \vdots &{}\quad \vdots \\ B(t-v_Nh),&{}\quad t_{N-1}\le t< t_N.\\ \end{array}\right. \end{aligned}$$

For evaluating $v_j$ first we choose $i$ as the smallest positive integer number such that

$$\begin{aligned} 1+\sum _{l=0}^{i-1}N_l\le j\le \sum _{l=0}^{i}N_l. \end{aligned}$$

Then we choose $v_j$ in such a way that

$$\begin{aligned} t_i=ih,\quad v_j=\frac{\xi _i}{h},\quad i=1,2,\ldots ,s,\quad j=1,2,\ldots ,N. \end{aligned}$$

In order to construct the matrix $Q$, we first find the matrix $Q_i$ for $i=1,2,\ldots ,N$ in such a way that the following relation is satisfied:

$$\begin{aligned} B(t-v_ih)=Q_iB(t),\quad t_{i-1}\le t<t_i. \end{aligned}$$

With the aid of Eq. (1), it is noted that for the case $t_{i-1}\le t<t_i,$ the only terms with nonzero values are $b_{(i-v_i)m}(t-v_ih)$, for $m=0,1,\ldots ,M$. Since

$$\begin{aligned} b_{(i-v_i)m}(t-v_ih)=b_{im}(t),\quad m=0,1,\ldots ,M, \end{aligned}$$

we have

$$\begin{aligned} Q_i=I_{M+1}\otimes S_i, \quad i=1,2,\ldots ,N, \end{aligned}$$

(22)

where $I_{M+1}$ is the $(M+1)$ dimensional identity matrix and $S_i$ is an $N\times N$ matrix in which the only nonzero entry is equal to one and located at the $(i-v_i)$th row and $i$th column and $\otimes$ denotes Kronecker product [25]. It is noted that if $i-v_i\le 0,$ then $S_i$ is a zero matrix of order $N\times N.$ Thus, if we expand $B(t-a(t))$ in terms of hybrid functions $B(t),$ we get

$$\begin{aligned} Q=Q_1+Q_2+\cdots +Q_N. \end{aligned}$$

Problem Statement

Consider the following linear time-varying delay system:

$$\begin{aligned} \dot{X}(t)&\!=\!&E(t)X(t)\!+\!\kappa _1\sum _{j\!=\!1}^{r}F_j(t)X(t\!-\!\eta _j)\!+\!\kappa _2H(t)X(t\!-\!a(t))\!+\!G(t)U(t),\quad 0\le t\le 1,\end{aligned}$$

(23)

$$\begin{aligned} X(0)&= X_{0},\end{aligned}$$

(24)

$$\begin{aligned} X(t)&= \phi (t), \quad t< 0, \end{aligned}$$

(25)

where $X(t)\in R^l,\,U(t)\in R^q,~E(t), F_j(t)\,\,j=1,2,\ldots ,r, H(t)$ and $G(t)$ are matrices of appropriate dimensions, $X_0$ is a constant specified vector, $\kappa _1$ and $\kappa _2$ are either $0$ or $1$ such that if $\kappa _1=1$ then $\kappa _2=0$ and vice versa, also if $\kappa _1=0$ then $\phi (t)=0$. The problem is to find $X(t),~0\le t\le 1,$ in Eq. (23) satisfying Eqs. (24) and (25). The method of this paper can also be extended to cases with delays in both state and control.

The Numerical Method

We approximate $X(t)$ in Eq. (23) as follows:

$$\begin{aligned} X(t)&= [x_{1}(t),x_{2}(t),\ldots ,x_{l}(t)]^{T},\quad U(t)=[u_{1}(t),u_{2}(t),\ldots ,u_{q}(t)]^{T},\end{aligned}$$

(26)

$$\begin{aligned} \hat{B}(t)&= I_{l}\otimes B(t),\quad \hat{B_{1}}(t)=I_{q}\otimes B(t), \end{aligned}$$

(27)

where $I_{l}$ and $I_{q}$ are the $l$- and $q$-dimensional identity matrices. Also, $\hat{B}(t)$ and $\hat{B_{1}}(t)$ are $l(M+1)N\times l$ and $q(M+1)N\times q$ matrices, respectively. By using Eq. (2) each of $x_{i}(t)$ and each of $u_{j}(t),\quad i=1,2,\ldots ,l,\quad j=1,2,\ldots ,q,$ can be written in terms of hybrid functions as

$$\begin{aligned} x_i(t)=B^T(t)X_i,\quad u_{j}(t)=B^T(t)U_j. \end{aligned}$$

From Eqs. (26) and (27) we get

$$\begin{aligned} X(t)=\hat{B}^{T}(t)X, \quad U(t)=\hat{B_{1}^{T}}(t)U, \end{aligned}$$

(28)

where $X$ and $U$ are vectors of order $l(M+1)N\times 1$ and $q(M+1)N\times 1,$ respectively, given by

$$\begin{aligned} X =[X_{1},X_{2},\ldots ,X_{l}]^{T},\quad U =[U_{1},U_{2},\ldots ,U_{q}]^{T}. \end{aligned}$$

Similarly we have

$$\begin{aligned} X(0)=\hat{B}^{T}(t)d,\quad \phi _j(t-\eta _j)=\hat{B}^{T}(t)R_j, \end{aligned}$$

(29)

where $d$ and $R_j,\,j=1,2,\ldots ,r$ are vectors of order $l(M+1)N\times 1$. We expand $E(t), F_j(t),\,H(t)$ and $G(t)$ by hybrid functions as follows:

$$\begin{aligned} E(t)=E^{T}\hat{B}(t), \quad F_j(t)=F_j^{T}\hat{B}(t),\quad H(t)=H^T\hat{B}(t),\quad G(t)=G^{T}\hat{B_{1}}(t), \end{aligned}$$

where $E^{T}, F_j^{T}, H^T$ and $G^{T}$ are of dimensions $l\!\times \! l(M\!+\!1)N, l\!\times \! l(M\!+\!1)N$ and $l\!\times \! q(M+1)N$, respectively. We can write $X(t-\eta _j)$ and $X(t-a(t))$ in terms of hybrid functions as

$$\begin{aligned} X(t-\eta _j)= \left\{ {\begin{array}{ll} \hat{B}^{T}(t)R_j, &{} \quad 0 \le t\le \eta _j, \\ \hat{B}^{T}(t)\hat{D}_j^{T}X, &{} \quad \eta _j \le t\le 1, \\ \end{array}} \right. \end{aligned}$$

and

$$\begin{aligned} X(t-a(t))=\hat{B}^{T}(t)\hat{Q}^{T}X, \end{aligned}$$

where

$$\begin{aligned} \hat{D}_j=I_{l}\otimes {D_j}, \quad \hat{Q}=I_{l}\otimes {Q}, \end{aligned}$$

${D_j},$ and $Q$ are the delay operational matrices given in Eqs. (18) and (20). Now we have

$$\begin{aligned} E(t)X(t)&= E^{T}\hat{B}(t)\hat{B}^{T}(t)X=\hat{B}^{T}(t)\tilde{E}^{T}X, \end{aligned}$$

(30)

$$\begin{aligned} G(t)U(t)&= G^{T}\hat{B_{1}}(t)\hat{B_{1}}^{T}(t)U=\hat{B}^{T}(t)\tilde{G}^{T}U, \end{aligned}$$

(31)

$$\begin{aligned} H(t)X(t-a(t))&= H^T\hat{B}(t)\hat{B}^{T}(t)\hat{Q}^TX=\hat{B}^{T}(t)\tilde{H}^T\hat{Q}^TX, \end{aligned}$$

(32)

where $\tilde{E},\,\tilde{G}$ and $\tilde{H}$ can be calculated similarly to matrix $\tilde{C}$ in Eq. (17). Also we have

$$\begin{aligned} \int \limits _{0}^{t}\hat{B}^{T}(t')dt'&= (I_{l}\otimes B^{T}(t))(I_{l}\otimes P^{T})=\hat{B}^{T}(t)\hat{P}^T, \end{aligned}$$

(33)

$$\begin{aligned} \int \limits _{0}^{t}F_j(t')X(t'-\eta _j)dt'&= \left\{ {\begin{array}{ll} \hat{B}^{T}(t)\hat{P}^T\tilde{F_j}^{T}R_j, &{} \quad \! 0 \le t\!\le \! \eta _j, \\ \hat{B}^{T}(t)Z_j\tilde{F_j}^{T}R_j+\hat{B}^{T}(t)\hat{P}^T\tilde{F_j}^{T}\hat{D_j}^{T}X, &{} \quad \! \eta _j \!\le \! t\!\le \! 1, \\ \end{array}} \right. \quad \quad \quad \end{aligned}$$

(34)

where $P$ is the operational matrix of integration given in Eq. (16) and

$$\begin{aligned} \int \limits _{0}^{\tau _j}\hat{B}^{T}(t)dt=\hat{B}^{T}(t)Z_j, \end{aligned}$$

where $Z_j$ is a constant matrix of order $l(M+1)N\times l(M+1)N$. By integrating Eq. (23) from $0$ to $t$ and using Eqs. (24–34) we have

$$\begin{aligned} \hat{B}^{T}(t)X-\hat{B}^{T}(t)d&= \hat{B}^{T}(t)\hat{P}^T\tilde{E}^{T}X+\kappa _1\displaystyle \sum \limits _{j=1}^{r}(\hat{B}^{T}(t)\hat{P}^T\tilde{F_j}^{T}R_j \nonumber \\&+\,\hat{B}^{T}(t)Z_j\tilde{F_j}^{T}R_j+\hat{B}^{T}(t)\hat{P}^T\tilde{F_j}^{T}\hat{D_j}^{T}X) \nonumber \\&+\,\kappa _2\hat{B}^{T}(t)\hat{P}^T\tilde{H}^T\hat{Q}^TX+\hat{B}^{T}(t)\hat{P}^T\tilde{G}^{T}U. \end{aligned}$$

(35)

From Eq. (35) we get $X$ as

$$\begin{aligned} X&= \left[ I-\hat{P}^T\tilde{E}^{T}-\kappa _1\sum _{j=1}^{r}\hat{P}^T\tilde{F_j}^{T}\hat{D_j}^{T}-\kappa _2\hat{P}^T\tilde{H}^T\hat{Q}^T\right] ^{-1}\\&\times \left[ d+\kappa _1\sum _{j=1}^{r}(\hat{P}^T\tilde{F_j}^{T}R_j+Z_j\tilde{F_j}^{T}R_j)+\hat{P}^T\tilde{G}^{T}U\right] . \end{aligned}$$

Hence, $X(t)$ in Eq. (28) can be obtained.

Discussion

Due to the nature of time-delay systems, the exact solutions of these systems are different functions on the distinct subintervals. In such situations, neither the continuous basis functions nor piecewise constant basis functions taken alone would form an efficient basis in the representation of such solutions. Datta and Mohan [26] have correctly pointed out that, in general, the computed response of the delay systems via continuous or piecewise constant basis functions is not in good agreement with the exact response of the system. To meet these situations, we choose a suitable hybrid system of basis functions inherently possessing the required features of the solutions corresponding to delay systems. In the proposed method, with the aid of Eqs. (19) and (21) we determine the appropriate value for $N$, the order of block-pulse functions for multi-delay and piecewise constant delay systems respectively. To select $M,$ we first choose an arbitrary number depending on the problem. If the exact solutions in each subinterval are polynomials we increase the value of $M$ by 1 until two consecutive results are the same in each subinterval. When the exact solutions in each subinterval are not polynomials, we evaluate the results for two consecutive $M$ for different $t$ in $[0,1]$ until the results are similar up to a required number of decimal places for each subinterval.

Illustrative Examples

In this “The Numerical Method” section, examples are given to demonstrate the applicability and accuracy of our method. Example 1 is a two-dimensional time-varying multi-delay system which was considered in [26]. The exact solutions in Examples 1 are polynomials for each subinterval. Example 2 is a delay system with delay in both control and state. Example 2 was first considered in [26] and also solved in [13–15] by using the hybrid of block-pulse with Chebyshev polynomials, with Legendre polynomials, and with Taylor series respectively. In this example we compare the solution obtained using the proposed method with [13–15]. The CPU time in each case are also given. Example 3 is a time-varying piecewise constant delay system whose solution is a polynomial for each subinterval and was considered in [5]. Example 4 is a piecewise constant delay system which was first considered in [26] and also solved in [5] by using the hybrid of block-pulse and Chebyshev polynomials. For example 4, we compare our findings with the numerical results in [5] together with the CPU time.

Example 1

Consider the multi-delay systems described by [26]

$$\begin{aligned} \left( {\begin{array}{l} \dot{x}_{1}(t)\\ \dot{x}_{2}(t)\\ \end{array}} \right) =\left( {\begin{array}{ll} t &{} 1 \\ t &{} 2t \\ \end{array}} \right) \left( {\begin{array}{l} x_{1}\left( t-\frac{1}{3}\right) \\ x_{2}\left( t-\frac{1}{3}\right) \\ \end{array}} \right) + \left( {\begin{array}{ll} 2 &{} t \\ t^2 &{} 0 \\ \end{array}} \right) \left( {\begin{array}{l} x_{1}\left( t-\frac{2}{3}\right) \\ x_{2}\left( t-\frac{2}{3}\right) \\ \end{array}} \right) + \left( {\begin{array}{l} 0\\ 1\\ \end{array}} \right) u(t), \end{aligned}$$

(36)

with

$$\begin{aligned} x_{1}(t)&= x_{2}(t)=u(t)=0,\,\quad t\in \left[ -\frac{2}{3},0\right] .\end{aligned}$$

(37)

$$\begin{aligned} u(t)&= 2t+1,\quad \,t>0. \end{aligned}$$

(38)

The exact solutions are [26]

$$\begin{aligned} x_1(t)&= \left\{ \begin{array}{ll} 0, &{}\quad 0\le t<\frac{1}{3},\\ \frac{7}{162}-\frac{2}{9}t+\frac{1}{6}t^2+\frac{1}{3}t^3, &{}\quad \frac{1}{3}\le t<\frac{2}{3},\\ \frac{11}{162}-\frac{58}{243}t+\frac{31}{162}t^2+\frac{1}{9}t^3+\frac{7}{72}t^4+\frac{1}{6}t^5, &{}\quad \frac{2}{3}\le t\le 1.\\ \end{array}\right. \\ x_2(t)&= \left\{ \begin{array}{ll} t+t^2, &{}\quad 0\le t<\frac{1}{3},\\ \frac{5}{486}+t+\frac{7}{9}t^2+\frac{2}{9}t^3+\frac{1}{2}t^4, &{}\quad \frac{1}{3}\le t<\frac{2}{3},\\ \frac{1}{486}+t+\frac{200}{243}t^2+\frac{20}{81}t^3+\frac{29}{72}t^4-\frac{1}{9}t^5+\frac{1}{6}t^6, &{}\quad \frac{2}{3}\le t\le 1.\\ \end{array}\right. \end{aligned}$$

By using Eq. (19) we have $\omega =3$ and $\lambda =1$, so we select $N=3$. We also choose $M=6$. Let

$$\begin{aligned} x_1(t)=C_{1}^{T}B(t),\quad x_2(t)=C_{2}^{T}B(t). \end{aligned}$$

(39)

By using Eq. (2) we get

$$\begin{aligned} u(t)= \left[ \frac{4}{3}, \frac{6}{3}, \frac{8}{3}, \frac{2}{3}, \frac{2}{3}, \frac{2}{3},\underbrace{ 0,\ldots , 0}_{15}\right] ^TB(t)=U_{1}^{T}B(t) \end{aligned}$$

(40)

and

$$\begin{aligned} t&= \left[ \frac{1}{6}, \frac{1}{2}, \frac{5}{6}, \frac{1}{3}, \frac{1}{3}, \frac{1}{3},\underbrace{ 0, \ldots , 0}_{15} \right] ^TB(t)=Y_{1}^{T}B(t),\end{aligned}$$

(41)

$$\begin{aligned} \quad t^2&= \left[ \frac{1}{27}, \frac{7}{27}, \frac{19}{27}, \frac{1}{9}, \frac{1}{3}, \frac{5}{9}, \frac{1}{9}, \frac{1}{9}, \frac{1}{9},\underbrace{ 0,\ldots ,0}_{12}\right] ^TB(t)= Y_{2}^{T}B(t). \end{aligned}$$

(42)

Also we have

$$\begin{aligned} x_1\left( t-\frac{1}{3}\right)&= C_{1}^{T}\underline{D}_1B(t),\quad x_2\left( t-\frac{1}{3}\right) =C_{2}^{T}\underline{D}_1B(t),\end{aligned}$$

(43)

$$\begin{aligned} x_1\left( t-\frac{2}{3}\right)&= C_{1}^{T}\underline{D}_2B(t),\quad x_2\left( t-\frac{2}{3}\right) =C_{2}^{T}\underline{D}_2B(t), \end{aligned}$$

(44)

where $\underline{D}_1$ and $\underline{D}_2$ are the delay operational matrices given in Eq. (18). By integrating Eq. (36) from 0 to $t$ and using Eqs. (37–44) we have

$$\begin{aligned} C_{1}^{T}&= C_{1}^{T}\underline{D}_1\widetilde{Y}_1P+C_{2}^{T}\underline{D}_1P+2C_{1}^{T}\underline{D}_2P+C_{2}^{T}\underline{D}_2\widetilde{Y}_1P, \end{aligned}$$

(45)

$$\begin{aligned} C_{2}^{T}&= C_{1}^{T}\underline{D}_1\widetilde{Y}_1P+2C_{2}^{T}\underline{D}_1\widetilde{Y}_1P+C_{2}^{T}\underline{D}_2\widetilde{Y}_2P+U_1^TP, \end{aligned}$$

(46)

where $\widetilde{Y}_1$ and $\widetilde{Y}_2$ can be obtained similarly to Eq. (17). Solving Eqs. (45) and (46), the same values as the exact values of $x_{1}(t)$ and $x_{2}(t)$ would be obtained.

Example 2

Consider the following delay system with delay in both control and state [26]

$$\begin{aligned} \dot{x}(t)&= -x(t)-2x\left( t-\frac{1}{4}\right) +2u\left( t-\frac{1}{4}\right) ,\quad u(t)=1,\quad t>0,\end{aligned}$$

(47)

$$\begin{aligned} x(t)&= u(t)=0,\quad -\frac{1}{4}\le t<0. \end{aligned}$$

(48)

The exact solution is

$$\begin{aligned} x(t)=\left\{ \begin{array}{ll} 0, &{} \quad 0\le t\le \frac{1}{4},\\ 2-2\exp \left[ -\left( t-\frac{1}{4}\right) \right] , &{} \quad \frac{1}{4}\le t\le \frac{1}{2},\\ -2-2\exp \left[ -\left( t-\frac{1}{4}\right) \right] +(2+4t)\exp \left[ -\left( t-\frac{1}{2}\right) \right] , &{} \quad \frac{1}{2}\le t\le \frac{3}{4},\\ 6-2\exp \left[ -\left( t-\frac{1}{4}\right) \right] +(2+4t)\exp \left[ -\left( t-\frac{1}{2}\right) \right] &{} \\ \quad -\left( \frac{17}{4}+2t+4t^{2}\right) \exp \left[ -\left( t-\frac{3}{4}\right) \right] , &{} \quad \frac{3}{4}\le t<1.\\ \end{array}\right. \end{aligned}$$

By using Eq. (19) we have $\omega =4$ and $\lambda =1$, so we select $N=4$. We also choose $M=5$. Let

$$\begin{aligned} x(t)=C_{3}^{T}B(t), \end{aligned}$$

(49)

by using Eq. (2) we have

$$\begin{aligned} u(t)=[1, 1, 1, 1, \underbrace{0, \ldots , 0}_{20}]^TB(t)=U_{2}^{T}B(t). \end{aligned}$$

(50)

Also we have

$$\begin{aligned} x\left( t-\frac{1}{4}\right)&= C_{3}^{T}\underline{D}_3B(t),\end{aligned}$$

(51)

$$\begin{aligned} u\left( t-\frac{1}{4}\right)&= U_{2}^{T}\underline{D}_3B(t), \end{aligned}$$

(52)

where $\underline{D}_3$ is the delay operational matrix given in Eq. (18). By integrating Eq. (47) from $0$ to $t$ and using Eqs. (48–52) we have

$$\begin{aligned} C_{3}^{T}=-C_{3}^{T}P-2C_{3}^{T}\underline{D}_3P+2U_{2}^{T}\underline{D}_3P. \end{aligned}$$

(53)

By solving Eq. (53) we obtain $C_{3}$. In Table 1, the solution obtained using the hybrid of block-pulse and Chebyshev polynomials in [13] with $N=4$ and $M_1=7$ and the hybrid of block-pulse and Legendre polynomials in [14] with $N=4$ and $M_2=7$ together with CPU time are given. In this table $M_1$ and $M_2$ denote the order of Chebyshev and Legendre polynomials respectively. In Table 2, the solution obtained using the hybrid of block-pulse and Taylor series in [15] with $N=4$ and $M_3=7$ and the proposed method with $N=4$ and $M=5$ together with CPU time and the exact solution of $x(t)$ for $\frac{1}{4}\le t\le 1$ are given. In this table $M_3$, denotes the order of Taylor series. In Tables 1 and 2, the approximate value of $x(t)$ on $[0,\frac{1}{4}]$ is equal to zero, which is the same as the exact solution.

Table 1 The solution obtained using the hybrid of block-pulse with Chebyshev and Legendre polynomials for Example 1

Table 2 The solution obtained using the hybrid of block-pulse with Taylor and Bernoulli polynomials for Example 1

Example 3

Consider the following piecewise constant delay system [5]

$$\begin{aligned} \dot{x}(t)&= t^2x(t-a(t))+u(t),\quad 0\le t\le 1,\end{aligned}$$

(54)

$$\begin{aligned} x(0)&= 1,\end{aligned}$$

(55)

$$\begin{aligned} u(t)&= 2t+1,\quad t\ge 0,\end{aligned}$$

(56)

$$\begin{aligned} a(t)&= \left\{ \begin{array}{ll} 0.2, &{}\quad 0\le t<0.3,\\ 0.7, &{}\quad 0.3\le t\le 1\\ \end{array}\right. \end{aligned}$$

(57)

The exact solution is

$$\begin{aligned} x(t)=\left\{ \begin{array}{ll} 1+t+t^2, &{} 0\le t<0.2,\\ \frac{62341}{62500}+t+t^2+\frac{7}{25}t^3+\frac{3}{20}t^4+\frac{1}{5}t^5,&{}0.2\le t <0.3,\\ \frac{1006717}{1000000}+t+t^2,&{}0.3\le t<0.7,\\ \frac{2720369}{3000000}+t+t^2+\frac{79}{300}t^3-\frac{1}{10}t^4+\frac{1}{5}t^5,&{}0.7\le t<0.9,\\ \frac{76256550101}{84000000000}+t+t^2+\frac{693817}{3000000}t^3+\frac{459}{40000}t^4\\ \quad +\frac{167}{5000}t^5+\frac{7}{50}t^6-\frac{11}{140}t^7+\frac{1}{40}t^8, &{}0.9\le t\le 1. \end{array}\right. \end{aligned}$$

By using Eqs. (21) and (57) we have $\gamma =10$ and $\delta =1$, so we choose $N=10$. We also choose $M=8$. Let

$$\begin{aligned} x(t)=C_{4}^{T}B(t), \end{aligned}$$

(58)

by using Eq. (2) we have

$$\begin{aligned} u(t)&= \left[ \frac{11}{10}, \frac{13}{10}, \frac{3}{2}, \frac{17}{10}, \frac{19}{10}, \frac{21}{10}, \frac{23}{10}, \frac{5}{2}, \frac{27}{10}, \frac{29}{10}, \frac{1}{5}, \frac{1}{5}, \frac{1}{5}, \frac{1}{5}, \frac{1}{5}, \frac{1}{5}, \frac{1}{5}, \frac{1}{5}, \frac{1}{5}, \frac{1}{5},\underbrace{ 0,\ldots ,0}_{70}\right] ^{\!T}\!\! B(t)\nonumber \\&= U_{3}^{T}B(t),\end{aligned}$$

(59)

$$\begin{aligned} t^2&= \left[ \frac{1}{300}, \frac{7}{300}, \frac{19}{300}, \frac{37}{300}, \frac{61}{300}, \frac{91}{300}, \frac{127}{300}, \frac{169}{300}, \frac{217}{300}, \frac{271}{300}, \frac{1}{100}, \frac{3}{100}, \frac{1}{20}, \frac{7}{100}, \frac{9}{100},\frac{11}{100}, \right. \nonumber \\&\left. \frac{13}{100},\frac{3}{20}, \frac{17}{100}, \frac{19}{100}, \frac{1}{100}, \frac{1}{100}, \frac{1}{100}, \frac{1}{100}, \frac{1}{100}, \frac{1}{100}, \frac{1}{100}, \frac{1}{100}, \frac{1}{100}, \frac{1}{100}, \underbrace{0,\ldots ,0}_{60}\right] ^{\!T}\!\! B(t)\!\!\!\nonumber \\&= Y_{3}^{T}B(t),\end{aligned}$$

(60)

$$\begin{aligned} 1&= [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, \underbrace{0,\ldots ,0}_{80}]^TB(t)=Y_{4}^{T}B(t). \end{aligned}$$

(61)

Also we have

$$\begin{aligned} x(t-a(t))=C_{4}^{T}\underline{D}_4B(t), \end{aligned}$$

(62)

where $\underline{D}_4$ is the delay operational matrix given in Eq. (20) and is obtained from

$$\begin{aligned} \underline{D}_5=\underline{Q}_1+\underline{Q}_2+\cdots +\underline{Q}_{10}, \end{aligned}$$

where $\underline{Q}_i,~~1\le i \le 10$ are calculated similarly to Eq. (22). For example $\underline{Q}_3$ is

$$\begin{aligned} \underline{Q}_3=I_9\otimes \underline{S}_3, \end{aligned}$$

where $I_9$ is the 9 dimensional identity matrix and $\underline{S}_3$ is a $10\times 10$ matrix given by

$$\begin{aligned} \underline{S}_3=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0&{}1&{}0&{}\ldots &{}0\\ 0 &{} 0&{}0&{}0&{}\ldots &{}0\\ \vdots &{} \vdots &{}\vdots &{}\vdots &{}\ldots &{}\vdots \\ 0 &{} 0&{}0&{}0&{}\ldots &{}0\\ \end{array}\right] . \end{aligned}$$

By integrating Eq. (54) from $0$ to $t$ and using Eqs. (55–62) we have

$$\begin{aligned} C_{4}^{T}-Y_{4}^{T}=C_{4}^{T}\underline{D}_4\widetilde{Y}_3P+U_{3}^{T}P, \end{aligned}$$

(63)

where $\widetilde{Y}_3$ can be obtained similarly to Eq. (17). By solving Eq. (63) the same value as the exact value of $x(t)$ would be obtained.

Example 4

Consider the following piecewise constant delay system [26]

$$\begin{aligned} \dot{x}(\tau )&= -5x(\tau )-5x(\tau -a(\tau ))+2u(\tau ),\quad 0\le \tau \le 2,\\ x(0)&= 1,\\ u(\tau )&= 1,\quad \tau \ge 0,\\ a(\tau )&= \left\{ \begin{array}{ll} 0, &{}\quad 0\le \tau <0.8,\\ 0.3,&{}\quad 0.8\le \tau <1.4,\\ 0.6,&{}\quad 1.4\le \tau < 1.7,\\ 0.9,&{}\quad 1.7\le \tau \le 2. \end{array}\right. \end{aligned}$$

The exact solution is

$$\begin{aligned} x(\tau )=\left\{ \begin{array}{ll} 0.2+0.8e^{-10\tau }, &{} 0\le \tau <0.8,\\ 0.2+0.8e^{3-10\tau }+0.8e^{-4}(1-e^3)e^{-5\tau },&{}0.8\le \tau <1.1,\\ 0.2+0.8e^{6-10\tau }-4e^{-2.5}(1-e^3)\tau e^{-5\tau }&{}1.1\le \tau <1.4,\\ \quad +\,0.8(1-e^3)(6.5e^{-2.5}+e^{-4})e^{-5\tau }, &{} \\ 0.2+0.8e^{9-10\tau }-4e^{-1}(1-e^3)\tau e^{-5\tau }&{} \\ \quad +\,0.8(1-e^3)(8e^{-1}-0.5e^{-2.5}+e^{-4})e^{-5\tau },&{} 1.4\le \tau <1.7,\\ 0.2+0.8e^{12-10\tau }-4e^{0.5}(1-e^3)\tau e^{-5\tau }&{} \\ \quad +\,0.8(1-e^3)(9.5e^{0.5}-0.5e^{-1}-0.5e^{-2.5}+e^{-4})e^{-5\tau },&{}\quad 1.7\le \tau \le 2.\\ \end{array}\right. \end{aligned}$$

By using transformation $\tau = 2t,\,0 \le t \le 1$, we have

$$\begin{aligned} \dot{x}(t)&= 2(-5x(t)-5x(t-a(t))+2u(t)),\quad 0\le t\le 1, \end{aligned}$$

(64)

$$\begin{aligned} x(0)&= 1,\end{aligned}$$

(65)

$$\begin{aligned} u(t)&= 1,\quad t\ge 0,\end{aligned}$$

(66)

$$\begin{aligned} a(t)&= \left\{ \begin{array}{ll} 0, &{} \quad 0\le t<0.4,\\ 0.3, &{} \quad 0.4\le t<0.7,\\ 0.6, &{} \quad 0.7\le t< 0.85,\\ 0.9, &{} \quad 0.85\le t\le 1. \end{array}\right. \end{aligned}$$

(67)

From Eqs. (21) and (67) we have $\gamma =100$ and $\delta =5$, so we select $N=20$. We also choose $M$ an arbitrary positive integer number. Let $M=1$ and

$$\begin{aligned} x(t)=C_{5}^{T}B(t), \end{aligned}$$

(68)

by using Eq. (2) we have

$$\begin{aligned} 1=[\underbrace{1, 1,\ldots , 1}_{20}]^TB(t)=Y_{5}^{T}B(t),\qquad u(t)=[\underbrace{1, 1,\ldots , 1}_{20}]^TB(t)=U_{4}^{T}B(t). \end{aligned}$$

(69)

Also we have

$$\begin{aligned} x(t-a(t))=C_{5}^{T}\underline{D}_5B(t), \end{aligned}$$

(70)

where $\underline{D}_5$ is the delay operational matrix given in Eq. (20). By integrating Eq. (64) from $0$ to $t$ and using Eqs. (65–70) we have,

$$\begin{aligned} C_{5}^{T}-Y_{5}^{T}=2\left( -5C_{5}^{T}P-5C_{5}^{T}\underline{D}_5P+2U_{4}^{T}P\right) . \end{aligned}$$

(71)

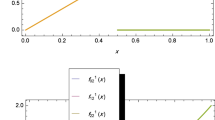
By solving Eq. (71) we obtain $C_{5}$. In Table 3, we compare maximum error obtained using the proposed method with the hybrid of block-pulse and Chebyshev polynomials in [5]. The approximate solution of $x(t)$, obtained by the proposed method for $M=1$ and 2, are shown in Figs. 1 and 2 respectively.

Fig. 1

Exact and approximate solution of $x (t)$ for $M=1$

Fig. 2

Exact and approximate solution of $x (t)$ for $M=2$

Table 3 The solution obtained using the hybrid of block-pulse with Chebyshev and Bernoulli polynomials for Example 4

Conclusion

In the present work, hybrid of block-pulse functions and Bernoulli polynomials are used to solve delay systems. The problem has been reduced to a problem of solving a system of algebraic equations. The matrix $P$ given in Eq. (16) has a large number of zero elements and is sparse. Hence, the present method is very attractive and reduces the CPU time and computer memory. Illustrative examples are given to demonstrate the validity and applicability of the proposed method. It is noted that the exact solutions obtained in the examples 1, 2 and 4 can not be obtained either with piecewise constant basis functions nor with continuous basis functions.