Fractional-order Fibonacci-hybrid functions approach for solving fractional delay differential equations

Abstract

The aim of the current paper is to propose an efficient method for finding the approximate solution of fractional delay differential equations. This technique is based on hybrid functions of block-pulse and fractional-order Fibonacci polynomials. First, we define fractional-order Fibonacci polynomials. Next, using Fibonacci polynomials of fractional-order, we introduce a new set of basis functions. These new functions are called fractional-order Fibonacci-hybrid functions (FFHFs) which are appropriate for the approximation of smooth and piecewise smooth functions. The Riemann–Liouville integral operational matrix and delay operational matrix of the FFHFs are obtained. Then, using these matrices and collocation method, the problem is reduced to a system of algebraic equations. Using Newton’s iterative method, we solve this system. Some examples are proposed to test the efficiency and effectiveness of the present method. Given the application of these kinds of fractional equations in the modeling of many phenomena, a numerical example of this work includes the Hutchinson model which describes the rate of population growth.

1 Introduction

In the last few decades, delay systems have been highly regarded by researchers. Because a lot of these time-delay systems appear in many systems and branches of various sciences such as engineering, chemistry, physics, disease models [1], traffic flow models [2], and so on.

Myshkis introduced the theory of a class of delay differential equations in 1949 [3]. In addition, Krasovski [4], Bellman and Cooke [5], El’sgol’c and Norkin [6], and Hale [7] studied in the field.

One of the branches of mathematical studies is the fractional calculus, which has attracted many researchers in recent years, because this branch of mathematics emerges in the modeling of many phenomena. For example, in [8], the authors presented fractional Sturm–Liouville boundary value problems. In [9], the authors discussed the fractional rumor spreading dynamical model, and in [10], they regularized long-wave equation has been studied. To find out more about fractional calculus, we can refer to [11]. Fractional calculus is obtained by the change of the derivative and integral order from the integer to the non-integer. In fact, the fractional calculus is the classical mathematical development. Some advantage of this branch of mathematics is explained in [12].

The fractional differential equation is a kind of fractional equations that appears in the modeling of many phenomena in the various sciences. Recently, these equations have been considered by many researchers and mathematicians, and this has led to the improvement and expansion of this kind of equations. The examples of these works can be found in [13, 14] and [15].

In addition, there are various analytic and numerical techniques to solve this type of fractional equations, such as fractional Lagrange polynomials [16], fractional-order of Legendre polynomials [17], fractional-order Taylor method [18], homotopy analysis transform method [19], q-fractional homotopy analysis transform method [20], Volterra integral equation method [21], homotopy analysis method [22], operational matrix of Legendre polynomials [23], the mixture homotopy analysis technique, Sumudu transform approach and homotopy polynomials [24], and so on.

Several numerical techniques have been presented for solving integer and non-integer order of delay differential equations, such as Legendre wavelet method [25], Chebyshev polynomials [26], Bernoulli wavelet [27], fractional-order Bernoulli wavelet [28], predictor-corrector method [29], Legendre spectral element method [30], finite difference/finite element method [31], etc.

Moreover, some scholars discussed the stability and analysis of the behavior of delay fractional differential equations or a system of delay fractional differential equations. This type of study can be seen in some works like [32, 33].

Delay fractional differential equations describe the effectiveness of some physical objects such as amorphous semiconductors, fractional random walk [34], and so on. Other applications of this kind of equation happen in some fields such as: fluid flow, viscoelasticity, electrical networks, probability and statistics, optics and signal processing, rheology, etc. Interested readers can find more details in Refs. [35,36,37,38].

Piecewise constant basis functions, orthogonal polynomials, and sine-cosine functions in the Fourier series are three classes of the orthogonal functions.

Utilizing the derivative or integration operational matrices of orthogonal functions, the dynamical system problems reduce to solving a system of algebraic equations. These operational matrices can be specified uniquely, using the special orthogonal functions [39]. The Fibonacci polynomials are not orthogonal functions. However, these polynomials have the fractional-order integration operational matrix. A Riemann–Liouville integral operational matrix of Fibonacci polynomials is proposed in [40].

Recently, hybrid functions have included a combination of pulse-block functions and some polynomials such as Legendre polynomials, Lagrange polynomials [41], Chebyshev polynomials [42], and Bernoulli polynomials [43], Bernstein polynomials [44], and Taylor series [45] as strong base functions in solving various kind of equations.

In the current study, we present fractional-order Fibonacci polynomials. Then, using these fractional functions, we introduce another new set of fractional functions, that is called fractional-order Fibonacci-hybrid functions.

FFHFs are appropriate for the approximation of smooth and piecewise smooth functions defined on symmetric and asymmetric subintervals. Moreover, the introduced fractional-order Fibonacci-hybrid functions have three free parameters ($N, M ,\alpha$), and so, by different choice of them especially $\alpha$, we can obtain more accurate solution for problems, while the previous hybrid functions are dependent to N and M.

The structure of this work is organized as follows. The next section includes some necessary definitions and mathematical preliminaries required for the next development. Section 3 is devoted to construct the Fibonacci polynomials of fractional-order and fractional-order Fibonacci-hybrid functions. In Sect. 4, we derive the FFHFs operational matrices of fractional integration and delay. In Sect. 5, we present the numerical technique for solving delay fractional differential equations. Section 6 is devoted to the error analysis. In Sect. 7, by considering some example, we propose the numerical results and display the effectiveness of this method. In addition, we employ this method for solving the Hutchinson model.

2 Preliminaries

Definition 1

Suppose that $f:\;[a,\;b] \rightarrow R$ be a function, $\nu \in R, \nu> 0$ and $n= \lceil \nu \rceil$, the fractional-order Riemann–Liouville integral is defined as follows [16]:

$$\begin{aligned} I^{\nu }f(x) = \left\{ \begin{array}{llll} \frac{1}{\varGamma ( \nu )} \int _{0}^{x} (x-t)^{ \nu -1}f (t) {\text {d}}t = \frac{1}{\varGamma (\nu )} x^{ \nu -1} * f(x) &{} \nu>0,\\ f(x) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad &{} \nu =0, \end{array}\right. \end{aligned}$$

(1)

where $*$ denotes the convolution product. In addition, we have the following: [16]

$$\begin{aligned} (D^{\nu } I^{\nu } f)(x)& = f(x), \end{aligned}$$

(2)

$$\begin{aligned} (I^{\nu }D^{\nu } f)(x)& = f(x) - \sum _{i=0}^{\lceil \nu \rceil -1}\frac{x^{i}}{i!} f^{(i)}(0). \end{aligned}$$

(3)

$D^{\nu }$ denotes fractional derivative in Caputo sense which is presented in [16].

Definition 2

(Generalized Taylor’s formula) [45] Let $D^{k \alpha }f(x) \in C (0,\;1]$ for $\small {k=0, 1, \ldots , n+1}$. Then, for $0 < \xi \le x, \forall x \in (0, 1]$, we have the following:

$$\begin{aligned} f(x) = \sum _{k=0}^{n} \frac{x^{k \alpha }}{\varGamma (k \alpha +1)} D^{k \alpha }f(0^{+}) + \frac{x^{(n+1) \alpha }}{\varGamma ((n+1) \alpha +1)} D^{(n+1) \alpha }f (\xi ), \end{aligned}$$

Moreover, we get

$$\begin{aligned} \vert f(x) - \sum _{k=0}^{n} \frac{x^{k \alpha }}{\varGamma (k \alpha +1)} D^{k \alpha }f(0^{+}) \vert \le M_{\alpha } \frac{x^{(n+1) \alpha }}{\varGamma ((n+1) \alpha +1)} , \end{aligned}$$

(4)

where $M_{\alpha } \ge \sup _{\xi \in (0, 1]} \vert D^{(n+1) \alpha }f (\xi ) \vert$.

3 Fractional-order Fibonacci-hybrid functions

Here, we recall the definitions of Fibonacci polynomials, and in continue, we introduce fractional-order Fibonacci polynomials. In the end, we propose the fractional-order Fibonacci-hybrid functions.

3.1 Fibonacci polynomials

Definition 3

For any $k \in R^{+}$, the recurrent form of k-Fibonacci sequence is as follows [46]:

$$\begin{aligned} \tilde{F}_{k,n+1} = k\tilde{F}_{k,n}+\tilde{F}_{k,n-1},\quad n \ge 1 \end{aligned}$$

(5)

subject to $\tilde{F}_{k,0}=0,\;\;\;\tilde{F}_{k,1}=1$.

If k is a real variable x in Eq. (5), then $\tilde{F}_{k,n} = \tilde{F}_{x,n}$. Therefore, the general formula of Fibonacci polynomials is as follows [46]:

$$\begin{aligned} \tilde{F}_{n}(x) = \left\{ \begin{array}{lll} 1, &{} n=0, \\ x, &{} n=1, \\ x\tilde{F}_{n-1}(x)+\tilde{F}_{n-2}(x), &{} n>1. \end{array}\right. \end{aligned}$$

(6)

or the power form representation of Fibonacci polynomials is as follows[46]:

$$\begin{aligned} \tilde{F}_{n}(x) =\sum _{i=0}^{\lfloor \frac{n}{2} \rfloor } \left( \begin{array}{ll} n-i \\ i \end{array} \right) x^{n-2i},\quad n \ge 0, \end{aligned}$$

(7)

Remark 1

The matrix form of Fibonacci polynomials is as follows:

$$\begin{aligned} \tilde{F}(x)= BT(x), \end{aligned}$$

(8)

in which

$$\begin{aligned} \tilde{F}(x)= [\tilde{F}_{0}(x),\;\tilde{F}_{1}(x),\;\tilde{F}_{2}(x),\ldots ]^{\text {T}},\;\;\;T(x)=[1,\;x,\;x^2,\;x^3,\ldots ]^{\text {T}}, \end{aligned}$$

and B is coefficients matrix which is the lower triangular matrix:

$$\begin{aligned} B= \left[ {\begin{array}{cccccccccccc} 1&{} 0&{} 0&{}0 &{}0 &{} 0&{}0 &{} \cdots \\ 0 &{} 1&{}0 &{} 0&{} 0&{}0 &{}0 &{} \cdots \\ 1&{}0&{}1&{}0 &{}0 &{}0 &{}0 &{} \cdots \\ 0 &{} 2 &{}0 &{} 1&{}0 &{}0 &{}0 &{} \cdots \\ 1&{}0&{} 3&{}0&{}1 &{}0 &{}0 &{} \cdots \\ 0 &{} 3 &{}0&{} 4 &{} 0 &{} 1 &{}0&{} \cdots \\ 1&{}0&{}6&{}0&{}5&{}0&{}1 &{} \cdots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots \\ \end{array}} \right] . \end{aligned}$$

(9)

In this matrix, the non-zero inputs exactly build the diagonals of the Pascal triangle and the sum of elements in each row is the same as the classical Fibonacci sequence [47].

3.2 Fractional-order Fibonacci polynomials

To construct fractional-order Fibonacci polynomials, we utilize the change of variable x to $x^{\alpha }$, $(\alpha>0)$, and we represent these fractional-order polynomials with $\tilde{F}_{n}^{\alpha }(x)$. Using Eq. (6), the analytic form of $\tilde{F}_{n}^{\alpha }(x)$ is as follows:

$$\begin{aligned} \tilde{F}^{\alpha }_{n}(x) = \left\{ \begin{array}{lll} 1, &{} n=0, \\ x^{\alpha }, &{} n=1, \\ x^{\alpha }\tilde{F}_{n-1}^{\alpha }(x)+\tilde{F}_{n-2}^{\alpha }(x), &{} n>1. \end{array}\right. \end{aligned}$$

(10)

In addition, using Eq. (7), we achieve

$$\begin{aligned} \tilde{F}_{n}^{\alpha }(x) =\sum _{i=0}^{\lfloor \frac{n}{2} \rfloor } \left( \begin{array}{ll} n-i \\ i \end{array} \right) x^{\alpha (n-2i)},\;\;\;\;n \ge 0, \end{aligned}$$

(11)

For example, the fractional-order Fibonacci polynomials for $n=3$ are as follows:

$$\begin{aligned} \tilde{F}_{0}^{\alpha }(x)=1, \quad \tilde{F}_{1}^{\alpha }(x)=x^{\alpha }, \quad \tilde{F}_{2}^{\alpha }(x)=x^{2\alpha }+1, \quad \tilde{F}_{3}^{\alpha }(x)=x^{3\alpha }+2x^{\alpha }. \end{aligned}$$

3.3 Fractional-order Fibonacci-hybrid functions

Now, a new set of functions called fractional-order Fibonacci-hybrid functions (FFHFs) is proposed. FFHFs are made by change of variable x to $x^{\alpha }$, $(0< \alpha \le 1)$, on the Fibonacci-hybrid functions. The FFHFs $f_{nm}(x^{\alpha })$ are specified by $f^{\alpha }_{nm}(x)$. Then, using the Fibonacci-hybrid functions and the fractional-order Fibonacci polynomials, we have the following:

$$\begin{aligned} f^{\alpha }_{nm}(x)= \left\{ \begin{array}{ll} \tilde{F}_{n}(Mx^{\alpha }-m+1),&{} \frac{m-1}{M} \le x^{\alpha } < \frac{m}{M}, \\ 0, &{} {\text {otherwise}}, \end{array} \right. \end{aligned}$$

(12)

where $n=0, 1, \ldots , N$ and $m=1, 2, \ldots , M$, and n is the order of fractional Fibonacci polynomials and the order of block-pulse function is denoted by m. In addition, we have Fibonacci-hybrid functions, for $\alpha =1$. For example, in $N=2,\;M=3,\alpha =\frac{1}{2}$, we obtain the following:

$$\begin{aligned} f^{\frac{1}{2}}_{01}(x)& = \left\{ \begin{array}{ll} 1,&{} 0 \le x< \frac{1}{9} \\ 0 &{} {\text {otherwise}} \end{array}\right. , \;\;\; f^{\frac{1}{2}}_{11}(x) =\left\{ \begin{array}{ll} 3 \sqrt{x},&{} 0 \le x< \frac{1}{9}\\ 0 &{} {\text {otherwise}} \end{array} \right. ,\;\;\;\\ f^{\frac{1}{2}}_{21}(x)& = \left\{ \begin{array}{ll} 9x+1,&{} 0 \le x< \frac{1}{9} \\ 0 &{} {\text {otherwise}} \end{array} \right. \\ f^{\frac{1}{2}}_{02}(x)& = \left\{ \begin{array}{ll} 1,&{} \frac{1}{9} \le x< \frac{4}{9} \\ 0 &{} {\text {otherwise}} \end{array}\right. , \;\;\; f^{\frac{1}{2}}_{12}(x) =\left\{ \begin{array}{ll} 3 \sqrt{x}-1,&{} \frac{1}{9} \le x< \frac{4}{9}\\ 0 &{} {\text {otherwise}} \end{array} \right. ,\;\;\; \\ f^{\frac{1}{2}}_{22}(x)& = \left\{ \begin{array}{ll} 9x-6\sqrt{x}+2,&{} \frac{1}{9} \le x< \frac{4}{9} \\ 0 &{} {\text {otherwise}} \end{array} \right. \\ f^{\frac{1}{2}}_{03}(x)& = \left\{ \begin{array}{ll} 1,&{} \frac{4}{9} \le x<1 \\ 0 &{} {\text {otherwise}} \end{array}\right. , \;\;\; f^{\frac{1}{2}}_{13}(x) =\left\{ \begin{array}{ll} 3 \sqrt{x}-2,&{} \frac{4}{9} \le x<1 \\ 0 &{} {\text {otherwise}} \end{array} \right. ,\;\;\;\\ f^{\frac{1}{2}}_{23}(x)& = \left\{ \begin{array}{ll} 9x-12\sqrt{x}+5,&{} \frac{4}{9} \le x <1 \\ 0 &{} {\text {otherwise}} \end{array} \right. \end{aligned}$$

Moreover, Figs. 1 and 2 show the FFHFs with $N=2, M=2$ and $\alpha =1, 0.5$

Fig. 1

Plot of the FFHFs with $N=2, M=2$ and $\alpha =1$

Fig. 2

Plot of the FFHFs with $N=2, M=2$ and $\alpha = 0.5$

3.4 Function approximation

Suppose that $H=L^{2}[0, 1]$, and $\{f^{\alpha }_{01}(x), f^{\alpha }_{11}(x), \ldots , f^{\alpha }_{NM}(x)\} \subset H$ is the set of Fibonacci-hybrid functions of fractional order, and $Y = span \{f^{\alpha }_{01}(x), f^{\alpha }_{11}(x), \ldots , f^{\alpha }_{NM}(x)\}$. Let g be an arbitrary element in H. Y is a finite-dimensional vector space, so $\tilde{g} \in Y$ is the unique best approximation out of Y, which is

$$\begin{aligned} \forall y \in Y,\;\;\;\; \Vert g- \tilde{g} \Vert \le \Vert g-y \Vert . \end{aligned}$$

Furthermore, since $\tilde{g} \in Y$, there exist coefficients $c_{01}, c_{11},\ldots , c_{NM}$, uniquely as follows:

$$\begin{aligned} g(x) \simeq \tilde{g}(x) = \sum _{n=0}^{N} \sum _{m=1}^{M} c_{nm}f^{\alpha }_{nm}(x) = C^{\text {T}}F^{\alpha }(x), \end{aligned}$$

(13)

where

$$\begin{aligned} C& = [c_{01}, c_{11}, \ldots , c_{N1}, c_{02}, c_{12}, \ldots , c_{N2}, \ldots , c_{0M}, \ldots , c_{NM}]^{\text {T}}\nonumber \\ F^{\alpha }(x)& = [f^{\alpha }_{01}(x), \ldots , f^{\alpha }_{N1}(x), \ldots , f^{\alpha }_{0M}(x), \ldots , f^{\alpha }_{NM}(x)]^{\text {T}}\nonumber \\& = [f^{\alpha }_{0}(x), f^{\alpha }_{1}(x), \ldots , f^{\alpha }_{NM}(x)]^{\text {T}}. \end{aligned}$$

(14)

The coefficient vector C can be obtained as $C^{\text {T}} = G^{\text {T}} D^{-1}$, where

$$\begin{aligned} D& = \langle F^{\alpha },\;F^{\alpha } \rangle = \int _{0}^{1} F^{\alpha }(x)F^{\alpha T}(x)x^{\alpha -1} {\text {d}}x, \nonumber \\ G& = [g_{01}, g_{11},\ldots , g_{N1}, g_{02}, g_{12},\ldots , g_{N2},\ldots , g_{0M},\ldots , g_{NM}]^{\text {T}}, \end{aligned}$$

(15)

and

$$\begin{aligned} g_{nm} = \int _{0}^{1} g(x) f^{\alpha }_{nm}(x)x^{\alpha -1} {\text {d}}x,\;\;n=0, 1, 2,\ldots , N,\;\;\;m=1, 2,\ldots , M. \end{aligned}$$

(16)

4 FFHF operational matrix of the Riemann–Liouville integral

Suppose $F^{\alpha }(x)$ is FFHFs vector presented in Eq. (7), then

$$\begin{aligned} I^{\nu }F^{\alpha }(x) \simeq P^{(\nu ,\;\alpha )} F^{\alpha }(x), \end{aligned}$$

(17)

where the fractional Riemann–Liouville integral operational matrix of order $\nu$ is denoted by $P^{(\nu ,\;\alpha )}$. Now, by using Eq. (1), we have the following:

$$\begin{aligned} I^{\nu }f^{\alpha }_{nm}(x) = \frac{1}{\varGamma (\nu )}x^{\nu -1} * f^{\alpha }_{nm}(x),\;\; n=0, 1, \ldots , N\;\;\;m=1, 2, \ldots , M. \end{aligned}$$

(18)

Taking the Laplace transform on Eq. (18), we obtain the following:

$$\begin{aligned} \mathcal {L}[I^{\nu }f_{nm}^{\alpha }(x)] = \mathcal {L}\left[ \frac{1}{\varGamma (\nu )}x^{\nu -1}\right] \mathcal {L}[ f^{\alpha }_{nm}(x)],\;\;\;n=0, 1, \ldots , N \quad m=1, 2, \ldots , M, \end{aligned}$$

(19)

where

$$\begin{aligned} \mathcal {L}\left[ \frac{1}{\varGamma (\nu )}x^{\nu -1}\right] = r^{-v}. \end{aligned}$$

(20)

In addition, for $f_{nm}^{\alpha }(x)$, we have the following:

$$\begin{aligned} f_{nm}^{\alpha }(x)& = \mu _{(\frac{m-1}{M})^{\frac{1}{\alpha }}}(x) \tilde{F}_{n}(Mx^{\alpha }-m+1)\nonumber \\&\quad -\mu _{(\frac{m}{M})^{\frac{1}{\alpha }}}(x) \tilde{F}_{n}(M x^{\alpha }-m+1) \nonumber \\& = \sum _{i=0}^{\lfloor \frac{n}{2} \rfloor } \left( \begin{array}{ccc} n-i\\ i \end{array} \right) (M x^{\alpha }-m+1)^{\alpha (n-2i)} \nonumber \\&\quad \biggl ( \mu _{(\frac{m-1}{M})^{\frac{1}{\alpha }}}(x)- \mu _{(\frac{m}{M})^{\frac{1}{\alpha }}}(x) \biggl ), \end{aligned}$$

(21)

where $\mu _{c}(x)$ is unit step function.

By employing the Laplace transform for Eq. (21) and using Eq. (19), we obtain $\mathcal {L} (I^{\nu } f_{nm}^{\alpha }(x))=\varphi ^{(\nu ,\alpha )}_{nm}(r)$. Now, utilizing the inverse Laplace transform of $\varphi ^{(\nu ,\alpha )}_{nm}(r)$, yields

$$\begin{aligned} I^{\nu }f_{nm}^{\alpha }(x) = \tilde{\varphi }^{(\nu ,\alpha )}_{nm}(x), \end{aligned}$$

(22)

where $\tilde{\varphi }^{(\nu ,\alpha )}_{nm}(x) =\mathcal {L}^{-1}(\varphi ^{(\nu ,\alpha )}_{nm}(r))$. We can expand $\tilde{\varphi }^{(\nu ,\alpha )}_{nm}(x)$ regarding FFHFs as follows:

$$\begin{aligned} \tilde{\varphi }^{(\nu ,\alpha )}_{nm}(x) \simeq \sum \limits _{\tau =0}^{N} \sum \limits _{\rho = 1}^{M} \tilde{c}_{\tau \rho } f_{\tau \rho }^{\alpha }(x)= \tilde{C}_{nm}^{\text {T}} F^{\alpha }(x). \end{aligned}$$

(23)

Hence, we have the following:

$$\begin{aligned} P^{(\nu , \alpha )}= [\tilde{C}_{nm}],\;\;n=0, 1, \ldots , N\;\;\;m=1, 2, \ldots , M. \end{aligned}$$

(24)

5 Delay operational matrix of FFHFs

For Taylor polynomials, we have the following [48]:

$$\begin{aligned} T_{N}(x- \xi ) = \theta (\xi ) T_{N}(x), \end{aligned}$$

(25)

where $\theta (\xi )$ is the following matrix:

$$\begin{aligned}\theta (\xi )=\left[ {\begin{array}{cccc} 1 &{}0&{}\ldots &{}0 \\ - \xi &{} 1&{} \ldots &{}0\\ (-\xi )^{2} &{}-2 \xi &{} \ldots &{}0\\ \vdots &{}\vdots &{}\ddots &{} \vdots \\ (- \xi )^{n} &{} \left( \begin{array}{ccc} N \\ N-1 \end{array} \right) (-\xi )^{n-1}&{}\ldots &{}1\\ \end{array}} \right] .\end{aligned}$$

and $T_{N}(x)=[1, x, x^2,\ldots , x^N]^{\text {T}}$.

According to Remark 1 and using Eq. (25), we obtain the following:

$$\begin{aligned} \tilde{F}(x- \xi ) = B \theta ( \xi ) T_{N}(x) = B \theta (\xi ) B^{-1} \tilde{F}(x). \end{aligned}$$

Then, we can rewrite

$$\begin{aligned} \tilde{F}^{\alpha }(x - \xi )= B \theta (\xi ) B^{-1} \tilde{F}^{\alpha }(x), \end{aligned}$$

(26)

where $\tilde{F}^{\alpha }(x)= [\tilde{F}_{0}^{\alpha }(x), \tilde{F}_{1}^{\alpha }(x),\ldots ,\tilde{F}_{N}^{\alpha }(x)]^{\text {T}}$.

We get $\varLambda _{\xi }= B \theta (\xi ) B^{-1}$, where $\varLambda _{\xi }$ is delay operational matrix of fractional Fibonacci polynomials. Moreover, we know

$$\begin{aligned} \tilde{F}_{n}(M (x^{\alpha }- \xi ) - m+1 )= \varLambda _{M\xi } \tilde{F}_{n}(Mx^{\alpha }-m+1),\;\;n=0, 1, \ldots , N; \end{aligned}$$

(27)

then, we obtain

$$\begin{aligned} F^{\alpha }(x-\xi ) = \varOmega _{\xi } F^{\alpha }(x), \end{aligned}$$

(28)

where $\varOmega _{\xi }$ is delay operational matrix of FFHFs and $\varOmega _{\xi }= diag[\underbrace{ \varLambda _{M\xi }, \varLambda _{M\xi }, \ldots , \varLambda _{M\xi }}_{M}]$.

6 Numerical method

We focus on the following fractional delay differential equation:

$$\begin{aligned} \left\{ \begin{array}{ll} F(x,\;y(x),\;y(x-\xi ),\;D^{\nu }y(x))=0,&{} 0 \le x \le 1,\;\;l-1< \nu \le l,\;0< \xi<1,\\ y^{(i)}(0)= \lambda _{i}, &{} i=0, 1,\ldots , l-1,\;\;l \in N\\ y(x)=\varPhi (x), &{} x <0. \end{array} \right. \end{aligned}$$

(29)

We can approximate $D^{\nu }y(x)$ in this problem with the FFHFs as follows:

$$\begin{aligned} D^{\nu }y(x) \simeq C^{\text {T}}F^{\alpha }(x), \end{aligned}$$

(30)

then, using Eq. (17) and property of fractional integration in Eq. (3), we achieve the following:

$$\begin{aligned} y(x) \simeq C^{\text {T}} P^{(\nu ,\alpha )} F^{\alpha }(x) +\sum _{i=0}^{l-1} \frac{x^{i}}{i!} \lambda _{i} \simeq C^{\text {T}} P^{(\nu ,\alpha )} F^{\alpha }(x) + E^{\text {T}} F^{\alpha }(x), \end{aligned}$$

(31)

where

$$\begin{aligned} E(x)=\sum _{i=0}^{l-1} \frac{x^{i}}{i!}\lambda _{i}, \quad E(x) \simeq E^{\text {T}} F^{\alpha }(x). \end{aligned}$$

In addition, for $\xi < x \le 1$ and using Eqs. (28) and (30):

$$\begin{aligned} y( x- \mu )& = C^{\text {T}} P^{(\nu ,\alpha )} F^{\alpha }(x- \mu )+ E^{\text {T}} F^{\alpha }(x- \mu ) \nonumber \\& = C^{\text {T}} P^{(\nu ,\alpha )}\varOmega _{\xi } F^{\alpha }(x)+ E^{\text {T}} \varOmega _{\xi }F^{\alpha }(x), \end{aligned}$$

and $\varPhi (x- \xi ) \simeq A^{\text {T}} F^{\alpha }(x), 0 \le x \le \xi$, then, we get

$$\begin{aligned} y(x- \xi ) \simeq \left\{ \begin{array}{ll} A^{\text {T}} F^{\alpha }(x), &{} 0 \le x \le \xi , \\ \\ C^{\text {T}} P^{(\nu ,\alpha )} \varOmega _{\xi } F^{\alpha }(x) + E^{\text {T}} \varOmega _{\xi } F^{\alpha }(x), &{} \xi < x \le 1 \end{array} \right. \end{aligned}$$

(32)

Substituting Eqs. (30)–(32) in Eq. (29), an algebraic equation is derived:

$$\begin{aligned} \left\{ \begin{array}{ll} F(x,\;C^{\text {T}} P^{(\nu ,\alpha )} F^{\alpha }(x) + E^{\text {T}} F^{\alpha }(x),\; A^{\text {T}} F^{\alpha }(x),\; C^{\text {T}}F^{\alpha }(x))=0, &{} 0 \le x \le \xi , \\ \\ F(x,\;C^{\text {T}} P^{(\nu ,\alpha )} F^{\alpha }(x) + E^{\text {T}} F^{\alpha }(x),\; C^{\text {T}} P^{(\nu ,\alpha )} \varOmega _{\xi } F^{\alpha }(x) + E^{\text {T}} \varOmega _{\xi } F^{\alpha }(x),\; C^{\text {T}}F^{\alpha }(x))=0, &{} \xi < x \le 1. \end{array} \right. \end{aligned}$$

Therefore, we collocate above equation at $x_{p}=\frac{p}{NM},\;\small {p=0, 1, 2,\ldots , NM}$. Thus, we get a system of algebraic equations. We solve this system and derive the vector C, using Newton’s iterative method.

7 Error analysis

Theorem 1

Let$D^{i \alpha }g \in C(0,\;1], i=0, 1,\ldots , N,\;\;(2N+1) \alpha \ge 1,\;\;(\widehat{N}=MN)$and$Y_{N}^{\alpha }=span \{F_{0}^{\alpha }(x), F_{1}^{\alpha }(x),\ldots , F_{N}^{\alpha }(x) \}$. If $g_{N}(x) =A^{\text {T}} \tilde{F} ^{\alpha }(x)$ is the best approximation ofg(x) out of$Y_{N}^{\alpha }$on$[\frac{m-1}{M}, \frac{m}{M}]$. Then, for the approximate solution$g_{\widehat{N}}(x)$using FFHFs series on [0, 1], we have the following:

$$\begin{aligned} \Vert g- g_{\widehat{N}} \Vert _{2} \le \frac{sup_{x \in [0,\;1]} \vert D^{(N+1) \alpha } g(x) \vert }{\varGamma ((N+1) \alpha +1) \sqrt{(2N+3) \alpha }}. \end{aligned}$$

(33)

Proof

We define the following:

$$\begin{aligned} g_{1}(x)= \sum _{i=0}^{N} \frac{x^{i \alpha }}{\varGamma (i \alpha +1)} D^{i \alpha }f(0^{+}), \end{aligned}$$

and by using Definition 2, we get the following:

$$\begin{aligned} \vert g(x)- g_{1}(x) \vert \le \frac{x^{(N+1) \alpha }}{\varGamma ((N+1)\alpha +1)} sup_{x \in I_{m,\;M}} \vert D^{(N+1)\alpha } g(x) \vert , \end{aligned}$$

where $I_{m,\;M}=[\frac{m-1}{M},\;\frac{m}{M}]$.

Given that $g_{N}(x) =A^{\text {T}} \tilde{F}^{\alpha }(x)$ is the best approximation of g(x) out of $Y_{N}^{\alpha }$ on the interval $I_{m,\;M}$, and $g_{1}(x) \in Y_{N}^{\alpha }$, then

$$\begin{aligned} \Vert g- g_{\widehat{N}} \Vert _{L^{2}[0,\;1]}^{2}& = \Vert g- C^{\text {T}} F^{\alpha } \Vert _{L^{2}[0,\;1]}^{2} = \sum _{m=1}^{M} \Vert g - A^{\text {T}} \tilde{F}^{\alpha } \Vert _{L^{2}[\frac{m-1}{M},\;\frac{m}{M}]}^{2} \le \sum _{m=1}^{M} \Vert g-g_{1} \Vert _{L^{2}[\frac{m-1}{M},\;\frac{m}{M}]}^{2} \\\le & {} \sum _{m=1}^{M} \int _{I_{m,\;M}} \biggl [\frac{x^{(N+1)\alpha }}{\varGamma ((N+1) \alpha +1)} sup_{x \in I_{m,\;M}} \vert D^{(N+1) \alpha }g(x) \vert \biggl ]^{2} x^{\alpha -1} {\text {d}}x \\\le & {} \int _{0}^{1} \biggl [\frac{x^{(N+1)\alpha }}{\varGamma ((N+1) \alpha +1)} sup_{x \in [0,\;1]} \vert D^{(N+1) \alpha }g(x) \vert \biggl ]^{2} x^{\alpha -1} {\text {d}}x \\\le & {} \frac{1}{\varGamma ((N+1) \alpha +1)^{2} (2N+3) \alpha } (sup_{x \in [0,\;1]} \vert D^{(N+1) \alpha }g(x) \vert )^{2}. \end{aligned}$$

$\square$

Lemma 1

Assume that$g \in L^{2}[0,\;1]$is approximated by fractional-order Fibonacci polynomials as follows:

$$\begin{aligned} g(x) \simeq g_{n}(x)= A^{\text {T}}\tilde{F}^{\alpha }(x); \end{aligned}$$

so, we have$\lim _{N \rightarrow \infty } e_{N}(g) =0$, where

$$\begin{aligned} e_{N}(g)= \int _{0}^{1}[g(x)-g_{N}(x)]^{2} {\text {d}}x. \end{aligned}$$

Theorem 2

LetHis a Hilbert space andYis a close subspace ofH, such that$dim Y < \infty$and$y_{1}, y_{2},\ldots , y_{n}$, is any basis forY. Letzbe an arbitrary element inH, and$y^{*}$be the unique best approximation tozout ofY. Therefore [49]

$$\begin{aligned} \Vert z-y^{*} \Vert _{2}^{2} = \frac{G(z, y_{1}, y_{2},\ldots , y_{n})}{G(y_{1}, y_{2},\ldots , y_{n})}, \end{aligned}$$

where

$$\begin{aligned} G( x, y_{1}, y_{2}, \ldots , y_{n}) = \left| \begin{array}{cccc} \langle x , x\rangle &{} \langle x , y_{1}\rangle &{} \cdots &{} \langle x , y_{n}\rangle \\ \langle y_{1} , x\rangle &{} \langle y_{1} , y_{1}\rangle &{} \cdots &{} \langle y_{1} , y_{n}\rangle \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ \langle y_{n} , x\rangle &{} \langle y_{n} , y_{1}\rangle &{} \cdots &{} \langle y_{n} , y_{n}\rangle \\ \end{array}\right| . \\ \end{aligned}$$

To obtain an upper bound for the error vector of $P^{(\nu ,\alpha )}$, we consider

$$\begin{aligned} E_{I}^{(\nu )} = P^{(\nu ,\,\alpha )}F^{\alpha }(x)-I^{\nu }F^{\alpha }(x),\,\,\,\,E_{I}^{(\nu )} =\left[ \begin{array}{c} e_{I0} \\ e_{I1} \\ \vdots \\ e_{INM}\\ \end{array}\right] , \end{aligned}$$

(34)

and, from Eqs. (15), (23) and approximated $\tilde{\varphi }_{i}^{(\nu ,\;\alpha )}(x)$, we get

$$\begin{aligned} \tilde{\varphi }_{i}^{(\nu ,\;\alpha )}(x) \simeq \sum _{i=0}^{NM} \tilde{c}_{i} f_{i}^{\alpha }(x), \end{aligned}$$

we obtain $\tilde{c}_{i}$ with the best approximation. From Theorem 2, we have the following:

$$\begin{aligned} \left\| \tilde{\varphi }_{i}^{(\nu ,\;\alpha )}(x) - \sum _{i=0}^{NM}\tilde{c}_{i} f^{\alpha }_{i}(x) \right\| _{2} = \biggl (\frac{G(\tilde{\varphi }_{i}^{(\nu , \alpha )}(x), f_{0}^{\alpha },\ldots , f_{NM}^{\alpha })}{G(f_{0}^{\alpha },\ldots , f_{NM}^{\alpha })} \biggl )^{\frac{1}{2}}. \end{aligned}$$

(35)

Then, from Eqs.  (22)–(29), we obtain the following:

$$\begin{aligned} \Vert e_{Ii} \Vert _{2}& = \bigg \Vert I^{\nu }f_{i}^{\alpha }(x) - \sum _{i=0}^{NM}\tilde{c}_{i} f^{\alpha }_{i}(x) \bigg \Vert \\\le & {} \bigg \Vert \tilde{\varphi }_{i}^{(\nu ,\;\alpha )}(x) - \sum _{i=0}^{NM} \tilde{c}_{i} f^{\alpha }_{i}(x) \bigg \Vert \\\le & {} \biggl (\frac{G(\tilde{\varphi }_{i}^{(\nu , \alpha )}(x) , f_{0}^{\alpha },\ldots , f_{NM}^{\alpha })}{G(f_{0}^{\alpha },\ldots , f_{NM}^{\alpha })} \biggl )^{\frac{1}{2}}. \end{aligned}$$

Therefore, considering Theorem 1, we can see that $E^{(\nu )}$ tends to zero by increasing the number of FFHFs. In addition, notice that we obtain delay operational matrix without any approximation, and then, the vector error of this operational matrix is zero.

For example, considering $N=2, M=3, 5$ and different values of $\nu , \alpha$, we obtain the upper bound of the error for this operational matrix. For $\alpha =\nu =1$, we have the following:

$$\begin{aligned} M& = 3, \quad E^{1}_{I} \le [0,0, 0,00223, 0,0,0.00223]^{\text {T}},\\ M& = 5, \quad E^{1}_{I} \le [0,0, 0, 0,8.64 \times 10^{-5}, 0,0,0,0,8.64 \times 10^{-5}]^{\text {T}}. \end{aligned}$$

For $\alpha =1, \nu =0.5$, we have the following:

$$\begin{aligned} M=3, \quad E^{0.5}_{I}\le & {} [0.011398, 0.001791, 0.013765, 2.57 \times 10^{-4} 5.05 \times 10^{-4}, 0.0024675]^{\text {T}},\\ M=5, \quad E^{0.5}_{I}\le & {} [0.004029, 1.87 \times 10^{-4}, 0.00441, 4.06 \times 10^{-4}, 0.0042, 3.59 \times 10^{-6},\\&\quad 4.73 \times 10^{-6}, 1.12 \times 10^{-5}, 2.63 \times 10^{-5}, 1.18 \times 10^{-5}]^{\text {T}}. \end{aligned}$$

For $\alpha =\nu =0.5$, we have the following:

$$\begin{aligned} M=3, \quad E^{0.5}_{I}\le & {} [0,0, 0,0.002686, 0,0,0.006006]^{\text {T}},\\ M=5, \quad E^{0.5}_{I}\le & {} [0,0, 0, 0,1.32 \times 10^{-4}, 0,0,0,0,3.07 \times 10^{-4}]^{\text {T}}. \end{aligned}$$

Then, in this example, we can see that, by increasing bases, the vector $E^{\nu }_{I}$ tends to zero.

8 Numerical results

Here, we employ the proposed technique for solving the following test examples.

Example 1

We consider the following fractional delay differential equation [28]:

$$\begin{aligned} \left\{ \begin{array}{ll} D^{\nu }y(x)=y(x - \xi )- y(x)+ \frac{2}{\varGamma (3- \nu )} x^{2- \nu } - \frac{1}{\varGamma (2- \nu )}x^{1- \nu } +2 \xi x - \xi ^2- \xi ,&{} 0 \le x \le 1,\;\;0< \nu \le 1, \\ y(x)=0, \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad &{} x\le 0 \quad \quad \quad \quad \quad \quad \quad \end{array} \right. \end{aligned}$$

(36)

For $\nu =1,\;\frac{1}{2}$, the analytic solution of Eq. (36) is $y(x)=x^2-x$.

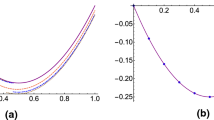
We apply this method for $\nu =\alpha =1$, various choices of $\xi$ and $N=2,\;M=2$. Figure 3 displays the numerical results achieved for various values of $\alpha =\nu$ and the exact solution in $\xi =0.01$.

Table 1 demonstrates the efficiency and accuracy of FFHFs to solve this problem. The numerical results show that the numerical solutions converge to the analytical solution.

Moreover, we solve this problem in $\nu =\frac{1}{2}$. In Table 2, our results show the effectiveness of our method in this problem.

Table 1 Absolute errors and CPU time (in seconds) of numerical solution in $N=2, M=2$ and different values of $\xi$ for Example 1

Table 2 Absolute errors and CPU time of numerical results in $N=4,\;M=2,\; \xi =0.1$ with different values of $\alpha$ for Example 1

Fig. 3

Comparison of our results for $N=2,\;M=2,\;\xi =0.01, \alpha =\nu$ and analytic solution in Example 1

Example 2

Consider the linear fractional delay differential equation as follows [28, 50]:

$$\begin{aligned} \left\{ \begin{array}{ll} D^{\nu }y(x)=-y(x)- y(x-0.3)+e^{-x+0.3},\quad \quad &{} 0 \le x \le 1,\;\;2< \nu \le 3, \\ y(x)=1, \quad y^{'}(0)=-1, \quad y^{''}(0)=1,\quad \quad \quad \quad &{} \\ y(x)=e^{-x}, \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad &{} x < 0. \quad \quad \quad \quad \quad \quad \quad \end{array} \right. \end{aligned}$$

(37)

For $\nu =3$, the analytic solution of Eq. (37) is $y(x)=e^{-x}$. We employ the proposed method for $M=1,\;N=6$ in $\alpha =1$.

Table 3 demonstrates the numerical results achieved for various values of x using our method in $M=1,\;N=6,\;\alpha =1$ or $\widehat{n}=7$, the Hermite wavelet method in $\widehat{n}=25$ [50], Bernoulli wavelets method with $k=2,\;M=7$ or $\widehat{n}=14$ [28], and the exact solution. In addition, Fig. 4 shows the numerical solutions obtained with various values of $\nu$ and the analytical solution for $N=7,\;M=1,\;\alpha =1$.

Moreover, maximum absolute error for this problem using our method for $n=6$ is $4.71097 \times 10^{-7}$, and this value obtained by one-point fifth-order predictor-corrector method and two-point fifth-order predictor-corrector method with $h=0.1$ are $8.692389 \times 10^{-5}$ and $8.804834 \times 10^{-5}$, respectively [29].

Table 3 Comparison of the numerical solution with analytical solution in Example 2

Fig. 4

Comparison of y(x) for $N=6,\;M=1,\;\nu =3$ and various of $\alpha$ and the analytical solution, in Example 2

Example 3

We consider the following fractional equation:

$$\begin{aligned} \left\{ \begin{array}{ccc} D^{\frac{1}{2}}y(x)= y(x - \xi )+f(x), \quad \quad \quad \quad \quad \quad &{} 0 \le x \le 1, \\ y(x)=\sqrt{x}, \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad &{} - \xi \le x \le 0 \end{array} \right. \end{aligned}$$

(38)

with

$$\begin{aligned} f(x)= \left\{ \begin{array}{ccc} \frac{\sqrt{\pi }}{2}+ \sqrt{x- \xi }, \quad \quad \quad \quad \quad \quad &{} 0 \le x < \frac{1}{4}, \\ \xi -\frac{2 \sqrt{x}}{\sqrt{\pi }} - x + \frac{8x^{\frac{3}{2}}}{3 \sqrt{\pi }}+(x-\xi )^{2}, &{} \frac{1}{4} \le x \le 1, \end{array} \right. \end{aligned}$$

and $\xi =0.000001$. The analytic solution of Eq. (38) is as follows:

$$\begin{aligned} y(x)= \left\{ \begin{array}{ccc} \sqrt{x}, \quad \quad \quad \quad \quad \quad &{} 0 \le x < \frac{1}{4}, \\ x^{2}-x, \quad \quad \quad \quad &{} \frac{1}{4} \le x \le 1. \end{array} \right. \end{aligned}$$

We employ our method to solve this equation in $N=4,\;M=2$, $\alpha = \frac{1}{2}$ and 1. Table 4 compares the numerical results in this method. We can see the effectiveness of presented method to solve this problem with piecewise smooth functions.

In addition, numerical results for $\alpha =\frac{1}{2}$ and exact solution are shown in Fig. 5.

Fig. 5

Comparison of y(x) for $N=4, M=2, \alpha = \frac{1}{2}$ and the analytical solution in Example 3

Table 4 Absolute errors and CPU time of our method for various values of $\alpha$ in Example 3

Example 4

Consider the Hutchinson model. This model describes the rate of population growth. In each particular time, the rate of population growth is dependent on some unique relationships at that time, and its equation is as follows [51]:

$$\begin{aligned} \left\{ \begin{array}{ccc} D^{\nu }y(x)=py(x)-\frac{p}{q}y(x)y(x-\xi ),&{} x \in [0,\;1],\\ y(x)=0.5, \quad \quad \quad \quad \quad \quad \quad \quad \quad &{} x \in [-\xi ,\;0]. \end{array} \right. \end{aligned}$$

(39)

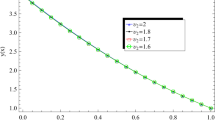
The analytical solution of Eq. (39) is not available [52], and then, our main purpose is to ensure the convergence of the proposed method. For this approach, consider the residual error norm as follows:

$$\begin{aligned} {\text {Res}}_{n}(x)& = C^{\text {T}}F^{\alpha }(x)-p (C^{\text {T}}P^{(\nu ,\alpha )} F^{\alpha }(x)+0.5)\\&\quad +\frac{p}{q}(C^{\text {T}}P^{(\nu ,\alpha )}F^{\alpha }(x)+0.5)(C^{\text {T}}P^{(\nu ,\alpha )} \varOmega _{\xi } F^{\alpha }(x)+0.5)^{\text {T}},\\ \Vert {\text {Res}}_{n} \Vert ^{2}& = \int _{0}^{1} {\text {Res}}_{n}^{2}(x) {\text {d}}x. \end{aligned}$$

The calculated residual error and numerical convergence order for the approximate solution of the considered models and CPU time (in seconds) are tabulated in Table 5 for $\xi =0.2,\;p=0.015,\;q=1$.

Table 5 The $\Vert Res_{n} \Vert ^{2}$ and CPU time with various values of $\nu ,\;\alpha$ for Example 4

9 Conclusion

In the current study, we introduced fractional-order Fibonacci polynomials. Next, we presented new functions called fractional-order Fibonacci-hybrid functions (FFHFs), based on block-pulse functions and fractional-order Fibonacci polynomials. The FFHF operational matrix of fractional-order integration and delay operational matrix of FFHFs have been obtained. These matrices and collocation method are used to numerical solution of linear and nonlinear delay fractional differential equations. Moreover, we employed this method for numerical solution of the Hutchinson model. The results displayed that the present method is more accurate than some existing method.