Pulsatile flow of blood through a stenosed tube: effect of periodic body acceleration and a magnetic field

Abstract

A proper understanding of the interactions of body acceleration and a magnetic field with blood flow could be useful in the diagnosis and treatment of some health problems. In the work reported in this paper we studied the pulsatile flow of blood through stenosed arteries, including the effects of body acceleration and a magnetic field. Blood is regarded as an electrically conducting, incompressible, couple-stress fluid in the presence of a magnetic field along the radius of the tube. The effects of the body acceleration and the magnetic field on the axial velocity, flow rate, and fluid acceleration were obtained analytically by use of the Hankel transform and the Laplace transform. Velocity variations under different conditions are shown graphically. The results have been compared with those from other theoretical models, and are in good agreement. Finally, our mathematical model gives a simple velocity expression for blood flow so it will help not only in the field of physiological fluid dynamics but will also help medical practitioners with elementary knowledge of mathematics.

Introduction

Many biological phenomena are being studied from the standpoint of fluid dynamics. One of these is blood flow through a stenosed tube under periodic body acceleration and in a magnetic field, which is of interest to mechanical engineers and to medical researchers. The red blood cell is a major biomagnetic substance, and blood flow may be affected by a magnetic field. A decrease in blood flow is caused by either an increase in blood resistance or a decrease in blood pressure. Therefore, a high static magnetic field increases blood resistance. The major mechanism of the effect of a static magnetic field on blood viscosity is based on the interaction between the induced magnetic moment of the RBC and the external magnetic field. The RBC has greater susceptibility along its long axis. Therefore, it tends to orient its long axis for larger magnetic susceptibility along the external magnetic field. This property in a static magnetic field increases the friction of the flowing blood, because the anisotropic orientation of the RBC in the static magnetic field disturbs the rolling of the cell in flowing blood, and so the blood viscosity increases. The magnetic properties of RBCs are important in the increase in blood viscosity during exposure to a static magnetic field [8]. Sud and Sekhon [15] studied blood flow through the human arterial system in the presence of a magnetic field. Stenosis, which is a frequent result of atherosclerosis, is a possible cause of arterial diseases such as post-stenotic dilatation and haemolysis. If a stenosis occurs in an artery, normal blood flow is disturbed. This fluid-dynamical factor is important in the development of arterial diseases. Although several hypotheses have been proposed to explain why arterial diseases occur locally at a stenosis or why a stenosis appears, there is not yet a definite theory. Therefore, it is of interest to clarify blood flow through a stenosed tube under the action of a magnetic field.

Ishikawa et al. [4] analysed periodic blood flow through a stenosed tube. Effects of pulsation and the rheology of the blood were considered. They obtained a flow pattern, a separated region, and the distributions of pressure and shear stress at the wall. They showed that the non-Newtonian property reduces the strength of the vortex downstream of the stenosis and this has a substantial effect on the flow, even at high Stokes and Reynolds numbers. El-Shahed [3] investigated the analytical expression for axial velocity, fluid acceleration, flow rate, and shear stress. Kumar and Singh [7] studied a mathematical model on arterial unsteady blood flow with mild stenosis in the presence of a magnetic field. Steady flow of blood through a rigid straight circular tube under the action of periodic body acceleration and a magnetic field was studied by Rathod et al. [11] by considering blood as a couple-stress fluid. Rathod and Pawar [10] studied the effect of periodic body acceleration on pulsatile blood flow through a stenosed narrow tube. Bali and Awasthi [1] researched the effect of magnetic field on blood flow in a stenotic artery taking into account the effect of a magnetic field in the direction transverse to the blood flow, and considering the viscosity of the blood as radial co-ordinate-dependent. The effects of the interaction between a magnetic field and the haemodynamics of the arterial system have been studied by Mishra and Shekhawat [9]. Numerical analysis of blood flow in realistic arteries subjected to a strong non-uniform magnetic fields has been studied by Kenjereš [6], who concluded that an imposed non-uniform magnetic field can create significant changes in the secondary flow patterns. Das and Saha [2] obtained the velocity and the maximum value of volumetric flow rate decreases with increasing Hartmann number and for a particular value of the phase angle; the maximum value of the wall shear stress increases with increasing Hartmann number but the effect is reversed for a fixed value of t. Rathod and Tanveer [12] used a mathematical model to study the effect of periodic body acceleration and a magnetic field on pulsatile blood flow through a porous medium, considering blood as a couple-stress fluid in a circular tube. The effect of body acceleration and an external magnetic field on two-dimensional flow of a non-Newtonian fluid through an asymmetric stenosed artery was analysed by Shaw et al. [13]. They treated the artery wall as an elastic (moving wall) cylindrical tube. The laminar, incompressible, fully developed non-Newtonian flow of blood in an artery with multiple stenoses under the action of a magnetic field has been studied numerically by use of a finite difference technique [16]. All the flow characteristics were found to be affected by the presence of multiple stenoses and exposure to magnetic fields of different intensities. There is a substantial difference between blood flow and water flow through a stenosed tube and the effect of the non-Newtonian property of blood should not be neglected. Non-Newtonian viscosity becomes significant in the low-shear stress region. Therefore, if there is a stagnant period, as in blood flow in vivo, the effect of the non-Newtonian property of blood should be considered together with pulsation of the flow rate.

In this work, pulsatile blood flow through a stenosed tube with periodic body acceleration in the presence of uniform transverse magnetic field was studied analytically, assuming blood to be a couple-stress fluid. The effect of the non-Newtonian property of blood was investigated.

Mathematical model

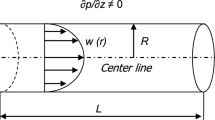
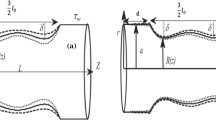
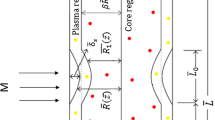
Let us consider a one-dimensional pulsatile flow of blood through a uniform straight and stenosed tube by considering blood as an electrically conducting, incompressible, couple-stress fluid. The magnetic field is acting along the radius of the tube and the flow is axially symmetric and fully developed. The stenosis is mild. The magnetic Reynolds number of the flow is assumed to be sufficiently small that the induced magnetic and electric fields can be neglected [10, 11].

The pressure gradient $\left( {\frac{\partial p}{\partial z}} \right)$ produced by the pumping action of the heart is given by:

$$ - \frac{\partial p}{\partial z} = A_{0} + A_{1} \cos (\omega_{1} t),\quad t \ge 0, $$

(2.1)

The time-periodic body acceleration is given by:

$$ G = a_{0} \cos (\omega_{2} t + \phi ),\quad t \ge 0, $$

(2.2)

A transverse magnetic field is applied as shown in Fig. 3.

The geometry of the stenosis is defined by [5]:

$$ R(z) = \left\{ \begin{array}{ll} a - \delta \left( {1 + \cos \frac{\pi z}{{2z_{0} }}} \right),& - 2z_{0} \le z \le 2z_{0} \\ a,& {\text{otherwise}} \hfill \\ \end{array} \right\}. $$

(2.3)

The governing equation in cylindrical polar coordinates in the presence of a transverse magnetic field and periodic body acceleration can be written in the form:

$$ \frac{\partial u}{\partial z} = 0, $$

(2.4)

$$ \frac{\partial p}{\partial r} = 0, $$

(2.5)

$$ \rho \frac{\partial u}{\partial t} = - \frac{\partial p}{\partial z} + \rho G + \mu \nabla^{2} u - \eta \nabla^{2} (\nabla^{2} u) - \sigma B_{0}^{2} u, $$

(2.6)

where

$$ \nabla^{2} = \frac{1}{r}\frac{\partial }{\partial r}\left\{ {r\frac{\partial }{\partial r}} \right\}. $$

The following dimensionless quantities are used:

$$ u^{*} = \frac{u}{\omega R},\quad t^{*} = t\omega ,\quad A_{0}^{*} = \frac{R}{\mu \omega }A_{0} ,\quad A_{1}^{*} = \frac{R}{\mu \omega }A_{1} ,\quad a_{0}^{*} = \frac{\rho R}{\mu \omega }a_{0} ,\quad z^{*} = \frac{z}{R}, \quad c = \frac{{\omega_{1} }}{\omega }, \quad b = \frac{{\omega_{2} }}{\omega }. $$

We now introduce a radial coordinate transformation given by:

$$ \xi = \frac{r}{R(z)}. $$

(2.7)

In terms of these variables, Eq. (2.6), on dropping the asterisks, becomes

$$ \begin{aligned} \bar{\alpha }^{2} \alpha^{2} \frac{\partial u}{\partial t} & = \bar{\alpha }^{2} A_{0} + \bar{\alpha }^{2} A_{1} \cos ct + \bar{\alpha }^{2} a_{0} \cos (bt + \phi ) \\ & \quad + \bar{\alpha }^{2} \left[ {\frac{1}{\xi }\frac{\partial }{\partial \xi }\left( {\xi \frac{\partial u}{\partial \xi }} \right)} \right] - \left[ {\frac{1}{\xi }\frac{\partial }{\partial \xi }\left( {\xi \frac{\partial }{\partial \xi }} \right)} \right]\left[ {\frac{1}{\xi }\frac{\partial }{\partial \xi }\left( {\xi \frac{\partial u}{\partial \xi }} \right)} \right] - \bar{\alpha }^{2} H^{2} u \\ \end{aligned} $$

(2.8)

The initial and boundary condition for solving Eq. (2.8) are:

$$ u(\xi ,0) = 2\sum\limits_{n = 1}^{\infty } {\frac{{J_{0} (\xi \lambda_{n} )\bar{\alpha }^{2} }}{{\lambda_{n} J_{1} (\lambda_{n} )}}} \left[ {\frac{{\left( {A_{0} + A_{1} + a_{0} \cos \phi } \right)}}{{\lambda_{n}^{4} + \bar{\alpha }^{2} \left( {\lambda_{n}^{2} + H^{2} } \right)}}} \right], $$

(2.9A)

(This is the result of steady flow of blood through a stenosed tube under periodic body acceleration and magnetic field.)

$$ u\;{\text{and}}\;\nabla^{2} u\;{\text{are}}\;{\text{finite}}\;{\text{at}}\;\xi = 0, $$

(2.9B)

$$ u\; {\text{and}}\;\nabla^{2} u = 0\;{\text{at}}\;\xi = 1. $$

(2.9C)

Required integral transform

If f(ξ) satisfies the Dirchlet condition in [0, 1] and if $f^{*} (\lambda_{n} )$ is the finite Hankel transform of f(ξ) then we have:

$$ f^{*} (\lambda_{n} ) = \int\limits_{0}^{1} {\xi f(\xi )J_{0} } (\xi \lambda_{n} ){\text{d}}\xi $$

(3.1)

where λ _n are the roots of the Bessel functions J ₀(ξ) = 0. Then, at each point of the interval in which f(ξ) is continuous:

$$ f(\xi ) = 2\sum\limits_{n = 1}^{\infty }\,{f^{*} } (\lambda_{n} )\frac{{J_{0} (\xi \lambda_{n} )}}{{J_{1}^{2} (\lambda_{n} )}}. $$

(3.2)

where the sum is taken over all positive roots of $J_0(\xi)=0$. The Laplace transform of any function is defined as [14]:

$$ \overline{f} (s) = \int\limits_{0}^{1} {{\text{e}}^{ - st} f(t)} {\text{d}}t,\quad s > 0 . $$

(3.3)

Analysis

Applying the Laplace transform to Eq. (2.8) in the light of Eq. (2.9B), we obtain:

$$ \begin{aligned} \bar{\alpha }^{2} \alpha^{2} [s\bar{u} - u(\xi ,0)] & \,=\, \bar{\alpha }^{2} \frac{{A_{0} }}{s} \,+\, \bar{\alpha }^{2} A_{1} \frac{s}{{s^{2} + c^{2} }} +\, \frac{{\bar{\alpha }^{2} a_{0} (s\cos \phi - b\sin \phi )}}{{s^{2} + b^{2} }} \\ & \quad \,+\, \bar{\alpha }^{2} \left[ {\frac{1}{\xi }\frac{\partial }{\partial \xi }\left( {\xi \frac{{\partial \bar{u}}}{\partial \xi }} \right)} \right] - \left[ {\frac{1}{\xi }\frac{\partial }{\partial \xi }\left( {\xi \frac{\partial }{\partial \xi }} \right)} \right]\left[ {\frac{1}{\xi }\frac{\partial }{\partial \xi }\left( {\xi \frac{{\partial \bar{u}}}{\partial \xi }} \right)} \right] - \bar{\alpha }^{2} H^{2} \bar{u}. \\ \end{aligned} $$

(4.1)

$$ {\text{where}}\quad \bar{u}(\xi ,s) = \int\limits_{0}^{\infty } {{\text{e}}^{ - st} u(\xi ,t){\text{d}}t} $$

(4.2)

Now applying the finite Hankel transform to Eq. (4.1), using Eq. (2.9C), we obtain:

$$ \begin{aligned} \bar{u}^{*} (\lambda_{n} ,s) & = \frac{{J_{1} (\lambda_{n} )}}{{\lambda_{n} }}\bar{\alpha }^{2} \left[ {\frac{{A_{0} }}{s} + A_{1} \frac{s}{{s^{2} + c^{2} }} + \frac{{a_{0} (s\cos \phi - b\sin \phi )}}{{s^{2} + b^{2} }} + m\sum\limits_{n = 1}^{\infty } {\frac{{A_{0} + A_{1} + a_{0} \cos \phi }}{{\lambda_{n}^{4} + \bar{\alpha }^{2} [\lambda_{n}^{2} + H^{2} ]}}} } \right] \\ & \quad . \, \frac{1}{{sm + \lambda_{n}^{4} + \bar{\alpha }^{2} [\lambda_{n}^{2} + H^{2} ]}} \\ \end{aligned} $$

$$ {\text{where}}\quad m = \bar{\alpha }^{2} \cdot \alpha^{2} . $$

(4.3)

Now rearranging the terms of Eq. (4.3) into a form convenient for taking the inverse Laplace transform we obtain:

$$ \begin{aligned} \bar{u}^{*} (\lambda_{n} ,s) & = \frac{{J_{1} (\lambda_{n})}}{{\lambda_{n} }}\bar{\alpha }^{2} \left[ {\frac{{A_{0} }}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]}}\left( {\frac{1}{s} - \frac{1}{s + p}} \right)} \right. \\ & \quad + A_{1} \frac{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]}}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]^{2} + m^{2} c^{2} }}\left( { - \frac{1}{s + p} + \frac{s}{{s^{2} + c^{2} }} + \frac{{mc^{2} }}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right](s^{2} + c^{2} )}}} \right) \\ & \quad + \frac{{a_{0} \left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} \left( {\lambda_{n}^{2} + H^{2} } \right)} \right]\cos \phi }}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} \left( {\lambda_{n}^{2} + H^{2} } \right)} \right]^{2} + m^{2} b^{2} }}\left( { - \frac{1}{s + p} + \frac{s}{{s^{2} + b^{2} }} + \frac{{mb^{2} }}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right](s^{2} + b^{2} )}}} \right) \\ & \quad - \frac{{a_{0} bm\sin \phi }}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]^{2} + m^{2} b^{2} }}\left( {\frac{1}{s + p} - \frac{s}{{s^{2} + b^{2} }} + \frac{{\left[ {\lambda_{n}^{4} + \alpha^{2} (\lambda_{n}^{2} + H^{2} )} \right]}}{{m(s^{2} + b^{2} )}}} \right) \\ & \quad \left. { + m\sum\limits_{n = 1}^{\infty } {\frac{{(A_{0} + A_{1} + a_{0} \cos \phi )}}{{[\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )]}}} \left( {\frac{1}{m}.\frac{1}{s + p}} \right)} \right], \\ \end{aligned} $$

$$ {\text{where}}\quad p = \frac{{\lambda_{n}^{4} + \bar{\alpha }^{2} [\lambda_{n}^{2} + H^{2} ]}}{m}. $$

(4.4)

Now taking the inverse Laplace transform of Eq. (4.4), we obtain:

$$ \begin{aligned} u^{*} (\lambda_{n} ) & = \frac{{J_{1} (\lambda_{n} )}}{{\lambda_{n} }}\bar{\alpha }^{2} \left[ {\left\{ {\frac{{A_{0} }}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]}}} \right.} \right. + A_{1} \frac{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]\cos ct + mc\sin ct}}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]^{2} + m^{2} c^{2} }} \\ & \quad \left. { + \frac{{a_{0} \left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]\cos (bt + \phi ) + mb\sin (bt + \phi )}}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]^{2} + m^{2} b^{2} }}} \right\} \\ & \quad - {\text{e}}^{ - pt} \left\{ {\frac{{A_{0} }}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]}}} \right. + A_{1} \frac{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]}}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]^{2} + m^{2} c^{2} }} \\ & \quad + \frac{{a_{0} \left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]\cos \phi + bm\sin \phi }}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]^{2} + m^{2} b^{2} }}\left. {\left. { - \sum\limits_{n = 1}^{\infty } {\frac{{(A_{0} + A_{1} + a_{0} \cos \phi )}}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]}}} } \right\}} \right]. \\ \end{aligned} $$

(4.5)

The finite Hankel inversion of Eq. (4.5) gives the final solution in the form:

$$ u(\xi ,t) = 2\sum\limits_{n = 1}^{\infty } {u^{*} (\lambda_{n} )\frac{{J_{0} (\xi \lambda_{n} )}}{{J_{1}^{2} (\lambda_{n} )}}} . $$

$$ \begin{aligned} u(\xi ,t) & = 2\sum\limits_{n = 1}^{\infty } {\frac{{A_{0} J_0(\xi \lambda_{n} )\bar{\alpha }^{2} }}{{J_1(\lambda_{n} )\lambda_{n} }}} \left[ {\left\{ {\frac{1}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]}}} \right.} \right. \\ & \quad + A_{1} /A_{0} \frac{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]\cos ct + mc\sin ct}}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]^{2} + m^{2} c^{2} }} \\ & \left. {\quad + \frac{{a_{0} /A_{0} \left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]\cos (bt + \phi ) + mb\sin (bt + \phi )}}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]^{2} + m^{2} b^{2} }}} \right\} \\ & \quad - {\text{e}}^{ - pt} \left\{ {\frac{1}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]}}} \right. + A_{1} /A_{0} \frac{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]}}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]^{2} + m^{2} c^{2} }} \\ & \quad \left. {\left. { + \frac{{a_{0} /A_{0} \left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]\cos \phi + bm\sin \phi }}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]^{2} + m^{2} b^{2} }} - \frac{{(1 + A_{1} /A_{0} + a_{0} /A_{0} \cos \phi )}}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]}}} \right\}} \right]. \\ \end{aligned} $$

(4.6)

The expression for the flow rate Q can be written in the form:

$$ Q = 2\pi \int\limits_{0}^{1} {\xi u\,{\text{d}}\xi } $$

(4.7)

using Eq. (4.6) in Eq. (4.7), we get the flow rate in the form:

$$ \begin{aligned} Q & = 4\pi \sum\limits_{n = 1}^{\infty } {\frac{{A_{0} \bar{\alpha }^{2} }}{{\lambda_{n} }}} \left[ {\left\{ {\frac{1}{{\left[ {\lambda_{n}^{4} \,+\, \bar{\alpha }^{2} (\lambda_{n}^{2} \,+\, H^{2} )} \right]}}} \right.} \right. \\ & \quad +\, A_{1} /A_{0} \frac{{\left[ {\lambda_{n}^{4} \,+\, \bar{\alpha }^{2} (\lambda_{n}^{2} \,+\, H^{2} )} \right]\cos ct \,+\, mc\sin ct}}{{\left[ {\lambda_{n}^{4} \,+\, \bar{\alpha }^{2} (\lambda_{n}^{2} \,+\, H^{2} )} \right]^{2} \,+\, m^{2} c^{2} }} \\ & \left. {\quad +\, \frac{{a_{0} /A_{0} \left[ {\lambda_{n}^{4} \,+\, \bar{\alpha }^{2} (\lambda_{n}^{2} \,+\, H^{2} )} \right]\cos (bt \,+\, \phi ) \,+\, mb\sin (bt \,+\, \phi )}}{{\left[ {\lambda_{n}^{4} \,+\, \bar{\alpha }^{2} (\lambda_{n}^{2} \,+\, H^{2} )} \right]^{2} \,+\, m^{2} b^{2} }}} \right\} \\ & \quad - {\text{e}}^{ - pt} \left\{ {\frac{1}{{\left[ {\lambda_{n}^{4} \,+\, \bar{\alpha }^{2} (\lambda_{n}^{2} \,+\, H^{2} )} \right]}}} \right. \,+\, A_{1} /A_{0} \frac{{\left[ {\lambda_{n}^{4} \,+\, \bar{\alpha }^{2} (\lambda_{n}^{2} \,+\, H^{2} )} \right]}}{{\left[ {\lambda_{n}^{4} \,+\, \bar{\alpha }^{2} (\lambda_{n}^{2} \,+\, H^{2} )} \right]^{2} \,+\, m^{2} c^{2} }} \\ & \left. {\left. {\quad +\, \frac{{a_{0} /A_{0} \left[ {\lambda_{n}^{4} \,+\, \bar{\alpha }^{2} (\lambda_{n}^{2} \,+\, H^{2} )} \right]\cos \phi \,+\, bm\sin \phi }}{{\left[ {\lambda_{n}^{4} \,+\, \bar{\alpha }^{2} (\lambda_{n}^{2} \,+\, H^{2} )} \right]^{2} \,+\, m^{2} b^{2} }} - \frac{{(1 \,+\, A_{1} /A_{0} \,+\, a_{0} /A_{0} \cos \phi )}}{{\left[ {\lambda_{n}^{4} \,+\, \bar{\alpha }^{2} (\lambda_{n}^{2} \,+\, H^{2} )} \right]}}} \right\}} \right]. \\ \end{aligned} $$

(4.8)

Similarly the expression for fluid acceleration F can be obtained in the form:

$$ \begin{aligned} F(\xi ,t) & = \frac{\partial u}{\partial t} = 2\sum\limits_{n = 1}^{\infty } {A_{0} \frac{{J_{0} (\xi \lambda_{n} )}}{{\lambda_{n} J_{1} (\lambda_{n} )}}} \bar{\alpha }^{2} \left[ {\frac{{A_{1} /A_{0} \left[ {c^{2} m\cos ct - \left\{ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right\}c\sin ct} \right]}}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]^{2} + m^{2} c^{2} }}} \right. \\ & \quad + \frac{{a_{0} /A_{0} b\left[ {mb\cos (bt + \phi ) - \left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]\sin (bt + \phi )} \right]}}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]^{2} + m^{2} b^{2} }} \\ & \quad + p{\text{e}}^{ - pt} \left\{ {\frac{1}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]}}} \right. + A_{1} /A_{0} \frac{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]}}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]^{2} + m^{2} c^{2} }} \\ & \quad + \frac{{a_{0} /A_{0} \left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]\cos \phi + bm\sin \phi }}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]^{2} + m^{2} b^{2} }}\left. {\left. { - \frac{{(1 + A_{1} /A_{0} + a_{0} /A_{0} \cos \phi )}}{{\left[ {\lambda_{n}^{4} + \bar{\alpha }^{2} (\lambda_{n}^{2} + H^{2} )} \right]}}} \right\}} \right]. \\ \end{aligned} $$

(4.9)

Numerical computations for theoretical analysis

As we know, λ _n are zeros/roots of the Bessel function J ₀(ξ) = 0. When we multiply ξ = 0.2 by λ ₁, i.e., 2.42 (0.2 × 2.42 = 0.484) and from a table of Bessel function we obtain J ₀(0.484). For ξ = 1 the Bessel function J ₀(λ ₁) will become zero, i.e., at the tube wall the velocity becomes 0. Similarly we can continue the computation for next sum n = 2, and so on.

In order to obtain physiological insight into the effect of stenosis, magnetic field, and periodic body acceleration on the velocity profile, the following values are taken:

Phase difference ϕ = 15⁰, b = 2, c = 2, etc.

Results and discussion

The velocity profile for a pulsatile flow of blood through a stenosed tube with periodic body acceleration in the presence of a magnetic field, computed by using Eq. (4.6) for different values of the amplitude of body acceleration a ₀, Womersley parameter α, steady state part of pressure gradient A ₀, amplitude of oscillatory part A ₁, couple stress parameter $(\bar{\alpha }),$ Hartmann number (H), time t, have been shown through graphs.

Figure 1 illustrates the variation of axial velocity profile for different values of the amplitude of body acceleration $\frac{{a_{0} }}{{A_{0} }}.$ It is observed that the velocity profile increase for increasing the amplitude of body acceleration. It can be seen from Fig. 2, that the velocity increases for increase in steady state part of pressure gradient and amplitude of body oscillatory part $\frac{{A_{1} }}{{A_{0} }}.$ Figure 3 shows that the velocity decreases as the transverse magnetic field (H) is increased. From Fig. 4 it is observed that the velocity increases as $\bar{\alpha }$ is increased. Figures 5 and 6 show the variation of the velocity profile with Womersley parameter α and time t.

Fig. 1

Variation of the axial velocity profile for different values of a ₀/A ₀ taking A ₁/A ₀ = 1, $\overline{\alpha } = 1,$ α = 1, ϕ = 15°, b = 2, c = 2, t = 3, H = 2, A ₀ = 4

Fig. 2

Variation of the axial velocity profile for different values of A ₁/A ₀ taking $\overline{\alpha } = 1,$ α = 1, ϕ = 15°, b = 2, c = 2, t = 3, H = 2, A ₀ = 4, a ₀/A ₀ = 0.5

Fig. 3

Variation of the axial velocity profile for different values of H taking $\overline{\alpha } = 1,$ α = 1, ϕ = 15°, b = 2, c = 2, t = 3, A ₀ = 4, a ₀/A ₀ = 0.5, A ₁/A ₀ = 1

Fig. 4

Variation of the axial velocity profile for different values of $\overline{\alpha }$ taking α = 1, ϕ = 15°, b = 2, c = 2, t = 3, H = 2, A ₀ = 4, a ₀/A ₀ = 0.5, A ₁/A ₀ = 1

Fig. 5

Variation of the axial velocity profile for different values of α taking $\overline{\alpha } = 1$, ϕ = 15°, b = 2, c = 2, t = 3, H = 2, A ₀ = 4, a ₀/A ₀ = 0.5, A ₁/A ₀ = 1

Fig. 6

Variation of the axial velocity profile for different values of t taking $\overline{\alpha } = 1$, α = 1, ϕ = 15°, b = 2, c = 2, H = 2, A ₀ = 4, a ₀/A ₀ = 0.5, A ₁/A ₀ = 1

Conclusion

In the present mathematical model the pulsatile blood flow through a stenosed narrow tube under the action of periodic body acceleration and a magnetic field has been studied. The velocity expression has been obtained in the Bessel–Fourier series form. The corresponding expressions to flow rate and fluid acceleration are also been obtained.