1 Introduction

The gradual accumulation of cholesterol and fatty substances in the inner walls of human arteries leads to the production of platelets in the blood vessels, which leads to the tightening and hardening of the arterial walls. This disease is called atherosclerosis. Over time, the increased deposition of fats can lead to the narrowing of the vessels. This phenomenon interferes with sufficient blood supply to the tissue, which is called stenosis. In some cases, this condition can cause a stroke. In fact, stenosis can be defined as the phenomenon of narrowing of blood vessels which causes to decline in blood flow.

Young [1] pioneered the analysis of blood flow via stenotic blood vessels. His study is predicated on the idea of moderate stenosis. Forrester and Young [2, 3] theoretically and experimentally analysed the flow of incompressible fluid (blood) via an axisymmetrically convergent–divergent tube and discussed the possible influences of this flow on the development of vascular diseases. Lee and Fung [4] investigated blood flow in a locally constricted cylindrical tube and described the numerical results for the distributions and streamlines of shear stress, pressure, velocity, and vorticity for various values of the Reynolds number in the range 0–25. Soda and Chow [5] analysed the atypical flow conditions in diseased arteries engendered by the boundary irregularities. They assumed a laminar incompressible (isochoric) blood flow in a medium of an irregular surface where the propagation of the surface roughness is significantly higher compared to the channel’s mean width. Young and Morgan [6] utilized an approximation integral momentum approach to estimate the axial velocity of the blood flow in the region of axisymmetric stenosis. Azuma and Fukushima [7] conducted a study to recognize circulatory disorder via narrowed blood vessels with various types of stenosis. The numerical evaluation of the time-dependent flow of blood via moderate arterial stenosis was performed by MacDonald [8]. The pulsating blood flow via arterial stenosis denoted by three different modelled narrowed walls was experimentally studied by Young and Yangchareon [9]. Chanaeu and Doffin [10] utilized an experimental setup and a theoretical approach to calculate the steady flow through a fusiform (spindle-shaped) obstruction to comprehend the unique flow conditions that might be formed by a blood clot in an artery. Their model consisted of axisymmetric stenosis and an elongated obstruction conducted by a small-diameter axial metal rod in various positions. The mathematical model for the comparison of blood flow in large blood vessels subjected to a periodic acceleration field was developed by Misra and Sahu [11]. The equations that characterize the flow are computed in combination with the expressions that describe the movement of various types of the vessel wall. The displacement of the arterial wall, fluid acceleration, volume flow rate, velocity profile, and shearing stresses on the wall are all computed numerically. Haemorheology in the aforementioned studies was described by Newtonian fluids.

Over time, the researchers experimentally observed that the blood demonstrates non-Newtonian properties such as thixotropy, viscoelasticity, and shear-thinning. At a moderate shear rate, the power-law fluid model revealed significant non-Newtonian behaviour, as shown by the experimental results of Perktold et al. [12]. But this model does not accurately describe the behaviour for extreme values of shear rate. This discrepancy can be rectified by choosing the models like Sisko, Cross, Carreau and Eyring Powell, etc. A numerical simulation of blood flow via stenosis was carried out by Tu et al. [13] by implementing Galerkin's finite element technique. The results analysed the impacts of variation in the degree of stenosis, length of a stenosis, and other dimensionless parameters. Prema and Usha [14] examined the pulsatile blood flow using the particle-liquid suspension model while taking into account the effects of the acceleration field. Moustafa [15] employed Laplace and Henkel transformations to examine the impact of the body acceleration at pulsatile (Womersley) blood flow in a stenotic porous channel. The two-dimensional flow of blood via the stenotic blood vessel is examined by Mandal [16]. He characterized the non-Newtonian blood rheology as a generalized Power-law model. Yilmaz and Gundogdu [17] conducted an important analysis of blood flowing in large vessels related to haemorheology and biological conditions. Mekheimer and El Kot [18] presented a study to investigate the impacts of radially symmetric but axially nonsymmetric moderate stenosis on blood flow features wherein the blood is characterized as a micropolar fluid. A mathematical model for the Womersley flow of non-Newtonian blood in a stenotic artery was developed by Sankar and Lee [19]. They considered Herschel–Bulkley constative equation for the rheology of blood and utilized the perturbation method to evaluate the flow. Ali et al. [20] examined the impacts of acceleration and magnetic fields on the unsteady pulsatile blood flow described by the constitutive equation of Carreau-Yasuda fluid model via an overlapping stenosed vessel. Zaman et al. [21] considered an electrically conductive fluid (blood) under the impact of an external magnetic force and studied the influence of slip over a time-dependent flow of non-Newtonian blood via inclined overlapping stenosed blood vessels. They used the power-law constitutive equation to characterize the rheology of blood. Roy et al. [22] numerically analysed the flow of Carreau-Yasuda fluid in stenosed artery and reported that a 90% thick blockage inside the arterial channel may turn the transient blood flow into turbulence one, which might be deadly to the patient.

The rheological characteristics of blood cannot be specified by a single constitutive relation between stress and shear rate due to the diversity of nature. Therefore, a variety of non-Newtonian models, demonstrating various rheological effects such as shear-thinning [23], thixotropic [24], and viscoelastic [25] properties, are available in the haemodynamics literature. Gijsen et al. [26] proposed that only the shear-thinning feature is crucial for blood flow simulations because the remaining listed qualities have no significant effect on the velocity profile. The shear-thinning behaviour of streaming blood can be successively characterized by utilizing generalized Newtonian models [27], in which the dynamic viscosity is simply dependent upon the shear-rate tensor. A typical example of these type of fluids is a so-called power-law model. This model has been used to simulate blood flow dynamics in the coronary artery [28], aorta-iliac bifurcation [29], thoracic aorta [30], carotid artery [31], and several types of stenotic arteries [32]. This model, however, falls short of accurately representing the entire rheological profiles of non-Newtonian fluids [33]. Further, the existence of upper and lower Newtonian zones, as well as a Power-law region, makes the evaluation and utilization of rheological data difficult.

Many studies employed four-parameter models with two asymptotic dynamic viscosity values corresponding to infinitely large and infinitely small shear rates. Examples of such models are the Carreau model, Carreau-Yasuda model, cross model, simplified cross model, modified cross model, and Yeleswarapu model. In general, four-parameter models are challenging to implement because there is rarely enough data to allow the model to fit well. They do, however, provide the finest results in forecasting the behaviour of non-Newtonian fluids and can span the whole shear-rate range [35].

Among these is the tangent hyperbolic model [36], which, despite its mathematical complexity, has the ability to characterize flow dynamics at both high and low shear rates. This model is preferred above other non-Newtonian models because: (1) it is based on the kinetic molecular model of fluids rather than an empirical relation. (2) This model accurately predicts shear-thinning characteristics and is best suited for predicting the rheology of foods beverages and blood. (3) It properly simplifies to Newtonian behaviour for high and law shear stress. For further research data on tangent hyperbolic fluid, the readers are recommended to study Refs. [37,38,39,40,41,42].

In the past few decades, researchers have become increasingly interested in biological heat transfer phenomena, especially for diagnostic and therapeutic applications. Based on modern computational methods, the development of intricate mathematical models has significantly increased our ability to evaluate different types of biological heat transfer processes. The cooperation between clinicians, physiologists, and engineers in the field of biological heat transport has greatly improved the treatment, prevention, preservation, and protection of biological systems, including the use of heat or cold therapy to annihilate tumours and improve patient outcomes, brain damage, and protecting humans from intense environmental conditions. A number of studies have been carried out to study heat transfer in blood vessels. The heat transfer properties of blood were experimentally studied by Charm et al. [43] by placing small capillary tubes with a diameter of 0.6 mm in a water tank. Chato [44] examined the transmission of heat to specific blood arteries in three different formations: a single blood artery, two blood vessels in counterflow, and a vessel close to the skin surface. Kolios et al. [45] employed a finite difference technique (FDT) for the evaluation of basic fluid flow and heat transfer equations to calculate temperature distribution across large blood vessels where the heat transfer coefficients change with temperature variations. Ogulu and Tamunoimi [46] investigated the impacts of heat transmission on stenosed vessel under the condition of sufficiently thin fluid. Garcia and Riahi [47] studied the behaviour of heat transfer in bi-phase blood flow via stenotic blood vessels including viscous heating effects. They figured out that the amount of heat generated in the fluid (blood) owing to the viscous heating effects is sufficient to raise the fluid temperature above the vessel’s surface temperature. The heat/mass transfer features of blood flowing through the conical stenotic artery characterized by a Cross-fluid model are analysed by Zaman et al. [48]. Jamali and Ismail [49] investigated the dynamic behaviour of heat exchange in a steady incompressible blood flow via bifurcated stenotic vessel. Liu and Liu [50] examined the impacts of mass and heat transport on the pulsatile flow on blood via tapered arterial stenosis utilizing non-Newtonian fluid model. Fahim et al. [51] studied the nonisothermal flow in a stenotic vessel caused by pulsating pressure gradient and periodic body acceleration while characterizing the non-Newtonian blood rheology as a Sisko fluid model.

The key objective of this work is to evaluate the impacts of non-Newtonian rheology, severity of stenosis, and body acceleration on blood flow via stenosed vessel, which is induced by the heart’s pumping action, which creates a pulsatile pressure gradient thorough the system. The affected arterial region is modelled by an overlapping \(\omega\)-shaped stenosed model. The transport of heat via arterial walls in the main bloodstream is also examined in this paper. Thus, the current study helps us to understand the impacts of viscous dissipation on the dynamics of blood in a stenotic vessel utilizing the tangent hyperbolic fluid model, which is one of the finest shear-thinning models for haemorheological suspensions. For the effective results, we did not expand the tangent term into its Taylor series to preserve only the leading terms. In this way, the present study is superior to the existing ones [37,38,39,40,41,42] and portrays a more realistic situation for blood rheology.

The article is structured as follows: Sect. 2 demonstrates the geometry of the flow and stenosed artery. Section 3 illustrates the mathematical formulation of the problem under appropriate assumptions. Section 4 grants the non-dimensional representation of the developed problem, which allows for the incorporation of essential scaling parameters. Section 5 delves into the numerical approach for solving the established equations. Section 6 contains a quantitative assessment of the implications of the graphical results. The major findings of the current investigation are summarized in Sect. 7.

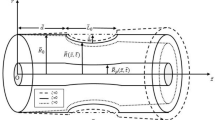
2 Geometry of the stenosed vessel

The geometrical model of the tapered artery with overlapping stenosis (Fig. 1(a)) is mathematically defined as

$$R\left( z \right) = \left\{ \begin{gathered} (\xi z + a)(1 - \frac{{64}}{{10}}\eta \left( {\frac{{11}}{{32}}l_{0}^{3} \left( {z - d} \right) - \frac{{47}}{{48}}l_{0}^{2} \left( {z - d} \right)^{2} + l_{0} \left( {z - d} \right)^{3} - \frac{1}{3}\left( {z - d} \right)^{4} } \right) \hfill \\ d \le z \le d + \frac{3}{2}l_{0} , \hfill \\ \left( {\xi z + a} \right)otherwise, \hfill \\ \end{gathered} \right.$$
(1)

where \(\xi =\mathrm{tan}\theta\) is the tapering parameter, a is the radius, \({l}_{0}\) is the stenotic section length, and d is refers to the length of the non-stenotic portion. The angle \(\theta\) refers to the tapered angle. The case \(\theta > 0\) is associated with the diverging tapered artery, \(\theta < 0\) is associated with the converging tapered artery, and \(\theta = 0\) associated with the nontapered artery (Fig. 2(b)). The parameter \(\eta\) can be expressed as

$$\eta = 4\delta /al_{0}^{4} ,$$
(2)

in which \(\delta\) indicates the maximum length of the stenosis located at

$$z = d + 8l_{0} /25\,{\text{and}}\,z = d + 61l_{0} /50,$$
(3)
Fig. 1
figure 1

Geometry of the problem for \(\omega\)-shaped tapered stenosed artery [48]

Full size image
Fig. 2
figure 2

Velocity \(\left(w\right)\) variations with \(We\)

Full size image

3 Problem formulation

Assume a time-dependent pulsatile (Womersley) flow in a \(\omega\)-shaped stenosed vessel of a finite length \(L\), under the impact of the body acceleration. The tangent hyperbolic model is appraised to characterize the rheology of incompressible blood. The polar coordinates system \((r,\phi , z)\) is preferred, where \(z\)-axis indicates the arterial axis and \(r\) specifies the radial direction. The velocity, pressure, stress, and temperature fields can be expressed as follows:

$${\mathbf{V}} = \left[ {u\left( {t,r,z} \right), 0, w\left( {t,r,z} \right)} \right], p = p\left( {t, r, z} \right), {\mathbf{S}} = {\mathbf{S}}\left( {t, r, z} \right), T = T\left( {t, r, z} \right).$$
(4)

The stress tensor \(\left( {\varvec{\tau}} \right)\) for the tangent hyperbolic model can be written as

$${\varvec{\tau}} = {\mathbf{S}} - p{\mathbf{I}}, {\mathbf{S}} = \left\{ {\mu_{\infty } + \left( {\mu_{0} - \mu_{\infty } } \right)\tanh \left( {{\Gamma }\left| {\dot{\gamma }} \right|^{n} } \right)} \right\}{\dot{\mathbf{\gamma }}},$$
(5)

where \(p\) is the pressure, \(\mathbf{I}\) refers to the identity tensor, and \(\mathbf{S}\) specifies the trace-free nonisotropic part of \({\varvec{\tau}}\). The parameter \(n\) is known as the power-law index, which ranges from 0 (Newtonian) to 1 (Infinitely shear thinning), and \({\mu }_{0}\) and \({\mu }_{\infty }\) are known as zero and infinite rates of shear viscosity, respectively. The values of shear rates that indicate the commencement of the upper and lower limiting viscosities are influenced by different parameters, including polymer type and concentration, solvent nature, and molecular weight distribution, etc. Therefore, making valid generalizations is challenging. In stable states, the viscosity limit \({\mu }_{0}\), which is difficult to quantify with existing experimental techniques, is approximately ten times larger than \({\mu }_{\infty }\) [52]. The viscosities \({\mu }_{0}= 0.56\) and \({\mu }_{\infty }= 0.0345\) have been proposed in several generalized Newtonian models for blood [53]. The first Rivlin–Ericksen tensor \(\dot{\varvec{\gamma}}\) can be written as.

$$\dot{\gamma } = \sqrt {\frac{1}{2}\mathop \sum \limits_{j} \mathop \sum \limits_{k} \gamma_{jk} \gamma_{kj} } = \sqrt {\frac{1}{2}\pi } ,$$
(6)
$$\pi = {\text{trac}}\left( {\left( {\nabla {\mathbf{V}}} \right)^{T} + \nabla {\mathbf{V}}} \right),$$
(7)

The basic equations of the fluid flow and heat transfer are given as.

$$\nabla .{\mathbf{V}} = 0,$$
(8)
$$\rho {\raise0.7ex\hbox{${{\text{d}}{\mathbf{V}}}$} \!\mathord{\left/ {\vphantom {{{\text{d}}{\mathbf{V}}} {{\text{d}}t}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{d}}t}$}} = \nabla .{\varvec{\tau}} + \rho {\mathbf{G}}\left( t \right),$$
(9)
$$\rho c_{p} {\raise0.7ex\hbox{${{\text{d}}T}$} \!\mathord{\left/ {\vphantom {{{\text{d}}T} {{\text{d}}t}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{d}}t}$}} = K\nabla^{2} T + {\varvec{\tau}}:\nabla {\mathbf{V}}.$$
(10)

In Eq. (9), \(\mathbf{G}(t)\) is the body acceleration per unit mass. Assume \(\mathbf{G}(t) = [0, 0, g(t)]\) and by incorporating Eqs. (4) and (5) into Eqs. (8–10), we obtain

$$\frac{1}{r}\frac{\partial }{\partial r}\left( {ru} \right) + \frac{\partial w}{{\partial z}} = 0,$$
(11)
$$\rho \left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}\right)=-\frac{\partial p}{\partial r}+\frac{1}{r}\frac{\partial }{\partial r}\left(r{\tau }_{rr}\right)+\frac{\partial }{\partial z}{\tau }_{rz}-\frac{{\tau }_{\phi \phi }}{r}$$
(12)
$$\rho \left(\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}\right)=-\frac{\partial p}{\partial z}+\frac{1}{r}\frac{\partial }{\partial r}\left(r{\tau }_{rz}\right)+\frac{\partial }{\partial z}{\tau }_{zz}+\rho g(t)$$
(13)
$$\rho {c}_{p}\left(\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}\right)={\tau }_{rr}\frac{\partial u}{\partial r}+{\tau }_{rz}\frac{\partial w}{\partial r}+{\tau }_{zr}\frac{\partial u}{\partial z}+{\tau }_{zz}\frac{\partial w}{\partial z}+K\left(\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right)+\frac{{\partial }^{2}T}{\partial {r}^{2}}\right)$$
(14)

The nonzero components of stress are:

$$\begin{aligned} \tau_{rr} & = \left\{ {\mu_{\infty } + \left( {\mu_{0} - \mu_{\infty } } \right)\tanh \left( {\Gamma \left| {2\left( {\frac{\partial u}{{\partial r}}} \right)^{2} + \left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)^{2} + 2\left( \frac{u}{r} \right)^{2} + 2\left( {\frac{\partial w}{{\partial z}}} \right)^{2} } \right|} \right)^{n} } \right\}\left( {2\frac{\partial u}{{\partial r}}} \right), \\ \tau_{rz} & = \left\{ {\mu_{\infty } + \left( {\mu_{0} - \mu_{\infty } } \right)\tanh \left( {\Gamma \left| {2\left( {\frac{\partial u}{{\partial r}}} \right)^{2} + \left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)^{2} + 2\left( \frac{u}{r} \right)^{2} + 2\left( {\frac{\partial w}{{\partial z}}} \right)^{2} } \right|} \right)^{n} } \right\}\left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right), \\ \tau_{\phi \phi } & = \left\{ {\mu_{\infty } + \left( {\mu_{0} - \mu_{\infty } } \right)\tanh \left( {\Gamma \left| {2\left( {\frac{\partial u}{{\partial r}}} \right)^{2} + \left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)^{2} + 2\left( \frac{u}{r} \right)^{2} + 2\left( {\frac{\partial w}{{\partial z}}} \right)^{2} } \right|} \right)^{n} } \right\}\left( {2\frac{u}{r}} \right), \\ \tau_{zz} & = \left\{ {\mu_{\infty } + \left( {\mu_{0} - \mu_{\infty } } \right)\tanh \left( {\Gamma \left| {2\left( {\frac{\partial u}{{\partial r}}} \right)^{2} + \left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)^{2} + 2\left( \frac{u}{r} \right)^{2} + 2\left( {\frac{\partial w}{{\partial z}}} \right)^{2} } \right|} \right)^{n} } \right\}\left( {2\frac{\partial w}{{\partial z}}} \right). \\ \end{aligned}$$
(15)

The term g(t) in Eq. (13) refers to the body acceleration acting per unit mass in the axial direction. Following [48], we assume

$$g\left( t \right) = a_{g} {\text{cos}}\left( {\omega_{b} t + \theta } \right),$$
(16)

where \({a}_{g}\) and \(\theta\) denote the amplitude and the leading angle of \(g(t)\) related to the heart action, and the parameter \({\omega }_{b}= 2\pi {f}_{b}\), where \({f}_{b}\) is the frequency.

The boundary/initial conditions linked to the modelled problem are

$$\begin{aligned} & \frac{\partial }{\partial r}w\left( {t, r, z} \right) = 0,\quad \frac{\partial }{\partial r}T\left( {t, r, z} \right) = 0\quad\,{\text{at}}\,r = 0,\\& w\left( {t, r, z} \right) = 0,\quad T\left( {t, r, z} \right) = T_{w} \quad\,{\text{at}}\,r = R\left( z \right), \\& w\left( {t, r, z} \right) = 0,\quad T\left( {t, r, z} \right) = 0,\quad\,{\text{at}}\,t = 0 \end{aligned}$$
(17)

4 Dimensionless transformations

To normalize the governing Eqs. (11–15) and the related boundary/initial conditions (17), we incorporate non-dimensional variables as follows:

$$\begin{aligned} r^{*} & = \frac{r}{a},\quad z^{*} = \frac{z}{{l_{0} }},\quad t^{*} = \frac{{\omega _{p} }}{{2\pi }}t, \quad w^{*} = \frac{w}{{U_{0} }},\quad u^{*} = \frac{{l_{0} }}{{\delta U_{0} }}u, \quad R^{*} = \frac{R}{a}, \\ p^{*} & = \frac{{a^{2} }}{{l_{0} U_{0} \mu _{0} }}p, \quad \Theta = \frac{T}{{T_{w} }},\quad \tau _{{rr}}^{*} = \frac{{l_{0} }}{{U_{0} \mu _{0} }}\tau _{{rr}} , \quad \tau _{{rz}}^{*} = \frac{a}{{U_{0} \mu _{0} }}\tau _{{rz}},\quad \tau _{{\phi \phi }}^{*} = \frac{{l_{0} }}{{U_{0} \mu _{0} }}\tau _{{\phi \phi }} \\ \tau _{{zz}}^{*} & = \frac{{l_{0} }}{{U_{0} \mu _{0} }}\tau _{{zz}} , \quad \omega _{r} = \frac{{\omega _{b} }}{{\omega _{p} }},\quad We = \frac{{\Gamma U_{0} }}{a},\quad m = \frac{{\mu _{\infty } }}{{\mu _{0} }},\quad \text{Re} = \frac{{\rho U_{0} a}}{{\mu _{0} }},\quad e = \frac{{a_{1} }}{{a_{0} }},\quad \delta ^{*} = \frac{\delta }{a} \\ \alpha & = \frac{{\rho \omega _{p} a^{2} }}{{2\pi \mu _{0} }},\quad B_{1} = \frac{{a_{0} a^{2} }}{{U_{0} \mu _{0} }},\quad B_{2} = \frac{{\rho a_{g} a^{2} }}{{U_{0} \mu _{0} }},\quad \Upsilon = \frac{a}{{l_{0} }},\quad \Pr = \frac{{c_{p} \mu _{0} }}{K},\quad B_{r} = \frac{{U_{0}^{2} \mu _{0} }}{{KT_{w} }},\quad f^{*} \left( t \right) = \frac{{af\left( t \right)}}{{\mu _{0} U_{0} }} \\ \end{aligned}$$
(18)

where \({U}_{0}\) is the reference velocity. By employing the above new variables and after dropping the asterisks, Eqs. (11–15), take the form.

$$\delta \frac{1}{r}\frac{\partial }{\partial r}\left(ru\right)+\frac{\partial w}{\partial z}=0,$$
(19)
$$\delta \Upsilon ^{2} \left\{ {\alpha \frac{{\partial u}}{{\partial t}} + \Upsilon \text{Re} \left( {\delta \left( {u\frac{{\partial u}}{{\partial r}}} \right) + w\frac{{\partial u}}{{\partial z}}} \right)} \right\} = - \frac{{\partial p}}{{\partial r}} + \Upsilon ^{2} \left\{ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\tau _{{rr}} } \right) + \frac{\partial }{{\partial z}}\tau _{{rz}} - \frac{{\tau _{{\phi \phi }} }}{r}} \right\},$$
(20)
$$\alpha \frac{{\partial w}}{{\partial t}} + \Upsilon \text{Re} \left\{ {\delta \left( {u\frac{{\partial w}}{{\partial r}}} \right) + w\frac{{\partial w}}{{\partial z}}} \right\} = - \frac{{\partial p}}{{\partial z}} + \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\tau _{{rr}} } \right) + \Upsilon ^{2} \frac{\partial }{{\partial z}}\tau _{{zz}} + f\left( t \right),$$
(21)
$$\Pr \left( {\alpha \frac{{\partial \Theta }}{{\partial t}} + \text{Re} \Upsilon \left( {\delta u\frac{{\partial \Theta }}{{\partial r}} + w\frac{{\partial \Theta }}{{\partial z}}} \right)} \right) = {\text{Br}}\left\{ {\delta \Upsilon ^{2} \tau _{{rr}} \frac{{\partial u}}{{\partial r}} + \tau _{{rz}} \frac{{\partial w}}{{\partial r}} + \Upsilon ^{2} \left( {\delta ~\tau _{{zr}} \frac{{\partial u}}{{\partial z}} + \tau _{{zz}} \frac{{\partial w}}{{\partial z}}} \right)} \right\} + \left( {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial \Theta }}{{\partial r}}} \right) + \Upsilon \frac{{\partial ^{2} \Theta }}{{\partial r^{2} }}} \right),$$
(22)
$$\begin{aligned} \tau_{rr} & = \left\{ {m + \left( {1 - m} \right)\tanh \left( {We\left| {2\delta \Upsilon \left\{ {\left( {\frac{\partial u}{{\partial r}}} \right)^{2} + \left( \frac{u}{r} \right)^{2} } \right\} + \left( {\delta \Upsilon^{2} \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)^{2} + 2\Upsilon^{2} \left( {\frac{\partial w}{{\partial z}}} \right)^{2} } \right|} \right)^{n} } \right\}\left( {2\delta \frac{\partial u}{{\partial r}}} \right), \\ \tau_{rz} & = \left\{ {m + \left( {1 - m} \right)\tanh \left( {We\left| {2\delta \Upsilon \left\{ {\left( {\frac{\partial u}{{\partial r}}} \right)^{2} + \left( \frac{u}{r} \right)^{2} } \right\} + \left( {\delta \Upsilon^{2} \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)^{2} + 2\Upsilon^{2} \left( {\frac{\partial w}{{\partial z}}} \right)^{2} } \right|} \right)^{n} } \right\}\left( {\delta {\Upsilon }^{2} \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right), \\ \tau_{\phi \phi } & = \left\{ {m + \left( {1 - m} \right)\tanh \left( {We\left| {2\delta \Upsilon \left\{ {\left( {\frac{\partial u}{{\partial r}}} \right)^{2} + \left( \frac{u}{r} \right)^{2} } \right\} + \left( {\delta \Upsilon^{2} \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)^{2} + 2\Upsilon^{2} \left( {\frac{\partial w}{{\partial z}}} \right)^{2} } \right|} \right)^{n} } \right\}\left( {2\delta \frac{u}{r}} \right), \\ \tau_{zz} & = \left\{ {m + \left( {1 - m} \right)\tanh \left( {We\left| {2\delta \Upsilon \left\{ {\left( {\frac{\partial u}{{\partial r}}} \right)^{2} + \left( \frac{u}{r} \right)^{2} } \right\} + \left( {\delta \Upsilon^{2} \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)^{2} + 2\Upsilon^{2} \left( {\frac{\partial w}{{\partial z}}} \right)^{2} } \right|} \right)^{n} } \right\}\left( {\frac{\partial w}{{\partial z}}} \right) \\ \end{aligned}$$
(23)

The expression for dimensionless body acceleration is:

$$g\left(t\right)={B}_{2}\left\{\mathrm{cos}\left(2{\omega }_{r}\pi t+\theta \right)\right\}$$
(24)

Applying the assumption of mild stenosis \((\delta/ a\ll 1)\) and the extra condition \((\Upsilon \cong 1)\), we obtain.

$$\frac{\partial p}{\partial r}=0$$
(25)
$$\alpha \frac{\partial w}{\partial t}=-\frac{\partial p}{\partial z}+\frac{1}{r}\frac{\partial }{\partial r}\left\{r\left(m+\left(1-m\right)\mathrm{tanh}{\left(We\left|\frac{\partial w}{\partial r}\right|\right)}^{n}\right)\frac{\partial w}{\partial r} \right\}+{B}_{2}\left\{\mathrm{cos}\left(2{\omega }_{r}\pi t+\theta \right)\right\}$$
(26)
$$\mathrm{Pr}\alpha \frac{\partial\Theta }{\partial t}=\mathrm{Br}\left\{m+\left(1-m\right)\mathrm{tanh}{\left(We\left|\frac{\partial w}{\partial r}\right|\right)}^{n}\right\}{\left(\frac{\partial w}{\partial r}\right)}^{2}+\frac{{\partial }^{2}\Theta }{\partial {r}^{2}}+\frac{1}{r}\frac{\partial\Theta }{\partial r}$$
(27)

In Eq. (26), \(p = p(z,t)\), \(p\) will only be a function of \(t\). Because the pressure waveform is periodic, therefore it is appropriate to represent the partial derivative of pressure utilizing Fourier series. A periodic function of such type is determined by the fundamental frequency of the signal \(({\omega }_{p})\), heart rate \((rad/s)\), and time \(t\) [54]. Thus following [48], we define the pressure gradient as.

$$-\frac{\partial p}{\partial z}={a}_{0}+{a}_{1}\mathrm{cos}({\omega }_{p}t)$$
(28)

where \({\omega }_{p}=2\pi {f}_{p}\) is also called pulse rate frequency, \({a}_{0}\) and \({a}_{1}\) specify the constant part and the magnitude of the pulsatile part of the pressure gradient, respectively. For more realistic analysis of blood flows, a multimode pressure gradient [55,56,57] can also be used in place of a single-mode pressure gradient defined by Eq. (28). An approximation of such pressure waveforms can be done with a Fourier series. Using the pressure waveform and a constant value at the vessel outlet, a pressure gradient can then be calculated.

In term of variables (18), Eq. (28) becomes:

$$-\frac{\partial p}{\partial z}={B}_{1}\left\{1+e\mathrm{cos}\left(2\pi t\right)\right\}$$
(29)

In terms of new variables (18), the boundary/initial conditions (17) are

$$\begin{aligned} \frac{\partial }{\partial r}w\left( {t, r} \right) & = 0,\,\frac{\partial }{\partial r}{\Theta }\left( {t, r} \right) = 0,\,{\text{at}}\,r = 0 \\ w\left( {t, r} \right) & = 0,\,{\Theta }\left( {t, r} \right) = 1,\,{\text{at}}\,r = R\left( z \right) \\ w\left( {t, r} \right) & = 0,\,{\Theta }\left( {t, r} \right) = 0,\,{\text{at}}\,t = 0 \\ \end{aligned}$$
(30)

The normalized form of the stenotic arterial portion is

$$R\left( z \right) = \left( {1 + \xi z} \right)\left( {1 - \frac{64}{{10}}\eta_{1} \left( {\frac{11}{{32}}\left( {z - \sigma } \right) - \frac{47}{{48}}\left( {z - \sigma } \right)^{2} - \left( {z - \sigma } \right)^{3} - \frac{1}{3}\left( {z - \sigma } \right)^{4} } \right)} \right),\,\sigma \le z \le \sigma + \frac{3}{2},$$
(31)
$${\text{where}}\,\eta_{1} = 4\delta ,\,\sigma = d/l_{0} ,\,\xi = \xi^{*} l_{0} /a.$$
(32)

The dimensionless expressions for WSS (τs), volume flow rate (Q), and resistive impendence (Λ) are [48]

$${\tau }_{s}={\left[\left(m+\left(1-m\right)\mathrm{tanh}{\left(We\left|\frac{\partial w}{\partial r}\right|\right)}^{n}\right)\frac{\partial w}{\partial r}\right]}_{r=R}$$
(33)
$$Q={\int }_{0}^{R}wr\mathrm{d}r$$
(34)
$$\Lambda =\frac{-\partial p/\partial z}{Q}$$
(35)

The computational domain is transformed from (0, R) to (0, 1) with the help of the following radial coordinate transformation.

$$x=\frac{r}{R\left(z\right)}$$
(36)

Equations (26, 27) in terms of the above variable are:

$$\alpha \frac{\partial w}{{\partial t}} = B_{1} \left\{ {1 + e\cos \left( {2\pi t} \right)} \right\} + B_{2} \left\{ {\cos \left( {2\omega_{r} \pi t + \theta } \right)} \right\} + \frac{1}{{xR^{2} }}\frac{\partial }{\partial x}\left\{ {x\left( {m + \left( {1 - m} \right)\tanh \left( {\frac{We}{R}\left| {\frac{\partial w}{{\partial x}}} \right|} \right)^{n} } \right)\frac{\partial w}{{\partial x}}} \right\},$$
(37)
$${\text{Pr}}\alpha \frac{{\partial {\Theta }}}{\partial t} = Br\frac{1}{{R^{2} }}\left\{ {m + \left( {1 - m} \right)\tanh \left( {\frac{We}{R}\left| {\frac{\partial w}{{\partial x}}} \right|} \right)^{n} } \right\}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \frac{1}{{R^{2} }}\left( {\frac{{\partial^{2} {\Theta }}}{{\partial x^{2} }} + \frac{1}{x}\frac{{\partial {\Theta }}}{\partial x}} \right),$$
(38)

whereas the boundary/initial conditions (300) turn into

$$\begin{aligned} w\left( {t, x} \right)\left. \right|_{t = 0} & = 0,\,w\left( {t, x} \right)\left. \right|_{x = 1} = 0,\partial w/\partial x\left. \right|_{x = 0} = 0, \\ {\Theta }\left( {t, x} \right)\left. \right|_{t = 0} & = 0,\,{\Theta }\left( {t, x} \right)\left. \right|_{x = 1} = 1,\,\partial {\Theta }/\partial x\left. \right|_{x = 0} = 0 \\ \end{aligned}$$
(39)

It is evident form Eqs. (37) and (38) that, unlike previous studies, we did not expand the Tanh-term to its Taylor series. Thusly this study is more superior to the existing ones and depicts a more realistic haemorheology situation. The WSS (33), flow rate (34), and resistive impendence (35) in terms of Eq. (36) can be expressed as:

$${\tau }_{s}={\left[\frac{1}{R}\left(m+\left(1-m\right)\mathrm{tanh}{\left(\frac{We}{R}\left|\frac{\partial w}{\partial x}\right|\right)}^{n}\right)\frac{\partial w}{\partial x}\right]}_{x=1}$$
(40)
$$Q={R}^{2}{\int }_{0}^{1}wx\mathrm{d}x$$
(41)
$$\Lambda =\frac{-\partial p/\partial z}{Q}$$
(42)

By incorporating the non-dimensional pressure gradient, Eq. (42) takes the form.

$$\Lambda =\frac{{B}_{1}\left(1+e\mathrm{cos}\left(2\pi t\right)\right)}{{R}^{2}{\int }_{0}^{1}wx\mathrm{d}x}$$
(43)

5 Numerical solution

The finite difference approximations of derivatives are one of the oldest and simplest approaches for solving differential equations. The advent of this technique in numerical applications began in the mid-1950s, and its advancement was stimulated by the development of computers which provided a suitable framework for solving complicated problems of engineering science and technology. In this technique, the forward difference formula is utilized to estimate a temporal derivative, whereas the central difference formula is utilized to estimate the spatial derivatives. The value of \(u\) at a time instant \({t}_{k}\) and a node \({x}_{j}\) is denoted by the symbol \({u}_{j}^{k}\). As a result, we write

$$\frac{\partial w}{\partial x}\cong \frac{{w}_{j+1}^{k}-{w}_{j-1}^{k}}{2\Delta x}={w}_{x}$$
(44)
$$\frac{{\partial }^{2}w}{\partial {x}^{2}}\cong \frac{{w}_{j+1}^{k}-2{w}_{j}^{k}+{w}_{j-1}^{k}}{(\Delta {x)}^{2}}={w}_{xx}$$
(45)
$$\frac{\partial w}{\partial t}\cong \frac{{w}_{j}^{k+1}-{w}_{j}^{k}}{\Delta t}$$
(46)

By inserting the above approximations (44–46) for spatial and temporal derivatives of \(w\) and \(\Theta\) in Eqs. (37) and (38), we attain the difference equations given below:

$$\begin{aligned}{w}_{j}^{k+1}\,=\,&{w}_{j}^{k}+\frac{\Delta t}{\alpha }[{B}_{1}\left\{1+e\mathrm{cos}\left(2\pi {t}^{k}\right)\right\}+{B}_{2}\left\{\mathrm{cos}\left(2{\omega }_{r}\pi {t}^{k}+\theta \right)\right\}+\frac{1}{x{R}^{2}}\left\{\left(m+\left(1-m\right)\mathrm{tanh}{\left(\frac{We}{R}\left|{w}_{x}\right|\right)}^{n}\right){w}_{x}\right\}\\&+\frac{1}{{R}^{2}}\left(m+\left(1-m\right)\mathrm{tanh}{\left(\frac{We}{R}\left|{w}_{x}\right|\right)}^{n}\right){w}_{xx}\\ &+\frac{1}{{R}^{2}}{w}_{x}\frac{\partial }{\partial x}\left(m+\left(1-m\right)\mathrm{tanh}{\left(\frac{We}{R}\left|{w}_{x}\right|\right)}^{n}\right)\end{aligned}$$
(47)
$${\Theta }_{j}^{k+1}={\Theta }_{j}^{k}+\frac{\Delta t}{\alpha Pr{R}^{2}}\left\{Br\left(m+\left(1-m\right)\mathrm{tanh}{\left(\frac{We}{R}\left|{w}_{x}\right|\right)}^{n}\right){\left({w}_{x}\right)}^{2}+{\Theta }_{xx}+\frac{1}{x}{\Theta }_{x}\right\}$$
(48)

The given boundary/initial conditions (39) can be discretized in the following way:

$$\begin{aligned} w_{j}^{1} & = {\Theta }_{j}^{1} = 0,{\text{at}}\,t = 0, \\ w_{1}^{k} & = w_{2}^{k} \,{\Theta }_{1}^{k} = {\Theta }_{2}^{k} ,{\text{at}}\,x = 0, \\ w_{N + 1}^{k} & = 0,\,{\Theta }_{N + 1}^{k} = 1,{\text{at}}\,x = 1, \\ \end{aligned}$$
(49)

Now with suitably defined space and time step-sizes, Eqs. (47, 48) can be used along with initial/boundary conditions (49) to compute \({w}_{j}^{k+1}\) and\({\Theta }_{j}^{k+1}\). Here the solutions are calculated for \((N + 1)\) uniformly discrete points \({x}_{j}\) with a grid size\(\Delta x = 1/(N + 1)\), where \(j = \mathrm{1,2},3, \ldots , N + 1\) at the time steps\({t}_{k}=(k-1)\Delta t\), where \(\Delta t\) and \(\Delta x\) are small increments in temporal and axial directions, respectively. We use the following time and spatial step sizes to achieve the accuracy of\(O({10}^{-7})\):

$$\Delta t = 0.00001,\,{\text{and}}\,\Delta x = 0.025.$$

6 Results and discussion

To analyse the quantitative effects of the power-law index \((n)\), Weisenberg number \((We)\), the amplitude of body acceleration \(({B}_{2})\), the height of stenosis \((\delta )\), and tapering angle \((\theta )\) on the velocity and temperature fields, WSS, resistive impedance, and volumetric flow rate we have sketched several graphs by taking the following set of values [48].

$$\begin{aligned} d & = 0.5,l_{0} = 1.0,L = 2.25,\delta = 0.1,\mu_{0} = 0.56,\mu_{\infty } = 0.0345,e = 0.5,z = 0.77 \\ f_{b} = f_{p} & = 1.2,B_{1} = 4,B_{2} = 1,We = 0.5,n = 0.5,{\text{Pr}} = 10,{\text{Br}} = 2. \\ \end{aligned}$$

The velocity profile is of particular importance to us since it includes comprehensive information about the flow field. Figure 2 designates that the blood velocity is a continuously diminishing function of \(We\). The dimensionless parameter \(We\) relates the elastic forces to the viscous forces, that is \(We\) characterize the viscoelastic features of the fluid. As a result, blood with higher viscoelasticity possesses lower velocity. This is most likely due to higher values of the Weissenberg number enhancing the shear-thinning characteristic of the blood, resulting in a drop in the blood's apparent viscosity. This viscosity drop causes a gradual decline of the blood axial velocity. This influence on the axial velocity of the Weissenberg number will obviously affect other major hemodynamic variables, such as wall shear stress (WSS), resistive impedance, and volumetric flow rate which will demonstrate oscillatory behaviour. Figure 3 demonstrates the velocity \((w)\) variations linked to the stenosis height \((\delta )\). It is indicated that the blood velocity is related inversely to the growth of stenosis. This plot also demonstrates that the blood velocity via a divergent tapering artery is larger in comparison with nontapered and converging tapering arteries. The fact is that the divergent geometry increases the momentum-flux and therefore facilitates the blood flow while, with the convergent one, the opposite tendency emerges. The influence of body acceleration over axial velocity is demonstrated in Fig. 4. This figure depicts that increasing the amplitude of the body acceleration \(({B}_{2})\) increases the axial velocity significantly. Figure 5 depicts the impact of power-law exponent \((n)\) on the distribution of the axial velocity. This plot demonstrates that as the magnitude of the power-law exponent increases, the blood velocity diminishes near the arterial wall while its amplitude tends to increase near the centre of the artery.

Fig. 3
figure 3

Velocity \(\left(w\right)\) variations with \(\delta\)

Full size image
Fig. 4
figure 4

Velocity \(\left(w\right)\) variations with \({B}_{2}\)

Full size image
Fig. 5
figure 5

Velocity \(\left(w\right)\) variations with \(n\)

Full size image

The impacts of related parameters on the volumetric flow rate at a particular axial position \(z = 0.77\) are presented in Figs. 6, 7, 8, 9. The flow rate behaviour for specific values of \(We\) is illustrated in Fig. 6. This plot reveals that the amplitude of \(Q\) diminishes by elevating the values of \(We\). Furthermore, this diminution is more pronounced for smaller values of \(We\). Figure 7 demonstrates the impact of the body acceleration \(({B}_{2})\) on the volumetric flow rate \((Q)\). Here the curves representing the time-evolution of \(Q\) indicate higher amplitudes with an increment in \({B}_{2}\). The flow rate \((Q)\) patterns for various values of \(\delta\) are exhibited in Fig. 8. It turns out that the flow rate curves diminish appreciably by magnifying the size of stenosis \((\delta )\). The flow rate \((Q)\) behavior for specific values of \(n\) is demonstrated in Fig. 9. From this figure, it is evident that the volumetric flow rate diminishes as the values of \(n\) increase.

Fig. 6
figure 6

Flow rate \(\left(Q\right)\) variation with \(We\)

Full size image
Fig. 7
figure 7

Flow rate \(\left(Q\right)\) variation with \({B}_{2}\)

Full size image
Fig. 8
figure 8

Flow rate \(\left(Q\right)\) variation with \(\delta\)

Full size image
Fig. 9
figure 9

Flow rate \(\left(Q\right)\) variation with \(n\)

Full size image

To see the impacts of the emergence parameters on the distribution of wall shear stress (WSS), we prepared Figs. 10, 11, 12, 13, 14. The influence of Weissenberg number \((We)\) over WSS is illustrated in Fig. 10. It is revealed that the curves of WSS increase by varying \(We\). The impacts of body acceleration \(({B}_{2})\) and size of stenosis \((\delta )\) are shown in Figs. 11 and 12, respectively. It is demonstrated that higher values of both \({B}_{2}\) and \(\delta\) elevate the magnitude of WSS. This change in the behaviour of WSS is quite significant with an escalation in the amplitude of \({B}_{2}\). The effect of the power-law exponent \((n)\) on WSS is revealed in Fig. 13. As expected, the magnitude of WSS adopts a reduced trend by stepping up the magnitude \(n\). Figure 14 shows the variation of WSS in the stenosed artery as a function of axial distance for specific values of \(We\) and \(n\) at time \(t = 0.5\). It is identified that increasing the values of \(We\) increases the magnitude of WSS, while this behavior is opposite with an escalation in \(n\).

Fig. 10
figure 10

Variation of WSS for specific values of \(We\)

Full size image
Fig. 11
figure 11

Variation of WSS for specific values of \(B2\)

Full size image
Fig. 12
figure 12

Distribution of WSS for specific values of \(\delta\)

Full size image
Fig. 13
figure 13

Distribution of WSS for specific values of \(n\)

Full size image
Fig. 14
figure 14

Distribution of WSS for specific values of \(We\) and \(n\)

Full size image

Figures 15 and 16 illustrate the behaviour of the resistive impedance \((\Lambda )\) to the flow. These plots show that the resistance \((\Lambda )\) to the flow increases almost linearly as the height of stenosis \((\delta )\) increases. Apart from this, in comparison with nontapered and diverging tapering arteries, the magnitude of \(\Lambda\) is greater in the case of a converging tapered artery. Moreover, these figures show that the blood rheology also affects the resistance to the flow, and the resistance increases by stepping up the degree of power-law exponent \((n)\), while it decreases with the escalation of \(We\).

Fig. 15
figure 15

Profile of resistive impendence for specific values of \(n\)

Full size image
Fig. 16
figure 16

Profile of resistive impendence for specific values of \(We\)

Full size image

Figures 17, 18, 19, 20, 21 show the temperature distribution relative to Brinkman number \((\mathrm{Br})\), Prandtl number \((\mathrm{Pr})\), Weissenberg number \((We)\), the amplitude of body acceleration \(({B}_{2})\), and the power-law exponent \((n)\) at a special axial station \(z = 0.77\) and at \(t = 0.5\). It is obvious from these plots that the blood temperature is maximum near the arterial surface and is minimum at the arterial centreline. Figure 17 exhibits the temperature distribution for various values of \(\mathrm{Br}\) in a stenosed blood vessel. It is examined that the blood temperature at the arterial centreline rises by amplifying \(\mathrm{Br}\) values. Figure 18 illustrates the behaviour of blood temperature for various values of \(\mathrm{Pr}\). The available literature on haemodynamics suggests that for blood flow, the values of \(Pr\) should be higher than \(10\), [48]. Therefore, the graphs of intra-arterial temperature are developed for \(\mathrm{Pr}\) = \(10\), \(15\), \(20\), and \(25\). It is spotted that the transport of heat from the vessel's wall to the blood diminishes, by escalating \(Pr\), which leads to the temperature drop of the streaming blood. This is since a higher Prandtl number \((Pr)\) usually results in a reduction in the blood thermal conductivity. This diminishes the proficiency of heat transmission from the wall to the flowing blood, which establishes itself in the prevention of the temperature. The influence of \(\delta\) on the temperature distribution is revealed in Fig. 19. This plot indicates that the temperature distribution escalates by varying \(\delta\). In addition, the converging artery offers higher temperature as compared to nontapered and diverging arteries. Figure 20 demonstrates that the fluid (blood) temperature diminishes slightly by improving the values of \(We\). Figure 21 indicates the increase in the temperature of the blood with the improvement in the \({B}_{2}\) amplitude. The effects of \(n\) on the blood temperature are shown in Fig. 22. It is noted that the magnitude of the blood temperature boosts marginally with an increase in \(n\).

Fig. 17
figure 17

Temperature variation with Br

Full size image
Fig. 18
figure 18

Temperature variation with \(Pr\)

Full size image
Fig. 19
figure 19

Temperature variation with \(\delta\)

Full size image
Fig. 20
figure 20

Temperature variation with \(We\)

Full size image
Fig. 21
figure 21

Temperature variation with \({B}_{2}\)

Full size image
Fig. 22
figure 22

Variation of temperature with \(n\)

Full size image

7 Concluding remarks

The pulsatile blood flow of the tangent hyperbolic fluid model in a narrowed arterial segment with overlapping stenosis is investigated including the impacts of the body acceleration and periodic pressure gradient. The numerical solution has been assessed by means of a finite difference approach. The primary goal of this study was to understand the impacts of non-Newtonian behaviour, body acceleration, and the degree of the stenosis on blood flow through arteries and to discover locations where blood velocity is low and resistance to flow is high. When the body acceleration is superimposed to the pulsatile flow, the intensity of shear stress at the blood vessels wall reduced significantly. As a result, the fluid velocity accelerates remarkably. Clearly, blood flow amplifies as the amplitude of body acceleration increases, causing the heart to beat faster. This change in flow behaviour signifies some additional pressure that must be considered while treating the affected regions. The distribution of wall shear stress over the stenotic region rises with axial distance upstream of the stenosis throat and achieves its highest magnitude at the throat (\(z=0.82\), and \(z=1.72\)). It then drops downstream of the throat and approaches the same magnitude at the endpoint \((z=2.0)\) of the constriction that was attained at the starting point \((z=0.5)\). The increment in stenosis height increases the wall shear stress \(({\tau }_{s})\), flow resistance, and heat transfer while it diminishes the velocity and flow rate in the stenosed region. This demonstrates how the intensity of stenosis changes flow characteristics. The analysis further reveals that these harmful effects of stenosis may be reduced by adjusting the values of Weissenberg number and power-law index.

Another goal of this work was to better understand the impacts of viscous dissipation on blood dynamics. Viscous dissipation can be computed in term of the so-called Brinkman number. It is recognized that the impacts of viscous dissipation are pretty important and always facilitate the warming up of the fluid (blood) from the channel wall. It is worth noting here that in the initial stages of temperature profile formation, for higher values of Br (for example, \(\mathrm{Br} = 6\)) temperature can reach its local maxima not at the channel wall but at some distance from it. Mostly there were the viscous dissipation achieves its maximum. It is concluded that the variation in the temperature can also be controlled by refining Weissenberg number and power-law index.

It is also worth mentioning that the diverging tapering artery has a higher temperature and greater flow resistance than the converging tapering and nontapering arteries. This illustrates that the tapering angle is a crucial component in predicting the flow variables. Therefore, the taper angle cannot be ignored during computations.

8 Drawbacks:

Tangent hyperbolic fluid falls into the class of generalized Newtonian fluid models, which are particularly good at predicting shear-thinning behaviour. However, it fails to forecast shear normal stresses as well as start-up or shutdown impacts (time-dependence, memory). In other words, this model cannot represent other rheological features of blood (such as thixotropic and viscoelastic) and can be supplemented with other particular models available in the literature. Furthermore, this study is based on the rigid tube notion and does not address the elastic aspects of the vessel’s wall.