A Geometric Errors Identification Method for the Rotating Axis of Five-Axis Welding Equipment

Abstract

This paper deals with the problems of high detection cost and low detection efficiency in geometric errors identification of five-axis welding equipment, proposing a new method for rotating axis equipment, based on screw theory and monocular vision. In this paper, a low-cost and high-precision pose measurement method is first proposed, while the screw theory is used to establish a kinematics model for five-axis welding equipment. Furthermore, an identification method for the kinematics parameters and geometric errors of the rotating axis is proposed. In order to verify the validity and feasibility of the proposed identification scheme, the high detection accuracy of the pose detection system is first verified. Following, the significant improvement of the motion accuracy, after geometric errors identification, is verified, based on sampling within the working range of the five-axis welding equipment. The experimental results show that, the average value of the relative direction error of the five-axis welding equipment is reduced from 0.5427°, prior to identification, to 0.0478°, post identification, while the average value of the relative position error is reduced from 0.1472 to 0.0174 mm, respectively. Therefore, the identification scheme is proven can effective in identifying the geometric errors for the rotating axis, while it significantly improves the motion accuracy of the five-axis welding equipment.

1 Introduction

Compared to the three-axis motion platform, the five-axis platform has higher processing flexibility and efficiency [1]. However, due to the introduction of two rotating axes, more geometric errors are generated, resulting in greater processing errors for the five-axis platform. The geometric errors in the rotating axes of the five-axis platform have a more complicated impact on the accuracy than those in the linear axes as they comprehensively affects the accuracy of the actuator's position and orientation relative to the workpiece and produce a highly nonlinear kinematics relationship. Therefore, the identification of the rotating axis error can significantly improve the motion accuracy of the five-axis welding equipment. Geometric errors are usually divided into position-dependent geometric errors (PDGEs) and position-independent geometric errors (PIGEs) [2, 3]. PDGEs are mainly caused by manufacturing defects relating to machine tools, while PIGEs are mainly caused by assembly defects [4,5,6]. The geometric error measurement methods of the five-axis platform are generally divided into direct measurement methods and indirect measurement methods [7, 8]. The direct measurement method, uses instruments to directly measure a single geometric error item. The method is simple but the measurement efficiency is low. The indirect measurement method solves the geometric errors by establishing a mathematical model of the error [9], exhibiting high detection efficiency. Many researchers have proposed different geometric errors identification methods based on different measuring instruments. M. Tsutsumi et al. [10] used a ballbar to identify the PIGEs of the five-axis platform, based on the indirect measurement method, while they verified the feasibility of this method through experiments. High-precision testing instruments, such as Capball [11, 12], laser tracker [13, 14], R-test [15, 16], etc. can be used to indirectly detect geometric errors. In recent years, the rapid developments in the computer vision field, provided achievements that have gradually been used in the research of parameter identification of industrial automation equipment. The use of computer vision as a detection method can largely reduce the cost and complexity of detection compared to the use of traditional expensive and precise detection instruments [17,18,19,20]. Wang et al. [21] proposed a robot identification method based on machine vision; Yusuke et al. [18] used a camera to measure the two-dimensional position error of a machine tool; Liu W et al. [22] used binocular vision to identify the PIGEs of a five-axis platform. As mentioned above, traditional high-precision measurement equipment requires a high degree of operational expertise and complexity. In addition, traditional measurement methods are time-consuming and difficult to meet the needs of industrial automation processes for high-volume error detection, while the use of vision methods provides great convenience, in terms of automated operation and programmability. The main contribution of this paper is to propose a low-cost and high-precision method for the identification of geometric errors in rotating axes, based on an improved pose measurement method. The goal is to achieve efficient calibration of a five-axis motion stage, in an automated process, so as to meet specific needs, such as five-axis welding processing.

The article is organized as follows: Sect. 2 proposes an optimized algorithm for pose measurement and establishes the kinematics model of the five-axis welding equipment. Section 3 proposes a geometric errors identification method of rotating axes. In Sect. 4, experiments are carried out on the five-axis welding equipment, in order to verify the feasibility and effectiveness of the proposed modeling and identification schemes. Finally, Sect. 5 summarizes the proposed concept.

2 Pose Measurement System and Kinematics Modeling of Five-Axis Welding EQUIPMENT

2.1 An Optimized Direct Linear Transform (DLT) Algorithm for Pose Measurement

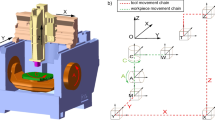
As shown in Fig. 1, the monocular camera is fixed at the end of the Z-axis actuator, the checkerboard target (hereafter referred to as the target) is fixed on the C-axis table. The spatial pose of the camera is determined by the amount of movement of the X, Y, and Z axes, while the spatial pose of the target is determined by the amount of movement of the A and C axes.

Fig. 1

Schematic diagram of five-axis welding equipment structure

The imaging of the target, according to the ideal camera imaging model, is shown in Fig. 2, including 4 coordinates systems: the camera coordinates system $O_{c} { - }X_{c} Y_{c} Z_{c}$, the target coordinates system $O_{b} { - }X_{b} Y_{b} Z_{b}$, the image physical coordinates system $o{ - }xy$ and the image pixel coordinates system $o{ - }uv$. The PnP(Perspective-n-Point) problem is described as knowing the 3D position point $\left( {\begin{array}{*{20}c} {X_{c} } \\ {Y_{c} } \\ {Z_{c} } \\ 1 \\ \end{array} } \right)$ and the corresponding 2D position $\left( {\begin{array}{*{20}c} u \\ v \\ 1 \\ \end{array} } \right)$ of the projection, and solving the pose matrix $M_{2}$ of the camera, as shown in Eq. (1):

$$\lambda \left[ {\begin{array}{*{20}c} u \\ v \\ 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {f_{x} } & 0 & {c_{u} } & 0 \\ 0 & {f_{y} } & {c_{v} } & 0 \\ 0 & 0 & 1 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {r_{3 \times 3} } & {t_{3 \times 1} } \\ {0^{T} } & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {X_{c} } \\ {Y_{c} } \\ {Z_{c} } \\ 1 \\ \end{array} } \right]{ = }M_{1} M_{2} \left[ {\begin{array}{*{20}c} {X_{c} } \\ {Y_{c} } \\ {Z_{c} } \\ 1 \\ \end{array} } \right]$$

(1)

where $M_{1} = \left[ {\begin{array}{*{20}c} {f_{x} } & 0 & {u_{0} } & 0 \\ 0 & {f_{y} } & {v_{0} } & 0 \\ 0 & 0 & 1 & 0 \\ \end{array} } \right]$ is the internal parameter matrix and $M_{2} = \left[ {\begin{array}{*{20}c} {r_{3 \times 3} } & {t_{3 \times 1} } \\ {0^{T} } & 1 \\ \end{array} } \right]$ is the external parameter matrix; $r_{3 \times 3} = \left[ {\begin{array}{*{20}c} {r_{11} } & {r_{12} } & {r_{13} } \\ {r_{21} } & {r_{22} } & {r_{23} } \\ {r_{31} } & {r_{32} } & {r_{33} } \\ \end{array} } \right]$ is the rotation matrix and $t_{3 \times 1} = \left[ {\begin{array}{*{20}c} {t_{1} } \\ {t_{2} } \\ {t_{3} } \\ \end{array} } \right]$ is the translation vector in the matrix $M_{2}$. The calibration method of Zhang Zhengyou [23] was used to calibrate the camera's internal parameter matrix $M_{1}$.

Fig. 2

Imaging model of monocular camera and target

Expanding the Eq. (1) and canceling out $\lambda$, the following equation can be obtained:

$$\left[ {\begin{array}{*{20}c} {X_{c} f_{x} } & 0 \\ {Y_{c} f_{x} } & 0 \\ {Z_{c} f_{x} } & 0 \\ {f_{x} } & 0 \\ 0 & {X_{c} f_{y} } \\ 0 & {Y_{c} f_{y} } \\ 0 & {Z_{c} f_{y} } \\ 0 & {f_{y} } \\ {X_{c} c_{u} - X_{c} u} & {X_{c} c_{v} - X_{c} v} \\ {Y_{c} c_{u} - Y_{c} u} & {Y_{c} c_{v} - Y_{c} v} \\ {Z_{c} c_{u} - Z_{c} u} & {Z_{c} c_{v} - Z_{c} v} \\ {c_{u} - u} & {c_{v} - v} \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {r_{11} } \\ {r_{12} } \\ {r_{13} } \\ {t_{1} } \\ {r_{21} } \\ {r_{22} } \\ {r_{23} } \\ {t_{2} } \\ {r_{31} } \\ {r_{32} } \\ {r_{33} } \\ {t_{3} } \\ \end{array} } \right] = 0$$

(2)

Since the number of corresponding points of 3D-2D is greater than 6, the pose matrix $M_{2}$ can be obtained by finding the least square solution of the above overdetermined equation. When the above-mentioned traditional DLT method is used to solve the external parameter matrix $M_{2}$, this is regarded as composed of 12 unknown numbers, and its connection is ignored. In fact, although the rotation matrix $r_{3 \times 3}$ in the matrix $M_{2}$ has 9 unknown numbers, it has only three degrees of freedom. Therefore, this paper proposes an optimized DLT algorithm to solve the pose matrix $M_{2}$. Considering the influence of noisy data, the following method is used to estimate the rotation matrix $r_{3 \times 3}$:

$$\tilde{r}_{3 \times 3} = \left( {r_{3 \times 3} \cdot r^{T}_{3 \times 3} } \right)^{{ - \frac{1}{2}}} \cdot r_{3 \times 3}$$

(3)

The solved rotation matrix $\tilde{r}_{3 \times 3}$ is substituted into Eq. (2) and then, the translation vector $t_{3 \times 1}$ is solved using the Singular Value Decomposition (SVD) method.

2.2 Kinematics Model of Five-Axis Welding Equipment

According to the principle of pose measurement system, the camera coordinates system on the Z axis can be defined as the actuator coordinates system{A}, while the target coordinates system on the C axis can be defined as the workbench coordinates system{W}. In order to obtain the kinematics model from the actuator coordinates system{A} to the workbench coordinates system{W}, the transformation relationship between the coordinates systems is required. The term $^{a} g_{w}$ represents the pose homogeneous transformation matrix of the workbench coordinates system{W} relative to the actuator coordinates system{A}. Based on product of exponentials formula [1], the forward kinematics model from the workbench coordinates system{W} to the actuator coordinates system{A} is:

$$^{a} {\text{g}}_{w} (x,y,z,\theta_{a} ,\theta_{c} ) = e^{{{\hat{\mathbf{\xi }}}_{z} \cdot z}} e^{{{\hat{\mathbf{\xi }}}_{x} \cdot x}} e^{{{\hat{\mathbf{\xi }}}_{y} \cdot y}} e^{{{\hat{\mathbf{\xi }}}_{a} \cdot \theta_{a} }} e^{{{\hat{\mathbf{\xi }}}_{c} \cdot \theta_{c} }} (^{a} g_{w} (0))$$

(4)

where the term $^{a} g_{w} (0)$ represents the initial pose matrix of the workbench coordinates system {W} relative to the actuator coordinates system {A}. ${{\varvec{\upxi}}}_{x}$, ${{\varvec{\upxi}}}_{y}$, ${{\varvec{\upxi}}}_{{\text{z}}}$, ${{\varvec{\upxi}}}_{a}$ and ${{\varvec{\upxi}}}_{c}$ represent the screw coordinates of the X, Y, Z, A and C axes respectively.$x$,$y$,$z$,$\theta_{a}$ and $\theta_{c}$ represent the motion components of X, Y, Z, A and C axes respectively.

In this section, a kinematics model of the five-axis welding machine is developed, based on the derivation of the screw theory (Appendix 1). The specific matrix form of forward kinematics model is mathematically expressed as:

$$\begin{gathered}^{a} {\text{g}}_{w} (x,y,z,\theta_{a} ,\theta_{c} ) = e^{{{\hat{\mathbf{\xi }}}_{z} \cdot z}} e^{{{\hat{\mathbf{\xi }}}_{x} \cdot x}} e^{{{\hat{\mathbf{\xi }}}_{y} \cdot y}} e^{{{\hat{\mathbf{\xi }}}_{a} \cdot \theta_{a} }} e^{{{\hat{\mathbf{\xi }}}_{c} \cdot \theta_{c} }} (^{a} g_{w} (0)) \hfill \\ = \left[ {\begin{array}{*{20}c} {I_{3 \times 3} } & {{\mathbf{v}}_{Z} \cdot z} \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {I_{3 \times 3} } & {{\mathbf{v}}_{x} \cdot x} \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {I_{3 \times 3} } & {{\mathbf{v}}_{y} \cdot y} \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right]. \hfill \\ \left[ {\begin{array}{*{20}c} {e^{{[{{\varvec{\upomega}}}_{{\mathbf{a}}} ]\theta_{a} }} } & {(I_{3 \times 3} - e^{{[{{\varvec{\upomega}}}_{{\mathbf{a}}} ]\theta_{a} }} ){\mathbf{q}}_{a} } \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {e^{{[{{\varvec{\upomega}}}_{{\mathbf{c}}} ]\theta_{c} }} } & {(I_{3 \times 3} - e^{{[{{\varvec{\upomega}}}_{{\mathbf{c}}} ]\theta_{c} }} ){\mathbf{q}}_{c} } \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right] \cdot \hfill \\ (^{a} g_{w} (0)) = \, \left[ {\begin{array}{*{20}c} {R_{3 \times 3} } & {{\mathbf{P}}_{3 \times 1} } \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right](^{a} g_{w} (0)) \hfill \\ \end{gathered}$$

(5)

where

$$R_{3 \times 3} = e^{{[{{\varvec{\upomega}}}_{{\mathbf{a}}} ]\theta_{a} }} e^{{[{{\varvec{\upomega}}}_{{\mathbf{c}}} ]\theta_{c} }}$$

(6)

$$\begin{gathered} {\mathbf{P}}_{3 \times 1} = (I_{3 \times 3} - e^{{[{{\varvec{\upomega}}}_{{\mathbf{a}}} ]\theta_{a} }} ){\mathbf{q}}_{a} + e^{{[{{\varvec{\upomega}}}_{{\mathbf{a}}} ]\theta_{a} }} (I_{3 \times 3} - e^{{[{{\varvec{\upomega}}}_{{\mathbf{c}}} ]\theta_{c} }} ){\mathbf{q}}_{c} \hfill \\ { + }({\mathbf{v}}_{{\mathbf{x}}} x + {\mathbf{v}}_{{\mathbf{y}}} y + {\mathbf{v}}_{{\mathbf{z}}} z) \hfill \\ \end{gathered}$$

(7)

The ideal kinematics parameters and screw coordinates are expressed as follows:

${{\varvec{\upxi}}}_{x} = \left[ {\begin{array}{*{20}c} {{\mathbf{v}}_{x} } \\ {0_{3 \times 1} } \\ \end{array} } \right]$,${\mathbf{v}}_{x} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ \end{array} } \right]^{T}$,${{\varvec{\upxi}}}_{y} = \left[ {\begin{array}{*{20}c} {{\mathbf{v}}_{y} } \\ {0_{3 \times 1} } \\ \end{array} } \right]$,${\mathbf{v}}_{y} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } \right]^{T}$,${{\varvec{\upxi}}}_{z} = \left[ {\begin{array}{*{20}c} {{\mathbf{v}}_{z} } \\ {0_{3 \times 1} } \\ \end{array} } \right]$,${\mathbf{v}}_{z} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right]^{T}$, ${{\varvec{\upxi}}}_{a} = \left[ {\begin{array}{*{20}c} { - {{\varvec{\upomega}}}_{a} \times {\mathbf{q}}_{a} } \\ {{{\varvec{\upomega}}}_{a} } \\ \end{array} } \right]$,${{\varvec{\upomega}}}_{a} { = }\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ \end{array} } \right]^{T}$,${\mathbf{q}}_{a} { = }\left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array} } \right]^{T}$,${{\varvec{\upxi}}}_{c} = \left[ {\begin{array}{*{20}c} { - {{\varvec{\upomega}}}_{c} \times {\mathbf{q}}_{c} } \\ {{{\varvec{\upomega}}}_{c} } \\ \end{array} } \right]$,${{\varvec{\upomega}}}_{c} { = }\left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right]^{T}$,${\mathbf{q}}_{c} { = }\left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array} } \right]^{T}$.

3 A Geometric Errors Identification Method of Rotating Axis

In this section, based on the pose measurement system of the monocular camera, a geometric errors identification scheme for the five-axis welding equipment is designed. Although it is difficult to identify the kinematics parameters directly by five-axis linkage, this paper proposes an analytical method, based on the least squares method, to identify the kinematics parameters. Then, the geometric errors of the A-axis and C-axis identification follows. The flowchart of the geometric errors identification method is shown in Fig. 3.

Fig. 3

Schematic diagram of the identification algorithm

3.1 Kinematics Parameters Identification Method for Kinematic Chain

Based on the principle of the monocular camera measurement, the target on the platform is fixed, while the monocular camera is used to take an image of the calibration target, to calculate the pose matrix $^{a} g_{w}$, based on the image information. The kinematic chain of the five-axis welding equipment is shown in Fig. 4.

Fig. 4

Kinematics chain of five-axis welding equipment

Equation (5) is simplified as follows:

$$^{a} {\text{g}}_{w} { = }\left[ {\begin{array}{*{20}c} {R_{3 \times 3} } & {{\mathbf{P}}_{3 \times 1} } \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right](^{a} g_{w} (0))$$

(8)

where

$$\left\{ {\begin{array}{*{20}c} {R_{3 \times 3} = e^{{[{{\varvec{\upomega}}}_{1} ]\theta_{1} }} e^{{[{{\varvec{\upomega}}}_{2} ]\theta_{2} }} } \\ \begin{gathered} {\mathbf{P}}_{3 \times 1} = (I_{3 \times 3} - e^{{[{{\varvec{\upomega}}}_{1} ]\theta_{1} }} ){\mathbf{q}}_{1} + e^{{[{{\varvec{\upomega}}}_{1} ]\theta_{1} }} (I_{3 \times 3} - e^{{[{{\varvec{\upomega}}}_{2} ]\theta_{2} }} ){\mathbf{q}}_{2} \, \hfill \\ { + }({\mathbf{v}}_{1} x + {\mathbf{v}}_{2} y + {\mathbf{v}}_{3} z) \hfill \\ \end{gathered} \\ \end{array} } \right.$$

(9)

where${{\varvec{\upomega}}}_{{\mathbf{1}}}$, ${{\varvec{\upomega}}}_{{\mathbf{2}}}$, $\theta_{1}$, $\theta_{2}$, ${\mathbf{q}}_{{\mathbf{1}}}$, ${\mathbf{q}}_{{\mathbf{2}}}$, ${\mathbf{v}}_{{\mathbf{1}}}$, ${\mathbf{v}}_{{\mathbf{2}}}$, ${\mathbf{v}}_{{\mathbf{3}}}$ are as listed in Table 1.

Table 1 The parameters value corresponding to the symbols

According to Eq. (8), the matrix $R_{3 \times 3}$ in Eq. (9) can be obtained as follows:

$$\begin{gathered} R_{3 \times 3} = (I_{3 \times 3} + \left[ {{{\varvec{\upomega}}}_{1} } \right]\sin (\theta_{1} ) + \left[ {{{\varvec{\upomega}}}_{1} } \right]^{2} (1 - \cos (\theta_{1} ))) \cdot \hfill \\ (I_{3 \times 3} + \left[ {{{\varvec{\upomega}}}_{2} } \right]\sin (\theta_{2} ) + \left[ {{{\varvec{\upomega}}}_{2} } \right]^{2} (1 - \cos (\theta_{2} ))) \hfill \\ = W_{1} + W_{2} \sin (\theta_{1} ) + W_{3} (1 - \cos (\theta_{1} )) + W_{4} \sin (\theta_{2} ) \hfill \\ + W_{5} \sin (\theta_{1} )\sin (\theta_{2} ) + W_{6} (1 - \cos (\theta_{1} ))\sin (\theta_{2} ) \hfill \\ + W_{7} (1 - \cos (\theta_{2} )) + W_{8} \sin (\theta_{1} )(1 - \cos (\theta_{2} )) \hfill \\ + W_{9} (1 - \cos (\theta_{1} ))(1 - \cos (\theta_{2} )) \hfill \\ \end{gathered}$$

(10)

The values of $W_{1}$,$W_{2}$,$W_{3}$,$W_{4}$,$W_{5}$,$W_{6}$,$W_{7}$,$W_{8}$,$W_{9}$ are listed in Table 2.

Table 2 The matrix symbol and value

According to Eq. (8), the following expression can be obtained:

$$\left[ {\begin{array}{*{20}c} {R_{3 \times 3} } & {{\mathbf{P}}_{3 \times 1} } \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right] = \left( {^{a} {\text{g}}_{w} } \right)\left( {^{a} g_{w} (0)} \right)^{ - 1}$$

(11)

where, $^{a} {\text{g}}_{w}$ represents the pose matrix, while the welding equipment is represented by $(x,y,z,\theta_{1} ,\theta_{2} )$;$^{a} g_{w} (0)$ represents the pose matrix as the motion component of each axis of the platform is $\left( {0,0,0,0,0} \right)$ in the initial state.

Let $^{a} G_{w} = \left( {^{a} {\text{g}}_{w} } \right)\left( {^{a} g_{w} (0)} \right)^{ - 1}$, then the following expression can be obtained:

$$^{a} G_{w} = \left[ {\begin{array}{*{20}c} {R_{3 \times 3} } & {{\mathbf{P}}_{3 \times 1} } \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right]$$

(12)

where, the pose matrix $^{a} {\text{g}}_{w}$ and $^{a} g_{w} (0)$ can be obtained by image data processing, provided by a camera, so $^{a} G_{w}$ can be measured by a monocular camera.

Regarding the matrix $R_{3 \times 3}$ in matrix $^{a} G_{w}$, it can be solved according to Eq. (10). For any $i \in \left\{ {1,2,3} \right\}$ and $j \in \left\{ {1,2,3} \right\}$,$^{a} G_{w}^{(i,j)} = R_{3 \times 3}^{(i,j)}$. Each element in the matrix $R_{3 \times 3}$ can be matched to a corresponding expression. Considering the element $^{a} G_{w}^{(1,1)}$ (which is also $R_{3 \times 3}^{(1,1)}$)in the first row and the first column of $^{a} G_{w}$ as an example, set:

$$W^{(1,1)} = \left[ {\begin{array}{*{20}c} {W_{1}^{(1,1)} } \\ {W_{2}^{(1,1)} } \\ {W_{3}^{(1,1)} } \\ {W_{4}^{(1,1)} } \\ {W_{5}^{(1,1)} } \\ {W_{6}^{(1,1)} } \\ {W_{7}^{(1,1)} } \\ {W_{8}^{(1,1)} } \\ {W_{9}^{(1,1)} } \\ \end{array} } \right]$$

(13)

$$\Theta _{1} = \left[ {\begin{array}{*{20}c} 1 \\ {\sin (\theta_{1} )} \\ {1 - \cos (\theta_{1} )} \\ {\sin (\theta_{2} )} \\ {\sin (\theta_{1} )\sin (\theta_{2} )} \\ {(1 - \cos (\theta_{1} ))\sin (\theta_{2} )} \\ {1 - \cos (\theta_{2} )} \\ {\sin (\theta_{1} )(1 - \cos (\theta_{2} ))} \\ {(1 - \cos (\theta_{1} ))(1 - \cos (\theta_{2} ))} \\ \end{array} } \right]$$

(14)

Next, the following expression can be obtained:

$$^{a} G_{w}^{(1,1)} =\Theta _{1}^{T} W^{(1,1)}$$

(15)

Actually, for any $i \in \left\{ {1,2,3} \right\}$ and $j \in \left\{ {1,2,3} \right\}$, the following expressions can be obtained:

$$\left\{ {\begin{array}{*{20}c} {^{a} G_{w}^{(i,j)} =\Theta _{1}^{T} W^{(i,j)} } \\ {W^{(i,j)} = \left[ {\begin{array}{*{20}c} {W_{1}^{(i,j)} } \\ {W_{2}^{(i,j)} } \\ {W_{3}^{(i,j)} } \\ {W_{4}^{(i,j)} } \\ {W_{5}^{(i,j)} } \\ {W_{6}^{(i,j)} } \\ {W_{7}^{(i,j)} } \\ {W_{8}^{(i,j)} } \\ {W_{9}^{(i,j)} } \\ \end{array} } \right]} \\ \end{array} } \right.$$

(16)

When the five-axis welding equipment is at the initial position, the initial pose matrix $^{a} g_{w} (0)$ can be obtained. As the five-axis welding equipment moves to different positions, the pose matrix $^{a} g_{w}$,corresponding to the different positions,is obtained, while then the matrixes $^{a} G_{w}^{(i,j)}$ and $\Theta _{1}$, corresponding to different positions, are obtained. Moreover, Eq. (16) is a linear type of equation, while the matrix $W^{(i,j)}$ can be obtained through multiple sets of different $^{a} G_{w}^{(i,j)}$ and $\Theta _{1}$, using the least square method. Therefore, according to Eqs. (17) (18) (19) and (20), the values of ${{\varvec{\upomega}}}_{1}$ and ${{\varvec{\upomega}}}_{2}$ are easily derived from matrix $W_{2}$ and matrix $W_{4}$,as shown in Table 2.

$$W_{2} = \left[ {\begin{array}{*{20}c} 0 & { - {{\varvec{\upomega}}}_{1}^{(z)} } & {{{\varvec{\upomega}}}_{1}^{(y)} } \\ {{{\varvec{\upomega}}}_{1}^{{\text{(z)}}} } & 0 & { - {{\varvec{\upomega}}}_{1}^{(x)} } \\ { - {{\varvec{\upomega}}}_{1}^{(y)} } & {{{\varvec{\upomega}}}_{1}^{{\left( {\text{x}} \right)}} } & 0 \\ \end{array} } \right]$$

(17)

$$W_{4} = \left[ {\begin{array}{*{20}c} 0 & { - {{\varvec{\upomega}}}_{2}^{(z)} } & {{{\varvec{\upomega}}}_{2}^{(y)} } \\ {{{\varvec{\upomega}}}_{2}^{{\left( {\text{z}} \right)}} } & 0 & { - {{\varvec{\upomega}}}_{2}^{(x)} } \\ { - {{\varvec{\upomega}}}_{2}^{(y)} } & {{{\varvec{\upomega}}}_{2}^{{\left( {\text{x}} \right)}} } & 0 \\ \end{array} } \right]$$

(18)

$${{\varvec{\upomega}}}_{1} = \left[ {\begin{array}{*{20}c} {{{\varvec{\upomega}}}_{1}^{\left( x \right)} } & {{{\varvec{\upomega}}}_{1}^{{\left( {\text{y}} \right)}} } & {{{\varvec{\upomega}}}_{1}^{\left( z \right)} } \\ \end{array} } \right]^{T}$$

(19)

$${{\varvec{\upomega}}}_{2} = \left[ {\begin{array}{*{20}c} {{{\varvec{\upomega}}}_{2}^{\left( x \right)} } & {{{\varvec{\upomega}}}_{2}^{{\left( {\text{y}} \right)}} } & {{{\varvec{\upomega}}}_{2}^{\left( z \right)} } \\ \end{array} } \right]^{T}$$

(20)

The vector ${\mathbf{P}}_{3 \times 1}$ in Eq. (12) is simplified into the following expression:

$${\mathbf{P}}_{3 \times 1} = \Omega_{ \, 1} {\mathbf{q}}_{{\mathbf{1}}} + \Omega_{ \, 2} {\mathbf{q}}_{{\mathbf{2}}} + W_{10} \left[ {\begin{array}{*{20}c} {\text{x}} & y & z \\ \end{array} } \right]^{T}$$

(21)

where vector ${\mathbf{q}}_{1} = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}_{1}^{(1,1)} } \\ {{\mathbf{q}}_{1}^{(2,1)} } \\ {{\mathbf{q}}_{1}^{(3,1)} } \\ \end{array} } \right]$,vector ${\mathbf{q}}_{2} = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}_{2}^{(1,1)} } \\ {{\mathbf{q}}_{2}^{(2,1)} } \\ {{\mathbf{q}}_{2}^{(3,1)} } \\ \end{array} } \right]$, the values of $\Omega_{ \, 1}$, $\Omega_{ \, 2}$ and $W_{10}$ are listed in Table.3.

Table 3 The value of $\Omega_{1}$,$\Omega_{2}$ and $W_{10}$

Each element in the vector ${\mathbf{P}}^{(1)}_{3 \times 1}$ can be matched to the corresponding expression. Considering the first element ${\mathbf{P}}^{(1)}_{3 \times 1}$ in the ${\mathbf{P}}_{3 \times 1}$ vector as an example, the following expression can be obtained:

$${\mathbf{P}}^{(1)}_{3 \times 1} = \Psi_{1}^{T} \Phi^{(1)}$$

(22)

where,

$$\Psi_{1} = \left[ {\begin{array}{*{20}c} {\Omega_{1}^{(1,1)} } \\ {\Omega_{1}^{(1,2)} } \\ {\Omega_{1}^{(1,3)} } \\ {\Omega_{2}^{(1,1)} } \\ {\Omega_{2}^{(1,2)} } \\ {\Omega_{2}^{(1,3)} } \\ x \\ y \\ z \\ \end{array} } \right]$$

(23)

$$\Phi^{(1)} { = }\left[ {\begin{array}{*{20}c} {{\mathbf{q}}_{1}^{(1,1)} } \\ {{\mathbf{q}}_{1}^{(2,1)} } \\ {{\mathbf{q}}_{1}^{(3,1)} } \\ {{\mathbf{q}}_{2}^{(1,1)} } \\ {{\mathbf{q}}_{2}^{(2,1)} } \\ {{\mathbf{q}}_{2}^{(3,1)} } \\ {{\mathbf{v}}_{1}^{(1,1)} } \\ {{\mathbf{v}}_{2}^{(1,1)} } \\ {{\mathbf{v}}_{3}^{(1,1)} } \\ \end{array} } \right]$$

(24)

For ${\mathbf{P}}^{(2)}_{3 \times 1}$ and ${\mathbf{P}}^{(3)}_{3 \times 1}$, the same expressions can be used:

$${\mathbf{P}}^{(2)}_{3 \times 1} = \Psi_{2}^{T} \Phi^{(2)}$$

(25)

$${\mathbf{P}}^{(3)}_{3 \times 1} = \Psi_{3}^{T} \Phi^{(3)}$$

(26)

The values of ${{\varvec{\upomega}}}_{1}$ and ${{\varvec{\upomega}}}_{2}$ have already been calculated, as previously described. Substituting the values of ${{\varvec{\upomega}}}_{1}$ and ${{\varvec{\upomega}}}_{2}$ into $\Omega_{1}$ and $\Omega_{2}$, and considering $\theta_{1}$、 $\theta_{2}$、$x$、$y$ and $z$ as the recorded components of each motion axis, the expressions of $\Psi_{1}$,$\Psi_{2}$ and $\Psi_{3}$ are derived. When the five-axis welding equipment moves to different positions, the $^{a} G_{w}$ is obtained, followed by the respective ${\mathbf{P}}^{(1)}_{3 \times 1}$ and $\Psi_{1}$. Considering that Eq. (22) is a linear equation, the $\Phi^{(1)}$ can be obtained through multiple sets of different ${\mathbf{P}}^{(1)}_{3 \times 1}$ and $\Psi_{1}$, using the least square method. The values of $\Phi^{(2)}$ and $\Phi^{(3)}$ can also be obtained. Therefore, vector ${\mathbf{q}}_{1}$ and vector ${\mathbf{q}}_{2}$ can be easily derived from $\Phi^{(1)}$,$\Phi^{(2)}$ and $\Phi^{(3)}$.

3.2 Identification of Geometric Errors for Rotating Axis

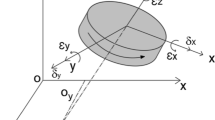
Considering the case of the C-axis as an example, a single rotating axis has 6 geometric errors, as shown in Fig. 5. It will produce errors in the six degrees of freedom in space, including one axial position error, which is represented by $\delta_{xc}$;two radial position errors, which are represented by $\delta_{yc}$ and $\delta_{zc}$; three angle errors, represented by $\varepsilon_{xc}$,$\varepsilon_{yc}$ and $\varepsilon_{zc}$, respectively were used to describe the angular error of the X-axis, Y-axis, and Z-axis of the coordinates system.

Fig. 5

Geometric errors of the C axis

The composite error matrix $T_{ec}^{D}$, formed by the 6 geometric errors on the C-axis, is as follows:

$$T_{ec}^{D} = T^{x} (\delta_{xc} )T^{y} (\delta_{yc} )T^{z} (\delta_{zc} )R^{x} (\varepsilon_{xc} )R^{y} (\varepsilon_{yc} )R^{z} (\varepsilon_{zc} )$$

(27)

where $T^{x} (*)$, $T^{y} (*)$ and $T^{z} (*)$, represent the $4 \times 4$ homogeneous transformation matrix of translational motion along the x-axis, y-axis and z-axis, respectively; $R^{x} (*)$,$R^{y} (*)$ and $R^{z} (*)$ represent the $4 \times 4$ homogeneous transformation matrix of the rotational motion around the X-axis, Y-axis and Z-axis, respectively. Since the geometric errors are very small quantities, expanding the expression $T_{ec}^{D}$ and ignoring the higher-order terms in $T_{ec}^{D}$, provides a simplified expression of the error matrix $T_{ec}^{D}$ as follows:

$$T_{ec}^{D} = \left[ {\begin{array}{*{20}c} 1 & { - \varepsilon_{zc} } & {\varepsilon_{yc} } & {\delta_{xc} } \\ {\varepsilon_{zc} } & 1 & { - \varepsilon_{xc} } & {\delta_{yc} } \\ { - \varepsilon_{yc} } & {\varepsilon_{xc} } & 1 & {\delta_{zc} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$

(28)

When identifying the geometric errors of a single axis, in order to prevent other axes from affecting the geometric errors measurement of the specific axis, the other axes are maintained in their initial position, while only the investigated axis is moved. Regarding the C-axis, the respective kinematics model can be established as:

$$^{a} {\text{g}}_{w} = e^{{{\hat{\mathbf{\xi }}}_{c} \theta_{c} }} (T_{ec}^{D} )(^{a} g_{w} (0))$$

(29)

Therefore, Eq. (29) can be obtained as:

$$T_{ec}^{D} = (e^{{{\hat{\mathbf{\xi }}}_{c} \theta_{c} }} )^{ - 1} (^{a} {\text{g}}_{w} )(^{a} g_{w} (0))^{ - 1}$$

(30)

where,

$$e^{{{\hat{\mathbf{\xi }}}_{c} \theta_{c} }} = \left[ {\begin{array}{*{20}c} {e^{{[{{\varvec{\upomega}}}_{c} ]\theta_{c} }} } & {(I_{3 \times 3} - e^{{[{{\varvec{\upomega}}}_{c} ]\theta_{c} }} ){\mathbf{q}}_{c} } \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right]$$

(31)

The terms ${{\varvec{\upomega}}}_{c}$ and ${\mathbf{q}}_{c}$ have been calculated in Sect. 3.1, whereas $^{a} {\text{g}}_{w}$ and $^{a} {\text{g}}_{w(0)}$ can be obtained by a monocular camera. Therefore, for any $\theta_{c}$, the corresponding $T_{ec}^{D}$ can be obtained according to Eq. (30). Therefore, when the axis is at $\theta_{c}$, 6 geometric errors of C-axis can be obtained from Eq. (28).

After measuring A-axis and C-axis geometric errors at different positions, each error term can be smoothed and fitted to obtain the expression for geometric errors compensation. For example, the C-axis can move within the range of 360°, while each error term can be considered as a periodic function of $\theta_{c}$ with a maximum period of 2π. The following finite term Fourier series can be selected to fit the various errors:

$$f(x) = \frac{{a_{0} }}{2} + \sum\limits_{k = 1}^{n} {(a_{k} \cos (kx) + b_{k} \sin (kx))}$$

(32)

4 Experiment

4.1 Inspection of Monocular Camera Measurement Accuracy

The vision measurement system in this article needs to have relatively high accuracy requirements for the pose measurement. Therefore, the measurement accuracy is analyzed by separately moving the axis to a specified distance in the five-axis welding equipment workspace. The feedback value by the motor encoder is regarded as the actual value $d_{a}$, while the value of the visual pose measurement is represented as $d_{m}$. The accuracy of the vision measurement system is detected by examining the difference $\Delta d$ between $d_{a}$ and $d_{m}$.

A single-axis motion experiment of the C-axis was performed. The specific motion control commands are: rotate 2 degree each time and rotate continuously for one cycle in a single direction, then calculate the angle error $\Delta d$ generated by sampling points. The actual value $d_{a}$ is obtained by calculating the change between two encoder counts, before and after. The measured value $d_{m}$ by monocular vision is obtained by calculating the change between the two camera external parameter matrices, before and after, as the pose matrix $M_{2} = \left[ {\begin{array}{*{20}c} {r_{3 \times 3} } & {t_{3 \times 1} } \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right]$ in Eq. (1). The measured value $d_{m}$ by monocular vision can be solved by the Eq. (33):

$$\left\{ {\begin{array}{*{20}c} {\Delta \left( t \right) = \left\| {t_{{0_{3 \times 1} }} - t_{{1_{3 \times 1} }} } \right\|} \\ {\Delta \left( r \right) = 2\arccos \left( {\sqrt {1 + tr\left( {r_{{0_{3 \times 3} }} r_{1\;3 \times 3}^{T} } \right)} } \right)/2} \\ \end{array} } \right.$$

(33)

where $r_{{0_{3 \times 3} }}$ represents the rotation matrix and $t_{{0_{3 \times 1} }}$ represents the translation vector in the previous pose matrix $M_{1}$;$r_{{1_{3 \times 3} }}$ represents the rotation matrix and $t_{{1_{3 \times 1} }}$ represents the translation vector in the latter pose matrix $M_{1}$.$\Delta \left( t \right)$ represents the displacement of this movement, while $\Delta \left( r \right)$ represents the respective rotation.

As shown in Fig. 6, the proposed optimized DLT algorithm proposed exhibits higher detection accuracy in pose measurement than the traditional DLT algorithm. As shown in Fig. 6, the angular error of the optimized DLT algorithm, caused by the single-axis rotation of the C-axis, is within 0.0025°, while the traditional DLT algorithm provides a slightly larger value. Comprehensive analysis shows that, the optimized DLT algorithm shows higher accuracy of pose measuring than the traditional algorithm, which meets the requirements of the process of parameter identification in a five-axis welding equipment, as presented in this paper.

Fig. 6

Angle error of rotation C-axis

4.2 Identification Experiment of Geometric Errors for Rotating Axis

In order to accurately identify the kinematics parameters, the following experiment is carried out. The physical map of the five-axis welding equipment is shown in Fig. 7, where a Basler monocular camera with a resolution of 5 million pixels is used; the target is a $15 \times 15$ black and white chessboard, with $2 \times 2\,{\text{mm}}$ squares. The sensor chip of the monocular camera is CMOS type and the frame rate is 14 fps. The closed-loop control of each single axis based on motion controllers, servo drives and motors, while the communication format is EtherCAT bus. Each motion axis provides real-time feedback of motor position signal based on incremental photoelectric encoder. The X, Y and Z axes are equipped with Panasonic AC servo motors and precision ball screw with a pitch of 5 mm, whereas their operating ranges are 425 mm, 375 mm and 220 mm, respectively. The motion assembly of A-axis consists of Panasonic AC servo motor and speed reducer, where the reduction ratio is 20:1. The motion of C-axis is realized by Akribis direct drive motor.

Fig. 7

Experimental setup

In the actual operation of the five-axis welding equipment, the working stroke range of the A-axis is ± 25°, and the operating range of the C-axis is ± 180°. The A axis is sampled every 0.5° according to the full stroke, while C axis is sampled every 1° across the full stroke path. Since the imaging of the monocular camera requires that the target is within the view field of the camera, it is necessary to roughly determine the positions of the translation axes X, Y, and Z according to the positions of the A-axis and the C-axis, as well as ensure that the target imaging is clear. Three items of data are recorded during sampling: the initial pose matrix $^{a} g_{w} (0)$ at the initial position, the pose matrix $^{a} g_{w}$ when the axes of the platform are located at each sampling point, and the components $(x,y,z,\theta_{1} ,\theta_{2} )$ of each axis at the respective sampling point. According to Eq. (8), the initial pose matrix $^{a} g_{w} (0)$ is a key data in the modeling process. In order to eliminate random errors, the average value of multiple measurements is considered in the calculation of $^{a} g_{w} (0)$. After identification, the actual kinematics parameters are listed in Table 4. The ideal and actual screw coordinates are shown in Table 5.

Table 4 Actual kinematics parameters

Table 5 Ideal and actual screw coordinates

4.2.1 Identification of C-Axis Geometric Errors

During the identification of geometric errors of the C axis, the other axes are remain at their initial positions, while the C axis is recorded every 1° within a range of ± 180°. According to the geometric errors identification method of the rotation axis, proposed in Sect. 3.2, the pose matrix of the target is measured at the sampling point, and the geometric errors of the C axis are calculated at each sampling points. Finally, considering n = 4, the various geometric errors of the C axis are fitted according to Eq. (32). Figure 8 illustrates the identified values of the geometric errors of the sampled C axis and the fitted curve. The points in Fig. 8 represent the identified values at each angle, while the curve represents the fitted curve.

Fig. 8

The identification value and fitting result of C-axis geometric errors

4.2.2 Identification of A-Axis Geometric Errors

The identification method of the A-axis geometric errors is similar to that of C-axis. For this experimental platform, if only the A-axis is rotated and the X, Y, and Z axes remain still, the target will move out of the camera's field of view after the A-axis is rotated to a certain angle, causing the camera to fail to measure the target's pose. Therefore, only a small range of geometric errors identification is performed on the A axis here. The A-axis records a sampling point every 0.1° within a range of ± 7°, and the geometric errors are calculated at each sampling point. Considering n = 1, the geometric errors of the A-axis are fitted according to Eq. (32). Figure 9 shows the identified values of the geometric errors of the A-axis and their fitted curves.

Fig. 9

The identification value and fitting result of A-axis geometric errors

4.3 Verification of the Identification Accuracy of Geometric Errors

In order to intuitively evaluate the motion accuracy of the five-axis welding equipment before and after the geometric errors identification, the relative position error and the relative direction error are defined, and used to evaluate the spatial pose accuracy. Figure 10 shows a common spiral-machining trajectory of a five-axis welding equipment in the actual workspace. The trajectory maintains the same pose at any position, while the sampling points are uniformly selected within the trajectory, in order to analyze the accuracy, before and after error identification.

Fig. 10

A common spiral-machining trajectory

For any sampling point $S_{i}$, the actual measured pose matrix of the workbench coordinates system {W} relative to the actuator coordinates system {A}, obtained by the monocular camera imaging is $(\tilde{R}_{wa}^{i} ,\tilde{T}_{wa}^{i} )$, where $\tilde{R}_{wa}^{i}$ denotes the rotation matrix and $\tilde{T}_{wa}^{i}$ denotes the position vector in the pose matrix. Before geometric errors identification, the theoretical pose matrix of the workbench coordinates system {W} relative to the actuator coordinates system {A}, obtained by the ideal model is $(\overline{R}_{wa}^{i} ,\overline{T}_{wa}^{i} )$. After geometric errors identification, the theoretical pose matrix of the workbench coordinates system {W} relative to the actuator coordinates system {A}, obtained by the actual model is $(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R}_{wa}^{i} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{wa}^{i} )$.

The relative direction error, before and after geometric errors identification, are defined as $\delta \overline{R}_{wa}^{i}$ and $\delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R}_{wa}^{i}$, respectively:

$$\delta \overline{R}_{wa}^{i} = \left\| {\log ((\tilde{R}_{wa}^{i} )^{ - 1} \cdot \overline{R}_{wa}^{i} )^{v} } \right\|^{{}}$$

(34)

$$\delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R}_{wa}^{i} = \left\| {\log ((\tilde{R}_{wa}^{i} )^{ - 1} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R}_{wa}^{i} )^{v} } \right\|$$

(35)

where ${\text{v}}$ denotes the transformation of rotation matrix to rotation vector according to the relationship between Lie group and Lie algebra.

The relative position error, before and after geometric errors identification, are defined as $\delta \overline{T}$ and $\delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}$, respectively:

$$\delta \overline{T} = \left\| {\tilde{T}_{wa}^{i} - \overline{T}_{wa}^{i} } \right\|$$

(36)

$$\delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} = \left\| {\tilde{T}_{wa}^{i} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{wa}^{i} } \right\|$$

(37)

Figure 11 shows the relative position error and relative direction error at each sampling point $S_{i}$, before and after geometric errors identification. Table 6 lists the average and maximum values of the relative position error and relative direction error. As shown in Table 6, the relative position error and relative direction error of the five-axis welding equipment have been significantly reduced after identification, compared to their respective values prior to identification. It is evident that, the identification method, as provided in this article, has a significant effect on improving the accuracy of the five-axis welding equipment.

Fig. 11

Errors at each sampling point before and after geometric errors identification

Table 6 Maximum and average values of errors before and after identification

5 Conclusions

In order to deal with the problems of high cost and low efficiency of geometric errors identification of five-axis welding equipment, this paper proposes a new method for rotating axes, based on screw theory and monocular vision.

• (1) Based on the structural characteristics of the five-axis welding equipment, this paper proposes an optimized DLT algorithm for pose measurement, based on the monocular camera.

  The proposed method demonstrates its low cost and high accuracy and contributes, to a certain extent, to the automated process of effective calibration of five-axis welding equipment.

• (2) According to the screw theory and the above mentioned pose measurement system, this papers proposes a geometric errors identification method for the rotating axis of five-axis welding equipment. The sampled experimental results show that, before identification, the average relative position error of the five-axis welding equipment is 0.1472 mm and the average value of the relative direction error is 0.5427°. After identification, the average relative position error of the five-axis welding equipment, is 0.0174 mm and decreased by 88.18%, while the average value of the relative direction error, is 0.0478° and decreased by 91.19%. Therefore, the accuracy and effectiveness of the identification scheme are verified.

Appendix 1. Derivation of Screw Theory

In the case of a rotary axis, the screw coordinate ${{\varvec{\upxi}}}$ can be expressed as:

$${{\varvec{\upxi}}} = \left[ {\begin{array}{*{20}c} {\mathbf{v}} \\ {{\varvec{\upomega}}} \\ \end{array} } \right],{\mathbf{v}} = {\mathbf{p}} \times {{\varvec{\upomega}}}$$

(38)

where ${{\varvec{\upomega}}}$ is the unit direction vector of the rotation axis-line and ${\mathbf{p}}$ is a point on the rotation axis-line.

The exponent $e^{{\hat{\xi }\theta }}$ of a spinor coordinate for a rotary axis, is expressed as follows:

$$e^{{{\hat{\mathbf{\xi }}}\theta }} = \left[ {\begin{array}{*{20}c} {{\text{e}}^{{[{{\varvec{\upomega}}}]\theta }} } & {({\text{I}}_{3 \times 3} - {\text{e}}^{{[{{\varvec{\upomega}}}]\theta }} )({{\varvec{\upomega}}} \times {\mathbf{v}}) + {\mathbf{\omega \omega }}^{T} {\mathbf{v}}\theta } \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right]$$

(39)

$${\text{e}}^{{[{{\varvec{\upomega}}}]\theta }} = I_{3 \times 3} + \left[ {{\varvec{\upomega}}} \right]\sin (\theta ) + \left[ {{\varvec{\upomega}}} \right]^{2} (1 - \cos (\theta ))$$

(40)

where

$${{\varvec{\upomega}}} = \left[ {\begin{array}{*{20}c} {{{\varvec{\upomega}}}^{(x)} } & {{{\varvec{\upomega}}}^{(y)} } & {{{\varvec{\upomega}}}^{(z)} } \\ \end{array} } \right]^{T}$$

(50)

$$\left[ {{\varvec{\upomega}}} \right] = \left[ {\begin{array}{*{20}c} 0 & { - {{\varvec{\upomega}}}^{(z)} } & { - {{\varvec{\upomega}}}^{(y)} } \\ {{{\varvec{\upomega}}}^{(z)} } & 0 & { - {{\varvec{\upomega}}}^{(x)} } \\ { - {{\varvec{\upomega}}}^{(y)} } & {{{\varvec{\upomega}}}^{(x)} } & 0 \\ \end{array} } \right]$$

(51)

$\theta$ is the rotation angle of the axis.

In the case of purely rotating motion, when $\left\| {\mathbf{v}} \right\| \ne 0$, ${{\varvec{\upomega}}}$ is orthogonal to ${\mathbf{v}}$, so ${{\varvec{\upomega}}}^{T} {\mathbf{v}} = 0$;when $\left\| {\mathbf{v}} \right\| = 0$, ${{\varvec{\upomega}}}^{T} {\mathbf{v}} = 0$ is still valid. Therefore, the following relation is obtained as:

$${\mathbf{\omega \omega }}^{T} {\mathbf{v}}\theta = 0_{1 \times 3}$$

(52)

Let ${\mathbf{q}} = {{\varvec{\upomega}}} \times {\mathbf{v}}$, while the geometric meaning of ${\mathbf{q}}$ is the vertical point between the origin and the line of the rotation axis. Thus, ${\mathbf{q}}$ represents the position of the vertical point of the rotation axis, while ${{\varvec{\upomega}}}$ represents the direction of the rotation axis.

The exponent $e^{{{\hat{\mathbf{\xi }}}\theta }}$ of a rotary axis can be simplified as follows:

$$e^{{{\hat{\mathbf{\xi }}}\theta }} = \left[ {\begin{array}{*{20}c} {{\text{e}}^{{[{{\varvec{\upomega}}}]\theta }} } & {({\text{I}}_{3 \times 3} - {\text{e}}^{{[{{\varvec{\upomega}}}]\theta }} ){\mathbf{q}}} \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right]$$

(53)

Regarding the translational axis, the screw coordinate ${{\varvec{\upxi}}}$ can be expressed as:

$${{\varvec{\upxi}}} = \left[ {\begin{array}{*{20}c} {\mathbf{v}} \\ {0_{3 \times 1} } \\ \end{array} } \right]$$

(54)

where ${\mathbf{v}}$ is the unit direction vector of the translational axis.

The exponent $e^{{{\hat{\mathbf{\xi }}}\theta }}$ of a translational axis is expressed as:

$$e^{{{\hat{\mathbf{\xi }}}\theta }} = \left[ {\begin{array}{*{20}c} {{\text{I}}_{3 \times 3} } & {{\mathbf{v}}\theta } \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right]$$

(55)