1 Introduction

With the increased machining accuracy and workpiece complexity, the importance of multi-axis CNC machine tools is becoming growingly prominent in the manufacturing industry. It enables efficient machining of complex parts by adding rotating parts on conventional three-axis type [1,2,3]. The machining accuracy is the main performance index for NC machine tools, and how to further elevate it has become a research hotspot. For the multi-axis machining, the geometric error of its rotary axis has a great influence on the overall machining accuracy, which can be improved effectively through measuring and compensating the corresponding errors. However, how to quickly and accurately identify it becomes a key scientific problem that has direct impact

on the compensation effect [4,5,6,7,8,9].

At present, there are various ways to separate the linear axis’ geometric errors of multi-axis machine tool, and the measurement technology is relatively mature. Whereas, study on detecting the rotary axis errors is rarely involved as a research difficulty [10], especially for simultaneous separation of the six geometric errors. The autocollimator, laser ball bar and R-test are generally used to detect the rotary axis errors. Combining an autocollimator with a polygon, the rotary axis’s position error can be assessed, but it’s not available for other errors evaluation. When measured with the ball bar, the remaining five geometric errors except the position error can be identified via the axial double-loop test and the cone test. Zargarbashi and Mayer, designed the five measurement modes based on the ball bar’s sensitive direction to detect A-axis’s motion error [11]. However, the interaction of multi-axis linkage and multi-mode measurement are required, making the measurement process and error identification model more complicate by this method. In addition, R-test was also adopted to measure the position-dependent geometric errors of rotary axis [12]. Then the multi-axis linkage and high-precision measuring devices are all required, which limits its application to a certain extent.

Since the 1980 s, the laser tracking measurement technology has rapid growth to meet the increasing needs of motion measurement of industrial robots, detection and assembly for some large workpieces, and so on [13,14,15,16]. With fast, dynamic and portable performance, the laser tracker now has been widely applied to large-scale metrology fields such as aerospace, ships, and automobiles. Currently, it is also applied to machine tool precision detecting [17,18,19,20].

In this work, the laser tracker is applied to realize rapid and accurate detection of the rotary axis’s geometric errors for the multi-axis NC machine tool. To overcome the influence of angle measurement error introduced by using the laser tracker, the multi-station and time-sharing measurement is adopted based on GPS principle. Then a novel separation method for the rotary axis’s six geometric errors is proposed in this investigation. Taking the identification of the turntable’s geometric errors as a precedent, the direction variations of the composed vectors during the rotation of turntable is measured, and the mutual mapping relationship is then established between the variations in the vector’s direction and the geometric errors of the turntable. The separation mathematical model of rotary axis’s geometric error with this novel method is established, and the corresponding measurement algorithms containing base station calibration, measuring point determination based on the hybrid genetic algorithm, six geometric errors separation algorithm are deduced and then validated by numerical simulations. Meanwhile, the experiment concerning on detecting the rotary axis’s geometric errors is implemented to further verify the feasibility and accuracy of the introduced approach.

2 The Relationship Between the Rotary Axis’s Geometric and the Vector’s Direction Variation

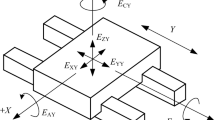
For a moving object, there exists 6 degrees of freedom. Figure 1 shows the turntable’s geometric errors rotating around z-axis. Where,\(\delta_{x} (\theta ),\;\delta_{y} (\theta ),\;\delta_{z} (\theta )\) refers to linear displacement errors, and \(\varepsilon_{x} (\theta ),\;\varepsilon_{y} (\theta ),\;\varepsilon_{z} (\theta )\) refers to angular displacement errors around x-axis, y-axis, z-axis respectively [21].

Fig. 1
figure 1

Turntable’s geometric errors rotating around z-axis

Full size image

There are three initial measuring points \(A_{0} ,\;B_{0}\) and \(C_{0}\) mounted on the turntable as shown in Fig. 2. Because of the existing turntable’s geometric errors, the direction of three vectors \(\overrightarrow {{A_{0} B_{0} }} ,\;\overrightarrow {{B_{0} C_{0} }} ,\;\overrightarrow {{C_{0} A_{0} }}\) would be varied during the rotation.

Fig. 2
figure 2

The variation of vectors’ direction during the motion of the turntable

Full size image

As the turntable rotates \(\theta\) angle around the z-axis, there exists a theoretical homogeneous transformation matrix shown in Eq. (1) [22]:

$$T_{1} = \left[ {\begin{array}{*{20}c} {\cos \theta } & { - \sin \theta } & 0 & 0 \\ {\sin \theta } & {\cos \theta } & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(1)

The error transformation matrix during the rotation is defined as [23]:

$$T_{2} = \left[ {\begin{array}{*{20}c} 1 & { - \varepsilon_{z} (\theta )} & {\varepsilon_{y} (\theta )} & {\delta_{x} (\theta )} \\ {\varepsilon_{z} (\theta )} & 1 & { - \varepsilon_{x} (\theta )} & {\delta_{y} (\theta )} \\ { - \varepsilon_{y} (\theta )} & {\varepsilon_{x} (\theta )} & 1 & {\delta_{z} (\theta )} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(2)

For the initial measuring point \(A_{0} (x_{a0} ,y_{a0} ,z_{a0} ),\) the actual coordinates of \(A_{i}^{{\prime }} (x_{ai}^{{\prime }} ,y_{ai}^{{\prime }} ,z_{ai}^{{\prime }} )\) with the turntable rotating different \(\theta_{i}\) angle can be calculated as shown in Eq. (3).

$$\left[ {\begin{array}{*{20}c} {x_{ai}^{{\prime }} } \\ {y_{ai}^{{\prime }} } \\ {z_{ai}^{{\prime }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {x_{a0} \cos \theta_{i} - x_{a0} \varepsilon_{z} (\theta_{i} )\sin \theta_{i} - y_{a0} \sin \theta_{i} - y_{a0} \varepsilon_{z} (\theta_{i} )\cos \theta_{i} + z_{a} \varepsilon_{y} (\theta_{i} ) + \delta_{x} (\theta_{i} )} \hfill \\ {x_{a0} \varepsilon_{z} (\theta_{i} )\cos \theta_{i} + x_{a0} \sin \theta_{i} - y_{a0} \varepsilon_{z} (\theta_{i} )\sin \theta_{i} + y_{a0} \cos \theta - z_{a} \varepsilon_{x} (\theta_{i} ) + \delta_{y} (\theta_{i} );} \hfill \\ { - x_{a0} \varepsilon_{y} (\theta_{i} )\cos \theta_{i} + x_{a0} \varepsilon_{x} (\theta_{i} )\sin \theta + y_{a0} \varepsilon_{y} (\theta_{i} )\sin \theta + y_{a0} \varepsilon_{x} (\theta_{i} )\sin \theta_{i} + z_{a} + \delta_{z} (\theta_{i} )} \hfill \\ \end{array} } \right]$$
(3)

Similarly, for the other initial measuring points \(B_{0}\) and \(C_{0}\), the actual coordinates of \(B_{i}^{{\prime }} (x_{bi}^{{\prime }} ,y_{bi}^{{\prime }} ,z_{bi}^{{\prime }} )\) and \(C_{i}^{{\prime }} (x_{ci}^{{\prime }} ,y_{ci}^{{\prime }} ,z_{ci}^{{\prime }} )\) with the turntable rotating \(\theta_{i}\) angle can be also calculated. Then, the directions of the vectors \(\overrightarrow {{A_{i} B_{i} }} ,\;\overrightarrow {{B_{i} C_{i} }}\) and \(\overrightarrow {{C_{i} A_{i} }}\) composed of the theoretical measuring points \(A_{i} ,\;B_{i}\) and \(C_{i}\) can be expressed respectively as:

$$\overrightarrow {{A_{i} B_{i} }} = \left[ {\begin{array}{*{20}l} {x_{b0} \cos \theta_{i} - y_{b0} \sin \theta_{i} - x_{a0} \cos \theta_{i} + y_{a} \sin \theta_{i} } \hfill \\ {x_{b0} \sin \theta + y_{b0} \cos \theta_{i} - x_{a0} \sin \theta - y_{a0} \cos \theta_{i} } \hfill \\ {z_{b0} - z_{a0} } \hfill \\ \end{array} } \right]$$
(4)
$$\overrightarrow {{B_{i} C_{i} }} = \left[ {\begin{array}{*{20}l} {x_{c0} \cos \theta_{i} - y_{c0} \sin \theta_{i} - x_{b0} \cos \theta_{i} + y_{b0} \sin \theta_{i} } \hfill \\ {x_{c0} \sin \theta + y_{c0} \cos \theta_{i} - x_{b0} \sin \theta - y_{b0} \cos \theta_{i} } \hfill \\ {z_{c0} - z_{b0} } \hfill \\ \end{array} } \right]$$
(5)
$$\overrightarrow {{C_{i} A_{i} }} = \left[ {\begin{array}{*{20}l} {x_{a0} \cos \theta_{i} - y_{a0} \sin \theta_{i} - x_{c0} \cos \theta_{i} + y_{c0} \sin \theta_{i} } \hfill \\ {x_{a0} \sin \theta + y_{a0} \cos \theta_{i} - x_{c0} \sin \theta - y_{c0} \cos \theta_{i} } \hfill \\ {z_{a0} - z_{c0} } \hfill \\ \end{array} } \right]$$
(6)

Accordingly, the directions of vectors \(\overrightarrow {{A_{i}^{{\prime }} B_{i}^{{\prime }} }} ,\;\overrightarrow {{B_{i}^{{\prime }} C_{i}^{{\prime }} }}\) and \(\overrightarrow {{C_{i}^{{\prime }} A_{i}^{{\prime }} }}\) composed of the actual measuring points \(A_{i}^{{\prime }} ,\;B_{i}^{{\prime }} ,\;C_{i}^{{\prime }}\) are determined. Then, the corresponding direction deviations of the vectors \(\overrightarrow {{A_{i} B_{i} }} ,\;\overrightarrow {{B_{i} C_{i} }} ,\;\overrightarrow {{C_{i} A_{i} }}\) during the rotation can be obtained as follows:

$$\Delta \overrightarrow {{A_{i} B_{i} }} = \left[ {\begin{array}{*{20}l} {\varepsilon_{z} (\theta_{i} )( - x_{b0} \sin \theta_{i} - y_{b0} \cos \theta_{i} + x_{a0} \sin \theta_{i} + y_{a0} \cos \theta_{i} ) + \varepsilon_{y} (\theta_{i} )(z_{b0} - z_{a0} )} \hfill \\ {\varepsilon_{z} (\theta_{i} )(x_{b0} \cos \theta_{i} - y_{b0} \sin \theta_{i} - x_{a0} \cos \theta_{i} + y_{a0} \sin \theta_{i} ) - \varepsilon_{x} (\theta_{i} )(z_{b0} - z_{a0} )} \hfill \\ {\varepsilon_{x} (\theta_{i} )(x_{b0} \sin \theta_{i} + y_{b0} \cos \theta_{i} - x_{a0} \sin \theta_{i} - y_{a0} \cos \theta_{i} ) - \varepsilon_{y} (\theta_{i} )(x_{b0} \cos \theta_{i} - y_{b0} \sin \theta_{i} - x_{a0} \cos \theta_{i} + y_{a0} \sin \theta_{i} )} \hfill \\ \end{array} } \right]$$
(7)
$$\Delta \overrightarrow {{B_{i} C_{i} }} = \left[ {\begin{array}{*{20}l} {\varepsilon_{z} (\theta_{i} )( - x_{c0} \sin \theta_{i} - y_{c0} \cos \theta_{i} + x_{b0} \sin \theta_{i} + y_{b0} \cos \theta_{i} ) + \varepsilon_{y} (\theta_{i} )(z_{c0} - z_{b0} )} \hfill \\ {\varepsilon_{z} (\theta_{i} )(x_{c0} \cos \theta_{i} - y_{c0} \sin \theta_{i} - x_{b0} \cos \theta_{i} + y_{b0} \sin \theta_{i} ) - \varepsilon_{x} (\theta_{i} )(z_{c0} - z_{b0} )} \hfill \\ {\varepsilon_{x} (\theta_{i} )(x_{c0} \sin \theta_{i} + y_{c0} \cos \theta_{i} - x_{b0} \sin \theta_{i} - y_{b0} \cos \theta_{i} ) - \varepsilon_{y} (\theta_{i} )(x_{c0} \cos \theta_{i} - y_{c0} \sin \theta_{i} - x_{b0} \cos \theta_{i} + y_{b0} \sin \theta_{i} )} \hfill \\ \end{array} } \right]$$
(8)
$$\Delta \overrightarrow {{C_{i} A_{i} }} = \left[ {\begin{array}{*{20}l} {\varepsilon_{z} (\theta_{i} )( - x_{a0} \sin \theta_{i} - y_{a0} \cos \theta_{i} + x_{c0} \sin \theta_{i} + y_{c0} \cos \theta_{i} ) + \varepsilon_{y} (\theta_{i} )(z_{a0} - z_{c0} )} \hfill \\ {\varepsilon_{z} (\theta_{i} )(x_{a0} \cos \theta_{i} - y_{a0} \sin \theta_{i} - x_{c0} \cos \theta_{i} + y_{c0} \sin \theta_{i} ) - \varepsilon_{x} (\theta_{i} )(z_{a0} - z_{c0} )} \hfill \\ {\varepsilon_{x} (\theta_{i} )(x_{a0} \sin \theta_{i} + y_{a0} \cos \theta_{i} - x_{c0} \sin \theta_{i} - y_{c0} \cos \theta_{i} ) - \varepsilon_{y} (\theta_{i} )(x_{a0} \cos \theta_{i} - y_{a0} \sin \theta_{i} - x_{c0} \cos \theta_{i} + y_{c0} \sin \theta_{i} )} \hfill \\ \end{array} } \right]$$
(9)

From Eq. (7) to (9), it can be obviously seen that the direction variations of \(\overrightarrow {{A_{i} B_{i} }} ,\;\overrightarrow {{B_{i} C_{i} }} ,\;\overrightarrow {{C_{i} A_{i} }}\) during the rotation are merely related to angular displacement errors rather than linear displacement errors. According to this characteristic, three angular displacement errors \(\varepsilon_{x} (\theta ),\;\varepsilon_{y} (\theta )\) and \(\varepsilon_{z} (\theta )\) can be firstly identified on the basis of the direction variation of a series of vectors, and three line displacement errors \(\delta_{x} (\theta ),\;\delta_{y} (\theta )\) and \(\delta_{z} (\theta )\) would be separated at last.

3 Measurement Principle and Algorithm

3.1 Measurement Principle

The coordinates of target point can be measured with the laser tracking system based on spherical coordinate, and the measuring accuracy is mostly affected by the angle measurement error [24, 25]. In order to overcome the effect of introduced angle measurement error, the multi-station and time-sharing method is applied. The target point can therefore be determined successively by collecting corresponding ranging data of laser tracker at different base stations based on the GPS principle. The direction of a series of vectors composed of adjacent measuring points during the rotation of turntable will be measured, then the turntable’s geometric errors can be separated respectively. In the measurement, quick and accurate calibration of each base station is critical, and then a precision NC turntable is designed to ensure it. Its axial and radial runout are less than 0.3 μm, meanwhile its position accuracy is ± 2″ with repeatability of ± 1″. The cat eye is set on the designed turntable and rotates accurately with different angles driven by the turntable. By using laser tracker to detect the rotary motion of the precision NC turntable, the accurate position of each base station will be calibrated and obtained. The geometric error measurement principle of the turntable by combining laser tracker with the designed precision turntable is shown in Figs. 3, and 4 gives the corresponding flowchart with this proposed method.

Fig. 3
figure 3

Geometric error measurement principle of the turntable by combining laser tracker with the designed turntable

Full size image
Fig. 4
figure 4

Measurement and identification process of turntable’s geometric error

Full size image

3.2 Measurement Algorithm

With this approach, the base station calibration and measurement point determination algorithms are mainly involved and studied [26, 27].

3.2.1 Base Station Calibration

According to the introduced measurement principle in Sect. 3.1, the corresponding calibration model of base station can be constructed as shown in Fig. 5. Where, \(Q_{1} ,\;Q_{2} \ldots Q_{n}\) are defined as the measuring points on the turntable, and P represents the position of base station.

Fig. 5
figure 5

Calibration mode of the base station

Full size image

Currently, the measurement principles of common laser trackers can be divided into two categories. For the laser trackers such as Leica, Faro and API, these instruments usually have the coordinate measurement function, and the absolute distance between the target point and the center of tracking mirror can be measured. For these laser trackers, the calibration equation of base station \(P_{1} (x_{p1} ,y_{p1} ,z_{p1} )\) can be established as follows:

$$\left\{ {\begin{array}{*{20}c} {\sqrt {(x_{p1} - R\cos \theta_{1} )^{2} + (y_{p1} - R\sin \theta_{1} )^{2} + z_{p1}^{2} } = l_{11} } \\ {\sqrt {(x_{p1} - R\cos \theta_{2} )^{2} + (y_{p1} - R\sin \theta_{2} )^{2} + z_{p1}^{2} } = l_{12} } \\ \vdots \\ {\sqrt {(x_{p1} - R\cos \theta_{i} )^{2} + (y_{p1} - R\sin \theta_{i} )^{2} + z_{p1}^{2} } = l_{1i} } \\ \end{array} } \right.$$
(10)

where \(R\) is defined as the distance between the center of designed turntable and cat eye, and \(\theta_{i}\) represents different rotating angles. \(l_{1i}\) represents the corresponding ranging data at each measuring point.

For the Etalon laser tracker, it is not available for angle measurement as well as the initial distance measurement between the target point and the center of tracking mirror. Thus, this distance value needs to be calibrated in the measurement. The corresponding calibration equation of base station \(P_{1} (x_{p1} ,y_{p1} ,z_{p1} )\) by Etalon laser tracker can also be attained:

$$\left\{ {\begin{array}{*{20}c} {\sqrt {(x_{p1} - R\cos \theta_{1} )^{2} + (y_{p1} - R\sin \theta_{1} )^{2} + z_{p1}^{2} } = L_{1} + \Delta l_{11} } \\ {\sqrt {(x_{p1} - R\cos \theta_{2} )^{2} + (y_{p1} - R\sin \theta_{2} )^{2} + z_{p1}^{2} } = L_{1} + \Delta l_{12} } \\ \vdots \\ {\sqrt {(x_{p1} - R\cos \theta_{i} )^{2} + (y_{p1} - R\sin \theta_{i} )^{2} + z_{p1}^{2} } = L_{1} + \Delta l_{1i} } \\ \end{array} } \right.$$
(11)

where \(L_{1}\) is the distance between the center of tracking mirror and initial measuring point, and \(\Delta l_{1i}\) is defined as the variation of the relative distance at different measuring points.

Equations (10) and (11) are nonlinear redundant equations, and how to solve these equations is a critical issue [28].

Genetic algorithm is a smart optimization algorithm to simulate the biological evolution [29, 30]. It is an iterative and adaptive probabilistic search method based on the principle of natural selection and genetic mechanism, which has been widely adopted in the optimization field [31]. However, premature convergence is prone to occur in the process of genetic manipulation, resulting in poor local search ability for genetic algorithm. When solving a large and complex problem, only local optimal solution could be often obtained [32].

In view of good local searching ability for the simplex method, the hybrid genetic algorithm combining simplex method with traditional genetic algorithm is adopted to calibrate the positions of base stations and determine the coordinates of each measuring point [33]. Then the good local and global searching ability can both be preserved for the new hybrid genetic algorithm, which can effectively overcome the deficiency of traditional genetic algorithm and further improve the calculation accuracy.

3.2.2 Measuring Point Determination

The rotation of the turntable can be measured after the base station calibration. In the same way as base station calibration, the equations for measuring point determination can also be established, and the coordinate of each measuring point can be obtained with the hybrid genetic algorithm mentioned above. Finally, the directions of a series of vectors composed of the adjacent measuring points can be easily determined.

4 Geometric Error Identification of the Turntable

The geometric error identification of the turntable consists of two parts: (1) angular displacement error identification; (2) linear displacement error identification.

4.1 Angular Displacement Error Identification

It is assumed that there exist three initial measuring points \(A_{0} (x_{a0} ,y_{a0} ,z_{a0} ),\;B_{0} (x_{b0} ,y_{b0} ,z_{b0} )\) and \(C_{0} (x_{c0} ,y_{c0} ,z_{c0} )\) at the initial position of the turntable as shown in Fig. 2. With different rotating angles of the turntable, the theoretical and actual coordinates of a series of measuring points are assumed as: \(A_{i} (x_{ai} ,y_{ai} ,z_{ai} ),\;B_{i} (x_{bi} ,y_{bi} ,z_{bi} ),\;C_{i} (x_{ci} ,y_{ci} ,z_{ci} ),\;A_{i}^{{\prime }} (x_{ai}^{{\prime }} ,y_{ai}^{{\prime }} ,z_{ai}^{{\prime }} ),\;B_{i}^{{\prime }} (x_{bi}^{{\prime }} ,y_{bi}^{{\prime }} ,z_{bi}^{{\prime }} )\) and \(C_{i}^{{\prime }} (x_{ci}^{{\prime }} ,y_{ci}^{{\prime }} ,z_{ci}^{{\prime }} )\) respectively.

At the initial position, the direction of vectors \(\overrightarrow {AB} ,\;\overrightarrow {BC}\) and \(\overrightarrow {CA}\) are:

$$\begin{array}{*{20}l} {\overrightarrow {AB} = (x_{b0} - x_{a0} ,y_{b0} - y_{a0} ,z_{b0} - z_{a0} ),} \hfill \\ {\overrightarrow {BC} = (x_{c0} - x_{b0} ,y_{c0} - y_{b0} ,z_{c0} - z_{b0} ),} \hfill \\ {\overrightarrow {CA} = (x_{a0} - x_{c0} ,y_{a0} - y_{c0} ,z_{a0} - z_{c0} ).} \hfill \\ \end{array}$$

During the rotation of turntable, the direction of actual vectors \(\overrightarrow {{A_{i}^{{\prime }} B_{i}^{{\prime }} }} ,\;\overrightarrow {{B_{i}^{{\prime }} C_{i}^{{\prime }} }}\), and \(\overrightarrow {{C_{i}^{'} A_{i}^{'} }}\) are:

$$\begin{aligned} & \overrightarrow {{A_{i}^{{\prime }} B_{i}^{{\prime }} }} = (x_{bi}^{{\prime }} - x_{ai}^{{\prime }} ,y_{bi}^{{\prime }} - y_{ai}^{{\prime }} ,z_{bi}^{{\prime }} - z_{ai}^{{\prime }} ), \\ & \overrightarrow {{B_{i}^{'} C_{i}^{'} }} = (x_{ci}^{{\prime }} - x_{bi}^{{\prime }} ,y_{ci}^{{\prime }} - y_{bi}^{{\prime }} ,z_{ci}^{{\prime }} - z_{bi}^{{\prime }} ), \\ & \overrightarrow {{C_{i}^{'} A_{i}^{'} }} = (x_{ai}^{{\prime }} - x_{ci}^{{\prime }} ,y_{ai}^{{\prime }} - y_{ci}^{{\prime }} ,z_{ai}^{{\prime }} - z_{ci}^{{\prime }} ). \\ \end{aligned}$$

According to the motion transformation matrix of turntable, the following relationship between \(\overrightarrow {AB}\) and \(\overrightarrow {{A_{i}^{{\prime }} B_{i}^{{\prime }} }}\) should exist.

$$\left[ {\begin{array}{*{20}c} {x_{bi}^{'} - x_{ai}^{'} } \\ {y_{bi}^{'} - y_{ai}^{'} } \\ {z_{bi}^{'} - z_{ai}^{'} } \\ 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} 1 \hfill & { - \varepsilon_{z} (\theta_{i} )} \hfill & {\varepsilon_{y} (\theta_{i} )} \hfill & 0 \hfill \\ {\varepsilon_{z} (\theta_{i} )} \hfill & 1 \hfill & { - \varepsilon_{x} (\theta_{i} )} \hfill & 0 \hfill \\ { - \varepsilon_{y} (\theta_{i} )} \hfill & {\varepsilon_{x} (\theta_{i} )} \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\cos \theta_{i} } \hfill & { - \sin \theta_{i} } \hfill & 0 \hfill & 0 \hfill \\ {\sin \theta_{i} } \hfill & {\cos \theta_{i} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{b0} - x{}_{a0}} \\ {y_{b0} - y{}_{a0}} \\ {z_{b0} - z{}_{a0}} \\ 1 \\ \end{array} } \right]$$
(12)

Then, it can be deduced that:

$$\left\{ {\begin{array}{*{20}l} {x_{bi}^{{\prime }} - x_{ai}^{{\prime }} = \varepsilon_{y} (\theta_{i} )(z_{b0} - z_{a0} ) + \varepsilon_{z} (\theta_{i} )(x_{a0} \sin \theta_{i} - x_{b0} \sin \theta_{i} + y_{a0} \cos \theta_{i} - y_{b0} \cos \theta_{i} ) + x_{b0} \cos \theta_{i} - x_{a0} \cos \theta_{i} - y_{b0} \sin \theta_{i} + y_{a0} \sin \theta } \hfill \\ {y_{bi}^{{\prime }} - y_{ai}^{{\prime }} = \varepsilon_{x} (\theta_{i} )(z_{a0} - z_{b0} ) + \varepsilon_{z} (\theta_{i} )(x_{b0} \cos \theta_{i} - x_{a0} \cos \theta_{i} - y_{b0} \sin \theta_{i} + y_{a0} \sin \theta_{i} ) + x_{b0} \sin \theta_{i} + y_{b0} \cos \theta_{i} - x_{a0} \sin \theta_{i} - y_{a0} \cos \theta } \hfill \\ {z_{bi}^{{\prime }} - z_{ai}^{{\prime }} = \varepsilon_{x} (\theta_{i} )(x_{b0} \sin \theta_{i} - x_{ao} \sin \theta_{i} + y_{b0} \cos \theta_{i} - y_{a0} \cos \theta_{i} ) - \varepsilon_{y} (\theta_{i} )(x_{b0} \cos \theta_{i} - x_{a0} \cos \theta_{i} - y_{b0} \sin \theta_{i} + y_{a0} \sin \theta_{i} ) + z_{b0} - z_{a0} } \hfill \\ \end{array} } \right.$$
(13)

In the same way, the relationship between the vectors \(\overrightarrow {BC}\) and \(\overrightarrow {{B_{i}^{\prime } C_{i}^{\prime } }}\), as well as \(\overrightarrow {CA}\) and \(\overrightarrow {{C_{i}^{\prime } A_{i}^{\prime } }}\) can also be established, then the equation concerning angular displacement errors \(\varepsilon_{x} (\theta ),\;\varepsilon_{y} (\theta )\) and \(\varepsilon_{z} (\theta )\) will be obtained. By solving this equation, three angular displacement errors during the rotation of turntable can be separated.

4.2 Linear Displacement Error Identification

During the rotation of turntable, the volumetric position error of each measuring point consists of two parts: one part is caused by the line displacement error, and the other part is caused by the angular displacement error. The corresponding position deviation induced by the identified angular displacement errors can be calculated at each measuring point. For the measuring point \(A_{i}\), it is assumed that the position deviations in the three directions caused by the angular displacement errors are \(t_{axi}\), \(t_{ayi}\) and \(t_{azi}\) respectively. Then the equality relationship on linear displacements errors exists:

$$\left\{ {\begin{array}{*{20}c} {x_{ai}^{\prime } - x_{ai} = \delta_{x} (\theta_{i} ) + t_{axi} } \\ {y_{ai}^{\prime } - y_{ai} = \delta_{y} (\theta_{i} ) + t_{ayi} } \\ {z_{ai}^{\prime } - z_{ai} = \delta_{z} (\theta_{i} ) + t_{azi} } \\ \end{array} } \right.$$
(14)

Similarly, the equations concerning the point \(B_{i}\) and \(C_{i}\) can be also established, then we can obtain the following equations:

$$\left\{ {\begin{array}{*{20}l} {x_{ai}^{\prime } - x_{ai} = \delta_{x} (\theta_{i} ) + t_{axi} } \hfill \\ {y_{ai}^{\prime } - y_{ai} = \delta_{y} (\theta_{i} ) + t_{ayi} } \hfill \\ {z_{ai}^{\prime } - z_{ai} = \delta_{z} (\theta_{i} ) + t_{azi} } \hfill \\ {x_{bi}^{\prime } - x_{bi} = \delta_{x} (\theta_{i} ) + t_{bxi} } \hfill \\ {y_{bi}^{\prime } - y_{bi} = \delta_{y} (\theta_{i} ) + t_{byi} } \hfill \\ {z_{bi}^{\prime } - z_{bi} = \delta_{z} (\theta_{i} ) + t_{bzi} } \hfill \\ {x_{ci}^{\prime } - x_{ci} = \delta_{x} (\theta_{i} ) + t_{cxi} } \hfill \\ {y_{ci}^{\prime } - y_{ci} = \delta_{y} (\theta_{i} ) + t_{cyi} } \hfill \\ {z_{ci}^{\prime } - z_{ci} = \delta_{z} (\theta_{i} ) + t_{czi} } \hfill \\ \end{array} } \right.$$
(15)

Three linear displacement errors \(\delta_{x} (\theta ),\;\delta_{y} (\theta )\) and \(\delta_{z} (\theta )\) can be separated by solving Eq. (15). In the above process, the identifications of angular and linear displacement errors of the rotary axis are decoupled, which is conducive to reduce the complexity of identification model and facilitate the accurate separation for each error.

5 Simulation for Measurement and Geometric Error Identification Algorithms of Rotary Axis

In order to validate the derived algorithms, the simulations regarding the measurement and geometric error identification algorithms are performed as follows.

5.1 Simulation for Measurement Algorithm of Rotary Axis

There exists certain similarity between the involved base station calibration and measuring point determination algorithms. Meanwhile, the measurement precision of this method largely depends on the calibration accuracy of base station. Therefore, the simulations and analysis on the base station calibration are typically given. Firstly, the positions of each base station are assumed as: \(P_{1} (800,600,1200),\;P_{2} (800,1800,1200),\;P_{3} ( - 1200,600,2200),\;P_{4} ( - 1200,1800,2200).\) The distance between the center of turntable and cat eye is 200 mm, and a measuring point is set for rotating each \(\theta { = }20^{ \circ }\) of the turntable. The following simulations are conducted under two conditions: considering the rotation error of the designed turntable or not.

  1. (1)

    Regardless of the turntable rotation error

The turntable can accurately rotate different angles according to the command without considering its motion error. The genetic algorithm is adopted to calibrate the base station. The main parameters involved in the calculation are: population size 150, deviations between initial parameters range and their true values ± 0.1 mm, crossover rate 0.6 and mutation rate 0.02 etc. Table 1 shows the calibration deviations of base station \(P_{1}\) with the genetic algorithm for three calculations.

Table 1 Calibration deviations of P1 with the genetic algorithm mm
Full size table

As shown in Table 1, large calibration deviations of base stations and the poor repeatability of calibration results for different times are presented. This can be attribute to random procedure used in the traditional genetic algorithm for searching the optimal solution. Meanwhile, prematurity phenomenon and poor local searching ability are both inevitable deficiencies for this algorithm.

To overcome the deficiencies, the constituted hybrid genetic algorithm mentioned above is adopted. Figure 6 illustrates the distribution of best fitness and mean fitness in the evolution, and the corresponding calibration deviations with this algorithm for three calculations are given in Table 2.

Fig. 6
figure 6

Distribution of best fitness and mean fitness in the evolution

Full size image
Table 2 Calibration deviations of \(P_{1}\) with the hybrid genetic algorithm mm
Full size table

It can be seen from Table 2 that, the calibration accuracy and repeatability are greatly enhanced compared with the traditional genetic algorithm, which is effective for multiple calculations. Taking base station \(P_{1}\) as an example, Table 3 shows the calibration uncertainty of \(P_{1}\) with genetic algorithm and hybrid genetic algorithm on the basis of Monte Carlo method respectively.

Table 3 Calibration uncertainty of \(P_{1}\) with genetic algorithm and hybrid genetic algorithm mm
Full size table

From Table 3, the calibration uncertainty of base station is smaller with the hybrid genetic algorithm, and the stability of the solution is good. Similar conclusions can be also obtained at other base stations. Accordingly, the calibration deviations of four base stations with this algorithm can be seen in Table 4.

Table 4 Calibration deviations of four base stations by the hybrid genetic algorithm mm
Full size table

Regardless of the rotation error of the designed turntable, accurate position calibration for each base station can be realized with small deviations by this hybrid algorithm.

In the base station calibration, the selected initial ranges of calibration parameters have certain effect on the calculation results. Here, the deviations between initial ranges of parameters and their true values are assumed as ± 0.1 mm, ± 10 mm, ± 100 mm and ± 1000 mm. Here, ± 0.1 mm, ± 10 mm, ± 100 mm and ± 1000 mm are defined as initial range 1, 2, 3, 4 respectively. In view of these different initial ranges, the corresponding simulations are conduced. Taking the calibration of base station \(P_{1}\) as an instance,the calibration deviations by the hybrid genetic algorithm with different initial ranges for the calibration parameters are shown in Table 5.

Table 5 Calibration deviations of P1 by the hybrid genetic algorithm with different initial ranges mm
Full size table

Less fluctuation in calibration results for different initial values of calibration parameter indicates the hybrid genetic algorithm is insensitive to the selected initial ranges of calibration parameters and has a certain robustness.

  1. (2)

    Considering the turntable rotation error

There exist certain deviations between the theoretical and actual rotation angles of the designed turntable. For ease of analysis, the position error of the designed turntable is supposed to obey random normal distribution within [0, 3′’] and [0, 5′’] respectively. In addition, the ranging error of laser tracker is also considered to obey random normal distribution within [0, 1 μm]. Table 6 gives the calibration deviations of four base stations under the first condition.

Table 6 Calibration deviations of four base stations under the first condition mm
Full size table

In Table 6, the calibration deviations are small under the condition, suggesting the base station calibration using the hybrid genetic algorithm is feasible and effective. Further simulations and analysis show the calibration accuracy gradually increases with increased position error of the turntable.

5.2 Simulation for Geometric Error Identification Algorithm of Rotary Axis

Taking the geometric error identification of rotary axis with rotating 30° as an example, the validation of the derived error identification algorithm is carried out. Firstly, each geometric error of the turntable with rotating 30° is assumed as: \(\delta_{x} (\theta ) = 0.030\) mm, \(\delta_{y} (\theta ) = 0.020\) mm, \(\delta_{z} (\theta ) = 0.010\) mm, \(\varepsilon_{x} (\theta ) = 2.0 \times 10^{ - 5}\) rad, \(\varepsilon_{y} (\theta ) = 3.5 \times 10^{ - 5}\) rad and \(\varepsilon_{z} (\theta ) = 4.5 \times 10^{ - 5}\) rad respectively. The simulations are then conducted under two cases: without or with considering the impact of random error during the rotation of turntable.

Under the first case, six geometric errors of turntable can be exactly separated. The maximum identification deviation is \(1.0 \times 10^{ - 14}\) mm for \(\delta_{y} (\theta )\).

Under the second case, a random error is introduced to each measuring point’s theoretical motion error. To simplify calculations, the random error is supposed to obey random normal distribution within [0, 3 μm] and [0, 5 μm]. Here, [0, 3 μm], [0, 5 μm] represents case 1 and 2 respectively. The identification deviations of six geometric errors under the two cases are listed in Table 7.

Table 7 Identification deviations of six geometric errors under different random error distributions
Full size table

From Table 7, the corresponding identification deviations of six geometric errors are relatively small for different random error distributions, revealing the feasibility of the derived identification algorithm.

6 Experimental Verification

The identification of geometric errors of the turntable with laser tracker is implemented by measuring vectors’ direction variations during the rotation as seen in Fig. 7.

Fig. 7
figure 7

Geometric error identification of the turntable

Full size image

The rotation of the turntable is successively measured by tracking at four different base stations. At each base station, the turntable rotates and stops at each interval of 10°, and the corresponding distance data of laser tracker is recorded every 120° of the turntable rotation. Entire measurement takes about 3 h with high efficiency. Each geometric error of rotary axis can therefore be separated through the proposed measurement algorithm and error identification algorithm.

To further validate the feasibility of the new approach, taking the identification of the position error as a case, the identification results by the proposed approach are compared to that by laser interferometer cooperating with Renishaw rotary measuring system RX10 as shown in Fig. 8.

Fig. 8
figure 8

Comparision of two mesurment methods

Full size image

From Fig. 8, it can be seen that the variation trend of the turntable’s position error curves measured by two methods are basically consistent, and the corresponding deviations at different measuring points are small. So the proposed method is feasible and effective.

Adopting the proposed method, the measurement uncertainty will be affected by time-sharing measurement, ranging error of laser tracker, designed turntable’s precision and repeatability, surrounding environment etc. In the measurement, the motion trajectory of turntable is measured by laser tracker at different base stations. Due to adopting the time-sharing measurement principle, the motion trajectories of the turntable measured at different base stations are different. In order to reduce the impact of time-sharing measurement, the motion of turntable will be measured for multiple times at each base station, then this error can be significantly reduced. To reduce the influence of the ranging error of laser tracker, the laser tracker can be set as close as possible to the tested turntable on the premise of keeping the measuring optical path uninterrupted. Meanwhile, the environmental compensation for temperature, pressure and humidity will ensure the ranging accuracy of laser tracker. In addition, the position precision and repeatability of the designed turntable have certain influence on the base station calibration. The designed turntable should have a certain precision requirement to ensure the measurement precision and repeatability. This proposed method can achieve the rapid measurement of the turntable’s error. Owing to the short measuring time, the measurement environment changes little, which has smaller effect on the measurement results.

7 Conclusions

  1. (1)

    A novel identification method with laser tracker is proposed to realize rapid and accurate separation of geometric errors of the rotary axis of multi-axis machine tool.

  2. (2)

    The identification mathematical model of rotary axis’s geometric error is established on the basis of measuring the direction variations of vectors. The measurement algorithms containing the base station calibration, the measuring point determination based on the hybrid genetic algorithm, as well as six geometric errors separation algorithm involving angular errors and displacement errors are deduced respectively and validated by simulations.

  3. (3)

    The geometric error measurement of the turntable by this method is completed in about 3 h, and then six geometric errors can be identified efficiently. Meanwhile, identifying the turntable’s position error as a case, the identification results by the proposed method are compared to that by laser interferometer cooperating with Renishaw rotary measuring system, which further confirms the feasibility of the introduced new approach.