1 Introduction

Modeling of flow curves during hot deformation is of crucial importance due to the applications in the simulation of hot deformation processes such as hot rolling. Constitutive modeling of metals and alloys during hot deformations can be categorized into three types; phenomenological models, physical-based models, and the models based on artificial neural networks (ANN) [1]. Phenomenological models have attracted great attention among other methods; they describe the relationship between flow stress and deformation parameters, namely, temperature, strain and strain rate.

Dynamic recrystallization (DRX) is one of the most important phenomena in hot deformation processes. DRX is a softening mechanism occurring during deformation with the driving force originating from the elimination of the stored energy of dislocations. It is the phenomenon observed most often in relatively low stacking sault energy (SFE) materials; it is mainly developed with nucleation and growth [2,3,4]. It modifies the microstructure greatly; hence, modeling of DRX is decisive for the prediction of microstructures and properties during and after deformation.

It is a common practice to interrelate the DRX fraction (XDRX) with a measure of softening represented below:

$$X_{DRX} = \frac{{\sigma_{WH} - \sigma }}{{\sigma_{s} - \sigma_{ss} }}\quad \left( {{\text{for}}\,\varepsilon > \varepsilon_{c} } \right),$$
(1)

where according to Fig. 1, σ is the experimental flow stress of the curve experiencing DRX (the DRX curve), and σWH is the flow stress of an imaginary curve (the DRV curve) obtained by considering dislocation generation and dynamic recovery (DRV) as the only hardening and softening mechanisms during deformation, respectively. Further, σss, which is known as the steady state stress, and σs, as the saturation stress, are the corresponding asymptotes of the DRX and DRV curves (Fig. 1). Equation (1) can be defined for strains higher than the critical strain (εc) of DRX initiation.

Fig. 1
figure 1

Schematic illustration of the DRV and DRX curves with characteristic stresses and strains

Full size image

There are different approaches for the determination of DRX kinetics, which is often a variation on the Kolmogorov–Johnson–Mehl–Avrami (KJMA) relationship. Most of these Models, such as those of Yada [5], Laasraoui and Jonas [6], Kim and Yoo [7], and Kim et al. [8], can be written in a general form as:

$$X_{DRX} = 1 - \exp \left( { - k\left[ { f\left( \varepsilon \right) } \right]^{p} } \right)\quad \left( {{\text{for}}\,\varepsilon > \varepsilon_{c} } \right),$$
(2)

where k and p are constants and f (ε) is a function of strain.

Development of low-carbon, copper-strengthened steels is of crucial importance for naval ships construction since these steels combine several attractive features such as high strength, good toughness, weldability and corrosion resistance. BA-160 steel is a newly designed steel in this class [9], showing the high strength of 160 ksi (~ 1100 MPa), while possessing the high Charpy v-notch impact toughness of 108 J at—40 °C [10]. It seems that the basis for the design of the novel BA-160 steel is the HSLA-100 steel, as compared with the key alloying elements. However, despite numerous investigations on the thermomechanical parameters and hot deformation characteristics of HSLA-100, there is not yet a similar systematic study on the BA-160 steel. Further understanding hardening and softening mechanisms as well as kinetics of DRX is of great importance in order to optimize the processing routes. Therefore, this work has been devoted to research on the hot deformation behavior of BA-160 steel using hot compression tests.

2 Experimental Procedure

2.1 Sample Preparation and Testing

5 kg of BA-160 steel was prepared in a vacuum induction melting furnace with the resulting chemical composition of Fe-0.04C-6.67Ni-3.6Cu-2Cr-0.65Mo-0.1V (in wt%). Homogenizing of the as-cast steel was performed at 1200 °C for 16 h; then, the ingot was forged into a plate with 17 mm thickness.

The plate thickness was reduced to 15 mm using a surface grinder to improve the flatness and parallelism of the two surfaces; afterwards, cylindrical samples were cut from the plate with the diameter and height of 10 and 15 mm, respectively. Concentric grooves and a small 45° bevel machined from both ends of the samples were intended for better lubrication, as well as developing the homogeneous deformation region. Glass powder was implemented as a lubricant material in order to minimize the friction between the anvils and the sample surface.

A fully computerized Zwick/Roell 250 testing machine was used to perform hot compression tests at temperatures ranging from 850 to 1100 °C with the steps of 50 °C, and under constant strain rates of 0.001, 0.01, 0.1 and 1 s−1. The samples were heated with a heating rate of 5 °C s−1 to a temperature of 1200 °C for a soaking duration of 10 min; they were cooled at a rate of 1 °C s−1 to the deformation temperature and held 3 min at that temperature before the beginning of straining for further thermal homogenization. Microstructural characterization of the samples was done through standard procedures using a Nikon Epiphot-300 optical microscope, a Tescan Mira 3-XMU field emission gun-scanning electron microscope (FEG-SEM) operating at 15 kV, and a JEOL 3200FS-HR field emission transmission electron microscope (TEM) working at 300 kV.

2.2 Corrections for Friction and Deformation Heating

Friction is an inevitable phenomenon during hot compression tests. It arises as an additional stress counteracting the straining process. The relation that obtains the applied average stress (σa) for an interfacial friction factor m is as follows [11]:

$$\sigma_{a} = \sigma_{0} \left( { 1 + 2\frac{m}{3\sqrt 3 }\frac{r}{h} } \right)$$
(3)

here σ0 is the flow stress, and r and h are the instantaneous radius and height of the sample during test, respectively. Evans and Scharning [12] used a modification of Eq. (3) for deformation at constant strain rates shown below:

$$\sigma_{a} = \sigma_{0} \left( { 1 + 2\frac{m}{3\sqrt 3 }\frac{{r_{0} }}{{h_{0} }}\exp \left( { \frac{3\varepsilon }{2} } \right) } \right) ,$$
(4)

where in Eq. (4), instantaneous dimensions introduced as r and h in Eq. (3) have been replaced with the initial dimensions, r0 and h0, and the true strain, ε. The calculation method of friction coefficients for each sample was adopted from the work of Ebrahimi and Najafizadeh [13].

Another source of error in the calculations of deformation data arises from deformation heating in the material. It is well accepted that less than 5% of the energy input to the material is consumed for deformation and the related metallurgical processes. Roughly, 95% of the energy is converted into heat during deformation. If adiabatic condition prevails, all of the heat is spent for the temperature rise of the material. Otherwise, there would be an adiabaticity factor (\(\eta = \frac{{\Delta T_{actual} }}{{\Delta T_{adiabatic} }}\)) that determines the ratio of the temperature rise in the actual conditions (ΔTactual) to the full adiabatic state (ΔTadiabatic). Therefore, the increase in sample temperature during deformation can be evaluated via Eq. (5):

$$\Delta T_{actual} = 0.95\eta /\rho C_{p } \smallint \sigma_{a} d\varepsilon$$
(5)

here ρ is the density and Cp is the specific heat of the material at constant pressure. The temperature rise equivalently decreases the strength of the metal by an amount of Δσ, which should be re-added to the flow stress in order to merely obtain the resistance of the metal against deformation. The amount of Δσ can be found using the relation \(\Delta \sigma = \Delta T_{actual} (d\sigma /dT)_{{\varepsilon ,\dot{\varepsilon }}}\) [14].

Some researchers have suggested that η in Eq. (5) is only a linear function of the logarithm of the strain rate [15,16,17], while it can be discerned that because of the change in sample dimensions during deformation and the dependence of the heat flux on the sample geometry, η is also a function of strain. Goetz and Semiatin [18] have adopted a different approach which includes instantaneous dimensional conditions. According to their work, η can be expressed as

$$\eta = \left( { 1 + \frac{H\Delta \varepsilon }{{x_{s} \rho C_{p} \dot{\varepsilon }}} } \right)^{ - 1} ,$$
(6)

where

$$H = \left( { \frac{{x_{s} }}{{k_{s} }} + \frac{1}{HTC} + \frac{{x_{d} }}{{k_{d} }} } \right)^{ - 1}$$
(7)
$$x_{s} = x_{0} { \exp }\left( { - \dot{\varepsilon }t} \right)$$
(8)

In Eqs. 6–8, H is an overall heat transfer coefficient that determines the heat flux from the sample to the environment, Δε is the strain corresponding to the elapsed time, xs is one-half of the instantaneous sample height, \(\dot{\varepsilon }\) is the strain rate, ks is the sample thermal conductivity, HTC is the heat-transfer coefficient between the sample and the die, xd is the length of constant temperature region in the die, as measured from the die surface, kd is the die thermal conductivity, x0 is the half of the initial sample height, and t is the elapsed time.

By using the above corrections, all of the hot compression data were re-calculated. Figure 2 shows the flow curve of the BA-160 steel at 1000 °C, as subjected to strain rates of 1 and 0.001 s−1, in comparison with their corrected curves.

Fig. 2
figure 2

Stress-strain curves obtained at 1000 °C and the strain rates of 1 and 0.001 s−1 in comparison with their friction modified (F-modified) and friction & deformation heating modified (F&DH-modified) curves

Full size image

2.3 Curve Fitting

In DRX curves, such as the schematic representation of Fig. 1, the onset of DRX is located at a critical strain before the strain of peak. Ryan and McQueen [19], as well as Poliak and Jonas [20,21,22,23], have shown that the critical strain corresponding to the onset of DRX could be obtained from the inflection in the plots of the strain hardening rate (\(\theta = (\partial \sigma /\partial \varepsilon )_{{\dot{\varepsilon }, T}}\)) versus true stress (σ). Determination of the inflections requires determining the double differentiation of θ with respect to σ (d2θ/dσ2) and finding zeroes of the second derivative. However, differentiation from the experimental data which include considerable noise may yield useless results. One way to tackle this problem is data smoothing using curve fitting [22, 24, 25], in which a suitable curve of \(\sigma = y\left( \varepsilon \right)\) could be fitted through the corrected experimental plot. In the present investigation, the inflection points were calculated using the fitted function y. Thus, the following equation was obtained (see the “Appendix” for derivation):

$$\left( {\frac{{\partial^{2} \theta }}{{\partial \sigma^{2} }}} \right)_{{\dot{\varepsilon },T}} = \left( {\frac{{y^{\prime\prime\prime}y^{\prime} - (y^{\prime\prime})^{2} }}{{(y^{\prime})^{3} }} } \right)_{{\dot{\varepsilon },T}} ,$$
(9)

where in Eq. (9), y′, y″ and y″′ are the first, second and third order derivatives of σ with respect to ε. Therefore, the critical strain could be calculated directly by finding the zero of the Eq. (9). In this work, ninth order polynomials were fitted to the nonlinear regions of the corrected hot compression curves from the yield point up to the steady state region, all of which yielded R2 values greater than 0.987.

3 Results and Discussion

3.1 Analysis of Flow Curves

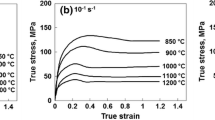
Figure 3 shows the corrected flow stress–strain curves of the BA-160 steel deformed at different deformation temperatures and the constant strain rates of 0.001, 0.01, 0.1 and 1 s−1. It is apparent from this figure that the flow stress was decreased with the elevation of deformation temperature or the decrease of the strain rate. Figure 3a shows that flow curves of samples deformed at the strain rate of 1 s−1 did not exhibit the characteristic DRX behavior, but other flow curves obtained under strain rates of 0.001, 0.01 and 0.1 s−1 (Fig. 3b–d) displayed the typical DRX behavior with a peak stress followed by a gradual fall towards a steady state stress. The peak became more pronounced when the deformation temperature was increased or strain rate was decreased. The Zener–Hollomon parameter including the simultaneous effects of deformation temperature and strain rate could be used to explain the variations of flow stress. It is represented as:

$$Z = \dot{\varepsilon } \,{ \exp }\left[ {Q/\left( {RT} \right)} \right],$$
(10)

where Q is the activation energy of deformation, R is the universal gas constant, and T is the absolute temperature. With a substantial decrease in Z value, the flow curves inclined to display multiple peaks as this could be obviously seen from the flow curve of 1100 °C and 0.001 s−1, which are shown in Fig. 4.

Fig. 3
figure 3

Flow curves of the BA-160 steel obtained from hot compression tests at different temperatures and strain rates of a 1 s−1, b 0.1 s−1, c 0.01 s−1, and d 0.001 s−1

Full size image
Fig. 4
figure 4

Double peaks in the flow curve of the BA-160 steel during hot compression at the temperature of 1100 °C and the strain rate of 0.001 s−1

Full size image

During deformation of metals, dislocation density was increased and the level of stress needed to precede the deformation was raised due to dislocation hardening. However, softening mechanisms during deformation, i.e. DRV and DRX, could activate and balance the extra dislocation density. Initially, DRV started to annihilate the dislocations through pathways requiring dislocation climb and cross slip, or rearrangement of them into a polygonized substructure. This could be the only mechanism needed to counteract the production of extra dislocations provided that the dislocations would have the sufficient mobility to participate in DRV processes. It could be understood that some alloying elements may have a decelerating effect on DRV, and some others could have a similar effect on DRX processes [26]. Of course, postponing DRX could lead to the extension of the DRV mechanism. Momeni and Abbasi [27] have attributed the difference between the activation energy of deformation of two comparable steels to their different alloying contents in connection with solute drag effects on the grain boundaries. They have proposed a compositional factor describing the effect of various alloying elements on the DRX process as a complementary study extending the work of Karjalainen et al. [28]. It indicated that elements such as Cu, Cr, Mo, and V followed an increasing order of impeding effect on DRX, while C facilitated this process. However, as a solute, Ni should have an impeding effect near Cr because of similar diffusivity and atomic radii difference with respect to the Iron atoms [27, 29]. On the other hand, elevated temperatures could be accompanied by the higher mobility of solute elements and the decrease in the solute drag effect, thereby increasing grain boundary mobility, giving rise to facilitating DRX [30]. However, mobility of dislocations is predominantly a function of the SFE of partial dislocations. The SFE value could be affected by solute elements such as C, Ni and Cr. It has been shown that carbon has a strong increasing effect on SFE [31,32,33]. Further, it has been pointed out that Ni can have a raising effect on SFE, whereas Cr tends to lower this energy [32, 34]. Lower SFE values are associated with the lesser mobility of dislocations due to the resistance of partial dislocations to rejoining, which is crucial for dislocation climb and cross slip. Thus, in low SFE materials, annihilation processes cannot keep pace with the dislocation production rate, leading to the accumulation of dislocations. Therefore, the free energy of the material is increased due to the generation and accumulation of dislocations. Eventually, the level of free energy reaches the critical activation energy required for the initiation of DRX. The critical free energy corresponds to a specific dislocation density equivalent to the critical strain (εc) which appears as the inflection point on the plot of θ versus σ [20].

Figure 5 shows the typical diagrams of θ against σ and \(d^{2} \theta /d\sigma^{2}\) versus ε according to Eq. (9); these are related to the hot deformation of the BA-160 steel at the temperature of 1100 °C and the strain rate of 0.01 s−1. The information could be acquired from the plots, which represent the critical and peak stresses and strains, i.e. σc, εc, σp and εp, respectively, as well as the steady state stress of DRX curve (σss). These parameters, which have been shown schematically in Fig. 1, are essential in DRX calculations. Most often, the microstructural evolution and its correlation with DRX characteristic points such as critical and peak points can be described using the concept of necklace mechanism. The critical point (εc, σc) corresponds to the onset of DRX, at which new grains start to nucleate on grain boundaries. Ponge and Gottstein [35] have indicated that the saturation of the grain surfaces with new-born DRX grains leading to the complete covering occurs around the peak point (εp, σp) forming the first layer of DRX grains. Successive necklaces would be formed between the previous necklaces and deformed grains until the DRX structure could be developed completely. This stage corresponds to the start of the steady state region of the flow curves, as established after (εss, σss) [35, 36].

Fig. 5
figure 5

The typical plots of a θ versus σ and b d2θ/dσ2 against ε based on Eq. (9) for the sample subjected to hot compression at the temperature of 1100 °C and the strain rate of 0.01 s−1

Full size image

By using diagrams of the type shown in Fig. 5, the characteristic points were attained for the different flow curves of Fig. 3. These characteristic stresses and strains are included in Table 1 for the conditions in which DRX calculations had been performed. The dependence of the flow stresses and strains of the critical and peak points on different working conditions with the Zener–Hollomon parameter is shown in Fig. 6. In accordance with the linear relationship on the logarithmic scale, the following equations can be expressed through regression analysis:

$$\varepsilon_{c} = 0.04\,Z^{0.056}$$
(11)
$$\sigma_{c} = 1.12\,Z^{0.125}$$
(12)
$$\varepsilon_{p} = 0.03\,Z^{0.084}$$
(13)
$$\sigma_{p} = 1.22\,Z^{0.125}$$
(14)
Table 1 Characteristic stresses and strains of different test conditions (stresses are in MPa)
Full size table
Fig. 6
figure 6

The dependence of a strains, and b stresses of peak and critical points of different hot compression conditions on the Zener–Hollomon parameter

Full size image

3.2 Constitutive Equations and Material Constants

It is a common practice to relate the flow stress in hot deformation to the Zener–Hollomon parameter (Z) through an equation of the following kind:

$$Z = Af\left( \sigma \right) ,$$
(15)

where A is a constant and f (σ) is a function defining the dependency of the Eq. (15) on the true stress (σ) via one of the following forms:

$$f\left( \sigma \right) = \left\{ {\begin{array}{*{20}l} {\sigma^{{n^{\prime}}} } \hfill & {\text{for low}}\,\sigma \hfill \\ {\exp \left( {\beta \sigma } \right) } \hfill & {\text{for high}}\,\sigma \hfill \\ {\left[ {\sinh \left( {\alpha \sigma } \right)} \right]^{n} } \hfill & {\text{for all}}\,\sigma \hfill \\ \end{array} } \right.,$$
(16)

in which n, α and n′ are material constants, and β is equal to n′α.

Combining Eqs. (15) and (16) with the extended form of the Zener–Hollomon parameter and taking natural logarithm from both sides of the final equation give:

$${ \ln }\left( {\dot{\varepsilon }} \right) = \left\{ {\begin{array}{*{20}l} {\ln A_{1} + n^{\prime}\ln \sigma - \frac{Q}{RT}} \hfill & {\text{for low}}\,\sigma \hfill \\ {\ln A_{2} + \beta \sigma - \frac{Q}{RT}} \hfill & {\text{for high}}\,\sigma \hfill \\ {\ln A_{3} + n\ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right] - \frac{Q}{RT}} \hfill & {\text{for all}}\,\sigma \hfill \\ \end{array} } \right.$$
(17)

As mentioned in Eq. (17), the first and second formulas are suitable for modeling lower and higher stress conditions, respectively. Therefore, to find the value of n′, a low level strain (corresponding to a low level of stress) the first formula of Eq. (17) should be used, and for β, a high level of strain, the second formula of Eq. (17) can be employed. Figure 7a shows a typical plot of ln σ − ln \(\dot{\varepsilon }\) for the strain level of 0.15, and Fig. 7b is another typical plot of σ − ln \(\dot{\varepsilon }\) for the strain level of 0.55. It could be deduced from Eq. (17) that the value of the constant n′ was obtained from the average slope of such plots, as shown in Fig. 7a, which was found to be 8.47. Also, the average slope of the plots of Fig. 7b showed the value of constant β to be 0.01; this, in turn, yielded the value of α to be 1.18 × 10−3. Then, according to the third formula of Eq. (17), the plot of \(\ln \dot{\varepsilon }\) versus ln [ sinh (ασ)] can be used to find the material constant n. This value was found to be 5.55 from the average slopes of the plots of Fig. 7c. Furthermore, Q/(nR) is the slope of the typical plots depicted in Fig. 7d, i.e. ln [ sinh (ασ)] against the inverse of the absolute temperature. Thus, the required activation energy for the hot deformation of the BA-160 steel was found to be ~ 390 kJ mol−1. Finally, by using one of the plots of Fig. 7c or d, the constant A3 could be obtained by means of the average of the intercepts of the fitted lines, which was calculated as 0.169 × 1014 s−1.

Fig. 7
figure 7

Dependence of ln \(\dot{\varepsilon }\) and a ln σ (at ε = 0.15), b σ (at ε = 0.55), and c ln sinh (ασ) (at ε = 0.55), and d is the variation of ln [sinh (ασ)] at ε = 0.55 versus the inverse of absolute temperature

Full size image

Figure 8 compares the natural logarithm of the Zener–Hollomon parameter versus the natural logarithm of the three different formula expressed by Eq. (16) at the low strain level (0.15), as well as the high strain level (0.55). The coefficient of determination (R2) of the fitted lines confirmed that the first formula had a good prediction of the experimental data of low strain (or stress) levels, while the second formula was the best at higher strain (or stress) levels; finally, the third one, i.e. the hyperbolic sine formula, could be the best at both low and high levels of strain. Based on the hyperbolic sine function, the constitutive equation of the BA-160 steel can be represented as:

$$\ln Z = \ln \dot{\varepsilon } + \frac{390000}{8.314 \times T} = 30.458 + 5.55 \times {\text{ln sinh }}\left( {1.18 \times 10^{ - 3} \sigma } \right)$$
(18)
Fig. 8
figure 8

Comparison of ln Z versus a ln σ at the strain of 0.15, b ln σ at the strain of 0.55, c σ at the strain of 0.15, d σ at the strain of 0.15, e ln sinh ασ at the strain of 0.15, and f ln sinh ασ at the strain of 0.15

Full size image

Momeni et al. [37] worked on the hot deformation of HSLA-100 steel, as a copper-strengthened steel almost possessing the same type of alloying elements at lower levels with respect to the BA-160 steel. They conducted a series of hot compression tests and used the exponential form of Eq. (16) to determine the constitutive response of the steel. The value of parameters β in their research was obtained to be 0.127. They found that the activation energy of the deformation of the steel was 377 kJ mol−1. This value was consistent with the activation energy of deformation obtained in the current research. The slight rise in the value obtained for BA-160 could be due to the higher alloying elements of this steel, as compared to the HSLA-100 steel. Mirzadeh et al. [25] also found the value of 442 kJ mol−1 by fitting the hyperbolic sine function on the experimental data for 17-4 PH stainless steel. It is a copper-strengthened steel with much higher Cr (15 wt%) and a high level of Nb (0.25 wt%) content, making hot deformation harder than the BA-160 steel. Comparison of HSLA-100, BA-160, and 17-4 PH steels indicated a reasonable trend in hot deformation activation energies with the increase in the alloying content of copper-strengthened steels, especially in the case of the elements effective in raising hot strength. It is noteworthy that Mirzadeh et al. obtained the activation energy of deformation using the three functions stated in Eq. (16), and the value of 337 kJ mol−1, which resulted from the power law function, was reported as the most accurate one. However, by referring to the very near R2 values for fittings through the power law and hyperbolic sine functions in their work and the high Nb content of the steel comparing to the steels which they considered for showing the justification of this value [38], it seemed that the value of 442 kJ mol−1 was more acceptable.

3.3 Kinetics of Dynamic Recrystallization

To find the recrystallization fraction according to Eq. (1), the flow stress of DRV curve (σWH) should be determined. Normally, this is done by a model defining the behavior of dislocation creation and destroying as deformation proceeds. There are few models that can be chosen for the definition of σWH [39]; however, the relation of Estrin and Mecking [40] is used for a material whose effective distance of dislocation motion is determined by obstacles other than dislocations; this is also the case for a precipitation hardened alloy:

$$\frac{d\rho }{d\varepsilon } = k_{1} - k_{2} \rho$$
(19)

here ρ is the dislocation density, and k1 is a coefficient representing the a thermal accumulation of mobile dislocations. These dislocations would be immobile through passing a certain distance. The coefficient k2, on the other hand, relates to the thermally activated processes of dynamic recovery such as dislocation annihilation and polygonization, which assume that it is a function of temperature and strain rate. Subsequently, the hypothetical stress σWH can be calculated from the following relation:

$$\sigma_{WH} = \alpha Gb\rho^{1/2} ,$$
(20)

where α is a material constant near unity, G is the shear modulus, and b is the length of Burgers vector. Combination of Eqs. (19) and (20) gives

$$\sigma_{\text{WH}} \theta_{\text{WH}} = k_{1}^{'} - k_{2}^{'} \sigma_{\text{WH}}^{2} ,$$
(21)

where θWH is \(d\sigma_{\text{WH}} /d\varepsilon\), and k1′ as well as k2′ are material constants. Integration of Eq. (21) with (ε1, σ1) to (ε, σ) gives

$$\sigma_{\text{WH}} = \left[ { \sigma_{\text{s}}^{2} + \left( { \sigma_{1}^{2} - \sigma_{\text{s}}^{2} } \right)\exp \left( { - 2k_{2}^{'} \Delta \varepsilon } \right) } \right]^{1/2}$$
(22)

here σ1 and ε1 are the stress and strain of a certain point on the nonlinear section of DRX curve before the critical point to be defined later, and Δε is the difference between ε and ε1. Equation (21) can be rearranged to be represented as (see the “Appendix” for derivation):

$$\sigma_{\text{WH}} \theta_{\text{WH}} = \frac{1}{2}k_{2} (\sigma_{s}^{2} - \sigma_{\text{WH}}^{2} )$$
(23)

This means that the slope of the plot of \(\sigma_{\text{WH}} \theta_{\text{WH}}\) versus \(\sigma_{\text{WH}}^{2}\) is − 0.5k2, and saturation stress can also be found from the intercept. Moreover, comparing Eqs. (21) and (23) results in \(k_{2}^{'} = k_{2} /2\). According to Estrin [39], there are several internal variables that can reach a steady state by progress in the deformation process, whereas dislocation density is the last one to equilibrate. Therefore, it can be expected that for strains greater than a certain strain, ε1, the only internal variable controlling the flow behavior of material is the dislocation density. This trend would be extended to the critical strain where DRX mechanism is activated. In other words, between ε1 and εc, there would be a complete accordance of DRV and DRX curves, showing that \(\sigma = \sigma_{\text{WH}}\) for strains between ε1 and εc. Therefore, Eq. (23) can be rewritten as:

$$\sigma \theta = \frac{1}{2}k_{2} (\sigma_{s}^{2} - \sigma^{2} )$$
(24)

Figure 9a shows a typical curve of the dependence of σθ against σ2 for the case of the hot compression of the BA-160 steel at the temperature of 1050 °C and the strain rate of 0.01 s−1. In order for Eq. (24) to be valid, the coefficient k2 should be constant, which requires that variations of σθ versus σ2 be linear. Thus, σ1, which is the stress corresponding to the strain ε1, was selected to be the beginning of the last linear part. Moreover, the constants k2 and σs (Table 1) were obtained from the slope and the intercept of the linear section, respectively. Figure 9b shows the flow curve of the BA-160 steel at the temperature of 1050 °C and the strain rate of 0.01 s−1, as compared with the calculated DRV curve from Eq. (21). It shows the complete correspondence between DRX and DRV curves in a range embracing strains between ε1 and εc. Such plots were depicted for different test conditions, and the parameters ε1, k2, and σs were obtained.

Fig. 9
figure 9

Plot of a σθ with respect to σ2 as related to the hot compression of the BA-160 steel at 1050 °C and the strain rate of 0.01 s−1, and b the corresponding DRV curve, as compared with DRX curve. σ0 and ε0 are the yield stress and the strain of the material at the test conditions

Full size image

Subsequently, the fraction of dynamic recrystallization XDRX was determined through Eq. (1) and further modeled using a Kolmogorov–Johnson–Mehl–Avrami (KJMA) type relation as

$$X_{DRX} = 1 - \exp \left( { - kt^{{n_{A} }} } \right) = 1 - \exp \left( { - k\left[ { \frac{{\varepsilon - \varepsilon_{c} }}{{\dot{\varepsilon }}} } \right]^{{n_{A} }} } \right)\quad {\text{for}}\,\varepsilon \ge \varepsilon_{c} ,$$
(25)

where k is a constant in isothermal transformations and nA is the Avrami exponent. Figure 10 shows the kinetics of dynamic recrystallization for different flow curves in comparison with Avrami kinetic models. It could be seen that the experimental data obeyed the typical sigmoidal behavior and the KJMA model was in a very good conformity with the experimental data.

Fig. 10
figure 10

Experimental DRX fraction of different hot compression tests as compared with the KJMA models. DRX fractions obtained a at the temperature of 1100 °C and different strain rates, and b at the strain rate of 0.01 s−1 and different testing temperatures

Full size image

The curves of Fig. 10a show that at a constant temperature, with the increase in the strain rate, the incubation times for recrystallization were decreased. This was due to the higher rate of dislocation accumulation at the higher strain rates, leading to the lower times needed to trigger recrystallization. However, at the constant strain rate of 0.01 s−1, the incubation times for recrystallization were not significantly different, which could be attributed to the lower effect of temperature variations in the applied range on the dislocation accumulation, as compared with the strain rate. Another fact in Fig. 10b is that decreasing the test temperature was accompanied with the lower fractions of DRX, which resulted from the lower mobility of dynamically recrystallized grain boundaries with the decrease in temperature, thereby leading to the lower fractions of DRX [41].

It should be noted that the DRX fraction of the sample 1100 °C–0.001 s−1 in Fig. 9a was calculated up to εss1 of the flow stress shown in Fig. 4. As can be seen from Fig. 4, the flow curve exhibited the multiple peaks phenomenon (here as two peaks in the strain range of the test). From the kinetic calculations point of view, incorporation of the region after εss1 into the kinetic determination would result in the failure of predictions through the KJMA model, since the second hardening regime would be inferred by the model as a zone in which a recrystallized fraction could be transformed back to a non-recrystallized state that might be obviously incorrect. However, at the strains εss1 and εss2, there were fully dynamic recrystallized conditions with different grain sizes [42]. Hence, in the outlined conditions, the KJMA model was applied up to εss1 as a complete DRX.

The coefficient k in the KJMA relation showed a direct correlation with strain rate, and it was raised with the increase in the strain rate. However, the Avrami exponent in the KJMA model was roughly constant for different test conditions, as it was obtained to be 1.8 ± 0.2. The values of the Avrami exponent indicated that the main regime of the DRX of the BA-160 steel in these experiments was of one of site saturation type on grain boundaries and grain edges [43].

3.4 Microstructural Characterization

Figure 11 shows the microstructures of the BA-160 steel after immediate water quenching of the samples subjected to a strain of 0.75 by hot compression tests at different temperatures and strain rates conditions. The high hardenability of the steel due to the relatively large amounts of alloying additions could give rise to a fully martensitic microstructure through water quenching. In the microstructures of prior austenite grains (PAG), new DRX grains (DRX-g) nucleated at prior austenite grain boundaries (PAGB) have been indicated by arrows. It could be seen that at the temperature of 850 °C, the microstructure obtained by the strain rate of 0.1 s−1 (Fig. 11b) was almost completely typical of DRV processes showing a pancake shaped grain structure. A small number of new DRX grains were nucleated, as indicated by arrows in the photomicrograph presenting the very early stages of necklace mechanism for the development of the DRX structure. At the lower strain rate of 0.001 s−1, a large number of tiny DRX grains were nucleated at some prior austenite grain boundaries (Fig. 11a). Similarly, at the temperature of 950 °C and the strain rate of 0.1 s−1 (Fig. 11c), it was observed that there was a prior austenite grain structure indicating a mix of deformed austenite and small DRX nucleating grains. This was, however, converted to a completely developed DRX structure with the increase in the strain rate (Fig. 11d). Higher deformation temperatures in the strain rates of 0.001 and 0.1 s−1 also resulted in totally dynamic recrystallized microstructures, as could be seen from Fig. 11e–h. In the microstructure of the dynamically recrystallized samples, it could be discerned that the increase in Zener–Hollomon parameter induced finer grain sizes. For instance, Fig. 11f shows the finer prior austenite grain size, as compared to Fig. 10e, h.

Fig. 11
figure 11

Optical micrographs of BA-160 steels at different strain rates of a, c, e, g 0.1 s−1, and b, d, f, h 0.01 s−1, and temperatures of 850 °C (a, b), 950 °C (c, d) 1000 °C (e, f), and 1050 °C (g, h) after the strain of 0.75. The axes of compression are vertical with respect to the scale bars

Full size image

It was also found that the microstructures of the BA-160 steel under different hot compression conditions after quenching consisted of diffused precipitates in a lath martensitic matrix with no significant differences between precipitate size and distribution. Figure 12a is a typical FEG-SEM micrograph illustrating clusters of the nanometric precipitates in a lath martensitic matrix after the hot compression test at the temperature of 1100 °C and the strain rate of 0.001 s−1. Moreover, Fig. 12b shows the bright field TEM image of the same sample exhibiting some of the precipitates (indicated by white arrows). Energy dispersive spectroscopy (EDS) evaluation of the precipitates using FEG-SEM and TEM microscopes revealed the copper rich and carbide nature of such precipitates. The EDS results using TEM also showed that the chemical composition of some of the precipitates were richer in copper, and some others were richer in carbide forming elements. Table 2 shows the typical records of the two kinds of chemical compositions.

Fig. 12
figure 12

Electron microscopy images of the BA-160 steel; a FEG-SEM micrograph after hot compression at 1050 °C–0.001 s−1, and b TEM image showing numerous nanometric precipitates. (A few of the precipitates in martensitic laths are indicated by white arrows in the TEM image)

Full size image
Table 2 EDS analysis of the precipitates using TEM revealing copper rich precipitates and those rich in carbide former elements types
Full size table

4 Conclusions

The flow curve behavior of the BA-160 steel was investigated and modeled. A high order polynomial was fitted to the flow curves and all of the required calculations were obtained through the fitted curve. In addition, the dynamic recrystallization kinetics of the steel in the range of test conditions was studied and the dynamically recrystallized fraction was modeled. The following conclusions could be drawn:

  1. 1.

    The tests with the strain rate of 1 s−1 showed the dynamic recovery type behavior of flow stress, while testing at lower strain rates led to the characteristic DRX behavior. The peaks of dynamic recrystallization became sharper with the increase in temperature and the decrease in the strain rate.

  2. 2.

    The flow curves of the BA-160 steel obtained in hot compression tests at different strain rates and temperatures were modeled perfectly with the hyperbolic sine formula. However, it was shown that the exponential function could also be fitted with the results very well.

  3. 3.

    The parameters of the hyperbolic sine equation model, n and α, were found to be 5.55 and 1.18 × 10−3 MPa−1, respectively, and the activation energy of hot deformation was obtained as 390 kJ mol−1.

  4. 4.

    Hypothetical DRV curves were found to have an excellent conformity with the experimental DRX curves by using the last linear parts of the plots of σθ versus σ2 for integrating and finding the constants of the DRV function formula.

  5. 5.

    The behavior of dynamic recrystallization was modeled successfully using the Kolmogorov–Johnson–Mehl–Avrami (KJMA) type relation.

  6. 6.

    The coefficient k of the KJMA model was changed significantly with the strain rate, while the Avrami exponent was roughly constant around 1.8, which implied that nucleation was mainly of the site saturation type on grain boundaries and edges.

  7. 7.

    Microstructures of hot deformed samples revealed that at lower temperatures and lower strains rates, partial DRX occurred and higher Zener–Hollomon parameters brought about the finer prior austenite grain sizes.