1 Introduction

The increasing demand for high-performance structural steels with good weldability and corrosion resistance has resulted in development of high-strength low-alloy (HSLA) steels.[1,2] Mechanical properties of these steels are improved by the cooperation of two factors: a carefully designed chemical composition and an optimized thermomechanical processing. These factors can result in a refined microstructure of austenite with high density of nucleation sites for ferrite in the following phase transformation. Consequently, a microstructure of very fine ferrite with excellent mechanical properties is formed by cooling. In terms of chemical composition, the addition of microalloying elements such as Niobium, Titanium, and Vanadium is one of the most effective approaches. Precipitation of fine niobium carbonitrides during thermomechanical processing of microalloyed steels is a great example of cooperation of these two factors to prevent austenite grain growth.[1]

The proper design of thermomechanical processing requires deep knowledge about the hot flow behavior of microalloyed steels which is, in fact, governed by several simultaneous microstructural phenomena. Hardening, dynamic recovery (DRV), and dynamic recrystallization (DRX) are known as major phenomena during hot deformation of austenite.[3,4,5] In order to incorporate such complicate phenomena into simulation tools, it is necessary to mathematically express them as proper constitutive equations or models. Constitutive models help to formulate the hot flow behavior at various deformation conditions. While several constitutive equations are developed for this purpose, most attention has been paid to the physically based models which try to formulate the contributions of the microstructural phenomena to the flow stress. Therefore, the flow stress is defined as a function of deformation parameters, i.e., the strain, strain rate, and temperature.[4,6,7] Several parameters are always introduced in these models to achieve a better match between the model and the experiments. Meanwhile, less attention has been paid to the physical meaning of the parameters.

Based on the deformation temperature, the microalloying elements can be in the form of either solute atoms or precipitates.[8,9] Effects of microalloying elements on the constitutive equations are usually disregarded in literature. Therefore, it is important to investigate the validity of the constitutive models in the whole range of temperature.

In this work, as an attempt to examine the potential effects of microalloying elements of Nb and Ti on the constitutive behavior, the hot deformation behavior of an Nb-Ti microalloyed steel is analyzed using hot compression test. It is also aimed to introduce an appropriate phenomenological constitutive model with a smaller number of parameters determined by curve fitting.

2 Experimental Procedure

As the primary material, a 16-mm-thick Nb-Ti microalloyed steel plate with the chemical composition of (wt pct) 0.055 C, 0.25 Si, 0.7 Mn, 0.17 Mo, 0.018 Nb, 0.023 Ti, 0.003 N has been prepared by vacuum arc melting, homogenization, and hot rolling.

In order to investigate hot deformation behavior of the steel, hot compression tests were performed on specimens with the length of 12 mm and diameter of 8 mm. A servo-hydraulic testing machine (Instron 8502) equipped with a furnace and a load cell of 100 kN (maximum load capacity) was used for the compression testing. Isothermal compression tests were performed at temperatures of 850 °C to 1200 °C and strain rates of 0.01 to 1 s−1 up to the high strain of 1.2 to ensure that DRX was completed. Before deformation, the specimens were held for 600 seconds at the test temperature. They were also immediately water quenched after the compression test to freeze the microstructure for further analyses. Scanning electron microscopy (SEM) was carried out on specimens deformed at the temperatures of 1000 °C and 1200 °C with strain rate of 0.1 s−1. A Schottky field emission SEM (JEOL JSM-7600F) equipped with an Energy-Dispersive Spectroscopy (EDS) X-ray analyser (Oxford Instruments X-max 50 mm2) was employed at 15 kV to study the specimens. Selected precipitates in these specimens were analyzed by EDS to follow their evolution in temperature ranges between T < 1100 °C and T > 1100 °C.

3 Hot Compression Flow Curves

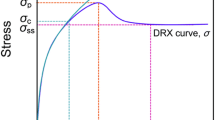
Compressive flow curves obtained at various strain rates and temperatures are presented in Figure 1. Note that the flow stresses were corrected for the effect of friction by the slab method formulation,[10] so that a plateau was obtained at large strains where a steady-state deformation was expected. As shown in this figure, the curves are characterized by the classic features of dynamic recrystallization. That is, the flow stress increases with strain up to the peak stress (σp) corresponding to the peak strain (εp) followed by a decrease until the steady-state stress (σss) is reached. Under the conditions of high temperatures and low strain rate, multiple peaks are distinguished which is a well-known feature of DRX at low Zener–Hollomon parameter.[4,11]

Fig. 1
figure 1

Stress–strain curves of the steel during hot compression at various temperatures and strain rates of (a) 10−2 s−1, (b) 10−1 s−1, and (c) 100 s−1

Full size image

4 Constitutive Model

In this study, DRV and DRX kinetic models are combined to establish the constitutive model for hot deformation of the studied steel. Therefore, by the onset of plastic deformation, the material undergoes hardening with a decreasing rate due to DRV phenomenon. The DRX starts at a critical strain (εc) and prevents the curve from reaching the common DRV stress saturation. As deformation continues, the progress of recrystallization provides softening additional to that provided by the DRV, so that the softening rate can overtake the hardening rate. This causes an extremum in the form of a peak in the flow curve followed by softening. Once the fraction of DRX is complete, the softening rate diminishes and the material continues to deform within a steady-state regime.[3,7,12]

The developed DRV and DRX combination model as proposed by Hernandez et al.[3] and used in other researches,[7,12,13,14] is based on the governing phenomena of hot deformation. In the present study, the Estrin and Mecking (EM) dislocation model[15] is taken as the DRV model and an Avrami type equation[16] as the DRX kinetic model.

4.1 DRV Model

Based on the EM model, the following differential equation expresses the relation between the dislocation density (ρ) and the plastic strain (ε)[15]:

$$ \frac{d\rho }{d\varepsilon } = h - r\rho $$
(1)

in which h and r represent the rate of a thermal hardening and the rate of dynamic recovery, respectively. Considering the relation between the flow stress and the dislocation density as

$$ \sigma \propto \sqrt \rho. $$
(2)

It can be shown that Eq. [1] leads to the following equation for the hardening rate, \( \theta = \frac{d\sigma }{d\varepsilon } \)[15]:

$$ \theta \sigma = A - B\sigma^{2} $$
(3)

in which A and B are constant parameters at fixed deformation conditions. Through integration, this model gives the following equation for the flow stress in the absence of DRX, i.e., the DRV flow stress (σDRV)[13]:

$$ \sigma_{\text{DRV}} = \left[ {\sigma_{\text{sat}}^{2} - \left( {\sigma_{\text{sat}}^{2} - \sigma_{0}^{2} } \right)\exp \left( { - 2B\varepsilon } \right)} \right]^{1/2}, $$
(4)

where σ0 and σsat are the yield and saturated stresses, respectively. The yield stress at each deformation condition can be determined by 0.2 pct strain offset from the experimental flow curves, or simply taken as zero in case of large deformation at high temperatures (assuming that the plastic strain is approximately equal to the total strain). Regarding the saturated stress, however, direct measurement from the flow curves is not possible because the occurrence of DRX prevents the curves from reaching the stress saturation. Alternatively, the saturated stress can be determined from extrapolation of the hardening rate vs the stress to θ = 0. It is necessary to note that such curves must be fitted to the experimental data before occurrence of DRX, i.e., at initial stage of hardening below εc. This is conducted in Figure 2 where the curves are fitted to the present compression data. Due to the low flow stresses and less difference between consecutive registered points, higher data scattering is seen at lower strain rates. The fitted curves in this figure are extrapolated to θ = 0. Note that, according to Eq. [3], these curves are in the form of

$$ \theta = \frac{A}{\sigma } - B\sigma. $$
(5)

By regressions according to Eq. [3], A and B can be obtained, respectively, from the intercept and the minus slope of the lines fitted to θσ vs σ2.

Fig. 2
figure 2

Experimental data and fitted curves of hardening rate vs stress at various temperatures and strain rates of (a) 10−2 s−1, (b) 10−1 s−1, and (c) 100 s−1

Full size image

4.2 DRX Model

The kinetics of softening by DRX is expressed by the Avrami type equation[3,12]

$$ X_{\text{DRX}} = 1 - \exp \left[ { - K\left( {\frac{{\varepsilon - \varepsilon_{\text{c}} }}{{\varepsilon_{\text{p}} }}} \right)^{N} } \right]. $$
(6)

Here, XDRX is the recrystallized volume fraction and K and N are material constants. It is assumed that the softening fraction caused by DRX is equal to the recrystallized volume fraction. Therefore, XDRX is related to the flow curves data as

$$ X_{\text{DRX}} = \left\{ \begin{array}{ll} 0& \varepsilon \le \varepsilon_{c} \\ \frac{{\sigma_{DRV} - \sigma }}{{\sigma_{sat} - \sigma_{ss} }} & \varepsilon > \varepsilon_{c}\\ \end{array} \right. $$
(7)

Fernandez et al.[17] studied the DRX behavior of Nb and Nb-Ti microalloyed steels and found that, at various deformation conditions, the critical strain was a constant fraction of the peak strain, i.e., εc = 0.77 εp. This relationship is employed in the present study. It is necessary to note that the effects of deformation conditions on the kinetics of DRX are implicitly taken into account in Eq. [6] by means of εp. Taking twice natural logarithm of Eq. [6] leads to

$$ \ln \ln \left( {\frac{1}{{1 - X_{\text{DRX}} }}} \right) = \ln K + N\ln \left( {\frac{{\varepsilon - \varepsilon_{\text{c}} }}{{\varepsilon_{\text{p}} }}} \right). $$
(8)

A plot of \( \ln \ln \left( {\frac{1}{{1 - X_{\text{DRX}} }}} \right) \) vs \( \ln \left( {\frac{{\varepsilon - \varepsilon_{\text{c}} }}{{\varepsilon_{\text{p}} }}} \right) \) can validate the reliability of this procedure. This is carried out in Figure 3 for flow data of all deformation conditions from the critical to the steady-state strains. As shown in this figure, a line can fit to the experimental data signifying the validity of Eq. [6] for the present experiments. In accordance with the fitted line and Eq. [8], the parameters K and N are obtained as 1.97 and 1.76, respectively.

Fig. 3
figure 3

Experimental data and fitted line of ln-ln(1/1 − X DRX ) vs ln((ε − ε c )/ε p )

Full size image

4.3 Constitutive Equation

The compact form of constitutive equation can be expressed by combining Eqs. [4], [6], and [7] as

$$ \sigma = \sigma_{\text{DRV}} - X_{\text{DRX}} \left( {\sigma_{\text{sat}} - \sigma_{\text{ss}} } \right). $$
(9)

In this constitutive equation, εc, εp, σsat, σss, and B are parameters depending on the deformation conditions. Therefore, they should be defined at arbitrary strain, strain rate, and temperature to calculate flow stress. A popular and successful approach is to define such parameters as functions of the Zener–Hollomon parameter (Z)

$$ Z = \dot{\varepsilon }\exp \left( {\frac{Q}{RT}} \right), $$
(10)

where \( \dot{\varepsilon } \) is the strain rate, T is the absolute temperature, R is the ideal gas constant, and Q is the activation energy of deformation.

4.4 Implementation of Predefined Values of Q and n

The activation energy, Q, is always determined through the evaluation of the Z parameter with respect to the experimental flow data. The following hyperbolic sine equation is found to give a good estimation over all range of stress (σ)[6,18]:

$$ Z = C\left[ {\sinh \left( {\alpha \sigma } \right)} \right]^{n}, $$
(11)

in which C, α, and n are material constants. Since strain is not specified in this equation, a characteristic stress such as the critical, the peak, or the steady-state stress should be used to fit with the experimental data. Among these stresses, the peak stress is the most widely used parameter. Since Eq. [11] is governed by deformation mechanisms, the parameters Q and n convey physical meanings. As shown by Cabrera et al.,[19,20] the constant exponent of n = 5 and the activation energy of self-diffusion can be considered as long as the deformation mechanism is controlled by dislocation glide and climb. Based on their investigations, these values are valid when temperature dependencies of the Young’s modulus (E) and the self-diffusion coefficient (D) are considered in the formulation. Therefore, \( \dot{\varepsilon } \) and σ are normalized by D and E, respectively, to modify Eq. [11] as

$$ \frac{{\dot{\varepsilon }}}{D} = C^{\prime}\left[ {\sinh \left( {\alpha^{\prime}\frac{\sigma }{E}} \right)} \right]^{n}, $$
(12)

in which the self-diffusion coefficient is defined by

$$ D = D_{0} \exp \left( {\frac{ - Q}{RT}} \right), $$
(13)

where D0 is the pre-exponential constant. Further investigations showed that the best coincidence with the predefined values of Q and n was attainable when, instead of the peak stress, the critical stress was used.[6] This approach is, therefore, implemented in this study to examine the predefined constants for flow data of the steel. For this purpose, dependence of D on temperature is considered by D0 = 1.8 × 10−5 m2/s and Q = 270 kJ/mol pertaining to γ-Iron.[21] Moreover, E is calculated for the used steel as a function of temperature as E = 233.7−100.36 T (GPa) within the used range of temperature.[22] According to Eq. [12], n is the slope of the line fitted in the plot of \( \ln (\dot{\varepsilon }/D) \) vs \( \ln \left[ {\sinh \left( {\alpha^{\prime}\frac{\sigma }{E}} \right)} \right] \). As demonstrated in Figure 4(a), the predefined values of Q = 270 kJ/mol and n = 5 coincide with the hot flow data of the present steel using α′ = 1610.

Fig. 4
figure 4

\( \ln (\dot{\varepsilon }/D) \) vs \( \ln \left[ {\sinh \left( {\alpha^{\prime}\frac{\sigma }{E}} \right)} \right] \) for σ c (a, b) and σ sat (c, d); (a) and (c) a single line fitted to all data and (b) and (d) two different lines fitted for distinct temperature domains

Full size image

Saturated stresses, σsat, were determined from the extrapolation of the hardening rate curves vs the stress to θ = 0 as mentioned in Section IV–A. It is interesting to examine whether the predefined values of Q and n can match with the evolution of this parameter, as well. Figure 4(c) shows that the variation of the saturated stress with the deformation conditions can well be expressed by Eq. [12] with the values of Q = 270 kJ/mol and n = 5. It is noteworthy that such a coincidence is achieved by the similar value of α′ = 1610.

Despite the admissible correlation of the data with the fitted lines shown in Figures 4(a) and (c), much better line fittings are achievable when hot deformation data of below and above 1100 °C are treated separately. This is shown in Figures 4(b) and (d). It is shown that the second line (≥ 1100 °C) is to some extent shifted to the right. In other words, at a specific strain rate and temperature (\( \dot{\varepsilon }/D \)), a higher normalized stress is expected by the line obtained from compression dataset of T ≥ 1100 °C. This finding will be discussed in accordance with the effects of Nb in the two temperature ranges. However, for the sake of simplicity and comprehensiveness, the single and yet acceptable line fitting of Figure 4(a) is taken for the constitutive equation.

4.5 Estimation of Z Dependent Parameters

Having the value of Q, parameter Z can be calculated at each strain rate and temperature. Accordingly, it is now possible to define the Z dependent parameters, i.e., σsat, σss, εp, and B. The dependency of σ sat to Z is, in fact, formulated by Eq. [12] (Figure 4(c)), because \( \frac{{\dot{\varepsilon }}}{D} \) is equal to Z/D0. Regarding B, σss, and εp, a power law equation is considered. In fact, it is well established in literature that Z dependency of many hot deformation parameters can be described by the following power law equation[23,24]:

$$ {\text{Parameter}} = aZ^{\text{b}}. $$
(14)

It is necessary to note that in accordance with the accepted procedure in this study, all stresses are normalized by E, so that, instead of σss, σss/E is treated by Eq. [14]. Accuracy of this relation for the mentioned parameters in the current study is shown in Figure 5 where a line can fit to the experimental results in ln-ln scales for B, σ ss /E, and εp vs Z. A large deviation from the fitted line is seen for data of ε p in Figure 5(c). Figure 5(d) shows that by the increase of the temperature up to 1000 °C, this parameter is decreased. At higher temperatures, however, this trend is suppressed so that εp does not decrease anymore. The relevant values of a and b for various parameters along with the other parameters of the constitutive model are summarized in Table I. The flow curves representing the derived constitutive equation considering the mentioned parameters are compared with the experimental curves shown in Figure 6. It is shown that the model shows a good agreement with the experiments.

Fig. 5
figure 5

Experimental data and fitted lines of (a) ln(B), (b) ln(σ ss /E), and (c) ln(ε p ) vs ln (Z) and (d) εp vs temperature at various strain rates

Full size image
Table I Parameters of the Constitutive Model Obtained by Fitting to the Experimental Data
Full size table
Fig. 6
figure 6

Comparison between the flow curves calculated from the model and the experimental data at various temperatures and strain rates of (a) 10−2 s−1, (b) 10−1 s−1, and (c) 100 s−1

Full size image

4.6 Constitutive Model with Reduced Number of Parameters

As explained in the last section, after setting the predefined values for Q and n, ten modeling parameters summarized in Table I have to be determined by fitting them to the experimental data. It would be interesting if the model could be modified so that the number of constants was decreased while staying in good agreement with the experiments.

Parameter B in the DRV model (Eq. [4]) is one possibility to reduce the number of parameters. As presented in the previous section, this parameter is defined as a power law function of Z, introducing two parameters to the model, i.e., aB and bB. An approach similar to the one implemented in Eq. [6] is suggested here by which the two parameters are reduced to one. A procedure to incorporate the effects of deformation conditions (strain rate and temperature) is to normalize strain by εp in Eq. [6]. In other words, the effects of deformation conditions on the kinetics of DRX are implicitly taken into account by means of εp, so that there is no need to define parameters K and N as functions of Z. Likewise, it can be expected that the Z dependency of B may be implemented in Eq. [4] by the same approach. Accordingly, this equation is suggested to be substituted by the following equation:

$$ \sigma_{\text{DRV}} = \left[ {\sigma_{\text{sat}}^{ 2} - \left( {\sigma_{\text{sat}}^{ 2} - \sigma_{0}^{2} } \right)\exp \left( { - 2B^{\prime}\frac{\varepsilon }{{\varepsilon_{\text{p}} }}} \right)} \right]^ {{1/2}}, $$
(15)

with a unique constant B′ over all deformation conditions. To demonstrate the accuracy of this approach, the experimental data of flow stresses taken from the curves of all deformation conditions before ε c are used to draw ln [(σ2 − σ 2 sat )/(σ 20  − σ 2 sat )] vs ɛ/ɛ p as shown in Figure 7. It is shown that a line is well fitted to this plot with the R-squared value of 0.96. Based on Eq. [15], the slope of this line is equal to − 2B′. Consequently, a value of 1.285 is obtained for parameter B′.

Fig. 7
figure 7

Experimental data and fitted line of \( { \ln }\left[ {{{\left( {\sigma^{ 2} - \sigma_{\text{sat}}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma^{ 2} - \sigma_{\text{sat}}^{2} } \right)} {\left( {\sigma_{0}^{ 2} - \sigma_{\text{sat}}^{2} } \right)}}} \right. \kern-0pt} {\left( {\sigma_{0}^{ 2} - \sigma_{\text{sat}}^{2} } \right)}}} \right] \) vs ε/εp

Full size image

In order to further reduce the number of modeling parameters, attention is paid to the fact that some of the parameters have similar dependency on Z, implying that they are not independent. In fact, parameters σsat, σss, and εp are functions of the same independent variable, i.e., parameter Z. Hence, each one introduces two parameters as presented in Table I. However, it is reasonable to consider the interconnections between these parameters to reduce their number. This was also addressed by Jonas et al.[16] through the examination of 26 different sets of data for various steels. They indicated that σc, σsat, σss, and σ0 can be linearly connected to σp. That εc is a fraction of εp, as found in Reference 17 and considered in this study, is also founded on the same ground. In the same way in the present study, σss/E and ε p are defined by a linear relation with σsat/E. Note that, according to the physical meaning, such a linear relation is constrained by zero intercept:

$$ {\text{Parameter}} = c\frac{{\sigma_{\text{sat}} }}{E}. $$
(16)

This interconnection is demonstrated to be accurate in Figure 8. The values of the modeling parameters are summarized in Table II. The flow curves representing the constitutive model with reduced number of parameters are compared with the experiments given in Figure 9. Obviously, with three fewer parameters, this model is in good accord with the experiments.

Fig. 8
figure 8

Experimental data and fitted lines of (a) σss/E and (b) εp vs σsat/E

Full size image
Table II Fitting Parameters and Their Values for the Model with Reduced Number of Parameters
Full size table
Fig. 9
figure 9

Comparison between the flow curves calculated from the model with reduced number of parameters and the experimental data at various temperatures and strain rates of (a) 10−2 s−1, (b) 10−1 s−1, and (c) 100 s−1

Full size image

5 SEM Analyses

SEM images of specimens deformed at 1000 °C and 1200 °C taken in back-scattered electrons mode are displayed in Figures 10(a) and (b), respectively. Regular-shaped precipitates can be found in both micrographs. Using EDS analyses, several precipitates of this kind were identified as Ti- and N-rich particles. The main distinction between the two temperatures is about the Nb distribution. As shown in the EDS element distribution maps of Figures 10(c) and (d), an obvious concentration of Nb is discernible on the particle in specimen deformed at 1000 °C. However, in the specimen tested at 1200 °C, no preferred concentration of Nb is seen on the particle. The same feature was recognized in several EDS analyses of similar precipitates in the two specimens.

Fig. 10
figure 10

SEM micrographs and EDS maps (N, Ti, and Nb) of specimens deformed at (a) and (c) 1000 °C, and (b) and (d) 1200 °C with strain rate of 0.1 s−1

Full size image

6 Discussion

6.1 Conformity of Flow Data and Predefined Values of Q and n

It was mentioned that, theoretically, Q of the self-diffusion activation energy and n = 5 were expected when the deformation mechanism was controlled by the dislocation glide and climb. As suggested by Cabrera et al.,[19,20] the approach of Eq. [12] can satisfy this expectation. In fact, as a result of variation of E by temperature, the parameters of Eq. [11] cannot be independent from the temperature. On the other hand, having σ as normalized by E, the parameters of Eq. [12], i.e., C′, α′, and n are independent from the temperature. This helps to attain the expected predefined values of Q and n. Mirzadeh et al.[6] conducted further explorations of this claim. They set the self-diffusion activation energy in Eq. [12] and found that, when the peak stress is employed, a deviation from the value of n = 5 may be resulted. Based on their investigations, when the critical stress is employed instead, the best coincidence with n = 5 is achievable. This is attributed to the fact that the simultaneous assumption of the self-diffusion coefficient and n = 5 is valid when the deformation mechanism is controlled by dislocation glide and climb. At these conditions, DRV is the only possible softening mechanism. Since this assumption is true before the onset of DRX, the critical stress is the best experimental parameter to fit with Eq. [12] and to find the relevant parameters. As shown in Figure 4(a), the experimental data of the present study confirm the validity of mentioned assumption.

Figure 4 shows that not only the critical stress, but also the saturation stress is in good agreement with the predefined values of Q and n with the same value of α′. This can be explained through the fact that σsat is also immune to the DRX influence. In other words, DRV is the only softening mechanism to make a balance with the hardening phenomena at the saturation stress. Therefore, the required conditions to achieve Q = 270 kJ/mol and n = 5 are satisfied by this parameter, too.

6.2 Distinct Temperature Domains

The results of hot flow data (Figures 4(b) and (d)) indicate a transition for variation of the normalized strain rate with the normalized stress between the two temperature ranges T < 1100 °C and T ≥ 1100 °C. From literature, it can be found that the most important metallurgical aspect, which is different in these two temperature ranges, is attributed to the Nb precipitation so that Nb-rich precipitates are thermodynamically stable in the first temperature range and soluble in the second one. Through a review of several investigations, the dissolution temperatures of Nb-rich precipitates in various steels are determined as presented in Table III. It is shown that the dissolution temperature of these precipitates, in particular the NbC, matches with the observed transition temperature of this work. Note that, based on this table, the NbC dissolution temperature in various microalloyed steels is in the range from 1050 °C to 1100 °C.

Table III Dissolution Temperature of Nb-Rich Precipitates in Various Steels
Full size table

Due to the considered Nb-Ti microalloyed steel in this study, it is necessary to discuss precipitates with respect to both microalloying elements. Yuan and Liang[33] found two types of precipitates in an as-forged Nb-Ti microalloyed steel. Coarse Ti-rich particles formed during solidification and fine strain-induced Nb-rich precipitates generally formed during hot deformation. Very fine Nb-rich particles also can precipitate during the austenite–ferrite phase transformation and/or in the ferrite during cooling.[34] Nitrides, carbides, and carbonitrides in Nb-Ti microalloyed steels can be generally shown as (Ti x Nb 1−x )(C y N 1−y ). Thermodynamic calculations and experimental results show the decrease of y along with the increase of x by temperature. Actually, above 1100 °C, the x value is higher than 0.95 and the y value is lower than 0.05, signifying that only TiN particles are stable at very high temperatures.[8] The EDS maps shown in Figure 10 are consistent with this evolution. Among various precipitates in microalloyed HSLA steels, TiN is known for its lowest solubility limit.[29]

Nb can be effective on hot flow stress in two ways: precipitation and solid solution strengthening. Dutta and Sellars[35] studied the individual strengthening contributions in Nb microalloyed steels. Their results show that Nb precipitation delivers significant strengthening provided that they are very small (< 2 to 3 nm) in size. By the formation of larger precipitates, this strengthening effect is lost and the flow stress is lower than before precipitation because the solid solution effect is also lost. Likewise, Fujita et al.[36] revealed that the increase of austenite strength caused by Nb addition is largely due to solid solution strengthening.

The observations of the present results, shown in Figures 4(b) and (d), can be explained through the above discussions. In fact, in the higher temperature range, where the highest content of solute Nb is expected, the solid solution strengthening plays its role in the flow stress. In the lower temperature range, however, the Nb solute atoms are expected to form precipitates, leading to the decreased effect of solid solution strengthening. Therefore, the potential strengthening by NbC precipitation is important in this temperature range. Strain-induced precipitation is considered as the most effective mechanism of NbC formation during hot deformation. In the case of Nb-Ti microalloyed steels, however, Ma et al.[25] revealed that TiN can act as substrate for epitaxial growth of NbC during cooling from hot temperatures, leading to absence of the strain-induced precipitation during the following hot rolling process. Similar effect is addressed by Hong et al.[37] regarding the heterogeneous nucleation of (Nb, Ti)C carbides in Nb-Ti microalloyed steels. This claim is also observable in Figure 10(c), where the Nb EDS map gives evidence of Nb concentration on TiN particle at 1000 °C. Therefore, it is believed that the existence of TiN particles in the present steel, as preferred cites of heterogeneous nucleation, inhibits the formation of very fine (< 2 to 3 nm) and dispersed NbC particles. Therefore, no significant strengthening is expected from either the Nb solid solution strengthening or the Nb precipitates at temperatures of T < 1100 °C. At T ≥ 1100 °C, however, as for example shown in Figure 10(d), Nb is dissolved from the preferred sites of TiN, leading to solid solution strengthening. That is why the lines related to the higher range of temperature in Figures 4(b) and (d) are on the right side of the ones related to the lower range of temperature.

The effects of microalloying elements on the retardation of both static and dynamic recrystallization processes are well known.[20,32,38] In this regard, Nb is the strongest element. The retardation effect of Nb on DRX is always quantitatively shown by the critical/peak strain, so that the critical/peak strain increases by the retardation of DRX.[39] Several studies revealed that, while the strain-induced Nb precipitation is more effective to inhibit static recrystallization between hot deformation passes, the solute Nb is more effective to retard DRX.[9,38,40] This is attributed to the pinning effect of Nb on the austenite grain boundaries. Thus, the strain can be accumulated up to higher levels before the occurrence of DRX.[31] The observation of the present study shown in Figure 5(d) can be explained according to this effect. In other words, as a result of the effect of solute Nb on retardation of DRX, the rapid decrease of εp by temperature is diminished at T ≥ 1100 °C. In fact, this observation can be taken as another evidence for solution of NbC precipitates in the higher range of temperature.

It is worthy to note that, despite the mentioned difference between the two ranges of temperature, a single constitutive model is developed for the whole deformation conditions. Based on the results, it can be said that no considerable error is imposed to the model by this approach. It is evident in Figures 6 and 9 that a single constitutive equation can be used for the whole tested temperatures of the present steel. However, more care is needed to extend this conclusion for other steels and conditions. In fact, it is quite possible to see much more significant change of flow behavior by the microalloying elements’ evolutions at various temperatures.

7 Conclusions

Hot deformation behavior of an Nb-Ti microalloyed steel is experimentally evaluated by a series of hot compression tests. Meanwhile, theoretical models are established to assess the hot flow behavior based on the contributing phenomena. The major conclusions can be listed as below:

  1. (1)

    The critical stress at the onset of DRX and the saturation stress of DRV can be derived as functions of the Zener–Hollomon parameter (Z) by the classical hyperbolic sine equation. The predefined activation energy of Q = 270 kJ/mol attributed to the austenite self-diffusion and the predefined exponent of n = 5 along with the same value of α′ fit well to the relationships. This is attributed to the fact that DRV is the only possible softening mechanism regarding the critical and the saturation stresses.

  2. (2)

    The phenomenological constitutive model developed by the combination of the DRV and the DRX models can well predict the experimental flow curves. In this model, Q and n are set to the predefined values and other parameters are determined by fitting them to the experiments.

  3. (3)

    The constitutive model is modified to reduce the number of parameters. For this purpose, a normalized strain is substituted in the DRV model. It is shown that, through this approach, a constant parameter B′ can be used for all deformation conditions. Moreover, the interconnections between dependent parameters are considered to further reduce the number of modeling parameters. Based on the results, despite having three fewer parameters, the modified model is in good agreement with the experiments.

  4. (4)

    There is a distinguished character between the hot flow behaviors in the two ranges T < 1100 °C and T ≥ 1100 °C. According to literature, and consistently with EDS analyses performed on the present material, this can be attributed to the heterogeneous formation of Nb precipitates on TiN particles in the lower range of temperature. Dissolution of Nb precipitates in the higher range of temperature leads to solid solution strengthening and the retardation of DRX. In spite of this, it is shown that a single constitutive equation is accurate enough at all tested temperatures for the studied steel.