Introduction

Numerical simulation technology has been widely applied to the study of metal deformation process in recent years. An accurate constitutive equation for flow stress is the key to improving the accuracy of the numerical simulation. Therefore, it is essential to establish an accurate functional relation between flow stress and deformation parameters. A number of constitutive equations were developed to describe the hot deformation behaviors of alloys (Ref 1-5). These equations can be classified into two groups, namely empirical and physical models. Empirical models focus on phenomenological modeling of the flow stress using mathematical methods. Physical models are based on the deformation mechanisms of alloys. When the physical models have been determined, it is possible to quantitatively explore the rules of materials science during hot deformation process.

The hot deformation of alloys is followed with work hardening (WH) and dynamic recovery (DRV). When the deformation degree exceeds a critical strain for a given temperature and strain rate, dynamic recrystallization (DRX) will occur. The stress-strain relationship in the stage of WH and DRV may be expressed by dislocation model (Ref 5, 6). It is found that the Avrami equation is applicable for describing the DRX kinetics (Ref 7, 8). Therefore, it is complete to establish the physical models to express the stress-strain relationship during high-temperature deformation of alloys once the critical strain for the onset of DRX is determined. When the strain hardening rate is expressed as \( \theta \), or \( \theta = d\sigma /d\varepsilon \), where the \( \sigma \) and \( \varepsilon \) are flow stress and strain, the critical values of flow stress and strain that correspond to the initiation of DRX under arbitrary conditions of deformation can be calculated by a criterion of \( \frac{\partial }{\partial \sigma }\left( { - \frac{\partial \theta }{\partial \sigma }} \right) = 0 \) based on the principles of irreversible thermodynamics (Ref 9). This criterion with a very clear physical meaning has been adopted by many literatures (Ref 10, 11). It also shows that the critical strain can be determined by the stress-strain curve. However, both the calculation of the critical strain and the subsection processing of stress-strain curve are very complicated, so it is necessary to look for a simple method.

The stress-strain curve is an external and comprehensive reflection of the microstructural evolution and deformation mechanisms (Ref 12). It can be used to find the material constants of a constitutive model describing the laws of WH, DRV and DRX, besides the critical strain of the onset of DRX. This set of material constants would be unique if the number of different experimental tests is not less than the constants to be determined in the constitutive model. With this set of constants, we are able not only to determine the constitutive equation of the investigated steel, but also to explore quantitatively the materials science problems of WH, DRV and DRV.

The alloy studied is a low carbon bainitic steel with moderate strength, superior plasticity and good weldability. Previous investigations give a profound attention on the effect of composition and thermodynamic parameters on microstructure and mechanical properties (Ref 13-15). In this paper, a constitutive model which can reflect the deformation mechanisms of the investigated steel has been established; the critical strain and the material constants in the model have been optimized by an inverse analysis of the experimental stress-strain curve, thereby gaining the constitutive equation and the materials models of WH, DRV and DRX for this steel. At the same time, the constitutive equation, the material models, and the methods of obtaining the constitutive equation and material constants have been verified by the experimental data under different deformation states.

Model Establishment

According to the linear theory of WH (Ref 16), the accumulation rate of the dislocation density is as follows:

$$ \frac{{\partial \rho^{ + } }}{\partial \varepsilon } = U\sqrt \rho $$
(1)

where \( U = U_{0} \exp \left( {Q_{u} /RT} \right) \); U 0 is a material constant, m−1; Q u is the activation energy of WH, J/mol; R is the gas constant, J/(mol K); T is the temperature, K; \( \rho \) is the dislocation density; and \( \varepsilon \) is the strain.

Suppose that the annihilation rate of dislocation density is a first-order reaction in DRV (Ref 17), then:

$$ \frac{{\partial \rho^{ - } }}{\partial \varepsilon } = - V\rho $$
(2)

where \( V = V_{0} d^{ - p} \dot{\varepsilon }^{ - q} \exp \left( {Q_{v} /RT} \right) \); V 0 and p are material constants; d is the grain diameter of austenite, μm; \( \dot{\varepsilon } \) is the strain rate, s−1; Q v is the activation energy of DRV, J/mol; and q can be expressed by

$$ q = c_{1} + c_{2} T $$
(3)

where c 1 and c 2 are material constants (Ref 18).

If WH and DRV occur simultaneously, and they are independent of each other, then the variation of dislocation density takes a form of \( d\rho = (U\sqrt \rho - V\rho )d\varepsilon \) (Ref 19, 20), and the dislocation density \( \rho \) can be obtained in the form:

$$ \sqrt \rho = \left[ {\frac{U}{V} + \left( {\sqrt {\rho_{0} } - \frac{U}{V}} \right)\exp \left( { - \frac{V}{2}\varepsilon } \right)} \right] $$
(4)

where \( \rho_{0} \) is the initial dislocation density, which is assumed to be 1012 m−2 (Ref 4).

For a coarse-grain, single-phase material, the relationship between flow stress and dislocation density can be expressed as follows (Ref 21, 22):

$$ \sigma = c\mu b\sqrt \rho $$
(5)

where c is a material constant; b is the magnitude of Burgers vector of dislocations, in the present work, b = 2.6 × 10−10 m (Ref 4); and the temperature-dependent shear modulus can be expressed by

$$ \mu = c_{3} - \frac{{c_{4} }}{{\exp (c_{5} /T) - 1}} $$
(6)

where c 3, c 4 and c 5 are material constants (Ref 23, 24).

Substituting Eq 4 into 5 yields the flow stress of DRV

$$ \sigma_{\text{DRV}} = \sigma_{\text{ss}} + (\sigma_{0} - \sigma_{\text{ss}} )\exp \left( { - \frac{V}{2}\varepsilon } \right) $$
(7)

where \( \sigma_{0} = c\mu b\sqrt {\rho_{0} } \) is the initial stress, MPa; \( \sigma_{\text{ss}} = c\mu bU /V \) is the steady flow stress.

The combined effects of forming temperature and strain rate on deformation behavior of an alloy can be characterized by a temperature-compensated strain rate factor:

$$ Z = \dot{\varepsilon }\exp (Q /RT) $$
(8)

where Q is the deformation activation energy of alloy. The peak stress can be described as \( \sigma_{p} = BZ^{D} \) (Ref 11), where B and D are material constants. Similarly, the stress of complete DRX can be written as

$$ \sigma_{sx} = AZ^{m} $$
(9)

where A and m are material constants (Ref 22).

The volume fraction of DRX can be expressed by \( X_{\text{DRX}} = 1 - \exp \left[ { - k((\varepsilon - \varepsilon_{c} ) /\varepsilon_{p} )^{n} } \right] \) (Ref 10), where \( \varepsilon_{p} \) and \( \varepsilon_{c} \) are the peak and critical strain, respectively, k and n are material constants. Because \( \varepsilon_{c} = \gamma \varepsilon_{p} \) (Ref 25), so

$$ X_{\text{DRX}} = 1 - \exp \left[ { - k(\varepsilon /\varepsilon_{p} - \gamma )^{n} } \right] $$
(10)

where \( \gamma \) is a material constant.

According to the law of mixtures (Ref 26), the flow stress of incomplete DRX can be expressed by

$$ \sigma_{\text{DRX}} = (1 - X_{\text{DRX}} )\sigma_{\text{DRV}} + X_{\text{DRX}} \sigma_{sx} $$
(11)

Because X DRX = 0 in the stage of WH and DRV, so the flow stress during the process of deformation can be written as

$$ \sigma = (1 - X_{\text{DRX}} )\sigma_{\text{DRV}} + X_{\text{DRX}} \sigma_{sx} $$
(12)

where \( \sigma_{\text{DRV}} ,\,\sigma_{sx} \), and \( X_{\text{DRX}} \) can be determined by Eq 7, 9, and 10, respectively.

Experiment Procedures

Materials

The alloy studied is a Mn-Mo-B series bainite steel, its chemical compositions (wt.%) are as follows: 0.053C-0.310Si-1.567Mn-0.014P-0.005S-0.246Mo-0.014Ti-0.236Ni-0.0012B. The steel was in the form of a 30 mm × 300 mm × 450 mm plate which had been hot-rolled. Cylindrical specimens with a height of 15 mm and a diameter of 10 mm were machined from the plate. The axis of the specimen is selected in the direction of the plate thickness.

Method

Hot compression tests were conducted on a Gleeble-1500 thermo-mechanical simulator. Four different temperatures (1173, 1273, 1373, 1473 K) and four different strain rates (0.01, 0.1, 1, 10 s−1) were used in hot compression tests. In order to minimize friction and try to keep the cylindrical shape of specimens unchanged during tests, graphite powder was put in the two grooves of a diameter of 6 mm and a height of 0.2 mm specially made on both ends of each specimen.

Specimens were first heated to 1473 K at a rate of 10 K/s, homogenized at that temperature for 5 min, and cooled to the deformation temperature at a rate of 3 K/s by cooling gas of He, then held isothermally for 2 min to eliminate the thermal gradient before deformation, and finally compressed to ε = ln(H/h) = 0.7 (Ref 11, 27).

After isothermal compression, specimens were immediately water-quenched to preserve the high-temperature microstructure. Selected deformed specimens were axially sectioned and prepared for metallographic examination using standard techniques. All microstructures were observed by optical microscopy of Axiovert 25.

Results

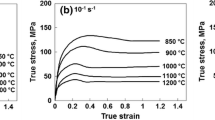
The true stress-true strain data were recorded automatically by the testing system in the isothermal compression process. The experimental results of a strain rate of 0.1 s−1 and a temperature of 1373 K are illustrated in Fig. 1(a) and (b), respectively. The microstructure of a specimen deformed at 1373 K and 0.1 s−1 is shown in Fig. 1(c).

Fig. 1
figure 1

Experimental stress-strain curves and microstructure of a specimen deformed at 1373 K and 0.1 s−1

Full size image

It can be found that there are three types of stress-strain curves: The first is characterized by the increase in flow stress with strain, which is demonstrated by the curve marked 10 s−1 shown in Fig. 1(b); the second is characterized by a saturation stress with increasing strain, which is displayed in the curve marked 1173 K shown in Fig. 1(a); and the last is composed of three stages: WH, softening and steady stage. In WH stage, the softening effect of DRV is too weak to balance the hardening effect of the continuous increase in dislocation, resulting in that the flow stress increases with the increase in strain. In the softening stage, the DRX occurs when the dislocation density reaches a critical value. The DRX will cause the annihilation of dislocations, and consequently, the flow stress will decrease. In the steady stage, the flow stress keeps a constant nearly due to the balance between the WH and dynamic softening (Ref 4).

Analysis

Data Treatment

There will be 16 constants to be determined for establishing a stress-strain relationship of the steel investigated; they are material constants of c, c 1, c 2, c 3, c 4, c 5, U 0, Q u , V 0 d −p, Q v , k, n, γ, Q, A and m. Let the stress measured by experiment and the one calculated from Eq 12 at a strain of \( \varepsilon_{i} \) be \( \sigma_{mi} \) and \( \sigma_{ci} \), respectively, the material constants can then be obtained by minimizing the value of function \( y = \sum\nolimits_{{i{ = 1}}}^{{n_{i} }} {\left( {1 - \sigma_{ci} /\sigma_{mi} } \right)^{2} } \)(where \( n_{i} \) is the group number of strain-stress measured experimentally). This optimizing procedure is to ensure that the stress-strain curves calculated from the material constants are the closest to those measured experimentally.

The coordinate rotation method is a common optimization technique. The computation is carried out along each coordinate direction alternately, in which only the value of the optimized coordinate is changed, whereas other variables remain unchanged. The optimal values obtained by the coordinate rotation method with a convergence accuracy of 0.5% for each optimization parameter are shown in Table 1.

Table 1 Optimal values
Full size table

The relationship between the shear modulus of steel and temperature can be determined by substituting the optimal material constants into Eq 6:

$$ \mu = 8881.92 - \frac{924.01}{{\exp \left[ {165.62 /T} \right] - 1}} $$
(13)

Parameter q can be determined by equation:

$$ q = 0.05066 + 6.87 \times 10^{ - 5} \,T $$
(14)

The activation energy of WH Q u  = 2.6177 × 104 J/mol, and

$$ U = 7.1104 \times 10^{8} \exp \left( { - \frac{{26{,}177.11}}{RT}} \right) $$
(15)

The activation energy of DRV Q v  = 3.7214 × 104 J/mol, so

$$ V = 1080.66\dot{\varepsilon }^{{ - 0.05066 - 6.87 \times 10^{ - 5} T}} \exp \left( { - \frac{{37{,}214.84}}{RT}} \right) $$
(16)

The volume fractions of DRX

$$ X_{\text{DRX}} = 1 - \exp \left[ { - 0.593085(\varepsilon /\varepsilon_{p} - 0.886463)^{1.833593} } \right] $$
(17)

The activation energy of deformation Q = 436,587.88 J/mol. The flow stress of complete DRX can be expressed by

$$ \sigma_{sx} = 0.0868332Z^{0.169886} $$
(18)

Besides, according to (Ref 18), the volume fractions of DRV

$$ X_{\text{DRV}} = 1 - \exp \left[ { - 540.33\dot{\varepsilon }^{{ - 0.05066 - 6.87 \times 10^{ - 5} T}} \exp \left( { - 37{,}214.84 /RT} \right)\varepsilon } \right] $$
(19)

Experimental Verification

A comparison between the experimental and calculated stress-strain curves was carried out in a wide range of strain, strain rate, and temperature to verify the accuracy of the constitutive equation. The results show a good agreement of the calculated and experimental curves under entire experimental conditions. As an example, the results of a temperature of 1273 K and a strain rate of 1 s−1 are shown in Fig. 2(a) and (b), respectively.

Fig. 2
figure 2

Comparison between calculated and experimental stresses

Full size image

Another comparison between the experimental and calculated values of flow stress is shown in Fig. 2(c). The slope of the regression line is 1.00506, showing that most of the data points lie fairly close to the best regression line. The correlation coefficient is 0.994862, indicating that a good correlation between the experimental and calculated data was achieved.

It is also shown that the relative errors of flow stress are mostly <3% except when the strain is <0.026, and the average absolute relative error is 3.56%. Obviously, the constitutive equation with its higher precision can be used to calculate the energy consumption and to analyze the deformation process of the steel. Average absolute relative error can be used as an unbiased statistical parameter for evaluating the deviation from the predicted flow stress; therefore, the constitutive equation based on dislocation theory, WH and DRV theory and softening mechanism of DRX can well describe the high-temperature deformation behavior of the investigated steel.

Discussion

The Material Constant

A comparison of material constants between literature (Ref 18) and this paper is shown in Table 2. It indicates that the values obtained by two different methods are similar.

Table 2 Comparison of material constants
Full size table

The Flow Stress of Complete DRX

A comparison of flow stresses of complete DRX between the experimental and calculated by Eq 18 is shown in Fig. 3(a). The correlation coefficient of 0.977328 indicates that the calculated values agree well with those measured, demonstrating that the material constants determined by the stress-strain curves and the constitutive model can capture the underlying materials science of high-temperature deformation.

Fig. 3
figure 3

Comparison between the calculated and experimental stresses of complete DRX (a) and initiation of DRX (b)

Full size image

The Critical Stress of DRX

The ratio of critical strain to peak strain equals to 0.886463 according to Eq 17, which is located between 0.6 and 0.9 as (Ref 28) indicated. The critical stress \( \sigma_{c} \) of DRX can be calculated by applying this relationship to the stress-strain data measured in different deformation parameters, or by using the criterion of \( \frac{\partial }{\partial \sigma }\left( { - \frac{\partial \theta }{\partial \sigma }} \right) = 0 \). A comparison of the critical stresses determined by the two methods is shown in Fig. 3(b). Clearly, both results are in good agreement.

The relation between \( \sigma_{c} \) and the peak stress \( \sigma_{p} \) is \( \sigma_{c} = (0.997658 \pm 0.0008502)\sigma_{p} \), meaning the critical stress is about 0.25% smaller than the peak one. The linear regression of the peak stresses measured and the values of Z determined by Eq 8 results in the material constants B = 0.434786 and D = 0.13326, meaning \( \sigma_{p} = 0.434786Z^{0.13326} \). Similarly, the critical stress can be expressed as \( \sigma_{c} = 0.436158Z^{0.1331} \), so \( \sigma_{c} /\sigma_{p} = 1.003155Z^{ - 0.00016} \), indicating that the smaller the Zener-Hollomon parameter is, the smaller the difference between \( \sigma_{c} \) and \( \sigma_{p} \).

Kinetics of DRV and DRX

The kinetics of DRV can be determined by Eq 19. The variations in the volume fraction of DRV with strain at deformation temperature of 1173 K are shown in Fig. 4(a). Similarly, the kinetics of DRX can be calculated by Eq 17. The variations in the volume fraction of DRX with strain at a strain rate of 0.1 s−1 are shown in Fig. 4(b). As expected, the volume fractions of DRV or DRX increase with the increase in strain. The smaller the strain rate is, the smaller the strain of complete DRV. The higher the deforming temperature is, the faster the process of DRX.

Fig. 4
figure 4

Variations of X DRV and X DRX with strain under different deformation parameters

Full size image

Conclusion

A constitutive model during high-temperature deformation can be established based on dislocation theory, work hardening and dynamic recovery theory, and softening mechanisms of dynamic recrystallization. An inverse analysis of the stress-strain curve measured experimentally has been proposed to determine the model constants for the relevant materials science and to establish the constitutive equation. Predictions of materials science models and the constitutive equation are in good agreement with the test results of stress-strain curves for a bainite steel. This agreement confirms that the constitutive model and the inverse analysis method are effective to determine the material constants and the constitutive equation from the measured stress-strain data. The analysis method can be extended to other coarse-grain, single-phase alloys.