Abstract
This paper presents a class of efficient Newton-type algorithms for solving the nonlinear programs (NLPs) arising from applying a direct collocation approach to continuous time optimal control. The idea is based on an implicit lifting technique including a condensing and expansion step, such that the structure of each subproblem corresponds to that of the multiple shooting method for direct optimal control. We establish the mathematical equivalence between the Newton iteration based on direct collocation and the proposed approach, and we discuss the computational advantages of a lifted collocation integrator. In addition, we investigate different inexact versions of the proposed scheme and study their convergence and computational properties. The presented algorithms are implemented as part of the open-source ACADO code generation software for embedded optimization. Their performance is illustrated on a benchmark case study of the optimal control for a chain of masses. Based on these results, the use of lifted collocation within direct multiple shooting allows for a computational speedup factor of about 10 compared to a standard collocation integrator and a factor in the range of 10–50 compared to direct collocation using a general-purpose sparse NLP solver.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Direct optimal control methods solve a continuous time optimal control problem (OCP) by first performing a discretization and then solving the resulting nonlinear program (NLP). This paper considers the direct numerical solution of a nonlinear OCP as it often appears in nonlinear model predictive control (NMPC), which reads as follows in continuous time:
where T is the control horizon length, \(x(t) \in {\mathbb {R}}^{n_{\mathrm {x}}}\) denotes the states of the system and \(u(t) \in {\mathbb {R}}^{n_{\mathrm {u}}}\) are the control inputs. This parametric OCP depends on the initial state \(\hat{x}_0\in {\mathbb {R}}^{n_{\mathrm {x}}}\) through Eq. (1b) and the objective in (1a) is defined by the stage cost \(\ell (\cdot )\). The nonlinear dynamics in Eq. (1c) are formulated as an implicit system of ordinary differential equations (ODE). The path constraints are defined by Eq. (1d) and can also be nonlinear in general. We assume in the following that the functions \(\ell (\cdot )\), \(f(\cdot )\) and \(h(\cdot )\) are twice continuously differentiable in all their arguments. The discussion in this paper can be easily extended to a general OCP formulation including an index 1 differential algebraic equation (DAE) [70] and a terminal cost or terminal constraint [20]. However, for the sake of simplicity regarding our presentation of the lifted collocation integrators, we omit these cases in the following, and even dismiss the path constraints (1d). A further discussion on the treatment of such inequality constraints in direct optimal control methods can, for example, be found in [9, 13, 61, 63].
Popular approaches to tackle the continuous time OCP in Eq. (1) are multiple shooting [17] and direct transcription [9, 11]. Both techniques treat the simulation and optimization problem simultaneously instead of sequentially. Note that this paper will not consider any sequential or quasi-sequential approaches, since they are generally difficult to apply to unstable systems [44]. While direct multiple shooting can employ any integration scheme, a popular transcription technique is known as direct collocation. It embeds the equations of a collocation method [42] directly into the constraints of the large-scale NLP [12]. A more detailed comparison will be made in the next section. In both cases, a Newton-type algorithm is able to find a locally optimal solution for the resulting NLP by solving the Karush–Kuhn–Tucker (KKT) conditions [56]. In the presence of inequality constraints for Newton-type optimization, the KKT conditions are solved via either the interior point (IP) method [13, 56] or sequential quadratic programming (SQP) [18].
Nonlinear model predictive control (NMPC) is an advanced technique for real-time control, which can directly handle nonlinear dynamics, objective and constraint functions [55]. For this purpose, one needs to solve an OCP of the form in Eq. (1) at each sampling instant, where \(\hat{x}_0\) denotes the current state estimate for the system of interest. Tailored online algorithms for direct optimal control have been proposed [30, 50] to solve such a sequence of parametric OCPs. These methods can rely on other tools to provide a good first initialization of all primal and dual variables in the optimization algorithm. By using a continuation technique [30, 57] for parametric optimization in combination with a shifting strategy to obtain an initial guess for the new OCP from the solution of the previous problem, the online algorithm can typically stay within its region of local convergence [14]. This paper therefore omits globalization strategies, even though the presented techniques can be extended to an offline framework including such global convergence guarantees [13, 56].
A real-time iteration (RTI) scheme for direct optimal control in the context of NMPC is proposed in [29], which uses the multiple shooting method in combination with SQP to solve the resulting NLP. Direct multiple shooting typically profits from using solvers for ODE or DAE with an efficient step size and order selection [17]. However, within a real-time framework for embedded applications, one can also implement multiple shooting using fixed step integrators [70, 74] to result in a deterministic runtime and to satisfy the real-time requirements. In case an implicit integration scheme is used for either stiff or implicitly defined dynamics, one needs to implement a Newton method for the integrator, which is used within the Newton-type optimization algorithm.
A novel approach based on the lifted Newton method [5] was recently proposed for embedding these implicit integrators within a Newton-type optimization framework [66]. It has been shown that direct multiple shooting using this lifted collocation method results in the same Newton-type iterations as for the direct collocation NLP formulation, and this based on either the Gauss-Newton (GN) [66] or an Exact Hessian scheme [68]. In Sect. 3 we review these results in a general framework, independent of the Newton-type optimization algorithm. An important advantage of the lifted collocation approach is that one solves subproblems having the structure and dimensions of the multiple shooting method, for which efficient embedded solvers exist, based on dense linear algebra routines such as qpOASES [35], FORCES [33], qpDUNES [36] and HPMPC [38]. The lifted collocation integrator can therefore be considered an alternative, parallelizable strategy to exploit the direct collocation problem structure within multiple shooting without relying on a generic permutation of matrices within sparse linear algebra packages. A similar idea of using specialized linear algebra to solve the KKT system for direct collocation has been proposed in [49, 77, 78], based on interior point methods and Schur complement techniques.
The lifted collocation scheme has been extended to exact Hessian based optimization by using a symmetric forward-backward propagation technique as discussed in [68]. In addition, it has been proposed in [65] that this lifting approach can be extended to the use of efficient inexact Newton-type methods for collocation. In the present paper, we will consider general techniques to obtain a Jacobian approximation for the collocation method, which is cheap to evaluate, factorize and reuse for the corresponding linear system solutions. Note that an alternative approach makes use of inexact solutions to the linearized subproblems in order to reduce the overall computational burden of the Newton-type scheme [23, 24]. Popular examples of an efficient Jacobian approximation are the Simplified Newton [10, 21] and Single Newton [22, 40] type iterations for implicit Runge–Kutta (IRK) methods. A standard inexact Newton-type optimization algorithm would rely on the computation of adjoints to allow convergence to a local minimizer of the original NLP [16, 32]. Instead, one could also implement a scheme to iteratively obtain the forward sensitivities [65], which we will refer to as the Inexact Newton scheme with Iterated Sensitivities (INIS) [67]. In the present article, we will consider these inexact lifted collocation schemes in a general Newton-type framework [25, 26], which allows us to summarize their local convergence properties.
Following the active development of tailored optimization algorithms, many software packages are currently available for direct optimal control. For example, MUSCOD-II [31] is a multistage dynamic optimization software based on direct multiple shooting and SQP [52]. The software dsoa [34] is an optimal control tool based on single shooting. In addition to these shooting-based software packages, there are other approaches based on direct collocation, which typically combine Algorithmic Differentiation (AD) [41] with a general-purpose sparse NLP solver such as Ipopt [75]. A few examples of such software packages are CasADi [7], GPOPS-II [60] and PROPT [73]. An important contribution of this article is the open-source implementation of the lifted collocation integrators in the ACADO Toolkit [46] for nonlinear optimal control, as a part of its code generation tool, originally presented in [47, 70]. Other software packages for real-time NMPC are, for example, OptCon [72], NEWCON [71] and VIATOC [48]. In the context of real-time optimal control on embedded hardware, the technique of automatic code generation has experienced an increasing popularity over the past decade [54, 58]. The ACADO code generation tool allows one to export efficient, self-contained C-code based on the RTI algorithm for real-time NMPC in the milli- or even microsecond range [6, 74].
1.1 Contributions and outline
This article presents a lifted collocation method. We discuss the connection of this scheme to multiple shooting and direct collocation in a general framework, independent of the Newton-type optimization method. This connection is illustrated in Fig. 2, while the advantages and disadvantages of using lifted collocation are detailed by Table 1. In addition, this article proposes and studies two alternative approaches for inexact lifted collocation based on either an adjoint derivative propagation or on iterated forward sensitivities. These variants of lifted collocation are detailed in Algorithms 1–4 and an overview is presented in Table 2. Another important contribution of this article is the open-source implementation of these novel lifting schemes within the ACADO code generation tool for embedded applications of real-time optimal control. The performance of this software package is illustrated on the benchmark case study of the optimal control for a chain of masses. Based on these numerical results, the use of lifted collocation within direct multiple shooting allows for a computational speedup factor of about 10 compared to a standard collocation integrator and a factor in the range of 10–50 compared to direct collocation using a general-purpose sparse NLP solver. In addition, these results illustrate that the INIS-type lifted collocation schemes from Algorithms 3 and 4 often show a considerably improved local contraction rate compared to an adjoint-based inexact Newton method, while using the same Jacobian approximation.
The paper is organized as follows. Section 2 briefly presents simultaneous approaches for direct optimal control and introduces Newton-type optimization. The exact lifted collocation integrator for direct multiple shooting is presented in Sect. 3, including a detailed discussion of its properties. Section 4 proposes a Newton-type optimization approach based on inexact lifted collocation and an adjoint derivative propagation. Advanced inexact lifted collocation methods based on an iterative scheme to compute sensitivities are discussed in Sect. 5. Section 6 presents an open-source software implementation of the proposed algorithms in the ACADO code generation tool, followed by a numerical case study in Sect. 7.
2 Direct optimal control methods
Direct optimal control [17] tackles the continuous time OCP (1) by forming a discrete approximation and solving the resulting NLP. As mentioned earlier, the inequality constraints (1d) will be omitted without loss of generality, because the presented integrators only affect the system dynamics in Eq. (1c). For the sake of simplicity, we consider here an equidistant grid over the control horizon consisting of the collection of time points \(t_i\), where \(t_{i+1}-t_i = \frac{T}{N} =: T_s\) for \(i=0, \ldots , N-1\). Additionally, we consider a piecewise constant control parametrization \(u(\tau ) = u_i\) for \(\tau \in [t_i,t_{i+1})\).
2.1 Implicit integration and collocation methods
This article considers the dynamic system in Eq. (1c) to be either stiff or implicitly defined, such that an implicit integration method is generally required to numerically simulate this set of differential equations [42]. The aim is to compute a numerical approximation of the terminal state \(x(t_{i+1})\) of the following initial value problem
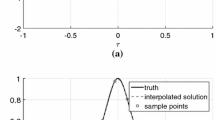
For this purpose, let us introduce the family of collocation methods, which form a subclass of Implicit Runge–Kutta (IRK) methods [42], even though the lifting techniques proposed in the present paper can be readily generalized to any implicit single-step integration method. The concept of a collocation method is illustrated by Fig. 1 for one specific shooting interval \([t_i,t_{i+1})\), where \(i = 0, \ldots , N-1\). The representation of the collocation polynomial is adopted from the textbook [42] and is referred to as the Runge–Kutta basis representation in [13]. To obtain the variables \(K_{i}\) describing this polynomial, one needs to solve the following system of collocation equations
where \(w_{i} := (x_i,u_i)\), q denotes the number of collocation nodes and the matrix \([A]_{ij} := a_{i,j}\) the coefficients of the method [42]. To later make a clear connection with the direct collocation parametrization for optimal control, this paper restricts itself to a constant integration step size \(T_{\mathrm {int}} := \frac{T_s}{N_{\mathrm {s}}}\) based on a fixed number of integration steps, \(N_{\mathrm {s}}\), which additionally simplifies the notation. The variables \(k_{i,j}^s \in {\mathbb {R}}^{n_{\mathrm {x}}}\) are collectively denoted by \(K_{i} := (K_{i,1}, \ldots , K_{i,N_{\mathrm {s}}}) \in {\mathbb {R}}^{n_{\mathrm {K}}}\) with \(K_{i,j} := (k_{i,j}^1, \ldots , k_{i,j}^q)\) for \(i = 0, \ldots , N-1\) and \(j = 1, \ldots , N_{\mathrm {s}}\). The intermediate values \(x_{i,j}\) are defined by the collocation variables and by the weights \(b_s\) of the q-stage method
where \(x_{i,0} = x_i\). The simulation result can then be obtained as \(x_{i,N_{\mathrm {s}}} = x_{i} + B \, K_{i}\) in which B is a constant matrix that depends on the fixed step size \(T_{\mathrm {int}}\) and the variables \(K_i\) satisfy the collocation equations \(G(w_{i},K_{i}) = 0\). Note that the Jacobian matrix \(\frac{\partial G(\cdot )}{\partial K_i}\) is nonsingular for a well defined set of differential equations in (2) and a sufficiently small integration step size [42].
2.2 Direct multiple shooting
A direct multiple shooting discretization [17] of the OCP in (1) results in the following NLP
with state \(X=[x_0^\top ,\ldots , x_N^\top ]^\top \) and control trajectory \(U=[u_0^\top ,\ldots , u_{N-1}^\top ]^\top \). In what follows, all the optimization variables for this NLP (5) can also be referred to as the concatenated vector \(W=[x_0^\top ,u_0^\top ,\ldots ,x_N^\top ]^\top \in {\mathbb {R}}^{n_{\mathrm {W}}}\), where \(n_{\mathrm {W}}= n_{\mathrm {x}}+N(n_{\mathrm {x}}+n_{\mathrm {u}})\). The function \(\phi (\cdot )\) denotes a numerical simulation of the dynamics, e.g., based on a fixed step collocation method as introduced in the previous subsection. Note that step size control can provide guarantees regarding the accuracy of the numerical simulation, which typically yields a reduced overall number of integration steps [42]. See, e.g., [4, 8, 43] for more details about the use of step size control especially within direct optimal control. The present paper restricts itself to the fixed step case of direct collocation [13], which is often acceptable for fast real-time applications [6, 74]. The absence of step size control will however be considered one of the disadvantages for the proposed lifting scheme in Table 1.
In the case of a fixed step collocation method, the function \(\phi (\cdot )\) can be defined as
where the collocation variables are obtained by solving the system of equations in (3), which depends on the state \(x_i\) and control input \(u_i\). The Lagrangian of the NLP in (5) is given by
where \(\lambda _i\) for \(i = 0, \ldots , N-1\) denote the multipliers corresponding to the continuity constraints (5c) and \(\lambda _{-1}\) denotes the multiplier of the initial value condition (5b). Note that the stage cost \(l(\cdot )\) in combination with the terminal cost \(m(\cdot )\), represents a discrete time approximation of the integral objective in Eq. (1a), which can be obtained efficiently by, e.g., extending the dynamics (1c) with quadrature states [43]. More information on quadrature variables and their efficient treatment within collocation methods, can be found in [64].
2.3 Direct collocation
Direct collocation differs from multiple shooting in the sense that it carries out the numerical simulation of the continuous time dynamics directly in the NLP, see [13]. More specifically, one treats the collocation equations (3) as constraints in the OCP, and the collocation variables as decision variables. The resulting structured NLP reads as
where \(w_{i} := (x_i,u_i)\) and \(z_{i} := (w_i,K_i)\) and all optimization variables can be concatenated into one vector
for which \(n_{\mathrm {Z}}= n_{\mathrm {W}}+Nn_{\mathrm {K}}= n_{\mathrm {x}}+N(n_{\mathrm {x}}+n_{\mathrm {u}}+n_{\mathrm {K}})\). The Lagrangian for the direct collocation NLP (8) is given by
where \(\lambda _i\) for \(i = 0, \ldots , N-1\) are defined as before in Eq. (7) and \(\mu _i\) for \(i = 0, \ldots , N-1\) denote the multipliers corresponding to the collocation equations (8c). For simplicity of notation, we assume in this paper that the stage cost does not depend on the collocation variables even though there exist optimal control formulations where this function instead reads \(\tilde{l}(w_i,K_i)\), e.g., based on continuous output formulas [70].
We further rely on the following definition and assumption, regarding the local minimizers of the NLPs in Eqs. (5) and (8).
Definition 1
A minimizer of an equality constrained NLP is called a regular KKT point if the linear independence constraint qualification (LICQ) and the second-order sufficient conditions (SOSC) are satisfied at this point [56].
Assumption 2
The local minimizers of the NLPs in Eqs. (5) and (8) are assumed to be regular KKT points.
Remark 3
Based on our expression for the continuity map \(\phi (x_i,u_i)\) in Eq. (5c) defining a fixed step collocation method, both multiple shooting and direct collocation solve the same nonlinear optimization problem. Therefore, a regular KKT point \((W^\star ,K^\star ,{\varLambda }^\star ,\mu ^\star )\) to the direct collocation based NLP (8) forms by definition also a regular KKT point \((W^\star ,{\varLambda }^\star )\) to the multiple shooting problem in Eq. (5) and vice versa.
2.4 Newton-type optimization
This paper considers the use of a Newton-type optimization method to solve the necessary Karush–Kuhn–Tucker (KKT) conditions of the nonlinear program [56]. Let us introduce this approach for equality constrained optimization for both the multiple shooting (5) and collocation based (8) NLPs. In case of direct multiple shooting, a Newton-type scheme iterates by sequentially solving the following linearized system

using the compact notation \({\varDelta }W := ({\varDelta }w_0, \ldots , {\varDelta }w_N)\), \(w_{i} := (x_i,u_i)\), \({\varDelta }w_i := w_i - \bar{w}_i\) for \(i = 0, \ldots , N-1\) and \({\varDelta }w_N := {\varDelta }x_N\). The values \(\bar{w}_{i} := (\bar{x}_i,\bar{u}_i)\) denote the current linearization point instead of the optimization variables \(w_i\) and they are updated in each iteration by solving the QP subproblem (11), i.e., \(\bar{W}^+ = \bar{W} + {\varDelta }W\) in the case of a full Newton step [56]. The matrices \(A \in {\mathbb {R}}^{n_{\mathrm {W}}\times n_{\mathrm {W}}}\), \(C \in {\mathbb {R}}^{(N+1)n_{\mathrm {x}}\times n_{\mathrm {W}}}\) are defined as

in which \(C_i := \left[ \frac{\partial \phi (\bar{w}_i)}{\partial w_i}, \, -{\mathbbm {1}}_{n_{\mathrm {x}}}\right] \) and \(A_i := \nabla _{w_i}^2 {\mathcal L}_i(\bar{w}_i,\bar{\lambda }_i)\), \(A_N := \nabla _{x_N}^2 m(\bar{x}_N)\) when using an exact Hessian based Newton method [56]. The Lagrangian term on each shooting interval is thereby defined as \({\mathcal L}_i(\bar{w}_i,\bar{\lambda }_i) = l(\bar{w}_i) + \bar{\lambda }_i^\top \left( \phi (\bar{w}_i) - \bar{x}_{i+1}\right) \). Note that the initial value condition is included with a term \(\bar{\lambda }_{-1}^\top \left( \bar{x}_0 - \hat{x}_0\right) \) for the first shooting interval \(i=0\), as in Eq. (7). In case of a least squares objective \(l(w_i) = \frac{1}{2}\Vert F(w_i)\Vert _2^2\), one could alternatively use a Gauss-Newton Hessian approximation such that \(A_i := \frac{\partial F(\bar{w}_i)}{\partial w_i}^\top \frac{\partial F(\bar{w}_i)}{\partial w_i}\) [15]. The right-hand side in the KKT system (11) consists of \(a \in {\mathbb {R}}^{n_{\mathrm {W}}}\) and \(c \in {\mathbb {R}}^{(N+1)n_{\mathrm {x}}}\) defined by
in which \(c_i := \phi (\bar{w}_i) - \bar{x}_{i+1}\) and \(a_i := \nabla _{w_i} {\mathcal L}(\bar{W},\bar{{\varLambda }})\), \(a_N := \nabla _{x_N} {\mathcal L}(\bar{W},\bar{{\varLambda }})\).
In a similar fashion, the linearized KKT system can be determined for the direct collocation based NLP (8) as

where the matrices \(A_\mathrm {c} \in {\mathbb {R}}^{n_{\mathrm {Z}}\times n_{\mathrm {Z}}}\), \(D \in {\mathbb {R}}^{Nn_{\mathrm {K}}\times n_{\mathrm {Z}}}\) are block diagonal and defined by \(A_{\mathrm {c},i} := \nabla _{z_i}^2 {\mathcal L}_i^{\mathrm {c}}(\bar{z}_i,\bar{\lambda }_i,\bar{\mu }_i)\) and \(D_i := \frac{\partial G(\bar{z}_i)}{\partial z_i}\). In case of a Gauss–Newton Hessian approximation when \(l(w_i) = \frac{1}{2}\Vert F(w_i)\Vert _2^2\), one has  instead. The constant matrix \(E \in {\mathbb {R}}^{(N+1)n_{\mathrm {x}}\times n_{\mathrm {Z}}}\) corresponds to the Jacobian for the continuity constraints (8d) and is given by
instead. The constant matrix \(E \in {\mathbb {R}}^{(N+1)n_{\mathrm {x}}\times n_{\mathrm {Z}}}\) corresponds to the Jacobian for the continuity constraints (8d) and is given by

The Lagrangian term on each shooting interval now reads as \({\mathcal L}_i^{\mathrm {c}}(\bar{z}_i,\bar{\lambda }_i,\bar{\mu }_i) = l(\bar{w}_i) + \bar{\lambda }_i^\top \left( \bar{x}_{i} + B \, \bar{K}_{i} - \bar{x}_{i+1}\right) + \bar{\mu }_i^\top G(\bar{w}_{i},\bar{K}_{i})\) in Eq. (10). The right-hand side components \(a_\mathrm {c} \in {\mathbb {R}}^{n_{\mathrm {Z}}}\), \(e \in {\mathbb {R}}^{(N+1)n_{\mathrm {x}}}\) and \(d \in {\mathbb {R}}^{Nn_{\mathrm {K}}}\) in the linear system (12) can be defined similarly to those of (11) in which \(a_{\mathrm {c},i} := \nabla _{z_i} {\mathcal L}^{\mathrm {c}}(\bar{Z},\bar{{\varLambda }},\bar{\mu })\), \(a_{\mathrm {c},N} := \nabla _{x_N} {\mathcal L}^{\mathrm {c}}(\bar{Z},\bar{{\varLambda }},\bar{\mu })\), \(d_i := G(\bar{w}_{i},\bar{K}_{i})\) and \(e_i := \bar{x}_{i} + B \, \bar{K}_{i} - \bar{x}_{i+1}\).
3 Exact lifted collocation integrator for multiple shooting
Unlike [66, 68], let us derive the proposed lifted collocation scheme directly from the subproblem in Eq. (12) arising from the Newton steps on the direct collocation problem formulation. Figure 2 provides an overview of the equations for direct collocation and multiple shooting, both using the standard integrator and with the proposed lifted collocation method.
3.1 Structure exploitation for direct collocation
We propose a condensing technique deployed on the Newton step for the direct collocation problem. This allows for the transformation of Eq. (12) into the form of (11) and thereby application of the tools developed for the multiple shooting approach. We present this result as the following proposition.
Proposition 4
Algorithm 1 solves the linearized direct collocation KKT system in Eq. (12) by performing a condensing technique, followed by solving a multiple shooting type KKT system of the form (11) and a corresponding expansion procedure to obtain the full solution \(\left( {\varDelta }Z, {\varDelta }{\varLambda }, {\varDelta }\mu \right) \).
Proof
Let us start with the following expressions resulting from the continuity and collocation equations on the second and third line of the direct collocation based KKT system (12), i.e.,
for each \(i = 0, \ldots , N-1\), where the previous definition of the matrices \(D_i\) and E has been used and, additionally, \(d_i = G(\bar{z}_i)\) and \(e_i = \bar{x}_{i} + B \, \bar{K}_{i} - \bar{x}_{i+1}\). Since the Jacobian \(\frac{\partial G(\bar{z}_i)}{\partial K_i}\) is nonsingular [42], one can eliminate the collocation variables \({\varDelta }K_i = {\varDelta }\tilde{K}_i + K_i^w {\varDelta }w_i\) from the subsystem, which reads as
where \(\tilde{e}_i := e_i + B\, {\varDelta }\tilde{K}_i\) and the auxiliary variables
have been defined. Subsequently, let us look at the first line of the direct collocation based KKT system (12),

where the matrix  is defined. Since \({\varDelta }K_i = {\varDelta }\tilde{K}_i + K_i^w {\varDelta }w_i\), we may write
is defined. Since \({\varDelta }K_i = {\varDelta }\tilde{K}_i + K_i^w {\varDelta }w_i\), we may write  which, when applied to (15), yields
which, when applied to (15), yields

Additionally, we observe that
where \(\frac{{\mathrm {d}}z_i}{{\mathrm {d}}w_i}^\top = \begin{bmatrix} {\mathbbm {1}}_{n_{\mathrm {w}}}&K_i^{w^\top } \end{bmatrix}\). This can be used to simplify Eq. (16). Left multiplying both sides of (16) with \(\frac{{\mathrm {d}}z_i}{{\mathrm {d}}w_i}^\top \) results in

where the Hessian matrix can be written as
in which \(H_i := \frac{{\mathrm {d}}z_i}{{\mathrm {d}}w_i}^\top \langle \bar{\mu }_i,\nabla _{z_i}^2 G_{i} \rangle \, \frac{{\mathrm {d}}z_i}{{\mathrm {d}}w_i}\) is the condensed Hessian contribution from the collocation equations. Here, the notation \(\langle \bar{\mu },\nabla _{z}^2 G \rangle = \sum _{r=1}^{n_{\mathrm {K}}} \bar{\mu }_r \frac{\partial ^2 G_r}{\partial z^2}\) is used. The right-hand side reads as

where we used \(\frac{\partial G(\bar{z}_i)}{\partial z_i}\frac{{\mathrm {d}}z_i}{{\mathrm {d}}w_i} = 0\) and \(h_i := \frac{{\mathrm {d}}z_i}{{\mathrm {d}}w_i}^\top \langle \bar{\mu }_i,\nabla _{z_i,K_i}^2 G_{i} \rangle \, {\varDelta }\tilde{K}_i\).
Based on this numerical elimination or condensing of the collocation variables \({\varDelta }K_i\), the KKT system from Eq. (12) can be rewritten in the multiple-shooting form of Eq. (11), where the matrices C and A are defined by
respectively. The vectors c and a on the right-hand side of the system are defined by

for each \(i = 0, \ldots , N-1\). After solving the resulting multiple shooting type KKT system (11), one can obtain the full direct collocation solution by performing the following expansion step for the lifted variables K and \(\mu \):
using the Newton step \(({\varDelta }W,{\varDelta }{\varLambda })\) and \(\bar{\lambda }_i^+ = \bar{\lambda }_i + {\varDelta }\lambda _i\). The expansion step (21) for the Lagrange multipliers \(\mu _i\) can be obtained by looking at the lower part of the KKT conditions in Eq. (15),
which can be rewritten as
\(\square \)

Remark 5
Algorithm 1 can be readily extended to nonlinear inequality constrained optimization, since the lifted collocation integrator is not directly affected by such inequality constraints. More specifically, the presence of inequality constraints only influences the computation of the step direction based on the KKT conditions [56]. Therefore, the lifted collocation scheme can, for example, be implemented within an SQP method [18] by linearizing the inequality constraints and solving the resulting QP subproblem to compute the step direction in Algorithm 1. Note that such an SQP type implementation is performed in the ACADO Toolkit as presented later in Sect. 6. Similarly, an IP method [13] could be implemented based on the lifted collocation integrator so that the step direction computation in Algorithm 1 involves the solution of the primal-dual interior point system.
Remark 6
Proposition 4 presents a specific condensing and expansion technique that can also be interpreted as a parallelizable linear algebra routine to exploit the specific direct collocation structure in the Newton method. The elimination of the collocation variables by computing the corresponding quantities in Eqs. (19) and (20) can be performed independently and therefore in parallel for each shooting interval \(i = 0, \ldots , N-1\) as illustrated by Fig. 3. The same holds true for the expansion step in Eq. (21) to recover the full solution.
3.2 The exact lifted collocation algorithm
Algorithm 1 presents the exact lifted collocation scheme (LC–EN), which can be used within direct multiple shooting based on the results of Proposition 4. The resulting Newton-type optimization algorithm takes steps \(\left( {\varDelta }W, {\varDelta }K, {\varDelta }{\varLambda }, {\varDelta }\mu \right) \) that are equivalent to those for Newton-type optimization applied to the direct collocation based NLP. Given a regular KKT point, \((W^\star ,K^\star ,{\varLambda }^\star ,\mu ^\star )\), as in Definition 1 for this NLP (8), the lifted collocation algorithm therefore converges locally with a linear rate to this minimizer in the case of a Gauss–Newton Hessian approximation or with a quadratic convergence rate in the case of an exact Hessian method [56]. Note that more recent results on inexact Newton-type optimization algorithms exist, e.g., allowing locally superlinear [32] or even quadratic convergence rates [45] under some conditions.
3.2.1 Connection to the standard lifted Newton method
The lifted Newton method [5] identifies intermediate values in the constraints and objective functions and introduces them as additional degrees of freedom in the NLP. Instead of solving the resulting equivalent (but higher dimensional) optimization problem directly, a condensing and expansion step are proposed to give a computational burden similar to the non-lifted Newton type optimization algorithm. The present paper proposes an extension of that concept to intermediate variables that are instead defined implicitly, namely the collocation variables on each shooting interval. Similar to the discussion for the lifted Newton method in [5], the lifted collocation integrator offers multiple advantages over the non-lifted method such as an improved local convergence. Unlike the standard lifted Newton method, the lifting of implicitly defined variables avoids the need for an iterative scheme within each iteration of the Newton-type optimization algorithm, and therefore typically reduces the computational effort. These properties will be detailed next.
3.2.2 Comparison with direct collocation and multiple shooting
This section compares multiple shooting (MS), lifted collocation (LC) and direct collocation (DC), all aimed at solving the same nonlinear optimization problem in Eq. (8) (see Remark 3). Proposition 4 shows that lifted and direct collocation result in the exact same Newton-type iterations and therefore share the same convergence properties. The arguments proposed in [5] for the lifted Newton method suggest that this local convergence can be better than for direct multiple shooting based on a collocation method. However, the main motivation for using lifting in this paper is that, internally, multiple shooting requires Newton-type iterations to solve the collocation equations (3) within each NLP iteration to evaluate the continuity map while lifted collocation avoids such internal iterations. In addition, let us mention some of the other advantages of lifted collocation over the use of direct collocation:
-
The elimination of the collocation variables, i.e., the condensing, can be performed in a tailored, structure-exploiting manner. Similarly to direct multiple shooting, the proposed condensing technique can be highly and straightforwardly parallelized since the elimination of the variables \({\varDelta }K_i\) on each shooting interval can be done independently.
-
The resulting condensed subproblem is smaller but still block structured, since it is of the multiple-shooting form (11). It therefore offers the additional practical advantage that one can deploy any of the embedded solvers tailored for the multi-stage quadratic subproblem with a specific optimal control structure, such as FORCES [33], qpDUNES [36] or HPMPC [38].
-
An important advantage of multiple shooting over direct collocation is the possibility of using any ODE or DAE solver, including step size and order control to guarantee a specific integration accuracy [17, 42]. Such an adaptive approach becomes more difficult, but can be combined with direct collocation where the problem dimensions change in terms of the step size and order of the polynomial [11, 53, 59]. Even though it is out of the scope of this work, the presented lifting technique allows one to implement similar approaches while keeping the collocation variables hidden from the NLP solver based on condensing and expansion.
The main advantage of direct collocation over multiple shooting is the better preservation of sparsity in the derivative matrices. Additionally, the evaluation of derivatives for the collocation equations is typically cheaper than the propagation of sensitivities for an integration scheme. These observations are summarized in Table 1, which lists advantages and disadvantages for all three approaches. It is important to note that direct collocation is also highly parallelizable, although one needs to rely on an advanced linear algebra package for detecting the sparsity structure of Eq. (12), exploiting it and performing the parallelization. In contrast, the lifted collocation approach is parallelizable in a natural way and independently of the chosen linear algebra. The relative performance of using a general-purpose sparse linear algebra routine for direct collocation versus the proposed approach depends very much on the specific problem dimensions and structure, and on the solver used. It has been shown in specific contexts that structure exploiting implementations of optimal control methods based on dense linear algebra routines typically outperform general-purpose solvers [37]. This topic will be discussed further for direct collocation in the numerical case study of Sect. 7.
3.3 Forward-backward propagation
The efficient computation of second-order derivatives using algorithmic differentiation (AD) is typically based on a forward sweep, followed by a backward propagation of the derivatives as detailed in [41]. Inspired by this approach, Algorithm 1 proposes to perform the condensing and expansion step using such a forward-backward propagation. To reveal these forward and backward sweeps in Algorithm 1 explicitly, let us recall the structure of the collocation equations from the formulation in (3), where we omit the shooting index, \(i = 0, \ldots , N-1\), to obtain the compact notation
Here, \(w_0 = (x,u)\), \(w_n = (x_n,u)\) and \(x_n = x_{n-1} + B_n K_n\) denotes the intermediate state values in Eq. (4) such that the numerical simulation result \(\phi (w) = x_{N_{\mathrm {s}}}\) is defined. Let us briefly present the forward-backward propagation scheme for respectively the condensing and expansion step of Algorithm 1 within one shooting interval.
3.3.1 Condensing the lifted variables: forward sweep
The condensing procedure in Algorithm 1 aims to compute the data \(C = \left[ \frac{{\mathrm {d}}x_{N_{\mathrm {s}}}}{{\mathrm {d}}w_0}, \, -{\mathbbm {1}}_{n_{\mathrm {x}}}\right] \) and \(A = \nabla _{w}^2 l(w) + H\), where the matrix \(H = \frac{{\mathrm {d}}z}{{\mathrm {d}}w}^\top \langle \mu ,\nabla _{z}^2 G \rangle \, \frac{{\mathrm {d}}z}{{\mathrm {d}}w}\) is defined similar to Eq. (17). In addition, the vectors \(c = e_{i} + B\, {\varDelta }\tilde{K}\) and  , in which \(h = \frac{{\mathrm {d}}z}{{\mathrm {d}}w}^\top \langle \mu ,\nabla _{z,K}^2 G \rangle \, {\varDelta }\tilde{K}\), are needed to form the linearized multiple shooting type KKT system (11). Note that this forms a simplified formulation of the condensed expressions in Eqs. (19) and (20) within one shooting interval.
, in which \(h = \frac{{\mathrm {d}}z}{{\mathrm {d}}w}^\top \langle \mu ,\nabla _{z,K}^2 G \rangle \, {\varDelta }\tilde{K}\), are needed to form the linearized multiple shooting type KKT system (11). Note that this forms a simplified formulation of the condensed expressions in Eqs. (19) and (20) within one shooting interval.
Given the particular structure of the collocation equations in (23) for \(N_{\mathrm {s}}\) integration steps, the variables \(K_n\) can be eliminated sequentially for \(n = 1, \ldots , N_{\mathrm {s}}\). The lifted Newton step \({\varDelta }\tilde{K} = -\frac{\partial G}{\partial K}^{-1} G(\bar{z})\) can therefore be written as the following forward sequence
for \(n = 1, \ldots , N_{\mathrm {s}}\) and where \(g_n := g_n(\bar{w}_{n-1}, \bar{K}_{n})\) and \({\varDelta }\tilde{x}_{0} = 0\) so that \({\varDelta }\tilde{x}_{n} = {\varDelta }\tilde{x}_{n-1} + B_n \, {\varDelta }\tilde{K}_n\). The same holds for the corresponding first order forward sensitivities \(K^w = -\frac{\partial G}{\partial K}^{-1} \frac{\partial G}{\partial w}\), which read as
where the first order derivatives  and \(S_n = \frac{{\mathrm {d}}x_{n}}{{\mathrm {d}}w_0}\) are defined. These sensitivities are used to propagate the state derivatives
and \(S_n = \frac{{\mathrm {d}}x_{n}}{{\mathrm {d}}w_0}\) are defined. These sensitivities are used to propagate the state derivatives
for \(n = 1, \ldots , N_{\mathrm {s}}\). This forward sequence, starting at  , results in the complete Jacobian \(S_{N_{\mathrm {s}}} = \frac{{\mathrm {d}}x_{N_{\mathrm {s}}}}{{\mathrm {d}}w_0}\).
, results in the complete Jacobian \(S_{N_{\mathrm {s}}} = \frac{{\mathrm {d}}x_{N_{\mathrm {s}}}}{{\mathrm {d}}w_0}\).
After introducing the compact notation \(\mu _{n}^\top g_n(\bar{w}_{n-1}, \bar{K}_{n}) = \sum _{r=1}^q \,\mu _{n,r}^\top f_{n,r}\), where \(f_{n,r} := f(\bar{k}_{n,r}, \bar{w}_{n,r})\) denote the dynamic function evaluations in (3), the expressions for the second-order sensitivities are
where \(z_{n,r} := (k_{n,r}, w_{n,r})\), \(w_{n,r} := (x_{n,r},u)\) and the stage values are defined by \(x_{n,r} = x_{n-1} + T_{\mathrm {int}} \sum _{s=1}^{q} a_{r,s} k_{n,s}\). The derivatives \(\frac{{\mathrm {d}}z_{n,r}}{{\mathrm {d}}w_{0}}\) are based on the first-order forward sensitivity information in Eqs. (25) and (26). In a similar way to that described in [68, 69], one can additionally perform a forward symmetric Hessian propagation sweep,
for  such that \(H_{N_{\mathrm {s}}} = \sum _{n=1}^{N_{\mathrm {s}}} K_n^{w,w}\). Regarding the gradient contribution, one can propagate the following sequence
such that \(H_{N_{\mathrm {s}}} = \sum _{n=1}^{N_{\mathrm {s}}} K_n^{w,w}\). Regarding the gradient contribution, one can propagate the following sequence
for \(n = 1, \ldots , N_{\mathrm {s}}\), where the values \({\varDelta }\tilde{x}_{n,r} = {\varDelta }\tilde{x}_{n-1} + T_{\mathrm {int}} \sum _{s=1}^{q} a_{r,s} {\varDelta }\tilde{k}_{n,s}\) are defined. Given the initial values  and
and  , the forward sweeps (28)–(29) result in \(H_{N_{\mathrm {s}}} = \frac{{\mathrm {d}}z}{{\mathrm {d}}w}^\top \langle \bar{\mu }, \nabla _z^2 G \rangle \, \frac{{\mathrm {d}}z}{{\mathrm {d}}w}\) and \(h_{N_{\mathrm {s}}} = \frac{{\mathrm {d}}z}{{\mathrm {d}}w}^\top \langle \bar{\mu }, \nabla _{z,K}^2 G \rangle \, {\varDelta }\tilde{K}\).
, the forward sweeps (28)–(29) result in \(H_{N_{\mathrm {s}}} = \frac{{\mathrm {d}}z}{{\mathrm {d}}w}^\top \langle \bar{\mu }, \nabla _z^2 G \rangle \, \frac{{\mathrm {d}}z}{{\mathrm {d}}w}\) and \(h_{N_{\mathrm {s}}} = \frac{{\mathrm {d}}z}{{\mathrm {d}}w}^\top \langle \bar{\mu }, \nabla _{z,K}^2 G \rangle \, {\varDelta }\tilde{K}\).
Remark 7
The above computations to evaluate the condensed Hessian contribution show a resemblance with the classical condensing method to eliminate the state variables in direct optimal control [17]. The main difference is that the above condensing procedure is carried out independently for the state and control variable within each shooting interval, such that the number of optimization variables does not increase in this case.
3.3.2 Expansion step for the lifted variables: backward sweep
Note that the first and second order sensitivities can be propagated together in the forward condensing scheme, which avoids unnecessary additional storage requirements. We show next that the expansion phase of Algorithm 1 can be seen as the subsequent backward propagation sweep. For this purpose, certain variables from the forward scheme still need to be stored.
The expansion step \(\bar{K}^+ = \bar{K} + {\varDelta }\tilde{K} + K^w {\varDelta }w\) for the lifted collocation variables can be performed as follows
where the values \({\varDelta }\tilde{K}_n\) and \(K_n^w\) are stored from the condensing procedure and \({\varDelta }w_0\) denotes the primal update from the subproblem solution in Algorithm 1. The expansion step \(\bar{\mu }^+ = -\frac{\partial G}{\partial K}^{-\top }\left( B^\top \bar{\lambda }^+ + \langle \bar{\mu }, \nabla _{K,z}^2 G \rangle \, {\varDelta }z\right) \) for the lifted dual variables can be performed as a backward propagation
for \(n = N_{\mathrm {s}}, \ldots , 1\), based on the initial value \(\bar{\lambda }_{N_{\mathrm {s}}}^+ = \bar{\lambda }^+\) from the subproblem solution, and where \({\varDelta }x_{n} = {\varDelta }x_{n-1} + B_n \, {\varDelta }K_n\) and \({\varDelta }z_n = ({\varDelta }w_n, {\varDelta }K_n)\). Note that the factorization of the Jacobian \(\frac{\partial g_n}{\partial K_n}\) is needed from the forward propagation to efficiently perform this backward sweep.
3.4 Lifted collocation integrator within a Gauss–Newton method
The previous subsection detailed how the expressions in Algorithm 1 can be computed by a forward-backward propagation, which exploits the symmetry of the exact Hessian contribution. In the case when a Gauss–Newton or Quasi-Newton type optimization method is used, the Hessian contribution from the dynamic constraints is \(H_i = 0\) and the gradient \(h_i = 0\) for \(i = 0, \ldots , N-1\), since no second-order derivative propagation is needed. The multipliers \(\mu \) corresponding to the collocation equations are then not needed either, so that only the collocation variables are lifted. In this context, Algorithm 1 boils down to a forward sweep for both the condensing and the expansion steps of the scheme without the need for additional storage of intermediate values, except for the lifted variables K and their forward sensitivities \(K^w\).
4 Adjoint-based inexact lifted collocation integrator
Any implementation of a collocation method needs to compute the collocation variables \(K_i\) from the nonlinear equations \(G(w_i,K_i) = 0\), given the current values for \(w_i\). The earlier definition of the auxiliary variable \({\varDelta }\tilde{K}_i\) in Eq. (14) corresponds to an exact Newton step \({\varDelta }\tilde{K}_i = -\frac{\partial G(\bar{w}_i,\bar{K}_i)}{\partial K_i}^{-1} G(\bar{w}_i,\bar{K}_i)\). It is, however, common in practical implementations of collocation methods or implicit Runge–Kutta (IRK) schemes in general to use inexact derivative information to approximate the Jacobian matrix, \(M_i \approx \frac{\partial G(\bar{w}_i,\bar{K}_i)}{\partial K_i}\), resulting in the inexact Newton step
This Jacobian approximation can allow for a computationally cheaper LU factorization, which can be reused throughout the iterations [42]. Monitoring strategies on when to reuse such a Jacobian approximation is a research topic of its own, e.g., see [4, 8]. Note that an alternative approach makes use of inexact solutions to the linearized subproblems in order to reduce the overall computational burden [23, 24]. Additionally, there exist iterative ways of updating the Jacobian approximation, e.g., based on Broyden’s method [19]. Efficient implementations of IRK methods based on such a tailored Jacobian approximation \(M_i\), are, for example, known as the Simplified Newton [10, 21] and the Single Newton type iteration [22, 40].
4.1 Adjoint-based inexact lifting algorithm
Even though it can be computationally attractive to use the inexact Newton scheme from Eq. (32) instead of the exact method, its impact on the convergence of the resulting Newton-type optimization algorithm is an important topic that is addressed in more detail by [14, 26, 32, 62]. A Newton-type scheme with inexact derivatives does not converge to a solution of the original direct collocation NLP (8), unless adjoint derivatives are evaluated in order to compute the correct gradient of the Lagrangian \(a_{\mathrm {c},i} = \nabla _{z_i} {\mathcal L}^{\mathrm {c}}(\bar{Z},\bar{{\varLambda }},\bar{\mu })\) on the right-hand side of the KKT system (12) [16, 32].
Let us introduce the Jacobian approximation \(\tilde{D}_i = [\frac{\partial G(\bar{z}_i)}{\partial w_i}, M_i] \approx \frac{\partial G(\bar{z}_i)}{\partial z_i} \in {\mathbb {R}}^{n_{\mathrm {K}}\times n_{\mathrm {z}}}\), where \(M_i \approx \frac{\partial G(\bar{z}_i)}{\partial K_i}\) is invertible for each \(i = 0, \ldots , N-1\), and which is possibly fixed. One then obtains the inexact KKT system

where all matrices and vectors are defined as for the direct collocation based KKT system in Eq. (12), with the exception of \(\tilde{D}\), where the Jacobian approximations \(M_i\) are used instead of \(\frac{\partial G(\bar{z}_i)}{\partial K_i}\). This is known as an adjoint-based inexact Newton method [16, 32] applied to the direct collocation NLP in Eq. (8) because the right-hand side is evaluated exactly, including the gradient of the Lagrangian, \(a_{\mathrm {c},i} = \nabla _{z_i} {\mathcal L}^{\mathrm {c}}(\bar{Z},\bar{{\varLambda }},\bar{\mu })\). We detail this approach in Algorithm 2 and motivate it by the following proposition.
Proposition 8
Algorithm 2 presents a condensing technique for the inexact KKT system (33), which allows one to instead solve a system of the multiple-shooting form in Eq. (11). The solution \(\left( {\varDelta }Z, {\varDelta }{\varLambda }, {\varDelta }\mu \right) \) to the original system (33) can be obtained by use of the corresponding expansion technique.
Proof
The proof here follows similar arguments as that used for Proposition 4, with the difference that the update of the collocation variables is instead given by \({\varDelta }K_i = {\varDelta }\tilde{K}_i + \tilde{K}_i^w {\varDelta }w_i\), where
and where \(\tilde{K}_i^w\) denotes the inexact forward sensitivities. To obtain the multiple shooting type form of the KKT system in Eq. (11), the resulting condensing and expansion step can be found in Algorithm 2. An important difference with the exact lifted collocation integrator from Algorithm 1 is that the gradient term \(h_i\) is now defined as
where \({z_i^w}^\top := \begin{bmatrix} {\mathbbm {1}}_{n_{\mathrm {w}}}&\tilde{K}_i^{w^\top } \end{bmatrix}\) and includes a correction term resulting from the inexact sensitivities \(\tilde{K}_i^w\). In addition, the expansion step for the Lagrange multipliers corresponding to the collocation equations is now
which corresponds to a Newton-type iteration on the exact Newton based expression from Eq. (22). \(\square \)

Table 2 shows an overview of the presented variants of lifted collocation including the exact method (LC–EN) in Algorithm 1, which can be compared to the adjoint based inexact lifting scheme (LC–IN) in Algorithm 2.
4.2 Local convergence for inexact Newton-type methods (IN)
Let us briefly present the local contraction result for Newton-type methods, which we will use throughout this paper to study local convergence for inexact lifted collocation. To discuss the local convergence of the adjoint-based inexact lifting scheme, we will first write it in a more compact notation starting with the KKT equations
where \(Y := (Z,{\varLambda },\mu )\) denotes the concatenated variables. Then, each Newton-type iteration from Eq. (33) can be written as
Given a guess, \(\bar{Y}\), the Jacobian approximation from Eq. (33) is

Because the system of equations in (37) denotes the KKT conditions [56] for the direct collocation NLP in Eq. (8), a solution \(\mathcal {F}(Y^\star ) = 0\) by definition also needs to be a KKT point \((Z^\star ,{\varLambda }^\star ,\mu ^\star )\) for the original NLP.
The Newton-type optimization method in Algorithm 2 can now be rewritten as the compact iteration (38). The convergence of this scheme then follows the classical and well-known local contraction theorem from [14, 26, 32, 62]. We use the following version of this theorem from [27], providing sufficient and necessary conditions for the existence of a neighborhood of the solution where the Newton-type iteration converges. Let us define the spectral radius, \(\rho (P)\), as the maximum absolute value of the eigenvalues of the square matrix P.
Theorem 9
(Local Newton-type contraction [27]) Let us consider the twice continuously differentiable function \(\mathcal {F}(Y)\) from Eq. (37) and the solution point \(Y^\star \) with \(\mathcal {F}(Y^\star ) = 0\). We then consider the Newton-type iteration \(Y_{k+1} = - \tilde{J}(Y_k)^{-1} \mathcal {F}(Y_k)\) starting with the initial value \(Y_0\), where \(\tilde{J}(Y) \approx J(Y)\) is continuously differentiable and invertible in a neighborhood of the solution. If all eigenvalues of the iteration matrix have a modulus smaller than one, i.e., if the spectral radius
then this fixed point \(Y^\star \) is asymptotically stable. Additionally, the iterates \(Y_{k}\) converge linearly to \(Y^\star \) with the asymptotic contraction rate \(\kappa ^\star \) if \(Y_0\) is sufficiently close. On the other hand, if \(\kappa ^\star > 1\), then the fixed point \(Y^\star \) is unstable.
Theorem 9 provides a simple means of assessing the stability of a solution point \(Y^\star \) and therefore provides a guarantee of the existence of a neighborhood of \(Y^\star \) where the Newton-type iteration converges linearly to \(Y^\star \) with the asymptotic contraction rate \(\kappa ^\star \).
Remark 10
The adjoint-based inexact lifting scheme converges locally to a solution of the direct collocation NLP if the assumptions of Theorem 9 and condition (40) are satisfied. As mentioned earlier, it is therefore possible to use a fixed Jacobian approximation \(\tilde{D}_i := [G_{w_i}, M_i]\) over the different Newton-type iterations [16] in Eq. (33) where, additionally, \(G_{w_i} \approx \frac{\partial G(\bar{z}_i)}{\partial w_i}\). Theorem 9 still holds for this case. It results in the computational advantage that the factorization of \(\tilde{D}_i\) needs to be computed only once. Additionally, the inexact forward sensitivities \(\tilde{K}_i^w = -M_i^{-1} G_{w_i}\) remain fixed and can be computed offline. The use of fixed sensitivity approximations can also reduce the memory requirement for the lifted collocation integrator considerably [66].
5 Inexact lifted collocation integrator with iterated sensitivities
This section presents an extension of the Gauss–Newton based iterative inexact lifting scheme to the general Newton-type optimization framework. Unlike the discussion in [65], we include the option to additionally propagate second-order sensitivities within this iterative lifted Newton-type algorithm. We formulate this approach as an inexact Newton method for an augmented KKT system and discuss its local convergence properties. Based on the same principles of condensing and expansion, this inexact lifting scheme can be implemented similar to a direct multiple shooting based Newton-type optimization algorithm. Finally, we discuss the adjoint-free iterative inexact lifted collocation integrator [65] as a special case of this approach.
5.1 Iterative inexact lifted collocation scheme
An inexact Newton scheme uses the factorization of one of the aforementioned approximations of the Jacobian, \(M_i \approx \frac{\partial G(\bar{w}_i,\bar{K}_i)}{\partial K_i}\), for each linear system solution. To recover the correct sensitivities in the Newton-type optimization algorithm, our proposed Inexact Newton scheme with iterated sensitivities (INIS) additionally includes the lifting of the forward sensitivities \(K_i^w\). More specifically, the forward sensitivities \(K_i^w\) are introduced as additional variables into the NLP, which can be iteratively obtained by applying a Newton-type iteration, \(\bar{K}_i^w \leftarrow \bar{K}_i^w + {\varDelta }K_i^w\), to the linear equation \(\frac{\partial G_i}{\partial w_i} + \frac{\partial G_i}{\partial K_i} K_i^w = 0\). The lifting of the sensitivities results in additional degrees of freedom such that the update for the collocation variables becomes \({\varDelta }K_i = {\varDelta }\tilde{K}_i + \bar{K}_i^w {\varDelta }w_i\), where \(\bar{K}_i^w\) are the current values for the lifted sensitivities. The forward sweep of the condensing procedure in Algorithm 2 can then be written as
instead of the standard inexact Newton step in Eq. (34).
In the case of a Newton-type optimization algorithm, which requires the propagation of second-order sensitivities, one can apply a similar inexact update to the Lagrange multipliers \(\mu _i\) corresponding to the collocation equations. The Newton-type scheme can equivalently be applied to the expression from Eq. (21), to result in the following iterative update
where \(\bar{\mu }_i\) denotes the current values of the Lagrange multipliers corresponding to the collocation equations. The inexact Newton iteration (42) only requires the factorization of the Jacobian approximation \(M_i\) and corresponds to the expansion step in Eq. (36) for the adjoint-based inexact lifting scheme. The Newton-type optimization algorithm based on the iterative inexact lifting scheme (LC–INIS) within direct multiple shooting is detailed in Algorithm 3.
5.1.1 Iterative inexact lifting as an augmented Newton scheme
By introducing the (possibly fixed) Jacobian approximation \(M_i \approx \frac{\partial G(\bar{w}_i,\bar{K}_i)}{\partial K_i}\) and the lifted variables for the forward sensitivities \(K_i^w\) for \(i = 0, \ldots , N-1\), let us define the following augmented and inexact version of the linearized KKT system (12) for direct collocation

where the matrix \(A_\mathrm {c} \in {\mathbb {R}}^{n_{\mathrm {Z}}\times n_{\mathrm {Z}}}\) is block diagonal and defined earlier in Eq. (12), and where \(A_{\mathrm {c},i} := \nabla _{z_i}^2 {\mathcal L}_i^{\mathrm {c}}(\bar{z}_i,\bar{\lambda }_i,\bar{\mu }_i)\) and \({\mathcal L}_i^{\mathrm {c}}(\bar{z}_i,\bar{\lambda }_i,\bar{\mu }_i) = l(\bar{w}_i) + \bar{\lambda }_i^\top \left( \bar{x}_{i} + B \, \bar{K}_{i} - \bar{x}_{i+1}\right) + \bar{\mu }_i^\top G(\bar{w}_{i},\bar{K}_{i})\). Also, the constant matrix \(E \in {\mathbb {R}}^{(N+1)n_{\mathrm {x}}\times n_{\mathrm {Z}}}\) is defined as before in Eq. (13). In addition, the block diagonal matrix \(\tilde{D}\) is defined by \(\tilde{D}_i = \left[ -M_i \bar{K}_i^w, \,M_i\right] \in {\mathbb {R}}^{n_{\mathrm {K}}\times n_{\mathrm {z}}}\) for each \(i = 0, \ldots , N-1\), because
where the Jacobian approximation \(M_i \approx \frac{\partial G(\bar{w}_i,\bar{K}_i)}{\partial K_i}\) is used. The following terms on the right-hand side are defined as before in Eq. (12) where \(a_{\mathrm {c},i} := \nabla _{z_i} {\mathcal L}^{\mathrm {c}}(\bar{Z},\bar{{\varLambda }},\bar{\mu })\), \(e_i := \bar{x}_{i} + B \, \bar{K}_{i} - \bar{x}_{i+1}\) and \(d_i := G(\bar{z}_i)\). In addition, the remaining terms are \(d_{\mathrm {f}, i} := \mathrm {vec}(\frac{\partial G(\bar{z}_i)}{\partial w_i} + \frac{\partial G(\bar{z}_i)}{\partial K_i} \bar{K}_i^w)\). The following proposition states the connection between this augmented KKT system (43) and Algorithm 3 for an iterative inexact lifted collocation integrator.
Proposition 11
Algorithm 3 presents a condensing technique for the augmented and inexact KKT system (43), which allows one to instead solve the multiple shooting type system (11). The original solution \(\left( {\varDelta }Z, {\varDelta }{\varLambda }, {\varDelta }\mu , {\varDelta }K^w\right) \) can be obtained by use of the corresponding expansion step.
Proof
Similar to the proof for Proposition 4, let us look closely at the first line of the KKT system in Eq. (43),

For the inexact Newton case, we observe that the following holds
where the approximate Jacobian matrices \({z_i^w}^\top = \begin{bmatrix} {\mathbbm {1}}_{n_{\mathrm {w}}}&\bar{K}_i^{w^\top } \end{bmatrix}\) and \(\tilde{D}_i = \left[ -M_i \bar{K}_i^w, M_i\right] \). We can multiply Eq. (45) on the left by \({z_i^w}^\top \) and use  to obtain the expression
to obtain the expression

where the Hessian matrix \(\tilde{A}_i = \nabla _{w_i}^2 l(\bar{w}_i) + H_i\) with \(H_i = {z_i^w}^\top \langle \bar{\mu }_i,\nabla _{z_i}^2 G_{i} \rangle \, {z_i^w}\). Furthermore, the right-hand side reads

where \(\tilde{h}_i = {z_i^w}^\top \langle \bar{\mu }_i,\nabla _{z_i,K_i}^2 G_{i} \rangle \, {\varDelta }\tilde{K}_i + \left( \frac{\partial G_i}{\partial w_i} + \frac{\partial G_i}{\partial K_i} \bar{K}_i^w \right) ^\top \bar{\mu }_i\). The augmented KKT system (43) can therefore indeed be reduced to the multiple shooting type form in Eq. (11), using the condensing step as described in Algorithm 3.
The expansion step for the lifted K variables follows from \(\tilde{D}_i {\varDelta }z_i = - d_i\) and becomes \({\varDelta }K_i = {\varDelta }\tilde{K}_i + \bar{K}_i^w {\varDelta }w_i\). To update the Lagrange multipliers \(\mu _i\), let us look at the lower part of Eq. (45):
which can be rewritten as \({\varDelta }\mu _i = - M_i^{-\top } \left( \frac{\partial G(\bar{z}_i)}{\partial K_i}^\top \bar{\mu }_i + B^\top \bar{\lambda }_i^+ + \langle \bar{\mu }_i,\nabla _{K_i,z_i}^2 G_{i} \rangle \, {\varDelta }z_i \right) \) in Equation (42). Finally, the update of the lifted sensitivities \(K_i^w\) follows from the last equation of the KKT system in (43)
\(\square \)

Remark 12
To be precise, Algorithm 3 is an adjoint-based iterative inexact lifting scheme since it corrects the gradient in the condensed problem (46) using the expression \(\left( \frac{\partial G_i}{\partial w_i} + \frac{\partial G_i}{\partial K_i} \bar{K}_i^w \right) ^\top \bar{\mu }_i\) similar to Eq. (35) for the adjoint-based inexact scheme. This correction term is equal to zero whenever the lifted sensitivities are exact, i.e., \(K_i^{w^\star } = -\frac{\partial G_i}{\partial K_i}^{-1}\frac{\partial G_i}{\partial w_i}\). The overview in Table 2 allows one to compare this novel approach for inexact Newton based lifted collocation with the previously presented lifting schemes.
Remark 13
The updates of the lifted forward sensitivities,
are independent of the updates for any of the other primal or dual variables, so that (47) can be implemented separately. More specifically, one can carry out multiple Newton-type iterations for the lifted variables \(\bar{K}_i^w\) followed by an update of the remaining variables or the other way around. To simplify our discussion on the local convergence for this INIS type scheme, we will however not consider such variations further.
5.2 Local convergence for inexact Newton with iterated sensitivities (INIS)
Similar to Sect. 4.2, let us introduce a more compact notation for the Newton-type iteration from Algorithm 3. For this purpose, we define the following augmented system of KKT equations:
where the concatenated variables \(Y_{\mathrm {a}}:= (Z,{\varLambda },\mu ,K^w)\) are defined. The INIS type iteration then reads as \(\tilde{J}_{\mathrm {a}}(\bar{Y}_{\mathrm {a}}) {\varDelta }Y_{\mathrm {a}}= - \mathcal {F}_{\mathrm {a}}(\bar{Y}_{\mathrm {a}})\) and uses the following Jacobian approximation

where \(Y := (Z,{\varLambda },\mu )\) and using the Jacobian approximations \(M_i(\bar{z}_i) \approx \frac{\partial G(\bar{z}_i)}{\partial K_i}\). We show next that a solution to the augmented system \(\mathcal {F}_{\mathrm {a}}(Y_{\mathrm {a}}) = 0\) also forms a solution to the direct collocation NLP in Eq. (8).
Proposition 14
A solution \(Y_{\mathrm {a}}^\star = (Z^\star ,{\varLambda }^\star ,\mu ^\star ,K^{w^\star })\), which satisfies the LICQ and SOSC conditions [56] for the nonlinear system \(\mathcal {F}_{\mathrm {a}}(Y_{\mathrm {a}}) = 0\), forms a regular KKT point \((Z^\star ,{\varLambda }^\star ,\mu ^\star )\) for the direct collocation NLP in Eq. (8).
Proof
The proof follows directly from observing that the first three equations of the augmented system (48) correspond to the KKT conditions for the direct collocation NLP in Eq. (8). A solution \(Y_\mathrm {a}^\star \) of the system \(\mathcal {F}_{\mathrm {a}}(Y_{\mathrm {a}}) = 0\) then provides a regular KKT point \((Z^\star ,{\varLambda }^\star ,\mu ^\star )\) for this NLP (8). \(\square \)
The Newton-type optimization method from Algorithm 3 has been rewritten as the compact iteration \(\tilde{J}_{\mathrm {a}}(\bar{Y}_{\mathrm {a}}) {\varDelta }Y_{\mathrm {a}}= - \mathcal {F}_{\mathrm {a}}(\bar{Y}_{\mathrm {a}})\). The local convergence properties of this scheme are described by the classical Newton-type contraction theory [14]. Under the conditions from Theorem 9, the iterates converge linearly to the solution \(Y_{\mathrm {a}}^\star \) with the asymptotic contraction rate
A more detailed discussion on the contraction rate for an INIS type optimization algorithm and a comparison to standard adjoint-based inexact Newton schemes is out of scope, but can instead be found in [67]. The numerical case study in Sect. 7 shows that the INIS algorithm typically results in better local contraction properties, i.e., \(\kappa _{\mathrm {a}}^\star \ll \kappa ^\star < 1\) in that case.
5.3 An adjoint-free iterative inexact lifted collocation scheme
The inexact Newton scheme with iterated sensitivities from Algorithm 3 is based on an adjoint propagation to compute the correct gradient of the Lagrangian on the right-hand side of the KKT system from Eq. (43). Because of the lifting of the forward sensitivities \(K_i^w\) for \(i = 0, \ldots , N-1\), one can however avoid the computation of such an adjoint and still obtain a Newton-type algorithm that converges to a solution of the direct collocation NLP (8).
For this purpose, let us introduce the following adjoint-free approximation of the augmented KKT system in Eq. (43),

where all quantities are defined as in Eq. (43), but an approximate Lagrangian gradient term is used, i.e.,

where \(\hat{D}_i = \left[ -\frac{\partial G(\bar{z}_i)}{\partial K_i} \bar{K}_i^w, \,\frac{\partial G(\bar{z}_i)}{\partial K_i}\right] \approx \frac{\partial G(\bar{z}_i)}{\partial z_i}\). Proposition 11 then still holds for this variant of lifted collocation, where the multiple shooting type gradient is instead defined without the adjoint-based correction term. The resulting algorithm is therefore referred to as an adjoint-free scheme (LC–AF–INIS) and it is detailed further in Algorithm 4 based on a Gauss–Newton Hessian approximation. It is important for the study of its local convergence that \(\hat{D}_i \ne \tilde{D}_i = \left[ -M_i \bar{K}_i^w, \,M_i\right] \), where \(\tilde{D}_i\) is used in the Jacobian approximation and \(\hat{D}_i\) is merely used to define the augmented KKT system in Eq. (51).

5.3.1 Local convergence for adjoint-free INIS scheme (AF–INIS)
To study the local convergence properties for the adjoint-free variant of the INIS based lifted collocation scheme, we need to investigate the approximate augmented KKT system from Eq. (51). It is written as \(\tilde{J}_{\mathrm {a}}(\bar{Y}_{\mathrm {a}}) {\varDelta }Y_{\mathrm {a}}= - \hat{\mathcal {F}}_{\mathrm {a}}(\bar{Y}_{\mathrm {a}})\) in its compact form, where \(\hat{\mathcal {F}}_{\mathrm {a}}(Y_{\mathrm {a}}) = 0\) represents the following approximate augmented system of KKT equations,
where the incomplete Lagrangian \(\tilde{{\mathcal L}}_i^{\mathrm {c}}(\bar{z}_i,\bar{\lambda }_i) = l(\bar{w}_i) + \bar{\lambda }_i^\top \left( \bar{x}_{i} + B \, \bar{K}_{i} - \bar{x}_{i+1}\right) \) and the approximate Jacobian \(\hat{D}_i = \left[ -\frac{\partial G(\bar{z}_i)}{\partial K_i} \bar{K}_i^w, \,\frac{\partial G(\bar{z}_i)}{\partial K_i}\right] \) are defined. Note that the Jacobian approximation \(\tilde{J}_{\mathrm {a}}(\bar{Y}_{\mathrm {a}})\) in the Newton-type iteration is still defined by Eq. (49), equivalent to the adjoint-based INIS scheme. The following proposition then shows that a solution to the approximate augmented system \(\hat{\mathcal {F}}_{\mathrm {a}}(Y_{\mathrm {a}}) = 0\) is also a local minimizer for the direct collocation NLP (8):
Proposition 15
A solution \(Y_{\mathrm {a}}^\star = (Z^\star ,{\varLambda }^\star ,\mu ^\star ,K^{w^\star })\), which satisfies the LICQ and SOSC conditions [56] for the system of nonlinear equations \(\hat{\mathcal {F}}_{\mathrm {a}}(Y_{\mathrm {a}}) = 0\), also forms a solution to the nonlinear system \(\mathcal {F}_{\mathrm {a}}(Y_{\mathrm {a}}) = 0\) and therefore forms a regular KKT point \((Z^\star ,{\varLambda }^\star ,\mu ^\star )\) for the direct collocation NLP in Eq. (8).
Proof
We observe that the lower part of the KKT system in Eq. (53) for the solution point \(Y_{\mathrm {a}}^\star \) reads as
so that \(K_i^{w^\star } = -\frac{\partial G(z_i^\star )}{\partial K_i}^{-1}\frac{\partial G(z_i^\star )}{\partial w_i}\) holds at any solution of \(\hat{\mathcal {F}}_{\mathrm {a}}(Y_{\mathrm {a}}) = 0\). The same holds at a solution of \(\mathcal {F}_{\mathrm {a}}(Y_{\mathrm {a}}) = 0\). Subsequently, we observe that \(\hat{D}_i(z_i^\star ,K_i^{w^\star }) = \left[ -\frac{\partial G(z_i^\star )}{\partial K_i} K_i^{w^\star }, \,\frac{\partial G(z_i^\star )}{\partial K_i}\right] = \frac{\partial G(z_i^\star )}{\partial z_i}\), such that the following equality holds at the solution
It follows that \(Y_{\mathrm {a}}^\star \) forms a solution to the original augmented KKT system from Eq. (48). The result then follows directly from Proposition 14. \(\square \)
Under the conditions of Theorem 9, the iterates defined by the Newton-type iteration \(\tilde{J}_{\mathrm {a}}(\bar{Y}_{\mathrm {a}}) {\varDelta }Y_{\mathrm {a}}= - \hat{\mathcal {F}}_{\mathrm {a}}(\bar{Y}_{\mathrm {a}})\) converge linearly to the solution \(Y_{\mathrm {a}}^\star \) with the asymptotic contraction rate
based on the Jacobian approximation \(\tilde{J}_{\mathrm {a}}(Y_{\mathrm {a}}) \approx \hat{J}_{\mathrm {a}}(Y_{\mathrm {a}}) := \frac{\partial \hat{\mathcal {F}}_{\mathrm {a}}(Y_{\mathrm {a}})}{\partial Y_{\mathrm {a}}}\) from (49).
5.3.2 Adjoint-free and multiplier-free INIS based on Gauss–Newton
The motivation for the alternative INIS-type lifting scheme proposed in the previous subsection is to avoid the computation of any adjoint derivatives, while maintaining a Newton-type optimization algorithm that converges to a local minimizer of the direct collocation NLP (8). This equivalence result has been established in Proposition 15. However, the propagation of second-order sensitivities still requires the iterative update of the Lagrange multipliers, \({\varDelta }\mu _i = - M_i^{-\top }\left( \frac{\partial G(\bar{z}_i)}{\partial K_i}^\top \bar{\mu }_i + B^\top \bar{\lambda }_i^+ + \nabla _{K_i,z_i}^2 {\mathcal L}_i^{\mathrm {c}} {\varDelta }z_i \right) \), based on adjoint differentiation. This alternative implementation would therefore not result in a considerable advantage over the standard INIS method.
Instead, the benefits for this adjoint-free scheme are more clear in the case of a least squares objective \(l(w_i) = \frac{1}{2}\Vert F(w_i)\Vert _2^2\) where one can use a Gauss–Newton (GN) approximation  for the Hessian of the Lagrangian [15]. In that case, the Jacobian approximation for the augmented KKT system (49) is independent of the Lagrange multipliers as discussed in Sect. 3.4. After applying Proposition 11 to condense this approximate augmented KKT system of the form of Eq. (51) to the multiple shooting type system in (11), the resulting scheme therefore does not depend on any of the Lagrange multipliers. This adjoint-free and multiplier-free implementation of Gauss–Newton based INIS type lifted collocation is detailed in Algorithm 4.
for the Hessian of the Lagrangian [15]. In that case, the Jacobian approximation for the augmented KKT system (49) is independent of the Lagrange multipliers as discussed in Sect. 3.4. After applying Proposition 11 to condense this approximate augmented KKT system of the form of Eq. (51) to the multiple shooting type system in (11), the resulting scheme therefore does not depend on any of the Lagrange multipliers. This adjoint-free and multiplier-free implementation of Gauss–Newton based INIS type lifted collocation is detailed in Algorithm 4.
6 ACADO toolkit: code generation software
Let us provide a brief overview of the different proposed schemes for lifted collocation, including a discussion on their relative advantages and disadvantages. In addition, we will comment on the open-source implementation of these algorithms in the code generation tool of the ACADO Toolkit. The software is free of charge and can be downloaded from www.acadotoolkit.org.
6.1 Classification of lifted collocation integrators
Table 4 presents a classification of all the variants of lifted collocation integrators presented in this article. The most distinguishing characteristic is whether the algorithm is based on exact (LC–EN) or inexact lifting, discussed respectively in Sect. 3 and in Sects. 4 and 5. Unlike the inexact lifting techniques, exact lifted collocation relies on computing a factorization of the Jacobian of the collocation equations. However, one can still choose either an exact Hessian or a Gauss–Newton type approximation within the optimization algorithm as shown in Table 4. Among the inexact lifting schemes, we make a distinction between the standard adjoint-based technique (LC–IN) from Sect. 4 and the inexact Newton scheme with INIS from Sect. 5. The latter INIS-type algorithm allows for an adjoint-based (LC–INIS) as well as an adjoint-free and multiplier-free (LC–AF–INIS) implementation using Gauss–Newton. Table 4 additionally includes multiple shooting (MS) without lifting the collocation variables and direct collocation (DC). For the standard (MS) implementation, a method to solve the nonlinear system of collocation equations needs to be embedded within the Newton-type optimization Algorithm [66, 70]. Similar to (DC), all lifted collocation type schemes avoid such internal iterations as mentioned also in Table 1.
The main advantage of the inexact schemes (LC–IN) and (LC–INIS) over the exact lifted collocation (LC–EN) is the reduced computational effort. Even though their local convergence is generally slower (due to the results from Theorem 9), the cost per iteration can be reduced considerably based on the use of a Jacobian approximation for the system of collocation equations. Since a relatively low accuracy of the solution is often sufficient, e.g., for real-time optimal control on embedded applications [30, 74], the overall computational cost can be much better for inexact Newton-based lifting. This is illustrated in Table 3, which shows the computational complexity per integration step and for different Newton-type iterations. The comparison here assumes that an LU factorization is used which, for a matrix of dimension n, requires \(\sim \frac{2}{3} n^3\) flops and the back substitutions accordingly require \(\sim 2 n^2\) flops. The table has been constructed for the Gauss collocation method, for which the coefficient matrix A has \(\frac{q}{2}\) complex conjugate pairs of eigenvalues when the number of stages q is even or it has one real eigenvalue and \(\frac{q-1}{2}\) complex conjugate pairs in case q is odd [42]. More information on the use of Simplified and Single Newton iterations within lifted collocation can be found in [65]. Between the two families of inexact schemes, the INIS algorithm results typically in better local contraction properties as illustrated by the numerical case study in the next section. In addition, it allows for an adjoint-free implementation in Scheme (LC–AF–INIS) for optimal control problems involving a least squares type objective as described by Algorithm 4. This method is both easy to implement based on forward differentiation and computationally efficient.
Regarding memory requirements for the various lifting schemes in Table 4, it is important to note that any algorithm based on an adjoint sweep requires the storage of variables during the preceding forward sweep as discussed in Sect. 3.3. This is a benefit for the GN based exact lifting (LC–EN) and adjoint-free INIS scheme (LC–AF–INIS), because both rely only on forward propagation of sensitivities. Another noticeable effect is the storage of the first-order forward sensitivities \(K^w\) in both exact and INIS-type lifting. The adjoint-based inexact lifting (LC–IN) has the advantage that one could use Jacobian approximations, which are precomputed and fixed, in order to further reduce the memory requirements of the corresponding implementation at the cost of possibly slowing down the convergence. In the case of an inexact INIS type algorithm, these forward sensitivities are additionally lifted and therefore need to be stored from one iteration to the next.
6.2 Open-source ACADO code generation tool
All variants of the lifted collocation method from Table 4 are implemented in the ACADO Toolkit [46] and are made available as open-source software. The collocation methods are based on either Gauss-Legendre or Radau IIA points [42] and the proposed Jacobian approximations are based on either Simplified or Single Newton-type iterations as discussed in [65]. The software can be downloaded freely from [1] and can be discussed on an active forum [3]. The ACADO code generation tool is a specific part of this toolkit, which can be used to obtain real-time feasible codes for dynamic optimization on embedded control hardware. In particular, it pursues the export of highly efficient C-code based on the RTI scheme for Nonlinear MPC (NMPC) [47]. As illustrated in Fig. 4, a user friendly MATLAB interface is available that allows one to export, compile and use auto generated code in an intuitive way and without direct interaction with C/C++ programming [70]. It remains however possible to use the tool directly from its C++ interface.
The ACADO software package supports many algorithmic features for nonlinear optimal control, including the real-time iteration (RTI) scheme for NMPC [28]. This online algorithm is based on sequential quadratic programming (SQP) to solve the nonlinear optimization problem within direct multiple shooting [15]. Note that the code generation tool targets fast embedded applications, with relatively small to medium-scale problem dimensions. Dense linear algebra routines are used to exploit the collocation based optimal control problem structure or the structure in the form of dynamic subsystems [64]. Therefore, it is currently not recommended to use this particular software implementation for rather large scale problems, e.g., involving hundreds of states or more. Our implementation is mostly self-contained, except for relying on tailored QP solvers for solving the multiple-shooting structured subproblems [51]. In addition to AD [46] and efficient integration schemes with sensitivity propagation [70], the convex solver used is important to obtain a high performance for the overall SQP method [51]. More specifically, the open-source solvers qpOASES [35], qpDUNES [36] and HPMPC [38] are interfaced to the ACADO code generation tool. This algorithmic framework lends itself perfectly to the use of the proposed lifted collocation integrators, to improve both the convergence and the computational properties without changing the code for the SQP type algorithm.
7 Case study: chain of masses
This section illustrates the performance of the proposed variants of lifted implicit integrators on the benchmark optimal control example, which consists of a chain of spring connected masses. For this purpose, a multiple shooting type SQP method is generated using the ACADO code generation tool. In the numerical results of this article, the QP solutions are obtained using the active-set solver qpOASES [35] in combination with a condensing technique to numerically eliminate the state variables as proposed by [17]. Mainly as a reference, the direct collocation problem is additionally solved using the general-purpose sparse NLP solver Ipopt [75] from the software package CasADi [7]. Note however that both implementations cannot be compared directly, since Ipopt is a general-purpose solver and therefore includes many different features. On the other hand, the ACADO generated SQP method can be warm started more easily and respects all linearized constraints at each iteration, which are both important features for real-time applications of optimal control [30]. We will therefore additionally report the computation times for solving the direct collocation QP subproblem, using a general-purpose sparse solver in the OOQP software [39]. Note that both the numerical results with OOQP and with Ipopt are based on the MA27 linear algebra code from the HSL library [2], in order to solve the sparse linear system at each interior point iteration.
All numerical simulations are carried out on a standard computer, equipped with Intel i7-3720QM processor, using a 64-bit version of Ubuntu 14.04 and the g++ compiler version 4.8.4. Note that the timings to set up the problem, generate the solver and compile the resulting code, are further not reported. Instead, the focus is on the numerical performance of the proposed algorithm implementations. The presented results can be verified by running the MATLAB simulation scripts, which can be found on the following public repository: https://github.com/rienq/liftedCollocation.
7.1 Optimal control problem formulation
We consider the chain mass control problem [76], which was already used to illustrate exact lifted collocation in [66]. The task of the controller is to return a chain of \(n_{\mathrm {m}}\) masses connected with springs to its steady state, starting from a perturbed initial configuration. The mass at one end is fixed, while the control input \(u \in {\mathbb {R}}^{3}\) to the system is the direct force applied to the mass at the other end of the chain. The state of each free mass \(x^j := [p^{j^\top },v^{j^\top }]^\top \in {\mathbb {R}}^{6}\) consists in its position \(p^j := [p_x^j,p_y^j,p_z^j]^\top \in {\mathbb {R}}^{3}\) and velocity \(v^j \in {\mathbb {R}}^{3}\) for \(j=1,\ldots ,n_{\mathrm {m}}-1\), such that the dynamic system can be described by the concatenated state vector \(x(t) \in {\mathbb {R}}^{6(n_{\mathrm {m}}-1)}\). More details on the resulting nonlinear ODE model \(\dot{x}(t) = f_{\mathrm {chain}}(x(t),u(t))\) can be found in [76].
The OCP problem formulation includes simple bounds on the control inputs \(u_x,u_y,u_z \in [-10,10]\) and the state constraint that the chain should not hit a wall placed close to the equilibrium state as illustrated by Fig. 5, i.e., \(p_y^j > -0.01\) for \(j=1,\ldots ,n_{\mathrm {m}}-1\). In addition, both the initial and terminal state are constrained resulting in a point-to-point motion
where \(\hat{x}_0\) and \(\hat{x}_T\) denote respectively the initial perturbed and the terminal equilibrium state values. The stage cost in the objective represents minimizing the control effort, such that \(\ell _{\mathrm {ME}}(\cdot ) := \Vert u(t) \Vert _2^2\) is defined. Note that such a least squares type objective will allow us to validate the Gauss–Newton based algorithms for this minimum-effort (ME) type OCP. Alternatively, we include a time optimal reformulation where we introduce the additional state variable \(T_{\mathrm {opt}}\) such that the scaled dynamics read as
which then replaces the original ODE model in Eq. (56c). The time scaling variable itself is not constrained, but instead forms the optimization objective \(\ell _{\mathrm {TO}}(\cdot ) := T_{\mathrm {opt}}\) in the time optimal (TO) formulation.
The horizon length is chosen to be \(T = 5 \mathrm {s}\) and a multiple shooting method is applied to the OCP (56), using \(N=20\) equidistant intervals. This results in a shooting interval of size \(T_s = 0.25 \mathrm {s}\) for the minimum-effort problem. In case of the time optimal formulation, the horizon length is instead taken \(T = 1 \mathrm {s}\) such that the scaling variable \(T_{\mathrm {opt}}\) directly represents the time in which the point-to-point motion is carried out. Note that the definition of this additional state variable \(T_{\mathrm {opt}}\), allows us to preserve the block banded structure in the discrete time OCP (5). In both cases, three integration steps \(N_{\mathrm {s}}= 3\) of a Gauss-Legendre collocation method using \(q = 4\) stages, i.e., of order 8, are used within each shooting interval. The resulting nonlinear OCP will be solved for different numbers of masses \(n_{\mathrm {m}}\) to illustrate the numerical performance of the lifted collocation integrators from Table 4. Figure 6 additionally shows the solution trajectories of the minimum-effort versus time optimal OCP formulation for \(n_{\mathrm {m}}= 8\) masses, including the position \(p^{n_{\mathrm {m}}-1}\) of the free mass at the controlled end of the chain.
7.2 Numerical simulation results
Table 5 shows the average computation times for the Gauss–Newton type SQP method on the minimum-effort OCP problem formulation. The table shows the average computation time per SQP iteration and this for different numbers of masses \(n_{\mathrm {m}}= 3,\ldots ,7\). It includes the standard multiple shooting method (MS) without lifting, as well as exact lifted collocation (LC–EN) and the inexact lifting schemes (LC–IN) and (LC–AF–INIS). The table illustrates that for systems with more states, the computational benefit of using inexact Newton based lifting schemes can be considerably higher. Note that the Jacobian approximation in the (LC–IN) and the (LC–AF–INIS) schemes is based on the Single Newton-type iteration in these experiments, as discussed in more detail also in [65]. For a specific instance of the chain mass problem where \(n_{\mathrm {m}}= 5\), more detailed timing results are shown in Table 6. It includes the average computation time spent in each component of the algorithm per SQP iteration, including the simulation with sensitivity propagation, condensing of the structured QP subproblem and the solution of the resulting condensed problem using qpOASES. It is the simulation time that can be reduced considerably by using lifted collocation integrators, which appears to account for the highest portion of the total computational effort for this numerical case study. More specifically, a speedup factor of about 2 can be observed when using lifted collocation instead of the standard method without lifting. When using the INIS-type lifting scheme, this computational speedup increases to a factor of about 10. Note that one iteration of the general-purpose sparse NLP solver Ipopt takes about 500 ms in this case, while the solution of one direct collocation based QP takes about 2.4 s using the sparse OOQP solver.
Table 7 shows the average computation times for an exact Hessian based SQP iteration on the time optimal OCP using different numbers of masses \(n_{\mathrm {m}}\) while Table 8 presents the detailed timing results using \(n_{\mathrm {m}}= 5\) masses. In a similar way as before for the Gauss–Newton based implementation, it can be observed from the latter table that both the exact and inexact lifting schemes can reduce the computational effort over the standard multiple shooting method. More specifically, a speedup factor of almost 2 can be observed when using the (LC–EN) scheme instead of the standard collocation integrator without lifting. The table additionally shows that the inexact lifted collocation integrators (LC–IN) and (LC–INIS) reduce the computation time less in the context of second-order sensitivity propagation, compared to the Gauss–Newton based implementation in Tables 5 and 6. However, a computational speedup factor of about 5 can still be observed in Table 8 when using, for example, the INIS-type lifting scheme over the standard (MS) method. Note that these timing results include a block based regularization of the Hessian to guarantee a convex structured QP subproblem in the exact Hessian based SQP implementation [69]. A more detailed discussion on how the algorithm is affected by different techniques to perform a sparsity preserving Hessian regularization is outside the scope of this article. Note that one iteration of the general-purpose sparse NLP solver Ipopt on the time optimal OCP problem takes about 300 ms in this case, while the solution of one direct collocation based QP takes about 5 s using the sparse OOQP solver.
The convergence of the SQP method using the different variants of lifted collocation is illustrated in Fig. 7 for both the minimum effort and the time optimal OCP formulation. The figure shows the distance \(\Vert W - W^\star \Vert _\infty \) of the current iterate W from the local minimum \(W^\star \) of the direct collocation NLP for the continuous time OCP in Eq. (56). Since the exact lifting scheme (LC–EN) is equivalent to direct collocation as shown in Proposition 4, it is expected that its convergence is close to that of the standard multiple shooting method (MS), which is also confirmed by the results in Fig. 7. In addition, the reduction in convergence speed by using a Jacobian approximation in the INIS based lifted collocation integrators appears to be relatively small for this numerical case study. More information on the design and use of efficient Jacobian approximations for collocation methods, taking into account the resulting convergence and stability properties, can be found in [10, 21, 22, 40]. In contrast to INIS, the adjoint-based IN scheme from Algorithm 2 shows a considerably slower local convergence rate based on the same Jacobian approximation for this example. This advantage of INIS over the standard IN implementation is shown also theoretically in [67].
8 Conclusions
This article presents a novel family of lifted Newton-type optimization algorithms for direct optimal control, based on collocation within direct multiple shooting. The schemes result in multiple shooting type subproblems, while they all converge locally to the solution of the direct collocation NLP. In case of the exact lifting scheme in Algorithm 1, the iterates are shown to be equivalent to those of a Newton-type optimization method for direct collocation. As summarized by Table 1, the main motivation for lifted collocation is the use of tailored solvers for the multiple shooting type optimal control structure, as well as the possibility to include efficient Newton-type implementations. This article proposes two types of inexact lifting schemes, using either an adjoint-based implementation in Algorithm 2 or the inexact Newton method with iterated sensitivities in Algorithms 3 and 4. In addition to discussing their implementation as summarized by Table 2 and discussing their corresponding properties, a connection has been made to Newton-type convergence theory.
Another important contribution of this article is the open-source software implementation of the proposed algorithms within the ACADO code generation tool for real-time optimal control. The performance of the lifted collocation integrators within this package has been illustrated based on the benchmark case study of the optimal control for a chain of masses. Based on these numerical results, a computational speedup of factor 2 is typically observed when using the exact lifting scheme instead of the standard collocation integrator within direct multiple shooting. In addition, a further speedup factor in the range of 5–10 per iteration has been observed when using the inexact Newton based lifted collocation schemes on this benchmark example.
References
ACADO Toolkit. http://www.acadotoolkit.org (2009–2016)
HSL. A collection of Fortran codes for large scale scientific computation. http://www.hsl.rl.ac.uk (2011)
ACADO Toolkit discussion. www.sourceforge.net/p/acado/discussion (2012–2016)
Albersmeyer, J., Bock, H.: Sensitivity generation in an adaptive BDF-method. In: Modeling, Simulation and Optimization of Complex Processes: Proceedings of the International Conference on High Performance Scientific Computing, March 6–10, 2006, Hanoi, Vietnam, pp. 15–24. Springer (2008)
Albersmeyer, J., Diehl, M.: The lifted Newton method and its application in optimization. SIAM J. Optim. 20(3), 1655–1684 (2010)
Albin, T., Ritter, D., Abel, D., Liberda, N., Quirynen, R., Diehl, M.: Nonlinear MPC for a two-stage turbocharged gasoline engine airpath. In: Proceedings of the IEEE Conference on Decision and Control (CDC), pp. 849–856 (2015)
Andersson, J., Akesson, J., Diehl, M.: CasADi—a symbolic package for automatic differentiation and optimal control. In: Recent Advances in Algorithmic Differentiation, Lecture Notes in Computational Science and Engineering, vol. 87, pp. 297–307. Springer (2012)
Bauer, I., Bock, H., Schlöder, J.: DAESOL—a BDF-code for the numerical solution of differential algebraic equations. Internal Report, IWR, SFB 359, University of Heidelberg (1999)
Betts, J.: Practical Methods for Optimal Control and Estimation Using Nonlinear Programming, 2nd edn. SIAM, Philadelphia (2010)
Bickart, T.A.: An efficient solution process for implicit Runge–Kutta methods. SIAM J. Numer. Anal. 14(6), 1022–1027 (1977)
Biegler, L.: Solution of dynamic optimization problems by successive quadratic programming and orthogonal collocation. Comput. Chem. Eng. 8(3–4), 243–248 (1984)
Biegler, L., Zavala, V.: Large-scale nonlinear programming using IPOPT: an integrating framework for enterprise-wide dynamic optimization. Comput. Chem. Eng. 33(3), 575–582 (2009). Selected Papers from the 17th European Symposium on Computer Aided Process Engineering held in Bucharest, Romania, May 2007
Biegler, L.T.: Nonlinear Programming, MOS-SIAM Series on Optimization. SIAM, Philadelphia (2010)
Bock, H.: Randwertproblemmethoden zur Parameteridentifizierung in Systemen nichtlinearer Differentialgleichungen, Bonner Mathematische Schriften, vol. 183. Universität Bonn, Bonn (1987)
Bock, H.G.: Numerical treatment of inverse problems in differential and integral equations. In: Progress in Scientific Computing, vol. 2, pp. 95–121. Birkhäuser, Boston (1983)
Bock, H.G., Diehl, M., Kostina, E.A., Schlöder, J.P.: Constrained optimal feedback control of systems governed by large differential algebraic equations. In: Real-Time and Online PDE-Constrained Optimization, pp. 3–22. SIAM, Philadelphia (2007)
Bock, H.G., Plitt, K.J.: A multiple shooting algorithm for direct solution of optimal control problems. In: Proceedings of the IFAC World Congress, pp. 242–247. Pergamon Press (1984)
Boggs, P.T., Tolle, J.W.: Sequential quadratic programming. Acta Numer. 4, 1–51 (1995)
Broyden, C.G.: Quasi-Newton methods and their application to function minimization. Math. Comput. 21, 368–381 (1967)
Büskens, C., Maurer, H.: SQP-methods for solving optimal control problems with control and state constraints: adjoint variables, sensitivity analysis and real-time control. J. Comput. Appl. Math. 120(1–2), 85–108 (2000)
Butcher, J.: On the implementation of implicit Runge–Kutta methods. BIT Numer. Math. 16(3), 237–240 (1976)
Cooper, G., Vignesvaran, R.: Some schemes for the implementation of implicit Runge–Kutta methods. J. Comput. Appl. Math. 45(1–2), 213–225 (1993)
Curtis, F.E., Johnson, T.C., Robinson, D.P., Wächter, A.: An inexact sequential quadratic optimization algorithm for nonlinear optimization. SIAM J. Optim. 24(3), 1041–1074 (2014)
Dembo, R., Eisenstat, S., Steihaug, T.: Inexact Newton methods. SIAM J. Numer. Anal. 19(2), 400–408 (1982)
Dennis, J.E.: On Newton-like methods. Numer. Math. 11(4), 324–330 (1968)
Deuflhard, P.: Newton Methods for Nonlinear Problems: Affine Invariance and Adaptive Algorithms, vol. 35. Springer, Berlin (2011)
Diehl, M.: Lecture Notes on Numerical Optimization. http://cdn.syscop.de/publications/Diehl2016.pdf (2016)
Diehl, M., Bock, H.G., Schlöder, J., Findeisen, R., Nagy, Z., Allgöwer, F.: Real-time optimization and nonlinear model predictive control of processes governed by differential-algebraic equations. J. Process Control 12(4), 577–585 (2002)
Diehl, M., Bock, H.G., Schlöder, J.P.: A real-time iteration scheme for nonlinear optimization in optimal feedback control. SIAM J. Control Optim. 43(5), 1714–1736 (2005)
Diehl, M., Ferreau, H.J., Haverbeke, N.: Efficient numerical methods for nonlinear MPC and moving horizon estimation. In: Magni, L., Raimondo, M., Allgöwer, F. (eds.) Nonlinear Model Predictive Control, Lecture Notes in Control and Information Sciences, pp. 391–417. Springer, Berlin (2009)
Diehl, M., Leineweber, D., Schäfer, A.: MUSCOD-II Users’ Manual. IWR-Preprint 2001–2025. University of Heidelberg (2001)
Diehl, M., Walther, A., Bock, H.G., Kostina, E.: An adjoint-based SQP algorithm with Quasi-Newton Jacobian updates for inequality constrained optimization. Optim. Methods Softw. 25(4), 531–552 (2010)
Domahidi, A., Perez, J.: FORCES professional. embotech GmbH. http://embotech.com/FORCES-Pro (2014)
Fabien, B.: dsoa: the implementation of a dynamic system optimization algorithm. Optim. Control Appl. Methods 31, 231–247 (2010)
Ferreau, H.J., Kirches, C., Potschka, A., Bock, H.G., Diehl, M.: qpOASES: a parametric active-set algorithm for quadratic programming. Math. Program. Comput. 6(4), 327–363 (2014)
Frasch, J.V., Sager, S., Diehl, M.: A parallel quadratic programming method for dynamic optimization problems. Math. Program. Comput. 7(3), 289–329 (2015)
Frison, G.: Algorithms and methods for high-performance model predictive control. Ph.D. thesis, Technical University of Denmark (DTU) (2015)
Frison, G., Sorensen, H.B., Dammann, B., Jørgensen, J.B.: High-performance small-scale solvers for linear model predictive control. In: Proceedings of the European Control Conference (ECC), pp. 128–133 (2014)
Gertz, E.M., Wright, S.J.: Object-oriented software for quadratic programming. ACM Trans. Math. Softw. 29(1), 58–81 (2003)
González-Pinto, S., Montijano, J.I., Rández, L.: Iterative schemes for three-stage implicit Runge–Kutta methods. Appl. Numer. Math. 17(4), 363–382 (1995)
Griewank, A.: Evaluating Derivatives, Principles and Techniques of Algorithmic Differentiation. No. 19 in Frontiers in Applied Mathematics. SIAM, Philadelphia (2000)
Hairer, E., Wanner, G.: Solving Ordinary Differential Equations II—Stiff and Differential-Algebraic Problems, 2nd edn. Springer, Berlin (1991)
Hindmarsh, A., Brown, P., Grant, K., Lee, S., Serban, R., Shumaker, D., Woodward, C.: SUNDIALS: suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. 31(3), 363–396 (2005)
Hong, W., Wang, S., Li, P., Wozny, G., Biegler, L.: A quasi-sequential approach to large-scale dynamic optimization problems. AIChE J. 52(1), 255–268 (2006)
Houska, B., Diehl, M.: A quadratically convergent inexact SQP method for optimal control of differential algebraic equations. Optim. Control Appl. Methods 34(4), 396–414 (2013)
Houska, B., Ferreau, H.J., Diehl, M.: ACADO toolkit—an open source framework for automatic control and dynamic optimization. Optim. Control Appl. Methods 32(3), 298–312 (2011)
Houska, B., Ferreau, H.J., Diehl, M.: An auto-generated real-time iteration algorithm for nonlinear MPC in the microsecond range. Automatica 47(10), 2279–2285 (2011)
Kalmari, J., Backman, J., Visala, A.: A toolkit for nonlinear model predictive control using gradient projection and code generation. Control Eng. Pract. 39, 56–66 (2015)
Kang, J., Cao, Y., Word, D.P., Laird, C.D.: An interior-point method for efficient solution of block-structured NLP problems using an implicit Schur-complement decomposition. Comput. Chem. Eng. 71, 563–573 (2014)
Kirches, C., Wirsching, L., Sager, S., Bock, H.: Efficient numerics for nonlinear model predictive control. In: Recent Advances in Optimization and its Applications in Engineering, pp. 339–357. Springer (2010)
Kouzoupis, D., Quirynen, R., Frasch, J.V., Diehl, M.: Block condensing for fast nonlinear MPC with the dual Newton strategy. In: Proceedings of the IFAC Conference on Nonlinear Model Predictive Control (NMPC), vol. 48, pp. 26–31 (2015)
Leineweber, D., Schäfer, A., Bock, H., Schlöder, J.: An efficient multiple shooting based reduced SQP strategy for large-scale dynamic process optimization. Part II: software aspects and applications. Comput. Chem. Eng. 27, 167–174 (2003)
Liu, F., Hager, W.W., Rao, A.V.: Adaptive mesh refinement method for optimal control using nonsmoothness detection and mesh size reduction. J. Frankl. Inst. 352(10), 4081–4106 (2015)
Mattingley, J., Wang, Y., Boyd, S.: Code generation for receding horizon control. In: Proceedings of the IEEE International Symposium on Computer-Aided Control System Design, pp. 985–992. Yokohama, Japan (2010)
Mayne, D., Rawlings, J.: Model Predictive Control. Nob Hill Publishing, Madison, WI (2013)
Nocedal, J., Wright, S.J.: Numerical Optimization, Springer Series in Operations Research and Financial Engineering, 2nd edn. Springer, Berlin (2006)
Ohtsuka, T.: A continuation/GMRES method for fast computation of nonlinear receding horizon control. Automatica 40(4), 563–574 (2004)
Ohtsuka, T., Kodama, A.: Automatic code generation system for nonlinear receding horizon control. Trans. Soc. Instrum. Control Eng. 38(7), 617–623 (2002)
Patterson, M.A., Hager, W.W., Rao, A.V.: A ph mesh refinement method for optimal control. Optim. Control Appl. Methods 36(4), 398–421 (2015)
Patterson, M.A., Rao, A.V.: GPOPS-II: a MATLAB software for solving multiple-phase optimal control problems using hp-adaptive gaussian quadrature collocation methods and sparse nonlinear programming. ACM Trans. Math. Softw. 41(1), 1–37 (2014)
Potschka, A.: Handling Path Constraints in a Direct Multiple Shooting Method for Optimal Control Problems. Diplomarbeit, University of Heidelberg (2006)
Potschka, A.: A direct method for the numerical solution of optimization problems with time-periodic PDE constraints. Ph.D. thesis, University of Heidelberg (2011)
Pytlak, R.: Numerical Methods for Optimal Control Problems with State Constraints, Lecture Notes in Mathematics. Springer, Berlin (1999)
Quirynen, R., Gros, S., Diehl, M.: Efficient NMPC for nonlinear models with linear subsystems. In: Proceedings of the IEEE Conference on Decision and Control (CDC), pp. 5101–5106 (2013)
Quirynen, R., Gros, S., Diehl, M.: Inexact Newton based lifted implicit integrators for fast nonlinear MPC. In: Proceedings of the IFAC Conference on Nonlinear Model Predictive Control (NMPC), pp. 32–38 (2015)
Quirynen, R., Gros, S., Diehl, M.: Lifted implicit integrators for direct optimal control. In: Proceedings of the IEEE Conference on Decision and Control (CDC), pp. 3212–3217 (2015)
Quirynen, R., Gros, S., Diehl, M.: Inexact Newton-type optimization with iterated sensitivities. SIAM J. Optim. (accepted, preprint available at Optimization Online, 2016-06-5502) (2016)
Quirynen, R., Houska, B., Diehl, M.: Symmetric hessian propagation for lifted collocation integrators in direct optimal control. In: Proceedings of the American Control Conference (ACC), pp. 1117–1123 (2016)
Quirynen, R., Houska, B., Vallerio, M., Telen, D., Logist, F., Impe, J.V., Diehl, M.: Symmetric algorithmic differentiation based exact Hessian SQP method and software for economic MPC. In: Proceedings of the IEEE Conference on Decision and Control (CDC), pp. 2752–2757 (2014)
Quirynen, R., Vukov, M., Zanon, M., Diehl, M.: Autogenerating microsecond solvers for nonlinear MPC: a tutorial using ACADO integrators. Optim. Control Appl. Methods 36, 685–704 (2014)
Romanenko, A., Pedrosa, N., Leal, J., Santos, L.: Seminario de Aplicaciones Industriales de Control Avanzado, chap. A Linux Based Nonlinear Model Predictive Control Framework, pp. 229–236 (2007)
Simon, L., Nagy, Z., Hungerbuehler, K.: Nonlinear Model Predictive Control, Lecture Notes in Control and Information Sciences, vol. 384, chap. Swelling Constrained Control of an Industrial Batch Reactor Using a Dedicated NMPC Environment: OptCon, pp. 531–539. Springer (2009)
Tomlab Optimization: PROPT: Matlab Optimal Control Software (ODE,DAE). http://tomdyn.com (2009–2011)
Vukov, M., Gros, S., Horn, G., Frison, G., Geebelen, K., Jørgensen, J.B., Swevers, J., Diehl, M.: Real-time nonlinear MPC and MHE for a large-scale mechatronic application. Control Eng. Pract. 45, 64–78 (2015)
Wächter, A., Biegler, L.T.: On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 106(1), 25–57 (2006)
Wirsching, L., Bock, H.G., Diehl, M.: Fast NMPC of a chain of masses connected by springs. In: Proceedings of the IEEE International Conference on Control Applications, Munich, pp. 591–596 (2006)
Word, D.P., Kang, J., Akesson, J., Laird, C.D.: Efficient parallel solution of large-scale nonlinear dynamic optimization problems. Comput. Optim. Appl. 59(3), 667–688 (2014)
Zavala, V.M., Laird, C.D., Biegler, L.T.: Interior-point decomposition approaches for parallel solution of large-scale nonlinear parameter estimation problems. Chem. Eng. Sci. 63(19), 4834–4845 (2008)
Author information
Authors and Affiliations
Corresponding author
Additional information
The software that was reviewed as part of this submission has been issued the Digital Object Identifier doi:10.5281/zenodo.321691.
This research was supported by the EU via ERC-HIGHWIND (259 166), FP7-ITN-TEMPO (607 957), H2020-ITN-AWESCO (642 682) and by the DFG in context of the Research Unit FOR 2401. At the time of initial submission, the first author held a Ph.D. fellowship of the Research Foundation—Flanders (FWO) and he is currently affiliated with the Mitsubishi Electric Research Laboratories (MERL) in Cambridge, MA.
Rights and permissions
About this article
Cite this article
Quirynen, R., Gros, S., Houska, B. et al. Lifted collocation integrators for direct optimal control in ACADO toolkit. Math. Prog. Comp. 9, 527–571 (2017). https://doi.org/10.1007/s12532-017-0119-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12532-017-0119-0