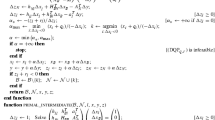qpOASES: a parametric active-set algorithm for quadratic programming

Abstract

Many practical applications lead to optimization problems that can either be stated as quadratic programming (QP) problems or require the solution of QP problems on a lower algorithmic level. One relatively recent approach to solve QP problems are parametric active-set methods that are based on tracing the solution along a linear homotopy between a QP problem with known solution and the QP problem to be solved. This approach seems to make them particularly suited for applications where a-priori information can be used to speed-up the QP solution or where high solution accuracy is required. In this paper we describe the open-source C++ software package qpOASES, which implements a parametric active-set method in a reliable and efficient way. Numerical tests show that qpOASES can outperform other popular academic and commercial QP solvers on small- to medium-scale convex test examples of the Maros-Mészáros QP collection. Moreover, various interfaces to third-party software packages make it easy to use, even on embedded computer hardware. Finally, we describe how qpOASES can be used to compute critical points of nonconvex QP problems.

1 Introduction

This paper describes the current release 3.0 of the open-source software package qpOASES ¹. This software package implements a parametric active-set method for solving convex quadratic programming (QP) problems and for computing critical points of nonconvex quadratic programming problems.

The class of convex QP problems is important in its own right. Gould and Toint maintain a bibliography [30] of currently about 1000 publications that comprise many application papers from disciplines as diverse as portfolio analysis, structural analysis, VLSI design, discrete-time stabilization, optimal and fuzzy control, finite impulse response design, optimal power flow or economic dispatch. The Maros-Mészáros QP test set [44] collects a number of benchmark and application problems that can be accessed through the CUTEr testing environment [32]. Linear model predictive control (MPC) problems constitute another important subclass of convex QP problems. As MPC is frequently applied to processes with very fast dynamics, it becomes crucial to solve the resulting convex QP problems at very high rates; possibly within a millisecond or less [57]. Moreover, as MPC controllers typically need to run autonomously without further user-interaction, QP solution needs to be highly reliable.

QP problems also arise as subproblems in sequential quadratic programming (SQP) methods. SQP methods aim at solving nonlinear optimization problems by using a linear-quadratic approximation of the original problem in each iteration. Depending on the way the nonlinear objective function is approximated, the resulting QP problems are often convex but may also become nonconvex for certain SQP-type schemes. Again, the fast and reliable solution of QP problems is crucial to make such nonlinear optimization algorithms work efficiently.

1.1 Problem description

We consider quadratic programming problems of the following form,

$$\begin{aligned}&\mathop {\hbox {min}}\limits _{x \in \mathbb {R}^n}&\frac{1}{2}\; x^THx + g^Tx \end{aligned}$$

(1a)

$$\begin{aligned}&\mathop {\hbox {s. t.}}&a^{\text{ l }}\le Ax\le a^{\text{ u }}, \end{aligned}$$

(1b)

comprising a symmetric Hessian matrix $H\in \mathbb {R}^{n\times n}$, a constraint matrix $A\in \mathbb {R}^{m \times n}$, a gradient vector $g\in \mathbb {R}^n$, and lower and upper constraint bound vectors $a^{\text{ l }}, a^{\text{ u }}\in \mathbb {R}^{m}\cup \{\infty ,-\infty \}^{m}$. Throughout this paper, inequality signs between vectors are to be understood element-wise.

For reasons of efficiency, it is important to exploit box constraints on the problem variables that lend the special substructure $A^T=(I \; \; \tilde{A}^T)$ to the constraint matrix. qpOASES exploits this substructure in the numerical linear algebra methods.

It is appropriate to introduce some notation at this point. Throughout this article, vectors are column vectors; an index subscript $i$ on a vector denotes the $i$-th element; a set subscript on a vector denotes the subvector of elements; the operator $\circ$ denotes element-wise multiplication of vectors. We will need to encode a working set $W$ as an $m$-vector with entries from $\{-1,0,+1\}$, whose $i$-th component indicates whether constraint $i$ of the matrix $A$ is inactive ($W_i= 0$) or active at the lower $(W_i = -1)$ or upper $(W_i = +1)$ bound. We further denote by $A_W$ the matrix that consists of the rows of $A$ indicated by $W_i \ne 0$.

1.2 Optimality conditions

A quadratic program of the form (1) is convex (strictly convex) if and only if its Hessian matrix $H$ is positive semidefinite (positive definite); it is nonconvex otherwise. If feasible, strictly convex QP problems are known to possess a unique global minimum. Uniqueness still holds for feasible convex QP problems if $H$ is positive definite on the null-space of the strictly active constraints in the solution. For nonconvex QP problems, finding the global minimum is NP-hard [45], as is the verification of local optimality of a constrained critical point in the case of weakly active constraints [10]. In these cases, we only strive to find a locally optimal solution or a critical point, respectively.

For the characterization of solutions of QP (1) we partition the index set $\overline{m} = \{1, \ldots , m\}$ for a feasible point $x$ into four disjoint sets

$$\begin{aligned} \fancyscript{A}^\mathrm{e}(x)&= \{ i \in \overline{m} \,|\, a^{\text{ l }}_i = (Ax)_i = a^{\text{ u }}_i \},&\fancyscript{A}^\mathrm{l}(x)&= \{ i \in \overline{m} \,|\, a^{\text{ l }}_i = (Ax)_i < a^{\text{ u }}_i \},\\ \fancyscript{A}^\mathrm{u}(x)&= \{ i \in \overline{m} \,|\, a^{\text{ l }}_i < (Ax)_i = a^{\text{ u }}_i \},&\fancyscript{A}^\mathrm{f}(x)&= \{ i \in \overline{m} \,|\, a^{\text{ l }}_i < (Ax)_i < a^{\text{ u }}_i \} \end{aligned}$$

of equality, lower active, upper active, and free constraint indices, respectively. It is well known [see, e.g., 48] that for any solution $x^*$ of QP (1) there exists a vector $y^* \in \mathbb {R}^m$ of Lagrange multipliers or dual variables such that

$$\begin{aligned} H x^* + g - A^Ty^*&= 0,&a^{\text{ l }}&\le Ax^* \le a^{\text{ u }}, \end{aligned}$$

(2a)

$$\begin{aligned} (Ax^* - a^{\text{ l }})_i y^*_i&= 0, \quad i \in \fancyscript{A}^\mathrm{l}(x^*),&y^*_i&\ge 0, \quad i \in \fancyscript{A}^\mathrm{l}(x^*),\end{aligned}$$

(2b)

$$\begin{aligned} (Ax^* - a^{\text{ u }})_i y^*_i&= 0, \quad i \in \fancyscript{A}^\mathrm{u}(x^*),&y^*_i&\le 0, \quad i \in \fancyscript{A}^\mathrm{u}(x^*), \end{aligned}$$

(2c)

$$\begin{aligned}&y^*_i&= 0, \quad i \in \fancyscript{A}^\mathrm{f}(x^*). \end{aligned}$$

(2d)

A pair $(x^*, y^*) \in \mathbb {R}^{n+m}$ that satisfies (2) is called a critical point. In the convex case it additionally holds that every critical point is a global solution of QP (1). The primal-dual solution is furthermore unique if and only if the following two conditions are satisfied:

• 1. The active constraint rows $A_i, i \in \fancyscript{A}^\mathrm{e}\cup \fancyscript{A}^\mathrm{l}\cup \fancyscript{A}^\mathrm{u}$, are linearly independent.

• 2. Matrix $H$ is positive definite on the null space of the strictly active constraints.

For the nonconvex case, critical points are not necessarily local minima. To verify local optimality, we can use a sufficient condition of second order. We specialize a result from nonlinear constrained optimization [20, Theorem 9.3.1 and the following remark] to the QP case: Let $(x^*, y^*) \in \mathbb {R}^{n+m}$ be a critical point and define the set of strongly active inequality constraints

$$\begin{aligned} \fancyscript{A}^\mathrm{l}_+(x^*,y^*)&= \fancyscript{A}^\mathrm{l}(x^*) \cap \{i \in \overline{m} \,|\, y^*_i > 0\}, \\ \fancyscript{A}^\mathrm{u}_-(x^*,y^*)&= \fancyscript{A}^\mathrm{u}(x^*) \cap \{i \in \overline{m} \,|\, y^*_i < 0\}. \end{aligned}$$

Then $x^*$ is a strict local minimizer of (1), if

$$\begin{aligned} s^TH s \!>\! 0 \quad \!\forall \! s \in \mathbb {R}^n\quad \text {with } s \!\ne \! 0, A_i s\!=\! 0, i \in \fancyscript{A}^\mathrm{e}(x^*) \cup \fancyscript{A}^\mathrm{l}_+(x^*,y^*) \cup \fancyscript{A}^\mathrm{u}_-(x^*,y^*). \end{aligned}$$

(3)

1.3 Existing methods

A great variety of methods for solving QP problems exists. Many of them can be categorized into one of two main families, namely active-set and interior-point methods, but other approaches, such as fast gradient methods, exist and have important applications, see for example [46].

Interior-point methods were initially developed for linear programming [39] and were later extended to convex quadratic and general nonlinear programming. They are mainly used in two different variants: primal barrier methods and primal-dual methods. Barrier methods replace the inequality constraints (1b) of the QP problem by a weighted barrier function in the objective. This barrier function is constructed such that it becomes (infinitely) expensive to violate the constraints; typically, a logarithmic barrier is used. The resulting equality constrained nonlinear problem is then solved by Newton’s method. In order to ensure convergence to the solution of the original QP problem, this procedure is repeated with a decreased weight on the barrier function. That way, IP methods follow the so-called central path, a nonlinear path from a strictly feasible point towards the solution. If the weight is changed only moderately in each step of the outer loop, then the inner Newton iterations can be shown to always remain in the region of quadratic convergence and thus solve the inner problem within very few iterations, cf. [59]. A polynomial runtime guarantee can be given for certain update schemes of the weight, as shown in [47]. Primal-dual IP methods combine the inner and outer loop of primal barrier methods by reducing the weight on the barrier in each iteration of Newton’s method.

Active-set methods were originally developed as extensions of the simplex method for solving LP problems [11, 58]. The fundamental idea of all active-set methods is to fix a working set, a maximal linearly independent subset of the active constraints, and to solve the resulting equality constrained QP problem. The working set is then updated repeatedly until optimality is reached. Active-set methods can be divided into primal, dual, and parametric methods. Once a feasible starting point has been found, primal active-set methods generate a sequence of primal feasible iterates until dual feasibility and hence an optimal solution is obtained [48]. If no feasible starting point is available, a so-called Phase I is employed to generate one or to detect infeasibility; see e.g. [20]. Dual active-set methods for convex QP problems generate a sequence of dual-feasible iterates until primal feasibility and hence an optimal solution is obtained. In the strictly convex case, this is equivalent to solving the dual of the QP problem (1) with a primal active-set method [28].

The numerical behavior of active-set and interior-point methods is usually quite different: While active-set methods need on average substantially more iterations than interior-point methods, each active-set iteration is computationally much cheaper. Often, one or the other method will perform favorably on a certain problem instance, indicating that both approaches are important. An advantage of active-set methods is the possibility to warm-start or hot-start² the iterations when solving a sequence of related QP problems, which can lead to substantial speed-ups. Contrary to primal active-set or primal barrier methods, dual active-set methods do not require a possibly expensive Phase I.

An up-to-date list of available quadratic programming codes can be found on the web page [31].

A variant of the active-set method that has received comparably little attention are parametric active-set methods, which are centered around the idea of tracing the solution of a linear homotopy parameterized by $\tau \in [0,1]$ between a QP problem with known solution $(\tau =0)$ and the QP problem to be solved $(\tau =1)$,

$$\begin{aligned} \mathop {\hbox {min}}\limits _{x(\tau ) \in \mathbb {R}^n}&\frac{1}{2} x(\tau )^THx(\tau ) + g(\tau )^Tx(\tau ) \end{aligned}$$

(4a)

$$\begin{aligned} \mathop {\hbox {s. t.}}&a^{\text{ l }}(\tau ) \le Ax(\tau ) \le a^{\text{ u }}(\tau ). \end{aligned}$$

(4b)

If $g(\tau ),\; a^{\text{ l }}(\tau )$, and $a^{\text{ u }}(\tau )$ are affine-linear functions of the homotopy parameter $\tau$, it can be shown that the optimal solutions $x(\tau )$ depend piecewise affine-linearly on $\tau$. The algorithm considered in this paper has been proposed in [7] in the form of the primal-dual Parametric Quadratic Programming (PQP) method, and was later adapted for use in model predictive control (MPC), see [19].

In MPC, one is interested in the on-line optimization of a dynamic process over a prediction horizon in time,

$$\begin{aligned}&\mathop {\mathop {\min }\limits _{v\in \mathbb {R}^{n_\text {v}\times (N+1)},}}\limits _{u \in \mathbb {R}^{n_\text {u}\times N}}\;&\frac{1}{2}\sum \limits _{k=0}^{N-1} \left( ||v_k-v^{\text {r}}_k||_{Q_k}^2\!+||u_k-u^{\text {r}}_k||_{R_k}^2\right) \!+\! \frac{1}{2}||v_N-v^{\text {r}}_N||_P^2 \end{aligned}$$

(5a)

$$\begin{aligned}&\mathop {\hbox {s. t.}}\;&v_0 = v_\text {est}, \end{aligned}$$

(5b)

$$\begin{aligned}&v_{k+1} = A_kv_k+B_ku_k +c_k\quad \forall \,k\in \left\{ 0,\ldots ,N-1\right\} \!, \end{aligned}$$

(5c)

$$\begin{aligned}&d^{\text {l}}_k \le C_kv_k + D_ku_k \le d^{\text {u}}_k \quad \forall \,k\in \left\{ 0,\ldots ,N-1\right\} \!, \end{aligned}$$

(5d)

$$\begin{aligned}&d^{\text {l}}_N \le C_Nv_N ~\le ~ d^{\text {u}}_N. \end{aligned}$$

(5e)

Here, the process is described by the discrete-time dynamic system (5c) on $N$ time intervals $[t_i,t_{i+1}]$, $0\le i \le N-1$, which defines the vector $v=(v_0,\ldots ,v_N)\in \mathbb {R}^{n_\text {v}\times (N+1)}$ of state predictions. The process is affected by a sequence of future control inputs $u=(u_0,\ldots ,u_{N-1})\in \mathbb {R}^{n_\text {u}\times N}$ to be determined such that a convex objective function (5a) is minimized subject to process constraints (5d)–(5e) that must be satisfied.

Problem (5) is a quadratic problem that depends parametrically on the initial state vector $v_\text {est}\in \mathbb {R}^{n_\text {v}}$. Using the dynamic equations (5c) to eliminate the process states $v$ from the problem yields the following equivalent QP problem:

$$\begin{aligned} \mathop {\hbox {min}}\limits _{u(v_0) \in \mathbb {R}^n}&\frac{1}{2} u(v_0)^THu(v_0) + g(y_0)^Tu(v_0) \end{aligned}$$

(6a)

$$\begin{aligned} \mathop {\hbox {s. t.}}&a^{\text{ l }}(v_0) \le Au(v_0) \le a^{\text{ u }}(v_0), \end{aligned}$$

(6b)

which can be easily re-parameterized to yield the standard form (4) of a parametric QP problem. The current state vector $v_0$ is repeatedly estimated from real-world measurements, and at each sampling instant problem (6) is solved on-line to find the optimal feedback control $u_0\in \mathbb {R}^{n_\text {u}}$. This optimized control is then used to control the process, until the next, more recent feedback control has been computed from the next state observation. As measurements of $v_\text {est}$ typically vary slowly, one can expect the optimal solution of the parametric QP problem (6) to also change only moderately with time. Therefore, it is beneficial to exploit the parametric hot-starting capabilities of active-set methods for MPC in order to meet the hard real-time constraints on the available on-line computation time, see [12, 19] for further details.

1.4 Structure and contribution of this article

This article presents the open-source software package qpOASES, first mentioned in [14, 19], in its most recent release 3.0. In this paper, the new release of qpOASES is shown to constitute a reliable and efficient, object-oriented C++ implementation of a parametric primal-dual active-set method. Section 2 starts by recalling the parametric quadratic programming algorithm as described in [7]. In Sect. 3 we describe new algorithmic extensions that were introduced in release 3.0 of qpOASES. We elaborate on the mathematical background of these extensions and present numerical details of the implementation details. Section 4 outlines the object-oriented design of the C++ implementation in more detail. Small code examples for typical use cases of qpOASES are given, and we mention possibilities for extending the functionality of qpOASES by deriving from existing C++ classes, providing an opportunity to tailor important parts of the code to special problem structures. Section 4.5 discusses important parameters of the algorithm and the qpOASES code. They are based on numerical improvements that allow a trade-off between efficiency and reliability of the algorithm, tailored to the numerical characteristics of the specific QP problem to be solved. Section 5 contains details about interfaces to various third-party software packages and mentions a number of applications of qpOASES to real-world problems, partly on embedded computer hardware. We show in Sect. 6 that qpOASES performs competitively with popular academic and commercial QP solvers on small- to medium-scale test examples. We also present results of qpOASES finding stationary points of nonconvex QP problems. In addition, we discuss how the homotopy framework can be efficiently exploited for hot-starting QP problems within a given sequence of problems, for example, QP problems arising in model predictive control applications. We briefly address in Sect. 7 how to obtain a copy of qpOASES and how to install it.

2 Algorithm

In this section we describe the PQP method due to [7], which forms the basis for the new algorithmic developments that we discuss in Sect. 3. The choice of matrix decompositions for the linear algebra employed in the computation of step directions is entirely decoupled from the PQP method itself. We briefly address the null-space method implemented in qpOASES and give details on the handling of QP problems with sparse matrix data.

From now on, we generally assume convexity, i.e., positive semi-definiteness of $H$, unless explicitly stated otherwise.

2.1 The parametric programming paradigm

The idea behind parametric active-set methods is to trace optimal solutions on a homotopy path between two QP instances, parameterized by $\tau \in [0, 1]$. Denote the set of affine-linear functions from $[0,1]$ to $\mathbb {R}^k$ by

$$\begin{aligned} \fancyscript{H}^k = \{ f: [0,1] \rightarrow \mathbb {R}^k ~|~ f(\tau ) = (1-\tau ) f(0) + \tau f(1), \ \tau \in [0,1] \}, \end{aligned}$$

(7)

and let $g(\tau )\in \fancyscript{H}^n,\; a^{\text{ l }}(\tau ), a^{\text{ u }}(\tau )\in \fancyscript{H}^m$. We are interested in the solution of the one-parametric family of QP problems

$$\begin{aligned}&\mathop {\hbox {min}}\limits _{x(\tau ) \in \mathbb {R}^n}&\frac{1}{2} x(\tau )^THx(\tau ) + g(\tau )^Tx(\tau ) \end{aligned}$$

(8a)

$$\begin{aligned}&\mathop {\hbox {s. t.}}&a^{\text{ l }}(\tau ) \le Ax(\tau ) \le a^{\text{ u }}(\tau ). \end{aligned}$$

(8b)

For fixed $\tau$, denote an optimal primal-dual solution by $z(\tau ) = (x(\tau ), y(\tau ))$, where $y(\tau )$ are the Lagrange multipliers of the inequality constraints (8b). It can be shown that optimal solutions $z(\tau )$ depend piecewise linearly but not necessarily continuously on $\tau$, see [7]. The active set is constant on each linear segment. Parametric active-set algorithms follow $z(\tau )$ by jumping from the beginning of one segment to the next, updating the working set $W(\tau )$ accordingly. We take the liberty of dropping the argument $\tau$ whenever this does not create ambiguities.

We can immediately observe that this approach allows in a natural way to hot-start the QP solver after modifications to the QP vectors. In addition, no Phase 1 is needed to begin with. We could always recede to the homotopy start $g(0) = 0,\; a^{\text{ l }}(0) = 0,\; a^{\text{ u }}(0) = 0,\; x(0) = 0,\; y(0) = 0$, although better choices are discussed in Sect. 3.

2.2 The classic parametric quadratic programming method

A parametric active-set method was first described by [7] for convex QP under the name parametric quadratic programming algorithm. We restate it here using the notation of problem (8).

• 1. Start with an optimal primal-dual solution $z(0)=(x(0),y(0))$ and associated working set $W(0)\in \{-1,0,1\}^{m}$ of the previously solved QP. Let $\tau :=0$.

• 2. Determine the step direction $\varDelta z= (\varDelta x, \varDelta y)$ using the current working set $W(\tau )$.

• 3. Determine the maximum homotopy step length $\varDelta \tau$ and possibly the index of a blocking constraint, $l$, or a blocking multipliers sign change, $k$.

• 4. If $\varDelta \tau \ge 1 - \tau$, then stop with $z(1) := z(\tau ) + (1 - \tau ) \varDelta z$ as the solution of (8).

• 5. Set $\tau ^+ := \tau +\varDelta \tau ,\; z(\tau ^+) := z(\tau ) + {\varDelta \tau }\varDelta z$, and $W(\tau ^+) := W(\tau )$.

• 6. If constraint $l$ is blocking:

  • (a) Set $W(\tau ^+)_l := \pm 1$ (depending on whether an upper or lower constraint is blocking).

  • (b) If the new working set $W(\tau ^+)$ is linear dependent, find an exchange constraint index $k$ or stop due to infeasibility of (8) for all $\tau >\tau ^+$. Adjust dual variables $y(\tau ^+)$ and set $W(\tau ^+)_k := 0$.

• 7. If sign change of $y(\tau ^+)_k$ is blocking:

  • (a) Set $W(\tau ^+)_k := 0$.

  • (b) If $H$ has nonpositive curvature on the null-space of $W(\tau ^+)$, find an exchange constraint index $l$ or stop due to unboundedness of (8) for all $\tau >\tau ^+$. Adjust primal variables $x(\tau ^+)$ and set $W(\tau ^+)_l := \pm 1$.

• 8. Set $\tau := \tau ^+$ and $W(\tau ) := W(\tau ^+)$. Continue with step 2.

Several steps in this algorithm deserve a more detailed explanation.

2.2.1 Computing the step direction (Step 2)

Denote by $a_W(\tau )$ the vector that consists of entries $a^{\text{ l }}_i(\tau )$ or $a^{\text{ u }}_i(\tau )$ depending on what bounds (if any) are marked active in $W_i(\tau )$. We can then determine the step direction $(\varDelta x, \varDelta y)$ by solving

$$\begin{aligned} K_{W} \begin{pmatrix} \varDelta x \\ -\varDelta y_W\end{pmatrix} = \begin{pmatrix} H &{} A_W^T\\ A_W&{} 0 \end{pmatrix} \begin{pmatrix} \varDelta x \\ -\varDelta y_W\end{pmatrix} = \begin{pmatrix} -(g(1) - g(\tau )) \\ a_W(1) - a _W(\tau ) \end{pmatrix} \end{aligned}$$

(9)

and letting $\varDelta y_i=0$ if $W_i(\tau )=0$. Given invertibility of the matrix $K_W$ for $W(0)$, see Sect. 3.2, steps 6 and 7 ensure that this property is maintained for all $\tau >0$. More details on the numerical linear algebra involved in solving (9) can be found in Sect. 2.3.

2.2.2 Determining the homotopy step length (Step 3)

We can follow $z(\tau )$ in direction $\varDelta z$ along the current segment until either an inactive constraint becomes active (primal blocking), or a dual variable of an active constraint changes its sign (dual blocking).

The step length $\varDelta \tau$ onto the first blocking constraint can be determined by ratio tests,

$$\begin{aligned} \mathrm{RT}: \mathbb {R}^{m}\times \mathbb {R}^{m} \rightarrow \mathbb {R}\cup \{\infty \}, \quad (u, v) \mapsto \min \{ u_i / v_i ~|~ 1 \le i \le m, v_i > 0 \}. \end{aligned}$$

(10)

The minimum yields $\infty$ by convention if the set of ratios is empty. With the help of Eq. (10), the maximum step towards the first blocking constraint is given by

$$\begin{aligned} \varDelta \tau _\text {p} = \min \left\{ \mathrm{RT}\left( Ax(\tau ) - a^{\text{ l }}(\tau ), -A\varDelta x\right) , \mathrm{RT}\left( a^{\text{ u }}(\tau ) - Ax(\tau ), A\varDelta x\right) \right\} \end{aligned}$$

(11)

and towards the first blocking sign change by

$$\begin{aligned} \varDelta \tau _\text {d} = \mathrm{RT}(W(\tau ) \circ y(\tau ), W(\tau ) \circ \varDelta y), \end{aligned}$$

(12)

There might be more than one limiting blocking constraint or sign change. This situation, referred to as a tie, will be addressed in Sect. 3. The maximum step allowed $\varDelta \tau = \min \{\varDelta \tau _\text {p}, \varDelta \tau _\text {d}\}$, however, is unique.

2.2.3 Determining linear dependence and an exchange constraint (Step 6)

The new working set $W^+:=W(\tau ^+)$ is formed by addition of a new constraint $l$ to the working set $W$, which can lead to rank deficiency of the matrix $A_{W^+}$ and thus loss of invertibility in Eq. (9). We can check for linear dependence of $A_l$ on $A_W$ by solving

$$\begin{aligned} \begin{pmatrix} H &{} A_W^T\\ A_W&{} 0 \end{pmatrix} \begin{pmatrix} p \\ q_W\end{pmatrix} = \begin{pmatrix} A_l^T\\ 0 \end{pmatrix}. \end{aligned}$$

(13)

This test can be carried out cheaply by reusing the factorization employed to solve (9). $A_l$ is linearly dependent on $A_W$ if and only if $p = 0$. In this case, to determine an exchange constraint resolving linear dependency, let $q$ be constructed from $q_W$ like $\varDelta y$ from $\varDelta y_W$. Equation (13) then yields

$$\begin{aligned} 0 = -A_l^T+ \sum _{i: W_i \ne 0}^{} q_i A_i^T. \end{aligned}$$

(14)

Multiplying Eq. (14) by $\lambda W^+_l$ with an arbitrary $\lambda \ge 0$ and adding this as a special form of zero to the stationarity condition in Eqs. (2a) yields

$$\begin{aligned} H (x(\tau ) + \varDelta \tau \varDelta x) + g(\tau ^+)&= \sum _{i:W_i \ne 0}^{} y_i(\tau ^+) A_i^T\nonumber \\&= -\lambda W^+_l A_l^T+ \sum _{i: W_i \ne 0}^{} (y_i(\tau ^+) + \lambda W^+_l q_i) A_i^T. \end{aligned}$$

(15)

All coefficients of $A_i, i: W^+_i \ne 0$ on the right hand side of Eq. (15) are also valid choices $\tilde{y}$ for the dual variables as long as they satisfy the sign condition $W^+_i \tilde{y}_i \le 0$. Hence, we need to compute the index $k$ and multiplier $\lambda$ of the exchange constraint. For this, we obtain $q$ from $q_W$ by letting $q_i=0$ if $W^+_i=0$, and carry out the ratio test

$$\begin{aligned} \lambda ^{\star } := \mathrm{RT}\left( -W^+_l (W \circ y(\tau ^+)), W^+_l (W \circ q)\right) , \end{aligned}$$

(16)

If $\lambda ^{\star } = \infty$, then the parametric QP is infeasible beyond $\tau ^+$, in particular in $\tau =1$ by convexity of the feasible set. Otherwise, let $k$ be a minimizing index of the ratio set and let $y(\tau ^+) := \tilde{y}$ where

$$\begin{aligned} \tilde{y}_l = -\lambda ^{\star } W^+_l,\quad \tilde{y}_i = y_i(\tau ^+) + \lambda ^{\star } W^+_i q_i\quad \text {for}\quad i: W_i \ne 0. \end{aligned}$$

(17)

Furthermore, $\tilde{y}_k$ vanishes by construction of $\lambda ^{\star }$. Removing constraint $k$ from $W^+$ restores linear independence. For a proof, we refer to [7].

2.2.4 Determining zero curvature and an exchange constraint (Step 7)

The new working set $W^+$ is formed by removal of a constraint from $W$. This may lead to exposition of a direction of zero curvature in the null-space of $A_{W^+}$, which has higher dimension than the null-space of $A_W$, again leading to loss of invertibility in Eq. (9). Directions of zero curvature can be detected by solving

$$\begin{aligned} \begin{pmatrix} H &{} A_W^T\\ A_W&{} 0 \end{pmatrix} \begin{pmatrix} s \\ \xi _W\end{pmatrix} = \begin{pmatrix} 0 \\ -(e_k)_W \end{pmatrix}, \end{aligned}$$

(18)

where $e_k\in \mathbb {R}^m$ denotes the $k$-th unit vector. $H$ is singular on the null-space of $A_{W^+}$ if and only if $\xi _W= 0$, see [7]. Then, $s$ solves

$$\begin{aligned} H s = 0, \quad A_k s = -1, \quad A_{W^+} s = 0 \end{aligned}$$

(19)

and all points $\tilde{x} = x(\tau ^+) + \sigma s$, $\sigma >0$ are also optimal solutions if $\tilde{x}$ is primal feasible. We can determine the largest such $\sigma = \min \{\sigma ^\text{ l }, \sigma ^\text{ u }\}$ from the ratio tests

$$\begin{aligned} \sigma ^\text{ l } = \mathrm{RT}(Ax(\tau ^+) - a^{\text{ l }}, -As), \quad \sigma ^\text{ u } = \mathrm{RT}(a^{\text{ u }}- Ax(\tau ^+), As). \end{aligned}$$

(20)

If $\sigma = \infty$, then the parametric QP is unbounded beyond $\tau ^+$, and in particular in $\tau =1$. Otherwise, let $l$ be a minimizing index of a ratio set that delivered the minimizer $\sigma$, and let $x(\tau ^+) := x(\tau ^+) + \sigma s$. By construction of $\sigma$, the constraint row $l$ is active in $x(\tau ^+)$ and can be added to the working set via $W^+_l := \pm 1$. Again, we refer to [7] for a proof.

As for the linear independence test, the nonzero curvature test can be evaluated cheaply by reusing the factorization computed for Eq. (9). Note that this procedure only guarantees regularity of $Z^THZ$, but not existence of a Cholesky factor if $H$ is not positive semidefinite. An extension to the case of directions of negative curvature is addressed in Sect. 3.

2.3 Linear algebra

The factorization of $K_W$ in Sect. 2.2 is the basis for determination of the step direction, the linear independence test, and the nonzero curvature test. In this section, we describe the computation of dense null-space factors from both dense and sparse matrices, the exploitation of simple bounds on the QP variables, and quicker version of linear independence tests.

2.3.1 Null-space factorization

In qpOASES, for solving the saddle-point problem $K_W$ we implement a null-space method that can be expected to be numerically stable [6]. In each step, to exploit active simple bounds on the QP variables, we permute and partition $\varDelta x=(\varDelta x_X,\varDelta x_F)$ into fixed and free variables according to the working set $W$, and $\varDelta y_W=(\varDelta y_A,\varDelta y_X)$ into multipliers for active linear constraints and fixed simple bounds in $W$. Gradient $g=(g_X,g_F)$ and residual $a=(a_A,a_X)$ as well as Hessian $H$ and constraints submatrix $\tilde{A}$ (see Sect. ) are permuted and partitioned accordingly,

$$\begin{aligned} H=\begin{pmatrix} H_X &{} H_M^T \\ H_M &{} H_F\end{pmatrix},\quad \tilde{A} = \begin{pmatrix} A_X&A_F \end{pmatrix}. \end{aligned}$$

(21)

We use the representation $x_F = Z x_Z + Y x_Y$ based on a TQ factorization $A_F(Z\,\,Y)=(0\,\,T)$ of the working set constraints matrix, wherein $Z$ and $Y$ are column-orthonormal bases of the null-space and the range-space of $A_F$, and $T$ is southeast triangular (as proposed in [26] to facilitate matrix updates). Finally, a Cholesky factorization $R^TR=Z^TH_FZ$ of the null-space projection of the Hessian yields

$$\begin{aligned} \begin{pmatrix} H_X &{} H_M^TY &{} H_M^TZ &{} A_X^T&{} I &{} \\ Y^TH_M &{} Y^TH_FY &{} Y^TH_FZ &{} T^T\\ Z^TH_M &{} Z^TH_FY &{} R^TR &{} &{} \\ A_X &{} T &{} &{} &{} \\ I &{} &{} &{} &{} \end{pmatrix} \begin{pmatrix} \varDelta x_X \\ \varDelta x_Y \\ \varDelta x_Z \\ -\varDelta y_A \\ -\varDelta y_X \end{pmatrix} = \begin{pmatrix} -g_X \\ -Y^Tg_F \\ -Z^Tg_F \\ a_A \\ a_X \end{pmatrix}, \end{aligned}$$

(22)

to be solved by block-wise backward substitution. Herein, the right hand side vectors $g_X,\; g_F,\; a_A$, and $a_X$ are generic, to be replaced by the appropriate right hand sides in step 2, step 6b, and step 7b of the PQP algorithm.

2.3.2 Fast linear independence tests

During the linear independence tests, see step 6, a backsolve with the special right hand side $a_W=(a_A,a_X)=0$ has to be carried out. Hence $(\varDelta x_X,\varDelta x_Y)=0$ in (22) and we obtain a test of a nonzero component of $\varDelta x_Z=-(R^TR)^{-1}Z^Tg_F$ in which we may safely ignore the basis transformation $(R^TR)^{-1}$. Hence, as mentioned in [14], step 6 may be carried out by simply looking for a nonzero entry in the matrix-vector product $Z^TA_l^T$ in (13).

2.3.3 Special shapes of the Hessian and constraint matrices

In the code qpOASES we automatically detect and exploit special structure of the Hessian matrix $H$: diagonal and unit diagonal Hessian matrices. In the first case, the Cholesky factorization $R^TR=H_F$ is trivial. In the second case, the KKT system (22) reduces to the much simpler system (23),

$$\begin{aligned} \begin{pmatrix} I &{} &{} &{} A_X^T&{} I &{} \\ &{} I &{} &{} T^T\\ &{} &{} I &{} &{} \\ A_X &{} T &{} &{} &{} \\ I &{} &{} &{} &{} \end{pmatrix} \begin{pmatrix} \varDelta x_X \\ \varDelta x_Y \\ \varDelta x_Z \\ -\varDelta y_A \\ -\varDelta y_X \end{pmatrix} = \begin{pmatrix} -g_X \\ -Y^Tg_F \\ -Z^Tg_F \\ a_A \\ a_X \end{pmatrix} \end{aligned}$$

(23)

that can be factorized and solved at greatly reduced cost. For the case of bound-constrained QP problems, i.e. problems that do not comprise linear constraints, the KKT system (22) reduces to

$$\begin{aligned} \begin{pmatrix} H_X &{} H_M^T &{} I &{} \\ H_M &{} R^TR &{} \\ I &{} &{} &{} \end{pmatrix} \begin{pmatrix} \varDelta x_X \\ \varDelta x_F \\ -\varDelta y_X \end{pmatrix} = \begin{pmatrix} -g_X \\ -g_F \\ a_X \end{pmatrix}, \end{aligned}$$

(24)

again factorized and solved at greatly reduced cost.

2.3.4 Matrix updates

After an active-set exchange, the block KKT matrix of the working set $W$ in (22) changes in a single row and column only. Hence, instead of recomputing this factorization with cubic runtime effort, it is possible to recover it from a previous one by orthogonal transformations and rank one updates involving only a quadratic runtime effort. This technique is central to the efficiency of active-set methods and goes back to [4, 25]. It has since been investigated for different factorizations, e.g. [22, 23, 27, 29, 36, 40]. A detailed presentation of the update techniques implemented in our code qpOASES can be found in [14, 26] and fundamentals for null-space updates can be found in [48].

2.3.5 Sparse matrices

In the new release of qpOASES we adopt the paradigm of computing dense factors of sparse matrices, see e.g. [21]. Both the Hessian matrix $H$ and the constraint matrix $A$ may be stored in a compressed row or compressed column storage format to reduce the amount of memory bandwidth and floating-point operations required during computation of the dense TQ and Cholesky factors as well as during formation of matrix-vector products with $H$ and $A$.

2.3.6 Limitations and alternatives

The dense factorizations implemented in qpOASES yield satisfactory runtimes only for problems that are not too large in terms of the numbers $n$ of unknowns and $m$ of constraints. The current implementation can be expected to show satisfactory performance for (typically dense) problems with up to about 1,000 unknowns and constraints. Obviously, any exploitation of special structures arising in the Hessian or constraints matrix that extends beyond sparse representation of the QP matrices would result in significant speed-ups. One prominent example is a condensing preprocessing step that exploits block structures arising in optimal control and MPC problems, see [9, 42], before passing a significantly smaller QP on to the solver. An alternative is the direct exploitation of such structures in a block structured KKT solve in place of (22), see, for example, [5, 40]. Finally, the effective treatment of large-scale sparse QPs with an active-set method is only possible using sparse factorizations with suitable update schemes such as those presented in [22, 36].

3 New algorithmic developments in qpOASES

In this section we describe the numerical challenges that occur in the PQP algorithm and present countermeasures implemented in qpOASES. Although these challenges are closely interconnected, they can be roughly broken up into a few individual issues: We address the treatment of equality constraints in Sect. 3.1, the choice of the initial working set in Sect. 3.2; the far bounds strategy in Sect. 3.3; rounding errors and ill-conditioning in Sects. 3.4, 3.5, 3.6, and 3.7; comparison with zero in Sects. 3.8 and 3.9; and cycling and ties in Sect. 3.10. These algorithmic developments address the reliability of the PQP algorithm and extend its applicability to nonconvex QP problems. Finally, an alternative strategy for handling positive semidefiniteness of the Hessian matrix as well as an extension of the homotopy framework to varying QP matrices are mentioned. We also relate the new algorithmic developments to caller-accessible parameters of qpOASES solver options.

3.1 Equality constraints

Many QPs contain equality constraints of the form $a^{\text{ l }}_i = a^{\text{ u }}_i$. Obviously, constraint $i$ must be contained in the optimal active set. If the considered QP is non-degenerate, it must also be in the optimal working set, and $W_i\ne 0$. It may hence be beneficial to exclude $W_i$ from modifications in order to reduce the combinatorial complexity of the active set identification. In the degenerate case, however, it may be necessary to keep constraint $i$ out of the working set if, for example, there are more equalities than variables. qpOASES considers constraints with lower and upper bound differing by less than boundTolerance as equalities. Disabling the switch enableEqualities leads to relaxation of equalities to $a^{\text{ l }}_i(\tau ) \le Ax(\tau ) \le a^{\text{ u }}_i(\tau )$ in the initial point $\tau =0$ of the homotopy, and enforces $a^{\text{ l }}_i(1)=a^{\text{ u }}_i(1)$ only. The amount of relaxation is set through boundRelaxation and may be further changed if ramping is enabled. This may facilitate the choice of a numerically more stable initial working set, e.g., variable bounds only.

3.2 Initial working set

Step 2 of Sect. 2.2 requires the matrix $K_W$ to be regular for the initial working set $W(0)$. Suitable choices may be computed by the caller, using, for example, crashing techniques, see [60] for example. In the event that the caller of qpOASES does not provide a suitable initial $W(0)$, we choose $W(0)$ such that all simple bounds are marked active. Existence of finite bounds on every variable is ensured by the far bounds strategy, see Sect. 3.3. Then the matrix $A_W$ is the $n$-by-$n$ identity matrix, its null-space is {0}, and the projected Hessian $Z^TH_FZ$ is vacuous. In this case, simple bounds in the initial active set are active at their lower bounds by default. This may be changed by setting initialStatusBounds accordingly.

3.3 Far bounds

For QP problems that are missing bounds on one or more of the variables or constraints, $a^{\text{ l }}_i = -\infty$ or $a^{\text{ u }}_i = \infty$, we employ a far bounds strategy. It consists of clipping infinite or large entries in $a^{\text{ l }}_i$ and $a^{\text{ u }}_i$ to finite, moderately large values $-M^\mathrm{l}_i \approx -10^6$ and $M^\mathrm{u}_i \approx 10^6$, respectively. We then solve the QP with far bounds and distinguish three cases:

• 1. If we find a solution with no far bounds active, then this solution also solves the original QP.

• 2. If the QP with far bounds is infeasible, we enlarge the values $M^\mathrm{l}_i$ and $M^\mathrm{u}_i$ by a certain growth factor, for example by $10^3$ and solve again.

• 3. If the first case has not occurred even after having grown the far bounds to very large value considered to constitute infinity, for example $10^{20}$, then the original problem is declared infeasible or unbounded. We declare infeasibility if the last QP with far bounds was infeasible, and unboundedness if at least one of the far bounds is still active in the last optimal solution.

The far bounds strategy can be carried out efficiently by exploiting the parametric nature of the algorithm. We can reuse the current working set and current matrix factorizations via hot-starts for the sequence of QPs with growing far bounds (see also Sect. 6.3). We also apply the far bounds strategy to general linear constraints in order to facilitate flipping, as described in Sect. 3.7.

The far bounds strategy may be enabled using the switch enableFarBounds. The initial size of the far bounds box is initialFarBounds, and the growth factor is growFarBounds.

3.4 Iterative refinement

If the KKT matrix $K_W$ has a high condition number, then small perturbations of the right hand side in Eq. (9) due to, for example, truncation errors, can lead to large changes in the solution $\varDelta z$. As a consequence, the ratio tests (11) and (12) can become unstable, yielding different results for only small perturbations of the right hand side in equation (9). This undesirable behavior can be mitigated by, for example, reducing the forward error of $\varDelta z$ through iterative refinement [56]. Other possibilities for stabilizing ratio tests have been presented, in the framework of the simplex method for linear programming, by [33] and [60].

Iterative refinement can be enabled by setting numRefinementSteps to a positive value. Early termination of refinement iterations happens if the KKT residual $2$-norm falls below epsIterRef.

3.5 Drift correction

Rounding errors can also accumulate over several iterations and lead to a parametric “solution” $z(\tau )$ that is optimal with an accuracy significantly worse than machine precision. We call this phenomenon drift. Large drift can even lead to breakdown of the algorithm because the general assumption of optimality of $z(\tau )$ is violated. However, the parametric homotopy framework allows for reducing the drift to zero immediately by perturbing the current dual variables, the current constraint vectors, and the current gradient appropriately such that $z(\tau )$ is optimal again. We directly carry out this backwards analysis by requiring for $i = 1, \ldots , m$ exact primal feasibility,

$$\begin{aligned} a^{\text{ l }}_i(\tau )&:= {\left\{ \begin{array}{ll} A_i x(\tau ) &{} \text {if } W_i = -1,\\ \min (a^{\text{ l }}_i(\tau ), A_i x(\tau )) &{} \text {if } W_i \in \{ 0, +1\}, \end{array}\right. }\end{aligned}$$

(25a)

$$\begin{aligned} a^{\text{ u }}_i(\tau )&:= {\left\{ \begin{array}{ll} A_i x(\tau ) &{} \text {if } W_i = +1,\\ \max (a^{\text{ u }}_i(\tau ), A_i x(\tau )) &{} \text {if } W_i \in \{ -1, 0\}, \end{array}\right. } \end{aligned}$$

(25b)

exact dual feasibility,

$$\begin{aligned} y_i(\tau ) := {\left\{ \begin{array}{ll} \max (y_i(\tau ), 0) &{} \text {if } W_i = -1,\\ 0 &{} \text {if } W_i = 0,\\ \min (y_i(\tau ), 0) &{} \text {if } W_i = +1, \end{array}\right. } \end{aligned}$$

(26)

and afterwards repairing stationarity via the gradient modification,

$$\begin{aligned} g(\tau ) := A^Ty(\tau ) - H x(\tau ). \end{aligned}$$

(27)

In case the multiplication with $A,\; A^T$, and $H$ is numerically at least as expensive as the remainder of the iteration, drift correction should be applied only infrequently, i.e. every $n_\text {DC} \gg 1$ iterations.

Drift correction may be enabled by setting the option enableDriftCorrection to a positive value.

3.6 Termination check

A well-designed termination criterion must work reliably on both well- and ill-conditioned problems. While it is tempting to use the homotopy parameter $\tau$ in the termination criterion as done in Sect. 2.2, this choice renders the criterion dependent on the choice of the homotopy start. We instead propose to use the relative distance $\delta$ in the QP data space

$$\begin{aligned} \varDelta ^{\tau }&= (g(\tau ), a^{\text{ l }}(\tau ), a^{\text{ u }}(\tau )),&\nonumber \\ s_j&= (\varDelta ^1_j - \varDelta ^{\tau }_j) / \max \{1, |\varDelta ^1_j| \}, \quad j=1,\ldots ,n+2m,&\delta&= ||s||_\infty , \end{aligned}$$

(28)

which yields a termination criterion that is independent of $\mathrm{cond}(K_W(1))$. This modified termination criterion does not give a guarantee for the distance to the exact solution. Instead, a backwards analysis result holds: The computed solution is the exact solution to a perturbed QP that deviates by no more than $\delta$ from the one to be solved.

The threshold of the condition-independent termination check may be set through terminationTolerance.

3.7 Flipping bounds

Flipping bounds is a strategy similar to long steps in the dual simplex method [41, 51], where one variable changes in the working set from upper to lower bound immediately without becoming inactive in between, i.e., it flips. Flipping bounds only need to be employed if $H$ is indefinite or positive semidefinite.

Obviously, flipping is only possible if $a^{\text{ l }}_i(1)$ and $a^{\text{ u }}_i(1)$ have finite entries. We ensure finiteness of the constraint vectors via the far bounds strategy, see Sect. 3.3.

We then perform flipping in the following way: If we remove a constraint $l$ from the active set and no other constraint $k$ enters, we monitor the size of the smallest diagonal entry $r_{i}$ of the Cholesky factor $R$ that grows by a row and column. If for some $\delta _\text {curv} > 0$ it holds that $r_i^2 < \delta _\text {curv}$, then we introduce a jump in the QP homotopy by moving the opposite bound of constraint $l$ such that it becomes active immediately. This is easily achieved by setting

$$\begin{aligned} a^{\text{ l }}_l(\tau ^+)&:= a^{\text{ u }}_l(\tau ^+),\ W^+_l := -1, \qquad \text {if } W_l = +1,\end{aligned}$$

(29a)

$$\begin{aligned} a^{\text{ u }}_l(\tau ^+)&:= a^{\text{ l }}_l(\tau ^+),\ W^+_l := +1, \qquad \text { if } W_l = -1. \end{aligned}$$

(29b)

Consequently, the Cholesky decomposition from the previous step stays valid for the current projected Hessian. We can thus successfully avoid small diagonal entries in the Cholesky factors $R$.

We employ the same strategy if the Cholesky decomposition breaks down due to a negative eigenvalue in the projected Hessian $Z^TH_F Z$. This allows one to move along the direction of negative curvature onto the opposite bound and hence permits the treatment of nonconvex QP problems, for which we identify a parametric path of critical points.

The flipping bounds strategy can be enabled using the switch enableFlippingBounds; the threshold $\delta _\text {curv}$ for the Cholesky diagonal elements is epsFlipping.

3.8 Ratio tests

In the ideal ratio test (10) we take a minimum over a subset of $k$ quotients with strictly positive denominators. The presence of round-off error however makes it necessary to substitute this ideal ratio test by an expression with adjustable tolerances,

$$\begin{aligned} u^\text {cut}_i&= \max (u_i, 0), \quad i = 1, \ldots , k,\nonumber \\ \mathrm{RT}_\text {r}(u, v, \varepsilon _\text {den}, \varepsilon _\text {num})&= \min \{ u^\text {cut}_i/v_i ~|~ i = 1, \cdots , k, v_i \ge \varepsilon _\text {den}, u^\text {cut}_i \ge \varepsilon _\text {num}\}. \end{aligned}$$

(30)

The denominator tolerance $\varepsilon _\text {den} > 0$ is a threshold to consider tiny positive values $v_i$ to be equal to zero. Such values are discarded as candidates for the minimum.

Negative numerators are cut off at zero before the quotients are taken, yielding a nonnegative minimum. For the ratio tests for determination of the step length (11) and (12), this choice is motivated by the fact that, in exact arithmetic, $u_i \ge 0$ for all $i = 1, \ldots , k$ with $v_i > 0$ holds. Hence, only values $u_i$ that are negative due to round-off are manipulated, and the step length satisfies $\varDelta \tau \ge 0$ also in finite precision arithmetic.

The tolerances $\varepsilon _\text {num}$ and $\varepsilon _\text {den}$ for numerators and denominators in ratio tests may be set using the options epsNum and epsDen, respectively.

3.9 Linear independence test and nonzero curvature test

After solving system (13) for $(p,q_W)$ or system (18) for $(s, \xi _W)$, we must compare the norm of $p$ or $\xi _W$ with zero to detect linear dependence of $A_W$ or a direction of zero curvature in its null-space, respectively. We use the relative conditions

$$\begin{aligned} ||p||_\infty&\le \varepsilon _\text {LI} ||\zeta _q||_\infty ,\ \zeta _q^T= (p^T, q^T)&\text {for the linear independence test, and}\end{aligned}$$

(31a)

$$\begin{aligned} ||\xi _W||_\infty&\le \varepsilon _\text {NZC} ||\zeta _s||_\infty ,\ \zeta _s^T= (s^T, \xi _W^T)&\text {for the nonzero curvature test.} \end{aligned}$$

(31b)

We also remark that $||\zeta _q||_\infty = ||q||_\infty$ if $p = 0$ and $||\zeta _s||_\infty = ||s||_\infty$ if $\xi _W= 0$. In the implementation, we may thus replace $||\zeta _q||_\infty$ by $||q||_\infty$ for test (31a) and $||\zeta _s||_\infty$ by $||s||_\infty$ for test (31b). If we perform the cheaper linear independence test (see Sect. 2.3.2), we compute $\tilde{p}^T = A_l Z$. We declare linear independence of constraint $l$ from the constraints in $W$ if there exists an index $i$ such that

$$\begin{aligned} |\tilde{p}_i| > \varepsilon _\text {LI} ||A_l^T||_2^2. \end{aligned}$$

(32)

Users may choose between the full variant (13) and the fast variant of Sect. 2.3.2 by toggling the switch enableFullLITests. The threshold $\varepsilon _\text {LI}$ for $p$ is epsLITests, and invoked dual jumps $\lambda ^{\star }$ must be smaller than maxDualJump. Nonzero curvature tests may be enabled through the switch enableNZCTests. The threshold $\varepsilon _\text {NZC}$ for $\xi _W$ is epsNZCTests, and invoked primal jumps $\sigma$ must be smaller than maxPrimalJump.

3.10 Ties and ramping

Instead of trying to treat ties (see Sect. 2.2) rigorously, which may be as computationally expensive as solving the QP itself [55], we try to avoid them in the first place: Let a homotopy start $g(0), a^{\text{ l }}(0), a^{\text{ u }}(0)$ with optimal solution $(x(0),y(0))$ and working set $W(0)$ be given. Then, for every triple of $m$-vectors $r^{(0)}, r^{(1)}, r^{(2)} \ge 0$, the primal-dual pair $(x(0), \tilde{y}(0))$ with

$$\begin{aligned} \tilde{y}_i(0) = {\left\{ \begin{array}{ll} y_i(0) + r^{(0)}_i &{} \text {if } W_i = -1,\\ y_i(0) &{} \text {if } W_i = 0,\\ y_i(0) - r^{(0)}_i &{} \text {if } W_i = +1,\\ \end{array}\right. } \qquad i = 1, \ldots , m, \end{aligned}$$

(33)

is an optimal solution for the homotopy start $\tilde{g}(0), \tilde{a}^\text{ l }(0), \tilde{a}^\text{ u }(0)$, where for $i = 1, \ldots , m$

$$\begin{aligned} \tilde{a}^\text{ l }_i(0)&= {\left\{ \begin{array}{ll} a^{\text{ l }}_i(0), &{} \text {if } W_i = -1,\\ a^{\text{ l }}_i(0) - r^{(1)}_i, &{} \text {otherwise},\\ \end{array}\right. }&\tilde{a}^\text{ u }_i(0)&= {\left\{ \begin{array}{ll} a^{\text{ u }}_i(0), &{} \text {if } W_i = +1,\\ a^{\text{ u }}_i(0) + r^{(2)}_i, &{} \text {otherwise},\\ \end{array}\right. }\end{aligned}$$

(34a)

$$\begin{aligned} \tilde{g}(0)&= A^T\tilde{y}(0) - H x(0). \end{aligned}$$

(34b)

In other words, if we move the inactive constraints’ bounds further away from $Ax(0)$, and the dual variables of the active constraints further away from zero, then $x(0)$ stays feasible and $g(0)$ can be adapted to restore stationarity of $(x(0), \tilde{y}(0))$ with the same working set $W(0)$.

Recall now that the ratio tests depend on the residuals of the inactive constraints and the dual variables of the active constraints. Many QP problems exhibit special structures such as, for example, identical bounds for several variables. To avoid primal ties for such special structures, it is important to avoid picking the same value for two entries of $r^{(j)}$. Hence, for given parameters $r_\text {final} > r_\text {initial} > 0$, we choose a linear ramp shape

$$\begin{aligned} r^{(j)}_i = r_\mathrm{initial}\frac{m-i}{m-1} + r_\mathrm{final}\frac{i-1}{m-1}, \quad j = 0, 1, 2, \quad i = 1, \ldots , m. \end{aligned}$$

(35)

This ramping ensures progress $\varDelta \tau > 0$ because $r_i^j > 0$ for all $j$, and if residuals are chosen such that all ratios are pairwise different, it also ensures absence of ties in the next iteration.

The ramping strategy may be enabled using the switch enableRamping and performs a linear interpolation between the values initialRamping and finalRamping.

3.11 Iterative regularization procedure

For solving QP problems where the Hessian matrix is positive semidefinite, an iterative regularization procedure that makes use of the homotopy framework has been proposed in [16]. The core idea is to add a regularization term to the objective function to arrive at the following regularized QP problem:

$$\begin{aligned}&\mathop {\hbox {min}}\limits _{x \in \mathbb {R}^n}&\frac{1}{2} x^THx + g^Tx + \tfrac{\varepsilon _\text {reg}}{2}(x-\bar{x})^T(x-\bar{x}) \end{aligned}$$

(36a)

$$\begin{aligned}&\mathop {\hbox {s. t.}}&a^{\text{ l }}\le Ax \le a^{\text{ u }}. \end{aligned}$$

(36b)

First, this problem is solved for $\bar{x}=0$ to yield a first approximation $x^{\star }$ to an optimal primal solution. Next, the regularization is “re-centered” by setting $\bar{x}=x^{\star }$ and problem (36) is solved again. Repeating this procedure yields a special case of a proximal point algorithm for which linear convergence towards an optimal solution of the original problem has been shown [50].

It is important to note that this iterative regularization procedure perfectly fits into the homotopy framework of qpOASES as it requires the solution of a sequence of QP problems with varying gradients. Thus, having solved the first regularized problem, the solution of the subsequent QP problems can be hot-started and typically requires only a few, if any, additional active-set iterations.

The iterative regularization strategy may be enabled using the switch enableRegularisation. The number of regularization steps may be set in numRegularisationSteps, and the regularization constant $\varepsilon _\text {reg}$ of equation (36) in epsRegularisation.

3.12 Warm-starts after changes to the QP matrices

During the solution of a sequence of QP problems, the parametric QP algorithm also allows for warm-starting, i.e. reuse of an available active set together with the primal-dual point, if the QP matrices $H$ or $A$ change [18]: Assume we have an optimal solution $z^*= (x^*,y^*)$ and an optimal working set $W^*$ for the QP problem

$$\begin{aligned} \mathop {\hbox {min}}\limits _{x \in \mathbb {R}^n} \tfrac{1}{2} x^T{H} x + {g}^Tx \quad \mathop {\hbox {s. t.}}\quad {a}^\mathrm{l} \le Ax \le {a}^\mathrm{u}, \end{aligned}$$

(37)

and want to solve the perturbed QP

$$\begin{aligned} \mathop {\hbox {min}}\limits _{x \in \mathbb {R}^n} \tfrac{1}{2} x^T\tilde{H} x + \tilde{g}^Tx \quad \mathop {\hbox {s. t.}}\quad \tilde{a}^\mathrm{l} \le \tilde{A} x \le \tilde{a}^\mathrm{u}. \end{aligned}$$

(38)

with new matrix data $\tilde{H},\; \tilde{A}$ and new vector data $\tilde{g},\; \tilde{a}_\mathrm{l},\; \tilde{a}_\mathrm{u}$. We may then compose a homotopy start $(\tau =0)$ for the second QP problem by setting

$$\begin{aligned} \tilde{a}^\mathrm{l}(0)&:= a^{\text{ l }}+ (\tilde{A} - A) x^*, \end{aligned}$$

(39a)

$$\begin{aligned} \tilde{a}^\mathrm{u}(0)&:= a^{\text{ u }}+ (\tilde{A} - A) x^*, \end{aligned}$$

(39b)

$$\begin{aligned} \tilde{g}(0)&:= g - (\tilde{H} - H) x^*+ (\tilde{A} - A)^Ty^*. \end{aligned}$$

(39c)

and (for $\tau =1$) let $\tilde{g}(1)=\tilde{g},\;\tilde{a}^\mathrm{l}(1)=\tilde{a}^\mathrm{l},\; \tilde{a}^\mathrm{u}(1)=\tilde{a}^\mathrm{u}$. The working set $W(0)=W^*$ remains unaltered. Alternatively, one could simply ramp an all-zero homotopy start, again keeping the working set $W(0)=W^*$, see Sect. 3.10.

As usual in sequential nonlinear methods, this approach requires the matrix $\tilde{K}_W$ for the given working set $W(0)$ to remain regular. If the initial factorization of $\tilde{K}_W$ reveals rank deficiency of $\tilde{K}_W$, we recede to a cold-start with a safe working set as described in Sect. 3.2.

4 Software design and algorithmic parameters

This section outlines the software design of qpOASES and briefly explains how to set up and solve QP problems. We also discuss its most important algorithmic parameters for adjusting the behavior of the solver as described in Sect. 3.

4.1 General remarks

qpOASES is an open-source C++ implementation of the parametric QP algorithm of Sect. 2 and all algorithmic enhancements as presented in Sect. 3. Its object-oriented design introduces separate classes for different QP problem types and encapsulates all matrix-vector operations, such that they can be easily adapted to the respective problem characteristics. Moreover, qpOASES has been implemented in a self-contained manner to facilitate compatibility with different, also embedded, hardware platforms. All matrix-vector operations within qpOASES are performed by customized C implementations of the required LAPACK/BLAS routines, but direct linking against the LAPACK or BLAS library [1, 8] is also possible.

qpOASES distinguishes two different ways of solving a QP problem of the form (1). First, it can be solved by performing a cold-start, i.e. without any prior solution information. This is the usual situation if just a single QP problem is to be solved. Second, provided that a QP problem with same dimensions has been already solved before, the current QP problem can be solved by performing a hot-start based on the optimal solution and the internal matrix factorizations of the previously solved QP problem. Hot-starts can be very efficient when solving whole sequences of parameterized QP problems as arising in model predictive control or within SQP algorithms.

4.2 QP solver classes

The current release 3.0 of qpOASES comes with three different QP solver classes that offer user-interfaces for tackling different QP problem formulations:

• 1. The QProblem class is designed for solving a single QP of the standard form (1). It also allows the user to efficiently solve whole sequences of QP problems with varying gradient or constraint vectors by performing hot-starts based on solution information of the previous QP problem.

• 2. The class QProblemB offers the same functionality as QProblem, but is tailored to QP problems (or sequences) that only comprise bounds on the variables $x$, often called box constraints. The distinction between bounds and general constraints arises naturally in many applications, such as model predictive control, and can lead to substantial computational savings.

• 3. Finally, the class SQProblem extents the functionality of the QProblem class to also allow hot-starts based on the previous QP solution in case of varying QP matrices (see Sect. 3.12).

All these three classes offer user-functions for passing the QP problem data, setting algorithmic options and for obtaining results and status information. All internal data members of the QP solver are hidden from the user. For example, these classes store information on the bounds and constraints of the QP problem by means of further auxiliary classes that manage lists of free and fixed variables or active and inactive constraints.

4.3 Linear algebra classes

qpOASES has originally been developed for small to medium-scale QP problems with dense Hessian and constraint matrices. Consequently, the internal matrix factorizations have been implemented as dense linear algebra routines.

For enhancing qpOASES ’s applicability to sparse QP problems, a minimal Matrix base class has been introduced that encapsulates all matrix-vector operations. This framework allows the user to easily switch between special linear algebra routines for dense and sparse QP matrices, and to exploit symmetry of the Hessian. For doing so, QP matrices can be passed as either of the following types: DenseMatrix, SparseMatrix, SymDenseMat, SymSparseMat. Through the ConstraintProduct class, the user may also provide a tailored routine that directly calculates the matrix-vector product $Ax$.

Internally, dense matrices are stored in arrays, while sparse matrices are stored in either a row compressed or a column compressed storage format.

4.4 Solving QP problems with qpOASES

The following code fragment illustrates the calling syntax of qpOASES for solving a QP problem with 10 variables and 25 constraints. It is assumed that QP data matrices H, A, and QP data vectors g, lb, ub, lbA, and ubA of appropriate dimension have already been defined.

First, the user needs to instantiate an object of the QProblem class by passing the dimension of QP problem. Then, the first QP problem is solved by calling the member function init, which takes the QP data as well as the maximum number of iterations as arguments. Afterwards, the optimal primal solution is retrieved from the QP object.

In case that a whole sequence of QP problems is to be solved, it is possible to hot-start the QP solution procedure based on solution information of the previously solved QP problem. This is done by calling the member function hotstart of the QProblem class, which takes the new QP gradient and constraint vectors as well as the maximum number of iterations as arguments:

For more details on the calling syntax and for a documentation of the classes QProblemB and SQProblem, we refer to the qpOASES User’s Manual [15]. Also information on how to specify the QP matrices in dense or sparse matrix format can be found therein.

4.5 Setting algorithmic parameters of qpOASES

In this subsection, we address the realization of the new algorithmic developments of Sect. 3 in our implementation qpOASES. We show how to set option parameters through the qpOASES interface, and we describe convenient pre-configured sets of options that are available for these parameters. Individual option parameters listed in Table 1, together with the default values they assume in the pre-configured sets. The respective meanings of the parameters are addressed in Sect. 3.

Table 1 Summary of algorithmic parameters in qpOASES with their respective default values in the MPC, default, and reliable pre-configurations. The constant $\varepsilon _\text {mach}$ denotes the machine precision

4.5.1 Setting options through the interface

The qpOASES interface provides access to many of the algorithmic details presented in Sects. 2 and 3 through the Options class as follows.

4.5.2 Pre-configured sets of options

Through the Options class, we provide quick access to three pre-configured sets of options: default, MPC, and reliable. They can be accessed by calls to the member functions setToDefault, setToMPC, or setToReliable. The respective options values are listed in Table 1.

The default options set collects recommended settings for qpOASES. All vital algorithmic features are enabled, and nonconvex QP problems can be handled by flipping bounds. If no explicit calls to Options are made, this is the configuration all computations will be carried out with.

The MPC set of options is designed for model predictive control applications in which we expect to solve strictly convex problems only. It ensures that a single iteration of the active-set method is carried out as fast as possible by disabling several of the more costly algorithmic features. Moreover, by disabling ramping at the cost of a possibly increased total iteration count, this set of options ensures that the primal homotopy path generated indeed is continuous and can hence be attributed with a physical interpretation [14].

The reliable options set deviates from the default one in only a few choices. The number of iterative refinement steps has been increased to address highly ill-conditioned systems, and full linear independence test are carried out instead of the fast tests of Sect. 2.3.2. Most important, the Cholesky factorization of $Z^THZ$ is recomputed in every iteration, thus greatly increasing the per-iteration cost of qpOASES at the benefit of increased numerical stability.

5 Interfaces and applications

The qpOASES distribution also includes several interfaces to widely-used third-party software packages in order to facilitate its use. This section gives an overview of these interfaces and outlines several real-world applications of qpOASES that have been completed in the past. For some of them qpOASES has been run on embedded computer hardware.

5.1 Interfaces for Matlab, Octave and Scilab

qpOASES can be directly used within Matlab $^{\circledR }$, allowing a user to run the solver without touching its C++ source code. For example, a single QP can be solved by calling

Besides the usual data specifying a QP of the form (1), a set of options and an initial guess for the primal solution can be passed. If no initial guess is given, the usual homotopy starting at the origin is performed. The output arguments contain the optimal primal solution vector as well as optionally the optimal objective function value, a status flag, the number of iterations actually performed, and the optimal dual solution vector, respectively.

Options can be generated using the qpOASES_options command in order to retrieve the full functionality of the C++ version, e.g.

for generating two sets of pre-defined algorithmic options that are tailored for fast MPC applications or most reliable QP solution, respectively. In the second case, also the default value for the maximum number of iterations is adapted.

The Matlab $^{\circledR }$ interface automatically detects whether the QP only comprises box constraints and internally instantiates the corresponding QP object. Moreover, it is possible to pass QP matrices in sparse format. This standard interface always performs a cold-start taking into account the guess for the primal solution (if specified), but also variants exist for solving whole sequences of QP problems using all features of the online active set strategy. For example, the following commands initialize a sequence of QP problems with the data of the initial () QP problem, perform a hot-start () for solving the second QP problem and clean-up () the internal memory of the Matlab $^{\circledR }$ interface:

In order to support open-source alternatives to Matlab $^{\circledR }$, qpOASES provides similar interfaces to Octave  [13] and scilab  [52].

5.2 Interfaces to YALMIP, the ACADO Toolkit, and MUSCOD-II

qpOASES also has been interfaced to YALMIP [43], a modelling language for solving convex and nonconvex optimization problems. Moreover, qpOASES is the default QP solver within the open-source package ACADO Toolkit for automatic control and dynamic optimization [35]. For solving nonlinear optimal control problems, MUSCOD-II [42] can use qpOASES as underlying QP solver.

5.3 Running qpOASES on dSPACE $^{\circledR }$ and xPC target

The qpOASES code also provides an interface to Simulink $^{\circledR }$ that allows the user to compile the code within a C mex S-function. This is particularly useful when using qpOASES to solve model predictive control problems. Different variants interfacing the QProblem, QProblemB and SQProblem class to the Simulink $^{\circledR }$ workspace are available. The S-function block expects all QP data to be given in signal form. It outputs the first piece of the primal solution as required in the MPC context, the optimal objective function value, a status flag and the number of actually performed QP iterations.

The Simulink $^{\circledR }$ interface also allows one to conveniently compile qpOASES onto dSPACE $^{\circledR }$ or xPC target hardware by means of the Simulink $^{\circledR }$ Real-Time Workshop [38]. The main requirement is the availability of a C++ compiler for the respective hardware. Compilation of qpOASES has been tested for dSPACE $^{\circledR }$ boards version 5.3 or higher together with the dSPACE $^{\circledR }$ C++ Integration Kit version 1.0.2 or higher. Also successful use on xPC target hardware has been reported, cf. Sect. 5.4.

5.4 Real-world applications

During the last few years, qpOASES has been used by a number of researchers for a wide range of applications. For example, it has been used for

• model predictive control of a Diesel engine test bench at the University of Linz, Austria, on dSPACE $^{\circledR }$ hardware at sampling times of 50 ms (dense QP problems comprising about 20 bounded variables and 20 constraints) [18];

• trajectory planning for a boom crane at the University of Stuttgart, Germany, similar to the one described in [3], on dSPACE $^{\circledR }$ hardware at sampling times in the order of 100 ms (about 57 bounded variables and 160 constraints);

• solving QP problems for controlling a tendon-driven robot platform at ETH Zurich, Switzerland, on a Standard PC [49];

• model predictive control of beam tip vibrations at the Slovak University of Technology, Bratislava, Slovakia, on an xPC target at sampling times of 10 ms (up to 150 bounded variables) [53];

• time-optimal control of machine tools at KU Leuven, on dSPACE $^{\circledR }$ and xPC hardware at sampling times in the order of 4–10 ms (about 45 bounded variables and 182 constraints) [54].

It is worth stressing that all given QP problem dimensions refer to the dense formulation (6) and that QP solution times were typically much lower than the reported sampling time.

Moreover, qpOASES has been used within several industrial applications solving QP problems with up to a few hundred variables and a few thousand constraints. Due to confidentiality reasons, we only mention its integration into an embedded engine controller developed by Hoerbiger Control Systems AB, Sweden, to control an integral gas engine in the pipeline network of the United States [2]. The dense QP problems comprised about 10–14 variables, up to several hundred constraints and have been solved on embedded hardware with very limited computational resources (compared to a standard PC).

6 Testing

6.1 Convex QP problems

qpOASES is mainly intended for sequences of small to medium size, dense QP problems. We discuss the case of QP sequences in Sect. 6.3 but it is of course also possible to use qpOASES to solve single QP instances. Figure 1 assesses the performance of qpOASES in comparison with other QP solvers. We chose QP solvers that have an appropriate license and provide a Matlab $^{\circledR }$ interface: The interior-point code OOQP [24] and the primal and dual active-set and barrier variants of Cplex [37] (CPLEXP, CPLEXD, CPLEXB). For each solver we use the default parameters. For qpOASES we test the default (qpOASES) and the “mpc” (qpOASESmpc) parameter variants, where we changed the initial working set of the mpc method from zero to all lower bounds active (as for the default variant) in order to make useful comparisons between the two versions of qpOASES calls. Unfortunately, the Cplex solvers’ interface exhibits a large calling overhead of around 1 s. In addition, the internal timing results of Cplex are rounded to 0.01 s (sometimes even down to 0 s), which makes an appropriate comparison hard to carry out. We have overcome this issue by implementing a wrapper file for the Cplex mex file in C, which carries out high resolution timings but discards “constructor” call timings within the mex file, which have been found responsible for the calling overhead.

Fig. 1

Performance graph of different QP solvers on all 43 problems of the Maros-Mészáros test set [44] with $n\le 250, m \le 1{,}001$; matrices passed in dense format

No particular starting points were provided to the solvers. We discard the primal and dual initial values from the CUTEr interface because they are zero for all considered problems. The solvers are allowed to find suitable starting points, for example via ramping (cf. Sect. 3.2).

Figure 1 shows a performance profile, which depicts how many percent of the test set problems (ordinate) are solved by each solver within a certain time factor (abscissa) of the fastest method on each problem. Generally, fast methods have their graph in the left hand part, reliable methods in the upper part of the diagram. All 43 problems from the Maros-Mészáros test set [44] with $n \le 250$ and $m \le 1,001$ were used and the matrices were given to the solvers in dense format. We believe that this size is reasonable for problems that can be solved in fast real-time applications. The quality of the solutions $(x^*, y^*)$ was measured using a residual $\rho$ of conditions (2) defined via

$$\begin{aligned} \rho _\text {stat}&\!=\! ||H x^* \!+\! g \!-\! A^Ty^*||_\infty ,&\rho _\text {cmpl}^\text{ l }&\!=\! \max \{ \min (|Ax^* \!-\! a^{\text{ l }}|_i, y^*_i) ~|~ y^*_i > 0 \},\\ \rho _\text {feas}&= \max ( 0, a^{\text{ l }}\!-\! Ax^*, Ax^* \!-\! a^{\text{ u }}),&\!\!\!\!\rho _\text {cmpl}^\text{ u }&\!=\! \max \{ \min (|Ax^* \!-\! a^{\text{ u }}|_i, -y^*_i) ~|~ y^*_i \!<\! 0 \},\\ \rho&\!=\! \max (\rho _\text {stat}, \rho _\text {feas}, \rho _\text {cmpl}^\text{ l }, \rho _\text {cmpl}^\text{ u }). \end{aligned}$$

For some problems, some solvers terminated without indication of failure but returned a low quality solution. Here, we only consider a problem solved if $\rho \le 10^{-4}$. We observe that qpOASES outperforms the other methods on this test set in terms of speed and reliability. The mpc version performs almost as well, even though no neighboring information of problems can be exploited for hot-starts.

Figure 2 shows the performance profiles for all 73 test problems with $n \le 1{,}000$ and $m \le 1{,}001$, passed to the solvers in sparse format. This size represents problems that qpOASES can solve in a reasonable time with its dense linear algebra subroutines. On these problems, OOQP and Cplex can exploit the sparsity of the problems efficiently. The sparse matrix vector products of qpOASES are still dominated by the cost of the dense linear algebra routines. In terms of speed, the active-set versions of Cplex are performing best. However, qpOASES is the most reliable method, closely followed by the active-set versions of Cplex. The mpc variant of qpOASES works less reliably, as expected on that kind of test collection.

Fig. 2

Performance graph of different QP solvers on all 73 problems of the Maros-Mészáros test set [44] with $n \le 1{,}000, m\le 1{,}001$; matrices passed in sparse format

Table 5 in the appendix to this paper lists the detailed results that served as the basis for the performance profiles in Figs. 1 and 2. For the Cplex solvers, the table only contains the results for the case that matrices were passed in sparse format, because Cplex seems to convert dense matrices to sparse format before starting the actual computation.

We have also tested qpOASES on the Netlib LP problem QAP8 $(n=1{,}632, m=912)$, which is known for its difficult, almost degenerate constraints: qpOASES successfully converges to the solution within 23,111 iterations, while the primal and dual active-set variants of Cplex need 29,736 and 39,495 iterations, respectively.

6.2 Nonconvex QP problems

Due to the flipping bounds strategy, qpOASES can be used to find critical points of nonconvex QP problems. In Table 2 we show the number of iterations for a few test problems from the CUTEr collection [32]. We also check the second order sufficient condition (3) which is satisfied for every critical point. In order to determine the strongly active inequality constraints, we required the numerical values of the Lagrange multipliers to satisfy $|y_i^*| > 10^{-8}$. The problems were solved with algorithmic parameters of qpOASES that are identical with the default settings except for the explicit treatment of equalities (enableEqualities), which was switched on.

Table 2 Iterations of qpOASES on nonconvex QP problems from the CUTEr test collection [32]

6.3 Sequences of QP problems

The parametric active-set strategy as implemented in qpOASES allows warm-starting and hot-starting the solution procedure at any given primal-dual iterate and with any given working set. This feature is particularly useful when solving sequences of QP problems whose optimal solutions are not expected to differ much from one problem to the next. We illustrate this fact by using qpOASES to solve all five test examples of the small online QP benchmark collection [17], which provides sequences of strictly convex QP problems as arising from different linear model predictive control applications. Within each of these QP sequences, the QP matrices are constant and only the QP vectors are varying.

Table 3 summarizes the problem dimensions of each benchmark example and also gives the length of each sequence in terms of number of QP problems. In the first four examples, the optimal active-set changes by up to 18 constraints between successive optimal solutions, while up to 154 changes in the optimal active-set can be observed in the last example.

Table 3 Number of variables ($n$), number of constraints ($m$) and number of QP instances for each problem of the online QP benchmark collection [17]

Table 4 lists both the maximum and the average number of iterations needed by qpOASES to find the optimal solution. These numbers are given once for cold-started QP solutions and once for QP solutions based on hot-starts as described in Sect. 4. It can be seen that hot-starting the QP solution can reduce both the average and the maximum number of iterations significantly. While interior-point solvers typically have limited warm-starting capabilities, also other active-set QP solvers can benefit from warm-starting. The positive impact on the maximum number of iterations is limited in case of sequences that feature a few situations where the optimal solution changes quite dramatically from one QP problem to the next.

Table 4 Maximum and average number of iterations when solving the problems of the online QP benchmark collection [17] with qpOASES

7 Distribution of qpOASES

7.1 Download

The qpOASES software package is available for download from

http://www.qpoases.org

and distributed under the GNU Lesser General Public License (LGPL) to allow linking against proprietary codes. Proceed to the menu point “Download” to obtain a gzipped tar archive of the most current version 3.0 of qpOASES. The user’s manual, license text, and extensive source code documentation generated from doxygen [34] are available here as well.

7.2 Installation

To install qpOASES on a 32-bit or 64-bit x86 machine running a standard Linux system, unpack the tar.gz archive to obtain a directory named qpOASES. Executing “make” there will build a static and a dynamic library named libqpOASES.a and libqpOASES.so, and will put them in the directory bin.

The static library libqpOASES.a contains solver code callable from a user-side C++ program that is statically linked against it. The dynamic librarylibqpOASES.so contains solver code callable from a user-side C++ program that is dynamically linked against it.

qpOASES can be built under the operating systems MacOS or Windows by a straightforward modification of the top-level make file Makefile to make use of the respective OS-specific make file make_osx.mk or make_windows.mk.

The source code of qpOASES is self-contained, but can be optionally linked against LAPACK [1] and BLAS [8] by modifying the appropriate operating system specific make file.

Interfaces to third-party software are excluded from the standard build process, and can be built separately from the subdirectory interfaces/matlab, interfaces /octave, etc. We refer the reader to the qpOASES User’s Manual [15] for further details.

8 Summary

We have described the open-source QP solver qpOASES in its most recent release 3.0. The new numerical features, including iterative refinement, data-space termination criterion, ramping, and flipping bounds, improve its reliability and even enable the determination of critical points of nonconvex QP problems. We have explained how the new algorithmic parameters can be modified through the various user interfaces for C, Matlab $^{\circledR }$, GNU Octave, and Scilab. Moreover, we have presented a numerical comparison with other popular QP solvers that shows the competitiveness of qpOASES as a stand-alone solver in terms of speed and reliability for small- to medium-scale, dense QP problems.

Appendix

See Table 5.

Table 5 Comparison of QP solvers on problems from the Maros-Mészáros test set ([44]) with at most $n = 1{,}000$ variables and $m=1{,}001$ two-sided inequality constraints (not counting variable bound constraints). The solution time in seconds and the optimality condition residual $\rho$ are given for each solver. Failure of the solver is denoted by blank time fields