Introduction

One of the most important issues in geotechnical engineering is the stability of reinforced soil slopes. Nowadays, reinforced soil slopes are widely popular because of some reasons like reasonable price, relatively easy construction and ideal resistance against earthquakes. Due to inadequate and inaccurate information about soil properties, and earthquake behaviour, it is difficult to precisely investigate the performance of reinforced soil structures against seismic forces.

In recent years, various methods have been proposed to examine the stability of reinforced soil slopes and walls. One of the conventional methods involves method of vertical slices using the limit equilibrium approach. The horizontal slice method (HSM) has several benefits against the vertical slice method. Unlike vertical slice method, the variations of soil properties in depth can be easily included in the HSM (Lo and Xu 1992; Shahgholi et al. 2001). Moreover, in the vertical slice method, the mobilized forces of reinforcements appear on the border between slices. In addition to the limit equilibrium, there are other numerical methods such as finite differences and finite element methods (Chen et al. 2003; Zheng et al. 2006; Li 2007), stress characteristics (Jahanandish and Keshavarz 2005), limit analysis method (Michalowski 1998a; Lin et al. 2010) and other methods (Bathurst et al. 2002) for the analysis of reinforced soil slopes.

One of the main problems in the limit equilibrium method (LEM) is how to determine the critical slip surface. The critical slip surface has been determined through various methods, including genetic algorithm (Zhu 2001; Zheng et al. 2009; Sengupta and Upadhyay 2009), Monte Carlo (Malkawi et al. 2001), particle swarm (Cheng et al. 2007; Kalatehjari et al. 2014) and fish swarm (Cheng et al. 2008).

There are some research works which were carried out on the stability of reinforced soil slopes. Ling et al. (1997) used the LEM in conjunction with the pseudo-static method to investigate the behaviour of reinforced soil slopes. Michalowski (1998b) analysed the stability of reinforced soil slopes through the kinematic theorem of limit analysis. He assumed that the slip surface was log-spiral, while using the pseudo-static method. Using the kinematic theorem of limit analysis and pseudo-static method, Ausilio et al. (2000) analysed the stability of reinforced soil slopes. Nouri et al. (2006) applied the HSM and proposed several formulations for reinforced soil slopes assuming the log-spiral slip surface. Azad et al. (2008) evaluated the effect of earthquake on the lateral earth pressure of unreinforced soil retaining walls using HSM through pseudo-dynamic method. Narasimha Reddy (2008) applied the HSM and pseudo-static methods to investigate the reinforced soil walls considering oblique load or displacement. Furthermore, Shekarian et al. (2008) applied HSM and pseudo-static method to analyse reinforced soil retaining walls. Li et al. (2015) assessed seismic stability of gravity retaining walls using pseudo-static method. Ghosh and Debnath (2016) analysed reinforced retaining walls assuming nonlinear failure surface. Seismic effects were considered through the pseudo-static method. Song et al. (2016) presented a new method using the LEM to evaluate the stability of geosynthetic-reinforced slopes. Using LEM and finite element method, Rawat and Gupta (2016) analysed the stability of nailed soil slop. Factor of safety and length of reinforcements of geocell-reinforced slope were calculated by Mehdipour et al. (2017) using the HSM under the static condition. Dey et al. (2017) evaluated seismic active earth pressure on retaining walls by considering conventional HSM. They used pseudo-static method to investigate seismic effects. Assuming log-spiral slip surface, Dong-ping et al. (2017) studied the stability of reinforced soil slope through LEM. Required micropiles to stabilize slopes under seismic condition were determined in their research. Pain et al. (2017) evaluated seismic passive earth pressure of inclined rigid retaining walls considering pseudo-static method. A planar slip surface was assumed as critical slip surface. Keshavarz et al. (2017) applied HSM in conjunction with the modified pseudo-dynamic method to compute the yield acceleration of reinforced soil slopes.

In this study, the seismic forces are applied as pseudo-static loads. Pseudo-static approach is one of the old methods used for the seismic stability of soil structures. In this method, the seismic loads are replaced by static forces and the dynamic nature of the seismic loads, time and phase difference and the damping ratio of soils are neglected. In the pseudo-static method, the earthquake force is equal to the soil weight multiplied by a seismic coefficient, which is a fraction of peak ground acceleration (PGA). Despite the disadvantages and simplicity of the pseudo-static method, numerous researches have been done using this method and the results of different investigations demonstrate that the pseudo-static method has appropriate accuracy (Duncan et al. 2014; Conte et al. 2017).

In this paper, the HSM is employed to examine the seismic stability of reinforced soil slopes. To this end, the 5N-1 formulation of Nouri et al. (2006) has been modified. Unlike the previous formulations, the proposed formulation in this study (i) can consider any type of the failure surface such as planar, log-spiral, circular and general slip surface; (ii) can take into consideration the effect of surcharge pressure; and (iii) is arranged such that the obtained system of nonlinear equations can be solved by the Newton-Raphson method or MATLAB optimization functions. The distribution of reinforcements in depth is assumed to be uniform and non-uniform. Moreover, in this study, the genetic algorithm is employed to optimize the critical slip surface and the calculations are performed for both general and log-spiral failure surfaces.

Proposed formulation

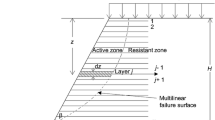
Figure 1 displays the geometry of the problem and all forces exerted on a horizontal slice. Table 1 presents all the number of unknowns and equations. As seen, the number of unknowns and equations are 5N-1, where N is the total number of horizontal slices. For each slice, the equilibrium of vertical and horizontal forces as well as moment around a hypothetical point is examined. Eqs. (1), (2) and (3) represent the equilibrium of forces in the vertical and horizontal directions and moment around point O, respectively.

$$ {V}_{i+1}-{V}_i-\left(1-{K}_{\mathrm{v}}\right){W}_i+{S}_i\sin {\alpha}_i+{N}_i\cos {\alpha}_i=0 $$
(1)
$$ {T}_j+{S}_i\cos {\alpha}_i-{N}_i\sin {\alpha}_i-{K}_{\mathrm{h}}{W}_i+{H}_{i+1}-{H}_i=0 $$
(2)
$$ {V}_{i+1}\left({x}_{i+1}-{x}_0-{L}_{i+1}-{x}_{v,i+1}\right)-{V}_i\left({x}_i-{x}_0-{L}_i-{x}_{v,i}\right)+{T}_j\left({y}_0-H+{Y}_{r,j}\right)+{H}_{i+1}\left({y}_0-{y}_{i+1}\right)-{H}_i\left({y}_0-{y}_i\right)+\left[{S}_i\sin {\alpha}_i+{N}_i\cos {\alpha}_i\right]\left({x}_{m,i}-{x}_0\right)+\left[{S}_i\cos {\alpha}_i-{N}_i\sin {\alpha}_i\right]\left({y}_0-{y}_{m,i}\right)-\left(1-{K}_{\mathrm{v}}\right){W}_i\left({x}_{G,i}-{x}_0\right)-{K}_{\mathrm{h}}{W}_i\left({y}_0-{y}_{G,i}\right)=0 $$
(3)

where Kh and Kv represent the horizontal and vertical pseudo-static coefficients, respectively. and Tj is the reinforcement force. Other parameters are shown in Fig. 1. Hi and Vi represent the interslice horizontal and vertical forces. The relationship between these two forces is assumed as follows (Morgenstern and Price 1965):

$$ {H}_i=\lambda {f}_i{V}_i $$
(4)

where λ is a scalar unknown parameter and fi is a function whose value is assumed to be 1, in this study. Si and Ni are tangential and normal forces exerted on the failure surface, respectively. Applying the Mohr-Coulomb failure criterion, the relation between these forces can be written as:

$$ {S}_i=\frac{N_i\tan \phi +c{b}_i}{F_{\mathrm{s}}} $$
(5)

where c and ϕ represent the soil cohesion and friction angle, respectively; Fs is the factor of safety and bi is the width of the slice base (\( {b}_i=\sqrt{{\left({x}_i-{x}_{i+1}\right)}^2+{\left({y}_i-{y}_{i+1}\right)}^2} \)).

Fig. 1
figure 1

a Geometry of the problem; b forces acting on each slice

Full size image
Table 1 Number of unknowns and equations in the proposed formulation
Full size table

In this study, the distribution of reinforcements along depth is assumed to be uniform or non-uniform (Fig. 2). In the uniform distribution, the vertical spacing between each reinforcement layer is constant (Fig. 2a):

$$ {Y}_{rj}=\left(j-0.5\right)\frac{H}{n};\kern1.25em j=1,2,\dots, n $$
(6)
Fig. 2
figure 2

Distribution of reinforcement in depth: a uniform spacing, and b variable spacing

Full size image

However, in the non-uniform distribution of reinforcement, the spacing between reinforcement layers decreases with depth (Fig. 2b) (Michalowski 1998b):

$$ {Y}_{rj}=\frac{2}{3} nH\left[\sqrt{{\left(\frac{j}{n}\right)}^3}-\sqrt{{\left(\frac{j-1}{n}\right)}^3}\right];\kern1.25em j=1,2,\dots, n $$
(7)

In Eqs. (6) and (7), Yrj is the depth of reinforcements (Fig. 1a) and n represents the total number of reinforcements. The normalized required reinforcement forces are computed as follows (Ling et al. 1997):

$$ K=\frac{\sum_{j=1}^n{T}_j}{0.5\gamma {H}^2} $$
(8a)
$$ {T}_j= K\gamma {Y}_{r,j}{D}_{r,j} $$
(8b)

where Dr,j is the space between two reinforcement layers (Fig. 1a).

By substituting Eqs. (4) and (5) into Eqs. (1)–(3) and after some algebraic manipulations, two sets of equations for each slice can be obtained as:

$$ \left\{\begin{array}{l}{A}_1K+\left(\lambda {f}_i-{A}_2\right)\left({V}_{i+1}-{V}_i\right)+{A}_3=0\\ {}\left[{A}_4+{x}_{v,i+1}+\lambda {f}_{i+1}\left({y}_0-{y}_{i+1}\right)\right]{V}_{i+1}-\left[{A}_5+{x}_{v,i}+\lambda {f}_i\left({y}_0-{y}_i\right)\right]{V}_i+{A}_1K\left({y}_0-H+{H}_{r,j}\right)+{A}_6=0\end{array}\right. $$
(9)

where:

$$ {\displaystyle \begin{array}{l}{A}_1=\gamma {Y}_{r,j}{D}_{r,j}\\ {}{A}_2={m}_i\left(\frac{\tan \phi }{F_s}\cos {\alpha}_i-\sin {\alpha}_i\right)\\ {}{A}_3={m}_i{A}_i\left(\frac{\tan \phi }{F_s}\cos {\alpha}_i-\sin {\alpha}_i\right)+\frac{c{b}_i}{F_s}\cos {\alpha}_i-{K}_h{W}_i\\ {}{A}_4={x}_{i+1}-{x}_0-{L}_{i+1}-{m}_i{B}_i\\ {}{A}_5={x}_i-{x}_0-{L}_i-{m}_i{B}_i\\ {}{A}_6={m}_i{A}_i{B}_i+\frac{c{b}_i}{F_s}\sin {\alpha}_i\left({x}_{m,i}-{x}_0\right)+\frac{c{b}_i}{F_s}\cos {\alpha}_i\left({y}_0-{y}_{m,i}\right)\\ {}-\left(1-{K}_v\right){W}_i\left({x}_{G,i}-{x}_0\right)-{K}_h{W}_i\left({y}_0-{y}_{G,i}\right)\\ {}{m}_i=\frac{1}{\cos {\alpha}_i+\frac{\tan \phi }{F_s}\sin {\alpha}_i}\\ {}{A}_i=\left(1-{K}_v\right){W}_i-\frac{c{b}_i}{F_s}\sin {\alpha}_i\\ {}{B}_i=\left(\frac{1}{m_i}\right)\left({x}_{m,i}-{x}_0\right)+\left(\frac{\tan \phi }{F_s}\cos {\alpha}_i-\sin {\alpha}_i\right)\left({y}_0-{y}_{m,i}\right)\end{array}} $$
(10)

Unknown parameters in Eq. (9) include V2, V3, …, VN, xv,2, xv,3, …, xv,N, λ, K. Therefore, the total number of unknowns is 2N. Two sets of Eq. (9) can be written for each slice and thus the total number of equations is equal to the total number of unknowns. In this way, the nonlinear system of 5N-1 equations in 5N-1 unknowns (Table 1) is reduced to 2N equations in 2N unknowns. Note that the values of VN + 1 and xv,N + 1 are 0. The values of H1, V1 and xv,1 for the first slice depend on the surcharge condition, which can be written as (see Fig. 1a):

$$ \left\{\begin{array}{l}\mathrm{if}\ {x}_1<\left(\mathrm{Hcot}\beta +{L}_0\right)\kern0.5em \mathrm{then}\kern0.5em {V}_1=0;{x}_{v1}=0\\ {}\mathrm{if}\ {x}_1>\left(\mathrm{Hcot}\beta +{L}_0+{L}_q\right)\kern0.5em \mathrm{then}\kern0.5em {V}_1={qL}_q\left(1-{K}_V\right);{x}_{v1}={L}_0+0.5{L}_q;{H}_1=q{L}_q{K}_h\\ {}\mathrm{if}\ \left(\mathrm{Hcot}\beta +{L}_0\right)<{x}_1<\left(\mathrm{Hcot}\beta +{L}_0+{L}_q\right)\kern0.5em \mathrm{then}\kern0.5em \\ {}\kern1em {V}_1=q\left({x}_1-\mathrm{Hcot}\beta -{L}_0\right)\left(1-{K}_V\right);\\ {}\kern1.25em {x}_{v1}=0.5\left({x}_1-\mathrm{Hcot}\beta +{L}_0\right);{H}_1=q\ \left({x}_1-\mathrm{Hcot}\beta -{L}_0\right){K}_h\end{array}\right. $$
(11)

where q indicates the surcharge pressure, and other parameters are shown in Fig. 1a.

The system of nonlinear equations can be written in the following form:

$$ \left[F\right]\left\{X\right\}=0 $$
(12)

where {X} is the unknown vector which is equal to:

$$ \left\{X\right\}={\left[{V}_2,{V}_3,\dots .,{V}_N,{x}_{v,2},{x}_{v,3},\dots .,{x}_{v,3},\lambda, K\right]}^T $$
(13)

In this study, the Newton-Raphson method is used to solve this nonlinear system of equations. In this method, the number of required trial and errors and convergence condition depend on the initial value of unknowns. To this end, the initial values of normal interslice forces (Vi) were assumed to be equal to the overburden pressure and xv,i = 0.5Li. The initial value of 0.5 was assumed for λ and K.

Critical slip surface

As mentioned before, the main challenge in examining the stability of soil slopes through the LEM is obtaining the critical slip surface. Several researchers have proposed different slip surfaces to investigate the stability of slopes. Nowadays, in the majority of studies, log-spiral is considered the critical slip surface particularly in the analysis of reinforced soil slopes.

Log-spiral slip surface

Figure 3a displays a log-spiral sliding surface divided into a number of parallel horizontal slices. The following equation demonstrates the log-spiral failure surface:

Fig. 3
figure 3

Types of failure surfaces: a log-spiral slip surface, and b general slip surface

Full size image
$$ {r}_i={r}_1\exp \left[\left({\theta}_{\mathrm{i}}-{\theta}_1\right)\tan \phi \right] $$
(14a)
$$ {\theta}_{\mathrm{i}}={\theta}_1+\left(\frac{\theta_{N+1}-{\theta}_1}{N}\right)\left(i-1\right) $$
(14b)

The parameters of this equation are shown in Fig. 3a. The value of r1 can be obtained as:

$$ {r}_1=\frac{H}{\sin {\theta}_{N+1}\exp \left[\left({\theta}_{N+1}-{\theta}_1\right)\tan \phi \right]-\sin {\theta}_1};{\theta}_1\le {\theta}_{N+1}\le \frac{\pi }{2}+\phi $$
(15)

The inclination angle of the base of the slice i can be calculated as:

$$ {\upalpha}_{\mathrm{i}}={\tan}^{-1}\left(\frac{r_{i+1}\sin {\theta}_{\mathrm{i}+1}-{r}_i\sin {\theta}_{\mathrm{i}}}{r_i\cos {\theta}_{\mathrm{i}}-{r}_{i+1}\cos {\theta}_{\mathrm{i}+1}}\right) $$
(16)

Having the values of H and ϕ, only the values of θ1 and θN + 1 are necessary to determine the log-spiral slip surface. To obtain the critical log-spiral slip surface which leads to the maximum value of K, the optimized values of θ1 and θN + 1 should be determined. In this study, genetic algorithm (GA) method is used to compute the optimized values of θ1 and θN + 1.

General slip surface

As mentioned earlier, the formulation presented in this study can be applicable to any type of failure surface. It is essential to generate numerous random sliding surfaces to obtain the most critical slip surface. In this paper, general sliding surfaces are generated through a method similar to that proposed by Chang et al. (Cheng et al. 2007, 2008). Figure 3b illustrates how a general sliding surface is generated. In this regard, PN + 1 is a known fixed point at the foot of the slope. To generate a general sliding surface, it is essential to first assume random initial values for α1 and αN and position of the point P1. In this study, the maximum value of L1 is assumed to be 2H. If the soil beneath the point PN + 1 is stiff enough, the slip surface will not extend below this point. Hence, the angle αN will be greater than 0. The value of angle α1 is chosen randomly between αN and π/2. Having the values of α1, αN and x1, the point P′1 can be obtained (see Fig. 3b). Then, a random value of δ1 in the interval [− 0.5, 0.5] is selected to determine the location of point PN (δ1 is equal to the ratio of difference between PN and midpoint of PN + 1P′1 to the difference between PN + 1 and P′1). Similarly, P′2 is specified on line P1P′1 by selecting a random value for δ2. This process continues until all points are specified on the slip surface. This method provides a kinematically admissible random slip surface. Therefore, to determine each random slip surface, the following random vector should be selected:

$$ U=\left[{x}_1,{\alpha}_1,{\alpha}_N,{\delta}_1,{\delta}_2,\dots .,{\delta}_{2N-4}\right] $$
(17)

To obtain the critical general slip surface which leads to the maximum value of K, the optimized value of vector U needs to be computed. Unlike the log-spiral slip surface which needs only two parameters to be optimized, 2N-1 parameters (vector U) should be optimized to obtain the critical general slip surface. Several optimization methods can be used to solve the problem. Genetic algorithm optimization method in MATLAB environment is adopted in this study.

Genetic algorithm (GA) is a search technique in computer science to find approximate solutions for optimization problems. It is a stochastic optimization method introduced by Holland (1975). The implementation process of genetic algorithm is as follows (Mathworks 2018):

  1. 1.

    Generating a random population

  2. 2.

    Scoring population members according to the fitness function

  3. 3.

    Identifying the best members and using them as parents

  4. 4.

    Generating the children and a new population using two mechanisms:

    1. a.

      Randomly changing a single parent (mutation)

    2. b.

      For a pair of parents, merging the vector entries (crossover)

  5. 5.

    Replacing the pervious population with the new population

  6. 6.

    Continuing the process until completion criterion is met

Results

In the following, the stability of reinforced granular soil slopes having the height H of 5 m is examined. The soil internal friction angle varies from 20 to 45°. The slope angle is assumed to be 40 to 90°. The horizontal pseudo-static seismic coefficient is assumed to vary from 0 to 0.3 and the vertical pseudo-static seismic coefficient is considered 0. Although the formulation presented in the previous section can be used for any c-ϕ soil, however, the following results are obtained for granular soils (c = 0). Furthermore, the safety factor Fs is assumed to be 1.

The slope stability is examined by developing a MATLAB code. Using GA optimization, the code determines the most critical log-spiral or general slip surface. After determining the optimum slip surface, the required amount of reinforcement and the length of reinforcements are calculated. Due to unavailability of previous experimental results, the results are compared with those obtained by other researchers.

Figure 4 compares the results of this paper assuming the log-spiral slip surface against those obtained from Nouri et al. (2006). The required reinforcement forces (K) versus ϕ are displayed for different slope angles corresponding to three pseudo-static horizontal coefficients namely 0, 0.15 and 0.3. As seen, the results obtained in this study are to a great extent consistent with those of Nouri et al. (2006) due to the similarity of the theory of these methods. The K values obtained in this study for the log-spiral slip surface is slightly higher than those obtained by Nouri et al. (2006).

Fig. 4
figure 4

Comparison between the results of this study with those of Nouri et al. (2006) for n = 9: aβ = 45°, bβ = 60°, cβ = 75° and dβ = 90°

Full size image

Assuming the log-spiral slip surface, Michalowski (1998b) evaluated the stability of reinforced soil slopes using the limit analysis method. The results of this study and those obtained by Michalowski (1998b) for uniform and non-uniform distribution of reinforcements are compared in Fig. 5 and Fig. 6, respectively. The values of K are compared with different values of slope angle, internal friction angle and horizontal pseudo-static coefficient. It can be observed that the results obtained from the present study are to a large extent consistent with those of Michalowski (1998b). In some cases, the results of two analyses are almost the same.

Fig. 5
figure 5

Comparison between the results of the present study with those of Michalowski (1998b) for uniform distribution of reinforcements and n = 12: aKh = 0, bKh = 0.1, cKh = 0.2 and dKh = 0.3

Full size image
Fig. 6
figure 6

Comparison between the results of the present study with those of Michalowski (1998b) for nonuniform distribution of reinforcements and n = 12: aKh = 0, bKh = 0.1, cKh = 0.2 and dKh = 0.3

Full size image

The values of K obtained from the present study against the results of Ling et al. (1997), Michalowski (1998b), Ausilio et al. (2000) and Nouri et al. (2006) are shown in Fig. 7. Comparisons are made for β = 45, 60 and 75 degrees assuming Kh = 0.2. Accordingly, the results of these methods are close to each other. Furthermore, the values of K of Ausilio et al. (2000) are smaller than those of others. The results of the current study are more close to the results of Michalowski (1998b).

Fig. 7
figure 7

For the log-spiral slip surface, Kh = 0.2, and n = 9, comparison between the results of this study and those obtained by other research works: aβ = 45°, bβ = 60° and cβ = 75°

Full size image

In addition to the required amount of reinforcements, it is essential to specify the minimum required length of reinforcements. Figure 8 shows the required length of reinforcements in dimensionless form (L/H) for the uniform and variable spacing between reinforcements. In both cases, the value of Kh is assumed to be 0.1. As seen, the values of L/H obtained from the present study are very close to those of Michalowski (1998b).

Fig. 8
figure 8

For Kh = 0.1 and n = 12, Comparison between the reinforcements length obtained by Michalowski (1998b) and this study for a uniform distribution of reinforcements and b variable distribution on reinforcements

Full size image

As discussed, the slip surface was assumed to be log-spiral in most previous studies. In the following, a few examples are analysed based on the general slip surface. Figures 9 and 10 display some results obtained in this paper for the uniform and non-uniform distribution of reinforcements, respectively. In these figures, the results are provided for both types of log-spiral and general slip surfaces. Evidently, the values of K for the general slip surface in all cases are higher than those for the log-spiral failure surface. It can be argued that the analysis carried out through the general slip surface is more conservative. Generally, the values of K obtained from the general slip surface are about 10 to 15% higher than those of the log-spiral slip surface.

Fig. 9
figure 9

Assuming the uniform distribution of reinforcements and n = 12, comparing the values of K for the log-spiral and general slip surface for aKh = 0, bKh = 0.1, cKh = 0.2 and dKh = 0.3

Full size image
Fig. 10
figure 10

Assuming the non-uniform distribution of reinforcements and n = 12, comparing the values of K for the log-spiral and general slip surface for aKh = 0, bKh = 0.1, cKh = 0.2 and dKh = 0.3

Full size image

Figure 11 shows four examples of the log-spiral and general slip surfaces for different values of the slope angle, namely, 40 and 65° and Kh = 0, 0.2. This figure compares the optimized log-spiral and general failure surfaces assuming uniform distribution of reinforcements. The soil friction angle is assumed to be 30°. As can be seen, the general failure surfaces expand beyond the log-spiral slip surface. Therefore, for the general slip surface, the larger lengths of the reinforcements are required.

Fig. 11
figure 11

Examples of the log-spiral and general slip surfaces for n = 12: aβ = 40° Kh = 0; bβ = 40°, Kh = 0.2; cβ = 65°, Kh = 0; and dβ = 65°, Kh = 0.2

Full size image

This study has, for the first time, examined the effects of surcharge pressure on the stability of reinforced soil slopes. Figure 12 shows the impacts of the surcharge pressure on the values of K. The calculations are conducted for a soil slope to a height of 5 m having the horizontal pseudo-static seismic coefficient of 0.15 and internal friction angle of 30°. The surcharge pressure is in the form of a uniform rectangular initiated at a distance of H/5 from the slope crest (L0 = H/5, Fig. 1). The slope stability is evaluated for loads extended to lengths Lq of 0.2H, 0.4H, 0.8H and infinite. The slip surface is log-spiral and spacing between reinforcements are constant. The values of the load intensities q are assumed to be 25, 50, 75 and 100 kPa. As shown in Fig. 12, increasing q or Lq leads to increase the value of K. Furthermore, the values of K increase more frequently in gentler slopes.

Fig. 12
figure 12

For H = 5 m, ϕ = 30°, Kh = 0.15, n = 12, the effect of the surcharge on the stability of reinforced soil slopes for aLq = 0.2H, bLq = 0.4H, cLq = 0.8H and dLq = ∞

Full size image

The calculations become extremely time-consuming when the general failure surface is adopted instead of the log-spiral slip surface. That is because a greater number of variables should be optimized for general slip surface. It is worth mentioned that the number of the optimization variables of the log-spiral and general slip surfaces are 2 and 2N-1, respectively. The analysis will be more precise as the number of slices (N) increases. However, the calculations become more time-consuming as the number of slices grows. Such slowdown is particularly significant for optimization of general slip surface. Figure 13 displays the effect of the number of slices on the value of K in two cases. This figure is prepared assuming the both general and log-spiral slip surfaces and uniform distribution of reinforcements. As seen, the solutions become more accurate as the number of slices increases. However, after a value of N, the results are almost constant. This specific value can be considered the best value for the number of slices. In both cases, the accurate solution can be achieved based on 6 and 14 slices for log-spiral and general slip surfaces, respectively.

Fig. 13
figure 13

The effect of the number of slices on the values of K for n = 12

Full size image

Conclusions

In recent years, various methods have been proposed to examine the stability of reinforced soil slopes and walls. The horizontal slice method was adopted in this paper to assess the stability of reinforced granular soil slopes. One of the problems in analysis of soil slopes through limit equilibrium method is how to determine the critical slip surface. The formulation proposed in this study may be used for any type of the slip surface. The seismic forces were modelled through a pseudo-static method.

The results in this study were verified by comparing the results (assuming a log-spiral slip surface) against those of other researchers. Comparisons indicate that the results of this study are desirably accurate. The comparison of results for the general and log-spiral slip surfaces demonstrated that considering the former will provide more conservative results. The normalized amount of reinforcement force (K) obtained from general slip surface is about 10 to 15% higher than that of log-spiral failure surface. This reflects that the log-spiral slip surface may lead to unconservative results.

Moreover, the shapes of the general and log-spiral slip surfaces were compared. The results demonstrated that the general slip surface covered larger areas of the soil mass. Thus, the general slip surface requires a larger length of reinforcements for achieving the stability of reinforced soil slopes.