Introduction

The stability of slopes has always been an issue of interest among scholars in different areas of geotechnical engineering (Kelarestaghi and Ahmadi 2009; Choobbasti et al. 2009; Sharma et al. 2012). The two main objectives of slope stability analysis are calculating factor of safety (FOS) for a given slip surface and determining the critical slip surface (CSS) for a given slope. FOS is usually obtained by limit equilibrium method (LEM) as the ratio of resistance forces by driving forces along the slip surface. The tendency for LEM in slope stability is because of the reliable results that it produces, its comprehensible procedure, and its flexible formulation (Baker 1980; Cheng et al. 2008; Sun et al. 2011). CSS is a unique slip surface with the minimum FOS that is determined by using deterministic search methods or approximate optimization techniques.

The most common LEMs are friction circle and methods of slices (Taylor 1948; Bishop 1955; Morgenstern and Price 1965; Spencer 1967; Janbu 1973; Sarma 1973, 1979, 1987; Fredlund and Krahn 1977; Chen and Morgenstern 1983). An appropriate method of analysis for a slope stability problem has to be able to model the shape of slip surface, the slope material, and any other involving condition. The scope of this paper is limited to simple homogeneous or layered slopes with circular slip surface, which is analyzed by simplified Bishop’s (1955) and Spencer’s (1967) methods.

The location and shape of CSS is not clearly defined in general slope stability problems. So, a large number of trial failure surfaces have to be evaluated to accomplish a reasonable search. The main steps of this search are generating trial slip surfaces as probable solutions and determining the CSS among the available solutions. Although researchers have paid intensive attention to the technique of determining the CSS (Goh 1999, 2000; Cheng 2003; Zolfaghari et al. 2005; Cheng et al. 2008, 2007a, b; Zhao et al. 2008; Kahatadeniya et al. 2009; Tian et al. 2009; Li and Chu 2010; Kalatehjari et al. 2011; Chen and Chen 2011), the significance of method of generating trial slip surfaces has not been investigated. We believe that the mentioned ignorance would affect the results of analysis even in the simplest slope stability problems with circular slip surface. Therefore, the circular slip surface was selected as the scope of this paper. Two other general shapes of slip surface are ellipse and polygon. The method of generating polygonal slip surface is almost the same in all studies, which is similar to the proposed approach by Hajiazizi (2010). The ellipse surface can be generated in two ways, by its center and semi-radiuses or by at least five points of its surface. In order to generate trial circular slip surfaces, conventional method (CM) and a proposed method, namely triple-point method (TPM), were used. The algorithm of both methods, their assumptions, and their limitations were described in this paper. Finally, the ability of these methods in determining the CSS was evaluated by example problems.

Theoretically, CSS can be determined by evaluating any available slip surfaces. Deterministic search methods provide fast and simple search by evaluating a limited number of trial slip surfaces that are selected based on a pattern. However, there is always a chance of losing the real CSS in available gaps between pattern nodes. Since these methods assess all the trial solutions to determine the best one, they act extremely slowly when the number of possible answers increased due to large searching spaces. Therefore, these methods are almost useless in large searching space. On the other hand, equation of FOS is a nonlinear function that makes it impossible to mathematically determine the approximate location of the global solution and cut the searching space into a smaller one. Thus, approximate optimization techniques with the ability of random searching are applied to the slope stability problem to remove the mentioned limitations.

CSS has been determined in research through Genetic Algorithm (Goh 1999, 2000; Zolfaghari et al. 2005), particle swarm optimization (PSO) (Cheng et al. 2007a, 2008), ant colony (Cheng et al. 2007b; Kahatadeniya et al. 2009), and Harmony Search (Li and Chu 2010). Cheng et al. (2007a, b) demonstrated that PSO is a powerful and reliable searching technique that can determine the CSS in different examples within an acceptable process time. The application of this method has continued in slope stability problems up to date (Cheng et al. 2008; Zhao et al. 2008; Tian et al. 2009; Li and Chu 2010; Kalatehjari et al. 2011; Chen and Chen 2011). We utilized PSO in this study as the searching technique to determine the CSS. Moreover, we developed a computer program to determine the CSS based on LEMs and PSO. This program can determine the circular CSS of complex soil slopes by using simplified Bishop’s (1955) and Spencer’s (1967) methods.

CM of generating circular slip surfaces

Optimization process is started by making the required number of initial trial slip surfaces that is usually greater than ten to prevent the failure in convergence of optimization process. The shape of trial slip surfaces mainly depends on the analysis method and the properties of slope material. Generally, a circular slip surface is assumed for slopes with homogeneous material. The easiest way to generate this kind of surface is to use three variables including the coordinates of center (X c and Y c) and the radius of circle (R c). The boundaries of these variables should be defined carefully. Trial slip surfaces are created by random selection of these variables throughout their boundaries. This method is the CM of generating trial circular slip surface that is shown in Fig. 1.

Fig. 1
figure 1

CM of generating circular slip surface

Full size image

In CM, the number of possible slip surfaces increases surprisingly by widening the boundaries of variables or extending the searching space. Although wider searching space provides more trial solutions and may lead to more accurate results, it increases the calculation time. Moreover, it is theoretically impossible to apply the infinite boundaries of variables and generate infinite trial slip surfaces. Therefore, there is a need to crop the searching space by estimating the position of the CSS and confining the boundaries of variables like what has been introduced by Fellenius (1927). This process has also some drawbacks. It inevitably sacrifices a number of possible solutions, which may cause failure in determining the real CSS of the slope.

Another limitation of CM is generating unacceptable slip surfaces. These surfaces are not practically feasible and should be excluded from the analysis, because they increases calculation time and cause delayed convergence in optimization process. Figure 1 shows even with using constant radius and confined boundaries for the center of circular slip surfaces, unacceptable slip surfaces may be generated by CM.

TPM to generate circular slip surfaces

Here, we presented a TPM for generating trial circular slip surfaces. The procedure of employing this method, which is also illustrated in Fig. 2, is as follows:

Fig. 2
figure 2

Generating circular slip surface by TPM

Full size image
  1. 1.

    Two points are selected on x-axis beneath the slope surface, between x min and x max.

  2. 2.

    The corresponding elevations of these points are calculated by interpolation between slope geometry points.

  3. 3.

    The coordinates of the two points are saved as points 1 (x 1 and y 1) and 2 (x 2 and y 2).

  4. 4.

    Initial coordinate of third point (x 3) is calculated as the middle of the two points or as a random point between them on x-axis.

  5. 5.

    The corresponding elevation of the third point is calculated by interpolation between slope geometry points as d max.

  6. 6.

    A random number between the base level and d max is generated as the height of the third point.

  7. 7.

    The coordinates of the third point is saved as point 3 (x 3 and y 3).

  8. 8.

    The confining circle of the three points is determined as a circular slip surface.

In order to determine the equation of a confining circle, the mentioned three points are sufficient. Firstly, two lines are formed by these three points and their equations are determined by calculating their gradients (m 1 and m 2). The first and the second lines pass through points 1 and 3 and points 2 and 3, respectively. Then, the coordinates of the center of circle (X c and Y c) are calculated as intersection point of normal vectors of mentioned lines. X c is calculated by Eq. 1; then Y c is determined by substituting X c into the equation of a normal vector. Finally, R c is determined as the distance from the center of circle to any of the initial points.

$$ {X_{\mathrm{c}}}={{{\left( {{m_1}{m_2}\left( {{y_1}-{y_2}} \right)+{m_2}\left( {{x_1}+{x_3}} \right)-{m_1}\left( {{x_3}+{x_2}} \right)} \right)}} \left/ {{2\left( {{m_2}-{m_1}} \right)}} \right.} $$
(1)

Where (also in Fig. 2) X c is the coordinate element of the center of the circle on x-axis; m 1 and m 2 are gradients of lines 1 and 2, respectively; x 1, x 2, and x 3 are the coordinate elements of points 1, 2, and 3 on x-axis, respectively; y 1 and y 2 are the coordinate elements of points 1 and 2 on y-axis, respectively.

TPM is able to eliminate the limitations of CM, because it does not need to define any boundary for the searching space. This independency allows TPM to generate trial slip surfaces without using any assumption or estimation in the location of the CSS. moreover, although TPM provides an independent searching space involving all possible slip surfaces, only three independent variables (x 1, x 2, and y 3) are required to make a circular slip surface. This is equal to the number of independent variables in CM (X c, Y c, and R). By having the geometry of slope, the presented method does not need any other information to generate a trial slip surface.

The application of TPM

The application of TPM in generating trial slip surfaces was compared with CM for a slope with irregular geometry (Fig. 3). The geometry of slope was extracted from Goshtasbi et al. (2008). This manmade wall of open pit mine had a height of 146.23 m along with a 261.294-m length. The boundaries of searching space of CM were set to X c (−30, 80) m, Y c (118,228) m, and R c (10, 210) m based on the original study. As mentioned earlier, TPM does not need any presetting of variable boundaries. Table 1 shows the percentages of unacceptable trial slip surfaces made by TPM and CM during five generations. The number of total generated slip surfaces in each generation was the same and equal to 20 for both methods. Since trial slip surfaces were generated by random function, their intersection points with the slope surface were not the same.

Fig. 3
figure 3

Irregular slope model

Full size image
Table 1 The percentages of unacceptable trial slip surfaces made by CM and TPM
Full size table

Table 1 shows that the average percentage of unacceptable trial slip surfaces in CM was 34 % while TPM did not generated any unacceptable trial slip surface in all generations. The difference in the results of TPM and CM is related to their process of generating trial slip surfaces, while their calculations process was identical. The obtained results confirmed the success of TPM in generating more acceptable trial slip surfaces than CM. Moreover, it is expected that TPM can increase the accuracy in determining the CSS, because each extra-acceptable trial slip surface represents an extra possible solution. It should be mentioned that unconcerned confining of searching space could make even more inferior results for CM.

Particle swarm optimization

In every problem involved with searching, an appropriate answer has to be found among potential solutions. Searching problem in engineering is usually defined as optimization problem to minimize or maximize a function, which is called the objective function. If this function got more than one optimum answer, the problem chances into global optimization. However, for several solutions that may satisfy the objective function in a neighboring area there is only one global answer.

Two main steps of determining the CSS with optimization techniques are generating trial slip surfaces, converting them into algorithm structure, evaluating the FOS and fitness of them, and determining the CSS with the lowest FOS by using operators of optimization algorithm. In the first step of optimization method, a certain number of trial slip surfaces are generated as candidate solutions in initial population. Then, each trial slip surface is coded into the algorithm structure to evaluate its fitness. The optimization operators work with the best trial slip surfaces to generate new candidate solutions and navigate the whole system into its goal. In slope stability analysis, this goal is determining the CSS.

PSO was initially introduced by Kennedy and Eberhart (1995) as a global optimization technique. This technique inspired by the behavior of social milieu. PSO simulates the activity of bird flocking when they try to find food randomly on their way. They follow the closest bird to the food by using a stochastic variable called craziness. Each bird is called a particle or individual, the whole flock is called swarm, and food is the objective. The objective function of PSO calculates the distance of each particle to the objective as its fitness value. PSO process is aimed to enhance the swarm fitness until meeting a termination criterion. These simple concepts of PSO help to solve optimization problems. Thus, PSO has been used increasingly as an effective technique for solving complex and difficult optimization problems. Kennedy and Eberhart (1995) showed that PSO is able to determine the global optimum with comparable result to the other successful optimization methods. In slope stability analysis, PSO was applied in several studies to determine the CSS (Cheng et al. 2008, 2007a, b; Zhao et al. 2008; Tian et al. 2009; Li and Chu 2010; Li et al. 2010a; Kalatehjari et al. 2011; Chen and Chen 2011). These studies have confirmed that PSO achieves satisfactory and reasonable results compare with other optimization techniques in slope stability problems.

Procedure of PSO

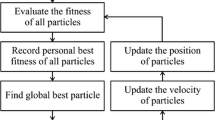
PSO starts by generating particles of first swarm. Each particle has two main variables as its position and velocity. Initial position of particles is determined inside the searching space by using a random function, while initial velocity of all particles is zero. The fitness value of each particle is evaluated by using an objective function where the greater fitness value belongs to the closer particle to the objective. In the next step, velocity and position of particles are updated based on their fitness values and their craziness for the next iteration. In the original form of PSO, velocity and position of particles are updated based on the following variables:

  1. (a)

    The best position of the particle so far as its personal best (p best)

  2. (b)

    The position of the best particle in swarm as global best (g best)

  3. (c)

    The random values of craziness (rand1 and rand2)

PSO uses simple concept of movement in updating the velocity and position of particles. Moreover, a stochastic variable is included to this process to avoid settlement of particles on a united, unchanging direction (Kennedy and Eberhart 1995). Therefore, PSO has the advantages of easy operation in comparison with the other population-based techniques that use complex evolutionary operations. In contrast to other population based optimization methods, particles never die in PSO. They continuously update their velocity and position to investigate new solutions inside the searching space. In the original form of PSO, position and velocity of particles are updated by using Eqs. 2 and 3, respectively. Later on, another variable as inertia weight (w) was added to original velocity equation to control the scope of the search (Poli et al. 2007). Equation 4 is the modified equation of velocity. The searching procedure of PSO continues to meet a termination criterion, which is usually set as a fixed number of iterations or a required accuracy. The workflow of original PSO is shown in Fig. 4.

Fig. 4
figure 4

The workflow of general PSO

Full size image
$$ \overrightarrow{{{v_{\mathrm{new}}}}}=\overrightarrow{v}+\mathrm{ran}{{\mathrm{d}}_1}\times \left( {\overrightarrow{{{p_{\mathrm{best}}}}}-\overrightarrow{p}} \right)+\mathrm{ran}{{\mathrm{d}}_2}\times \left( {\overrightarrow{{{g_{\mathrm{best}}}}}-\overrightarrow{p}} \right) $$
(2)
$$ \overrightarrow{{{p_{\mathrm{new}}}}}=\overrightarrow{p}+\overrightarrow{{{v_{\mathrm{new}}}}} $$
(3)
$$ \overrightarrow{{{v_{\mathrm{new}}}}}=\mathrm{w}.\overrightarrow{v}+\mathrm{ran}{{\mathrm{d}}_1}\times \left( {\overrightarrow{{{p_{\mathrm{best}}}}}-\overrightarrow{p}} \right)+\mathrm{ran}{{\mathrm{d}}_2}\times \left( {\overrightarrow{{{g_{\mathrm{best}}}}}-\overrightarrow{p}} \right) $$
(4)

Where v new is the updated velocity and v is the current velocity of a particle; both rand1 and rand2 are independent random numbers that stand limited in certain ranges; P new is the updated velocity and P is the current position of a particle; p best is the best position of a particle so far; and g best is the position of the best particle in the a swarm.

Two different particles were designed in the present study for CM and TPM. The anatomies of these particles are shown in Fig. 5. Regardless of the method of generating trial slip surfaces, each particle has four basic sections. The first section shows its current position with three subsections of (x c, y c, and R c) for CM and (x 1, x 2, and y 3) for TPM. These values are used to determine a trial slip surface. The next two sections are similar in both methods and contain the values of current and the best fitness of particle so far. Current velocity of particle that is in a similar form with position occupies the last section.

Fig. 5
figure 5

Anatomies of particles of PSO for CM and TPM

Full size image

The objective and fitness functions of PSO

Objective function is a mathematical function that works with the variables of problem within the boundaries of searching space. The aim of optimization technique is to minimize or maximize this function. Moreover, a fitness function related to objective function is defined to evaluate the fitness value of particles. The present study used simplified Bishop’s (1955) and Spencer’s (1967) methods as the objective functions of its optimization technique. In order to determine the CSS with the minimum FOS, a fitness function was defined to be maximized by the PSO (Fitness = 1/FOS). Consequently, PSO minimizes the value of FOS of either method by increasing the fitness value of particles during the optimization. Finally, the particle with the maximum fitness value represents the CSS with the lowest FOS.

Generally, simplified Bishop’s (1955) method is satisfactory to analyze the stability of simple slopes with circular slip surface. This method ignores the effect of intercolumn forces and calculates the FOS by using overall moment equilibrium. On the other hand, Spencer’s (1967) method is applied to make reasonable comparison with the results of other studies in slopes that are more complicated. This method considers the effect of interslice forces and is able to calculate FOS for layered soil with different shapes of slip surface including the circular one. Both mentioned methods are in the category of methods of slices. Based on the procedure of methods of slices, sliding body is divided into n slices and the value of FOS is calculated during an iterative process for trial factors of safety. In order to speed up the performance of algorithm, the upper and lower bounds of FOS are usually set to fixed values. These constriction values should be defined specifically for each problem. Figure 6 illustrates a typical slice that is used in simplified Bishop’s (1955) and Spencer’s (1967) methods.

Fig. 6
figure 6

A typical slice in method of slices

Full size image

Where b i is the horizontal width of the slice; h i and h i + 1 are the heights of action point of the interslice forces in the left and right sides of the slice, respectively; αi is the base inclination of the slice; N i and U i are the total normal force and pore-water force at the base of the slice, respectively; P i and P i + 1 are respectively the right and left interslice forces; ΔQ i and ΔW i are respectively the total horizontal and vertical forces; δ i and δ i + 1 are the inclination of the right and left interslice forces, respectively; and T i is the mobilized shear force at the base of the slice.

Initial parameters of PSO

The required program for PSO and slope modeling was written by the first author in MatLab software at Universiti Teknologi Malaysia. The following parameters were used to initialize the PSO algorithm based on the proposed values of original PSO of Kennedy and Eberhart (1995), modified velocity equation of Rini et al. (2011), extensive studies of Mendes et al. (2002) on the performance of PSO, and the results of some initial tests by the authors.

  1. (a)

    Two random methods to initialize the first population (CM and TPM)

  2. (b)

    A swarm size of 20 particles

  3. (c)

    An inertia weight of 0.4

  4. (d)

    Equal velocity coefficients of 2

  5. (e)

    A termination criterion as a fixed number of iterations

Although the results of some studies showed that PSO had immunity to change in its initial parameters, this parameters should be precisely initialized for the best performance in each specific problem (Kalatehjari et al. 2011; Cheng et al. 2007b). Apparently, the best performance of PSO is achieved by setting the optimum initial parameters that are achieved from sensitivity analysis.

The termination criteria should be carefully selected in each problem to avoid convergence problems. Except a fixed number of iterations, two more termination criteria are available based on observing the fitness value of the best particle during a certain iterations (observation period) similar to what was proposed by Cheng et al. (2007a, b) or observing the average fitness of the swarm during an observation period. In preliminary tests, the application of the other two criteria led to pre-mature convergence within short and medium observation periods. Since a long observation period is actually mutual with a fixed number of iterations, the termination criterion of this study was set to a fixed number of iterations. It should be noted that the actual performance of heuristic optimization methods depends on the minor tricks that are used by individual researchers.

Comparison of the results of CM and TPM

Although the main objective of this study was to compare the results of CM and TPM, the comparison studies were carried out to verify the results of these methods. Two well-known example problems were selected from the literature. The first example problem was extracted from Zolfaghari et al. (2005) as a natural homogeneous slope in dry condition. The geotechnical properties of example problem 1 were as friction angle of 20 , cohesion of 1,500 kg/m2, and unit weight of 1,900 kg/m3. Zolfaghari et al. (2005) used simple genetic algorithm (SGA) and (Morgenstern and Price 1965) method with constant interslice force function, equivalent to Spencer’s (1967) method to analyze the stability of slope. Later on, Cheng et al. (2007b) applied Spencer’s (1967) method with six huristic methods of global optimization including simulated annealing (SA), genetic algorithm (GA), PSO, simple and modified harmony methods (SHM and MHM), Tabu search (TS), and ant colony on the same slope to compare the application of these methods in determining the CSS. The results of the present analysis with both CM and TPM along with the results of the previous studies are presented in Table 2. For this study, the boundaries of searching space of CM were set as X c (0, 30), Y c (42, 60), and R c (2, 30).

Table 2 The results of different studies for example problem 1
Full size table

As Table 2 shows, the maximum difference between minimum FOS of the present study and previous methods did not exceed 1.15 %, which verifies the performance of the present study. The minimum factors of safety of simplified Bishop’s (1955) and Spencer’s (1967) methods were obtained as 1.7195 and 1.7393 for TPM and 1.7207 and 1.7402 for CM, respectively. A unique CSS was found for each of TPM and CM as X c = 17.77 m, Y c = 58.05 m, and R c  = 17.23 m and X c = 17.42 m, Y c = 17.63 m, and R c = 58.48 m, respectively. Although the FOS of simplified Bishop’s (1955) method for the present study was the lowest among the results of all methods, the corresponding value of Spencer’s (1967) method was between the other results. The results of the present study for Spencer’s (1967) method was smaller than the results of SGA, TS, and ant colony but greater than FOS of SA, PSO, SHM, and MHM. In fact, the differences between the results of Cheng et al. (2007b) and the present study with the same optimization technique and FOS function were only 0.62 and 0.69 % for TPM and CM, respectively. The authors believe that these small differences may be the result of using different shapes of slip surface in the analysis. Although the scope of the current study was set to circular slip surfaces to compare the results of CM and TPM, other mentioned studies were free to use both circular and noncircular slip surfaces in their analysis.

The obtained CSSs of example problem 1 are illustrated in Fig. 7. Both CSSs of the present study were deeper than the others. The CSSs of Cheng et al. (2007b) for SA, MSH, SHM, PSO, and GA were closer to the CSS of CM. The noncircular CSS of Zolfaghari et al. (2005) and the CSS of TS of (Cheng et al. 2007b) were partly adjacent to the CSS of CM in the middle parts. A comparison between the results of CM and TPM in Table 2 and Fig. 7 shows that the minimum factors of safety of both simplified Bishop’s (1955) and Spencer’s (1967) methods and the deeper CSS belongs to TPM.

Fig. 7
figure 7

The CSSs obtained by different studies for example problem 1

Full size image

The second example problem was a natural slope with complex layers that was originally presented by Zolfaghari et al. (2005). The slope involved four layers with different strength parameters as shown in Fig. 8. This problem was re-analyzed by Cheng et al. (2007a) and Li et al. (2010b). Zolfaghari et al. (2005) used SGA with Morgenstern–Price method (Morgenstern and Price 1965) same as example problem 1. With Spencer’s (1967) method as the function of FOS, Cheng et al. (2007a) applied PSO and Li et al. (2010b) used a real-coded genetic algorithm (RCGA) to analyze the stability of this slope. This study used PSO with Spencer’s (1967) method to re-analyze the mentioned problem. Table 3 shows the results of different studies for example problem 2.

Fig. 8
figure 8

The CSSs obtained by different studies for example problem 2

Full size image
Table 3 The results of different studies for example problem 2
Full size table

As Table 3 shows, the two different numbers of slices were used in example problem 2. Zolfaghari et al. (2005) used 40 slices and Cheng et al. (2007a) and Li et al. (2010b) applied 30 slices in their analyzes. The present study applied both numbers to make fair comparison with the results of each method. The values of FOS for TPM and CM by 30 slices were 1.4230 and 1.4301, respectively. By using 40 slices, TPM and CM obtained FOS as 1.4267 and 1.4313, respectively. Consequently, TPM successfully obtained smaller values of FOS compare with CM. By considering the results of 40 slices, the present study was able to achieve the smaller factors of safety by both CM and TPM compare with Zolfaghari et al. (2005) when the circular slip surfaces were used in both studies. However, the factors of safety of Cheng et al. (2007a) and Li et al. (2010b) which were obtained by using non-circular slip surfaces were slightly smaller than the results of TPM and CM by 6.59 and 7.12 %, respectively. As mentioned before, we believe that these differences may be the result of using different shapes of slip surface in these analyzes. It should be mentioned that the obtained locations of opening and ending points of CSSs in this study were always close to the results of the previous studies.

As Fig. 8 shows, TPM achieved similar critical surfaces for both 30 and 40 slices, but CM obtained two different CSSs. The coordinates of CSS of TPM were X c = 27.37 m, Y c = 54.92 m, and R c  = 10.92 m. The coordinates of CSS of CM with 30 slices were X c = 27.71 m, Y c = 55.61 m, and R c  = 11.61 m and with 40 slices were X c = 26.67 m, Y c = 56.41 m, and R c = 12.41 m. A comparison between the results of CM and TPM in Table 3 and Fig. 8 shows that the minimum factors of safety of both 30 and 40 slices and the deeper CSS belongs to TPM.

Discussion

During comparative studies, the present study showed that CM and TPM could determine the CSS and FOS by reasonable accuracies compare with the results of the previous studies. The small amount of differences between the results could verify the performance of both methods in determining the CSS. Apparently, the obtained factors of safety by CM and TPM were different, but TPM always achieved better results than CM. Although, these results verified the effect of method of generating trial slip surfaces in determining the CSS, a sensitivity test was conducted on the slope of example problem 1 to assess the performance of CM and TPM with more accuracy. This test was planned for five different iterations as 10, 20, 30, 40, and 100 and 20 repetitions for each one. The number of slices was set to 80 to produce more precise values of FOS compare to previously 40 applied slices. The results of sensitivity analysis for CM and TPM are shown in Tables 4 and 5, respectively.

Table 4 The results of sensitivity test for CM
Full size table
Table 5 The results of sensitivity test for TPM
Full size table

Table 4 shows that the average FOS of CM experienced fluctuation by raising the iteration number. It showed that CM did not provide convergence over a mutual value of FOS during different repetitions. Additionally, the global minimum FOS was changed over the analysis process of CM. While the value of FOS decreased continuously to 40 iterations, it unexpectedly increased at 100 iterations. These are the evidences of convergence problem. Failure in convergence, fluctuation in the average FOS, and instability of the global minimum could be the evidences of unreliability of CM.

Table 5 shows that the average FOS of TPM had a descending trend by increasing the iteration number. It shows the stability of this method in the convergence toward the minimum FOS. The value of the global minimum FOS had good stability during the process and converged to 1.7306 at 100 iterations. Comparing the results of Tables 4 and 5, TPM obtained the lower average and global minimum FOS in every step of the test. The only advantage of CM compare to TPM was less calculations time with around 6 min time saving in the whole process. Regarding the fact that a medium performance laptop computer (Intel Core i3 CPU, 2.40 GHz) performed the calculations of the present study, this little time saving may not be considered a victory.

Figure 9 shows the slip surfaces with minimum FOS in each swarm during 100 iterations. These surfaces were extracted from the results of sensitivity test with termination criterion of 100 iterations that obtained the global minimum FOS. It can be seen that TPM opened the boundaries to search freely through enormous sorts of trial slip surfaces, while CM was restricted by its boundaries within limited searching space. This could be the other significance of using TPM over CM in determining the CSS.

Fig. 9
figure 9

The slip surfaces with the minimum FOS in each swarm during 100 iterations

Full size image

Conclusions

This paper presented a new method of generating circular slip surfaces, namely TPM. Performance of this new method was compared with the CM of generating trial slip surfaces for a general slope. The results showed that TPM was more successful than CM in generating acceptable trial slip surfaces.

A computer program was written to determine the CSS of slopes with simplified Bishop’s (1955) and Spencer’s (1967) methods by using PSO. The performance of this program was verified during two comparative studies. The comparative analyzes showed that both TPM and CM are successful to determine the CSS with the comparative FOS with the previous studies. In example problem 1, the maximum difference between the FOS of the present study and previous methods did not exceed 1.15 %. In example problem 2, the difference between the FOS of TPM and CM and previous methods were at most 6.59 and 7.12 %, respectively. However, TPM achieved better results than CM in all tests. This result approves the effect of generating circular slip surface on determining the CSS.

The results of the sensitivity analysis showed that CM has the potential for failure in convergence, fluctuation in the average FOS, and instability of the global minimum FOS. The results also demonstrated that the ability of TPM in determining the CSS is more than CM. Observing the visual result of the sensitivity analysis showed that TPM could generate vast sorts of trial slip surfaces freely, while CM was restricted to its boundaries.

Based on the results of the present study, TPM eliminated some limitations of CM including defining the boundaries of searching space, losing the CSS in gaps of searching pattern, and generating unacceptable slip surfaces. The superiority of TPM has been demonstrated in terms of generating acceptable trial slip surfaces, determining the CSS with the lowest FOS, and better convergence in the procedure of optimization. The mentioned advantages have been achieved by changing the method of generating trial slip surfaces. Therefore, the effect of the applied method of generating trial slip surfaces on determining the CSS was confirmed.