Introduction

Karst fractures, the groundwater conduits, play an important role in groundwater flow. Therefore, the study on the spatial distribution of fractures is essential to understand groundwater migration (Berkowitz 2002). The karst fracture network model constructed by the integration of both surface fracture data and underground fracture data is the basis for simulating the migration of fissure water and pollutants in the fracture media. The discontinuity, inhomogeneity, and anisotropy in the development of karst fractures result in greatly different conditions of groundwater flow, which poses huge challenges to research groundwater seepage along fractures (Batu 2009; Brkic et al. 2018; Ford and Williams 2007). This paper aims at simulating crack seepage in karst areas and establishing a three-dimensional fracture network model to provide a solid theoretical basis for computer simulations of groundwater flow along with karst fractures.

Establishing an underground fracture seepage network model in a karst area is key to understanding the intensity and development mechanism of karst fractures (Karimzade et al. 2017), as well as underground transport of pollutants (Gellasch et al. 2013). Moreover, establishing a model can help decision-makers identify the development and distribution of fractures within the study area. The dispersion rate and diffusion edge, contaminant plume, and effects of groundwater flow on environment can be calculated and estimated by combining simulations with external factors like hydrogeological conditions in study field (He 1997; Chen 2011).

In the process of constructing large-scale fracture networks by computer, fractures characterized by connectivity which are important components of the seepage path must be found before determining seepage paths (Hyman et al. 2016; Medici et al. 2016). Huamei Liu provided the theoretical basis for fracture intersection determination using analytic geometry in which plane equations for two fractures were established. According to the knowledge on analytic geometry, if the two disks intersect, the sum of the distance between their centers to the intersecting line must be less than the sum of their radii, and their distances from the center to the intersection must be less than each radius; this can be used to determine whether two crevices intersect (Liu and Wang 2010). However, some fractures are isolated, meaning that they do not intersect with any other fractures. Further judgment is required every time these fractures are involved in the evaluation, which costs more time in calculation and reduces efficiency. To solve this problem, an R-tree index algorithm is used to exclude the isolated fractures and evaluate whether they truly intersect. Meanwhile, the consumption of computer memory begins to increase in the process of constructing an R-tree index, but it remarkably saves computing time. Zhiyu Li proposed and optimized an algorithm termed “bounding box” for rapid judgments of intersections, which also improved the efficiency of the system. The final judgment results were stored in an adjacency matrix or adjacency list and illustrated in a form of directed graphs, thus paving the way for groundwater seepage simulations in a karst area (Li et al. 2014).

To demonstrate data graphically and intuitively, three-dimensional visualization technology seen as a bridge to link multiple disciplines is a useful tool for analyzing, understanding, and duplicating data. A large amount of data can be used by it to check the continuity and authenticity of the material and find anomalies (Wang 2016). Different concrete or abstract fracture network models can be vividly presented in real time using 3D visualization technology to simulate a three-dimensional fracture network. Eliminating abnormal values and analyzing meaningful abnormal values allow one to better understand their results.

Generalized disk model for karst fractures

To intuitively present the karst fracture networks, the in situ data about fractures such as the coordinates, length, trace length, and separation distance, as well as the occurrence including dips and dip angles obtained from field measurements must be displayed in a three-dimensional form in visualization. Based on the acquired data mentioned above, fractures demonstrated on a spatial level by an appropriate and easily simulated model chosen for the study area provide a prerequisite for recognition of the flow path along the crevices.

The fracture surface morphology must be taken into account when it comes to the three-dimensional simulation of joint fracture, three-dimensional stability analysis of rock mass mechanics, underground fluid flow field, and material migration path characteristics, to name a few. In the field, the shape of the fracture plane varies and it is usually difficult to directly observe the specific geometry of an intact fracture surface. Therefore, computer simulation of the fracture data is required; otherwise, it is almost impossible to completely display a fracture surface through computer visualizations. First of all, it is necessary to simplify the structural plane to a regular shape such as a circle, an ellipse, or a polygon. Then, the relatively accurate structural parameters could be obtained through the method of probability statistics and spatial analysis.

The studies on fracture models began in the 1960s. A deterministic orthogonal model was first proposed, but this model is imprecise due to the limited number of random parameters and the assumption that the fracture is unbounded (Snow 1965). Bounded fracture models were later proposed, for instance, the three-dimensional seepage model of a disk fracture network by Long (Long et al. 1985), polygonal fracture network model by Dershowitz, Poisson plane model, and Mosaic board model by Einstein (Dershowitz and Einstein 1988). At present, researchers have been attaching importance to the uncertainty of the fracture surface and using probability modeling to simulate the fracture properties, such as its shape, length, and trace length, to name a few. As a result, the Monte Carlo method is widely used in karst fracture models gradually, bringing the method from pure mathematical analysis to practical application.

Studies show that fractures have a tendency to form a circular shape, and the real shape of a fracture is probably a rough oval (Baecher 1977). There is also evidence showing that the space length of a fracture along the strike direction is basically similar to that along dip direction (Robertson 1970). The disk model has its own unique advantages regarding construction of the fracture network in the study area (Zhangfang, Fangshan district in Beijing). Firstly, the fractures in this area are close to a disk shape. Secondly, the disk model can clearly display the fracture parameters. In other words, the center of the disk represents the location of the fracture in space and the radius of the disk indicates the size of the fracture. The length of the tangent line between the disk and the surface is the trace length, and the occurrence of the fracture can also be represented by the underground distribution of disks. Finally, the disk model is easy to simulate with a computer, thus reducing complexity.

Figure 1 shows the structural planes of fracture represented by disks, where the center of the disk is the location of the fracture; the radius of the disk is equal to that of the fracture; and the distribution direction in the underground space represents the occurrence.

Fig. 1
figure 1

Disk model

Full size image

At present, the disk fracture network model is most widely used to study karst fractures. Although fractures generally diverge from a circular shape when they expand to the boundary (e.g., ground surface, lithologic interface, etc.), this does not have a serious impact on the application of the disk model because the model puts emphasis on the entire fracture, ignoring the local deformation.

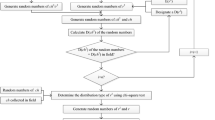
Many assumptions must be made in advance for a computer simulation due to the limitations to computer operation and display, measuring techniques and conditions, and differences in the development of the fracture structure in space. According to previous research results on karst fractures in Zhangfang, Fangshan district in Beijing (Dong et al. 2014; Qiao et al. 2014), the disk model was used to carry out a generalized simulation of the structural plane of fractures based on the merits of the disk model compared to the other fracture models. That is to say, fractures in the rock mass are assumed to be thin disk-shaped, and its growth level and spatial distribution are represented by the disk radius and occurrence.

Each fracture in the disk model is regarded as a thin space disk. The required data to three-dimensionally visualize fractures is stored in a database, which mainly include the center coordinates O(x, y, z) of the fracture disk, disk occurrence (α, β; where α means direction and β dip angle), disk radius R, and fracture density ρ. These parameters are shown in Fig. 2. Dip and dip angle are the primary elements of the occurrence of fractures. The dip indicates the inclination of the fracture surface and the dip angle indicates the degree of inclination. The parameters (α, β) need to be transformed into polar coordinates (θ, φ) when drawing a fracture disk. The corresponding relationship is shown in Eq. (1).

Fig. 2
figure 2

All parameters in the disk model (n is the normal vector)

Full size image

A simulation of a three-dimensional fracture network produces many intersecting thin circular disks with different sizes and orientations on three-dimensional space level. As it is impossible to directly measure all of the intact fracture planes, some properties of fractures are determined by probability distributions chosen, which include logarithmic normal distribution, uniform distribution, Fisher distribution, exponential distribution, and gamma distribution. After knowing the types of possible probability distributions for geometric parameters of the fracture system, random sampling by the Monte Carlo method is used to obtain the geometrical parameters to form a concrete fracture network. Consequently, a specific fracture network which has statistical hydraulic equivalence with the actual rock mass is generated in the study area.

Theoretically speaking, the combination of structural surface simulation and computer graphic technology can visualize the geological structure. Although many scholars have conducted a large amount of researches on 3D modeling of rock mass structures, these models are still not systematic or mature because the structural surface exists in the interior of the rock mass, indicating that measurements on the geometric parameters of the joint can only be taken in the area where bedrock is exposed. Therefore, local geometry parameters of joint were collected and used to construct an image of the joint network.

Based on the original data, Kriging interpolation was used to obtain surface fracture data for the entire karst area prior to the process and reconstruction by 3D simulation because in reality, the entire study field could not be sufficiently covered by sampling. As for underground data, the Monte Carlo method was used to simulate about 10,000 pieces of fracture data 500 m from surface down to underground. Afterwards, a seepage network can be built with a water flow path recognition algorithm.

$$ {\displaystyle \begin{array}{l}\phi =\frac{\pi }{2}-\alpha, \alpha \le \frac{\pi }{2}\\ {}\phi =2.5\pi -\alpha, \alpha \ge \frac{\pi }{2}\\ {}\theta =\beta \end{array}} $$
(1)

Optimization of fracture intersection judgment

Intersection judgment between two fractures

In the study of fluid flow in fractured rock masses, the mutual positional relationship of the fractures determines the continuity of fluid flow. The amount of seepage calculation exponentially increases with the number of fracture plane increases. As the number of fractures in nature is huge, when the number reaches hundred thousand levels, the corresponding seepage calculation is very time-consuming. However, the disjoint fractures do not contribute to the seepage and only the intersecting fractures draw our attention, meaning that the efficiency of the seepage calculation can be improved by retaining the intersecting cracks and eliminating the isolated fractures. Thus, fracture intersection judgment is the basis of seepage calculations.

To simplify the question, the intersection algorithm of two fracture disks is considered in this paper, Fig. 3 shows the sketch map of two intersecting fractures. In order to judge whether disks 1 and 2 are intersected in the space, assuming the geometric parameters of disk 1 and 2 as follows: the center coordinates of disk 1 is (X1, Y1, Z1), dip angle α1, dip β1, radius r1 and the center coordinates of disk 2 is (X2, Y2, Z2), dip angle α2, dip β2, radius r2. The plane of the fracture disk can be described as eq. (2).

$$ \mathrm{a}X+ bY+ cZ+\mathrm{d}=0 $$
(2)
Fig. 3
figure 3

Sketch map of two intersecting fractures

Full size image

where

a = sin α × sin β; b = sin α × cos β; c = cos α; d =  − (aX + bY + cZ).

So, the plane of two fracture disks in Fig. 3 can be expressed as formula (3).

$$ \Big\{{\displaystyle \begin{array}{c}{a}_1X+{b}_1Y+{c}_1Z+{d}_1=0\\ {}{a}_2X+{b}_2Y+{c}_2Z+{d}_2=0\end{array}} $$
(3)

The angle θ between two disk planes can be expressed by formula (4).

$$ \cos \theta =\frac{a_1{a}_2+{b}_1{b}_2+{c}_1{c}_2}{\sqrt{\left({a_1}^2+{b_1}^2+{c_1}^2\right)\left({a_2}^2+{b_2}^2+{c_2}^2\right)}} $$
(4)

When θ ≠ 0, the intersection of the plane can be calculated.

The distance from the center point of the disk to intersection line can be obtained by formula (5).

$$ {D}_i=\sqrt{\frac{{\left(\left({y}_i-{y}_0\right)p-\left({z}_i-{z}_0\right)n\right)}^2+{\left(\left({z}_i-{z}_0\right)m-\left({x}_i-{x}_0\right)p\right)}^2+{\left(\left({x}_i-{x}_0\right)n-\left({y}_i-{y}_0\right)m\right)}^2}{m^2+{n}^2+{p}^2}} $$
(5)

where x0, y0, z0 is any point in the intersection line, m, n, p is the direction vector of the intersection line, which can be represented as formula (6).

$$ \Big\{{\displaystyle \begin{array}{c}m={b}_1{c}_2-{b}_2{c}_1\\ {}n={a}_2{c}_1-{a}_1{c}_2\\ {}p={a}_1{b}_2-{a}_2{b}_1\end{array}} $$
(6)

According to the knowledge on analytic geometry, the two disks are not intersected if D1 + D2 > r1 + r2. Otherwise, the relationship between distance from the center point of two disks to the intersection line D1, D2 and their radius r1, r2 should be judged separately. The two disks are intersected only if D1 < r1and D2 < r2.

Highly efficient fracture intersection judgment method

Partition algorithm can further improve the seepage calculation efficiency. At present, the basic mechanism behind the commonly used partition algorithm is to reduce the size of the map and break it into parts. The purpose of a sub-block in this case is to reduce the number of fractures in every operation and speed up computation through batch processing, i.e., the unconnected graphs are artificially divided in space to reduce the value of n, which is the number of fractures in a sub-block. A study area is divided into several blocks, and the number of center points contained in a block is the size of a block. Although the computation time increases due to partitioning and splicing of the graph, the complexity of the original problem can be greatly reduced. However, because of the different structure of fractures, it is not possible to determine which block the intersection between fractures located at the boundary of two blocks belongs to during an actual calculation. The space can be divided into three-dimensional space, or it can be divided along one direction. Different block schemes have different impacts on the results of the algorithm, as shown in Fig. 4.

Fig. 4
figure 4

Intersection evaluation in different block schemes. a Block division in three directions. b Block division in one direction

Full size image

The partitioning relies on parallel computation, i.e., the entire model is broken into sub-blocks and the largest calculation time among all blocks is taken as the time complexity. Moreover, a blocking method is usually combined with the other optimization algorithms like axial bounding box algorithm which will be introduced in detail in “Simplification of path traversal”, because intersections between fracture disks also need determining in each individual block. The time complexity of the algorithm is O(n2) if the method of exhaustion is used in a sub-block, and the time complexity is O(n) if the axial bounding box algorithm is used in a sub-block. If the method of exhaustion and the axial bounding box algorithm are used in a sub-block, then the time complexity of the entire algorithm is max(O(n2), O(n)).

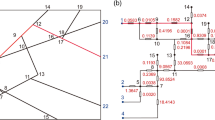
Another algorithm is the R-tree algorithm. R-tree is a type of highly balanced tree which is a natural expansion of a B-tree in K-dimensions. It uses a minimum bounding rectangle (MBR) to approximately represent an object in space. The object occupying a certain volume in space can be directly indexed with the R-tree algorithm based on the object’s MBR. The R-tree index algorithm can effectively exclude isolated fractures and quickly determine the set of fractures that may intersect to further evaluate intersections. In principle, the R-tree index algorithm is a type of combination of the axial bounding box algorithm and the block algorithm.

Figure 5a, b shows schematic of the fracture disk bounding box distribution in space and the corresponding R-tree graph. Each node in the R-tree index structure is a fracture disk corresponding to an MBR. All non-leaf nodes are MBRs of its child node. The R-tree index generally traverses down from the root node layer by layer and can quickly exclude features that do not meet the screening requirements and reduce unnecessary calculation. The time complexity of the R-tree index algorithm is O (log2n), which is greatly reduced compared with the blocking and axial bounding box algorithms. Especially when the amount of fracture data is huge, the R-tree indexing algorithm will greatly accelerate execution of the program.

Fig. 5
figure 5

a Fracture disk bounding box distribution in space. b R-tree corresponding to a

Full size image

Seepage identification of water flow along the fractures

After acquiring surface fracture data by Kriging interpolation and the underground fracture data with the Monte Carlo method, the fast intersecting algorithm was used to judge whether the two fracture surfaces intersect and a karst fracture seepage simulation based on the fast intersecting algorithm was applied to dynamically simulate groundwater flow direction and directly describe the distribution of underground fractures. In the data structure, a large-scale fracture network can be expanded to an unconnected graph in which each crevice point (center of circle) is the vertex of the graph, and the seepage path is the edge of the graph. Considering the groundwater flow direction, a directed graph can be used to simulate the entire underground fracture network.

Directed graphs to identify and store fractured networks

The arrow between two connecting fractures is the water flow path, as shown in Fig. 6. In the data structure, the directed graph is stored and traversed with an adjacency matrix or adjacency list. The connecting path between the fractures is shown in Fig. 7, and the lines between adjacent disks in the diagram indicate that adjacent disks are connected.

Fig. 6
figure 6

Underground fracture network generalized as a directed graph

Full size image
Fig. 7
figure 7

Centers of intersecting disks acting as path nodes

Full size image

The adjacency matrix represents adjacency between vertices. Supposing G = (v, e) is a graph, where v = {v1, v2,..., vn}. The connectivity between nodes can be stored in a two-dimensional array, which is the adjacency matrix. The length of each row (or each column) of the adjacency matrix is the number of vertices in the graph. Figure 8 shows a directed graph. According to the definition of the adjacency matrix, an adjacency matrix is created for this directed graph using Eq. (7).

Fig. 8
figure 8

Directed graph

Full size image

For two connecting vertices in the directed graph, the vertex where the arrow starts is the starting point, and the vertex pointed by the arrow is the ending point. Each position in the adjacency matrix indicates whether or not two vertices at that position are connected. For example, A, B, C, D, and E in Fig. 8 denote vertices; a, b, c, d, e, f, g, and h denote paths. There is a path between C and D, so 1 is placed at CD in the corresponding adjacency matrix. In contrast, there is no path between B and A, so 0 is stored at BA in the adjacency matrix. The adjacency matrix is stored in a linear table structure.

$$ {\displaystyle \begin{array}{l}\kern0.5em A\kern0.5em B\kern0.5em C\kern0.5em D\kern0.5em E\\ {}\begin{array}{c}A\\ {}B\\ {}C\\ {}D\\ {}E\end{array}\left\{\begin{array}{ccccc}0& 1& 1& 0& 0\\ {}0& 0& 0& 0& 1\\ {}0& 1& 0& 1& 0\\ {}0& 1& 0& 0& 0\\ {}1& 0& 1& 0& 0\end{array}\right\}\end{array}}. $$
(7)

The seepage path for fractures can also be stored in a form of an adjacency list, which is a single linked list. Although the application of an adjacency list can save storage space and is more convenient for basic graph operations such as adding and deleting vertices, the adjacency matrix is used to store the directed graph because the edge table relationship is involved in the adjacency list structure, which is not known in the system and can be a barrier to the usefulness of the subsequent algorithm.

According to the fast intersection algorithm for fractures, the intersected fractures are used to build paths between vertices in a directed graph. And based on the knowledge on hydromechanics, the fluid flows from high hydraulic head to low hydraulic head, determining the flow direction in networks. Intersection of fractures is evaluated and the results of judgment are stored in the adjacency matrix. If two fractures intersect, the hydraulic heads of the fractures are compared and the number “1” is placed at the position where vertex corresponding to fractures with higher hydraulic head and fractures with a lower one intersect in the adjacency matrix. After building the adjacency matrix, a seepage path is formed by connecting the two fractures with a value of 1 in the adjacency matrix.

Simplification of path traversal

During simulation of the seepage paths, there are more likely to have tens of thousands of fracture data records sampled in the field, not to speak of the random fracture data generated with Kriging interpolation and Monte Carlo stochastic simulation. Evaluating whether these fractures intersect with each other requires a considerable amount of time and consumes all available computer memory in an ordinary computer. Therefore, simplifying the calculation process can greatly improve the efficiency of the computer.

The fracture disk is intricate. There are many types of intersecting morphologies of fracture disks, including the existence of isolated fractures which do not intersect with other fractures. Isolated fractures are involved in the intersection evaluation process prior to seepage path identification algorithms. That is to say, if the number of fracture data is assumed to be n, there will be n-1 invalid operations for each isolated fracture, which means that the temporal and spatial complexity of the entire fracture recognition algorithm will increase by a power of 2 if the number of isolated fractures becomes large. In conclusion, the main measure for simplifying the seepage path and reduce the calculation of the intersection of fracture disks is to exclude isolated fractures as much as possible.

The method of exhaustion is the most direct intersection evaluation algorithm. Assuming that the number of fractures is n, the number of judgments to be performed is n2, and the time complexity is O(n2), which means that if the number of fractures is huge, the processing time of the computer can be tens of hours, or even days. Figure 9a shows the method of exhaustion for evaluating intersections. As a result, the most commonly used algorithm in 3D geology appears, which is referred to as the axial bounding box algorithm. The axial bounding box algorithm is considered a rough intersection evaluation algorithm. Each fracture disk has a minimum axial bounding box, i.e., their smallest external cube. If two fracture disks intersect, their minimum axial bounding boxes must intersect. The axial bounding box intersection evaluation algorithm is shown in Fig. 9b. The minimum axial bounding box algorithm can be used as an optimization algorithm to judge intersection because it is easier to determine the intersection of bounding boxes than to directly determine the intersection of fracture disks, thus reducing the calculation time. The time complexity of bounding box is O(n).

Fig. 9
figure 9

Evaluating intersections using axis-aligned bounding boxes

Full size image

Simulation of seepage water flow

In the graph structure, the center of fracture is represented as the vertex of the graph, and the seepage path is the edge of the graph. As shown in Fig. 10, the lines between the two intersecting fractures are the seepage paths.

Fig. 10
figure 10

Generalized underground fracture network as a directed graph

Full size image

Take the length of each fracture segment lj(j = 1,2, …,m) in the fracture network as the weight of the seepage flow in the fracture network, and the m-order diagonal matrix D represents the adjacency matrix of the weighted fracture network.

$$ D=\left[\begin{array}{c}\begin{array}{ccc}{l}_1& 0& \dots \\ {}0& {l}_2& \dots \\ {}\dots & \dots & \dots \end{array}\\ {}\begin{array}{ccc}0& 0& \dots \end{array}\end{array}\kern0.5em \begin{array}{c}\begin{array}{c}0\\ {}0\\ {}\dots \end{array}\\ {}{l}_m\end{array}\right] $$

Based on the fracture network model, the seepage velocity of each fracture segment is

$$ v=K\ast {D}^{-1}\ast {M}^T\ast \Delta H $$
(8)

where K represents the hydraulic conductivity, ∆H is the hydraulic-head difference between two points, and M is the adjacency matrix shown in eq. (7).

In addition to the hydraulic conductivity K, the seepage simulation also requires the use of water flow q, flow velocity v, permeability k, and permeability coefficient tensor \( \overrightarrow{k} \).

The hydraulic conductivity is an important hydrogeological parameter. In isotropic media, the value of K which is a scalar and independent of the direction of the percolation is defined as the unit flow rate per unit hydraulic gradient, indicating how easy the fluid passes through the porous media. The K value depends not only on the properties of the rock (i.e., particle size, texture, particle arrangement, filling condition, and development degree, etc.), but also on the physical properties (i.e., capacity, viscosity, etc.) of the osmotic liquid. Theoretical analysis shows that the size of the void plays a major role in the K value. Permeability is the penetration rate of a liquid in media with a dynamic viscosity coefficient of 1 and the pressure gradient of 1. However, in anisotropic media where the direction of the percolation is arbitrary, the K value is related to the direction of seepage. Since the hydraulic gradient disagrees with the seepage direction, a permeability coefficient tensor is introduced.

The methods to obtain these parameters mainly include in situ hydraulic experiments, fracture geometry measurement, and the numerical inversion of seepage in discrete fracture networks. This article uses the second method.

The hydraulic conductivity of fractures with width b can be obtained by

$$ {K}_f=\frac{\rho g}{12\mu }{b}^2{\left(\cos a\right)}^2=\frac{g}{12{v}_w}{b}^2{\left(\cos a\right)}^2 $$
(9)

And the flow volume is

$$ {q}_f={v}_f\ast b=\frac{g{b}^3}{12{v}_w}J $$
(10)

Flow velocity

$$ v= KJ $$
(11)

Permeability coefficient

$$ {k}_{ff}=\frac{b^2}{12}{\left(\cos a\right)}^2 $$
(12)

From above equations, the relation between K and permeability coefficient(k) is

$$ K=\frac{\rho g}{\mu }k=\frac{g}{v_w}k $$
(13)

In this paper, the Cartesian coordinate system is used, and the permeability coefficient tensor \( \overrightarrow{k} \) is set up based on the flow movement in a single fracture:

$$ \overrightarrow{K}=\left[\begin{array}{ccc}{k}_{xx}& {k}_{xy}& {k}_{xz}\\ {}{k}_{yx}& {k}_{yy}& {k}_{yz}\\ {}{k}_{zx}& {k}_{zy}& {k}_{zz}\end{array}\right] $$
$$ ={K}_e\left[\begin{array}{ccc}1-{\left(\cos \beta \sin \gamma \right)}^2& -\sin \beta \cos \beta {\left(\sin \gamma \right)}^2& -\cos \beta \sin \gamma \cos \gamma \\ {}-\sin \beta \cos \beta {\left(\sin \gamma \right)}^2& 1-{\left(\sin \beta \sin \gamma \right)}^2& -\sin \beta \sin \gamma \cos \gamma \\ {}-\cos \beta \sin \gamma \cos \gamma & -\sin \beta \sin \gamma \cos \gamma & 1-\cos {\gamma}^2\end{array}\right] $$
(14)

For the above equations, μ is the dynamic viscosity coefficient, J is the hydraulic gradient, vw is the viscosity coefficient for water, g is the gravity acceleration, a is the angle of fracture and water flow direction, b is the fracture width, ρ is density, β is the dip, and γ is the dip angle.

Case study of the algorithm

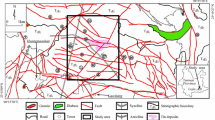
The karst area in Zhangfang, Fangshan district in Beijing, is a typical representative of northern karst, and fracture data was systematically collected to provide a reliable basis for accurately constructing the fracture network model and evaluating karst development. A total number of 2069 sets of joint data were obtained during field survey. Most fractures in the karst area are classified as joints, and the acquired joint data are assumed to give a comprehensive description of the properties of the fracture. These data include spatial attributes such as joint name, rock characteristics, dip, dip angle, frequency, silt width, extension length, latitude, and longitude. Surface fracture data covering the entire study area were obtained by interpolation. By comparison, data generated from Kriging interpolation highly coincide with the measured data. After that, the Monte Carlo method was used to extend the fracture data from surface into the ground to form a complete spatial distribution of the fracture in the karst area.

Zhangfang and its periphery area of Fangshan district in Beijing were chosen as the study area. The Zhangfang karst-water distributed area, as one of the seven karst distribution areas in Beijing, is a relatively independent hydrogeological unit. The study area is shown in Fig. 11 is about 20,000 m * 12,000 m and the karst fractures distribute from surface to 500 m underground. The processed remote sensing image from this area was used as the base map, where the yellow line denotes the fault zone, the blue part on the left being the lamprophyre vein, and the purple part on the right being the monzogranite vein. The surface fracture data was obtained mainly by fine outcrop exploration in the study area. The red part in Fig. 11 is the sampling routes, where the parameters of fractures such as the direction, dip, dip angle, width, length, and development density were sampled every 5 m. In total, more than 8000 sets of fracture data were measured.

Fig. 11
figure 11

Simulation map of the study area (with remote sensing base map)

Full size image

Interpolation of surface fractures

After sampling, the fractures on the surface can be interpolated by a quadrat based on Kriging method. In terms of the idea of quadrat, this paper proposed a fracture quadrat model dividing the study area into grid cells with specific size, as shown in Fig. 12. Fracture data statistics were carried out for each single grid cell. The cell was set up to null if no fractures were observed, otherwise the fracture data in the cell was counted. The statistical method was consistent with the method of drawing the fracture-density-rose diagram: The sampled data of fracture occurrence and density were grouped by spatial azimuth interval (such as 5° or 10°), and statistical information (i.e., the number of fractures, average dip, average width, and length) of each group was summarized. In this way, each grid cell containing the fracture data corresponds to a rose chart and this grid cell can be used as a known point to interpolate the other grid cells in the unknown area.

Fig. 12
figure 12

Quadrat model of fractures data and its statistics

Full size image

In the interpolation, each direction group in the fracture-rose-chart can be interpolated individually and sequentially, and statistic information mentioned above was used. Thus, the fracture-rose-charts for each of the other grid cells can be obtained by Kriging interpolation. The interpolated rose diagram is shown in Fig. 13.

Fig. 13
figure 13

Spatial distribution of surface joints

Full size image

Simulation of underground fractures

This paper assumes that uncertainty exists in the karst underground space. In the modeling process, only the original measured data of the outcrops near the surface and the interpolated surface fracture data were utilized. There is evidence showing that there is a spatial correlation between fractures in the underground space. The fact that the fractures are not independent, but have a certain spatial relation with each other provides a possibility for speculating underground fractures from surface data. This paper took the feature of dip angle as an example to illustrate the property simulation for the subsurface fracture. In this paper, the known geoscience knowledge, statistical methods and engineering experience can be regarded as the prior knowledge to speculate underground fracture data. The combination of prior knowledge with the measured data was achieved by the Bayesian theory and the problem of sampling fractures with spatial variability was solved by the Markov chain and Monte Carlo method.

The distribution of the dip angle of the underground fractures satisfies the normal distribution and the probability density function is

$$ f(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma}^2}}\kern1.25em -\infty <\mathrm{x}<\infty $$
(15)

where μ and σ are the expectation and the standard deviation of the dip, respectively, of which a rough estimate of the range can be given by the priori knowledge. For example, the expectation and standard deviation of the dip can be roughly estimated by the fracture-rose diagram.

There are many combinations of μ and σ, and each combination is possible. According to the maximum entropy theory, the more the uncertainty is retained in the probability model, the better the model will be. Given the a priori knowledge and the field data, from the total probability theorem, the probability of dip is

$$ {\displaystyle \begin{array}{l}P\left( dip| prior, test\right)=\\ {}{\int}_{\mu, \sigma }P\left( dip|\mu, \sigma \right)P\left(\mu, \sigma | prior, test\right) d\mu d\sigma \end{array}} $$
(16)

where P(dip| μ, σ) is the probability density distribution of the dip given a set of μ and σ. Since it conforms to the normal distribution, it can be expressed by the formula (1). P(μ, σ| prior, test) indicates the probability density distribution of μ and σ under the conditions of prior knowledge and measured data.

In statistics, the joint probability distribution of an event is equal to the product of the conditional probability and the marginal probability. Assume event A, B, event A represents the ground-truth probability distribution of model C, and event B represents the probability distribution obtained from measured data, then there is:

$$ P\left(A,B\right)=P\left(A|B\right)\ast P(B)=P\left(B|A\right)\ast P(A) $$
(17)

Thus:

$$ P\left(A|B\right)=P\left(B|A\right)\ast P(A)/P(B) $$
(18)

Since event B is the probability distribution of event C obtained through field observation, the marginal probability P(B) of event B is a fixed value, then there is

$$ P\left(A|B\right)\propto P\left(B|A\right)\ast P(A) $$
(19)

where P(A| B) is the posterior probability distribution of the model C, that is, the original probability distribution of the model C given the observation value; P(A) is the prior distribution of model C; P(B| A) is the likelihood distribution.

Thus:

$$ {\displaystyle \begin{array}{l}P\left(\mu, \sigma | prior, test\right)=\\ {} KP\left( prior, test|\mu, \sigma \right)P\left(\mu, \sigma \right)\end{array}} $$
(20)

where \( K=\frac{1}{\int_{\mu, \sigma }P\left( prior, test|\mu, \sigma \right)P\left(\mu, \sigma \right) d\mu d\sigma} \)is the constant。.

P(μ, σ) is the distribution probability without any measured data, that is, the prior probability distribution, or the joint probability distribution of μ and σ. This paper assumes that μ and σ conform to uniform joint distribution, and the probability distribution is

$$ P\left(\mu, \sigma \right)=\frac{1}{\left({\mu}_{\mathrm{max}}-{\mu}_{\mathrm{min}}\right)\left({\sigma}_{\mathrm{max}}-{\sigma}_{\mathrm{min}}\right)}\kern0.5em \mu \in \left[{\mu}_{\mathrm{min}},{\mu}_{\mathrm{max}}\right],\sigma \in \left[{\sigma}_{\mathrm{min}},{\sigma}_{\mathrm{max}}\right] $$
(21)

Therefore, P(μ, σ) can be calculated by obtaining the range of μ and σ based on priori knowledge.

P(prior, test| μ, σ) is the likelihood probability which can be obtained by maximum likelihood estimation. The maximum likelihood method argues that if only one test is performed and the result A occurs, the condition is considered to be favorable for the result A. This paper assumes that each fracture sample is independent, and its likelihood probability is consistent with:

$$ L\left(\theta \right)=L\left({x}_1,...{x}_n;\theta \right)=\prod \limits_{i=1}^nf\left({x}_i;\theta \right)\kern0.5em \theta \in \varTheta $$
(22)

where θ is the parameter to be estimated, Θ is the range of possible values of θ, x1, x2, …  … ,xn are sample values of events X1, X2, …  … ,Xn, \( \prod \limits_{i=1}^nf\left({x}_i;\theta \right) \) is the joint probability distribution when events X1, X2, …  … ,Xn takes value x1, x2, …  … ,xn, f(xi; θ) is the probability density function, i.e., P(dip| μ, σ) in this case. Finally, P(dip| prior, test) is specified.

To simulate the unknown properties of underground fractures from the measured fracture data, a random sampling based on the posterior probability distribution of the underground fracture is required. Since the process of generating random numbers by computer, which depends on certain algorithms, is not a random process in the actual sense, the generated random number is a pseudo-random number. And the Monte Carlo method is an important method to generate such a pseudo-random number.

In geostatistics, there is a correlation between fractures of which the spatial distribution exhibits inhomogeneity and complexity and conforms to certain spatial variability characteristics. That is to say, the properties between the fractures are mutually related. Monte Carlo random sampling based on Markov chain provides an effective way to deal with the complexity in sampling. The core idea is to construct a Markov chain in the initial state space, of which the stable distribution is the probability distribution of the target, and then transfer the current state to the next state by the state transition function (the next state only related to the current state). After a period of sampling, the probability distribution is approached to the distribution of target in the real situation, and the sample from this probability distribution is finally selected (Zhao 2014).

The fracture data is sampled based on the Gibbs sampling algorithm. Assuming that the k-dimensional sample spacex = (x1(0), x2(0), ……, xn(0)), and the probability distribution of its initial state is π(x1(0), x2(0), …  … , xn(0)). Then, according to the conditional transition probability P(xk + 1| x1(0), x2(0), ……, xk(0)), the (k + 1) th value is obtained, which is denoted as xk + 1(1). The (k + 2) th value, which is denoted as xk + 2(1), can also be obtained by the conditional transition probability P(xk + 2| x1(0), x2(0), ……, xk(0), xk + 1(1)) and repeating this process. According to the law of large numbers, when the number of samples is large enough, the probability distribution of the sample approximates the target distribution under real conditions (Li 2008).

The spatial distribution map of the speculated underground joints is shown in Fig. 14.

Fig. 14
figure 14

Underground fractured joint spatial distribution

Full size image

Results

Open Scene Graph (OSG) was used to construct the “karst fracture simulation system”. Terrain data was loaded as the base map in “Karst fracture simulation system of Zhangfang, Fangshan district in Beijing” as shown in Figs. 15 and 16. The number of fractures generated with the Monte Carlo simulation was around 65,000.

Fig. 15
figure 15

The simulation of the fracture in the whole study area

Full size image
Fig. 16
figure 16

Local fracture map

Full size image

Moreover, the efficiency of the algorithm proposed in this paper, R-tree index algorithm combined with the optimization of block algorithm, is compared with the exhaust algorithm and the R-tree index algorithm in terms of operation time. Figure 17 shows the result of different algorithms, where A represents exhaust algorithm; B represents R-tree index algorithm; C represents the optimized algorithm combining the R-tree index algorithm with block algorithm. The efficiency of C is higher than other two algorithms obviously.

Fig. 17
figure 17

Result on efficiency of different algorithms

Full size image

A dynamic flow direction diagram can be obtained by evaluating fracture intersections and the seepage flow path (Figs. 18 and 19). The arrows in the figure are dynamically updated by the callback function in OSG. The position of the arrow indicates the position of the fluid, and the direction of the arrow indicates the fluid flow direction.

Fig. 18
figure 18

Dynamic groundwater flow path in the fracture network

Full size image
Fig. 19
figure 19

Local map of the dynamic groundwater flow path in the fracture network

Full size image

Conclusions

Seepage simulations are an important aspect in the study of three-dimensional underground fractures and their permeability. Choosing a suitable fracture model is a prerequisite for accurately simulating the groundwater seepage field under different geological conditions.

From the seepage simulation results, the following conclusions can be drawn:

(1) In this paper, the disk model was used to simulate the fracture planes due to its simplicity and efficient evaluation of fracture intersections. However, this does not mean this model is better than the others. Nowadays, researches on the construction of a fracture plane have been more and more complicated. But in computer simulation, the convenience of the disk model makes the disk model more applicable to large study area and large amount of data.

(2) The fast intersection evaluation algorithm in this paper is based on the disk model and the associated optimization algorithm aims at rapidly evaluating intersections. The “karst fracture simulation system” was implemented and tested. The number of isolated fractures is large and most fractures were randomly simulated with the Monte Carlo algorithm. Therefore, the removal of isolated fractures and reduction of unnecessary intersections can greatly improve the efficiency of the system. When the boundary problem is neglected, optimization of the block algorithm can also assist with implementation of the R-tree algorithm.