1 Introduction

The uniaxial compression test is by far the most common experimental procedure for the mechanical characterization of those materials, such as rock, concrete or cohesive soil, usually called brittle or quasi-brittle. A common feature to this class is that, in general, the strength under uniaxial compression is much higher than under tension, so that accepted in modeling is to neglect their tensile resistance [1]. Since such an idealized response has been traditionally used for masonry works [2], a considerable part of the technical literature refers to the solids for which such a schematization is plausible as masonry-like materials [3]. The propagation of brittle fractures under compression in masonry-like solids has been the subject of a deep research for at least the last two centuries, but some fundamental aspects still remain unclear. The technical literature is so wide that it is practically impossible to present a reasonably complete summary of existing typical models (an excellent, though partial, review can be found in [4]). Consequently, the following considerations irremediably reflect a personal viewpoint, useful just to introduce our work.

Since the original work by Föppl et al. [5], it has been realized that end-confinement due to frictional contact of the loading-machine platens may substantially influence the strength and failure mode of compressed specimens [6]. If platens are lubricated [7], so that friction is avoided, the observed failure mode is the one usually named axial splitting [8], i.e., specimens fail under the formation of a perplex of fractures oriented in the axial direction crossing the specimen from one end to the other, as schematically represented in Fig. 1a. On the other hand, the result of end-confinement is to isolate conical or pyramidal sound material portions at the specimen bases (Fig. 1b), that define the classical hourglass shape. Such rupture has been observed in many materials: here we just mention the somehow unusual experiments on specimens made of ice [9], which are particularly interesting because of the transparency of the material. It is often understood that such portions are bounded by shear-induced inclined fracture surfaces, considered not only a consequence of end-restraint but a fundamental form of failure [10]; according to this rationale, it is their wedging action that possibly provokes the subsequent axial splitting in the central portion of the specimen. An alternative interpretation, first advanced in [11] to our knowledge, is that no shear occurs in uniaxial compression [12], being the so-called shear failure a secondary development, which occurs after the vertical splitting has begun. Consequently, the mechanism of initial cracking and ultimate failure may be different, but are not completely independent (this will be confirmed by our modeling).

Fig. 1
figure 1

Failure modes of quasi-brittle materials under compression: a axial splitting under lubricated loading platens; b formation of wedge-shaped portions at the bases due to frictional contact of dry platens

Full size image

The idea that uniaxially compressed specimens collapse following a dominant inclined fracture plane is historically attributed to Coulomb [13]. Later on, Mohr suggested [5] that materials fail under the combined action of shear and normal stress along characteristic planes and, according to this idea, it is friction induced by dry loading platens to be responsible of the observed inclined failure surfaces at the bases (notice here that we have used the term “failure” and not “fracture”, for reasons that will be clarified later on). However, by no means Mohr’s theory can account for axial-splitting failure-mode under frictionless lubricated platens, because any conceivable envelope of Mohr’s cycles in Mohr’s plane (σ, τ) would predict failure along some inclined set of surfaces, in which the critical combination of shear and normal stress is attained.

Indeed, any classical theory of strength based upon a macroscopic analysis of the state of stress would inevitably fail in the interpretation of axial-splitting failure. For example, resorting to De Saint Venant’s tensile-strain failure-criterion would result equally ineffective, because the observed lateral tensile strain at failure under compression is, as a rule, one order of magnitude higher than the axial strain at failure under direct uniaxial tension [14]. One may consider Galileo-Rankine’s maximum-stress failure-criterion, but axial-splitting would again lead to conceptual difficulties, because cracks would appear to propagate under the application of a null macroscopic stress normal to their plane.

In order to account for tensile stresses where splitting fractures occurs, one has to conceptually accept the presence of microscopic defects like cracks, inclusions, grain boundaries etc., whose effect in terms of stress is substantial, although it averages out to zero for planes parallel to the axis of compressed specimens. A number of different in kind models exists in this field. A famous one is that based upon the extension of an inclined crack [15], but it can be verified that the crack-tip driving force quickly diminishes when crack propagates, especially in the presence of frictional resistance between crack surfaces. Other models consider the presence of inclusions or heterogeneities [16]. A common feature to such models is that, in general, the defect is supposed to be isolated in a homogenous matrix, because evaluating the energy release rate in the complicated stress field of a microstructurally heterogeneous solids is hopelessly complicated. Other effective approaches consist in pseudo non-local continuum theories of fracture, such as that accounting for stress diffusion proposed in [17].

Here, we consider the problem of splitting failure of compressed cylinders by using a regularized variational model of fracture mechanics that accords to compressive fracture an energetic interpretation. As already remarked in the elegant approach of [18], the solid splits because in doing so it lowers the global energy by isolating independent load-bearing microscopic material columns. The driving force for this is due to the presence of heterogeneities, that are here included as elastic inclusions much stiffer than the surrounding matrix.

The model at hand has been recently proposed in [19] and consists in the minimization of a two-field pseudo-spatial dependent functional with a structure similar to that originally proposed by Bourdin et al. in [20], that translates to the case of fracture-mechanics the \(\Upgamma\)—convergence result of Ambrosio and Tortorelli [21] for the regularization of the Mumford-Shah functional. The model takes a smeared view of the effects of fractures by assuming that their gross consequence is associated with a positive-semidefinite strain component of the (average) strain in the representative volume element, to account for the fact that only inelastic dilatations due to micro-crack openings are permitted. This case is consistent with the constitutive equations for a classical no-tension masonry-like material as discussed in [22], because one can verify that the associated stress tensor is negative semidefinite and co-axial with the strain component associated with cracking. However, the present approach is different from the classical no-tension theory because it is based upon the competition between bulk-energy release and surface-energy production due to the nucleation and/or progression of cracks: since a certain energy has to be consumed to nucleate cracks, fracture localization is energetically favorable. The model is numerically implemented using a standard finite-element discretization and adopts an alternate minimization algorithm, adding an inequality constraint to impose crack irreversibility (fixed crack model).

Using this rationale, the phenomenon of axial splitting can be conveniently reproduced. The model also predicts the formation of the wedge-like portions contiguous to confining dry loading platens, but furnishes for this phenomenon an alternative explanation to the classical one, according to which such portions are delimited by shear-fracture surfaces as mentioned at the beginning. Indeed, here the leading phenomenon for both cases of dry- and lubricated-platens is always axial splitting; the possible presence of friction induces a confinement that compresses the end-portions and prevents axial-cracks from reaching the specimen bases. In other words, according to our interpretation in agreement with the original idea of [11], axial splitting is not provoked by the wedging action of the conically-shaped end-portions (isolated by shear-fracture surfaces), but it is axial splitting that is arrested by the lateral confinement due to friction in proximity of the conical surface. No shear fracture is induced in this model: specimen failure is eventually provoked by the buckling of the material columns resulting from axial splitting, while the conical portions at the specimen bases remain sound in the post-peak response because they are not affected by cracks.

Numerical experiments have been performed for prismatic solids under fixed lateral confinement and increasing uniaxial tension or compression up to failure. This simple model explains that lateral confinement is in general beneficial because it tends to close the axial cracks. Moreover, in our interpretation there is no need to call for a theory à la Mohr, assuming a priori the dependence of the failure state upon a proper combination of shear and normal stress in the failure plane. Our model is minimal because the only material parameters that are required are the elastic moduli, the value of the fracture energy and a third parameter representative of the material intrinsic length scale [23]. Despite its simplicity, the model is capable of reproducing most part of classical resistance domains for confined materials, such as Kupfer’s for concrete under biaxial stress [24], with no need of establishing a phenomenological dichotomy between shear and cleavage fracture.

2 The variational approach to fracture in masonry-like materials

The model used here has already been presented in [19], but for the sake of completeness the main features are briefly recalled. Denoting with \({\mathcal{D}, {\mathcal{D}}= 2\div3}\), the dimension of the Euclidean space where the problem is set, let \({\Upomega \subset {{\mathbb R}}^{\mathcal{D}} }\) be the undistorted natural reference configuration of the body \(\mathcal{B}\) for which the reference frame \({\{O, x_1,\ldots, x_{\mathcal{D}}\}}\) has been defined by the orthogonal base of unit vectors \(\{{\bf e}_1,\ldots,{\bf e}_{\cal D}\}\). The mapping \({{\bf y} ({\bf x}): \Upomega \rightarrow {{\mathbb R}}^{\cal D}}\) define the deformation so that \({{\bf u} ({\bf x})={\bf y} ({\bf x})-{\bf x}: \Upomega \rightarrow {{\mathbb R}}^{\cal D}}\) is the displacement of x.

We suppose that under assigned boundary conditions the body may damage and fracture. The resulting deformation is characterized by two different kinematics: the opening of micro- or macro-cracks and the distortion of the elastically bent lamellae delimited by the crack surfaces (elastic part of the deformation). We consider a smeared view of the phenomenon so that the corresponding strain fields result continuous and regular in any representative volume element (RVE). Under the hypothesis of infinitesimal deformations, the global strain is the symmetric gradient of the displacement field

$$ \nabla^s {\bf u}=(\nabla {\bf u} + \nabla {\bf u}^T)/2 , $$
(2.1)

for which a decomposition is assumed in the form

$$ \nabla^s {{\bf u}} {({\bf x})}= {\bf E}_e {({\bf x})} +{\bf E}_s {({\bf x})}, $$
(2.2)

where E e represents the elastic part of the strain, whereas E s is the inelastic part of the strain, associated with the formation of micro-cracks. In the language of the broader framework of the Theory of Structured Deformations [25], E s is that part of the strain representing the structured part of the deformation. This is why, in the following, E s will be referred to as the structured strain.

Let us introduce an internal damage state variable \({s({\bf x}): \Upomega \rightarrow [0,1]\subset {{\mathbb R}}}\), which varies from 0 to 1 and takes the 1 value in the undamaged region and 0 in a completely disaggregated zoneFootnote 1. If E c (x) represents the structured strain that would develop in a neighborhood of the particle x if, here, the material was completely disaggregated, the significance of the variable s is defined by the relation

$$ {\bf E}_s {({\bf x})} = \left[1- s({\bf x}) \right] {\bf E}_c {({\bf x})}. $$
(2.3)

In fact, s = 0 ⇒ E s  = E c and s = 1 ⇒ E s  = 0, while if s takes an intermediate value it means that material microstructure is only partially loosened. Particular expressions of the field E c (x) characterize the response of different-in-type materials, because a completely damaged body is composed of pieces in unilateral contact whose kinematics depends upon the underlying microstructure.

The energy functional is composed of two terms: the bulk energy stored in the elastically bent material and the surface energy associated with the formation of fractures. Such functional generally depends upon the displacement field u(x), the damage field s(x) and E c , according to a general expression of the form

$$ \Uppi_l ({\bf{u}},s,{\bf E}_c) = \int\limits_\Upomega {\Uppsi(\nabla^s{\bf{u}},s,{\bf E}_c)d{\bf{x}}} + \int\limits_\Upomega {\Upgamma_l (s)d{\bf{x}}}. $$
(2.4)

Here, \(\Uppsi({\nabla^s \bf{u}},s,{\bf E}_c)\) is the bulk part of the energy, a function of the displacement u, the damage field s and the structured part of the deformation E c as per (2.3), while \(\Upgamma_l(s)\) is the surface part. Following Griffith, this is proportional to the area of the fracture surface only, so that the dependence is upon the field s and the characteristic material internal length-scale l, representing the width of the process-zone band associated with the phenomenon of crack coalescence [23]. For reasons explained at length in [27], we take for \(\Upgamma_l(s)\) the expression

$$ \Upgamma_l (s) = {\frac{\gamma}{2}}\left[{l |\nabla s|^2 + {\frac{{(1 - s)^2}}{l}}} \right], $$
(2.5)

being γ the material parameter representative of the energy per unit area of fracture.

The derivation of the specific form of the bulk part of the energy requires more effort and the reader is directed to [19] for the details. In the simplest case, it can be inferred that for the given material the crack pattern is completely characterized by the average strain of the RVE, i.e., E c (x) is a function of ∇s u(x). In extreme synthesis, one may establish a relationship between the local value of the average stain ∇s u and a particular value of E c , say E * c  = E * c (∇s u), which corresponds to the structured strain that minimizes the stored elastic energy in the RVE under homogenous boundary condition, compatible with the local value of ∇s u.

In the particular case of masonry-like materials, one assumes that \({\bf E}_c \in Sym^+\), being Sym + the class of positive semi-definite symmetric tensors. Then, in case of a linear elastic isotropic matrix for which the elasticity tensor takes the form \({\mathbb{C}=2 \mu \mathbb{I} + \lambda {\bf I} \otimes {\bf I}}\), being λ and μ the Lamé’s elastic constants, it can be proved that

$$ {{\bf \nabla^s{\bf u}}} = \sum\limits_{i = 1}^{{\mathcal{D}}} {\varepsilon _i {\hat{ \bf{e}}}_i \otimes {\hat{ \bf{e}}}_i } \Rightarrow {\bf E}^*_c= \sum\limits_{i = 1}^{{\mathcal{D}}} {\alpha ^*_i {\hat{ \bf{e}}}_i \otimes {\hat{ \bf{e}}}_i }, $$
(2.6)

i.e., \(\varvec{\nabla}^s{\bf u}\) and E * c are coaxial. Moreover, for the case of plain strain for which \(\varepsilon_3=0\), it is possible to verify that, when λ ≥ 0, then

$$ \alpha _3^*= 0, \quad \left(\alpha _1^* ,\alpha _2^*\right)= \left\{\begin{array}{ll}(0,0)&{\rm{if}} \;(1-\nu)\varepsilon _1+\nu\varepsilon _2 \le 0,\\\left({\varepsilon _1 + {\frac{\nu}{1 - \nu}}}\varepsilon _2,\;0 \right)&{\rm if}\;(1-\nu)\varepsilon _1+\nu\varepsilon _2 > 0\;{\rm{and}}\;\varepsilon _2 <\;0,\\(\varepsilon_1,\;\varepsilon_2)&{\rm if}\;\varepsilon_2 \geq 0 , \end{array} \right. $$
(2.7)

having set, without loosing generality, \(\varepsilon _1 \geq \varepsilon _2\).

The final result is the definition of the relaxed bulk energy density in the form \(\Uppsi^{**} (\nabla^s{\bf{u}},s) \equiv \Uppsi\left(\nabla^s{\bf{u}},s,{\bf E}^*_c(\nabla^s {\bf u})\right)\), that reads [19]

$$ \Uppsi^{**} (\nabla^s {\bf {\bf u}},s) = {{1}\over {2}} {\mathbb{C}} \left[\nabla^s {\bf {\bf u}} - (1 - s)\;{\bf E}^*_c(\nabla^s {\bf u}) \right] \cdot \left({\nabla^s {\bf {\bf u}} - (1 - s)\;{\bf E}^*_c(\nabla^s {\bf u})} \right). $$
(2.8)

Remarkably, defining \({{\bf T}^{*}:=\mathbb{C}[\nabla^s{{\bf u}} -{\bf E}^*_c(\nabla^s {\bf u})]}\), one finds that (1) \({\bf E}^*_c(\nabla^s {\bf u}) \in Sym^+\); (2) \({\bf T}^{*} \in Sym^-\); (3) \({\nabla^s{\bf u} = \mathbb{C}^{-1}[{\bf T}^{*}]+{\bf E}_c^{*}}\); (4) \({\bf T}^{*} \cdot {\bf E}_c^{*}= 0\). These conditions imply that T * and E * c are, in general, coaxial. Moreover, in the particular case of isotropic elasticity, then (5) also ∇s u is coaxial with T * and E * c . If one establish a correspondence between the tensor T * and the Cauchy stress in completely damaged body (s = 0), these conditions coincide with the definition of the constitutive equations for a classical linear elastic masonry-like material, established in [22].

Going back to the energy functional (2.4), we can now introduce the relaxed free energy functional, obtained from (2.4) by substitution of \(\Uppsi^{**}\) for \(\Uppsi\), that is

$$ \Uppi_{l}^{**} ({\bf{u}},s) = \int\limits_\Upomega {\Uppsi^{**} (\nabla^s {\bf{u}},s)d{\bf{x}}} + \int\limits_\Upomega {\Upgamma_l (s)d{\bf{x}}}, $$
(2.9)

where \(\Uppsi^{**} (\cdot,\cdot)\) and \(\Upgamma_l (\cdot)\) are defined in (2.8) and (2.5), respectively.

In conclusion, the variational problem results to be

$$ \mathop{\min}\limits_{({\bf{u}},s) \in {{\mathcal{A}}}}\Uppi_l^{**} ({\bf{u}},s), $$
(2.10)

where \(\mathcal{A}\) represents the admissible class of functions, which also contains indication of the specific conditions for the fields u(x) and s(x) on the boundary \(\partial \Upomega\) of \(\Upomega\) with \(\dot s \leq 0\) where \(\left\langle \cdot \right\rangle\) represents derivative with respect to time.

It can be verified [19] that the Cauchy stress T, which is dual in energy with respect to the strain ∇s u, reads

$$ \begin{aligned} {{\bf T}} &= {{\mathbb{C}}}\left[{\nabla^s {\bf{u}}} \right] - (1 - s^2 ){{\mathbb{C}}}\left[{{\bf E}^{*}_{c}(\nabla^s {\bf u})} \right]\\ &= {\bf T}^*+s^2 {{\mathbb{C}}}\left[{{\bf E}^*_c(\nabla^s {\bf u})} \right]. \end{aligned} $$
(2.11)

Notice that when s = 1 one finds the stress in a sound elastic material, whereas when s = 0 one obtains the aforementioned T * for a classical masonry-like material [22]. There are however two major novelties of this model with respect to the classical no-tension theory. First, the term in (2.9) representative of surface-energy implies that the opening of fractures (i.e., s passing from 1 to 0) is associated with an energy consumption; second, there may be regions where the material is only partially damaged (s between 0 and 1).

The model has been implemented in an appositely conceived program based upon the Open Source package deal.II [28], for which the numerical details can be found in [19].

3 The influence of heterogeneities. Numerical experiments

In the numerical experiments, we consider the two-dimensional rectangular domain \(\Upomega\) of Fig. 2, with sides d and h, which represents a section of a prismatic specimen in plane strain.

Fig. 2
figure 2

Layout of the prismatic specimen in plane strain under uniaxial tension or compression

Full size image

The element is uniaxially loaded at the bases \(\Upgamma_2\) and \(\Upgamma_1\), while the vertical borders \(\Upgamma_3\) and \(\Upgamma_4\) are unconstrained and stress free. The considered boundary conditions reflect the borderline cases of perfectly lubricated (slippery) and perfectly bonded (frictional) loading plates. For the first case of slippery plates they take the form

$$ \left\{\begin{array}{llll}{\bf u} \cdot {\bf e}_2 = 0, & {\bf t}_n \cdot {\bf e}_1 = {\bf 0},& s = 1, & {\rm on}\;\Upgamma_1,\\{\bf u} \cdot {\bf e}_2 = t\overline{u},& {\bf t}_n \cdot {\bf e}_1= {\bf 0}, & s = 1,& {\rm on} \;\Upgamma_2,\\{\bf t}_n = {\bf 0},&\nabla s \cdot {\bf n} = 0,& {\rm on} \;\Upgamma_3\;{\rm and}\; \Upgamma_4,\\ \end{array} \right. $$
(3.1)

where e 1 and e 2 are the horizontal and vertical unit vectors respectively, n is the outward normal to the boundary, t n  = Tn is the normal traction with T the Cauchy stress defined in (2.11), while t is the dimensionless parameter correlated with the imposed displacement, associated with the length-scale \(\overline{u}\). The case of bonded dry platens is simply obtained through

$$ \left\{\begin{array}{lll}{\bf u} = {\bf 0},& s = 1,& {\rm on} \;\Upgamma_1,\\{\bf u} = t\overline{u} {\bf e}_2, & s = 1,& {\rm on} \;\Upgamma_2,\\{\bf t}_n = {\bf 0},&\nabla s \cdot {\bf n} = 0,& {\rm on} \;\Upgamma_3 \;{\rm{and}}\;\Upgamma_4.\\\end{array} \right.$$
(3.2)

The setting s = 1 on \(\Upgamma_1\) and \(\Upgamma_2\) means that the body cannot damage at the constrained borders and it is remindful of the fact that contact of loading platens can strengthen the material at the interface, but the distinction is of scarce relevance because the degradation may in any case occur in a neighboring portion. The following experiments refer to the case d = 50 mm, h = 100 mm, with elastic constants μ = 12,500 N/mm2 and λ = 8,333 N/mm2 (corresponding to Young’s modulus E = 30,000 N/mm2 and Poisson’s ratio ν = 0.2). For fracture toughness and intrinsic length scale, we set γ = 10−4 N/mm and l = 1 mm and we define \(\overline{u}=2.5\times10^{-4} \text {mm}\) for a traction test and \(\overline{u}=-2.5\times10^{-3} {\hbox{mm}}\) in compressionFootnote 2. In the numerical discretization, we adopted a structured and homogeneous finite element mesh composed of 80,000 quadrilaterals, with in total 3 × 80,601 degrees of freedoms. The size of the element is \(5\times10^{-3}{d}\), that is 0.25 l.

Figure 3 summarize the results of a traction test on the homogeneous isotropic specimen under the slippery platen conditions of (3.1). Two horizontal cracks appear in a neighborhood of the lower and upper bases (Fig. 3a) and the formation of such cracks is evidenced by an energetic transfer à la Griffith from the bulk to the surface energy part. This is clearly illustrated in the energy graphs of Fig. 3b, which represent the bulk, surface and total energy, respectively associated with the first and second integral in the energy functional of (2.9) and with their sum.

Fig. 3
figure 3

Failure mode of homogeneous isotropic specimen under traction: a map of s; b surface energy diagram as a function of the loading parameter t

Full size image

The corresponding compression test is illustrated in Fig. 4. Remarkably, no crack occurs in practice because the body is under a uniaxial state of stress (Fig. 4a). The total energy grows quadratically as represented in Fig. 4b, where there is no evident sign of transfer from the bulk to the surface part.

Fig. 4
figure 4

Behaviour of quasi-brittle homogeneous material under compression: a map of s; b surface energy diagram as a function of t

Full size image

The model predictions under compression are clearly unsatisfactory and consequently, as mentioned in the Introduction, we need to consider the presence of defects. In a first experiment, we simply add three small square inclusions with side equal to one millimeter inside the prism in the position indicated in Fig. 5. The inclusions are made of a material much stiffer than the matrix, for which we choose E = 60,000 MPa and γ = 10−3 N/mm.

Fig. 5
figure 5

Rectangular prism in plane strain with three small inclusions under uniaxial tension or compression (strain-driven test)

Full size image

Figure 6 describes for increasing load the evolution of the damage parameter s for the case of slippery platens, which is clearly associated with the crack path. Looking for energy minimization, the specimen splits following vertical cracks that isolate material columns that render the presence of inclusions ineffective, because they annihilate the hoop stress due to the kinematic compatibility with the inhomogeneities.

Fig. 6
figure 6

Rectangular prism in plane strain under compression with three small inclusions. Evolution of s for the case of lubricated platens

Full size image

The corresponding case for bonded-platen boundary conditions is particularly interesting. To render even more evident the comparison with the previous case, Fig. 7 report the evolution of the field s for a mixed problem, for which the slippery boundary condition of (3.1) has been adopted on the upper base \(\Upgamma_2\), whereas the bonded platen condition of (3.2) has been used on the lower base \(\Upgamma_1\). Since the specimen is relatively high, the two conditions, as confirmed by the numerical results, do not influence one-another.

Fig. 7
figure 7

Rectangular prism in plane strain with three small inclusions under compression (dry lower platen and lubricated upper platen): evolution of s

Full size image

What should be noted here is that cracks do not develop down to the lower base, simply because here the material is under biaxial compression due to frictional contact. From the energetic point of view, the development of cracks for both cases is evidenced by a gradual increase of the surface energy, as it is clear from observation of Fig. 8 which reports the integral over the whole body of the term (2.5). In substance there is not a qualitative differences between the cases of dry and lubricated platens, because in both cases the leading phenomenon is axial splitting.

Fig. 8
figure 8

Rectangular prism with three small inclusions in plane strain under compression: surface-energy diagram as a function of the loading parameter t. a Case of lubricated platens; b case of dry lower platen and lubricated upper platen

Full size image

To investigate further, we now consider the effect of multiple square inclusions with side equal to 1 mm, arranged according to a regular scheme as indicated in Fig. 9 (the horizontal distance of the inclusion is 6 mm and each line of inclusions are 3 mm equally spaced) the mechanical properties of the inclusion being the same as before.

Fig. 9
figure 9

Layout of the prismatic specimen with multiple small inclusions in plane strain under uniaxial tension or compression (strain-driven test)

Full size image

The corresponding crack path for the case of compression with lubricated platens is represented in Fig 10. The phenomenon of axial splitting is clearly evident. Final failure of the specimen is associated with the buckling of the materials columns isolated by the crack surfaces, but the present model cannot reproduce this effect because the quadratic form (2.8) of the bulk strain energy cannot account for geometric non-linearities.

Fig. 10
figure 10

Prism with multiple small inclusions in plane strain under compression. Evolution of s for the case of lubricated platens

Full size image

If one considers the same case but under dry-platens condition, the evolution of s would be as represented in Fig. 11. Again, the confinement at the specimen ends prevents the propagation of cracks at the bases under biaxial compression. It is remarkable that two triangular-shaped sound material portions are isolated at the bases, but this shape is not due to shear cracks but it is simply delimited by the tips of propagating cracks, that arrest where the material is bi-axially compressed. The classical hourglass shape that is commonly experienced in compression tests with dry platens is consequently not due to shear but rather to cleavage fractures, with no substantial difference with the case of lubricated platens.

Fig. 11
figure 11

Prism with multiple small inclusions in plane strain under compression. Evolution of s for the case of dry platens

Full size image

The substantial analogy between the two cases of slippery and dry platens is again confirmed from an energetic point of view by the surface energy graphs of Fig. 12. Of course the progression of cracks is quite restrained by frictional contact because, for the same value of t, the fracture energy expended in the material is smaller in dry than in lubricated platen conditions.

Fig. 12
figure 12

Prism with multiple small inclusions in plane strain under compression. Surface-energy diagram as a function of t for: a lubricated platens; b dry platens

Full size image

4 The domain of resistance under biaxial stress

Despite its simplicity, the model can also account for the influence of lateral confinement. For this tests plane strain conditions have been used. To illustrate, consider now the same prism with multiple inclusions of Fig. 9 for which, with the same notation of (3.1) and (3.2), we assume boundary conditions of the form

$$ \left\{\begin{array}{l} {{\bf t}}_n = \sigma_2 {\bf n},\quad s = 1,\quad {\rm on} \;\Upgamma_1 \quad \hbox{and} \;\Upgamma_2 ,\\ {{\bf t}}_n = \sigma_1 {\bf n},\quad s = 1,\quad {\rm on}\; \Upgamma_3 \quad \hbox{and} \;\Upgamma_4 , \end{array} \right. $$
(4.1)

as schematically represented in Fig. 13a.

Fig. 13
figure 13

Rectangular prism in plane stress with multiple small inclusions: a state of stress; b Biaxial stress state; c Particular of the biaxial stress state under traction

Full size image

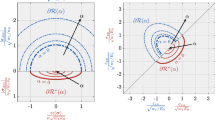
The scope now is to calculate the combination of σ1 and σ2 that provokes the onset of cracks. This is conventionally revealed, as already discussed for Figs. 8 and 12, by a sudden increase of the total surface energy, calculated as the body integral of the term (2.5). The resulting resistance domain is represented in Fig. 13b, where an indication of the failure mode is also furnished in the small pictures, representing a collapsing RVE in proximity of the corresponding branch of the domain. Figure 13c represents a magnification of the domain when tractions are applied (σ1 > 0 and/or σ2 > 0).

Observing the domain, it is clear that the strength under compression is one order of magnitude higher than under traction and that the lateral confinement increases the compression strength. In fact, material crisis occurs when the compression reaches a threshold value that linearly increases with the lateral confining actions. The failure mode for this case, as evident in the corresponding pictures of the RVE, is multiple axial splitting according to the direction of maximal compression.

It should be mentioned that in this model the material exhibits unbounded compression strength if the lateral confinement is correspondingly high. In fact, this model does not account for the possibility of material crushing under exceptionally high compression because only crack openings are contemplated. If crushing failure was taken into account by a convenient enrichment of the model, the negative branches of the domain would be delimited by the dashed lines represented, at a pure qualitative level, in Fig. 13b. This will be not considered here, but will be the subject of further research.

Under the combination of traction and compression (sectors where \(\sigma_1 \cdot \sigma_2\;<\;0\)), it is evident from the picture that even a moderate lateral tensile component drastically diminishes the associated compression strength. More in particular, increasing the lateral traction component decreases the corresponding compression strength with a pseudo-linear dependence. Failure again occurs by cracking that develops parallel to the compression direction or, equivalently, at right angle to the direction of tension. However, as evidenced in the small RVE pictures, failure is associated with the formation of one dominant crack, instead of multiple axial splitting as in the previous case. This is because the tensile component favors the fracture localization under pure mode I opening.

Finally, let us consider the case of biaxial tension, magnified in Fig. 13c. Again, failure occurs across one dominating crack that develops at right angle to the direction of maximal tension. A contemporaneous lateral traction renders the material slightly stronger, but the effect is of scarce relevance, being the ultimate tensile strength practically independent of the applied lateral stress.

Moreover, for the reasons mentioned above, the present approach cannot predict the final failure of the specimen under high compression because material crushing is not contemplated.

The response predicted by the model in the elastic range is reminiscent of the classic Kupfer domain [25], that is almost unanimously recognized as the typical domain of resistance for quasi-brittle materials under generalized plane stress. As a matter of fact, the elastic domain of Fig. 13 shows a slight deviation from convexity especially in the transition zone between the tension-tension range and the tension-compression regime, whereas the Kupfer-like domains are usually assumed to be convex. However, here the non-convexity is just perceptible and it is difficult to understand whether it is due to numerical approximation or it is physically motivated. To our knowledge, the experimental results, such as the most famous ones on brick masonry by Page [29–31], reveal a rather scattered ensemble of experimental points, that only qualitatively can be interpolated by a convex contour. The issue of the convexity of the elastic domain is very important and certainly deserves further investigation that goes beyond the scope of this paper.

5 Discussion and conclusions

The uniaxial compression test on brittle and quasi-brittle solids is of such importance and complexity that it is practically impossible to account for all the proposed models, ranging from phenomenological models to micro-mechanically motivated theories, possibly based upon a multiscale approach. In general, the response of diverse materials is different in type, so that no model can be considered of universal value, even if our present interpretation accords with a wide experimental evidence.

Perhaps, the major result here consists in having shown the potentiality of the regularized variational approach to fracture mechanics, as adapted to the case of masonry-like material as per [19]. The model is minimal, because the only required material parameters are the elastic moduli, the overall fracture energy and the intrinsic material length scale. Nevertheless, with a proper consideration of micro-defects, here simply considered as elastic inclusions, the model is able to reproduce a great number of aspects, capturing the onset of axial splitting and the possible influence of end frictional constraints of loading platens. In particular, for what the latter aspect is concerned, the classical hourglass shape is justified by an interpretation that is alternative to the classical one accounting to shear cracks, being it attributed to the arrest of splitting cracks in the bi-axially compressed portions.

The variational masonry-like model is in practice analogous to a no-tension material with an energetic barrier, so that a balance à la Griffith results to be equivalent to moderate tensile strength. The model can capture the defect-induced axial splitting because the heterogenous microstructure gives rise to a complex stress distribution: the material fractures to relax the excess of elastic energy associated with this. Indeed, the proposed approach is a regularized formulation of fracture mechanics in the sense stated by [20], that can be numerically implemented and take into account an extraordinary complex distribution of stress, that would be very complicated with a conventional sharp fixed-crack model.

Remarkably, without any need to resort to more complexity or to phenomenological laws, the simple model can also give an elementary explanation of the effects of confinement, interpreting at least at the qualitative level a considerable part of the Kupfer-like failure domains [24], representing by far the most used description of failure under biaxial stress for a wide class of quasi-brittle solids.

Of course, the model is still far from being exhaustive. Further necessary developments consist in the implementation of failure due to material crushing and in the introduction of geometric non-linearities, to account for the possibility of buckling of material columns isolated by axial splitting. Possible further immediate applications could be the analysis of the effect of reinforcement rings in compressed structural columns.