Abstract
Phase-field models of brittle fracture can be regarded as gradient damage models including an intrinsic internal length. This length determines the stability threshold of solutions with homogeneous damage and thus the strength of the material, and is often tuned to retrieve the experimental strength in uniaxial tensile tests. In this paper, we focus on multiaxial stress states and show that the available energy decompositions, introduced to avoid crack interpenetration and to allow for unsymmetric fracture behavior in tension and compression, lead to multiaxial strength surfaces of different but fixed shapes. Thus, once the length scale is tailored to recover the experimental tensile strength, it is not possible to match the experimental compressive or shear strength. We propose a new energy decomposition that enables the straightforward calibration of a multi-axial failure surface of the Drucker-Prager type. The new decomposition, which hinges upon the theory of structured deformations, encompasses the volumetric-deviatoric and the no-tension models as special cases. Preserving the variational structure of the model, it includes an additional free parameter that can be calibrated based on the experimental ratio of the compressive to the tensile strength (or, if possible, of the shear to the tensile strength), as successfully demonstrated on two data sets taken from the literature.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The variational phase-field approach to fracture, pioneered by Bourdin et al. (2000a) and first proposed as the regularization of Francfort and Marigo’s variational fracture formulation (Francfort and Marigo 1998; Francfort et al. 2008), has recently established itself as a game changer in the field of computational fracture mechanics. The computational framework stemming from the variational phase-field formulation is able to handle crack topologies of arbitrary complexity in two and three dimensions, with no need for complicated crack tracking procedures nor for additional criteria to guide the occurrence of crack branching or merging phenomena. Thus, the approach enables fracture computations of unprecedented flexibility, which is probably the key reason for its success.
Another desirable feature of the associated computational framework is the capability to automatically handle both nucleation and propagation. However, the understanding of the underlying nucleation criteria and the discussion of their physical pertinence is subtle. This point is currently the subject of an open debate in the community. The present paper intends to be a contribution in this context, focusing on the discussion of the nucleation criteria under multiaxial loading.
Variational phase-field models can be interpreted as a special class of gradient-damage models including a length-scale parameter. Gamma-Convergence results show that when this parameter tends to zero, the global minimizers of the damage energy functional approach the global minimizers of the energy of the sharp interface Griffith model. For rate-independent processes, this notion of convergence applies also to quasi-static evolutions, passing through a time-discretisation (Giacomini 2005). However, the convergence of evolutions of phase-field towards sharp-interface models is retrieved only in terms of global minimizers, i.e. by requiring that the current state achieves the smallest possible energy level among all admissible competitors at a given time step. Global minimization is at the basis of the variational approach proposed by Francfort and Marigo (1998). It is of fundamental utility from the mathematical point of view, allowing for the application of the direct methods of the calculus of variation. However, the global minimality requirement is neither consistent with experimental evidence nor it corresponds to the numerical practice. From the numerical standpoint, global minimization is not feasible in large-scale computations and all the available numerical approaches attempt to retrieve at best local minimizers of the energy. From the physical point of view, local minimization, or meta-stability, appears as a more appropriate criterion to select experimentally observable states. These issues were anticipated already in (Bourdin et al. 2000a; Francfort and Marigo 1998) and are discussed in detail in (Francfort et al. 2008) and by several other authors (see e.g. Larsen n.d.; Negri 2010). This motivates us and many other authors to define evolutions in terms of local minimizers of the total energy functional. We discuss the nucleation criterion accordingly, in the footsteps of Tanné et al. (2018).
Nucleation of a crack within the variational phase-field framework is identified with the localization of the phase-field variable. When considering local minimization as a criterion to select the stable states during a quasi-static evolution, localization events are associated to the loss of the stability of the solution with an almost uniform damage level. The corresponding nucleation loading is the one at which the current solution branch ceases to be a local minimum of the energy. This load can be unrelated to the critical load obtained within an evolution law based on the global minimization as a stability criterion. The critical load with local minimization depends on the internal length scale of the phase-fied model, whilst it converges to a value independent of this regularization length when considering global minimization. Several authors embraced the idea of local minimization as a stability criterion and set this length scale to such a value as to achieve nucleation at a desired level of stress in uniaxial conditions (i.e. at the level of the known uniaxial tensile strength of a given material). This approach leads to the interpretation of the length scale as a material parameter, a concept that was adopted in several studies, see (Amor et al. 2009; Borden et al. 2012; Mesgarnejad et al. 2015; Nguyen et al. 2016; Pham et al. 2011b, c, 2017; Tanné et al. 2018; Wu et al. 2017) among others. The effect of this length scale is tantamount to the effect of the size of the process zone in cohesive fracture models.
The study by Tanné et al. (2018) is the most comprehensive investigation conducted to date on crack nucleation under mode-I loading with variational phase-field models of brittle fracture. The authors concluded that, with the above interpretation of the length scale and adopting a stability condition in terms of local minimizers, variational phase-field models are capable of quantitatively predicting crack nucleation in mode-I conditions in a wide range of geometries with various types of notches and for several brittle materials.
However, it is well-known that the available variational phase-field models are not able to faithfully predict the nucleation threshold under multi-axial loading. In standard isotropic phase-field models (Bourdin et al. 2000b), the nucleation threshold is symmetric in tension and compression. More complex models have been developed to avoid crack interpenetration in compression and to obtain an unsymmetric behavior in tension and compression. The most widely used of these models (Amor et al. 2009; Freddi and Royer-Carfagni 2010; Miehe et al. 2010) are variational and include the decomposition (also denoted as split) of the strain energy density into positive and negative (or active and inactive, or tensile and compressive) parts (Amor et al. 2009; Freddi and Royer-Carfagni 2010; Miehe et al. 2010). Even when using these models it is not possible to independently set tension and compression nucleation thresholds to match the experimental data (see e.g. Amor et al. 2009, Sect. 4.4). Moreover, the available literature discussed especially the influence of the energy split on crack propagation, whereas its influence on crack nucleation remained largely unexplored.
The above limitation motivated several authors to propose non-variational models to retrieve the experimental strength surfaces under multi-axial loading, as done in more classical damage models (Comi and Perego 2001). In non-variational approaches, the damage criterion does not come as consequence of an energy minimization principle. In this framework, Lorentz (2017) proposed a damage model with gradient damage regularization featuring the correct strength surface of plain concrete under multi-axial tension, by introducing a residual elastic energy in compressive states. Kumar et al. (2020) advocates the use of non-variational models, claiming explicitly that the strength cannot be solely a result of energy minimization, criticizing the approach proposed in (Amor et al. 2009; Pham et al. 2011b, c; Tanné et al. 2018). In short their arguments are the following: (i) when using the standard isotropic variational phase-field model of Bourdin et al. (2000b) (i.e. the model with no decomposition of the elastic strain energy), tension and compression nucleation thresholds cannot be set independently (ii) in the incompressible limit the strength under isotropic stress loading is infinite. Hence, they proposed a non-variational model supplementing the equation which governs the evolution of the phase field with an additional driving force, which is not associated to an elastic energy release rate. With their non-variational approach they were able to recover a multiaxial failure surface of the Drucker-Prager type, which they opposed to the elliptical failure surface obtained in two dimensions (2D) with the isotropic model of Bourdin et al. (2000b).
In variational approaches, both the equilibrium equations and the damage criterion are expressed as optimality conditions on a total energy functional. As a result, the damage criterion is expressed as a threshold on the elastic energy release rate. Non-variational approaches give a great flexibility for straightforwardly defining arbitrary strength surfaces, independently of the elastic energy release rate. However, this flexibility comes with a price. First, the symmetry property of the global tangent stiffness is not guaranteed in general. This implies fundamental difficulties in the mathematical and numerical analysis, as it happens, for example, in contact mechanics (Ballard 2013). Non-variational approaches do not allow for the application of the direct methods of the calculus of variations to discuss the existence of solutions or to derive asymptotic Gamma-convergence results, nor the use of the methods of optimization theory to devise numerical solution schemes for the coupled damage-elasticity problem. Marigo (1989) relates the Drucker-Ilyushin postulate to the variational structure of the model, showing that the strain work in a closed cycle in the strain space is non-negative only if the damage criterion comes from a variational model, where the strain work is a state function (see also Pham and Marigo 2010b). Although this does not imply that non-variational models violate the second principle of thermodynamics, it provides a strong fundamental theoretical argument in favor of variational formulations for nonlinear material models. Hence, even though non-variational approaches should not be banned, we believe that variational approaches are preferable from the theoretical and practical point of view and therefore should be aimed for whenever possible.
The objective of this paper is twofold. First, we carry out an in-depth analysis and comparison of the strength surfaces of the most widely used variational phase-field models. Then, we propose a novel variational model featuring a generalized energy density decomposition which leads to a strength surface of the Drucker-Prager type, where the ratio between the shear and the tensile strengths (or the compressive and the tensile strengths) can be freely tuned to match the experimental data. The identification procedure and the capability of the model to match the experimental multiaxial strength surface are illustrated on the same examples used in Kumar et al. (2020). The new decomposition encompasses those proposed in Amor et al. (2009) and (in two dimensions) Freddi and Royer-Carfagni (2010) as special cases. The specific form of the strain energy density is obtained by extending the ideas of Freddi and Royer-Carfagni (2010) of using the theory of structured deformations (Del Piero and Owen 1993) to define the residual elastic energy in the fully damaged state. Altough the theory of structured deformations has been originally formulated only in the sharp-interface context, here we simply use it as an effective tool to define a damage model featuring a strength surface of Drucker-Prager type. We refrain from giving any specific theoretical or physical justification to this approach. Providing a variational model where tension and compression nucleation thresholds can indeed be set independently, we challenge one of the main claims of Kumar et al. (2020) on the variational approach to fracture not being able to correctly retrieve crack nucleation.
This paper is organized as follows: in Sect. 2, we briefly summarize the main ingredients of the variational phase-field approach to brittle fracture. In Sect. 3, we recall the most widely used approaches for the decomposition of the elastic strain energy density in variational phase-field models, and we determine and compare their respective crack nucleation criteria. In Sect. 4, we propose a new generalized energy decomposition able to enhance the flexibility of the available decompositions in terms of multiaxial failure criteria and recovering two of them as special cases. We finally draw the main conclusions in Sect. 5.
As follows, we report a brief overview of the notation and some useful relations. Vectors and second-order tensors will be both denoted by boldface fonts, e.g. \({\mathbf {u}}\) and \(\varvec{\varepsilon }\) for the displacement vector and strain tensor. For the standard orthogonal decomposition of second-order tensors in spherical and deviatoric parts we will use the following notation (exemplified on \(\varvec{\varepsilon }\))
where \({\mathbf {I}}\) is the second-order identity tensor and n is the number of space dimensions. For \(n=3\), denoting with \((\varepsilon _1,\varepsilon _2,\varepsilon _3)\) the eigenvalues of the symmetric tensor \(\varvec{\varepsilon }\), we have the following relations:
with \(\Vert \varvec{\varepsilon }_{\mathrm {dev}}\Vert ^2{=} \frac{2}{3} \left( \varepsilon _1^2{+}\varepsilon _2^2+\varepsilon _3^2-\varepsilon _1 \varepsilon _2-\varepsilon _2\varepsilon _3-\varepsilon _1\varepsilon _3\right) \). For an isotropic linearly elastic material with Young’s modulus E and Poisson’s ratio \(\nu \), we denote by \((\lambda ,\mu ,\kappa )\) the Lamé and the bulk moduli given by
Given a scalar valued function \(f:x\rightarrow f(x)\in {\mathbb {R}}\), we define its positive and negative parts as
2 Basic variational phase-field models of brittle fracture
Variational phase-field models of brittle fracture can be obtained in two alternative ways: (i) from the regularization of the variational approach to fracture (Francfort et al. 2008), or (ii) as a special class of gradient damage models, see e.g. (Pham et al. 2011a; Pham and Marigo 2010a, b). As follows, we briefly recall the main ingredients of the formulation taking the latter point of view, following the presentation given in Marigo et al. (2016).
2.1 General formulation
Let us consider a body \(\Omega \subset {\mathbb {R}}^{n}\) made of a damageable rate-independent material whose current state is characterized by the vector-valued displacement field \({\mathbf {u}}:{\mathbf {x}}\in {\mathbb {R}}^{n}\rightarrow {\mathbf {u}}({\mathbf {x}})\in {\mathbb {R}}^{n}\), and the irreversible scalar damage field \({\alpha }:{\mathbf {x}}\in {\mathbb {R}}^{n} \rightarrow \alpha ({\mathbf {x}})\in [0,1]\). Assuming a geometrically linear model, the strain measure is the infinitesimal strain tensor \(\varvec{\varepsilon }\left( {\mathbf {u}}\right) =\nabla ^{s}{\mathbf {u}}\), with \({\nabla ^{s}\left( \bullet \right) =}\frac{1}{2}\left[ \nabla \left( \bullet \right) +\nabla ^{T}\left( \bullet \right) \right] \) as the symmetric gradient operator. The strain energy density of the material is assumed to be a differentiable function of the strain, the damage, and the gradient of the damage in the form:
where \(\varphi \) is the elastic energy density of the material, which is assumed to be a monotonically decreasing function of \(\alpha \), \(\varphi _0(\varvec{\varepsilon }):=\varphi (\varvec{\varepsilon },0)\) being the elastic energy of the pristine material and \(\varphi _1(\varvec{\varepsilon }):=\varphi (\varvec{\varepsilon },1)\) the elastic energy of the fully damaged material. We assume that the elastic energy density is a convex function of the strain at each fixed \(\alpha \), and that it is positively homogeneous of degree 2, i.e. that \(\varphi (s\,\varvec{\varepsilon },\alpha )=s^2\varphi (\varvec{\varepsilon },\alpha ), \forall s\ge 0\). The dissipated energy is composed of an homogeneous part, represented by the monotonically increasing function \(w(\alpha )\) with \(w(0)=0\) and \(w(1)=1\), and a term depending on the gradient of the damage introducing an internal length \(\ell \). The constant \(w_1\) is the specific energy dissipation, representing the energy dissipated per unit volume to reach the fully damaged state from the pristine material during a homogeneous process.
The body \(\Omega \) is subjected to a time-dependent boundary displacement \(\bar{{\mathbf {u}}}_t\) on the Dirichlet portion \(\partial _{D}\Omega \) of the boundary, to a traction \({\mathbf {f}}_t\) on the remaining (Neumann) portion \(\partial _{N}\Omega \) and to a body force \({\mathbf {b}}_t\) in \(\Omega \). In the time-discrete version of the variational approach to gradient damage models, given the damage field \(\alpha _{p}\) at the previous time-step \(t_{p}\) and a (small) time increment \(\Delta t>0\), the quasi-static equilibrium displacement \({\mathbf {u}}\) and the damage field \({\alpha }\) at the new time step \(t=t_p+\Delta t\) are given by the solution of the energy minimization problem
where
is the total energy functional including the work of the external forces and
are the spaces of the admissible displacement and damage fields at time t from the previous state with damage \(\alpha _p\). Here \(H^1(\Omega ;{\mathbb {R}}^n)\) denotes the usual Sobolev space of functions with square integrable first derivatives taking values in \({\mathbb {R}}^n\). In the energy minimization principle (3), loc min stands for local unilateral minimization, meaning that the solution \(({\mathbf {u}},\alpha )\in {\mathcal {C}}_t\times {\mathcal {D}}({\alpha }_{p})\) should be such that
Retaining only the first-order series expansion of the energy increment in (5) gives the following variational inequality as a necessary condition for optimality:
where
denotes the directional derivative of the functional \({\mathcal {E}}_{t}({\mathbf {u}},{\alpha })\) in the direction \(({\mathbf {v}},{\beta })\).
By suitably selecting the variations \({\mathbf {v}},{\beta }\) and applying standard localization arguments, one can show that, for smooth solutions, the first-order optimality condition (6) is equivalent to the following equilibrium equation and equilibrium boundary condition
and to the damage criterion
where \({\mathbf {n}}\) is the outer unit normal to the boundary, \(\Delta \alpha \) denotes the Laplacian of the damage field, and
are the stress tensor and the damage energy release rate, respectively. Equivalent conditions are obtained in a time-continuous setting as a consequence of an evolution principle based on irreversibility, energy balance, and stability. We refer the reader to (Pham and Marigo 2010b, a; Marigo et al. 2016) for further details.
For homogeneous states for which \(\Delta \alpha =0\), the damage criterion implies that damage can evolve only if the stress and the strain are on the boundary of the following elastic domains:
where we introduced the complementary elastic energy density defined as the conjugate function of \(\varphi \):
The positive homogeneity of degree 2 of the elastic energy density implies the positive homogeneity of degree 1 of the stress-strain relationship in (8) and that
where, here and henceforth, \(\varvec{\varepsilon }(\varvec{\sigma },\alpha )\) denotes the inverse of the stress-strain relationship in (8), which is well defined because of the assumed convexity of \(\varphi \) with respect to \(\varvec{\varepsilon }\).
A damage law is defined as stress-softening or stress-hardening if the domain of the admissible stresses \({\mathcal {R}}^*(\alpha )\) is a decreasing or an increasing function of \(\alpha \), respectively; analogous definitions of strain-softening or strain-hardening apply to the domain of the admissible strains \({\mathcal {R}}(\alpha )\). Damage models used for a phase-field model of fracture should include a stress-softening phase, at least for sufficiently high damage levels.
2.2 Basic gradient damage model used for phase-field fracture
Basic phase-field fracture models assume isotropic linear elasticity and an elastic energy density in the form
with
for which the elastic domains read as
In a uniaxial stress state \(\varvec{\sigma }=\sigma {\mathbf {e}}_1\otimes {\mathbf {e}}_1\), the inequalities in (13) give:
In-depth analytical solutions of the one-dimensional tension test, including stability and bifurcation analysis (Pham et al. 2011b, c), show that when loading an initially undamaged bar of length \(L\gg \ell \) with an imposed end displacement, at a critical stress \(\sigma _c\) the homogeneous solution becomes unstable and the damage localizes in a band assimilable to a crack. The localized solution has a well-defined dissipated energy density, that can be identified with the fracture toughness \(G_c\). The critical stress \(\sigma _c\) can be interpreted as the strength of the material. It coincides with the elastic limit \(\sigma _e(0)\) when the material is stress-softening for any \(\alpha \), while it corresponds to the transition from the stress-hardening (\(\sigma _e'(\alpha )>0\)) to the stress-softening (\(\sigma _e'(\alpha )<0\)) regimes when the material has an initial stress-hardening phase, i.e.:
where \(\varepsilon _c\) is the corresponding critical strain and \(\alpha _c\) is the critical damage for entering the stress-softening phase. The critical stress and the equivalent fracture toughness obtained for two popular choices of the damage constitutive functions, which exemplify these two behaviors, are
The first model has an initial purely elastic phase followed by stress-softening, whereas the second model has an initial stress-hardening phase followed by stress-softening. The critical stress corresponds to the instability of the homogeneous solution, that is regarded as the basic mechanism explaining crack nucleation in gradient damage models (Amor et al. 2009; Pham et al. 2011c). According to this interpretation, one can use (15) to select the material parameters \(w_1\) and \(\ell \) of the gradient damage model using the values of the fracture toughness \(G_c\) and the strength \(\sigma _c\) of brittle materials provided by material databases. Recently, it has been shown that with this choice it is possible to correctly reproduce the nucleation phenomena and size effect under mode-I loading with several types of pre-existing notches (Tanné et al. 2018), and explain the morphogenesis of complex tensile crack patterns (Sicsic et al. 2014).
Under multi-axial loading, for sufficiently large structures, homogeneous states can loose their stability only when the stress and the strain are on the boundary of the elastic domain and the material is in the stress-softening phase (Pham and Marigo 2013). Hence, recalling the definition in (14) of \(\alpha _c\) as the critical value of the damage for the transition to the stress-softening phase, we define the strength surfaces under multi-axial loading as follows
They give respectively the maximum allowable strain and stress for homogeneous states. We assimilate these surfaces to the nucleation threshold, even though it can be rigorously proved that being on the strength surface is only a necessary condition for crack nucleation.
Since the strength surfaces coincide with the boundary of the elastic domains for \(\alpha =\alpha _c\), i.e. \({\mathcal {S}}=\partial {\mathcal {R}}(\alpha _c)\), \({\mathcal {S}}^*=\partial {\mathcal {R}}^*(\alpha _c)\), in the following we will derive \({\mathcal {R}}\left( \alpha \right) \) and \({\mathcal {R}}^{*}\left( \alpha \right) \) for the various considered models, from which the strength surfaces can be immediately obtained. In this paper, the strength surfaces will be plotted for \(\alpha _c=0\) assuming an \(\mathtt {AT}_1\)-type model.
3 The available energy decompositions and their influence on the strength surface under multi-axial loading
A fundamental limitation of the basic phase-field fracture model is to have a symmetric behavior in tension and in compression. This has two direct negative consequences, which are clearly unphysical: (i) the possible crack interpenetration under compressive loading, (ii) the critical stress for nucleating a crack under uniaxial compression is the same required for uniaxial tension. For this reason, several modifications of the basic model (11) have been proposed in the literature. A possible strategy to avoid unphysical interpenetration of the crack lips is to introduce a decomposition of the elastic energy density into a compressive (or inactive, or negative) and a tensile (or active, or positive) part, and let the damage affect only the latter part. The most pertinent way to perform this decomposition is still an open issue in the literature and a subject of ongoing debate, see (Li 2016) for an overview of the main drawbacks of the different approaches. In this section, we recall the most widely used decompositions proposed in the literature and derive and compare their strength surfaces. While the decomposition affects both the nucleation and the propagation phases, in this work we only discuss its implications on crack nucleation, a point which, to the best of our knowledge, has not been clearly addressed in the literature yet.
3.1 Energy decompositions and the corresponding elastic domains
The decompositions of the elastic energy density (2) proposed in the literature are in the form:
where only the portion \(\varphi _D\) of the elastic strain energy is affected by the damage, while \(\varphi _R\) is a residual elastic energy, independent of the damage variable. In the following, we will focus on the case of materials which are isotropic in the undamaged states, i.e. with \(\varphi _0\) in the form (12a). However, the elastic energy \(\varphi (\varvec{\varepsilon },\alpha )\) can be anisotropic for \(\alpha >0\).
The decomposition of the elastic energy induces an analogue decomposition for the stress tensor and the damage energy release rate appearing in the equilibrium equation and the damage criterion (8):
The main idea is to associate \(\varphi _{D}\) to tension-like states and \(\varphi _R\) to compression-like states, in order to obtain a residual stiffness in compression for completely damaged states. Because of the associate nature of the damage model, this kind of decomposition affects directly the damage criteria (7) and the domains of admissible strains and stresses (9). Indeed, only \(\varphi _{D}\) contributes to the energy release rate Y, providing a driving force for the nucleation and evolution of damage. The elastic domain in the strain space is directly given by (9)
Obtaining the elastic domain in the stress space requires to compute \(\varvec{\varepsilon }(\varvec{\sigma },\alpha )\) as the inverse of the constitutive equation in (17) and substitute it back in the strain domain (18) as follows:
Assuming the decomposition in the form (16) ensures that, for varying \(\alpha \), \({\mathcal {R}}(\alpha )\) is transformed with a simple homothety centered in the origin. This is not true in general for \({\mathcal {R}}^*(\alpha )\). The stress domain \({\mathcal {R}}^*(\alpha )\) enjoys the same property if \(\varvec{\varepsilon }(\varvec{\sigma },\alpha )\) can be decomposed in the form \(s(\alpha )\,\varvec{\varepsilon }_D(\varvec{\sigma })+\varvec{\varepsilon }_R(\varvec{\sigma })\).
3.2 The volumetric-deviatoric strain energy decomposition
The decompositions proposed by Lancioni and Royer-Carfagni (2009) and by Amor et al. (2009) are both based on the orthogonal decomposition of the infinitesimal strain tensor in spherical and deviatoric components. The model by Lancioni and Royer-Carfagni (2009) allows only for shear fracture by taking:
The model by Amor et al. (2009) combines the above model with the basic fracture model (11), allowing for total fracture if the volumetric part of the deformation is positive and only shear fracture if the volumetric part of the deformation is negative. This is obtained by setting:
where \(\mathrm {tr}^+\) and \(\mathrm {tr}^-\) respectively denote the positive and negative parts of the trace, see (1).
The stress-strain relationship is given by Equation (17)a with
from which \(\mathrm {tr}^{+}(\varvec{\varepsilon }) = \mathrm {tr}^{+}(\varvec{\sigma })/(n\,\kappa \,a(\alpha ))\), \(\mathrm {tr}^{-}(\varvec{\varepsilon }) = \mathrm {tr}^{-}(\varvec{\sigma })/(n\,\kappa )\), and \(\varvec{\varepsilon }_{\mathrm {dev}}= \varvec{\sigma }_{\mathrm {dev}}/(2\, \mu \,a(\alpha ))\). Hence, one can compute the elastic strain and stress domains to obtain:
In this case, both domains transform with \(\alpha \) as homotheties centered in the origin.
3.3 The spectral strain energy decomposition
This model, proposed by Miehe et al. (2010), is based on the following expressions
with \({\varvec{\varepsilon }}^{+}=\sum _{i} \varepsilon _{i}^+{\mathbf {e}}_{i}\otimes {\mathbf {e}}_{i}\) and \({\varvec{\varepsilon }}^{-}=\sum _{i} \varepsilon _{i}^-{\mathbf {e}}_{i}\otimes {\mathbf {e}}_{i}\), \(\varepsilon _{i}\) being the eigenvalues of the strain tensor and \({\mathbf {e}}_{i}\) the corresponding eigenvectors.
For this model, the stress domain does not transform with \(\alpha \) as an homothety centered in the origin, thus the hardening or softening character of the model is more complex to evaluate. We can compute the elastic domains \({\mathcal {R}}\left( \alpha \right) \) and \({\mathcal {R}}^{*}\left( \alpha \right) \), but obtaining from them the strength surfaces requires additional considerations and is not further pursued here. The drawbacks of this decomposition and its induced stress-strain behavior under uniaxial stress states have been analyzed in Li (2016), where it is also shown that this model (unlike the others considered in this paper) does not fit in the variational framework of structured deformations that will be outlined in Sects. 3.4 and 4. For completeness, we report the elastic domains \({\mathcal {R}}\left( \alpha \right) \) and \({\mathcal {R}}^{*}\left( \alpha \right) \) in Appendix A and include \(\partial {\mathcal {R}}(0)\), \(\partial {\mathcal {R}}^*(0)\) in the plots to follow, so that they can be compared with the strength surfaces of the other decompositions.
3.4 The no-tension model
In (Freddi and Royer-Carfagni 2010), the authors applied the theory of structured deformations (Del Piero and Owen 1993) to the formulation of damage models. In this framework, they proposed an energy decomposition in the form (16) in order to reproduce at the fully damaged state the behavior of the so-called no-tension materials, i.e. materials that cannot withstand tensile stresses.
They assume that, because of micro-cracking, the elastic energy density of the pristine material, \(\varphi _0(\varvec{\varepsilon })\), is reduced by the presence of inelastic deformations \(\varvec{\eta }\), which are called structured deformations. The structured deformations are characterized by being constrained in a convex set \({\mathcal {K}}_{\varepsilon }\), which specifies the “structure” of the admissible micro-cracks. Given \(\varphi _0\) and \({\mathcal {K}}_{\varepsilon }\), the elastic energy of the fully cracked body is computed by solving the following minimization problem:
No-tension materials are defined by choosing \({\mathcal {K}}_{\varepsilon }=\mathrm {Sym}^{+}\), the convex cone of symmetric positive semi-definite second-order tensors. As shown later, the optimality conditions of (23) imply that the corresponding stress tensor must be in the convex cone of symmetric negative semi-definite second-order tensors \(\mathrm {Sym}^{-}\), i.e. that the material cannot sustain tension. For their application to the modeling of masonry structures, no-tension materials have been the object of many interesting works within the Italian community of theoretical solid mechanics (Sacco 1990; Angelillo 1993; Giaquinta and Giusti 1985; Lucchesi et al. 1996; Cuomo and Ventura 2000; Del Piero 1989). The solution of the problem (23) with \({\mathcal {K}}_{\varepsilon }=\mathrm {Sym}^{+}\) for the three-dimensional case is given in (Sacco 1990). Assuming without loss of generality to order the eigenvalues of \(\varvec{\varepsilon }\) such that \(\varepsilon _{1}\ge \varepsilon _{2}\ge \varepsilon _{3}\), this solution reads as follows
-
if \(\varepsilon _{3}\ge 0\), then \(\bar{\varvec{\eta }}=\varvec{\varepsilon }\),
-
else if \(\varepsilon _{2}+\nu \varepsilon _{3}\ge 0\), then \({\bar{\eta }}_{1}=\varepsilon _{1}+\nu \varepsilon _{3}\), \({\bar{\eta }}_{2}=\varepsilon _{2}+\nu \varepsilon _{3}\) and \({\bar{\eta }}_{3}=0\),
-
else if \(\varepsilon _{1}+\frac{\nu }{1-\nu }\left( \varepsilon _{2}+\varepsilon _{3}\right) \ge 0\) , then \({\bar{\eta }}_{1}=\varepsilon _{1}+\frac{\nu }{1-\nu }\left( \varepsilon _{2}+\varepsilon _{3}\right) \) and \({\bar{\eta }}_{2}={\bar{\eta }}_{3}=0\),
-
else, \(\bar{\varvec{\eta }}={\mathbf {0}}\).
Freddi and Royer-Carfagni (2010) proposed to define the elastic energy density for a partial damage level \(\alpha \) by linearly modulating the optimal inelastic deformation \(\bar{\varvec{\eta }}\) with \(\alpha \). They obtained in this way an energy in the form (16) with \(a(\alpha )=(1-\alpha )^2\). This idea can be easily generalized to an arbitrary \(a(\alpha )\) by setting
We will discuss this point and the main properties of this approach in the following section, where we will extend it to propose a new model obtained with a different choice of \({\mathcal {K}}_{\varepsilon }\).
Substituting \(\bar{\varvec{\eta }}\left( \varvec{\varepsilon }\right) \) in (24), the boundary of the elastic domain \({\mathcal {R}}\left( \alpha \right) \) is obtained as the set of \(\varvec{\varepsilon }\in Sym\) such that
-
if \(\varepsilon _{3}\ge 0\), \(\frac{1}{2}\kappa \left[ \mathrm {tr}\left( \varvec{\varepsilon }\right) \right] ^{2}+\mu \varvec{\varepsilon }_{\mathrm {dev}}\cdot \varvec{\varepsilon }_{\mathrm {dev}}\le -\frac{w_{1}w'\left( \alpha \right) }{a'\left( \alpha \right) }\),
-
else if \(\varepsilon _{2}+\nu \varepsilon _{3}\ge 0\), \(\frac{\lambda ^{2}}{2\left( \lambda +\mu \right) }\varepsilon _{3}^{2}+ \frac{\lambda }{2}\varepsilon _{3}\left( \varepsilon _{1}+\varepsilon _{2}\right) +\frac{\lambda }{2}\left( \varepsilon _{1}+\varepsilon _{2}\right) ^{2}+\mu \left( \varepsilon _{1}^{2}+\varepsilon _{2}^{2}\right) \le -\frac{w_{1}w'\left( \alpha \right) }{a'\left( \alpha \right) }\),
-
else if \(\varepsilon _{1}+\frac{\nu }{1-\nu }\left( \varepsilon _{2}+\varepsilon _{3}\right) \ge 0\), \(\frac{1}{2\left( \lambda +\mu \right) }\left[ \left( \lambda +2\mu \right) \varepsilon _{1}+\right. \left. \lambda \left( \varepsilon _{2}+\varepsilon _{3}\right) \right] ^{2}\le -\frac{w_{1}w'\left( \alpha \right) }{a'\left( \alpha \right) }\).
The boundary of the elastic domain in terms of stresses is found by computing \(\varvec{\sigma }\left( \varvec{\varepsilon },\alpha \right) \) from (8) and (24), inverting it to obtain \(\varvec{\varepsilon }\left( \varvec{\sigma },\alpha \right) \), and substituting it back in the strain domain. The resulting \({\mathcal {R}}^{*}\left( \alpha \right) \) is obtained as the set of \(\varvec{\sigma }\in Sym\) such that
-
if \(\sigma _{3}-\nu \left( \sigma _{1}+\sigma _{2}\right) \ge 0\), \(\frac{1}{18\kappa }\left[ \mathrm {tr}\left( \varvec{\sigma }\right) \right] ^{2}+\frac{1}{4\mu }\left\| \varvec{\sigma }_{\mathrm {dev}}\right\| ^{2}\le \frac{w_{1}w'\left( \alpha \right) }{s'\left( \alpha \right) }\),
-
else if \(\sigma _{2}-\frac{\nu }{1-\nu }\sigma _{1}\ge 0\), \(\frac{1}{8\mu \left( \lambda +\mu \right) }\left[ \lambda \left( \sigma _{1}-\sigma _{2}\right) ^{2}+2\mu \right. \left. \times \left( \sigma _{1}^{2}+\sigma _{2}^{2}\right) \right] \le \frac{w_{1}w'\left( \alpha \right) }{s'\left( \alpha \right) }\),
-
else if \(\sigma _{1}\ge 0\), \(\frac{1}{2\left( \lambda +2\mu \right) }\sigma _{1}^{2}\le \frac{w_{1}w'\left( \alpha \right) }{s'\left( \alpha \right) }\).
Freddi and Royer-Carfagni (2010) also demonstrated that with the above approach the energy decompositions in the previous sections, except for the spectral one, can be recovered by different choices of the convex cone \({\mathcal {K}}_{\varepsilon }\). In particular, the formulation with no energy decomposition is obtained with \({\mathcal {K}}_{\varepsilon }=\mathrm {Sym}\) (the space of all symmetric second-order tensors), whereas the split in (20) is recovered for \({\mathcal {K}}_{\varepsilon }=\mathrm {Sym}_{\mathrm {dev}}\) (the space of symmetric second-order tensors with no spherical component) and the one in (21) results from taking \( {\mathcal {K}}_{\varepsilon }=\{ \mathrm {Sym}\;\mathrm { if }\,\mathrm {tr}\left( \varvec{\varepsilon }\right) \ge 0,\; \mathrm {Sym}_{\mathrm {dev}} \; \mathrm {if}\;\mathrm {tr}\left( \varvec{\varepsilon }\right) <0\} \). More details on the above approach can be found in the original paper and some are recalled in Sect. 4, as the proposed generalized energy decomposition fits in this framework as well.
3.5 Strength surfaces
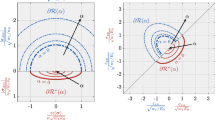
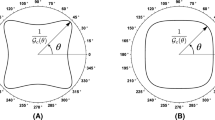
The key results of this section are summarized in Figs. 1 and 2, which report the strength surfaces for the considered models in the general three-dimensional case and in plane stress (\(\sigma _{3}=0\)), respectively. From these surfaces we can also compute the uniaxial tensile and compressive strengths \(\sigma _{tens}\) and \(\sigma _{compr}\) (the latter taken as absolute value), which are obtained from the conditions \(\sigma _{2}=\sigma _{3}=0\) with \(\sigma _{1}>0\) and \(\sigma _{1}<0\), respectively, and the shear strength in plane stress \(\sigma _{shear}\) (again in absolute value), which follows from the conditions \(\sigma _{2}=-\sigma _{1}\) and \(\sigma _{3}=0\). Their expressions are reported in Table 1 and in Appendix B.
For all the considered models, the calibration procedure alluded to in the introduction is carried out as follows: for given (experimentally known) values of the elastic properties (E and \(\nu \)) of the material, the tensile strength given in Table 1 is equated to the experimentally known tensile strength, which delivers the value of \(w_1\). From this, for a given (experimentally known) value of the fracture toughness \(G_c\), the value of the length scale is set using (15a) or (15b) (or the appropriate relationships if other models are used). It is clear that, after this calibration, the compressive and the shear strengths of the material automatically result from the expressions in Table 1 and typically do not match the experimental values for common brittle materials. For example, the ratio of compressive to tensile strengths delivered by the volumetric-deviatoric energy decomposition is only slightly larger than the unity, whereas the one predicted by the no-tension model is infinite. This lack of flexibility has already been recognized, see e.g. Sect. 4.4 in (Amor et al. 2009), (Li 2016), (Lorentz 2017), and, more recently, (Kumar et al. 2020). It limits the possibility of currently available phase-field models to quantitatively predict nucleation under states of stress that are far from pure tension. As a side note, we can remark also that the spectral energy decomposition proposed in Miehe et al. (2010) can lead to non-convex strength surfaces for extreme values of the Poisson’s ratio, as shown in Fig. 2 for \(\nu =-0.25\).
4 A novel energy decomposition giving a parametric strength surface à la Drucker–Prager.
As mentioned earlier, Freddi and Royer-Carfagni (2010) showed that some of the available energy density decompositions can be obtained as special cases of a general formulation involving the variational problem (23). The roots of this formulation are in the theory of structured deformations of Del Piero and Owen (1993) - which was developed within a framework with sharp discontinuities, and not within a regularized setting - as well as in a plethora of works on the behavior of no-tension materials, with masonry as envisioned application (Sacco 1990; Lucchesi et al. 1996; Cuomo and Ventura 2000; Del Piero 1989). The formulation is based on the following steps:
-
1.
The definition of the strain density of the pristine material \(\varphi _0(\varvec{\varepsilon })\);
-
2.
The definition of the set of admissible deformations \({\mathcal {K}}_\varepsilon \) which determines the residual strain energy of the fully damaged material, \(\varphi _R(\varvec{\varepsilon })\), as the solution of the minimization problem (23);
-
3.
The definition of the energy of the partially damaged material by modulating the amplitude of the structured deformation with the damage variable, as in (24).
As follows, we exploit this approach to formulate a novel energy decomposition featuring a strength surface à la Drucker–Prager, in which the ratio between the strengths in tension and in compression can be modulated by suitably setting an additional material parameter. Before presenting the new model, we illustrate some general properties of the optimal solution of the structured deformation problem (23) and of the corresponding elastic energy density (24).
4.1 Optimality conditions for the structured deformation \(\varvec{\eta }\)
In the theory of structured deformations, the elastic energy density is defined by solving the minimization problem (23), where \(\varphi _0\) is the convex elastic energy density of the pristine material. We recall below the basic notions of convex optimization theory needed to solve this problem, focusing on the case in which \({\mathcal {K}}_\varepsilon \) is a convex cone, which means that \(\forall \eta _1,\eta _2\in {\mathcal {K}}_\varepsilon \), \(\forall c_1,c_2\ge 0\), \(c_1\eta _1+c_2\eta _2\in {\mathcal {K}}_\varepsilon \).
The convexity of the strain energy function and of the cone \({\mathcal {K}}_\varepsilon \) implies the uniqueness of the solution of the minimization problem for any given \(\varvec{\varepsilon }\). Let us call this solution \(\bar{\varvec{\eta }}(\varvec{\varepsilon })\). By definition of minimality, it must verify the following condition:
where we introduced the following definitions:
The optimal inelastic deformation \(\bar{\varvec{\eta }}(\varvec{\varepsilon })\) and the optimal stress-strain relationship \(\bar{\varvec{\sigma }}(\varvec{\varepsilon })\) are characterized by the following proposition, which is a classical result of convex optimization (Boyd and Vandenberghe 2004):
Proposition 1
For a given \(\varvec{\varepsilon }\), the solution of the convex optimization problem (23) defined on the convex cone \({\mathcal {K}}_{\varepsilon }\) is unique and must verify the following conditions:
where
is the negative dual cone (or polar cone) of \({\mathcal {K}}_{\varepsilon }\). Moreover, if \(\bar{\varvec{\eta }}(\varvec{\varepsilon }) \in \mathring{{\mathcal {K}}}_\varepsilon \) (the interior of \({\mathcal {K}}_{\varepsilon }\)), then \(\bar{\varvec{\sigma }}(\varvec{\varepsilon })={\varvec{0}}\), if \(\bar{\varvec{\sigma }}(\varvec{\varepsilon }) \in \mathring{{\mathcal {K}}}_\sigma \) (the interior of \({\mathcal {K}}_{\sigma }\)), then \(\bar{\varvec{\eta }}(\varvec{\varepsilon })={\varvec{0}}\).
Proof
Neglecting higher order terms, (25) gives the following variational inequality:
Taking once \(\varvec{\eta }={\varvec{0}}\) and once \(\varvec{\eta }=2\,\bar{\varvec{\eta }}(\varvec{\varepsilon })\) to test (28) gives the following orthogonality condition for the solution:
Hence, the inequality (28) implies that \( \bar{\varvec{\sigma }}(\varvec{\varepsilon }) \in {\mathcal {K}}_\sigma \).
Moreover, if \(\bar{\varvec{\eta }}(\varvec{\varepsilon })\in \mathring{{\mathcal {K}}}_\varepsilon \), then for each \(\hat{\varvec{\eta }}\in {\mathcal {K}}_{\varepsilon }\), for h sufficiently small, \(\varvec{\eta }=\bar{\varvec{\eta }}(\varvec{\varepsilon })\pm h\hat{\varvec{\eta }}\in {\mathcal {K}}_{\varepsilon }\) can be used to test (28). This implies that if \(\bar{\varvec{\eta }}(\varvec{\varepsilon })\in \mathring{{\mathcal {K}}}_\varepsilon \), then \(\bar{\varvec{\sigma }}(\varvec{\varepsilon })={\varvec{0}}\). Vice versa, if \(\bar{\varvec{\sigma }}(\varvec{\varepsilon })\in \mathring{{\mathcal {K}}}_\sigma \), the inequality in the definition of \({\mathcal {K}}_\sigma \) must be strict, i.e. \(\bar{\varvec{\sigma }}(\varvec{\varepsilon })\cdot {\varvec{\eta }} < 0\), \(\forall {\varvec{\eta }}\in {\mathcal {K}}_\varepsilon \setminus {\mathbf {0}}\). Hence, if \(\bar{\varvec{\sigma }}(\varvec{\varepsilon })\in \mathring{{\mathcal {K}}}_\sigma \), the orthogonality condition implies that \(\bar{\varvec{\eta }}(\varvec{\varepsilon })={\mathbf {0}}\). \(\square \)
The following proposition uses the optimality condition above to characterize the energy of the damaged material defined in (24).
Proposition 2
The definition (24) for the energy of the damaged material, with \(\bar{\varvec{\eta }}(\varvec{\varepsilon })\) solution of the structured deformation problem (23) and \(\varphi _0(\varvec{\varepsilon })\) a positively homogeneous function of degree 2, gives
with
\(\varvec{\sigma }_0\) and \(\bar{\varvec{\sigma }}\) being defined in (26).
Proof
Being \(\varphi _0\) 2-homogeneous, one can use (10) and the 1-homogeneity of the stress to obtain

where the last term vanishes because of the orthogonality condition in (27). \(\square \)
4.2 The choice of the admissible structured deformations \({\mathcal {K}}_{\varepsilon }\)
For masonry materials, \({\mathcal {K}}_{\varepsilon }\) is the convex cone of positive semi-definite symmetric tensors and \({\mathcal {K}}_{\sigma }\) is the convex cone of negative semi-definite symmetric tensors. Hence, the structured deformation \(\varvec{\eta }\) has only non-negative eigenvalues (opening strains, also called “cracking strains” in the original papers, see e.g. Sacco (1990)) and the eigenvalues of the stress tensor \(\varvec{\sigma }(\varvec{\varepsilon })\) are all non-positive (compressive), which mirrors the expected behavior of a no-tension material.
Our aim is to generalize this behavior to a Drucker-Prager-like criterion for the admissible strain and stress. The Drucker-Prager failure model is inspired by the Coulomb friction law and is widely used to model compressive failure of a large class of cohesive-frictional materials, like rocks or concrete. It constraints the admissible shear stress \(\tau \) and the admissible normal stress \(\sigma \) by an inequality of the type \(\tau \le -\sigma \tan (\phi )+c\), where \(\phi \) is called friction angle and c cohesion.
As follows, we formulate a damage model leading to a similar behavior, with vanishing cohesion (\(c=0\)). To this end, we assume that the energy of the fully damaged material is the result of the structured deformation problem (23) where we define the convex cone of admissible structured deformations as follows:
This choice is justified by the following proposition, which gives the negative dual cone of sustainable stresses for the fully damaged material:
Proposition 3
\({\mathcal {K}}_{\varepsilon }\) is a convex cone. Its negative dual cone is
Proof
To show that \({\mathcal {K}}_{\varepsilon }\) is a convex cone, we can use the triangle inequality for any \(c_1,c_2\ge 0\)
Moreover, expanding the tensor scalar product using the volumetric-deviatoric decomposition, knowing that the scalar product cannot exceed the product of the norms and using the definition (33) gives
where the inequalities are satisfied as equalities taking \(\varvec{\eta }_{\mathrm {dev}} =\dfrac{\mathrm {tr}(\varvec{\eta })}{\gamma } \dfrac{\varvec{\sigma }_{\mathrm {dev}}}{\Vert \varvec{\sigma }_{\mathrm {dev}}\Vert }\). Hence, we get
which gives (34). \(\square \)
4.3 The solution of the structured deformation problem
Assuming that the pristine material is linearly elastic and isotropic, the structured deformation problem reads as
The following Lemma allows us to express the structured deformation in terms of only two scalar unknowns, the trace of the inelastic deformation \(\mathrm {tr}(\varvec{\eta })\) and the norm of its deviatoric part \(\Vert \varvec{\eta }_{\mathrm {dev}}\Vert \), by eliminating the dependence on the orientation of \(\varvec{\eta }_{\mathrm {dev}}\).
Lemma 1
Let \(\hat{\varvec{\varepsilon }}_{\mathrm {dev}}={\varvec{\varepsilon }_{\mathrm {dev}}}/{\Vert \varvec{\varepsilon }_{\mathrm {dev}}\Vert }\) be the director of \(\varvec{\varepsilon }_{\mathrm {dev}}\). The solution of the problem (35) is in the form \( \bar{\varvec{\eta }}_{\mathrm {dev}}(\varvec{\varepsilon }) = {\Vert \bar{\varvec{\eta }}_{\mathrm {dev}}(\varvec{\varepsilon })\Vert }\,\hat{\varvec{\varepsilon }}_{\mathrm {dev}} \) and \( \bar{\varvec{\sigma }}_{\mathrm {dev}}(\varvec{\varepsilon }) = {\Vert \bar{\varvec{\sigma }}_{\mathrm {dev}}(\varvec{\varepsilon })\Vert }\,\hat{\varvec{\varepsilon }}_{\mathrm {dev}} \). Hence, \(\Vert \varvec{\varepsilon }_{\mathrm {dev}} - \bar{\varvec{\eta }}_{\mathrm {dev}}(\varvec{\varepsilon }) \Vert ^2=\left( \Vert \varvec{\varepsilon }_{\mathrm {dev}}\right. \left. \Vert -\Vert \bar{\varvec{\eta }}_{\mathrm {dev}}(\varvec{\varepsilon }) \Vert \right) ^2\) and \({\Vert \bar{\varvec{\sigma }}_{\mathrm {dev}}\Vert } = 2\mu (\Vert \varvec{\varepsilon }_{\mathrm {dev}}\Vert - \Vert \bar{\varvec{\eta }}_{\mathrm {dev}}(\varvec{\varepsilon }) \Vert )\).
Proof
The orientation of the tensor \(\varvec{\varepsilon }_{\mathrm {dev}}\) appears in the minimization problem only in the last term of the energy, for which we have
where the last inequality is satisfied as an equality if and only if \(\varvec{\eta }_{\mathrm {dev}}\) is collinear to \(\varvec{\varepsilon }_{\mathrm {dev}}\), and such an \(\varvec{\eta }\) is admissible for any \(\varvec{\varepsilon }\in \mathrm {Sym}\). Hence, \(\varvec{\eta }\) cannot be a minimizer if it does not verify this condition. Because of its definition (8) and the isotropy of the energy density, \(\bar{\varvec{\sigma }}_{\mathrm {dev}}(\varvec{\varepsilon })=2\,\mu (\varvec{\varepsilon }_{\mathrm {dev}}-\bar{\varvec{\eta }}_{\mathrm {dev}}(\varvec{\varepsilon }))\), which implies that \(\left\| \bar{\varvec{\sigma }}_{\mathrm {dev}}\left( \varvec{\varepsilon }\right) \right\| = 2\mu \left( \left\| \varvec{\varepsilon }_{\mathrm {dev}}\right\| - \left\| \bar{\varvec{\eta }}_{\mathrm {dev}}\left( \varvec{\varepsilon }\right) \right\| \right) \), where \(\left\| \bar{\varvec{\eta }}_{\mathrm {dev}}\left( \varvec{\varepsilon }\right) \right\| \le \left\| \varvec{\varepsilon }_{\mathrm {dev}}\right\| \). The proof of the remaining part of the statement follows immediately. \(\square \)
The remaining optimal parameters of the inelastic deformation (\(\Vert \bar{\varvec{\eta }}_{\mathrm {dev}}\Vert \), \(\mathrm {tr}(\bar{\varvec{\eta }})\)) and the stress (\(\Vert \bar{\varvec{\sigma }}_{\mathrm {dev}}\Vert \), \(\mathrm {tr}(\bar{\varvec{\sigma }})\)) can be determined by applying the results of Proposition 1, which can be summarized saying that either the inelastic deformation and the stress are on the boundary of the respective cones, or the respective dual variables vanish. With the cone of admissible deformations (33) and the corresponding negative dual cone of admissible stresses (34) we obtain:
with the following constitutive relations:
Because of the Proposition 1, if one of the two inequalities is verified strictly, the corresponding dual variable vanishes. Hence, we have three cases:
-
1.
\(\gamma \Vert \varvec{{\bar{\eta }}}_{\mathrm {dev}}\Vert < {\mathrm {tr}(\varvec{{\bar{\eta }}})}\), hence \(\varvec{{\bar{\sigma }}}={\varvec{0}}\) and \(\varvec{{\bar{\eta }}}=\varvec{\varepsilon }\), which is admissible for \(\Vert \varvec{\varepsilon }_{\mathrm {dev}}\Vert < {\mathrm {tr}(\varvec{\varepsilon })}/\gamma \).
-
2.
\(\Vert \varvec{{\bar{\sigma }}}_{\mathrm {dev}}\Vert <-{\gamma }\,\mathrm {tr}(\varvec{{\bar{\sigma }}})/n\), hence \(\varvec{{\bar{\eta }}}={\varvec{0}}\), \(\mathrm {tr}({\varvec{{\bar{\sigma }}}})=n\,\kappa \, \mathrm {tr}(\varvec{\varepsilon })\), and \(\Vert \varvec{{\bar{\sigma }}}_{\mathrm {dev}}\Vert =2\mu \,\Vert \varvec{\varepsilon }_{\mathrm {dev}}\Vert \), which is admissible for \(\Vert \varvec{\varepsilon }_{\mathrm {dev}}\Vert < -\frac{\gamma \,\kappa }{2\,\mu }\,{\mathrm {tr}(\varvec{\varepsilon })}\).
-
3.
\(\Vert \varvec{{\bar{\eta }}}_{\mathrm {dev}}\Vert = {\mathrm {tr}(\varvec{{\bar{\eta }}})}/{\gamma }\) and \(\Vert \varvec{{\bar{\sigma }}}_{\mathrm {dev}}\Vert =-{\gamma }\mathrm {tr}(\varvec{{\bar{\sigma }}})/n\). These relations and the constitutive equations (36) form a linear system that can be solved to obtain
$$\begin{aligned}&\Vert \varvec{{\bar{\eta }}}_{\mathrm {dev}}\Vert = \frac{\mathrm {tr}(\varvec{\varepsilon })+\dfrac{2\mu }{k\gamma }\Vert \varvec{\varepsilon }_{\mathrm {dev}}\Vert }{\gamma +\frac{2\mu }{k\gamma }}, \quad \mathrm {tr}(\varvec{{\bar{\eta }}})=\gamma \,\Vert \varvec{{\bar{\eta }}}_{\mathrm {dev}}\Vert ,\\&\Vert \varvec{{\bar{\sigma }}}_{\mathrm {dev}}\Vert = \frac{2\mu (\gamma \,\Vert \varvec{\varepsilon }_{\mathrm {dev}}\Vert -\mathrm {tr}(\varvec{\varepsilon }))}{\gamma +\frac{2\mu }{k\gamma }},\\&\mathrm {tr}(\varvec{{\bar{\sigma }}})=-\frac{n}{\gamma }\Vert \varvec{{\bar{\sigma }}}_{\mathrm {dev}}\Vert . \end{aligned}$$This solution is admissible if and only if the expressions for the norm are non-negative, i.e. for \(\Vert \varvec{\varepsilon }_{\mathrm {dev}}\Vert \ge -\frac{\gamma \,\kappa }{2\,\mu }\,{\mathrm {tr}(\varvec{\varepsilon })}\) and \(\Vert \varvec{\varepsilon }_{\mathrm {dev}}\Vert \ge {\mathrm {tr}(\varvec{\varepsilon })}/\gamma \).
In conclusion, we have that the optimal inelastic deformation is
and the stress-strain relationship for the fully damaged material is
4.4 The proposed damage model and its elastic domains
The energy of the proposed damage model is readily obtained replacing (37) and (38) in the general expression (31). From this we obtain:
Thus, \({\mathcal {R}}\left( \alpha \right) \) is obtained as the set of \(\varvec{\varepsilon }\in Sym\) such that
-
if \(\mathrm {tr}\left( \varvec{\varepsilon }\right) -\gamma \left\| \varvec{\varepsilon }_{\mathrm {dev}}\right\| >0\), \(\frac{\kappa }{2}\mathrm {tr}^{2}\left( \varvec{\varepsilon }\right) +\mu \left\| \varvec{\varepsilon }_{\mathrm {dev}}\right\| ^{2}\le -\frac{w_{1}w'\left( \alpha \right) }{a'\left( \alpha \right) }\),
-
else if \(\mathrm {tr}\left( \varvec{\varepsilon }\right) +\frac{2\mu }{\gamma \kappa }\left\| \varvec{\varepsilon }_{\mathrm {dev}}\right\| \ge 0\), \(\frac{1}{2\left( \kappa \gamma ^{2}+2\mu \right) }\big [\kappa \gamma \mathrm {tr}\big (\varvec{\varepsilon }\big )+2\mu \big \Vert \varvec{\varepsilon }_{\mathrm {dev}}\big \Vert \big ]^{2}\le -\frac{w_{1}w'\big (\alpha \big )}{a'\big (\alpha \big )}\).
\({\mathcal {R}}^{*}\left( \alpha \right) \) is obtained as the set of \(\varvec{\sigma }\in Sym\) such that
-
if \(\mathrm {tr}\left( \varvec{\sigma }\right) -\frac{n\gamma \kappa }{2\mu }\left\| \varvec{\sigma }_{\mathrm {dev}}\right\| >0\), \(\frac{1}{2n^{2}\kappa }\mathrm {tr}^{2}\left( \varvec{\sigma }\right) +\frac{1}{4\mu }\left\| \varvec{\sigma }_{\mathrm {dev}}\right\| ^{2}\le \frac{w_{1}w'\left( \alpha \right) }{s'\left( \alpha \right) }\),
-
else if \(\mathrm {tr}\left( \varvec{\sigma }\right) +\frac{n}{\gamma }\left\| \varvec{\sigma }_{\mathrm {dev}}\right\| \ge 0\), \(\frac{1}{2n^{2}\left( \kappa \gamma ^{2}+2\mu \right) }\big [\gamma \mathrm {tr}\big (\varvec{\sigma }\big )+n\big \Vert \varvec{\sigma }_{\mathrm {dev}}\big \Vert \big ]^{2}\le \frac{w_{1}w'\big (\alpha \big )}{s'\big (\alpha \big )}\).
Now recall that the strength surfaces coincide with the boundaries of the elastic domains for \(\alpha = \alpha _c\). A comparison with (13) shows immediately that, as the volumetric-deviatoric and the no-tension energy decompositions, also the proposed generalized model shares part of its strength surface (the part for which \(\mathrm {tr}\left( \varvec{\sigma }\right) -\frac{n\gamma \kappa }{2\mu }\left\| \varvec{\sigma }_{\mathrm {dev}}\right\| >0\)) with the model without energy decomposition, whereas the remaining part will be shown in Sect. 4.5 to be of Drucker-Prager type.
4.4.1 Limit cases
Recalling Sect. 3.4, it is straightforward to show that the proposed generalized formulation admits the model by Amor et al. (2009) as limit case for \(\gamma =0\). In fact, for \(\gamma =0\) the convex cone reduces to \({\mathcal {K}}_{\varepsilon }=\left\{ \varvec{\eta }\in Sym:\mathrm {tr}\left( \varvec{\eta }\right) \ge 0\right\} \) which can be shown to be equivalent to (21). For \(n=2\) it can also be shown that the special case \(\gamma =\sqrt{2}\) delivers \({\mathcal {K}}_{\varepsilon }=Sym^{+}\) which corresponds to the model by (Freddi and Royer-Carfagni 2010).
4.5 Nucleation domains and discussion
The nucleation domains, i.e. the strength surfaces, are illustrated for different values of \(\gamma \) in Figs. 3 and 4 in the general three-dimensional case and in plane stress (\(\sigma _3=0\)), respectively. The generalized model enhances the flexibility of the available models on the nucleation under multiaxial stress states, by introducing the possibility to taylor the slope of the surfaces (or, under plane stress or plane strain conditions, the lines) delimiting the nucleation domains in order to conveniently match experimental results. Hence, one can control the ratio of the compressive to the tensile strength in uniaxial conditions, or alternatively the ratio of the shear strength in plane stress to the uniaxial tensile strength. These ratios are given in Table 2 and depend on the free parameter \(\gamma \), so that one of them can be matched to the experimentally known value by setting \(\gamma \) appropriately (and the other one will result automatically).
Once \(\gamma \) is calibrated to match one of these ratios, the specific fracture energy \(w_1\) can be set to match the tensile strength to the experimental value. Finally, the internal length \(\ell \) will determine the experimental fracture toughness \(G_c\) for the dissipated energy in the localized solution. The analysis of the localized solution is out of the scope of the present work. For the sake of simplicity, and without any formal justification, we apply here the relation in (15a) for the identification of the internal length \(\ell \) from the values of \(G_c\) and \(w_1\). An in-depth analysis of this point will be the subject of future work.
The table containing the expressions of \(\sigma _{tens}\), \(\sigma _{compr}\) and \(\sigma _{shear}\) is reported in AppendixB. Note that, for \(0\le \gamma \le \sqrt{\frac{3}{2}}\frac{1-2\nu }{1+\nu }\), the conditions for the uniaxial tensile strength satisfy \(\mathrm {tr}\left( \varvec{\sigma }\right) -\frac{n\gamma \kappa }{2\mu }\left\| \varvec{\sigma }_{\mathrm {dev}}\right\| >0\), thus the corresponding point belongs to the strength surface of the phase-field model without energy decomposition. Instead, for \(\gamma \ge \sqrt{\frac{3}{2}}\frac{1-2\nu }{1+\nu }\), the uniaxial tensile strength conditions fall within the new strength surface. The point corresponding to the uniaxial compressive strength conditions always satisfies \(\mathrm {tr}\left( \varvec{\sigma }\right) -\frac{n\gamma \kappa }{2\mu }\left\| \varvec{\sigma }_{\mathrm {dev}}\right\| <0\) regardless of the value of \(\gamma \), hence, it never falls within the strength surface of the model without energy decomposition. On the other hand, simple calculations show that for \(\gamma >\sqrt{6}\) it is always \(\mathrm {tr}\left( \varvec{\sigma }\right) +\frac{n}{\gamma }\left\| \varvec{\sigma }_{\mathrm {dev}}\right\| <0\), so that no damage ever develops under uniaxial compression. For \(0\le \gamma <\sqrt{6}\), the uniaxial compressive strength is attained on the new strength surface. Finally, the point corresponding to the shear strength in plane stress is always attained on the new strength surface, regardless of the value of \(\gamma \).
As follows, we show with simple calculations that for \(\sqrt{\frac{3}{2}}\frac{1-2\nu }{1+\nu }\le \gamma \le \sqrt{6}\) (assuming \(\nu \ge -1/4\)), i.e. within the range of \(\gamma \) for which the points corresponding to the uniaxial tensile strength and the uniaxial compressive strength both fall within the new strength surface, part of the strength surface of the generalized model (i.e. the new strength surface) is of Drucker-Prager type, i.e. it corresponds to
with \(I_{1}\) and \(J_{2}\) as the first invariant of \(\varvec{\sigma }\) and the second invariant of \(\varvec{\sigma }_{\mathrm {dev}}\), respectively. As commented at the end of Sect. 4.4, the strength surface of the generalized model coincides with the strength surface of the model with no energy decomposition for \(\mathrm {tr}\left( \varvec{\sigma }\right) -\frac{n\gamma \kappa }{2\mu }\left\| \varvec{\sigma }_{\mathrm {dev}}\right\| >0\). Instead, for \(\mathrm {tr}\left( \varvec{\sigma }\right) -\frac{n\gamma \kappa }{2\mu }\left\| \varvec{\sigma }_{\mathrm {dev}}\right\| \le 0\) and \(\mathrm {tr}\left( \varvec{\sigma }\right) +\frac{n}{\gamma }\left\| \varvec{\sigma }_{\mathrm {dev}}\right\| \ge 0\), it reads
where we have accounted for the relationships \(\left\| \varvec{\sigma }_{dev}\right\| =\sqrt{2J_{2}}\), \(\mathrm {tr}\left( \varvec{\sigma }\right) =I_{1}\) and we have considered the three-dimensional case \(n=3\). Now note that for this range of \(\gamma \) it is \(\frac{\sigma _{compr}}{\sigma _{tens}}=\frac{\sqrt{6}+\gamma }{\sqrt{6}-\gamma }\) (see Table 1), which can be rewritten as
so that we easily obtain
Moreover, the uniaxial compressive strength is given by \(\sigma _{comp}=\sqrt{\frac{18\left( \kappa \gamma ^{2}+2\mu \right) }{\left( \sqrt{6}-\gamma \right) ^{2}}\frac{w_{1}w'\left( \alpha _{c}\right) }{s'\left( \alpha _{c}\right) }}\) (see Appendix B), so that it is also
Normalized strength surface of the generalized model in the principal stress space (\(\nu =0.25\)) for a \(\gamma =0.05\) , b \(\gamma =0.3\), c \(\gamma =1\), d \(\gamma =2.5\). For both a and b it is \(\gamma <\sqrt{\frac{3}{2}}\frac{1-2\nu }{1+\nu }\); these models are close to the one with volumetric-deviatoric decomposition (attained exactly for \(\gamma =0\)); for the model in (c) it is \(\sqrt{\frac{3}{2}}\frac{1-2\nu }{1+\nu }<\gamma <\sqrt{6}\), hence part of the strength surface is exactly of the Drucker-Prager type (the Drucker-Prager surface is plotted in light grey for comparison); the model in (d) has \(\gamma >\sqrt{6}\) which gives unlimited strength in uniaxial compression. The ratio of compressive to tensile strength, \(\sigma _{compr}/\sigma _{tens}\), is equal to 1.12, 1.29, 2.38 and \(\infty \) for (a), (b), (c) and (d), respectively
The comparison between the strength surface of the generalized model and the Drucker-Prager strength surface in the stress space for \(\sqrt{\frac{3}{2}}\frac{1-2\nu }{1+\nu }\le \gamma \le \sqrt{6}\) is shown in Fig. 3c (for \(\nu = 0.25\)). The difference between the two surfaces is limited to the region close to the vertex of the Drucker-Prager cone, where the surface of the generalized model features a rounded termination which corresponds to the stress range where the model with no energy decomposition applies. From the same figure it can be easily inferred that this deviation is no longer visible in plane stress conditions, e.g. for \(\sigma _3=0\), as the corresponding cross-sections of both surfaces are identical.
We finally exemplify calibration of the new model for the experimental results in Fig. 5, which are the same shown in Kumar et al. (2020), corresponding to titania (Ely 1972) and graphite (Sato et al. 1987). The materials have experimentally known values of elastic constants and strengths that are reported in Table 3. We decide to use the \(\mathtt {AT}_1\) model, thus \(\alpha _{c}=0\) and \(\frac{w_{1}w'\left( 0\right) }{s'\left( 0\right) }=\frac{w_{1}}{2}\).
For titania, based on the experimental ratio of the compressive to the tensile strength and using (43), we calibrate \(\gamma =2.08\). This value is then verified to fall within the range \(\sqrt{\frac{3}{2}}\frac{1-2\nu }{1+\nu }\le \gamma \le \sqrt{6}\), which is the condition for the validity of (43). Then, based on the expression of the tensile strength in Table 1 and on the experimental tensile strength in Table 3, we calibrate \(w_{1}=0.0217\,\mathrm {MPa}\), which can eventually be used to compute \(\ell =0.62\,\mathrm {mm}\) when assuming the expression in (15a) for \(G_c\). The exact same procedure can be repeated for graphite finding \(\gamma =1.18\), \(w_{1}=0.0725\,\mathrm {MPa}\), and \(\ell =0.47\,\mathrm {mm}\). The strength surfaces in plane stress are reported for both materials in Fig. 5, where they can be noticed to fit very well the experimental results. As noted above, these are exactly Drucker-Prager strength surfaces.
Normalized strength surfaces of the generalized model in the principal stress space in plane stress for Poisson’s ratios \(\nu =-\,0.25\) (left), \(\nu =0.25\) (center), and \(\nu =0.49\) (right) and various values of the parameter \(\gamma \). For \(\nu =-0.25\), the ratio of compressive to tensile strength, \(\sigma _{compr}/\sigma _{tens}\), is equal to 1.44, 1.62, 2.58 and \(\infty \) for \(\gamma \) equal to 0.05, 0.3, 1.0 and 2.5, respectively. For \(\nu =0.25\), \(\sigma _{compr}/\sigma _{tens}\) is equal to 1.12, 1.29, 2.38 and \(\infty \) for \(\gamma \) equal to 0.05, 0.3, 1.0 and 2.5, respectively. For \(\nu =0.49\), \(\sigma _{compr}/\sigma _{tens}\) is equal to 1.04, 1.28, 2.38 and \(\infty \) for \(\gamma \) equal to 0.05, 0.3, 1.0 and 2.5, respectively
Comparison between the calibrated strength surfaces of the generalized model in plane stress with experimental results for a titania (Ely 1972) and b graphite (Sato et al. 1987). These strength surfaces exactly coincide with the Drucker-Prager strength surfaces corresponding to the compressive and tensile strengths of the materials, see Eq. (41)
5 Conclusions
We derived and proposed a generalized energy density decomposition for variational phase-field modeling of brittle fracture, which encompasses those by Amor et al. (2009) and Freddi and Royer-Carfagni (2010) as special cases. The newly proposed decomposition hinges upon the application of the theory of structured deformations and no-tension materials to the formulation of variational damage models proposed by Freddi and Royer-Carfagni (2010). In comparison to the previously available decompositions, the proposed one introduces a generalization whose flexibility enables the straightforward calibration of a multiaxial failure surface of the Drucker-Prager type. We thus demonstrate that a fully variational phase-field formulation is indeed able to correctly reproduce the multi-axial nucleation threshold of real materials characterized by a strength surface \(\grave{a}\) la Drucker-Prager, provided that it is endowed with a sufficiently general strain energy decomposition. This finding is in contrast with the claim of Kumar et al. (2020), which advocates the necessity of a non-energetic model to recover a similar behavior.
The presented investigation paves the way for many further developments. We only explored the consequences of the generalized decomposition on the strength surfaces, and ignored the following behavior featuring localization and crack propagation. Future research will focus on this subsequent phase, with the aim of relieving or possibly suppressing the known drawbacks of the available strain energy decompositions. It goes without saying that numerical and experimental investigations would be mandatory to complement and support the present analytical study. They are currently in progress and will be reported in forthcoming publications. Moreover, more complex and flexible multiaxial failure surfaces can be envisioned along the lines of the proposed formulation, by appropriately choosing the convex space where the minimization problem leading to the structured strain in fully damaged conditions is carried out. Finally, future work should aim at addressing the other fundamental issue pointed out by Kumar et al. (2020) about the nucleation threshold under isotropic loading in the incompressible limit within a variational approach.
References
Amor H, Marigo J-J, Maurini C (2009) Regularized formulation of the variational brittle fracture with unilateral contact: numerical experiments. J Mech Phys Solids 57(8):1209–1229
Angelillo M (1993) Constitutive relations for no-tension materials. Meccanica 28(3):195–202
Ballard P (2013) Steady sliding frictional contact problems in linear elasticity. J Elast 110(1):33–61
Borden MJ, Verhoosel CV, Scott MA, Hughes TJ, Landis CM (2012) A phase-field description of dynamic brittle fracture. Comput Methods Appl Mech Eng 217–220:77–95
Bourdin B, Francfort G-A, Marigo J-J (2000a) Numerical experiments in revisited brittle fracture. J Mech Phys Solids 48:787–826
Bourdin B, Francfort G, Marigo J-J (2000b) Numerical experiments in revisited brittle fracture. J Mech Phys Solids 48(4):797–826
Boyd S, Vandenberghe L (2004) Convex Optimization. Cambridge University Press, Cambridge
Comi C, Perego U (2001) Fracture energy based bi-dissipative damage model for con-crete. Int J Solids Struct 38(36):6427–6454
Cuomo M, Ventura G (2000) A complementary energy formulation of no tension masonry-like solids. Comput Methods Appl Mech Eng 189(1):313–339
Del Piero G (1989) Constitutive equation and compatibility of the external loads for linear elastic masonry-like materials. Meccanica 24(3):150–162
Del Piero G, Owen DR (1993) Structured deformations of continua. Arch Rational Mech Anal 124(2):99–155
Ely RE (1972) Strength of titania and aluminum silicate under combined stresses. J Am Ceramic Soc 55(7):347–350
Francfort G, Bourdin B, Marigo J-J (2008) The variational approach to fracture. J Elast 91(1–3):5–148
Francfort G, Marigo J-J (1998) Revisiting brittle fracture as an energy minimization problem. J Mech Phys Solids 46(8):1319–1342
Freddi F, Royer-Carfagni G (2010) Regularized variational theories of fracture: a unified approach. J Mech Phys Solids 58:1154–1174
Giacomini A (2005) Ambrosio-Tortorelli approximation of quasi-static evolution of brittle fractures. Calc Variations Partial Differ Equ 22:129–172
Giaquinta M, Giusti E (1985) Researches on the equilibrium of masonry structures. Arch Rational Mech Anal 88(4):359–392
Goggin PR, Reynolds WN (1967) The elastic constants of reactor graphites. Philos Mag 16(140):317–330
Iuga M, Steinle-Neumann G, Meinhardt J (2007) Ab-initio simulation of elastic constants for some ceramic materials. Eur Phys J B 58(2):127–133
Kumar A, Bourdin B, Francfort GA, Lopez-Pamies O (2020) Revisiting nucleation in the phase-field approach to brittle fracture. J Mech Phys Solids 142:104027
Lancioni G, Royer-Carfagni G (2009) The variational approach to fracture mechanics. A practical application to the French Panthéon in Paris. J Elast 95:1–30
Larsen CJ (2010) Epsilon-stable quasi-static brittle fracture evolution. Commun Pure Appl Math 63(5):630–654
Li T (2016) Gradient-damage modeling of dynamic brittle fracture: variational principles and numerical simulations. PhD thesis
Lorentz E (2017) A nonlocal damage model for plain concrete consistent with cohesive fracture. Int J Fract 207(2):123–159
Lucchesi M, Padovani C, Zani N (1996) Masonry-like solids with bounded compressive strength. Int J Solids Struct 33(14):1961–1994
Marigo J (1989) Constitutive relations in plasticity, damage and fracture mechanics based on a work property. Nuclear Eng Des 114(3):249–272
Marigo J-J, Maurini C, Pham K (2016) An overview of the modelling of fracture by gradient damage models. en. Meccanica 51(12):3107–3128
Mesgarnejad A, Bourdin B, Khonsari MM (2015) Validation simulations for the variational approach to fracture. Comput Methods Appl Mech Eng 290:420–437
Miehe C, Welschinger F, Hofacker M (2010) Thermodynamically consistent phase-field models of fracture: variational principles and multi-field FE implementations. Int J Numeri Methods Eng 83(10):1273–1311
Negri M (2010) A comparative analysis on variational models for quasi-static brittle crack propagation. Adv Calc Variations 3(2):149–212
Nguyen TT, Yvonnet J, Bornert M, Chateau C, Sab K, Romani R, Le Roy R (2016) On the choice of parameters in the phase field method for simulating crack initiation with experimental validation. Int J Fracture 197(2):213–226
Pham K, Amor H, Marigo J-J, Maurini C (2011a) Gradient damage models and their use to approximate brittle fracture. Int J Damage Mech 20(4):618–652
Pham K, Marigo J-J (2010a) The variational approach to damage: II. The gradient damage models [Approche variationnelle de l’endommagement: II. Les modèles à gradient]. Comptes Rendus Mécanique 338(4):199–206
Pham K, Marigo J-J (2013) Stability of homogeneous states with gradient damage models: size effects and shape effects in the three-dimensional setting. J Elast 110(1):63–93
Pham K, Marigo J-J, Maurini C (2011b) The issues of the uniqueness and the stability of the homogeneous response in uniaxial tests with gradient damage models. J Mech Phys Solids 59(6):1163–1190
Pham KH, Ravi-Chandar K, Landis CM (2017) Experimental validation of a phase-field model for fracture. Int J Fracture 205(1):83–101
Pham K, Amor H, Marigo J-J, Maurini C (2011c) Gradient damage models and their use to approximate brittle fracture. Int J Damage Mech 20(4):618–652
Pham K, Marigo J-J (2010b) Approche variationnelle de l’endommagement: II. Les modèles à gradient. Comptes Rendus Mecanique 338(4):199–206
Sacco E (1990) Modellazione e calcolo di strutture in materiale non resistente a trazione. ita. In: Atti della Accademia Nazionale dei Lincei. Classe di Scienze Fisiche, Matematiche e Naturali. Rendiconti Lincei. Matematica e Applicazioni 1(3), 235–258
Sato S, Awaji H, Kawamata K, Kurumada A, Oku T (1987) Fracture criteria of reactor graphite under multiaxial stesses. Nuclear Eng Des 103(3):291–300
Sicsic P, Marigo J-J, Maurini C (2014) Initiation of a periodic array of cracks in the thermal shock problem: a gradient damage modeling. J Mech Phys Solids 63:256–284
Tanné E, Li T, Bourdin B, Marigo J-J, Maurini C (2018) Crack nucleation in variational phase-field models of brittle fracture. J Mech Phys Solids 110:80–99
Wu T, Carpiuc-Prisacari A, Poncelet M, De Lorenzis L (2017) Phase-field simulation of interactive mixed-mode fracture tests on cement mortar with full-field displacement boundary conditions. Eng Fracture Mech 182:658–688
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
The spectral strain energy decomposition
The stress-strain relationship is again given by Eq.(17a17b) with
which can be inverted most easily in component form. Thus, whereas the strain domain is directly obtained as
the stress domain must be found componentwise by distinguishing several cases. Assuming, without loss of generality, \(\varepsilon _{1}\ge \varepsilon _{2}\ge \varepsilon _{3}\), \({\mathcal {R}}^{*}\left( \alpha \right) \) is obtained as the set of \(\varvec{\sigma }\in Sym\) such that
-
if \(\sigma _{3}-\nu \left( \sigma _{1}+\sigma _{2}\right) \ge 0\)
$$\begin{aligned} \frac{1}{18\kappa }\mathrm {tr}^{2}\left( \varvec{\sigma }\right) +\frac{1}{4\mu }\left\| \varvec{\sigma }_{\mathrm {dev}}\right\| ^{2} \le \frac{w_{1}w'\left( \alpha \right) }{s'\left( \alpha \right) } \end{aligned}$$ -
else if \(\left[ \left( 1+a\left( \alpha \right) \right) \lambda +2\mu \right] \sigma _{2}-\lambda \sigma _{1}-a\left( \alpha \right) \lambda \sigma _{3}\ge 0\) and \(\sigma _{1}+\sigma _{2}+a\left( \alpha \right) \sigma _{3}\ge 0\)
$$\begin{aligned}&\frac{1}{4a^{2}\left( \alpha \right) \mu \left[ \left( 2+a\left( \alpha \right) \right) \lambda +2\mu \right] ^{2}}\\&\qquad \cdot \left\{ 4\mu ^{2}\left( \sigma _{1}^{2}+\sigma _{2}^{2}\right) +2\lambda \mu \left[ \left( 3+2a\left( \alpha \right) \right) \sigma _{1}^{2}\right. \right. \\&\left. \qquad -2\sigma _{1}\sigma _{2}+\left( 3+2a\left( \alpha \right) \right) \sigma _{2}^{2}+a^{2}\left( \alpha \right) \sigma _{3}^{2}\right] \\&\qquad +\lambda ^{2}\left[ \left( 2+2a\left( \alpha \right) +a^{2}\left( \alpha \right) \right) \left( \sigma _{1}^{2}+\sigma _{2}^{2}\right) \right. \\&\qquad -2a^{2}\left( \alpha \right) \sigma _{2}\sigma _{3}+2a^{2}\left( \alpha \right) \sigma _{3}^{2}\\&\qquad \left. \left. -2\sigma _{1}\left( 2\sigma _{2}+2a\left( \alpha \right) \sigma _{2}+a^{2}\left( \alpha \right) \sigma _{3}\right) \right] \right\} \\&\quad \le -\frac{w_{1}w'\left( \alpha \right) }{a'\left( \alpha \right) } \end{aligned}$$ -
else if \(\left[ \left( 1+a\left( \alpha \right) \right) \lambda +2a\left( \alpha \right) \mu \right] \sigma _{2}-\lambda \sigma _{1}-a\left( \alpha \right) \lambda \sigma _{3}\ge 0\) and \(\sigma _{1}+\sigma _{2}+a\left( \alpha \right) \sigma _{3}\le 0\)
Table 4 Tensile, compressive and shear strengths according to all considered models (we assume here \(\nu >-1/4\)) $$\begin{aligned}&\frac{1}{4a^{2}\left( \alpha \right) \mu \left[ \left( 2+a\left( \alpha \right) \right) \lambda +2a\left( \alpha \right) \mu \right] ^{2}}\\&\quad \cdot \left\{ \left[ \left( \lambda +a\left( \alpha \right) \lambda +2a\left( \alpha \right) \mu \right) \sigma _{1}-\lambda \sigma _{2}-a\left( \alpha \right) \lambda \sigma _{3}\right] ^{2}\right. \\&\qquad +\left. \left[ \left( \lambda \!+\!a\left( \alpha \right) \lambda \!+\!2a\left( \alpha \right) \mu \right) \sigma _{2}\!-\!\lambda \sigma _{1}\!-\!a\left( \alpha \right) \lambda \sigma _{3}\right] ^{2}\right\} \\&\quad \le -\frac{w_{1}w'\left( \alpha \right) }{a'\left( \alpha \right) } \end{aligned}$$ -
else if \(2\mu \sigma _{1}+a\left( \alpha \right) \lambda \left( 2\sigma _{1}-\sigma _{2}-\sigma _{3}\right) \ge 0\) and \(\sigma _{1}+a\left( \alpha \right) \left( \sigma _{2}+\sigma _{3}\right) \ge 0\)
$$\begin{aligned}&\frac{1}{4a^{2}\left( \alpha \right) \mu \left[ \left( 1+2a\left( \alpha \right) \right) \lambda +2\mu \right] ^{2}}\\&\quad \cdot \left\{ \left[ \left( 8a\left( \alpha \right) +2\right) \lambda \mu +4\mu ^{2}\right] \sigma _{1}^{2}\right. \\&\quad +\left. a^{2}\left( \alpha \right) \lambda \left[ 2\mu \left( \sigma _{2}\!+\!\sigma _{3}\right) ^{2}\!+\!\lambda \left( \!-2\sigma _{1}\!+\!\sigma _{2}\!+\!\sigma _{3}\right) ^{2}\right] \right\} \\&\le -\frac{w_{1}w'\left( \alpha \right) }{a'\left( \alpha \right) } \end{aligned}$$ -
else if \(2\left( \lambda +\mu \right) \sigma _{1}-\lambda \left( \sigma _{2}+\sigma _{3}\right) \ge 0\) and \(\sigma _{1}+a\left( \alpha \right) \left( \sigma _{2}+\sigma _{3}\right) \le 0\)
$$\begin{aligned}&\frac{1}{4\mu \left[ \left( 1+2a\left( \alpha \right) \right) \lambda +2a\left( \alpha \right) \mu \right] ^{2}}\\&\quad \cdot \left[ 2\left( \lambda +\mu \right) \sigma _{1}-\lambda \left( \sigma _{2}+\sigma _{3}\right) \right] ^{2}\le -\frac{w_{1}w'\left( \alpha \right) }{a'\left( \alpha \right) } \end{aligned}$$
Tensile, compressive and shear strengths according to all models considered in this paper, including the newly proposed generalized one.
Rights and permissions
About this article
Cite this article
De Lorenzis, L., Maurini, C. Nucleation under multi-axial loading in variational phase-field models of brittle fracture. Int J Fract 237, 61–81 (2022). https://doi.org/10.1007/s10704-021-00555-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10704-021-00555-6