Optimal replenishment policy and preservation technology investment for a non-instantaneous deteriorating item with stock-dependent demand

Abstract

An inventory model with stock-dependent demand and non-instantaneous deterioration is developed in this paper. It is assumed that the item starts deteriorating at a constant rate after a certain period of time from the instant of receiving the delivery by the retailer. The retailer can reduce the rate of deterioration by investing in preservation technology. Depending on the fact that the on-hand stock may be finished before or after deterioration starts, two different inventory scenarios have been considered and analyzed. Optimal length of an inventory cycle as well as investment in preservation technology have been obtained in both the scenarios. Certain conditions have also been derived to identify situations where the retailer should or should not invest in preservation technology. The proposed model is illustrated with a numerical example.

1 Introduction

Market demand has been one of the major concerns of the managerial decision makers as well as researchers over decades. In the literature, different demand patterns have been assumed and studied for different types of products to reflect the real world scenarios. There are certain parameters such as price, quality, post-purchase support, credit facility, etc. on which the demand largely depends. On-hand stock display is one such parameter which affects market demand. Display of greater quantity of an item tends to attract more customers (Zhou and Yang 2005) in practice. Such kind of demand is particularly observed in fashion apparel industries, electronic items, supermarkets and convenience stores, etc. It is the visibility and variety of products that attract more customers. Levin et al. (1972) mentioned that large piles of consumer goods displayed would attract the customers to buy more. Silver and Peterson (1985) showed that sales at the retail level tend to be proportional to stock displayed. Baker and Urban (2009), Pal et al. (1993), and Giri et al. (1966) studied inventory models where market demand is a function of on-hand inventory. An order-level inventory model was developed by Ray et al. (1998) assuming the demand rate to be stock-dependent and the retailer could use two warehouses. Hwang and Hahn (2000) investigated an optimal procurement policy for items with an inventory-level-dependent demand rate and fixed lifetime. Chang (2004) discussed inventory models with stock-dependent demand and non-linear holding cost for deteriorating items. Wu et al. (2006) developed optimal replenishment policy incorporating the effects of deterioration and partial backlogging under stock-dependent demand scenario. Ouyang et al. (2008) dealt with an inventory problem for non-instantaneous deteriorating items with stock-dependent demand when supplier offers an all-unit quantity discount. Sajadieh et al. (2010) studied an integrated vendor-buyer model with stock-dependent demand. Pando et al. (2012) and Yang (2014) developed inventory models with the assumption that the holding cost is also stock-dependent. Yang et al. (2013) examined the effect of credit incentives on a two-echelon supply chain with stock-dependent demand. Ghiami et al. (2013) developed and analyzed inventory model for a deteriorating item with stock-dependent demand under capacity constraint and partial backlogging. Jiangtao et al. (2014) derived optimal ordering policy for multiple perishable items under stock-dependent demand and two-level trade credit. Choudhury et al. (2015) framed an inventory model considering stock-dependent demand rate with allowable shortages. Singh et al. (2016a) developed an inventory model for deteriorating items having seasonal and stock-dependent demand with allowable shortages.

Deterioration is a natural phenomenon particularly for inventories of food items, volatile liquids, agricultural products, pharmaceutical products, etc. The deterioration occurs due to evaporation, damage, spoilage, dryness, etc, and it reduces the quality and/or quantity of stored items. In general, the items are considered to deteriorate continuously with time, pharmaceutical products being exception as they are considered to be of identical quality until their expiry dates, and completely useless thereafter. Ghare and Schrader (1963) were the first to incorporate the idea of deterioration in inventory models. They studied an exponentially decaying inventory model with constant demand. Since then numerous researches have been carried out considering the effect of deterioration on on-hand stock. Tenga et al. (2002) presented an optimal replenishment policy for deteriorating items with time-varying demand and partial backlogging. Mandal et al. (2006) developed an inventory model for deteriorating items under a constraint with a different approach of Geometric Programming. Panda et al. (2008) considered an inventory model for a seasonal product with ramp-type demand. Min et al. (2010) developed an inventory model for deteriorating item under stock-dependent demand and two-level trade credit. Liang and Zhou (2011) considered a different model for deteriorating items with two warehouses under conditionally permissible delay in payment. More works on deterioration have been done by Mirzazadeh et al. (2009), Sicilia et al. (2014), Chakraborty et al. (2015), Annadurai and Uthayakumar (2015) and many other researchers. We refer to Raafat (1991) and Goyal and Giri (2001) for detailed review on the trends in modeling deteriorating inventory.

Although most of the researchers assumed that deterioration starts as soon as the the items are produced or those are received by the retailer, the reality reveals something different. In practice, most of the items start deteriorating after certain time period, which is termed as ‘non-instantaneous deterioration’. For example, fresh fruits or vegetables do not deteriorate during the early stage of storage. The time period after which deterioration would start plays an important role while setting optimal strategies. Wu et al. (2006) derived an optimal replenishment policy for items with non-instantaneous deterioration, stock-dependent demand and partial backlogging, which was further extended by Geetha and Uthayakumar (2010) by considering reciprocal time-dependent partial backlogging rate. Ouyang et al. (2006) developed an inventory model for non-instantaneously deteriorating items with permissible delay in payment which was later extended by Maihami and Kamalabadi (2012) by considering price- and time-dependent demand. Rabbani et al. (2015) developed coordinated replenishment and marketing policies for non-instantaneous stock deterioration problem. However, in all these works, the deterioration rate was assumed to be an exogenous variable. In reality, the deterioration rate may be controlled by taking certain measures in preserving the items. As higher deterioration rate has considerable impact on system profit, supply chain managers may think of using technology to reduce the effective deterioration. To the best of authors’ knowledge, Hsu et al. (2010) first derived an inventory policy allowing the retailer to invest in preservation technology when the demand and deterioration rates were both constant. Dye and Hsieh (2012) extended Hsu et al.’s (2010) work by considering time-varying deterioration rate and partial backlogging. Lee and Dye (2012) considered an inventory model for deteriorating items under stock-dependent demand and controllable deterioration rate. Hsieh and Dye (2013) developed inventory model under time-dependent demand rate and constant deterioration rate. Dye (2013) generalized non-instantaneous deteriorating inventory system with constant demand and time-dependent deterioration with allowable shortages and waiting time-dependent partial backlogging. He and Huang (2013) studied the effect of investment in preservation technology in a price-dependent demand and constant deterioration rate scenario. Singh and Sharma (2013) provided a global optimizing policy for constantly decaying items with ramp-type demand under two-level trade credit financing. Mishra (2014) developed an inventory model with controllable deterioration rate under time-dependent demand and time-varying holding cost. Liu et al. (2015) provided joint dynamic pricing and investment strategy for foods perishing at a constant rate with price and quality dependent demand. Singh and Rathore (2015) developed a model with preservation technology investment for constantly deteriorating inventory permitting shortage under the effect of inflation and trade credit with time-varying demand. Yang et al. (2015) examined an optimal dynamic decision making problem under trade credit and preservation technology allocation for a deteriorating item, the demand rate of which varies simultaneously with time. Recently Singh et al. (2016b) developed an economic order quantity (EOQ) model for deteriorating products having stock-dependent demand with trade credit period and preservation technology.

Shah and Shah (2014) developed an inventory model with price- and stock-dependent demand. However, they couldn’t prove the existence of the optimal solution analytically. Moreover, they considered deterioration to start from the very beginning of replenishment time (i.e. instantaneous deterioration) which is a simplified assumption. There are products for which price is not that much influential parameter compared to the variety or quality; a stock-dependent demand pattern is more appropriate to reflect the realistic scenario. The decision of investing (or not investing) in preservation technology in order to reduce deterioration rate is always a concern for the retailer, particularly when the selling season is sufficiently short. The retailer may shorten the replenishment period in order to reduce deterioration in his inventory, and thereby bears less preservation cost. The effects of uncontrollable parameters such as stock-sensitivity, holding cost or production cost on the investment as well as business period would also be interesting to examine as those will help the decision maker to have a better overview of the whole system dynamics. We aim to study all these aspects in this paper. We have developed and analyzed an inventory model with exponentially stock-dependent demand where the item starts perishing after a certain time period. The present work is a two-step generalization of Hsu et al. (2010) as setting stock sensitivity to zero would convert the demand to be constant, and setting ‘non-deterioration time period’ to zero would turn the item into an instantaneously deteriorating one. It is also a generalization of Lee and Dye (2012) where they considered stock-dependency to be linear, since very small values of the exponent produces curves almost identical with straight lines. It may somewhat be considered as a partial extension of the work of Dye (2013) too, where the demand rate has been considered constant.

Table 1 A comparison of the present article with the existing literature on preservation technology

In this paper, we have considered the deterioration rate to be constant for ease of calculation. We have allowed the retailer to invest in preservation technology to reduce the deterioration. We have considered the stock-dependent demand scenario with exponential form of dependence. We have examined how the optimal decisions change in order to cope up with the variation of other uncontrollable parameters. The contribution of the present work with respect to the existing literature is shown in Table 1. The rest of the paper is designed as follows. Section 2 provides the notations and assumptions used to formulate the model. The model is formulated and analyzed in Sect. 3. The proposed model is illustrated through a numerical example in Sect. 4. Finally, conclusions are made and future research directions are suggested in Sect. 5.

2 Notations and assumptions

We use the following notations throughout the paper:

I(t)	Inventory level at time t
$\theta$	Constant deterioration rate at time t, $0\le \theta < 1$
$\xi$	Preservation technology cost per unit time for reducing the deterioration rate
$m(\xi )$	Proportion of reduced deterioration rate, $0 \le m(\xi ) \le 1$
Q	Total ordered quantity
$Q_d$	Total quantity of deteriorated items in a cycle
$Q_s$	Total number of items sold in a cycle
$c_{d}$	Unit deterioration cost of the retailer per unit time
h	Unit holding cost per unit time ($/unit item/ year)
k	Ordering cost per order ($/order)
c	Unit purchase cost
p	Unit selling price
T	Length of a cycle
$t_d$	Time length during which the product has no deterioration
$\Pi _1(\xi ,T)$	Average profit when deterioration starts before stock-out occurs
$\Pi _2(T)$	Average profit when stock-out occurs before deterioration starts

Assumptions

To develop the proposed model, we make the following assumptions:

• (i) The market demand is completely deterministic, and it is of the form $D=\alpha [I(t)]^{\beta }$, $\alpha >0$, $0\le \beta <1$, where I(t) denotes the inventory level of the buyer at time t, $\alpha$ is the scale parameter, and $\beta$ is the shape parameter which is a measure of responsiveness of the demand rate to changes in the inventory level. Some of the advantages of this kind of demand pattern, as mentioned in Baker and Urban (2009), are diminishing returns (marginal increment in demand rate decreases for larger values of inventory level), richness (good approximate demand in many practical situations), and intrinsic linearity (linear regression can be used for parameter estimation after taking logarithm).

• (ii) No deterioration takes place during the time period [$0, t_d$]. After the period, the product deteriorates at a constant rate $\theta$ of the on-hand inventory.

• (iii) There is no repair or replacement of deteriorated units during the inventory cycle.

• (iv) The proportion of reduced deterioration rate $m(\xi )$ is a continuous, concave, increasing function of retailer’s capital investment $\xi$, with $m(0)=0$ and $\lim _{\xi \rightarrow \infty } m(\xi )=1$. We assume $m'(\xi )>0$ so as to make the retailer lean to invest in it, and $m''(\xi )<0$ to ensure diminishing return from capital investment in preservation.

• (v) There is no information asymmetry among the channel members.

• (vi) Lead time is deterministic and we assume it as zero.

• (vii) Shortages are not allowed in inventory.

Note 1. :

Here we make the assumption of demand pattern similar to Zhou et al. (2008), and that of preservation technology investment similar to Dye (2013).

Note 2. :

Unlike most of the existing research works done considering the effect of preservation technology, we do not put any restriction on the maximum amount of money to be spent on preservation technology. The reason is that if the retailer has budget constraint, i.e. capital limit W (say), he may just choose the optimal preservation investment as $\min \{W,\xi ^*\}$, where $\xi ^*$ is the optimal cost obtained under unrestricted scenario.

3 Model formulation

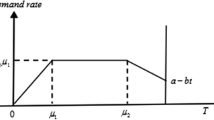
As the time point $t_d$ at which the deterioration starts is exogenous, the profit function will take different forms depending on whether the on-hand stock reaches zero level after or before deterioration starts. We shall obtain and analyze the profit functions in both cases separately (Fig. 1).

Fig. 1

Schematic diagram of the inventory level

Case 1:

$t_d<T$

In this case, the time period during which the product has no deterioration is shorter than the length of in-stock period. During the interval $(0,t_d)$, the inventory is depleted due to the demand only, whereas during $(t_d,T)$, the inventory level decreases due to the combined effect of demand and deterioration. As per the assumption, spending $\xi$ amount of money on preservation technology reduces the effective deterioration rate to $(1-m(\xi ))\theta$. The variation of inventory with time t can thus be described by the following differential equation:

$$\begin{aligned} \frac{dI(t)}{dt}= \left\{ \begin{array}{ll} -\alpha {I(t)}^{\beta }, &{} \qquad \quad 0 \le t< t_d\\ -\alpha {I(t)}^{\beta }-(1-m(\xi ))\theta I(t), &{} \qquad \quad t_d\le t <T\\ \end{array}\right. \end{aligned}$$

(1)

with the condition $I(T)=0$. Solving (1) and writing m instead of $m(\xi )$ for simplicity, we get the inventory level at any time t as

$$\begin{aligned} I(t)= \left\{ \begin{array}{ll} \left[ \frac{\alpha }{(1-m)\theta }\left\{ e^{(1-m)(1-\beta )\theta (T-t_d)}-1\right\} +\alpha (t_d-t)(1-\beta )\right] ^{\frac{1}{1-\beta }},&{} \quad 0\le t<t_d\\ \left[ \frac{\alpha }{(1-m)\theta }\left\{ e^{(1-m)(1-\beta )\theta (T-t)}-1\right\} \right] ^{\frac{1}{1-\beta }},&{}\quad t_d\le t\le T\\ \end{array}\right. \end{aligned}$$

(2)

See Appendix 1 for detailed calculation.

We obtain the total inventory during the interval (0, T) as given below:

$$\begin{aligned} I_1= & {} \int _{0}^{T}{I(t)}dt\\= & {} \int _{0}^{t_d}\left[ \frac{\alpha }{(1-m)\theta }\left\{ e^{(1-m)(1-\beta )\theta (T-t_d)}-1\right\} +\alpha (t_d-t)(1-\beta )\right] ^{\frac{1}{1-\beta }} dt \\&+\int _{t_d}^{T}\left[ \frac{\alpha }{(1-m)\theta }\left\{ e^{(1-m)(1-\beta )\theta (T-t)}-1\right\} \right] ^{\frac{1}{1-\beta }}dt . \end{aligned}$$

Total number of items ordered is obtained as

$$\begin{aligned} Q=I(0)=\left[ \alpha (1-\beta )\left\{ \frac{1}{(1-\beta )(1-m)\theta }\left( e^{(1-m)(1-\beta )\theta (T-t_d)}-1\right) + t_d\right\} \right] ^{\frac{1}{1-\beta }} . \end{aligned}$$

Total number of items deteriorated during $(t_d,T)$ is

$$\begin{aligned} Q_d=(1-m)\theta \int _{t_d}^{T} {\left\{ \frac{\alpha }{(1-m)\theta }(e^{(1-m)(1-\beta )\theta (T-t)}-1)\right\} ^{\frac{1}{1-\beta }}}dt . \end{aligned}$$

Total number of items sold is thus $Q_s=Q-Q_d$, and the average profit of the retailer is obtained as

$$\begin{aligned} \Pi _1(T,\xi )= & {} \frac{1}{T}\left( pQ_s-k-T\xi -h I_1-c Q-c_dQ_d\right) \\= & {} \frac{1}{T}\left[ (p-c)\left[ \alpha (1-\beta )\left\{ \frac{1}{(1-\beta )(1-m)\theta }\left( e^{(1-m)(1-\beta )\theta (T-t_d)}-1\right) + t_d\right\} \right] ^{\frac{1}{1-\beta }}\right. \\&-(p+c_d)(1-m)\theta \int _{t_d}^{T} {\left\{ \frac{\alpha }{(1-m)\theta }(e^{(1-m)(1-\beta )\theta (T-t)}-1)\right\} ^{\frac{1}{1-\beta }}}dt\\&-k-T\xi -h\int _{0}^{t_d}\left[ \frac{\alpha }{(1-m)\theta }\left\{ e^{(1-m)(1-\beta )\theta (T-t_d)}-1\right\} +\alpha (t_d-t)(1-\beta )\right] ^{\frac{1}{1-\beta }} dt \\&\left. -h\int _{t_d}^{T}\left[ \frac{\alpha }{(1-m)\theta }\left\{ e^{(1-m)(1-\beta )\theta (T-t)}-1\right\} \right] ^{\frac{1}{1-\beta }}dt\right] . \end{aligned}$$

Approximating $e^{(1-m)(1-\beta )\theta (T-t_d)}$ by $1+(1-m)(1-\beta )\theta (T-t_d)$ and $e^{(1-m)(1-\beta )\theta (T-t)}$ by $1+(1-m)(1-\beta )\theta (T-t)$, and neglecting the higher order terms, the average profit function can be simplified as (see Appendix 2 for detailed calculation)

$$\begin{aligned} \Pi _1(T,\xi )= & {} \frac{1}{T}\left[ (p-c)\left\{ \alpha (1-\beta )\right\} ^{\frac{1}{1-\beta }}T^{\frac{1}{1-\beta }}- \frac{(p+c_d)(1-m)\theta \{\alpha (1-\beta )\}^{\frac{2-\beta }{1-\beta }}}{\alpha (2-\beta )}(T-t_d) ^{\frac{2-\beta }{1-\beta }} \right. \nonumber \\&\left. -k-T\xi -h\frac{\{\alpha (1-\beta )\}^{\frac{2-\beta }{1-\beta }}}{\alpha (2-\beta )}T^ {\frac{2-\beta }{1-\beta }}\right] \,. \end{aligned}$$

(3)

The following proposition can be stated straightforwardly.

Proposition 1

For any given feasibleT, $\Pi _1(\xi |T)$is strictly concave in$\xi$.

Proof

We have, from (3),

$$\begin{aligned} \frac{\partial \Pi _1(\xi |T)}{\partial \xi }= & {} \frac{1}{T}m'(\xi )\frac{(p+c_d)\theta \{\alpha (1-\beta )\}^{\frac{2-\beta }{1-\beta }}}{\alpha (2-\beta )}(T-t_d) ^{\frac{2-\beta }{1-\beta }}-1,\\ \hbox { and }\frac{\partial ^2 \Pi _1(\xi |T)}{\partial \xi ^2}= & {} \frac{1}{T}m''(\xi )\frac{(p+c_d)\theta \{\alpha (1-\beta )\}^{\frac{2-\beta }{1-\beta }}}{\alpha (2-\beta )}(T-t_d)^{\frac{2-\beta }{1-\beta }}<0, \end{aligned}$$

since $m''(\xi )<0$. Hence the proposition is proved. $\square$

Before proceeding to prove the concavity of the average profit function, let us recall the definition of fractional program given in Dye (2013).

Definition

For the ratio $q(x)=\frac{f(x)}{g(x)}$ over a set $S=\{x\in X: h(x)\le 0\}$, if g(x) is positive on X, then the nonlinear program

(P) $\sup \{q(x):x \in S \}$ is called a fractional program. If $f(x) ({\ge} 0)$ is concave and both $g(x) (>0)$ and h(x) are convex, then (P) is called a concave fractional program.

We now state the following propositions which are due to Schaible (1983) and Cambini and Martein (1988):

Proposition 2

Iff(x) andg(x) are differentiable in a concave fractional program then the objective functionq(x) is pseudoconcave on S. It is strictly pseudoconcave if eitherf(x) is strictly concave org(x) is strictly convex.

Proposition 3

In a concave fractional program (P), any local maximum is a global maximum, and (P) has at most one maximum iff(x) is strictly concave org(x) is strictly convex. In a differentiable concave fractional program, a solution of the Karush–Kuhn–Tucker (KKT) conditions is a maximum of (P).

In light of the definition of fractional program and Propositions 2 and 3, we see that for given feasible $\xi$, maximizing $\Pi _1(T|\xi )=\frac{TP_1(T|\xi )}{T}$ is a fractional program with $h(T)=t_d-T$. If $TP_1(T|\xi )$ is (strictly) concave on a set $S_1\subseteq S$, the problem is a concave fractional one, and from Proposition 2, $\Pi _1(T|\xi )$ is (strictly) pseudoconcave on $S_1$, because of the differentiability of $TP_1$ and T. Now, we have, from (3),

$$\begin{aligned} \frac{\partial TP_1(T|\xi )}{\partial T}= & {} \frac{(p-c)\{\alpha (1-\beta )\}^{\frac{1}{1-\beta }}}{1-\beta }T^{\frac{\beta }{1-\beta }} -\frac{(p+c_d)(1-m)\theta \{\alpha (1-\beta )\}^{\frac{2-\beta }{1-\beta }}}{\alpha (1-\beta )}(T-t_d)^{\frac{1}{1-\beta }}\nonumber \\&-\xi -h\frac{\{\alpha (1-\beta )\}^{\frac{2-\beta }{1-\beta }}}{\alpha (1-\beta )}T^{\frac{1}{1-\beta }}\nonumber \\= \,& {} B_1 T^{\frac{\beta }{1-\beta }}-B_2(T-t_d)^{\frac{1}{1-\beta }}-\xi -B_3 T^{\frac{1}{1-\beta }} \hbox { (say), so that} \end{aligned}$$

(4)

$$\begin{aligned} \frac{\partial ^2 TP_1(T|\xi )}{\partial T^2}= & {} \frac{B_1\beta }{1-\beta }T^{\frac{2\beta -1}{1-\beta }} -\frac{B_2}{1-\beta }(T-t_d)^{\frac{\beta }{1-\beta }}-\frac{B_3}{1-\beta }T^{\frac{\beta }{1-\beta }} \nonumber \\= & {} \frac{T^{\frac{\beta }{1-\beta }}}{1-\beta }\left[ \frac{B_1 \beta }{T}-B_2\left( 1-\frac{t_d}{T}\right) ^{\frac{\beta }{1-\beta }}-B_3\right] . \end{aligned}$$

(5)

Note that the function $\frac{B_1 \beta }{T}-B_2\left( 1-\frac{t_d}{T}\right) ^{\frac{\beta }{1-\beta }}-B_3$ is strictly decreasing in T, all $B_i$’s being positive. We have, from (5), $\frac{\partial ^2 TP_1(T|\xi )}{\partial T^2}\rightarrow -\infty$ as $T\rightarrow \infty$. Also, $\frac{\partial ^2 TP_1(T|\xi )}{\partial T^2}\left| \right. _{T=t_d}<0$ if and only if $\frac{B_1 \beta }{t_d}-B_3<0$, i.e. if $\frac{(p-c)\beta }{h(1-\beta )}<t_d$. For $t_d<\frac{(p-c)\beta }{h(1-\beta )}$, the existence of T$(>t_d)$, the unique (guaranteed by the strictness in T) solution of the equation $\frac{B_1 \beta }{T}-B_2\left( 1-\frac{t_d}{T}\right) ^{\frac{\beta }{1-\beta }}-B_3=0$ is ensured due to continuity of $\frac{\partial ^2 TP_1(T|\xi )}{\partial T^2}$ in any positive domain. Hence $TP_1(T|\xi )$ is strictly concave.

The finding is summarized in the following proposition.

Proposition 4

For any given feasible$\xi$, if$\frac{(p-c)\beta }{h(1-\beta )}<t_d$, $\Pi _1(T|\xi )$is strictly concave in$(t_d,\infty )$; otherwise, it is strictly concave in$(\underline{T},\infty )$, where$\underline{T}$is the only solution of (5).

We are now in a position to prove the concavity of the average profit function. Let us write $\Pi _1(T,\xi )=\frac{TP_1(T,\xi )}{T}$. We shall first show that $TP_1(T,\xi )$ is jointly concave in T and $\xi$. We have

$$\begin{aligned} \frac{\partial ^2 TP_1(T,\xi )}{\partial T^2}= & {} \frac{(p-c)\beta \{\alpha (1-\beta )\}^{\frac{1}{1-\beta }}}{(1-\beta )^2}T^{\frac{2\beta -1}{1-\beta }} -h\frac{\{\alpha (1-\beta )\}^{\frac{1}{1-\beta }}}{(1-\beta )}T^{\frac{\beta }{1-\beta }}\\&-\frac{(p+c_d)(1-m(\xi ))\theta \{\alpha (1-\beta )\}^{\frac{1}{1-\beta }}}{(1-\beta )}(T-t_d)^{\frac{\beta }{1-\beta }}\\ \frac{\partial ^2 TP_1(T,\xi )}{\partial \xi ^2}= \,& {} m''(\xi )\frac{(p+c_d)\theta \{\alpha (1-\beta )\}^{\frac{2-\beta }{1-\beta }}}{\alpha (2-\beta )}(T-t_d)^{\frac{2-\beta }{1-\beta }}\\ \frac{\partial ^2 TP_1(T,\xi )}{\partial \xi \partial T}= \,& {} m'(\xi ) (p+c_d)\theta \{\alpha (1-\beta )\}^{\frac{1}{1-\beta }} (T-t_d)^{\frac{1}{1-\beta }}-1. \end{aligned}$$

For the Hessian matrix $\left( \begin{array}{cc} \frac{\partial ^2 TP_1(T,\xi )}{\partial \xi ^2} &{} \frac{\partial ^2 TP_1(T,\xi )}{\partial T \partial \xi } \\ \frac{\partial ^2 TP_1(T,\xi )}{\partial \xi \partial T} &{} \frac{\partial ^2 TP_1(T,\xi )}{\partial T^2} \\ \end{array} \right)$, $|H_1|<0$, following Proposition 1.

Before calculating $|H_2|$, let us simplify the above second order partial derivatives as follows:

$$\begin{aligned} \frac{\partial ^2 TP_1(T,\xi )}{\partial T^2}= \,& {} A_2T^{\frac{2\beta -1}{1-\beta }}-A_3(T-t_d)^{\frac{\beta }{1-\beta }}-A_4 T^{\frac{\beta }{1-\beta }},\\ \frac{\partial ^2 TP_1(T,\xi )}{\partial \xi ^2}=\, & {} m''(\xi )A_1(T-t_d)^{\frac{2-\beta }{1-\beta }}, \\ \hbox {and }\frac{\partial ^2 TP_1(T,\xi )}{\partial \xi \partial T}=\, & {} m'(\xi )A_5(T-t_d)^{\frac{1}{1-\beta }}-1, \end{aligned}$$

where $A_1=\frac{(p+c_d)\theta \{\alpha (1-\beta )\}^{\frac{2-\beta }{1-\beta }}}{\alpha (2-\beta )}$, $A_2=\frac{(p-c)\beta \{\alpha (1-\beta )\}^{\frac{1}{1-\beta }}}{(1-\beta )^2}$, $A_3=\frac{(p+c_d)(1-m(\xi _1))\theta \{\alpha (1-\beta )\}^{\frac{1}{1-\beta }}}{1-\beta }$, $A_4=\frac{h\{\alpha (1-\beta )\}^{\frac{1}{1-\beta }}}{1-\beta }$, and $A_5= (p+c_d)\theta \{\alpha (1-\beta )\}^{\frac{1}{1-\beta }}$, so that

$$\begin{aligned} |H_2|=\, & {} m''(\xi )A_1 (T-t_d)^{\frac{2-\beta }{1-\beta }}\left[ A_2 T^{\frac{2\beta -1}{1-\beta }}-A_3 (T-t_d)^{\frac{\beta }{1-\beta }}-A_4T^{\frac{\beta }{1-\beta }}\right] -\{m'(\xi )A_5 (T-t_d)^{\frac{1}{1-\beta }}-1\}^2\\=\, & {} m''(\xi )A_1A_2T^{\frac{1+\beta }{1-\beta }}\left( 1-\frac{t_d}{T}\right) ^{\frac{2-\beta }{1-\beta }} -m''(\xi )A_1A_3T^{\frac{2}{1-\beta }}\left( 1-\frac{t_d}{T}\right) ^{\frac{2}{1-\beta }}-m''(\xi )A_1A_4T^{\frac{2}{1-\beta }} \left( 1-\frac{t_d}{T}\right) ^{\frac{2-\beta }{1-\beta }}\\&-{m'(\xi )}^2A_5^2T^{\frac{2}{1-\beta }}\left( 1-\frac{t_d}{T}\right) ^{\frac{2}{1-\beta }}+2m'(\xi )A_5T^{\frac{1}{1-\beta }} \left( 1-\frac{t_d}{T}\right) ^{\frac{1}{1-\beta }}-1\\=\, & {} T^{\frac{2}{1-\beta }}\left[ m''(\xi )\frac{A_1A_2}{T}\left( 1-\frac{t_d}{T}\right) ^{\frac{2-\beta }{1-\beta }}-m''(\xi )A_1A_3 \left( 1-\frac{t_d}{T}\right) ^{\frac{2}{1-\beta }}-m''(\xi )A_1A_4\left( 1-\frac{t_d}{T}\right) ^{\frac{2-\beta }{1-\beta }}\right. \\&\left. -{m'(\xi )}^2A_5^2\left( 1-\frac{t_d}{T}\right) ^{\frac{2}{1-\beta }}+2m'(\xi )A_5\left( \frac{1}{T}-\frac{t_d}{T^2}\right) ^{\frac{1}{1-\beta }}\right] -1\\=\, & {} T^{\frac{2}{1-\beta }}f(T)-1, \end{aligned}$$

where

$$\begin{aligned} f(T)=\, & {} m''(\xi )\frac{A_1A_2}{T}\left( 1-\frac{t_d}{T}\right) ^{\frac{2-\beta }{1-\beta }}-m''(\xi )A_1A_3 \left( 1-\frac{t_d}{T}\right) ^{\frac{2}{1-\beta }}-m''(\xi )A_1A_4\left( 1-\frac{t_d}{T}\right) ^{\frac{2-\beta }{1-\beta }}\nonumber \\&-{m'(\xi )}^2A_5^2\left( 1-\frac{t_d}{T}\right) ^{\frac{2}{1-\beta }}+2m'(\xi )A_5\left( \frac{1}{T}-\frac{t_d}{T^2}\right) ^ {\frac{1}{1-\beta }}. \end{aligned}$$

(6)

Clearly, $f(t_d)=0$, so that $|H_2|=-1<0$ at $T=t_d$. Also,

$$\begin{aligned} \lim _{T\rightarrow \infty } f(T)=-m''(\xi )A_1A_3-m''(\xi )A_1A_4-{m'(\xi )}^2A_5^2, \end{aligned}$$

which means $|H_2| \rightarrow \infty$ as $T\rightarrow \infty$ if and only if $-m''(\xi )A_1A_3-m''(\xi )A_1A_4-{m'(\xi )}^2A_5^2>0$,

or $\frac{M}{{m'(\xi )}^2}>\frac{A_5^2}{A_1(A_3+A_4)}$, where $M(=-m''(\xi ))>0$. Simple calculation reveals that

$$\begin{aligned} \frac{A_5^2}{A_1(A_3+A_4)}= & {} \frac{(p+c_d)\theta (2-\beta )}{(p+c_d)\theta (1-m)+h}, \hbox { so that}\nonumber \\ \hbox {if } \frac{M}{{m'(\xi )}^2}> & {} \frac{(p+c_d)\theta (2-\beta )}{(p+c_d)\theta (1-m)+h}\nonumber \\ \hbox {or if } \frac{{m'(\xi )}^2}{M}+\frac{m}{2-\beta }< & {} \frac{1}{2-\beta }+\frac{h}{(p+c_d)\theta (2-\beta )}, \end{aligned}$$

(7)

$|H_2|\rightarrow \infty$ as T increases. It is easy to deduce that $\frac{\partial }{\partial \xi }\left[ \frac{{m'(\xi )}^2}{M}+\frac{m}{2-\beta }\right] =-\frac{(3-2\beta )m'}{2-\beta }-\frac{M'm'^2}{M^2}<0$ when $M'>0$, so that there exists a particular value $\bar{\xi }$ of $\xi$ such that equation (7) is satisfied whenever $\xi >\bar{\xi }$. Therefore, $|H_2|\rightarrow \infty$ with T, whenever $\xi >\bar{\xi }$. If f(T) is strictly increasing in T, there exists a value of T, say $\bar{T}$, such that $|H_2|(\bar{T})=0$, and $|H_2|>0$ for all $T\in (\bar{T},\infty )$. Therefore, $\Pi _1(T,\xi )$ is strictly pseudoconcave due to Proposition 2, and has at most one maximum due to Proposition 3.

We shall now provide an iterative search method to find optimal values of T and $\xi$ (say $T^*$ and $\xi ^*$) with the help of propositions 1 and 4. Numerical example proves that the method is a convergent one, providing optimal values for both the decision variables. As $m(0)=0$ and $\lim _{\xi \rightarrow \infty }m(\xi )=1$, we choose initial value of $\xi$ to be such that $m(\xi )=0.5$.

Algorithm

Step 1: :

Start with $j=0$ and the initial trial value of $\xi _0$, where $m(\xi _0)=0.5$.

Step 2: :

For given $\xi _j$, find optimal T (by virtue of Proposition 4).

Step 3: :

Using the result obtained from Step 2, determine optimal value of $\xi _{j+1}$ (by virtue of Proposition 1).

Step 4: :

If the difference between $\xi _j$ and $\xi _{j+1}$ is sufficiently small, set $\xi ^*=\xi _{j+1}$ and $T^*=T$. Then $(T^*, \xi ^*)$ is the optimal solution and stop. Otherwise, set $j=j+1$ and return to Step 2.

We summarize the findings in the following proposition:

Proposition 5

If$m'''(\xi )>0$, then the average profit function is jointly concave inTand$\xi$on$S=\{(\bar{T},\infty )\times (\bar{\xi },\infty )\}$, where$\bar{\xi }$is the least value of$\xi$satisfying (7), and$\bar{T}$is the only solution of$f(T)=0$of Eq. (6). The optimal solution$(T_1^*,\xi ^*)$is given by

$$\begin{aligned} (T_1^*,\xi ^*)= \left\{ \begin{array}{ll} (T^*,\xi ^*), &{} \hbox {if }\bar{T}<T^* \,\hbox { and }\, \bar{\xi }<\xi ^*;\\ (\bar{T},\xi ^*), &{} \hbox {if } T^*<\bar{T} \,\hbox { and }\, \bar{\xi }<\xi ^*; \\ (T^*,\bar{\xi }), &{} \hbox {if } \bar{T}<T^* \,\hbox { and }\, \xi ^*<\bar{\xi }; \\ (\bar{T},\bar{\xi }), &{} \hbox {if } T^*<\bar{T}\,\hbox { and }\, \xi ^*<\bar{\xi }. \end{array} \right. \end{aligned}$$

Case 2:

$T<t_d$

Under this assumption, the stock-in-hand will be depleted totally before deterioration starts. Hence there is no need to invest in preserving the items, so that we may set $\xi =0$. Also, the change in inventory level during (0, T) is due to demand only, with boundary condition $I(T)=0$. The average profit takes the form

$$\begin{aligned} \Pi _2(T)=\frac{1}{T}\left[ (p-c)\{\alpha (1-\beta )\}^{\frac{1}{1-\beta }}T^{\frac{1}{1-\beta }} -k-h\frac{\{\alpha (1-\beta )\}^{\frac{2-\beta }{1-\beta }}}{\alpha (2-\beta )}T^{\frac{2-\beta }{1-\beta }}\right] . \end{aligned}$$

(8)

We have, from (8),

$$\begin{aligned} \frac{d\Pi _2(T)}{dT}= & {} -\frac{1}{T^2}\left[ (p-c)\{\alpha (1-\beta )\}^{\frac{1}{1-\beta }}T^{\frac{1}{1-\beta }} -k-h\frac{\{\alpha (1-\beta )\}^{\frac{2-\beta }{1-\beta }}}{\alpha (2-\beta )}T^{\frac{2-\beta }{1-\beta }}\right] \nonumber \\&+\frac{1}{T}\left[ (p-c)\frac{\{\alpha (1-\beta )\}^{\frac{1}{1-\beta }}T^{\frac{1}{1-\beta }-1}}{1-\beta }-\frac{h\{\alpha (1-\beta ) \}^{\frac{2-\beta }{1-\beta }}T^{\frac{2-\beta }{1-\beta }-1}}{\alpha (1-\beta )}\right] . \end{aligned}$$

Let the solution of the equation $\frac{d\Pi _2(T)}{dT}=0$ be $T_2$. We then have

$$\begin{aligned} \frac{d^2 \Pi _2}{dT^2}= & {} -\frac{2}{T}\frac{\partial \Pi _2}{\partial T}+\frac{1}{T}\left[ (p-c)\{\alpha (1-\beta )\}^{\frac{1}{1-\beta }} \frac{1}{1-\beta }\frac{\beta }{1-\beta }T^{(\frac{1}{1-\beta }-1-1)}\right. \\&\left. -\frac{h\{\alpha (1-\beta )\}^{\frac{2-\beta }{1-\beta }}}{\alpha (1-\beta )}\frac{1}{1-\beta }T^{(\frac{1}{1-\beta }-1)}\right] , \end{aligned}$$

so that $\frac{d^2 \Pi _2}{dT^2}\left| \right. _{T=T_2}=\frac{1}{T_2}\left[ (p-c)\alpha ^{\frac{1}{1-\beta }}\beta (1-\beta )^{\frac{2\beta -1}{1-\beta }} T^{\frac{2\beta -1}{1-\beta }}_2-h\alpha ^{\frac{1}{1-\beta }}(1-\beta )^{\frac{\beta }{1-\beta }}T_2{^{\frac{\beta }{1-\beta }}}\right]$. Clearly, $\frac{d^2 \Pi _2}{dT^2}|_{T=T_2}<0$ if and only if $T_2>\left( \frac{p-c}{h}\right) \frac{\beta }{1-\beta }$. Also, as per the assumption, $T_2<t_d$. The finding is summarized in the following proposition.

Proposition 6

In absence of investment on preservation, the profit function is concave if $T_2>\left( \frac{p-c}{h}\right) \frac{\beta }{1-\beta }$ , where $T_2$ is the solution of first order condition. The optimal cycle length is given by $T^*_2=\left\{ \begin{array}{ll} \left( \frac{p-c}{h}\right) \frac{\beta }{1-\beta }, &{} \hbox {if } T_2<\left( \frac{p-c}{h}\right) \frac{\beta }{1-\beta }; \\ T_2, &{} \hbox {if }\left( \frac{p-c}{h}\right) \frac{\beta }{1-\beta }<T_2<t_d; \\ t_d, &{} \hbox {if }t_d<T_2. \end{array} \right.$

From propositions 5 and 6, the optimal average profit of the retailer is given by

$\Pi (T,\xi )=\max \{\Pi _1(T_1^*,\xi ^*), \Pi _2(T_2^*)\}$, i.e., the retailer should separately calculate the cases to take the decision whether to invest in preservation technology or not. However, there are certain situations where one has limited option for judgement. For example, if deterioration starts too early, the retailer is almost bound to invest in preservation in order to reduce deterioration.

Proposition 7

It is always beneficiary for the retailer to invest in preservation technology if$t_d<\left( \frac{p-c}{h}\right) \frac{\beta }{1-\beta }$.

The proof follows directly from Proposition 6. Proposition 7 has a valuable managerial insight for the retailer. It provides a lower limit for the non-deterioration time period, violation of which would lead to considerable amount of loss due to spoilage.

4 Numerical illustration

In this section, we aim to illustrate the proposed model by a numerical example. The following parameter-values are considered: $c=20$, $h=3$, $t_d=0.0417$, $k=120$, $p=35$, $\alpha =1000$, $\beta =0.1$, $c_d=0.2$, $\theta =0.2$ in appropriate units. The reduced deterioration rate is $m(\xi )=1-e^{-a\xi }$ with $a=0.01$, where a is the simulation coefficient representing the change in the reduced deterioration rate per unit change in capital (Dye 2013).

Table 2 Computational results

Using the algorithm provided in the earlier section, we obtain Table 2 starting with $\xi _0=69.3147$, from which it is easy to deduce that the optimal values of the decision variables in the first case are $\xi ^*=367.35$, $T^*_1=1.052$ and $\Pi _1=25446.4$. Also, we obtain $T^*_2=0.0417$ and $\Pi _2=17238.5$ in the second case, so that the retailer would bag more profit if he invests in preservation technology.

Fig. 2

Sensitivity of optimal results w.r.t. $\beta$. a$\beta$ versus cycle length, b$\beta$ versus total profit, c$\beta$ versus preservation investment

Fig. 3

Sensitivity of optimal results w.r.t. $\theta$. a$\theta$ versus cycle length, b$\theta$ versus total profit, c$\theta$ versus preservation investment

Fig. 4

Sensitivity of optimal results w.r.t. $t_d$. a$t_d$ versus cycle length, b$t_d$ versus total profit, c$t_d$ versus preservation investment

Fig. 5

Sensitivity of optimal results w.r.t. h. ah versus cycle length, bh versus total profit, ch versus preservation investment

Fig. 6

Sensitivity of optimal results w.r.t. p. ap versus cycle length, bp versus total profit, cp versus preservation investment

We now examine the effects of changes in the parameter-values on the optimal decision variables as well as on the average profit. We change the value of one parameter at a time while keeping the other parameter-values unchanged. In all the Figs. 2, 3, 4, 5 and 6, results obtained from case 1 ($t_d<T$) is compared with the results obtained by setting $\xi =0$, i.e. a situation when the opportunity to invest in preservation technology is not available, or the retailer is simply unwilling to spend on it. Based on the behavioral changes as reflected in Figs. 2, 3, 4, 5 and 6, we derive the following managerial insights.

• 1. The more the demand is stock-sensitive, the more is the need of investment in preservation, as the difference between optimal profits obtained in two cases increases (Fig. 2b). The higher value of $\beta$ makes the retailer lean to order more; eventually, he is bound to spend more on preservation to reduce the effect of deterioration (Fig. 2c). Higher preservation technology investment as well as higher stock-sensitivity make a good sales volume, resulting in increment in profit. Also, the initial order quantity being larger, the cycle length increases in order to allow the inventory level to reach zero (Fig. 2a).

• 2. Increasing deterioration rate has negative effect on the total profit, which is obvious; however, in presence of investment in preservation, the optimal cycle length as well as profit are less vulnerable compared to the case of zero preservation investment (Fig. 3a, b). The reduced vulnerability comes at a higher cost which is due to higher investment in preservation technology. Higher deterioration rate enforces the retailer to invest more in preservation technology in order to keep the profit margin unaffected as much as possible (Fig. 3c). With higher deterioration rate, the retailer should realign his business strategy to sell the product as soon as possible which results in reduced cycle length.

• 3. With higher values of $t_d$, i.e. longer ‘no deterioration period’, cycle length decreases in case 1. On the contrary, due to the fact that deterioration starts at a later time-point which eventually implies lower deterioration cost as well as lesser amount of spoilage, the retailer earns some extra profit by widening cycle length when there is zero investment in preservation (Fig. 4a). Both the cases produce higher profit as $t_d$ increases (Fig. 4b). It is also seen that when $t_d$ crosses a threshold value, it is not profitable to invest in preservation, so that investment amount becomes zero then, which is evident from Fig. 4c. Also, if the deterioration starts at a later time, lesser preservation investment is then necessary, indicating that preservation cost should decrease significantly with increasing $t_d$, which is corroborated by Fig. 4c.

• 4. With higher holding cost, the order quantity as well as cycle length decrease (Fig. 5a), resulting in lesser profit (Fig. 5b). However, due to lower order level and shorter cycle length, the retailer has to invest lesser in preservation technology (Fig. 5c).

• 5. With higher selling price, increase in total profit is obvious (Fig. 6b). The order level is also increased aiming to gain more profit, resulting in longer cycle length (Fig. 6a) and higher investment in preservation to fight against deterioration for longer time period (Fig. 6c).

5 Discussion and conclusion

The present paper develops an inventory model for non-instantaneously deteriorating item with preservation technology investment under stock-dependent demand scenario. Two cases depending on whether stock out occurs before or after deterioration starts are considered, and optimal values of the decision variables are determined. The paper suggests that the retailer should maximize average profit in both cases in order to determine which of the schemes should be adopted. We have derived a condition on $t_d$ which acts as a lower bound. If $t_d$ goes down beyond that lower limit indicating ‘too early occurrence’ of deterioration, we see that it is always beneficial to invest in reducing deterioration. The proposed model is illustrated through a numerical example and the optimal cycle length and investment for preservation are obtained. The sensitivity analysis exhibits that the solution of the model is quite stable. The numerical results demonstrate that investing in preservation technology substantially aids managers in developing a competitive advantage and improves their total profit. The results provide managerial insights towards determining optimal strategies with changed market scenario.

The present model may be extended in various ways. One can incorporate into the model some other parameters such as food quality or price, on which demand depends. The model may also be extended to two-echelon scenario where the vendor may allow permissible delay in payments. Another interesting direction would be to consider variable lead time which can be controlled through extra investment. Extending the model under stock-dependent stochastic demand scenario would be a challenging task but worth studying.

Appendices

Appendix 1

During $t_d\le t\le T$, we have

$$\begin{aligned} &\frac{dI(t)}{dt}= {} -\alpha {I(t)}^\beta -(1-m)\theta I(t)\\ &\hbox {or, } \frac{dI(t)}{dt}+(1-m)\theta I(t)= {} -\alpha {I(t)}^\beta \end{aligned}$$

Substituting $y={I(t)}^{1-\beta }$ and using the boundary condition $y(T)=0$, we get

$$\begin{aligned} y= & {} \frac{\alpha }{(1-m)\theta }\left[ e^{(1-m)(1-\beta )\theta (T-t)}-1\right] \\ \hbox {or}, I(t)= & {} \left[ \frac{\alpha }{(1-m)\theta }\left\{ e^{(1-m)(1-\beta )\theta (T-t)}-1\right\} \right] ^{\frac{1}{1-\beta }} . \end{aligned}$$

At $t=t_d$, we have $I(t_d)=\left[ \frac{\alpha }{(1-m)\theta }\left\{ e^{(1-m)(1-\beta )\theta (T-t_d)}-1\right\} \right] ^{\frac{1}{1-\beta }}$

During $0\le t<t_d$, we have,

$$\begin{aligned} \frac{dI(t)}{dt}= & {} {-}\alpha \{I(t)\}^\beta \\ \hbox {so that }\, \{I(t)\}^{1-\beta }= \,& {} \{I(t_d)\}^{1-\beta }+\alpha (t_d-t)(1-\beta )\\= & {} \frac{\alpha }{(1-m)\theta }\left\{ e^{(1-m)(1-\beta )\theta (T-t_d)}-1\right\} +\alpha (t_d-t)(1-\beta ) . \end{aligned}$$

Hence Eq. (2) is obtained.

Appendix 2

Substituting $e^{(1-m)(1-\beta )\theta (T-t_d)}=1+(1-m)(1-\beta )\theta (T-t_d)$ and $e^{(1-m)(1-\beta )\theta (T-t)}=1+(1-m)(1-\beta )\theta (T-t)$, and neglecting higher order terms, we get

$$\begin{aligned} \Pi _1(T,\xi )= & {} \frac{1}{T}\left[ (p-c)\left[ \alpha (1-\beta )\left\{ \frac{1}{(1-\beta )(1-m)\theta }(1-\beta )(1-m)\theta (T-t_d)+t_d\right\} \right] ^{\frac{1}{1-\beta }}\right. \\&-(p+c_d)(1-m)\theta \int _{t_d}^{T} {\left\{ \frac{\alpha }{(1-m)\theta }(1-\beta )(1-m)\theta (T-t)\right\} ^{\frac{1}{1-\beta }}}dt-k-T\xi \\&-h\int _{0}^{t_d}\left[ \frac{\alpha }{(1-m)\theta }(1-\beta )(1-m)\theta (T-t_d)+\alpha (1-\beta )(t_d-t)\right] ^{\frac{1}{1-\beta }} dt\\&\left. -h\int _{t_d}^{T}\left\{ \frac{\alpha }{(1-m)\theta }(1-\beta )(1-m)\theta (T-t)\right\} ^{\frac{1}{1-\beta }} dt\right] \\=\, & {} \frac{1}{T}\left[ (p-c)\{\alpha (1-\beta )T\}^{\frac{1}{1-\beta }}-(p+c_d)(1-m)\theta \int _{t_d}^{T}\{\alpha (1-\beta )(T-t)\}^{\frac{1}{1-\beta }}dt\right. \\&-k-T\xi -h\int _{0}^{T}\{\alpha (1-\beta )(T-t)\}^{\frac{1}{1-\beta }}dt\\=\, & {} \frac{1}{T}\left[ (p-c)\left\{ \alpha (1-\beta )\right\} ^{\frac{1}{1-\beta }}T^{\frac{1}{1-\beta }}-\frac{(p+c_d)(1-m)\theta \{\alpha (1-\beta )\}^{\frac{2-\beta }{1-\beta }}}{\alpha (2-\beta )}(T-t_d) ^{\frac{2-\beta }{1-\beta }}\right. \\&\left. -k-T\xi -h\frac{\{\alpha (1-\beta )\}^{\frac{2-\beta }{1-\beta }}}{\alpha (2-\beta )}T^{\frac{2-\beta }{1-\beta }}\right] . \end{aligned}$$