1 Introduction

Shortest path problem is a widely used application of graph theory in real-world networks e.g. transportation networks, routing, communication networks, supply chain networks, etc. A network of the problem is denoted by weighted direct graph \(G = \left( {V,E} \right)\), where \(V = \left\{ {1,2, \ldots m} \right\}\) is the set of m vertices and \(E \subseteq V \times V\) is the set of n arcs. Each arc has a length with the unit of distance, time, weight, cost, etc., based on the concepts of the network which is being studied. In the shortest path problem, the length of each arc is represented by a real number. A path between any pair of nodes of the network is a collection of consecutive arcs which connect that pair of nodes. Clearly, the distance of each path is the sum of lengths of its arcs. The shortest path problem aims to find the path which has the shortest length among all possible paths connecting the first and last nodes of the network. The problem has many real-world applications in the fields of transportation, traffic routing, robotic systems, etc. (see Cappanera and Scaparra 2011; Hassanzadeh et al. 2013).

Fuzzy theory has many applications in real-world problems (see Fullér et al. 2012; Sakawa et al. 2012; Carlsson and Fullér 2013; Atsalakis 2014: Mahmoodi-Rad et al. 2014). In the case of the shortest path problem as a real-world application, the lengths of arcs may not have an exact value e.g. it can vary in a range of values or it may be determined stochastically. Consider a traffic network where the cities are the vertices of the network and the roads between them are the arcs. The uncertainty of the time for driving between the cities can suit the network to be an example of such cases of the shortest path problem with non-exact arc length. This uncertainty may not be only limited to the geometric distance, as the factors like weather conditions and other unexpected factors can be cause to consider the driving time between the cities as a fuzzy variable (see Deng et al. 2012 for this example and Jayswal et al. 2015 as another example). Therefore, in such cases, the shortest path problem is remodeled as fuzzy shortest path problem. In the fuzzy shortest path problem the obtained shortest path will have a fuzzy length which is the sum of fuzzy lengths of its arcs. Comparing to the shortest path problem, the fuzzy shortest path problem has more difficulties to be solved. Comparison between fuzzy numbers for finding the shortest path is more difficult than exact numbers because of variety of the methods which compare fuzzy numbers.

The fuzzy shortest path problem has been studied in many studies. Dubois and Prade (1980) may be the first studies which introduced the fuzzy shortest path problem. Okada and Soper (2000) introduced a fuzzy set based solution for the fuzzy shortest path problem where nondominated paths or Pareto optimal paths with no guideline to select one of them as the best one. Blue et al. (2002) introduced an algorithm to find a cut value in order to limit and decrease the number of paths that are being analyzed. Okada (2004) applied a method based on the degree of possibility of the arcs of shortest path with the purpose of finding the shortest path. The study of Nayeem and Pal (2005) introduced a solution method for the fuzzy shortest path problem based on the acceptance index which was proposed by Sengupta and Pal (2000). The method introduces a single fuzzy shortest path for the problem. A dynamic programming solution method was proposed by Mahdavi et al. (2009) to tackle the fuzzy shortest path problem by applying an appropriate ranking method. Tajdin et al. (2010) applied a dynamic programming model to find the fuzzy shortest path in a network in existence of mixed fuzzy arc lengths by α-cuts. Kumar and Kaur (2011) proposed an iterative heuristic algorithm to solve the shortest path problem on a network where the arcs have imprecise length. Zareei et al. (2011) studied fuzzy shortest path (critical path) problem in project scheduling. Dou et al. (2012) applied a multi-criteria decision making approach which was based on value similarity measure to solve the fuzzy shortest path problem. Hassanzadeh et al. (2013) proposed a genetic algorithm metaheuristic to solve the fuzzy shortest path problem when mixed fuzzy arc lengths exist. In addition to the above-mentioned studies, Yano and Sakawa (2014) applied an interactive fuzzy programming to multiobjective fuzzy random linear programming problems using possibility-based probability maximization.

Clearly, when the lengths of the arcs in a network are fuzzy numbers, the length of the shortest path of that network is a fuzzy number. In this study, a new solution approach is proposed for the fuzzy shortest path problem which calculates the fuzzy objective value of the fuzzy shortest path problem, where the lengths of the arcs in the network are fuzzy numbers. The solution approach applies Zadeh’s extension principle (see Zadeh 1987; Yager 1986; Ramik 1986; Zimmermann 1996) which was extensively used in the literature of fuzzy combinatorial optimization problems (see Liu and Kao 2004; Liu 2008, 2015). The fuzzy shortest path problem is formulated as a pair of two-level mathematical models to calculate a single lower and upper bound of any \(\alpha -\) cut (\(0 \le \alpha \le 1\)) of the objective function value which cover the shortcomings of the literature of the shortest path problem. The membership function of the fuzzy objective function value is obtained numerically by applying different values of \(\,\alpha\).

The rest of this paper is organized as follows. Section 2 reminds some initial concepts of fuzzy sets and numbers. The shortest path problem and its fuzzy version is formulated in Sect. 3. Section 4 describes the proposed solution methodology. In Sect. 5, some numerical examples from the literature of fuzzy shortest path problem is solved by the proposed method and the comparison of the results by the literature is discussed. Section 6 discusses some advantages of the proposed method. Finally, the paper is ended by conclusion.

2 Preliminaries

In this section, some initial concepts of fuzzy set theory are presented which are used while dealing with problems with fuzzy parameters (Zadeh 1987; Zimmermann 1996; Fullér et al. 2011; Hadi-Vencheh and Mokhtarian 2011; Kumar and Kaur 2012).

2.1 Initial definitions

Definition 1:

Considering \(X\) as a collection of objects that is generically shown by \(x\), a fuzzy set on \(X\) is a set of pairs such that \(\tilde{A} = \left\{ {\left( {x,\mu_{{\tilde{A}}} \left( x \right)} \right)|x \in X} \right\}\) and \(\mu_{{\tilde{A}}} \left( x \right)\) is the membership function that relates each \(x\) to a number from \(\left[ {0, 1} \right]\).

Definition 2:

Support of a fuzzy set \(\tilde{A}\) which is denoted by \(S\left( {\tilde{A}} \right)\), is a set of elements in \({\mathbb{R}}\) that result in positive value of \(\mu_{{\tilde{A}}} \left( x \right)\). It is defined as \(S\left( {\tilde{A}} \right) = \left\{ {x \in {\mathbb{R}}|\mu_{{\tilde{A}}} \left( x \right)\text{ > }0} \right\}\).

Definition 3:

Core of a fuzzy set \(\,\tilde{A}\) is denoted by \(C\left( {\tilde{A}} \right)\) and defined as \(C\left( {\tilde{A}} \right) = \left\{ {x \in X|\mu_{{\tilde{A}}} \left( x \right) = 1} \right\}\).

Definition 4:

The (crisp) set of elements that belong to the fuzzy set \(\,\tilde{A}\) by at least the degree of \(\alpha\) is called the \(\alpha\)-level set as \(A_{\alpha } = \left\{ {x \in X|\,\mu_{{\tilde{A}}} \left( x \right) \ge \alpha } \right\}\).

Definition 5:

A fuzzy set \(\tilde{A}\) is convex if

$$\forall x_{1} ,x_{2} \in X\;{\text{and}}\;\lambda \in [0,1]:\;\,\mu_{{\tilde{A}}} \left( {\lambda x_{1} + \left( {1 - \lambda } \right)x_{2} } \right) \ge \hbox{min} \left\{ {\mu_{{\tilde{A}}} \left( {x_{1} } \right),\,\mu_{{\tilde{A}}} \left( {x_{2} } \right)} \right\}.$$

Definition 6:

A trapezoidal fuzzy number is denoted by \(\,\tilde{A} = \left( {a_{1} ,\;a,\;b,\;b_{1} } \right)\) and shown by Fig. 1. The core of this trapezoidal fuzzy set is \(\left[ {a, b} \right]\) and its support is \(\left( {a_{1} , b_{1} } \right)\). Its membership function is as follow,

Fig. 1
figure 1

A trapezoidal fuzzy number

Full size image
$$\mu _{{\tilde{A}}} \left( x \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill &\quad {if\,x \le a_{1} } \hfill \\ {\frac{{x - a_{1} }}{{a - a_{1} }}} \hfill &\quad {if\,a_{1} \le x \le a} \hfill \\ 1 \hfill & \quad {if\,a \le x \le b} \hfill \\ {\frac{{b_{1} - x}}{{b_{1} - b}}} \hfill &\quad {if\,b \le x \le b_{1} } \hfill \\ 0 \hfill &\quad {if\,x \ge b_{1} } \hfill \\ \end{array} } \right.$$

Definition 7:

Let \(\left( {a_{1} ,\;a,\;b,\;b_{1} } \right)\) and \(\left( {c_{1} ,\;c,\;d,\;d_{1} } \right)\) be two positive trapezoidal fuzzy numbers. Some fuzzy operators are defined as follow,

$$\begin{aligned} \left( {a_{1} ,\;a,\;b,\;b_{1} } \right) \oplus \left( {c_{1} ,\;c,\;d,\;d_{1} } \right) & = \left( {a_{1} + c_{1} ,\;a + c,\;b + d,\;b_{1} + d_{1} } \right) \\ \left( {a_{1} ,\;a,\;b,\;b_{1} } \right){ \ominus }\left( {c_{1} ,\;c,\;d,\;d_{1} } \right) & = \left( {a_{1} - d_{1} ,\;a - d,\;b - c,\;b_{1} - c_{1} } \right) \\ k{\kern 1pt} {\kern 1pt} \left( {a_{1} ,\;a,\;b,\;b_{1} } \right) & = \left\{ \begin{aligned} \left( {ka_{1} ,\;ka,\;kb,\;kb_{1} } \right)\quad k > 0, \hfill \\ \left( {kb_{1} ,\;kb,\;ka,\;ka_{1} } \right)\quad k < 0. \hfill \\ \end{aligned} \right. \\ \end{aligned}$$

2.2 Extension principle

One of the most important concepts in fuzzy set theory that can be used to generalize crisp mathematical concepts to fuzzy sets is Zadeh’s extension principle. The Zadeh’s extension principle is described here.

Let X be a Cartesian product of some universes \(X = X_{1} \times \cdots \times X_{n}\), and \(\tilde{A}_{1} , \ldots ,\tilde{A}_{n}\) be n fuzzy sets in \(X_{1} , \ldots ,X_{n}\), respectively. f is a mapping function from X to a universe Y such that \(y = f\left( {x_{1} , \ldots ,x_{n} } \right)\). Then the extension principle allows us to define a fuzzy set \(\tilde{B}\) in Y by

$$\tilde{B} = \left\{ {\left( {y,\mu_{{\tilde{B}}} \left( y \right)} \right)|\,y = f\left( {x_{1} , \ldots ,x_{n} } \right),\,\left( {x_{1} , \ldots ,x_{n} } \right) \in X} \right\}$$

where

$$\mu _{{\tilde{B}}} \left( y \right) = \left\{ {\begin{array}{*{20}l} {\mathop {\sup }\limits_{{(x_{1} , \ldots ,x_{n} ) \in f^{{ - 1}} (y)}} \min \left\{ {\mu _{{\tilde{A}_{1} }} \left( {x_{1} } \right), \ldots ,\mu _{{\tilde{A}_{n} }} \left( {x_{n} } \right)} \right\}} \hfill & {if\,f^{{ - 1}} \left( y \right) \ne \emptyset } \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

where \(f^{ - 1}\) is the inverse form of f.

3 Fuzzy shortest path problem

Consider a weighted direct graph \(G = \left( {V,E} \right)\), where \(V = \left\{ {1,2, \ldots ,m} \right\}\) is the set of m vertices and \(E \subseteq V \times V\) is the set of n arcs. Each arc is denoted by an ordered pair \(\left( {i, \, j} \right)\), where \(i,j \in \,\,V\). It is supposed that there is only one directed arc \(\left( {i, \, j} \right)\) from node i to node j. Let the nodes 1 and m be the source and destination nodes, respectively. A path \(p_{ij}\) is defined as a sequence of alternating nodes and arcs, from i to j. We denote length of the paths between two specified vertices by \(c_{ij}\) associated with each arc \(\left( {i, \, j} \right)\) in direct graph G. So, the shortest path problem with the crisp arc lengths \(c_{ij}\) can be linearly formulated as (Bazaraa et al. 2010),

$$\begin{aligned} & \min \;Z = \sum\limits_{{i = 1}}^{m} {\sum\limits_{{j = 1,j \ne i}}^{m} {c_{{ij}} } } x_{{ij}} \\ & {\text{s}}{\text{.t}}{\text{.}}\sum\limits_{{j = 1,j \ne i}}^{m} {x_{{ij}} } - \sum\limits_{{k = 1,k \ne i}}^{m} {x_{{ki}} } = \left\{ {\begin{array}{*{20}l} 1 \hfill & {if\;i = 1} \hfill \\ 0 \hfill & {if\;i = 2, \ldots ,m - 1} \hfill \\ { - 1} \hfill & {if\;i = m} \hfill \\ \end{array} } \right. \\ & x_{{ij}} \ge 0\quad i,j = 1,2, \ldots ,m \\ \end{aligned}$$
(1)

The variable \(x_{ij}\) is the decision variable of the arc \(\left( {i, \, j} \right)\). It takes a positive value if the arc \(\left( {i, \, j} \right)\) is a part of the shortest path in the solution of the problem. Otherwise, its value is zero.

The problem is dualized as (Bazaraa et al. 2010),

$$\begin{aligned} & \hbox{max} \;w_{1} - w_{m} \\ & {\text{s}} . {\text{t}} .\quad w_{i} - w_{j} \le c_{ij} \quad i \ne j,\quad i,j = 1,2, \ldots ,m \\ \end{aligned}$$
(2)

where \(w_{i}\) denotes the dual variable of vertex i with no restriction on its sign.

In conventional shortest path problems the main assumption is that the decision maker is sure about the arc length of the paths between two specified vertices. In real world problems, some arc length in the shortest path problems may not be known precisely due to some uncontrollable factors. In these problems, the arc length may be shown by units of cost, time, distance, etc.

Intuitively, if because of uncontrollable factors the arc length from the i-th vertex to the j-th vertex varies from its certain value, fuzzy sets can be used to model it. In such cases, the shortest path problem is converted to a fuzzy shortest path problem (see Okada and Soper 2000).

Suppose the arc length between vertices is approximately known and can be represented by the convex fuzzy sets, \(\tilde{C}_{ij}\). Furthermore, let \(\mu_{{\tilde{C}_{ij} }}\) denote its membership function. So,

$$\tilde{C}_{ij} = \left\{ {\left( {c_{ij} ,\mu_{{\tilde{C}_{ij} }} \left( {c_{ij} } \right)} \right)|c_{ij} \in S\left( {\tilde{C}_{ij} } \right)} \right\}$$

where \(S\left( {\tilde{C}_{ij} } \right)\) is the support of \(\tilde{C}_{ij}\) which denote the universe sets of the unit shipping cost between the vertices. Then, the fuzzy shortest path problem can be formulated as,

$$\begin{aligned} & \min \;\tilde{Z} = \sum\limits_{{i = 1}}^{m} {\sum\limits_{{j = 1,j \ne i}}^{m} {\tilde{C}_{{ij}} } } x_{{ij}} \\ & {\text{s}}{\text{.t}}{\text{.}}\sum\limits_{{j = 1,j \ne i}}^{m} {x_{{ij}} } - \sum\limits_{{k = 1,k \ne i}}^{m} {x_{{ki}} } = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,i = 1} \hfill \\ 0 \hfill & {{\text{if}}\,i = 2, \ldots ,m - 1} \hfill \\ { - 1} \hfill & {{\text{if}}\,i = m} \hfill \\ \end{array} } \right. \\ & x_{{ij}} \ge 0\quad i,j = 1,2, \ldots ,m \\ \end{aligned}$$
(3)

where the sign \({\sum }\) in the objective function is the \({ \oplus }\) operator of the fuzzy sets.There are different methods in the literature which solved fuzzy shortest path problems (see Okada and Soper 2000; Chuang and Kung 2006; Moazeni 2006; Ji et al. 2007) but none of them applied the extension principle to find the fuzzy optimal solution for the problem. In the next section, a solution approach based on the extension principle is developed for the fuzzy shortest path problem.

4 The proposed solution methodology

A solution approach based on the extension principle of Zadeh (Zadeh 1987; Yager 1986) is used to solve the fuzzy shortest path problem in this section.

If an \(\alpha\)-cut for the fuzzy set \(\tilde{C}_{ij}\) is defined by,

$$\left( {C_{ij} } \right)_{\alpha }\,=\, \left[ {\left( {C_{ij} } \right)_{\alpha }^{L} ,\left( {C_{ij} } \right)_{\alpha }^{U} } \right] = \left[ {\mathop {\hbox{min} }\limits_{{c_{ij} }} \left\{ {c_{ij} \in S\left( {\tilde{C}_{ij} } \right)|\,\mu_{{\tilde{C}_{ij} }} \left( {c_{ij} } \right) \ge \alpha } \right\},\,\mathop {\hbox{max} }\limits_{{c_{ij} }} \left\{ {c_{ij} \in S\left( {\tilde{C}_{ij} } \right)|\,\mu_{{\tilde{C}_{ij} }} \left( {c_{ij} } \right) \ge \alpha } \right\}} \right]$$

the interval shows where the cost value at the given possibility level \(\alpha\). As the aim is to derive the membership function of the total shortest path \(\tilde{Z}\), the main difficulty arises when dealing with the varying ranges of the unit shipping costs. One way to solve such difficulty is to use Zadeh’s extension principle. Therefore, based on extension principle, the membership function \(\mu_{{\tilde{Z}}}\) is defined by,

$$\mu_{{\tilde{Z}}} \left( z \right) = \mathop {\sup}\limits_{c} \,\hbox{min} \,\left\{ {\mu_{{_{{\tilde{C}_{ij} }} }} \left( {c_{ij} } \right),\quad \forall i,j|\,z = Z\left( c \right)} \right\}$$
(4)

where \(Z\left( c \right)\) is the objective function for the shortest path of the problem (1). The objective function value of the fuzzy shortest path problem (3) is a fuzzy number if the \(\alpha\)-cuts of \(\tilde{Z}\) do not degenerate to a similar point. Otherwise, it is a crisp value. Equation (4) implies that \(\mu_{{\tilde{Z}}}\) is the minimum of \(\mu_{{_{{\tilde{C}_{ij} }} }} \left( {c_{ij} } \right)\) for all pairs of \(i,j\). So, for an \(\alpha\)-cut the following conditions must be held in order to have \(\mu_{{\tilde{Z}}} \left( z \right) = \alpha\),

  • \(\forall i,j:\, \mu_{{_{{\tilde{C}_{ij} }} }} \left( {c_{ij} } \right) \ge \alpha\),

  • \(\forall i,j:\) at least one \(\mu_{{_{{\tilde{C}_{ij} }} }} \left( {c_{ij} } \right) = \alpha\).

Now, to calculate the membership function \(\mu_{{\tilde{Z}}}\), it is enough to calculate the left shape and right shape functions of \(\mu_{{\tilde{Z}}}\), that is the same as finding the lower and upper bound (\(Z_{\alpha }^{L}\) and \(Z_{\alpha }^{U}\)) for the \(\alpha\)-cuts of \(\tilde{Z}\). As \(Z_{\alpha }^{L}\) and \(Z_{\alpha }^{U}\) are the minimum and maximum of \(Z\left( c \right)\), respectively, those are defined by,

$$Z_{\alpha }^{L} = \hbox{min} \left\{ {Z\left( c \right)|\left( {C_{ij} } \right)_{\alpha }^{L} \le c_{ij} \le \left( {C_{ij} } \right)_{\alpha }^{U} ,\quad \forall i,j} \right\}$$

and

$$Z_{\alpha }^{U} = \hbox{max} \left\{ {Z\left( c \right)|\left( {C_{ij} } \right)_{\alpha }^{L} \le c_{ij} \le \left( {C_{ij} } \right)_{\alpha }^{U} ,\quad \forall i,j} \right\}$$

that are modeled by the following two-level mathematical models:

$$Z_{\alpha }^{L} = \mathop {\min }\limits_{{(C_{{ij}} )_{\alpha }^{L} \le \,\,c_{{ij}} \le (C_{{ij}} )_{\alpha }^{U} }} \left\{ \begin{gathered} {\text{min}}\;Z = \sum\limits_{{i = 1}}^{m} {\sum\limits_{{j = 1}}^{m} {c_{{ij}} } } x_{{ij}} \hfill \\ s.t.\quad \sum\limits_{{j = 1}}^{m} {x_{{ij}} } - \sum\limits_{{k = 1}}^{m} {x_{{ki}} } = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,i = 1} \hfill \\ 0 \hfill & {{\text{if}}\,i = 2, \ldots ,m - 1} \hfill \\ { - 1} \hfill & {{\text{if}}\,\;i = m} \hfill \\ \end{array} } \right. \hfill \\ x_{{ij}} \ge 0\quad i,j = 1,2, \ldots ,m~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \hfill \\ \end{gathered} \right.$$
(5)
$$Z_{\alpha }^{U} = \mathop {\max }\limits_{{(C_{{ij}} )_{\alpha }^{L} \le c_{{ij}} \le (C_{{ij}} )_{\alpha }^{U} }} \left\{ \begin{gathered} {\text{min}}~\;Z = \sum\limits_{{i = 1}}^{m} {\sum\limits_{{j = 1}}^{m} {c_{{ij}} } } x_{{ij}} \hfill \\ s.t.\quad \sum\limits_{{j = 1}}^{m} {x_{{ij}} } - \sum\limits_{{k = 1}}^{m} {x_{{ki}} } = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,i = 1} \hfill \\ 0 \hfill & {{\text{if}}\,i = 2, \ldots ,m - 1} \hfill \\ { - 1} \hfill & {{\text{if}}\,i = m} \hfill \\ \end{array} } \right. \hfill \\ x_{{ij}} \ge 0\quad i,j = 1,2, \ldots ,m~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \hfill \\ \end{gathered} \right.$$
(6)

4.1 One-level transformation

As \(Z_{\alpha }^{L}\) and \(Z_{\alpha }^{U}\) are obtained by the two-level mathematical model (5) and (6), the models are transformed to one-level models in this subsection.

4.1.1 Transformation of the lower bound model

The two-level problem (5) consists of an outer-level problem and an inner-level problem of minimization type objective function. As both levels has the same type objective function, those can be easily transformed to a one-level problem respect to the constraints of the both problems simultaneously. To do this transformation as the objective function of the both problems is minimization, each \(c_{ij}\) is replaced by its lower bound value \(\left( {C_{ij} } \right)_{\alpha }^{L}\). Therefore, the two-level problem (5) is transformed to a one-level problem such as,

$$\begin{aligned} & \min \;Z_{\alpha }^{L} = \sum\limits_{{i = 1}}^{m} {\sum\limits_{{j = 1,j \ne i}}^{m} {\left( {C_{{ij}} } \right)_{\alpha }^{L} } } x_{{ij}} \\ & {\text{s}}{\text{.t}}{\text{.}}\quad \sum\limits_{{j = 1,j \ne i}}^{m} {x_{{ij}} } - \sum\limits_{{k = 1,k \ne i}}^{m} {x_{{ki}} } = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,i = 1} \hfill \\ 0 \hfill & {{\text{if}}\,i = 2, \ldots ,m - 1} \hfill \\ { - 1} \hfill & {{\text{if}}\,i = m} \hfill \\ \end{array} } \right. \\ & x_{{ij}} \ge 0\quad i,j = 1,2, \ldots ,m \\ \end{aligned}$$
(7)

As the model (7) is a conventional shortest path problem (Bazaraa et al. 2010), it can be solved easily by any solver. In the model, as each \(c_{ij}\) is replaced by the lower bounds of its \(\alpha\)-cut, that means \(\mu_{{\tilde{C}_{ij} }} \left( {c_{ij} } \right) = \alpha\), therefore, the requirement of Eq. (4) is satisfied as \(\mu_{{\tilde{Z}}} \left( z \right) = \mathop {\sup}\nolimits_{c} \,\hbox{min} \,\{ {\mu_{{_{{\tilde{C}_{ij} }} }} \left( {c_{ij} } \right),\,\forall i,j|\,z = Z\left( c \right)} \} = \alpha\).

4.1.2 Transformation of the upper bound model

The procedure to transform the two-level model of the upper bound to a one-level model is different than what was used for the lower bound model. The difference arises because in the model (6) the outer-level model and the inner-level model have different optimization directions of maximization and minimization respectively. So, the model (6) cannot be solved straightforwardly.

Based on the duality principle in linear programming (Bazaraa et al. 2010), a primal problem and its dual problem which has opposite optimization direction, have the same objective function value (in optimality condition). So, the duality principle is used here to transform the model (6) to a one-level mathematical model by replacing the inner-level problem by its dual version. The dual problem of the inner-level problem of the model (6) is problem (2). Therefore, the model (6) is rewritten as,

$$Z_{\alpha }^{U} = \mathop {\hbox{max} }\limits_{{(C_{ij} )_{\alpha }^{L} \le c_{ij} \le (C_{ij} )_{\alpha }^{U} }} \left\{ \begin{aligned} { \hbox{max} } w_{1} - w_{m} \hfill \\ s.t.\quad w_{i} - w_{j} \le c_{ij} \quad \forall i,j \hfill \\ \end{aligned} \right.$$
(8)

In the model (8), as both levels have the same type objective function, those can be easily transformed to a one-level problem respect to the constraints of the both problems simultaneously. For this transformation as the objective function of the both problems is of maximization type, each \(c_{ij}\) is replaced by its upper bound value \(\left( {C_{ij} } \right)_{\alpha }^{U}\). Therefore, the two-level problems (6) and (8) is transformed to the following one-level problem,

$$\begin{aligned} & { \hbox{max} } Z_{\alpha }^{U} = w_{1} - w_{m} \\ & {\text{s}} . {\text{t}} .\quad w_{i} - w_{j} \le \left( {C_{ij} } \right)_{\alpha }^{U} \quad \forall i,j \\ \end{aligned}$$
(9)

As the model (9) is dual of a conventional shortest path problem, it can be solved easily by any solver. In the model (8), as each \(c_{ij}\) is replaced by the upper bounds of its \(\alpha\)-cut, that means \(\mu_{{\tilde{C}_{ij} }} \left( {c_{ij} } \right) = \alpha\), therefore, the requirement of Eq. (4) is also satisfied as \(\mu_{{\tilde{Z}}} \left( z \right) = \mathop {\sup }\nolimits_{c} \,\hbox{min} \,\{ {\mu_{{_{{\tilde{C}_{ij} }} }} \left( {c_{ij} } \right),\,\forall i,j|\,z = Z\left( c \right)} \} = \alpha\).

If two \(\alpha\)-cuts of \(\alpha_{1}\) and \(\alpha_{2}\) such that \(0 \le \alpha_{1} \text{ < }\alpha_{2} \le 1\) is considered, according to the models (7) and (9) the following relations is true,

$$Z_{{\alpha_{1} }}^{L} \le Z_{{\alpha_{2} }}^{L}$$

and

$$Z_{{\alpha_{2} }}^{U} \le Z_{{\alpha_{1} }}^{U}$$

It means that the left side function according to the \(\alpha\)-cuts does not decreased and the right side one does not increased. Referring to the definition of “convex fuzzy set” (see Zimmermann 1996), the above relations prove the convexity of \(\tilde{Z}\). As, \(Z_{\alpha }^{L}\) and \(Z_{\alpha }^{U}\) are inverted according to \(\alpha\) values, the left and right side functions of \(L\left( Z \right) = \left( {Z_{\alpha }^{L} } \right)^{ - 1}\) and \(L\left( R \right) = \left( {Z_{\alpha }^{U} } \right)^{ - 1}\) can be defined respectively. Therefore, the membership function of \(\mu_{{\tilde{Z}}}\) is defined by the following relation,

$$\mu _{{\tilde{Z}}} \left( z \right) = \left\{ {\begin{array}{*{20}l} {L\left( Z \right)} \hfill & {Z_{{\alpha = 0}}^{L} \le Z \le Z_{{\alpha = 1}}^{L} } \hfill \\ 1 \hfill & {Z_{{\alpha = 1}}^{L} \le Z \le Z_{{\alpha = 1}}^{U} } \hfill \\ {L\left( R \right)} \hfill & {Z_{{\alpha = 1}}^{U} \le Z \le Z_{{\alpha = 0}}^{U} } \hfill \\ \end{array} } \right.$$
(10)

Using the models (7) and (9) and different \(\alpha\)-cut values, the solutions obtained for \(Z_{\alpha }^{L}\) and \(Z_{\alpha }^{U}\) are collected to show the shape of \(L\left( Z \right)\) and \(L\left( R \right)\) as a fuzzy number.

4.2 Overall solution procedure

The overall procedure of the proposed solution methodology to find the shortest path of a fuzzy shortest path problem and its associated fuzzy length is summarized in the flowchart of Fig. 2.

Fig. 2
figure 2

The flowchart of the proposed solution methodology

Full size image

For any fuzzy shortest path problem, the models (7) and (9) are to be solved for different \(\alpha\) confidence levels (\(\alpha\)-cuts). For all \(\alpha\)-cuts, the same shortest path is obtained while unique trapezoidal fuzzy path length for each \(\alpha\)-cut is obtained by, \(\tilde{Z} = \left( {Z_{\alpha = 0}^{L} ,Z_{\alpha = 1}^{L} ,Z_{\alpha = 1}^{U} ,Z_{\alpha = 0}^{U} } \right).\) Furthermore, for any \(\alpha\)-cut other than 0 and 1, lower and upper bounds can be obtained by \(Z_{\alpha }^{L}\) and \(Z_{\alpha }^{U}\) from the models (7) and (9) for that \(\alpha\)-cut.

5 Numerical examples

In this section, in order to test efficiency of the proposed method, two examples from the literature of fuzzy shortest path problem is considered. Examples 1 is taken from the study of Okada and Soper (2000) where Example 2 was solved previously by Ji et al. (2007), Mahdavi et al. (2009), Deng et al. (2012). To perform the computations of this section all of the mathematical models are solved using GAMS 23.5 software.

Example 1.

This example was tackled by Okada and Soper (2000). It has a transportation network consisting of six nodes with their lengths represented by trapezoidal fuzzy numbers. The aim is to find its shortest path and the associated fuzzy length. The network is illustrated by Fig. 3.

Fig. 3
figure 3

The transportation network of Example 1 (Okada and Soper 2000)

Full size image

The models (7) and (9) are required to be solved to obtain the shortest path of the example. So, the models (3), (7) and (9) using the data of the example are written as, model (3):

$$\begin{aligned} & \hbox{min} \;Z = \,\left( {10,20,20,30} \right)\,x_{12} + \left( {52,62,65,70} \right)\,x_{13} \, + \left( {35,38,40,45} \right)\,x_{23} \, + \,\left( {10,13,17,20} \right)\,x_{34} \\ & \quad \quad + \left( {52,55,60,65} \right)\,x_{25} + \left( {8,9,9,10} \right)\,x_{35} \, + \,\left( {70,75,85,97} \right)\,x_{46} \, + \left( {50,70,80,100} \right)\,x_{56} \\ & {\text{s}} . {\text{t}} .\quad x_{12} + x_{13} = 1 \\ & x_{25} + x_{23} - x_{12} = 0 \\ & x_{34} + x_{35} - x_{23} - x_{13} = 0 \\ & x_{46} - x_{34} = 0 \\ & x_{56} - x_{34} - x_{25} & = 0 \\ & - x_{46} - x_{56} = - 1 \\ & x_{ij} \ge 0\quad \forall i,j \\ \end{aligned}$$
(11)

The lower bound based on the model (7) is as follows:

$$\begin{aligned} & \hbox{min} \;Z_{\alpha }^{L} = \left( {10 + 10\alpha } \right)x_{12} + \left( {52 + 10\alpha } \right)\,x_{13} \, + \left( {35 + 3\alpha } \right)x_{23} \, + \,\left( {10 + 3\alpha } \right)\,x_{34} \, \\ & \quad \quad + \left( {52 + 3\alpha } \right)\,x_{25} + \left( {8 + \alpha } \right)\,x_{35} \, + \,\left( {70 + 5\alpha } \right)\,x_{46} \, + \left( {50 + 20\alpha } \right)\,x_{56} \\ & {\text{s}} . {\text{t}} .\quad x_{12} + x_{13} = 1 \\ & x_{25} + x_{23} - x_{12} = 0 \\ & x_{34} + x_{35} - x_{23} - x_{13} = 0 \\ & x_{46} - x_{34} = 0 \\ & x_{56} - x_{34} - x_{25} = 0 \\ & - x_{46} - x_{56} = - 1 \\ & x_{ij} \ge 0\quad \forall i,j \\ \end{aligned}$$
(12)

The upper bound based on the model (9) is as follows:

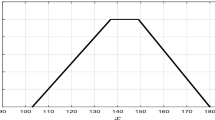
$$\begin{aligned} & \hbox{max} \;Z_{\alpha }^{U} \, = w_{1} \, - w_{6} \\ & {\text{s}} . {\text{t}} .\quad w_{1} \, - w_{2} \le 30 - 10\alpha \\ & w_{1} \, - w_{3} \le 70 - 5\alpha \\ & w_{2} \, - w_{3} \le 45 - 5\alpha \\ & w_{2} \, - w_{5} \le 65 - 5\alpha \\ & w_{3} \, - w_{4} \le 20 - 3\alpha \\ & w_{3} \, - w_{4} \le 20 - 3\alpha \\ & w_{3} \, - w_{5} \le 10 - \alpha \\ & w_{4} \, - w_{6} \le 97 - 12\alpha \\ & w_{5} \, - w_{6} \le 100 - 20\alpha \\ \end{aligned}$$
(13)

The models (12) and (13) for the Example 1 are solved using different values of \(\alpha\), so, different objective function values for upper and lower bound problems are obtained. The results are shown by Table 1. The results are plotted to reflect a fully trapezoidal fuzzy number with core of [137, 149] and support of [103, 180] which are obtained in \(\alpha\)-cuts of 1 and 0 respectively. This trapezoidal fuzzy number is illustrated by Fig. 4.

Table 1 The upper bound and lower bound obtained by different \(\alpha\)-cuts for Example 1
Full size table
Fig. 4
figure 4

The membership function obtained for Example 1 by different \(\alpha\)-cuts

Full size image

In this example, the length of obtained shortest path is impossible to be out of the interval [103, 180] and its most likely value lies within the interval [137, 149]. The shortest path introduced by the models (12) and (13) are the same for different \(\alpha\)-cuts. Here, we focus on the paths obtained by \(\alpha\)-cuts 0 and 1.

For \(\alpha = 0\) cut of \(\tilde{Z}\), the lower bound of \(Z_{\alpha }^{L*} = 103\) occurs in the shortest path \(1 \to 2 \to 3 \to 5 \to 6\) and the upper bound of \(Z_{\alpha }^{U*} = 180\) occurs in the shortest path \(1 \to 3 \to 5 \to 6\). In the case of \(\alpha = 1\) cut of \(\tilde{Z}\), the lower bound of \(Z_{\alpha }^{L*} = 137\) occurs in the shortest path \(1 \to 2 \to 3 \to 5 \to 6\) and the upper bound of \(Z_{\alpha }^{U*} = 149\) occurs in the shortest path \(1 \to 2 \to 3 \to 5 \to 6\). So, for \(\alpha = 0\) cut, two non-dominated shortest paths and for \(\alpha = 1\) cut a single shortest path is obtained by the models (12) and (13). The obtained shortest paths is the same as what reported by Okada and Soper (2000) as is explained here.

In Okada and Soper (2000) two non-dominated shortest paths is obtained for this example. These shortest paths are, path 1: \(1 \to 2 \to 3 \to 5 \to 6\) and path 2: \(1 \to 3 \to 5 \to 6\). The paths are the same as what our proposed method results. It should be mentioned that, in the proposed method, we obtain a lower and upper bound to the fuzzy shortest path for all \(\alpha\) levels starting from 0 to 1 which is no done in the method of Okada and Soper (2000). For \(\alpha = 0\) cut of \(\tilde{Z}\), the proposed method gives unique lower and upper bounds of 103 and 180 respectively, where the lower and upper bounds in Okada and Soper (2000) vary in the shortest paths. They obtained the lower and upper bounds of 103 and 185 for path 1 and the lower and upper bounds of 110 and 180 for path 2. So, although the shortest paths obtained by both methods are the same, the proposed method in this paper show better results for the lower and upper bounds obtained for the minimum \(\alpha\)-cut level (\(\alpha = 0\)) than the method used by Okada and Soper (2000).

The same superiority of the method of this paper is proved in the maximum \(\alpha\)-cut level (\(\alpha = 1\)). For \(\alpha = 1\) cut of \(\tilde{Z}\), the unique lower and upper bounds of 137 and 149 respectively, where the lower and upper bounds in Okada and Soper (2000) is different for each shortest path. They obtained the lower and upper bounds of 137 and 149 for path 1 and the lower and upper bounds of 141 and 154 for path 2.

Example 2.

Another transportation network from the literature of the fuzzy shortest path problem where the length of each arc is a trapezoidal fuzzy number, is considered to test the efficiency of the proposed method. The method previously was solved by Ji et al. (2007), Mahdavi et al. (2009) and Deng et al. (2012). The network and its input data are presented by Fig. 5 and Table 2.

Fig. 5
figure 5

The transportation network of Example 2 (Ji et al. 2007; Mahdavi et al. 2009; Deng et al. 2012)

Full size image
Table 2 The arc lengths for the network of Example 2
Full size table

The lower bound and upper bound models (7) and (9) were coded by the data of Example 2. The models were solved for different levels of \(\alpha\)-cut. The obtained lower and upper bound values are reported in Table 3. In this example, the length of obtained shortest path is impossible to be out of the interval [38, 65] and its most likely value lies within the interval [49, 58]. The shortest path introduced by the models (7) and (9) are the same for different \(\alpha\)-cuts. Here, we focus on the paths obtained by \(\alpha\)-cuts 0 and 1.

Table 3 The lower and upper bounds obtained by different \(\alpha\)-cuts for Example 2
Full size table

For \(\alpha = 0\) cut of \(\tilde{Z}\), the lower bound of \(Z_{\alpha }^{L*} = 38\) occurs in the shortest path \(1 \to 5 \to 11 \to 17 \to 21 \to 23\) and the upper bound of \(Z_{\alpha }^{U*} = 65\) occurs in the shortest path \(1 \to 5 \to 11 \to 17 \to 21 \to 23\). In the case of \(\alpha = 1\) cut of \(\tilde{Z}\), the lower bound of \(Z_{\alpha }^{L*} = 49\) occurs in the shortest path \(1 \to 5 \to 11 \to 17 \to 21 \to 23\) and the upper bound of \(Z_{\alpha }^{U*} = 58\) occurs in the shortest path \(1 \to 5 \to 11 \to 17 \to 21 \to 23\). Therefore, the shortest path of the example is \(1 \to 5 \to 11 \to 17 \to 21 \to 23\) with trapezoidal length of (38, 49, 58, 65) which is exactly the same as what reported by Ji et al. (2007), Mahdavi et al. (2009) and Deng et al. (2012).

6 Discussion and conclusion

A typical shortest path problem which has fuzzy arc lengths naming fuzzy shortest path problem was studied in this paper. The problem has many real-world applications. The objective of the problem was to introduce the shortest path connecting the first and last vertices of the network which has minimum fuzzy sum of arc lengths among all possible paths. A solution algorithm based on Zadeh’s extension principle was developed to solve the problem. The algorithm uses a decomposition scheme by dividing the problem into two lower bound and upper bound sub-problems.

The algorithm has the following advantages that can be distinguished from the numerical examples of Sect. 5.

  • No ranking function is applied in the procedure of the algorithm.

  • The proposed method can be easily solved using any optimization software.

  • There is no need to have high information of fuzzy linear programming, Zimmermann method and crisp linear programming.

  • The proposed method can be applied to the real-world problems that can be formulated by shortest path problem.

  • For each \(\alpha\)-cut, we obtain a unique lower and upper bound for fuzzy length of shortest path(s).

  • When the fuzzy shortest path model is defuzzified, in this case, two crisp models are solved and therefore, all the algorithms introduced for shortest path problem can be applied.

  • The method is of single-criteria type methods, while, some studies of the literature (see Okada and Soper 2000) considered a multi-criteria method.

  • In the proposed method the fuzzy lower and upper bound models can be solved by parametric analysis approaches. In the previous methods of the literature parametric analysis approaches cannot be used.

The algorithm was tested over some well-known networks from the literature and its performance is superior to the existent methods.