Heuristics for Shortest Path Problem with Intuitionistic Fuzzy Arc Weights

Abstract

This paper is concerned with shortest path problem in a network where arc weights are taken as intuitionistic fuzzy numbers instead of crisp values. Although shortest path problem is very important and well known problem in graph theory but the approach of taking arc weights as intuitionistic fuzzy numbers is new and make this problem more realistic as theoretically these numbers has been proved very useful to deal with distinct real life factors. So this problem deals with real life situations more effectively. In this paper, a population based genetic algorithm (GA) and a single solution based tabu search algorithm are proposed to find the shortest path in a given network having trapezoidal intuitionistic fuzzy arc weights. The performance of both the algorithms is tested on randomly generated graphs as no benchmark graph is available for this problem so far. Further, the results of these algorithms are also compared to find out the significance of the proposed approaches.

1 Introduction

Shortest path problem (SPP) is a well known problem where path with least cost is found in a given graph (network) from one vertex to another where cost of the path is equal to the sum of the weights of all edges (arcs) consisting in the path. These weights may be travelling time, travelling cost, capacity, demand etc. This is a fundamental problem in graph theory which have been drawn attention of many scientists from beginning as transportation problem, routing problem, communication, supply chain management, wire length minimization problems etc. can be converted into this problem.

Although, in traditional shortest path problem, the arc weights are crisp values but in real life situations arc weights may represent time, cost, capacity, demand etc. Due to variations in different variables, the arc weights cannot be represented as a single value. In this condition, fuzzy numbers may better represent the arc weights and the shortest path problem where the arc weights are fuzzy numbers is generally known as fuzzy shortest path problem (FSPP). But the concept of fuzzy numbers is very much different from crisp numbers as one cannot simply add and compare two fuzzy numbers. To deal with fuzzy numbers the concept of fuzzy set theory has been introduced by Zadeh [21]. Dubois and Prade [4] were first who analyzed fuzzy shortest path problem.

Later Atanassov in 1983 [1] extended fuzzy sets to intuitionistic fuzzy sets to solve fuzzy shortest path problem more precisely with the help of degree of membership, degree of non-membership and degree of hesitation. Since last two decades it has been become topic of great interest for many scientists. Intuitionistic fuzzy set theory has successfully used to solve problems in many areas like logical programming, medical diagnosis, artificial intelligence, decision making problems etc. Since comparison of intuitionistic fuzzy numbers (IFNs) is a difficult task, a lot of attention has been paid to develop ranking methods for comparison of IFNs. Although ranking of intuitionistic fuzzy numbers has been started since late seventies of last century but complete ranking method is developed in 2014 by Wang and Westmant [19]. Since then few other ranking methods have appeared in the literature [2, 11, 15,16,17,18]. In this paper, we have used ranking methods given in [15] to compare the costs of paths in a given network with trapezoidal intuitionistic fuzzy arc weights.

Yu and Wei [20] proposed a fuzzy linear programming approach to find fuzzy shortest path in a graph. Liu and Kao [10] calculated Yager ranking indices for fuzzy arcs to change fuzzy formulation in crisp formulation. A fuzzy algorithm based on multiple labeling methods was proposed by Okada and Soper [14] to extract shortest paths in a given graph. Nayeem and Pal [13] also proposed an algorithm to deal with fuzzy shortest path problem with two different types of intuitionistic numbers. A dynamic programing algorithm for solving FSPP has been proposed in [17]. Later they proposed a genetic algorithm [7] to solve FSPP with mixed fuzzy arc weights in 2013. A particle swarm optimization algorithm to solve FSPP is proposed in [5]. For other papers on fuzzy shortest path problems, see [6, 8, 9]. It is worth to note that no metaheuristic has been proposed for SPP with intuitionistic fuzzy arc weights.

In this paper, we proposed two metaheuristic approaches: a genetic algorithm (GAIFSP) and a tabu search based algorithm (TSIFSP) to solve intuitionistic fuzzy shortest path problem. As there is no benchmark graph available for this problem, we performed experiments for both the proposed algorithms on randomly generated graphs. Furthermore, there is no previously proposed metaheuristic approach available for FSPP to compare the results with our proposed algorithms so we have compared the performance of our proposed GAIFSP with that of TSIFSP.

Organization of the paper is as follows: Some useful basic definitions are given in Sect. 2 to understand the problem and proposed algorithms. A genetic algorithm is described briefly in Sect. 3 followed by explanation of its application on shortest path problem step by step. Basic structure of tabu search algorithm is explained in Sect. 4 followed by explanation of proposed TSIFSP step by step. Experimentation and results are discussed in Sect. 5. The work is concluded in Sect. 6.

2 Some Basic Definitions

In this section some basic definitions regarding graph theory and fuzzy theory are presented as follows:

Graph: A graph G(V, E) is a combination of a set of n vertices $V \,{=}\, \{v_{1}, v_{2}, \ldots , v_{n}\}$ together with a set of m edges $E =\{e_{1}, e_{2}, \ldots , e_{m}\},$ such that each edge $e_{k}$ is represented as a pair of vertices $(v_{i}, v_{j})$ and is denoted by $v_{i} v_{j}$ for convenience. Cardinality of the graph is denoted as $|V|= n$.

Directed Graph: A simple graph where each edge has a direction i.e. each edge is represented by an ordered pair of vertex is called directed graph. In other words if an edge $(v_i, v_j)$ connects vertex $v_i$ to $v_j$ then it is not necessary that it also connects vertex $v_j$ to vertex $v_i$. In this paper, we have considered only directed networks and call them simply a network.

Path: A $u-v$ path is defined as a sequence of vertices starting at u and ending at v, where consecutive vertices in the sequence are adjacent vertices in the graph and no vertex is repeated.

Intuitionistic Fuzzy Sets: An intuitionistic fuzzy set X in universal set Y is defined as $X = \{y,\mu '_{X} (y),\nu '_{X} (y)\in Y \}$, where $\mu '_{X} (y): Y\rightarrow [0,1]$ and $\nu '_{X} (y): Y\rightarrow [0,1]$ are called the membership and non-membership grades respectively and $\forall y \in Y, 0 \le \mu '_{X} (y)+\nu '_{X} (y)\le 1$. Pair $(\mu '_{X} (y),\nu '_{X} (y))$ is called an intuitionistic fuzzy number. For any intuitionistic fuzzy number B let eight numbers $a'_1, a'_2, a'_3, a'_4, b'_1, b'_2, b'_3, b'_4 \in \mathrm{I\!R}$ such that $b'_1 \le a'_1 \le b'_2 \le a'_2 \le a'_3 \le b'_3 \le a'_4 \le b'_4$ and four functions $f_B, g_B, h_B, k_B : \mathrm{I\!R} \rightarrow [0,1]$, such that $f_B$ and $k_B$ are non decreasing and $g_B$ and $h_B$ are non increasing then the membership function $\mu '_B$ can be described as

$$\begin{aligned} \mu '_{B}(y)= {\left\{ \begin{array}{ll} 0, \text { if }y< a'_{1} \\ f_{B}(y), \text { if }a'_{1}\le y \le a'_{2} \\ 1, \text { if }a'_{2}\le y \le a'_{3} \\ g_{B}(y), \text { if } a'_{3}\le y \le a'_{4} \\ 0, \text { if } a'_{4}< y \end{array}\right. } \end{aligned}$$

and non-membership function $\nu '_B$ as

$$\begin{aligned} \nu '_{B}(y)= {\left\{ \begin{array}{ll} 0, \text { if }y< b'_{1} \\ h_{B}(y), \text { if }b'_{1}\le y \le b'_{2} \\ 1, \text { if }b'_{2}\le y \le b'_{3} \\ k_{B}(y), \text { if } b'_{3}\le y \le b'_{4} \\ 0, \text { if } b'_{4}< y \end{array}\right. } \end{aligned}$$

Graphical representation of the intuitionistic fuzzy number is shown in Fig. 1.

Fig. 1

Graphical representation of the intuitionistic fuzzy number

2.1 Trapezoidal Intuitionistic Fuzzy Number

A trapezoidal intuitionistic fuzzy number with parameters $b'_{1} \le a'_{1} \le b'_{2} = a'_{2} \le a'_{3} = b'_{3} \le a'_{4}\le b'_{4}$ is denoted by $X \,{=}\, (< a'_{1}, a'_{2}, a'_{3}, a'_{4}>, < b'_{1}, b'_{2}, b'_{3}, b'_{4}>)$ where, membership function is defined as

$$\begin{aligned} \mu '_{X}(y)= {\left\{ \begin{array}{ll} 0, \text { if }y< a'_{1} \\ \frac{y-a'_{1}}{a'_{2} - a'_{1}}, \text { if }a'_{1}\le y \le a'_{2} \\ 1, \text { if }a'_{2}\le y \le a'_{3} \\ \frac{y-a'_{4}}{a'_{3} - a'_{4}}, \text { if } a'_{3}\le y \le a'_{4} \\ 0, \text { if } a'_{4}< y \end{array}\right. } \end{aligned}$$

and the non-membership function is given by

$$\begin{aligned} \nu '_{X}(y)= {\left\{ \begin{array}{ll} 0, \text { if }y< b'_{1} \\ \frac{y-b'_{1}}{b'_{1} - b'_{2}}, \text { if }b'_{1}\le y \le b'_{2} \\ 1, \text { if }b'_{2}\le y \le b'_{3} \\ \frac{y-b'_{4}}{b'_{3} - b'_{4}}, \text { if } b'_{3}\le y \le b'_{4} \\ 0, \text { if } b'_{4}< y \end{array}\right. } \end{aligned}$$

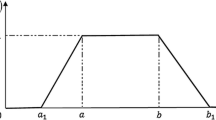
Figure 2 shows the graphical representation of trapezoidal intuitionistic fuzzy number.

Fig. 2

Graphical representation of the trapezoidal intuitionistic fuzzy number

2.2 Addition of Two Trapezoidal Intuitionistic Fuzzy Numbers

Let $X = (< a'_1, a'_2, a'_3, a'_4>, < a'_5, a'_6, a'_7, a'_8>)$ and $Y = (< b'_1, b'_2, b'_3, b'_4>, < b'_5, b'_6, b'_7, b'_8>)$ be two trapezoidal intuitionistic fuzzy numbers then addition of X and Y, denoted by $X\bigoplus Y$, is defined as $X\bigoplus Y = (< a'_1+b'_1, a'_2+b'_2, a'_3+b'_3, a'_4+b'_4>, < a'_5+b'_5, a'_6+b'_6, a'_7+b'_7, a'_8+b'_8>)$.

2.3 Centroid Ranking Technique

Let $X = (\langle a'_1, a'_2, a'_3, a'_4\rangle , \langle b'_1, b'_2, b'_3, b'_4\rangle )$, where $b'_1 \le a'_1 \le b'_2 = a'_2 \le a'_3 = b'_3 \le a'_4 \le b'_4$ and $a'_1, a'_2, a'_3, a'_4, b'_1, b'_2, b'_3, b'_4 \in \mathrm{I\!R}^{+}$ be a trapezoidal intuitionistic fuzzy number. Then centroid of X is defined by four relations given as follows [15]:

$$\begin{aligned} p_{\mu '}(X)=\frac{1}{3}\left[ \frac{a_3^{'2}+a_4^{'2}-a_1^{'2}-a_2^{'2}-a'_1 a'_2+a'_3 a'_4}{a'_4+a'_3-a'_2-a'_1}\right] \end{aligned}$$

$$\begin{aligned} p_{\nu '}(X)=\frac{1}{3}\left[ \frac{2b_4^{'2}-2b_1^{'2}+2b_2^{'2}+2b_3^{'2}+b'_1 b'_2-b'_3 b'_4}{b'_3+b'_4-b'_1-b'_2}\right] \end{aligned}$$

$$\begin{aligned} q_{\mu '}(X)=\frac{1}{3}\left[ \frac{a'_1+2a'_2-2a'_3 -a'_4}{a'_1+a'_2-a'_3-a'_4}\right] \end{aligned}$$

$$\begin{aligned} q_{\nu '}(X)=\frac{1}{3}[\frac{2b'_1+b'_2-b'_3-2b'_4}{b'_1+b'_2-b'_3-b'_4}] \end{aligned}$$

The ranking function of the trapezoidal intuitionistic fuzzy number A is defined by

$$\begin{aligned} R(X)=\sqrt{\frac{1}{2}([p_{\mu '}(X)-q_{\mu '}(X)]^{2}+[p_{\nu '}(X)-q_{\nu '}(X)]^{2})} \end{aligned}$$

3 Genetic Algorithm

Genetic algorithm (GA) is a heuristic search procedure and an optimization technique which is inspired from the process of natural evolution and generally used to generate high quality solution to a problem. It is a type of evolutionary algorithm based on the principle of evolution via natural selection. This process begins with initialization of a population of randomly generated solutions. It is an iterative process where each iteration generates a population of new generation. A fitness function is concerned with the problem is defined to evaluate each solution in each generation and a comparison takes place between each two solutions of the current population which selects the solution with better fitness value and rejects the other one keeping the population size constant. Population obtained after this process is modified by reproduction (crossover) and mutation operators to generate the population of next generation. The new generated population is then used in the next iteration of the algorithm. In general, the procedure continued until there is no change in the best observed fitness value or number of iterations are less than the pre-defined fixed value. The flow chart of genetic algorithm is shown in Fig. 3. To know more about genetic algorithm see [3].

Fig. 3

A flow chart of genetic algorithm

3.1 Genetic Algorithm for Solving Intuitionistic Fuzzy Shortest Path Problem

In this section, the proposed genetic algorithm for shortest path problem with intuitionistic fuzzy arc weights, is explained with description of genetic operators such as initialization of the parent population, selection, crossover, and mutation operator etc.

3.1.1 Initial Population

In general, a solution in the population of genetic algorithm is represented as a chromosome of binary numbers. But in case of FSPP, solution is a path in a given network. So it is not convenient to generate the solution randomly as the random sequence of vertices may not correspond to a path in a given network. Also the length of the path is not a fixed number as it may vary from two to $n -1$ in a given network with n vertices. So, there is a necessity to use some strategy to generate a solution. Here, an approach given in [7] is used to obtain various paths in a given network. The algorithm starts with first vertex of the network and ends with the last vertex or terminating vertex by applying specific steps in between. This algorithm is called repeatedly to generate desired population of paths. The framework of the algorithm is given below [7]:

At the end of execution of this algorithm the population of paths is stored in a matrix namely $\text {par}_{-}\text {pop}$. The algorithm is explained below with the help of a network shown in Fig. 4 where A is the adjacency matrix of this network.

Fig. 4

An example of a network

$$A = \begin{bmatrix} 0&{}1&{}1&{}0&{}1&{}0&{}0&{}0\\ 0&{}0&{}0&{}1&{}1&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}1&{}1&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}1&{}1&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ \end{bmatrix} $$

Here $n =$ 8. Initially set $l = i = p(l) = 1$. Then $a^{1}(1) = \{2, 3, 5\}$. Select an element of this set randomly say $j =$ 5. Set $l = l+$1 i.e. $l =$2 and $p(2) =$ 5. Since 5$\ne$8, set $i =$ 5 and $a^{1}(5) = \{6, 7\}$. Now let $j =$ 6. Set $l =$3 and $p(3) =$6. Since 6 $\ne$8, set $i =$ 6 and $a^{1}(6) = \{8\}$. Now $j =$ 8, $l =$ 4 and $p(4) =$ 8. Since $p(4) =$ 8, procedure stops. The generated path is 1-5-6-8. In this paper, we call it as a solution.

3.1.2 Fitness of a Solution

For selection of good solutions, it is necessary to define their fitness which we call as the cost in this paper. To find the fitness (cost) of each solution in $\text {par}_{-}\text {pop}$, a centroid ranking technique defined in Sect. 2 is used. To understand it, let us consider one of the solution 1-5-6-8 of network shown in Fig. 4. The trapezoidal intuitionistic fuzzy weights of all the arcs of this network are generated randomly and shown in Table 1. Using this table, fitness of the solution 1-5-6-8 is calculated as follows:

Table 1 Edges of a network (Fig. 4) and their corresponding weights

First add all the arc weights corresponding to each edge of the solution, by applying addition procedure defined in Sect. 2. So total arc weight of the solution 1-5-6-8 is $(\langle 72, 87, 107, 120\rangle ,\langle 55, 87, 107, 133\rangle )$. Fitness of the solution 1-5-6-8 calculated by centroid ranking technique mentioned in Sect. 2 is 154.579. So the cost of the solution 1-5-6-8 is 154.579. In context of the problem presented here, the solution with lower cost is more fit than the solution with greater cost. Note that the minimum cost is maintained at each iteration of the algorithm which is treated as the $\text {Best}_{-}\text {cost}$ and the corresponding path is treated as the $\text {Best}_{-}\text {solution}$ at the end of the algorithm. Note that the $\text {Best}_{-}{\text {cost}}$ obtained at the end of the execution of the algorithm is treated as $\text {final}_{-}\text {cost}$.

3.1.3 Selection

This process aims to keep good solutions in the population by omitting the poor ones without reducing the population size. In this work, tournament operator is used for selection procedure wherein a comparison has been made between each two consecutive solutions of $\text {par}_{-}\text {pop}$ and the best one (with lower cost) is placed in a dummy matrix namely $\text {new}_{-}\text {pop}$ with same size as that of $\text {par}_{-}\text {pop}$. It is worthy to note that each solution in $\text {par}_{-}\text {pop}$ participates two times in a tournament and the best solution is placed in $\text {new}_{-}\text {pop}$. In this way $\text {new}_{-}\text {pop}$ may have one, two or zero copy of a solution in $\text {par}_{-}\text {pop}$.

3.1.4 Crossover

Crossover combines properties of two parent solutions and generate two child solutions having some common properties with parent solutions. In this step two new solutions are produced by using any two randomly selected solutions from $\text {new}_{-}\text {pop}$. Crossover rate $(p_c)$ is used to determine the frequency of this job. In our proposed GAIFSP, one point crossover is used. This is a very common crossover technique used in genetic algorithms where two random paths (parent solutions) are selected from the population obtained after selection and if any vertex is common between them except from the first and the last vertex, left or right parts of the common vertex of both parent solutions are exchanged.

Example: Consider two solutions 1-5-7-8 and 1-2-4-5-6-8 of network shown in Fig. 4. Here vertex 5 is common in both solutions. Then exchanging right part of vertex 5 of both the solutions two new solutions are 1-5-6-8 and 1-2-4-5-7-8.

Note that in this process two new child solutions are generated and replaced their parent solutions in a dummy matrix of $\text {new}_{-}\text {pop}$ if child solutions are more fit than parent solutions. This crossover procedure is repeated $p_c \times \text {pop}_{-}\text {size}$ number of times on $\text {new}_{-}\text {pop}$ and at the end dummy $\text {new}_{-}\text {pop}$ is copied back to original $\text {new}_{-}\text {pop}$.

3.1.5 Mutation

This function systematically changes the vertices of a solution which results either a positive direction towards the optimal solution or resulted in the deviation from the optimal solution i.e. the mutated solution can be better than the previous one or not. In proposed heuristic, mutation is addressed effectively. In this process, a mutation rate or mutation probability ($p_m$) is fixed initially so that the frequency of application of this operator is $q = \text {pop}_{-}\text {size} \times p_{m}$. Mutation is applied on $\text {new}_{-}\text {pop}$ obtained after crossover for q number of times. Firstly q number of solutions are selected from $\text {new}_{-}\text {pop}$ by producing q different random integers between 1 and $\text {pop}_{-}\text {size}$. To apply the mutation on a solution, a random number, say k, is generated between 1 and length of the path of the current solution. After that, a new path is searched using Algorithm 1 from kth vertex to the last vertex of the solution keeping vertices prior to kth vertex remain same. Now so obtained mutated solution replaced the original one if it is more fit in concerned to FSPP.

For an example, consider a randomly selected solution 1-2-4-6-8 of network shown in Fig. 4. This is called as current solution with cost = 201.67. Here path length is 5, therefore a random number (say 4) is generated between 1 and 5. Then, the first three vertices 1, 2 and 4 are remain at their places and random path is evolved starting with vertex 6 at position 4 using Algorithm 1. So the new obtained mutated solution is 1-2-4-5-7-8. The cost of this solution is 242.35. Since cost of mutated solution is more than the original one, it wouldn’t be replace the parent solution (original one).

4 Tabu Search

Tabu search (TS) is a single solution based metaheuristic that guides a local search heuristic procedure to escape from local optima and to explore the solution space. This method was proposed by Grover in 1986 [12]. Tabu search is an extension of previously existing local search approaches. In fact it can be seen that basic tabu search is a combination of local search with short term memories. The process starts with initializing a random solution. A candidate list of moves is created by applying some specific steps. In each iteration, each move from candidate list generates a new solution from current solution. This set of solutions is regarded as tabu list and a solution from it is recorded as best solution if it improves the previous best and tabu list is updated. The process stops if solution remains unchanged for some specific number of iterations or the optimal solution is found.

4.1 Tabu Search for Solving Intuitionistic Fuzzy Shortest Path Problem (TSIFSP)

In this section the proposed tabu search algorithm to solve intuitionistic fuzzy shortest path problem is explained. The TSIFSP algorithm starts with generating an initial solution using Algorithm 1. Initially, this solution is called $\text {current}_{-}\text {solution}$ and cost of this solution is considered as $\text {current}_{-}\text {cost}$ and this solution is saved in a tabu list for some time period or for few number of iterations which is called tabu tenure (t) so that this solution is not selected for t number of iterations and new area of search space can be explored. The tabu list is used to prevent looping of solutions and to guide the algorithm to explore the global solution space. To improve the $\text {current}_{-}\text {solution}$, N number of neighbouring solutions of $\text {current}_{-}\text {solution}$ are generated and best solution (solution with lowest cost) among these neighbouring solutions is determined which is referred to as $\text {best}_{-}\text {solution}$ and cost associated with it is called $\text {best}_{-}\text {cost}$. Now this $\text {best}_{-}\text {solution}$ replaces the $\text {current}_{-}\text {solution}$ and $\text {best}_{-}\text {cost}$ replaces the $\text {current}_{-}\text {cost}$ if $\text {best}_{-}\text {cost}$ is less than $\text {current}_{-}\text {cost}$. Once a $\text {best}_{-}\text {solution}$ becomes $\text {current}_{-}\text {solution}$, it is inserted into the tabu list for tabu tenure t to escape from getting stuck in local optima. This process is repeated until $\text {current}_{-}\text {solution}$ remains unchanged for $K_{\max }$ number of iterations. After stoping the process $\text {current}_{-}\text {solution}$ obtained in last iteration is desired final solution and cost associated is $\text {final}_{-}\text {cost}$ of the problem. Some components of TSIFSP are explained below:

4.1.1 Initial Solution

Here, Algorithm 1 is used to generate an initial solution.

4.1.2 Neighbouring Solution

To generate neighboring solution of $\text {current}_{-}\text {solution}$, two vertices of the current solution are selected randomly and path between these two vertices is regenerated using Algorithm 1, where these randomly selected vertices are taken as initial vertex and final vertex.

As an example, consider a path 1-2-4-5-7-8 of network shown in Fig. 4 and let two randomly selected vertices are 2 and 7. Algorithm 1 generates a new path between vertex 2 and vertex 7. Suppose this path is 2-5-7. So a neighbourhood solution of current solution 1-2-4-5-7-8 will be 1-2-5-7-8.

4.1.3 Tabu List

Once a solution is considered as $\text {current}_{-}\text {solution}$, it is sent to tabu list for tabu tenure t so that the algorithm do not select same solution repeatedly as searching around some fixed solutions can prevent to explore new search space that may contain the optimal solution. Apart from this $\text {current}_{-}\text {solution}$, the randomly selected vertices in an iteration which are used to find neighbouring solution, are also inserted in the tabu list for short period of time $tv = n/10$ to escape from generating similar neighboring solution repeatedly.

4.1.4 Termination Criteria

The TSIFSP algorithm stops when $\text {current}_{-}\text {solution}$ remains unchanged for $K_{\max }$ number of iterations i.e. $\text {current}_{-}\text {solution}$ is not improved for $K_{\max }$ number of iterations.

5 Experimentations and Results

All computational experiments have been carried out on an Intel i3, 2.40 GHz quadcore processor with 2 GB RAM. All algorithms in this paper are coded in C++ and compiled with Dev C++. Tuning of parameters for better performance of GAIFSP and TSIFSP is discussed as follows.

Fig. 5

Experimental results of GAIFSP with different values of a $p_c$ and b $p_m$

5.1 Parameter Setting

For parameter setting we have used randomly generated networks with vertices 20, 40, 60, 80, 100 and edges equal to 40, 78, 185, 210 and 329 respectively. Weights on each edge of graphs as trapezoidal inuitionistic fuzzy numbers are also generated randomly. For tuning the parameters used in GAIFSP, experiments have been done for setting crossover rate $p_c$ and mutation rate $p_m$. Number of generation is set to 100 for all the experiments of GAIFSP. In Fig. 5a, results of tuning crossover rate $p_c$ are shown where $p_c$ is set to 0.2, 0.5 and 1 by fixing $p_m$ as 0.2. From the figure it can be seen that GAIFSP performed well for $p_c = 0.5$, so this value of $p_c$ is fixed for further experiments. Fig. 5b shows the results of tuning mutation rate $p_m$ which is set to 0.1, 0.2 and 0.3 and it is observed that best results are obtained when $p_m$ is 0.2 so it is fixed for further experiments. For tuning the parameters used in TSIFSP, first experiment is carried out for setting number of neighboring solutions N by fixing N equal to n/10, n/5 and n/2 with $K_{\max } = 100$. Results of this experiment shown in Fig. 6a clearly depict that least $\text {final}_{-}\text {cost}$ is obtained when number of neighboring solutions is n/5 or n/2. So N has been fixed as n/5. After fixing N, experiments are carried out for tuning $K_{\max }$. For this TSIFSP is executed with $K_{\max }$=25, 50, 100 and 200. From Fig. 6b it can be observed that $\text {final}_{-}\text {cost}$ of an instance is least for $K_{\max } = 100$. After that performance of TSIFSP is stable. So $K_{\max } = 100$ is fixed for TSIFSP. Summary of the parameters, for both the algorithms, with their fine tuned values is given in Table 2.

Fig. 6

Experimental results of TSIFSP with different values of a N and b $K_{\max }$

Table 2 Parameter setting

Fig. 7

Elapsed time comparison of GAIFSP and TSIFSP

5.2 Comparison of GAIFSP and TSIFSP

As there is no benchmark graph available for FSPP with intuitionistic fuzzy arc weights, performance of both GAIFSP and TSIFSP is tested on same network instances as used to fine tune the parameters in the previous section. Since performance of both the algorithms is comparable in obtaining $\text {final}_{-}\text {cost}$ for all the instances, elapsed time has been noted for both GAIFSP and TSIFSP. Value of elapsed time for both the algorithms shown in Fig. 7 concluded that GAIFSP is faster than TSIFSP in terms of finding shortest path having intuitionistic arc weights in a given network.

6 Conclusion

We have considered a new shortest path problem with intuitionistic fuzzy arc weights in this paper and proposed two heuristics for solving it. One is population based and the other one is single solution based heuristic. Experiments on randomly generated graphs show that both algorithms are equally capable of finding shortest path in a given network but computation time of GAIFSP is less than that of TSIFSP. For future work, some more effective heuristics can be designed and compared for this problem.