1 Introduction

The study of nonlinear partial differential equations (NPDEs) are widely growing for its direct relevance with various physical phenomena like plasma physics, nonlinear optics, fluid mechanics, elastic media, optical fibers etc. [1,2,3,4,5,6,7,8,9,10,11,12]. Due to high nonlinear behavior, these NPDEs do not follow superposition principles and are difficult to be analyzed. To obtain their exact solution plays a vital role in understanding the phenomena physically. Therefore, a number of effective tools such as tanh method [1, 2], extended mapping method [3], bifurcation method [4, 5], Exp-function method [6], \((G^{'}/G)\)-expansion method [7], Hirota’s method [8, 9] and Lie symmetry method [10, 11, 13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28] have been evolved for reliable treatments of these NPDEs.

The motive with present study is to obtain invariant solutions of (2+1)-dimensional KP-BBM equation

$$\begin{aligned}&(u_t+u_x-a(u^2)_x-bu_{xxt})_x+ku_{yy}=0 \end{aligned}$$
(1.1)

where a, b, k are constants while u represents wave amplitude. It describes propagation of bidirectional small amplitude waves in nonlinear dispersive medium. The KP-BBM equation was first discovered by A.M. Wazwaz [1] by combining Kadomtsov- Petviashvili (KP) and Benjamin-Bona-Mahony (BBM) equations

\((u_t+auu_x+u_{xxx})_x+u_{yy}=0\) and \(u_t+u_x-a{(u^2)}_{x}-bu_{xxt}=0\) respectively. The KP equation is weakly two dimensional integrable generalization of unidirectional KdV equation [29]. It represents propagation of long waves and admits quadratic nonlinearity with dissipation [30]. While, BBM equation is unidirectional dispersive long-wave equation, known as associative KdV equation for small amplitude, long surface wave propagation. [31].

A.M. Wazwaz [1] investigated KP-BBM equation and its generalized form as well as derived some exact solutions using tanh and sine-cosine methods. Continuing, A.M Wazwaz [2] used extended tanh method to extract soliton solutions of Eq. (1.1). Some periodic wave solutions were found by M.A. Abdou [3]. Tang et al. [4] studied generalized KP-BBM equation and extracted soliton solutions with aid of bifurcation theory. Proceeding with same spirit, Song et al. [5] employed bifurcation method and listed some new soliton solution of Eq. (1.1). Moreover, some exact periodic solutions were constructed by Yu and Ma [6]. Alam and Akbar [7] proposed \((G^{'}/G)\)-expansion method and used it to derive travelling wave solutions of KP-BBM equation. Thereafter, Manafian et al. [8] used Hirota’s method to derive bilinear form of Eq. (1.1) and analyzed its stability. Proceeding with same methodology, Manafian et al. [9] described the intraction between solitons and lumps. Recently, Tanwar and Wazwaz [10] derived optimal system via Lie symmetries and generated some exact soliton solution of Eq. (1.1). Some more solutions were found by Kumar et al. [11]. Apart, Mekki and Ali [12] analyzed numerical results of KP-BBM equation using finite difference scheme and Crank-Nicholson method.

The above findings [1,2,3,4,5,6,7,8,9,10,11,12] motivate us to derive some exact solutions with aid of Lie point symmetries. The main idea of method is based on invariance under various symmetries. The method reduces the independent variables. Thus, repeated applications lead to determining ODEs, which result into exact solutions. These exact solutions describe doubly soliton, multisoliton, compacton, soliton fusion and parabolic nature. Solitons are localized solitary wave packets retaining their shapes when propagating with constant velocity. It is experimentally reported as result of balancing in dispersion effect and nonlinearity. Solitons are widely used in shallow water waves, long-distance transmission and optical switching device due to its high stability. The compactons are newly evolved class of solitons having compact support without exponential tails or wings [32]. It shows the completely elastic interaction behavior similar to solitons. Compactons have wide applications in super deformed nuclei, cluster in hydrodynamic models, inertial fusion and the fission of liquid drops. Substantially, the non elastic behavior of solitons are observed in some specific phenomena. It may show fusion of two or more solitons in one soliton as well as fission of one soliton into two or more.

The remaining paper is organized as: Sect. 2 deals with Lie symmetries. The exact invariant solutions are reported in Sect. 3. In Sect. 4, the obtained results are analyzed. The conclusions and remarks are furnished in the end.

2 Lie Symmetries

In this section, we aim to discuss about basic terminology to produce infinitesimal generators. For, one parameter transformations are

$$\begin{aligned}&t^{*}=t+\epsilon {\xi }^t+O({\epsilon }^2)\\&y^{*}=y+\epsilon {\xi }^y+O({\epsilon }^2)\\&x^{*}=x+\epsilon {\xi }^x+O({\epsilon }^2)\\&u^{*}=u+\epsilon {\theta }+O({\epsilon }^2) \end{aligned}$$

where \({\xi }^t\), \({\xi }^y\), \({\xi }^x\), \(\theta \) are corresponding infinitesimals to keep PDEs invariant.

The associated vector field is

$$\begin{aligned}&\psi ={\xi }^t\,\frac{\partial }{\partial t}+{\xi }^y\,\frac{\partial }{\partial y}+{\xi }^x\,\frac{\partial }{\partial x}+\theta \, \frac{\partial }{\partial u}. \end{aligned}$$

Employing prolongation \(Pr^{(3)}(\Delta )=0\) on Eq. (1.1), the invariant surface is

$$\begin{aligned}&{\theta }^{xt}+{\theta }^{xx}-2a(u\,{\theta }^{xx}+u_{xx}\,\theta )-4au_x\,{\theta }^{x}-b\,{\theta }^{xxxt}+k\,{\theta }^{yy}=0 \end{aligned}$$
(2.1)

where

$$\begin{aligned} {\theta }^{x}&=D_x{\theta }-u_x\,D_x{\xi }^{x}-u_y\,D_y{\xi }^{y}-u_t\,D_t{\xi }^{t}\\ {\theta }^{xx}&=D_x^2{\theta }-2u_{xx}\,D_x{\xi }^{x}-u_x\,D_x^2{\xi }^x-2u_{xy}\,D_x{\xi }^{y}\\&\quad -u_y\,D_x^2{\xi }^{y}-2u_{xt}\,D_x{\xi }^{t}-u_t\,D_x^2{\xi }^{t}\\ {\theta }^{yy}&=D_y^2{\theta }-2u_{xy}\,D_y{\xi }^{x}-u_x\,D_y^2{\xi }^x-2u_{yy}\,D_y{\xi }^{y}\\&\quad -u_y\,D_y^2{\xi }^{y}-2u_{yt}\,D_y{\xi }^{t}-u_t\,D_y^2{\xi }^{t} \\ {\theta }^{xt}&=D_xD_t{\theta }-u_{xx}\,D_t{\xi }^{x}-u_{xt}\,D_x{\xi }^x-u_{x}\,D_xD_t{\xi }^{x}\\&\quad -u_{xy}\,D_t{\xi }^{y}-u_{yt}\,D_x{\xi }^{y}-u_y\,D_xD_t{\xi }^{y}-u_{xt}D_t{\xi }^{t}\\ {}&\quad -u_{tt}D_x{\xi }^{t}-u_{t}D_xD_t{\xi }^{t} \\ {\theta }^{xxt}&=D_x^2D_t{\theta }-u_{x}\,D_x^2D_t{\xi }^{x}-u_{xt}\,D_x^2{\xi }^x-2u_{xx}\,D_xD_t{\xi }^{x}\\&\quad -2u_{xxt}\,D_x{\xi }^{x}-u_{xxx}\,D_t{\xi }^{x}-u_y\,D_x^2D_t{\xi }^{y}-u_{yt}D_x^2{\xi }^{y}\\ {}&\quad -2u_{xy}D_xD_t{\xi }^{y}-2u_{xyt}D_x{\xi }^{y}-u_{xxy}D_t{\xi }^{y}-u_{t}D_x^2D_t{\xi }^{t}\\&\quad -u_{tt}D_x^2{\xi }^{t}-2u_{xt}D_xD_t{\xi }^{t}-2u_{xtt}D_x{\xi }^{t}-u_{xxt}D_t{\xi }^{t} \end{aligned}$$

with total derivatives \(D_t\), \(D_y\), \(D_x\).

Using these extensions in Eq. (2.1), we get desired infinitesimals

$$\begin{aligned}&\xi ^x = b_1, \eta ^y=b_2+b_4y, \xi ^t=b_3+2b_4t, \theta =b_4(\frac{1}{a}-2u). \end{aligned}$$

with real constants \(b_1\), \(b_2\), \(b_3\) and \(b_4\).

The symmetry analysis for Eq. (1.1) is associated with following vectors

$$\begin{aligned} \alpha _1=\frac{\partial }{\partial x}, \alpha _2=\frac{\partial }{\partial y}, \alpha _3=\frac{\partial }{\partial t}, \alpha _4=y\frac{\partial }{\partial y}+2t\frac{\partial }{\partial t}+(\frac{1}{a}-2u)\frac{\partial }{\partial u}. \end{aligned}$$

The commutative relations of these vectors are given in Table 1, where \((i,j)^{th}\) entry of commutator table are represented by Lie brackets \([\alpha _i, \alpha _j]=\alpha _i\alpha _j-\alpha _j\alpha _i\).

Table 1 Commutative table
Full size table

The commutative table shows the closure property of vectors under Lie brackets.

3 Invariant Solutions

The auxiliary equation to determine invariant solutions is given as

$$\begin{aligned}&\frac{dx}{b_1} = \frac{dy}{b_2+b_4y}=\frac{dt}{b_3+2b_4t}= \frac{du}{b_4(\frac{1}{a}-2u)}. \end{aligned}$$
(3.1)

Case (I): For \(b_4 \ne 0\), the Eq. (3.1) can be written as

$$\begin{aligned}&\frac{dx}{B_1} = \frac{dy}{B_2+y}=\frac{dt}{B_3+2t}= \frac{du}{(\frac{1}{a}-2u)}. \end{aligned}$$

with \(B_1=\frac{b_1}{b_4}\), \(B_2=\frac{b_2}{b_4}\) and \(B_3=\frac{b_3}{b_4}\). Then, the similarity form is

$$\begin{aligned}&u=\frac{1}{2a}+\frac{P(\xi , \eta )}{2t+B_3} \end{aligned}$$
(3.2)

where similarity function \(P(\xi , \eta )\) consists of variables

$$\begin{aligned}&\xi =\frac{2}{B_1}x-\log (2t+B_3) \text{ and } \eta =\frac{(y+B_2)^2}{(2t+B_3)}. \end{aligned}$$

Availing Eq. (3.2) into Eq. (3.1), we have first reduction as

$$\begin{aligned}&8b\,(P_{\xi \xi \xi \xi }+\eta \,P_{\xi \xi \xi \eta }+P_{\xi \xi \xi })-4aB_1(PP_{\xi \xi }+P_{\xi }^2)-2B_1^2(P_{\xi \xi }\nonumber \\&\quad +\eta P_{\xi \eta }+P_{\xi })+kB_1^3(P_{\eta }+2\eta P_{\eta \eta })=0 \end{aligned}$$
(3.3)

Again applying STM on Eq. (3.3) , the infinitesimals are obtained as

$$\begin{aligned} {\hat{\xi }}^{x}=1, \hat{\xi ^{y}}=0, {\hat{\phi }}=0. \end{aligned}$$

Thus, characteristic equation is

$$\begin{aligned}&\frac{d \xi }{1}=\frac{d \eta }{0}=\frac{d P}{0} \end{aligned}$$

It follows similarity form

$$\begin{aligned} P=P_1(\chi ) \end{aligned}$$

with similarity variable \(\chi =\eta \). It transforms the Eq. (3.3) into

$$\begin{aligned}&2 \chi \bar{\bar{P_1}}+\bar{P_1}=0 \end{aligned}$$
(3.4)

which has the solution \(\displaystyle P_1=c_1\,{\chi }^{\frac{1}{2}}+c_2\).

Thus, KP-BBM equation has solution

$$\begin{aligned}&u=\frac{1}{2a}+\frac{c_1(y+B_2)}{(2t+B_3)^{\frac{3}{2}}}+\frac{c_2}{(2t+B_3)} \end{aligned}$$
(3.5)

Case (II): For \(b_4 = 0\) and \(b_3 \ne 0\), the Eq. (3.1) can be written as

$$\begin{aligned}&\frac{dx}{B_4} = \frac{dy}{B_5}=\frac{dt}{1}= \frac{du}{0} \end{aligned}$$

with \(B_4=\frac{b_1}{b_3}\) and \(B_5=\frac{b_2}{b_3}\).The similarity form yields

$$\begin{aligned}&u=P(\xi , \eta ) \end{aligned}$$
(3.6)

where \(P(\xi , \eta )\) is function of

$$\begin{aligned}&\xi =x-B_4\,t \text{ and } \eta =y-B_5\,t \end{aligned}$$

The Eqs. (1.1) and (3.6) lead towards first reduction of KP-BBM equation

$$\begin{aligned} b\,(B_4\,P_{\xi \xi \xi \xi }+B_5\,P_{\xi \xi \xi \eta })+(1-B_4)P_{\xi \xi }-B_5\, P_{\xi \eta }-2a(PP_{\xi \xi }+P_{\xi }^2)+k P_{\eta \eta }=0 \end{aligned}$$
(3.7)

A particular solution of Eq. (3.7) is

$$\begin{aligned}&P=c_3\,\xi +\frac{2ac_3^2}{k}{\eta }^2+c_4\,\eta +c_5 \end{aligned}$$

Thus, solution of Eq. (1.1) is

$$\begin{aligned}&u=c_3\,(x-B_4\,t)+\frac{2ac_3^2}{k}(y-B_5\,t)^2+c_4\,(y-B_5\,t)+c_5 \end{aligned}$$
(3.8)

To reduce Eq. (3.7) again, the characteristic equation is

$$\begin{aligned}&\frac{d \xi }{b_5}=\frac{d \eta }{b_6}=\frac{dP}{0} \end{aligned}$$
(3.9)

Case (IIa): If \(b_6 \ne 0\), the above characteristic is rewritten as

$$\begin{aligned}&\frac{d \xi }{B_6}=\frac{d \eta }{1}=\frac{d P}{0} \end{aligned}$$

such that \(\displaystyle P=P_1(\chi )\) with \(\chi =\xi -B_6\,\eta \) and \(B_6=\frac{b_5}{b_6}\).

Thus, Eq. (3.7) is transformed to

$$\begin{aligned}&b(B_4-B_5B_6)\bar{\bar{\bar{\bar{P_1}}}} -2a(P_1\bar{\bar{P_1}}+\bar{P_1}^2)+(1-B_4+B_5B_6+kB_6^2)\bar{\bar{P_1}}=0 \end{aligned}$$
(3.10)

Taking \(B_4-B_5B_6=0\) and \(1+kB_6^2=0\), a particular solution is

$$\begin{aligned}&P_1=\sqrt{c_6\,{\chi }+c_7}. \end{aligned}$$

Eventually, the solution of test equation is

$$\begin{aligned}&u=\sqrt{c_6\,(x-B_6\,y)+c_7}. \end{aligned}$$
(3.11)

Furthermore, the thrice integration of Eq. (3.10) provides

$$\begin{aligned}&\bar{P_1}^2-B_7(P_1^3-3B_8P_1^2+c_9P+c_{10})=0 \end{aligned}$$
(3.12)

where \(B_7=\frac{2a}{3b(B_4-B_5B_6)}\) and \(B_8=\frac{1-B_4+B_5B_6-kB_6^2}{2a}\).

Some solutions of Eq. (3.12) are addressed as follows:

Case (II\(a_1\)): For \(c_9=3B_8\) and \(c_{10}=-B_8^3\) in Eq. (3.12), we have

$$\begin{aligned}&\bar{P_1}^2-B_7(P_1-B_8)^3=0 \end{aligned}$$
(3.13)

which has a solution

$$\begin{aligned}&P_1=B_8+\frac{4}{B_7(\chi +c_{11})^2}. \end{aligned}$$

So, the required solution is

$$\begin{aligned}&u=B_8+\frac{4}{B_7[x-B_6\,y-(B_4-B_5B_6)t+c_{11}]^2}. \end{aligned}$$
(3.14)

Case (II\(a_2\)): For \(c_9=\frac{9B_8^2}{4}\) and \(c_{10}=0\) in Eq. (3.12), we have

$$\begin{aligned}&\bar{P_1}^2-B_7P_1(P_1-\frac{3B_8}{2})^2=0. \end{aligned}$$
(3.15)

The solution is

$$\begin{aligned}&P_1=\frac{3B_8}{2}\tanh ^2\,\Bigr (\frac{1}{2}\sqrt{\frac{3B_7B_8}{2}}\chi +c_{12}\Bigr ). \end{aligned}$$

So, the required solution is

$$\begin{aligned}&u=\frac{3B_8}{2}\tanh ^2\,\Bigr (\frac{1}{2}\sqrt{\frac{3B_7B_8}{2}}[x-B_6\,y-(B_4-B_5B_6)t]+c_{12}\Bigr ). \end{aligned}$$
(3.16)

Also, another solution is

$$\begin{aligned}&u=\frac{3B_8}{2}\coth ^2\,\Bigr (\frac{1}{2}\sqrt{\frac{3B_7B_8}{2}}[x-B_6\,y-(B_4-B_5B_6)t]+c_{13}\Bigr ). \end{aligned}$$
(3.17)

Case (II\(a_3\)): For \(c_9=0\) and \(c_{10}=0\) in Eq. (3.12), we have

$$\begin{aligned}&\bar{P_1}^2-B_7P_1^2(P_1-3B_8)=0. \end{aligned}$$
(3.18)

Then, it raises the solution

$$\begin{aligned}&P_1=3B_8\,\sec ^2\,\Bigr (\frac{\sqrt{3B_7B_8}}{2}\chi +c_{14}\Bigr ). \end{aligned}$$

So, the required solution is

$$\begin{aligned}&u=3B_8\,\sec ^2\,\Bigr (\frac{\sqrt{3B_7B_8}}{2}[x-B_6\,y-(B_4-B_5B_6)t]+c_{14}\Bigr ). \end{aligned}$$
(3.19)

Case (IIb): If \(b_6=0\), then Eq. (3.9) produces similarity function is \(P=P_1(\chi )\) with \(\chi =\eta \). So, Eq. (3.7) is converted to \(\bar{\bar{P_1}}=0\) and thus \(P_1=c_{15}\eta +c_{16}\).

Consequently, Eq. (1.1) gets the solution

$$\begin{aligned}&u=c_{15}(y-B_5\,t)+c_{16}. \end{aligned}$$
(3.20)

Case (III): For \(b_2 = 0\), \(b_4 = 0\) and \(b_3 \ne 0\), the Eq. (3.1) is rewritten as

$$\begin{aligned}&\frac{dx}{B_4} = \frac{dy}{0}=\frac{dt}{1}= \frac{du}{0}. \end{aligned}$$

The similarity form yields

$$\begin{aligned}&u=P(\xi , \eta ) \end{aligned}$$
(3.21)

where \(P(\xi , \eta )\) is function of

$$\begin{aligned}&\xi =x-B_4\,t \text{ and } \eta =y \end{aligned}$$

The Eqs. (1.1) and (3.21) lead towards following reduction

$$\begin{aligned} b\,B_4\,P_{\xi \xi \xi \xi }+(1-B_4)P_{\xi \xi }-2a(PP_{\xi \xi }+P_{\xi }^2)+k P_{\eta \eta }=0 \end{aligned}$$
(3.22)

A particular solution of Eq. (3.22) is

$$\begin{aligned}&P=c_{17}\,\xi \,\eta +\frac{ac_{17}^2}{6k}{\eta }^4+c_{18}\,\eta +c_{19} \end{aligned}$$

Thus, solution of Eq. (1.1) is

$$\begin{aligned}&u=c_{17}\,(x-B_4\,t)\,y+\frac{ac_{17}^2}{6k}\,y^4+c_{18}\,y+c_{19} \end{aligned}$$
(3.23)

An another solution is

$$\begin{aligned}&u=c_{20}\,(x-B_4\,t)+\frac{ac_{20}^2}{k}\,y^2+c_{21}\,y+c_{22} \end{aligned}$$
(3.24)

To reduce Eq. (3.22) again, the characterstic equation is

$$\begin{aligned}&\frac{d \xi }{\Bigr (\frac{b_7\,\xi }{2}+b_8\Bigr )}=\frac{d \eta }{b_7\,\eta +b_9}=\frac{dP}{b_7\Bigr (-P+\frac{1-B_4}{2a}\Bigr )} \end{aligned}$$
(3.25)

For \(b_7 \ne 0\), we have similarity form

$$\begin{aligned}&P=\frac{1-B_4}{2a}+\frac{P_1(\chi )}{\eta +B_{10}} \text{ with } \chi =\frac{\xi +2B_9}{(\eta +B_{10})^{\frac{1}{2}}} \text{ such } \text{ that } B_9=\frac{b_8}{b_7}, B_{10}=\frac{b_9}{b_7}. \end{aligned}$$

Thus, Eq. (3.22) is transformed to

$$\begin{aligned}&bB_4 \bar{\bar{\bar{\bar{P_1}}}}-2a(P_1\bar{\bar{P_1}}+\bar{P_1}^2)+\frac{k}{4}({\chi }^2\bar{\bar{P_1}}+ 7\chi \bar{P_1}+8P_1)=0 \end{aligned}$$
(3.26)

It has an exact solution

$$\begin{aligned}&P_1=-\frac{k}{2a}\,{\chi }^2 \end{aligned}$$

Consequently, the test equation has solution

$$\begin{aligned}&u=\frac{1-B_4}{2a}+\frac{k(x-B_4t+2B_9)^2}{2a(y+B_{10})^2}. \end{aligned}$$
(3.27)

Another solution of Eq. (3.26) is

$$\begin{aligned}&P_1=\frac{6\,b\,B_4}{a\,{\chi }^2}. \end{aligned}$$

Thus, the test equation has solution

$$\begin{aligned}&u=\frac{1-B_4}{2a}+\frac{6\,b\,B_4}{a\,(x-B_4t+2B_9)^2}. \end{aligned}$$
(3.28)

4 Analysis of Results

Explicit expressions are much significant to interpret the phenomena physically. In this section, we analyze graphical behavior of the solutions (3.5), (3.8), (3.14), (3.16), (3.17), (3.19), (3.27) while the solutions listed in Eqs. (3.11), (3.20), (3.23), (3.24), (3.28) are self-evident. All the derived results are new and never reported before. These solutions involve free parameters therefore we perform the numerical simulation for significant values of existing parameters as \(a=0.6596\), \(b=0.5185\), \(k=0.9729\) and rest are given in adjacent figures. The figures show doubly soliton, multisoliton, compacton, soliton fusion and parabolic nature, which are analyzed as follows:

Fig. 1
figure 1

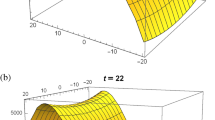
Soliton fusion for Eq. (3.5)

Full size image
Fig. 2
figure 2

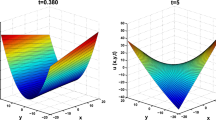
Parabolic nature of solution (3.8)

Full size image

Figure 1: The non elastic behavior of solution (3.5) is expressed in this spatio-temporal profile, which shows soliton fusion for \(B_2=0.9516\), \(B_3=0.9203\), \(c_1=0.0526\), \(c_2=0.7378\). It is clearly exhibited in 2D view that solitons are fused when interacting with others and show new phenomenon.

Figure 2: It demonstrates the parabolic nature of the solution profile (3.8) at \(t=0.7093\). The values assigned to parameters are \(B_4=0.6489\), \(B_5=0.8003\), \(c_3=0.7546\), \(c_4=0.276\), \(c_5=0.6797\). With passes of time, nonlinearity disappears and results into straight stripe for \(t=100\).

Fig. 3
figure 3

Intensive multisoliton profile for Eq. (3.14)

Full size image
Fig. 4
figure 4

Multisoliton annihilation profile for Eq. (3.16)

Full size image

Figure 3: It displays the intensive feature of solitary waves interacting with each others. The values to remaining constants are provided as \(B_4=0.6489\), \(B_5=0.8003\), \(B_6=0.7546\), \(B_7=18.8491\), \(B_8=1.1839\), \(c_{11}=0.6537\). The velocity component u features minimum and maximum amplitude of multisoliton at \(t=0.1076\). The minimum amplitude of wave is displayed in the centre and maximum amplitude in sides in \(x-u\) and \(y-u\) views.

Figure 4: The multisoliton profile for Eq. (3.16) is analyzed in this figure for \(B_4=0.6489\), \(B_5=0.8003\), \(B_6=0.7546\), \(B_7=18.8491\), \(B_8=1.1839\), \(c_{12}=0.4538\) at \(t=0.4598\). The slowly decay in profile with time is concluded. As time is bigger than \(t=879\), the solitons annihilate and profile becomes stationary.

Fig. 5
figure 5

Elastic multisoliton for Eq. (3.17)

Full size image
Fig. 6
figure 6

Compacton profile for Eq. (3.19)

Full size image

Figure 5: The physical behavior of solution (3.17) is illustrated via this profile at \(t=0.3648\). It shows multisoliton nature for \(B_4=0.6489\), \(B_5=0.8003\), \(B_6=0.7546\), \(B_7=18.8491\), \(B_8=1.1839\), \(c_{13}=0.6256\). The solitons seem completely elastic during mutual collision except phase shift, and the maximum and minimum amplitude of waves is shown in \(y-u\) view.

Figure 6: The elastic compacton behavior of Eq. (3.19) is represented at \(t=0.6554\). The values to constants are assigned as \(B_4=0.6489\), \(B_5=0.8003\), \(B_6=0.7546\), \(B_7=18.8491\), \(B_8=1.1839\), \(c_{14}=0.1711\). The amplitude of compactons remains unchanged during interaction with others and show its elastic behavior when the argument of \(\cos \) lies in \((-\frac{\pi }{2}, \frac{\pi }{2})\) displayed in \(y-u\) view.

Fig. 7
figure 7

Transition of doubly soliton in single soliton for (3.27)

Full size image

Figure 7: The transition of doubly soliton into single soliton with passage of time for Eq. (3.27) is recorded in this figure. It shows doubly soliton profile at \(t=0.2769\) for \(B_4=0.6489\), \(B_9=0.0462\), \(B_{10}=0.0971\). When time increases and passes over \(t=60\), the dynamical change happens in doubly soliton and transforms to single soliton.

5 Conclusions

In this work, Lie symmetry method is applied to construct infinitesimal generators, commutative relations and symmetry reductions of KP-BBM equation. The one parameter transformation enables to retain the invariance of PDEs under symmetry reductions. The twice reductions of KP-BBM equation provide determining ODEs and lead to exact solutions listed in Eqs. (3.5), (3.8), (3.11), (3.14), (3.16), (3.17), (3.19), (3.20), (3.23), (3.24), (3.27) and (3.28). All these results are novel and never reported earlier. Some of these results are examined graphically based on their numerical simulation. Eventually, mutisoliton, doubly soliton, compacton, soliton fusion and parabolic nature are analyzed to make these finding physically meaningful. Thus, Lie symmetry method may be treated as effective and versatile tool to derive exact solutions of highly nonlinear PDEs.