1 Introduction

The modern power distribution system is continuously facing ever-growing load demand, resulting in increased burden and reduced voltages. The voltages at buses or nodes reduces while moving away from a substation, due to an insufficient amount of reactive power. To improve this voltage profile, reactive compensation is required. The efficiency of power delivery is enhanced, and losses at distribution level are reduced by incorporating network reconfigurations, shunt capacitor placement, etc. The optimal capacitor placement supplies the part of reactive power demand which helps in reducing the energy losses, peak demand losses and improves the voltage profile, power factor (pf) and system stability [14]. Therefore, specific size capacitors are required to be placed at specific places in the distribution network to achieve the optimum reactive power.

To achieve this objective while maintaining the optimal economy, optimal placement of capacitor with proper sizing should be decided by some conventional [6] or non-conventional strategy [9, 14].

The shunt capacitor is a very common conventional strategy for distribution system. Further, the concept of loss minimization by a singly located capacitor was extended for multiple capacitors. Subsequently, combinational optimization strategy was developed to deal with the discrete capacitor placement problem. The described methods have their limitations of depending on the initial guess, lack of robustness, time-consuming, and many local optimal solutions for nonlinear optimization problems [6].

Swarm intelligence based meta-heuristics have impressed the researchers to apply them for solving the capacitor placement and sizing problems [24]. In past, the capacitor placement problem was solved by applying fuzzy approximate reasoning [18], genetic algorithm (GA) [29], artificial bee colony (ABC) algorithm [24], and particle swarm optimization (PSO) algorithm [23] etc. Recently, Bansal et al. [2] introduced a swarm intelligence based algorithm namely, spider monkey optimization (SMO) algorithm by taking inspiration from the social and food foraging behavior of spider monkeys. It has been shown that the SMO is competitive to the ABC, PSO, DE, and covariance matrix adaptation evolution strategies (CMA-ES) algorithms [2].

Though SMO performs well still, due to the presence of random components (\(\phi \) and \(\psi \)) in the position update process, there is a chance of skip of the true solution. So, integration of a local search strategy with SMO may improve the exploitation capability of the algorithm and, hence reduces the chance of skipping true solution. Therefore, in this paper, a new local search algorithm is proposed by modifying the limaçon curve equation and named as limaçon inspired local search (LLS). Further, the proposed local search is incorporated with SMO in expectation of improving exploitation capability. The proposed hybridized algorithm is named as Limaçon inspired spider monkey optimization algorithm (LSMO). The performance of LSMO is tested through various numerical experiments with respect to accuracy, reliability, and consistency. Then the LSMO is applied to solve the optimal placement and sizing problem of capacitors in the distribution network. The results are compared with un-capacitor and other existing methods for IEEE 14, 30 and 33 test bus cases with 3 and 5-capacitor placement and sizing conditions.

The detailed description may be categorized as follows: Basic SMO is explained in Sect. 2. Section 3 describes a brief review on local search strategies. Limaçon inspired local search strategy was proposed and incorporated to SMO in Sect. 4. In Sect. 5, the performance of proposed strategy is evaluated. Section 6 describes capacitor sizing and optimal allocation problem. Solution to the optimal placement and sizing problem of the capacitor is presented in Sect. 7. Finally, the conclusion of the work is given in Sect. 8.

2 Spider monkey optimization (SMO) Algorithm

SMO algorithm is based on the foraging behavior and social structure of spider monkeys [2]. Spider monkeys have been categorized as a fission-fusion social structure (FFSS) based animals, in which individuals form small, impermanent parties whose member belongs to a larger community. Monkeys split themselves from larger to smaller groups and vice versa based on scarcity and availability of food.

2.1 Main steps of SMO algorithm

The SMO algorithm consists of six phases: Local leader phase, Global leader phase, Local leader learning phase, Global leader learning phase, Local leader decision phase, and Global leader decision phase. Each of the phases is explained as follows:

2.1.1 Initialization of the Population

Initially, SMO generates an equally distributed initial population of N spider monkeys where each monkey \(SM_i\) (i \(= 1, 2, \ldots ,\) N) is a D-dimensional vector and \(SM_i\) represents the ith spider monkey (SM) in the population. SM represents the potential solution of the problem under consideration. Each \(SM_i\) is initialized as follows:

$$\begin{aligned} SM_{ij}=SM_{{ min} j}+U(0,1)\times (SM_{{ max} j}-SM_{{ min} j}) \end{aligned}$$
(1)

where \(SM_{{ min} j}\) and \(SM_{{ max} j}\) are respectively lower and upper bounds of \(SM_i\) in jth direction and U(0, 1) is a uniformly distributed random number in the range [0, 1].

2.1.2 Local leader phase (LLP)

In this phase, each SM updates it’s current position based on gathered information from local leader as well as local group members. The fitness value of so obtained new position is computed. If the fitness value of the new position is superior to the old position, then the SM modifies its position with the new one. The position update equation for ith SM (which is a member of kth local group) in this phase is

$$\begin{aligned} SM{ new}_{ij}= & {} SM_{ij}+U(0,1)\times (LL_{kj}-SM_{ij})\nonumber \\&+U(-1,1)\times (SM_{rj}-SM_{ij}) \end{aligned}$$
(2)

where \(SM_{ij}\) is the jth dimension of the ith SM, \(LL_{kj}\) represents the jth dimension of the kth local group leader position. \(SM_{rj}\) is the jth dimension of the rth SM which is chosen arbitrarily within kth group such that \(r \ne i\). U(0, 1) is a uniformly distributed random number between 0 and 1. Algorithm 1 shows position update process in the local leader phase.

figure a

In Algorithm 1, MG is the maximum number of groups in the swarm and pr is the perturbation rate which controls the amount of perturbation in the current position.

2.1.3 Global leader phase (GLP)

In this phase, all SMs update their positions using knowledge of global leader and local group members experience. The position update equation for this phase is as follows:

$$\begin{aligned} SMnew_{ij}= & {} SM_{ij}+U(0,1)\times (GL_{j}-SM_{ij})\nonumber \\&+U(-1,1)\times (SM_{rj}-SM_{ij}) \end{aligned}$$
(3)

where \(GL_j\) is the jth dimension of the global leader position and j is the randomly chosen index. The positions of spider monkeys (\(SM_i\)) are updated based on a probability \(prob_i\) which is a function of fitness. In this way, a better candidate will have more chance to make it better. The probability \(prob_i\) is calculated as shown in Eq. 4 [27].

$$\begin{aligned} { prob}_i=0.9\times \frac{{ fitness}_i}{max\_{ fitness}}+0.1, \end{aligned}$$
(4)

Here \({ fitness}_i\) is the fitness value of ith SM and \(max\_{ fitness}\) is the highest fitness in the group. The fitness of the newly generated \(SM_s\) is calculated and compared with the old one, and the better position is adopted. The position update process of this phase is explained in Algorithm 2.

figure b

2.1.4 Global leader learning phase (GLLP)

In this phase, the position of the SM having best fitness in the population is selected as the updated position of the global leader using greedy selection. Further, the position of global leader is checked whether it is updating or not and if not then the global limit count is incremented by 1.

2.1.5 Local leader learning phase (LLLP)

In this phase, the position of the SM having best fitness in that group is selected as the updated position of the local leader using greedy selection. Next, if the modified position of the local leader is compared with the old one and if the local leader is not updated then the local limit count is incremented by 1.

2.1.6 Local leader decision phase (LLDP)

If any local leader is not updated up to a preset threshold called local leader limit, then all the members of that minor group update their positions either by random initialization or by using combined information from global leader and local leader through Eq. 5.

$$\begin{aligned} SMnew_{ij}= & {} SM_{ij}+U(0,1)\times (GL_{j}-SM_{ij})\nonumber \\&+U(0,1)\times (SM_{ij}-LL_{kj}); \end{aligned}$$
(5)

It is clear from Eq. (5) that the updated dimension of this SM is attracted towards global leader and repels from the local leader.

2.1.7 Global leader decision (GLD) phase

In this phase, the global leader is monitored, and if it is not updated up to a preset number of iterations called global leader limit, then the global leader divides the population into minor groups. Firstly, the population is divided into two groups and then three groups and so on till the maximum number of groups (MG) are formed. After every division, LLL process is initiated to choose the local leader in the newly formed groups. The case in which a maximum number of groups are formed and even then the position of global leader is not updated then the global leader combines all the minor groups to form a single group.

The SMO algorithm is better represented by pseudo-code in Algorithm 3.

figure c

3 Significant recent local search modifications

A local search is thought of as an algorithmic structure converging to the closest local optimum while the global search should have the potential of detecting the global optimum. Therefore, to maintain the proper balance between exploration and exploitation behavior of an algorithm, it is always suggested to incorporate a local search approach in the basic population-based algorithm to exploit the identified region in a given search space. Therefore, the local search algorithms are applied to the global search algorithms to improve the exploitation capability of the global search algorithm. Here the main algorithm explores while the local search exploits the search space.

Researchers are constantly working in the field of memetic search approach. Natalio and Gustafson [11] discussed proofs of memetic concepts. Ong et al. [22], proposed a technique to maintain a balance between genetic search and local search. Ong et al. [21], listed classification of memes adaptation by the mechanism used and the level of historical knowledge on the memes employed. Lim presented a valuable discussion on memetic computing [15]. In the same year, Neri et al. [17], incorporated scale factor local search to improve exploitation capability of DE. Further Nguyen et al. [19], presented a novel probabilistic memetic framework to model MAs as a process involving in finalizing separate actions of evolution or individual learning and analyzing the probability of each process in locating the global optimum. Ong et al. [20] presented, an article to show several deployments of memetic computing methodologies to solve complex real world problems. In same year Mininno et al. [16] incorporated Memetic approach with DE in noisy optimization. Chen et al. [3], presented realization of memetic computing through memetic algorithm. Sharma et al. [26], included opposition based lévy flight local search with ABC. Sharma et al. [27], integrated lévy flight local search strategy with artificial bee colony algorithm. Recently, in 2016 Sharma et al. presented power law based local search in SMO (PLSMO) algorithm [25]. In the above presented local search strategies, the direction and distance (step size) of the individuals, which are going to update, are based on the inter-individual distance among the solutions. This may force the individuals to move towards a specific direction. Therefore, development of local search strategy, which properly exploit the identified search space is highly required. An angular rotation based search process may reduce the chance of trapping in a local optima. Therefore, in this paper limaçon curve inspired local search strategy (LLS) is developed and incorporated with SMO algorithm. In the proposed LLS, the direction and distance of the solutions are based on the fitness of the solution (sign), the distance between the individual, and an angle of rotation.

4 Limaçon inspired local search strategy and it’s incorporation to SMO

The word limaçon is a Latin word meaning snail. During it’s evolution, two important features were adapted by Limaçon or snail naturally. In the first process called torsion, most of the internal organs were twisted \(180^{\circ }\) anticlockwise. The another important feature is that the shell became more conical and then spirally coils. The shell is a line of defence for the limaçon. The foot of limaçon allows it to move forward and backward with muscle contracting and expanding movement with the help of mucus and slime. The limaçon’s basic specifications are the height of shell, width of shell, height of aperture, width of the aperture, the number of whorls, and apical angle. In this context, the height of the shell is it’s maximum measurement along the central axis. The width is the maximum measurement of the shell at right angles to the central axis. The central axis is an imaginary axis along the length of a shell, around which, in a coiled shell the whorls spiral. The central axis passes through the columella, the central pillar of the shell. Normally the whorls are circular or elliptical, but from compression and other causes a variety of forms can result. The spire can be high or low, broad or slender according to the way the coils of the shells are arranged and the apical angle of the shell varies accordingly. The whorls overlap the earlier whorls, such that they may be largely or wholly covered by the later ones. When an angulation occurs, the space between it and the suture above it constitute the area known as the shoulder of the shell. The shoulder angle may be simple or keeled, and may sometimes have nodes or spines. The limaçon and its single line diagram are shown in Fig. 1.

The proposed local search strategy is based on the limaçon curve. The limaçon curve was introduced by Etienne Pascal (1588–1651) [5]. The Limaçon curve is a botanical curve which resembles the snail. Here, both rolling circles are having the same radius and the curve thus obtained “epicycloid” is the traces of a point P fixed to a circle that rolls around another circle as shown in Fig. 2.

In literature, this curve already has been used in different ways [12]. But, in this paper, the first time the limaçon curve is used to develop a local search strategy and hybridized with the basic SMO to improve the exploitation capability of SMO.

Fig. 1
figure 1

a Limaçon (Snail) curve (this figure is accessed on Feb 2015 from http://entnemdept.ufl.edu/creatures/misc/whitegardensnail.htm), b single line curve (this figure is accessed on Feb. 2015 from http://www.clipartpanda.com/categories/snail-clipart-black-andwhite)

Full size image
Fig. 2
figure 2

Epicycloid curve (this figure is accessed on Feb 2015 from http://cf.ydcdn.net/1.0.1.42/images/main/epicycloid.jpg)

Full size image

The basic equations of limaçon curve are shown in equations 6 and 7 for vertical axis and horizontal axis curves respectively [30].

$$\begin{aligned} r= & {} a\pm b sin \theta \end{aligned}$$
(6)
$$\begin{aligned} r= & {} a\pm b cos \theta \end{aligned}$$
(7)

Here, r is the distance of the limaçon from the origin, a and b are constants and \(\theta \) is an angle of rotation. The curve has transient phases based on the value of b. From a circle, for \(b=0\) to cardioid for \(b=1\) and a noose on curve appears for \(b>a\).

In this paper, this limaçon curve is used to form a local search strategy into SMO. In the proposed local search strategy, the distance r is used as a new position of a solution which is going to update its position during the search process in the given search region. The detailed description of the proposed limaçon curve based local search strategy, named as limaçon local search (LLS) strategy is as follows:

In the proposed LLS, Eq. 6 of limaçon curve is adapted with some modifications as a position update equation of the proposed local search strategy. The modified equation is as follows:

$$\begin{aligned}&x_{new}=x_i\pm (x_i-x_k) \times sin \theta \quad \hbox {where},\nonumber \\&\quad k\in \hbox {randomly selected solution, but} \quad k\ne i. \end{aligned}$$
(8)

Here, \(a=x_i\) is the solution which is going to update its position, \(x_{new}\) is the updated position of the \(x_i\), \(b= (x_i-x_k)\) is the social influence of the solution \(x_i\) in the population and \(\theta \) is an angle of rotation.

In this paper, in each iteration, only the best solution will be allowed to update its position using the LLS strategy. The position update equation for the best solution is given by Eq. 9.

$$\begin{aligned} x_{{ new}} = x_{{ best}}\pm (x_{{ best}}-x_{k})\times sin\theta \end{aligned}$$
(9)

where \(\theta \) is calculated as

$$\begin{aligned} \theta =\frac{\pi }{2}\times \left( 1-\frac{t}{T}\right) \end{aligned}$$
(10)

Where, \(t=\) current iteration counter and \(T=\) total iterations of local search. The pseudo-code of the proposed LLS is shown in Algorithm 4.

As the step size is also based on sine of an angle, resembling apical angle of limaçon, the step size reduces based on decreasing angular values from \(\theta =90 ^{\circ }\) to \(\theta =0^{\circ }\) either in negative or positive direction. The higher height of spire shows a lesser apical angle for limaçon and vice versa. Similarly, the lesser angular step represents a small step size, while the higher angular step represents larger step size in the LLS strategy. This implies that in early iterations larger step sizes are allowed while smaller step sizes are allowed in later iterations.

figure d

In Algorithms 4 and 5, \(c_r\) is a perturbation rate (a number between 0 and 1) which controls the amount of perturbation in the best solution, U(0, 1) is a uniform distributed random number between 0 and 1, D is the dimension of the problem and \(x_{k}\) is a randomly selected solution within population. See Sect. 5.1 for details of these parameter settings.

The proposed LLS strategy is incorporated with the SMO after the global leader decision phase. The pseudo-code of the modified SMO named as limaçon inspired SMO (LSMO) algorithm is shown in Algorithm 6.

figure e
figure f

5 Performance evaluation of LSMO algorithm

The performance of proposed LSMO algorithm is evaluated on 25 different benchmark continuous optimization functions (\(f_1\) to \(f_{25}\)) having different degrees of complexity and multimodality as shown in Table 1. The acceptable errors of above functions are set to see the clear difference among the considered algorithms in terms of success rate and number of function evolutions. Here, the functions and acceptable errors are adopted from the literature [1, 2, 27]. To check the competitiveness of LSMO, it is compared with SMO [2], ABC [10], DE [28], \(PSO-2011\) [4], \(CMA-ES\) [7] and one significant variant of ABC namely, Gbest-guided ABC (GABC) [31] as well as two local search variants namely, memetic ABC (MeABC) [1], and Lévy flight ABC (LFABC) [27] and one recent local search variant of SMO namely, PLSMO [25]. The experimental setting is given in Sect. 5.1.

Table 1 Test problems
Full size table

5.1 Experimental setting

The experimental settings are as follows:

  • Population Size N \(=\) 50;

  • \(MG= N/10\).

  • \({ GlobalLeaderLimit} = 50 \),

  • \({ LocalLeaderLimit} = 1500 \),

  • pr(perturbation rate of main SMO algorithm) \(\in [0.1, 0.4]\), linearly increasing over iterations,

    $$\begin{aligned} pr_{G+1}=pr_{G}+(0.4-0.1)/MIR \end{aligned}$$
    (11)

    where, G is the iteration counter, MIR is the maximum number of iterations.,

  • The stopping criteria is either maximum number of function evaluations (which is set to be 200,000) is reached or the acceptable error of test problem has been achieved,

  • The number of simulations/run =100,

  • Parameter settings for the algorithm SMO, ABC, GABC, MeABC, LFABC, PLSMO, \(CMA-ES\), \(PSO-2011\), and DE are similar to their legitimate research papers respectively.

  • The maximum number of iterations of LLS is set through sensitivity analysis in terms of sum of success rate (SR). The performance of LSMO is measured for considered test problems on different values of T and results in terms of success are analyzed in Fig. 3. It is clear from Fig. 3 that \(T=20\) gives better results (highest value of sum of success). Therefore in this paper maximum local search iterations is set as T \(=\) 20.

  • In order to investigate the effect of parameter \(c_r\) (perturbation rate of local search), described by Algorithm 5 on the performance of LSMO, its sensitivity with respect to different values of \(c_r\) in the range [0.1, 0.9], is examined in the Fig. 4. It can be observed from Fig. 4 that the algorithm is very sensitive towards \(c_r\) and value 0.6 gives comparatively better results. Therefore \(c_r=0.6\) is selected for the experiments in this paper.

Fig. 3
figure 3

Effect of LLS termination criteria T on success rate

Full size image
Fig. 4
figure 4

Effect of parameter \(c_r\) on success rate

Full size image

5.2 Results comparison

The numerical results obtained are presented in Table 2 for success rate (SR), average number of function evaluations (AFE), mean error (ME), and standard deviation (SD).

LSMO, SMO, ABC, DE, PSO–2011, CMA-ES and one significant variant of \({ ABC}\) namely, \({ GABC}\), and two local search variants namely, \({ LFABC}\), and \({ MeABC}\), and one recent local search variant of \({ SMO}\) namely, \({ PLSMO}\) are compared in terms of \({ SR}\), \({ AFE}\), \({ ME}\), and \({ SD}\) as shown in Table 2. The results show that \({ LSMO}\) is competitive than \({ SMO}\) and other considered algorithms for most of the benchmark test problems irrespective of their nature either in terms of separability, modality and other parameters.

Table 2 Comparison of the results of test problems
Full size table

The considered algorithms are also compared through Mann–Whitney U rank sum test [27], acceleration rate and boxplot analysis. Mann–Whitney U rank sum test is applied on average number of function evaluations. For all considered algorithms the test is performed at 5 % significance level (\(\alpha =0.05\)) and the output results for 100 simulations are presented in Table 3. In this table ‘+’ sign indicates that LSMO is significantly better than the other considered algorithm while ‘−’ sign represents that the other considered algorithm is better. The LSMO outperforms as compared to all other considered algorithms for 10 test problems including \(f_1\), \(f_3\)–\(f_7\), \(f_9\), \(f_{12}\), \(f_{18}\), and \(f_{24}\). LSMO performs better than basic SMO for 18 test problems, \(f_1\)–\(f_9\), \(f_{11}, f_{12}, f_{14}\)–\(f_{16}, f_{18}\), and \(f_{23}\)–\(f_{25}\). The LSMO shows better results for 24 test problems when compared with basic ABC algorithm, \(f_1\)–\(f_{15}\) and \(f_{17}\)–\(f_{25}\). The LSMO performs better for 21 test problems, \(f_1\)–\(f_7\), \(f_9\)–\(f_{12}\), \(f_{14}\)–\(f_{18}\), and \(f_{20}\)–\(f_{24}\) in comparison with DE. The LSMO performs better for 23 test problems in comparison with PSO, \(f_1\)–\(f_{18}\) and \(f_{20}\)–\(f_{24}\). In comparison with \(CMA-ES\), LSMO performs better on 15 functions, \(f_1\)–\(f_7\), \(f_9\)–\(f_{12}\), \(f_{17}\), \(f_{18}\), \(f_{20}\), \(f_{22}\), and \(f_{24}\). While comparing with the variants of ABC, the LSMO performs better for 19 test problems than GABC, \(f_1\)–\(f_9\), \(f_{12}\)–\(f_{15}\), \(f_{18}\), \(f_{19}\), \(f_{22}\)–\(f_{25}\). The LSMO performs better than LFABC for 24 test problems \(f_1\)–\(f_9\) and \(f_{11}\)–\(f_{25}\). In comparison with MeABC, LSMO shows better results for 18 test problems \(f_1\), \(f_3\)–\(f_9\), \(f_{11}\)–\(f_{14}\), \(f_{17}\), \(f_{18}\), \(f_{22}\)–\(f_{25}\). The LSMO shows better results for 18 test problems, \(f_1\)–\(f_{12}\), \(f_{16}\)–\(f_{18}\), \(f_{23}\)–\(f_{25}\) when compared with PLSMO algorithm. The above discussion represents that LSMO may be a competitive candidate in the field of swarm intelligence.

Further, the convergence speed of considered algorithms are compared by analysis of AFEs. There is an inverse relation between AFEs and convergence speed, for smaller AFEs the convergence speed will be higher and vice-versa. For minimizing the effects of stochastic nature of algorithm, the reported AFEs are averaged for 100 runs for each considered test problems. The convergence speed is compared using acceleration rate (AR) for the considered algorithms. The AR which is calculated as follows:

$$\begin{aligned} AR=\frac{AFE_{ALGO}}{AFE_{LSMO}}, \end{aligned}$$
(12)

Here, \({ ALGO}\in \{ { SMO}, { ABC}, { PSO}, { DE}, { CMA}-{ ES}, { GbestABC}, { MeABC}, { LFABC}, { PLSMO}\}\) and \(AR>1\) represents that LSMO is faster than the compared algorithm. The AR results are shown in Table 4. The results in Table 4 shows that for most of the considered benchmark test functions, LSMO converge faster than the considered algorithms.

The boxplots analyses have also been carried out for all the considered algorithms for comparison regarding consolidated performance. In boxplot analysis tool [27] graphical distribution of empirical data is efficiently represented. The boxplots for LSMO and other considered algorithms are represented in Fig. 5. It is clear from this figure that LSMO performs better than the considered algorithms as interquartile range, and the median is quite low.

Table 3 Comparison based on Mann–Whitney U rank sum test at significant level \(\alpha =0.05\) and average number of function evolutions
Full size table
Table 4 Comparison based on acceleration rate (AR)
Full size table
Fig. 5
figure 5

Boxplots graphs for average number of function evaluation

Full size image

6 Capacitor sizing and optimal placement problem

The placement of capacitors in the distribution network is mainly needed, for improving power transfer capability, for properly serving to reactive loads, for the smooth working of power transformers, and for secure and stable transmission system in different network configurations. Further, these capacitors improve voltage profile and maintain contractual obligations for electrical equipments. The capacitors also help in reducing the energy consumption of voltage-dependent sources as well as technical losses [6]. The capacitors have been widely installed by utilities, to provide reactive power compensation, to enhance the efficiency of the power distribution, and to achieve deferral of construction. Economically, we can say that the capacitors installation in distribution network help in increasing, generation capacity, transmission capacity, and distribution substation capacity. Subsequently, it helps in increasing revenue generation. But the placement of capacitors exactly at required optimal position in a distribution system is a challenging task or can say a difficult problem for the distribution engineers. The objective of this problem is to minimize the energy losses while considering the capacitor installation costs. In other words, the goal is to achieve the optimal placement and sizing of capacitors with the system constraints in the distribution network. The problem is defined as follows:

The total loss in a distribution system having n number of branches is given by

$$\begin{aligned} {PL_t} = {\sum \limits _{i=1}^{n} [I_{i}^{2}]{R_i}} \end{aligned}$$
(13)

Here \(I_i\) and \(R_i\) are current magnitude and resistances respectively for the ith branch. The branch current obtained from load flow solution has two components; active \((I_a)\) and reactive \((I_r)\). In active and reactive branch currents, the associated losses are given by Eqs. 14 and 15 respectively.

$$\begin{aligned} {PL_a}= & {} {\sum \limits _{i=1}^{n} \left[ I_{ai}^{2}\right] {R_i}} \end{aligned}$$
(14)
$$\begin{aligned} {PL_r}= & {} {\sum \limits _{i=1}^{n} \left[ I_{ri}^{2}\right] {R_i}} \end{aligned}$$
(15)

In loss minimization technique of the capacitor placement, a single capacitor is repetitively placed by varying its size for determining a sequence of nodes in view of loss minimization of the distribution system. The concept of loss minimization by a singly located capacitor can be extended for multiple capacitors [6].

Let us consider the following [13]:

  • m = number of capacitor buses.

  • \(I_{c}\) = m dimensional vector consisting of capacitor currents.

  • \(\alpha _{j}\) = set of branches from the source bus to the \(j^{th}\) capacitor bus \((j=1, 2, \ldots m)\).

  • D = a matrix of dimension \(n\times m\).

The elements of D are considered as

  • \(D_{ij}\) = 1; if branch \(i \in {\alpha }\)

  • \(D_{ij}\) = 0; otherwise

When the capacitors are placed in the system, the new reactive component of branch currents is given by

$$\begin{aligned} {[}I_r^{new}] = [ I_r] + [D] [ I_c] \end{aligned}$$
(16)

The loss associated with the new reactive currents in the compensated system is

$$\begin{aligned} P_{L_r}^{com}=\sum \limits _{i=0}^{n}\left( I_{ri}+{D_{ij}{I_{cj}}}\right) ^2{R_i} \end{aligned}$$
(17)

The loss saving (S) is obtained by placing the optimal size capacitors in the distribution network. The loss saving is calculated by taking the difference of the Eqs. 15 and 17 and is shown as follows:

$$\begin{aligned} S=-\sum \limits _{i=1}^{n} \left[ \left( 2I_{ri} \sum \limits _{j=1}^{m}D_{ij} I_{cj} + \sum \limits _{j=1}^{m}D_{ij} I_{cj}\right) ^2\right] R_{i} \end{aligned}$$
(18)

For achieving the maximum loss saving, optimal capacitor currents can be obtained from the following equations:

$$\begin{aligned} \begin{aligned} \frac{\delta {S}}{\delta {I_{c1}}}=0\\ \frac{\delta {S}}{\delta {I_{c2}}}=0\\ ----\\ ----\\ \frac{\delta {S}}{\delta {I_{ck}}}=0 \end{aligned} \end{aligned}$$
(19)

After some mathematical manipulations, equation 19 can be expressed by a set of linear algebraic equations as follows:

$$\begin{aligned} {[}A] [I_c] = [B] \end{aligned}$$
(20)

Where A is a \(m\times m\) square matrix and B is a k-dimensional vector. The elements of A and B are given by

$$\begin{aligned} A_{jj}= & {} \sum \limits _{i\epsilon \alpha j} [R_i] \end{aligned}$$
(21)
$$\begin{aligned} A_{jj}= & {} \sum \limits _{i\epsilon (\alpha j\bigcap \alpha m)}[R_i] \end{aligned}$$
(22)
$$\begin{aligned} B_j= & {} \sum \limits _{i\epsilon \alpha j}[I_{ri} R_{i} ] \end{aligned}$$
(23)

Only the branch resistances and reactive currents in the original system are required to find the elements of A and B. The capacitor currents for the highest loss saving can be obtained from Eq. 20.

$$\begin{aligned}{}[I_c] = [A]^{-1} [B] \end{aligned}$$
(24)

Once the capacitor currents are known, the optimal capacitor sizes can be written as \({Q_c}\) in mega volt ampere reactive (MVAR) as equation 25

$$\begin{aligned} {Q_c} = {V_m }\times {I_c } \end{aligned}$$
(25)

Here \(V_m\) is the voltage magnitude vector of capacitor buses. The saving in the compensated system can be estimated from Eq. 18 using the value of \(I_c\) given by Eq. 24.

The objective function may be formulated using Eq. 18 in following manner :

$$\begin{aligned} {{ minf}\,(x_{{ location}}, x_{{ size}})} = S \end{aligned}$$
(26)

7 LSMO for optimal placement and sizing of capacitors

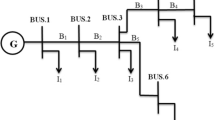
In this section, the LSMO and SMO algorithms are applied to solve the optimal placement and sizing problem of capacitors in the distribution network. First in LSMO, the solutions are generated randomly in a given range i.e. capacitors of given value are placed at random nodes in the distribution system. Here, each solution represents the size and location of capacitors in the distribution network, for example for 3-capacitor problem; a solution will be of six dimensions of which first three will represent the size of the capacitors while remaining three will show the locations of the capacitors. Here, it should be noted that the locations of the capacitors are represented by discrete values while size by continues values. Therefore, the first three real values are converted into discrete values by rounding off in the nearby integer value. In this way, a mixed representation of the solution is prepared. As the capacitor placement and the sizing problem is non-separable and multimodal in nature, SMO and its proposed variant are applied to solve it. In this paper, the loss minimization is carried out by providing the optimal size and location of the capacitors in the network. For testing, the performance of LSMO, it is applied on IEEE−14, 30 and 33 test bus radial distribution system. The LSMO is used to update the bus data of the considered bus systems iteratively for reducing the system losses. The reported results are compared with GA and SMO (The parameter settings of GA and SMO are same as their legitimate research papers [2, 8]) as shown in Tables 5, 6, 7, 8, 9, and 10. The better results are represented by bold values. The loss minimization curves are shown in Fig. 6. From these tables, it is clear that the size of the capacitor is determined in MVAR (i.e. \(10^6\) VAR) while power loss is measured in Mega Watts (i.e. \(10^6\) W). So, a little difference in power loss and capacitor size affects the performance significantly. The results show that the loss occurred using LSMO strategy is minimum among all the considered cases and algorithms. Therefore, the LSMO may be used for solving the capacitor placement and sizing problem of the distribution system.

Fig. 6
figure 6

LSMO for Optimal placement of capacitor of IEEE−14, IEEE−30 and IEEE−33 bus system respectively for a 3 capacitor, b 5 capacitor problems

Full size image
Table 5 Optimal placement and sizing of capacitor for IEEE 14 bus 3 capacitor problem
Full size table
Table 6 Optimal placement and sizing of capacitor for IEEE 14 bus 5 capacitor problem
Full size table
Table 7 Optimal placement and sizing of capacitor for IEEE 30 bus 3 capacitor problem
Full size table
Table 8 Optimal placement and sizing of capacitor for IEEE 30 bus 5 capacitor problem
Full size table
Table 9 Optimal placement and sizing of capacitor for IEEE 33 bus 3 capacitor problem
Full size table
Table 10 Optimal placement and sizing of capacitor for IEEE 33 bus 5 capacitor problem
Full size table

8 Conclusion

In this paper, a limaçon inspired local search (LLS) strategy is developed and hybridized with SMO. The proposed hybridized strategy is named as limaçon inspired SMO (LSMO). The performance of LSMO has evaluated over 25 well-known benchmark functions. Results indicate that the proposed LSMO is a significant candidate among most promising swarm intelligence based global optimization algorithms. Further, a complex real-world optimization problem, optimal placement and sizing of capacitors in distributed network is solved with IEEE 14, 30, and 33 bus test system using LSMO. Results have been compared with those of GA and SMO. It is observed that LSMO obtains minimum distribution and transmission losses while maintaining the minimum cost. This work may further be extended to an unbalanced radial system as a future research perspective.