Abstract
This work presents an algorithm based on the bio-inspired optimization technique known as monkey search (MS) for the optimal allocation of fixed and switched capacitor banks in distribution systems. The objectives are to minimize the energy loss, to improve the voltage levels and to reduce the carbon dioxide emission. The monkey search technique is a metaheuristic method that is inspired by the behavior of a monkey searching for food in a jungle. The applied method consists of a modified monkey search (MMS), which presents modifications and improvements for the original MS technique to represent in a suitable manner the features and constraints of the capacitor allocation problem. The proposed model considers different load levels, voltage limit constraints and practical values for fixed and switched capacitor banks, as well as for unit costs and emission coefficient. Case studies are performed by using test systems of the literature in order to assess the efficiency of the proposed algorithm, including a tutorial on the MMS algorithm.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The new paradigms of the energy sector, as the requirements for lower costs and higher quality of the energy supplying, as well as the technological advances, have leading to the search for more efficient solutions of common problems, as the network loss and the voltage drop. The distribution systems have an important role for the energy sector, because such systems impact appreciably on the electrical networks planning (Gonen 1986) and are more complex in respect of voltage control and loss (Grainger and Lee 1981; Lee and Grainger 1981).
The energy quality question has been handled by energy efficiency policies through the development of short-, medium- and long-term plans, in line with the strategic and business plans of energy companies. Such policies aim at the economy of resources and the postponement of investments in generation, transmission and distribution systems, which can reduce the environmental impact (Li et al. 2013). Moreover, the planning of modern systems should encourage the search for technological solutions through analyses of the social, economic and environmental impacts from the potential generation sources and respective conversion technologies. In this context, options for increasing the efficiency and quality of distribution systems with control of the environmental impact, as the capacitor allocation, should be considered.
The problem of optimal capacitor allocation in distribution systems comprises the determination of the location, the type of equipment that can be fixed or switched, and its capacity, so that the economic benefits are maximum, without violation of the operational constraints (Singh and Rao 2012). The following aspects give more complexity to the problem: (i) different capacities given by a series of tabulated values adopted by the distribution utilities, which implies more variables for the problem; (ii) different load levels during the operation, given by diary curves related to different kinds of costumers (Gerbec et al. 2005); and (iii) operation of the switched banks during the load variations.
Additionally, the nonlinear features of the objective function and constraints, as well as the existence of discrete variables that are related to the location, type and capacity options for the capacitor banks, result in a problem of combinatorial, nonlinear and mixed-integer mathematical programming, whose solution space is not convex. These features increase the difficulty of solving the problem (Oliveira et al. 2010), especially for larger networks. Therefore, the search for efficient capacitor allocation solutions that can combine suitable quality and processing times (Gallego et al. 2001) is important for the planning of modern distribution systems.
Given the characteristics of the capacitor allocation problem, metaheuristic techniques have been proposed for solving it, with the purpose of obtaining good quality solutions and computational efficiency (Arora et al. 1995). Some techniques are bio-inspired, i.e., based on the behavior of natural systems, as ant colony (Chang 2001; Chiou et al. 2004; Sirjani and Hassanpour 2012), particle swarm optimization (Eajal and El-Hawary 2010; Etemadi and Fotuhi-Firuzabad 2008; Ghadimi 2012) and genetic algorithms (Levitin et al. 2000; Haghifam and Malik 2007; Salama and Chikhani 2000; Sundhararajan and Pahwa 1994; Swarnkar et al. 2010). Artificial intelligence techniques, as neural networks (Salazar et al. 2006) and fuzzy logic (Mekhamer et al. 2003), as well as hybrid algorithms (Barukcic et al. 2010; Gerbec et al. 2005), have also been applied. Fuzzy logic and genetic algorithm are joint in (Das 2008; Souza et al. 2004; Su et al. 2001a) for the capacitor allocation, whereas (Bhattacharya and Goswami 2009) present the application of diffuse systems with tabu search.
In Huang and Liu (2012), it is presented a methodology based on a bio-inspired technique known as plant growth-based optimization approach for the capacitor allocation, which considers the reduction in the carbon dioxide emission among the objectives. The emission reduction can be achieved from the reactive support provided by capacitors. It can be highlighted that the consideration of contemporary objectives, as the gas emission reduction, is still not much investigated (Baghipour and Fallahian 2015; Huang and Liu 2012; Humbert et al. 2013).
From the application of bio-inspired optimization methods to determine the optimal capacitor allocation in distribution systems, this paper presents an algorithm based on the MS technique (Mucherino and Seref 2007) for the allocation of fixed and switched capacitor banks. The objectives comprise the minimization of energy loss considering different system load levels, the improvement of voltage and the reduction in gas emissions. The optimization method is known as MMS and consists on a modification of the original MS technique that allows performing the search process in a more efficient way according to the problem characteristics (Duque et al. 2015). The main contribution is the application of a technique still unexplored for the allocation of fixed and switched capacitors banks, in view of its successful application just for fixed banks (Duque et al. 2015). Moreover, the addition of present-day objectives as the gas emission minimization can also be included among the contributions. Case studies are made to evaluate the proposed approach.
The rest of the paper is organized as follows: Sect. 2 formulates the capacitor allocation problem, Sect. 3 describes the proposed methodology and details the procedures for the calculations, Sect. 4 presents the case studies and Sect. 5 the conclusions.
2 Formulation of the Problem
The mathematical formulation of the optimization problem considers the energy loss minimization for different load levels and incorporates the reduction in carbon dioxide \((\hbox {CO}_{2})\) emission, subject to the network and voltage limit constraints. This formulation is presented hereafter:

subject to:
where
- OBF :
-
Objective function ($);
- Nt :
-
Number of load levels;
- \(k_{e,u}\) :
-
Energy cost for load level u ($/kWh);
- \(T_{u}\) :
-
Duration time of load u (h);
- \(L_{ij,u}\) :
-
Active power loss of branch ij at load level u (pu kW);
- Bp :
-
Base power (kW);
- \(\beta \) :
-
\(\hbox {CO}_{2}\) emission coefficient \((\hbox {CO}_{2}\hbox {/kWh})\);
- \(k_{\mathrm{CO}_{2}}\) :
-
\(\hbox {CO}_{2}\) emission cost \((\$/\hbox {CO}_{2})\);
- Nb :
-
Number of candidate buses for capacitor bank allocation;
- \(k_{f}, k_{s}\) :
-
Unitary costs for fixed and switched capacitors, respectively ($/kvar);
- \(u_{i,f}, u_{i,s}\) :
-
Binary variables that represent allocation of fixed and switched capacitor at bus i, respectively (0—not allocated; 1—allocated);
- \(Qf_{i},Qs_{i}\) :
-
Capacity of the fixed or switched bank, respectively, at candidate bus i (pu kvar);
- \(Pg_{i,u}, Qg_{i,u}\) :
-
Active (pu kW) and reactive (pu kvar) power, respectively, generated at bus i at load level u;
- \(Pl_{i,u}, Ql_{i,u}\) :
-
Active (pu kW) and reactive (pu kvar) load demand, respectively, at bus i at load level u;
- \(p_{ij,u}, q_{ij,u}\) :
-
Active (pu kW) and reactive (pu kvar) power flows, respectively, at branch ij at load level u;
- \(\Omega i\) :
-
Set of the buses connected to bus i through distribution branches;
- \(\alpha _{i,u}\) :
-
Factor for obtaining the reactive support at bus i provided by switched capacitors at load level u;
- \(g_{ij}\) :
-
Conductance of branch ij (pu S);
- \(\theta _{ij,u}\) :
-
Phase angle between buses i and j at load level u (rad);
- \(V_{\min }, V_{\max }\) :
-
Lower and upper voltage limits at buses (pu V);
- \(b_{ij}\) :
-
Susceptance of branch ij (pu S); and
- \(bs_{ij}\) :
-
Shunt susceptance of branch ij (pu S).
The objective function (OBF) of (1) is also used in Huang and Liu (2012) and is formed by three cost terms. The first one refers to the cost associated with the total energy loss during the operation period, and the second term is related to the cost associated with the total volume of \(\hbox {CO}_{2}\) emitted into the atmosphere during the same period. The third term, in turn, consists on the total cost of investment in fixed and switched capacitors, whose unitary costs are different according to each option and are given by practical values (Huang and Liu 2012).
Equations (1a) and (1b) correspond to the active and reactive balance constraints in each bus, respectively, and are related to the Kirchhoff’s current law (KCL). The factor \(\alpha _{i,u}\le 1\) determines the reactive support at bus i and load level u provided by switched capacitor. For the higher load level, the reactive support corresponds to the capacity of the bank and \(\alpha _{i,u} = 1\). The constraint (1c) establishes that only one type of capacitor, fixed (\({u_{i,f} = 1}\)) or switched (\({u_{i,s} = 1}\)), is allowed for a same candidate bus—i, at most. The constraint in (1d) is used to calculate the active power loss at branch ij and load level u. The voltage limit constraints are formulated in (1e). Equations (1f) and (1g) are related to Kirchhoff’s voltage law (KVL) and consist of the active and reactive power flows at branch ij and load level u, respectively.
Notice that the loss minimization implies the improvement of the voltage levels. The load flow problem resulting from each solution proposal provided by the MMS is solved by using the Newton’s method (Tinney and Hart 1967), to calculate losses and the other quantities.
3 The Modified Monkey Search Algorithm
The MMS algorithm upgraded for the allocation of fixed and switched capacitor banks is presented hereafter, including the codification of the candidate solutions, the parameters and steps of the algorithm, the mechanisms of memory updating and convergence criteria.
3.1 Codification of the Candidate Solutions
The codification proposed for a candidate solution (m) of the MMS algorithm stores the capacity of reactive support provided by capacitors banks in each candidate bus, according to (2).
where \(Qb_{i}\) is the capacity of the bank allocated at candidate bus i that can be fixed \((Qb_{i} = Qf_{i})\) or switched \((Qb_{i} = Qs_{i})\). The determination of type is done by combining the candidate solution in m with a matrix \(\alpha \), which stores the multiplicative factors \(\alpha _{i,u}\) for obtaining the reactive support at each bus and load level. The matrix (3) is defined such that each line stores the factors associated with a bus in all load levels and each column stores the factors related to a load level in all candidate buses.
The factor \(\alpha _{i,u}.Qb_{i}\) can result in a value that is not among the discrete values for a capacitor bank. In this case, the factor \(\alpha _{i,u}.\hbox {Q}b_{i}\) is rounded to the nearest discrete number, in a similar procedure adopted in (Viana et al. 2013), as represented in (4).
where
- \(Qc_{i,u}\) :
-
Reactive support provided by capacitor bank at bus i and load level u; and
- round:
-
Operator that rounds to the nearest discrete value.
When the values of \(Qc_{i,u}\) for bus i, at the final of the optimization process, are different between load levels u, a switched capacitor bank is allocated at bus i, \(u_{i,s}\) is set at 1 and \(Qs_{i} = Qb_{i}\) in system of equations (1). On the other hand, when \(Qc_{i}\) is the same for all load levels u, a fixed capacitor bank is allocated at bus \(i, u_{i,f}\) is set at 1 and \(Qf_{i} = Qb_{i}\) in (1). The factors \(\alpha _{i,u}\) are randomly generated at the beginning of the optimization process for every bus and load level. As the algorithm evolves, the factors are fixed by a procedure known as intensification, which is described in this paper.
3.2 Parameters of the Initial Tree
The initial tree is defined as the set of candidate solutions that are used as starting point for the MMS algorithm. The base case is the condition where there is not capacitor allocation and it is defined as “root candidate solution”. From the “root”, the algorithm generates two new candidate solutions that along with the base case form the first level of the initial tree. The first-level solutions are derived from the base case through tree branches as pictured in Fig. 1. From that, the second level is obtained by deriving two new solutions from each point of the first level, and so on. Each level implies a new depth for the search. The mechanism to derive new candidate solutions from a current solution is known as perturbation.
In the initial tree of Fig. 1, the number of levels is equal to 3 because the “root” and the two first candidate solutions form a unique level. Therefore, the first level is formed by the candidate solutions “root”, “A” and “B”, the second one by solutions “C” to “F” and the third level is formed by eight candidate solutions (“G”–“N”). In an artificial tree, a branch consists of a link between two candidate solutions, whereas a path consists on a full sequence of solutions between the “root” and a solution of the last level. In the initial tree of Fig. 1, (“root”–“A”) e (“A”–“B”) represent two branches, whereas (“root”-“A”–“C”–“G”) define a path. In this way, the number of paths in an artificial tree can be formulated as:
where
- c :
-
Number of possible paths in an artificial tree;
- h :
-
Number of levels (height or top of the tree).
The search for candidate solutions in the initial tree is finished when all paths between the “root” and the last level are covered through a full search process.
3.3 Subsequent Trees
The first subsequent tree to be investigated in the MMS search process is obtained through perturbation in the best solution found in the initial tree, which is defined as the “root” of the first subsequent tree. In general, the starting point of any subsequent tree is the best candidate solution among all previous trees.
In a subsequent tree, the algorithm performs a search guided by the best candidate solutions obtained during the perturbation processes, avoiding the full search and increasing the efficiency of the method in relation to the original MS (Kammerdiner et al. 2009) for the capacitor allocation problem. The original MS performs the full search in all trees.
In Fig. 2, the candidate solution “root” is perturbed to generate solutions “A” and “B”. The algorithm compares the two generated solutions and “A” is the best. From that, the process continues from the candidate solution “A”, generating “C” and “D”, and so on until the top of the tree. Therefore, the candidate solution “D” and the respective derived branches are excluded from the search process by a pruning procedure.
3.4 Adaptive Memory
The adaptive memory is initialized by the ten best solutions obtained in the initial tree and is updated during the search in the subsequent trees. The adaptive memory after the full search in the initial tree is represented in (6).
where
- \(memo_{m1}\) :
-
Initial adaptive memory of tree m1;
- \(m_{n,mi}\) :
-
Candidate solution stored at position n of tree mi.
As previously described, the best candidate solution found in tree \(m1, m_{1,m1}\), is the “root” of subsequent tree m2. If a candidate solution found in tree m2 is better than any solution of \(memo_{m1}\), the memory is updated and the last position \(m_{10,m1}\) is discharged, maintaining the number of stored candidate solutions. As an example, two solutions of tree \(m2, m_{1,m2}\) e \(m_{2,m2}\), are assumed to be better than solutions \(m_{3,m1}\) and \(m_{6,m1}\) of the initial memory in (6), respectively. So the memory should be updated as in (7).

It can be observed that even if the candidate solutions found in m2 are not better than the first solution of \(memo_{m1}\), and the memory is updated if at least one solution of m2 is better than any candidate solution in set given by \([m_{2,m1} : m_{10,m1}]\), the adaptive memory is updated. This procedure makes the MMS method more efficient for the capacitor allocation problem and is a modification in relation to the original MS (Kammerdiner et al. 2009), which makes comparisons only with the best stored solution.
3.5 Perturbation Mechanism of the Current Solution
The perturbation process applied to a candidate solution to generate new solutions consists of increment and decrement operations in random positions of the solution code. Given the adopted codification for the candidate solutions, an increment operation changes the capacity of the capacitor bank at a random bus to the next higher capacity among the possible discrete values, provided that the new capacity does not exceed the maximum discrete value. Likewise, a decrement operation changes the current capacity to the next lower among the discrete values. The number of increment \((n_\mathrm{inc})\) or decrement \((n_\mathrm{dec})\) operations varies randomly from 1 to 3. Figure 3 is used to exemplify the perturbation mechanism, where the values modified by perturbations are highlighted. From the “root”, candidate solution “A” is generated through two increments and one decrement, whereas solution “B” is obtained by one increment and one decrement.
If a bus is selected two times for increment, its capacity will be changed to the second value above among the possible discrete values for capacitor bank. Analogous process is done when a bus is selected three times for increment or two times for decrement. The capacity limits are considered in such operations, i.e., if a new value goes out of the discrete values range, the respective operation is not done and new random values are generated until the numbers of increments—\(n_\mathrm{inc}\) and decrements—\(n_\mathrm{dec}\) are achieved, which are also randomly chosen.
Regarding the multiplicative factors \(\alpha _{i,u}\), which define the reactive support in each bus and load level, the candidate solutions “A” and “B” generated by the perturbation mechanism have distinct characteristics from one another. While “A” maintains the factors of “root”, new multiplicative factors are randomly generated for solution “B” from the beginning of the optimization process until the beginning of the intensification process that is described ahead. The differences in the generation of “A” and “B” avoid the algorithm from being limited to a nonoptimal solution given by the factors \(\alpha _{i,u}\) of the “root” in the first iterations. The same mechanism procedure applied to the “root” is extended to derive two solutions of any level in tree from a given solution of the previous level.
Figure 4 exemplifies the proposed perturbation mechanism of the MMS algorithm upgraded for fixed and switched capacitor banks allocation. The example assumes five candidate buses and the following discrete values: 0, 150, 300, 450. It is further considered that the candidate solution at level “k” of a given tree is codified as [150 0 0 300 150], which determines the allocation of 150 kvar banks at the first and fifth candidate buses \((Qb_{1}=Qb_{5}=150)\), besides a bank of 300 kvar at the fourth bus \((Qb_{4} =300)\). Solution “A” of level “\(k + 1\)” in the tree maintains the matrix of factors \(\alpha \) of level “k”, whereas solution “B” receives new random factors \(\alpha _{i,u}\), as pictured in Fig. 4 that also shows the factors \(\alpha _{i,u}.Qb_{i}\) for each solution and the respective reactive support values \(Qc_{i,u}\) after the rounding operations of (4). In this case, candidate solution “A” determines allocations of switched banks at buses 1 and 4, because the values of \(QC_{i,u}\) are different between two or more load levels for these buses, besides the allocation of a fixed bank at bus 3 because \(Qc_{3,1} = Qc_{3,2} = Qc_{3,3}\). Solution “B”, in turn, determines the allocation of switched banks at buses 1, 3 and 4.
3.6 Convergence
The convergence criteria for the search in the artificial trees of the MMS algorithm are summarized hereafter.
-
(i)
Initial tree The convergence is achieved when all paths are covered.
-
(ii)
Subsequent tree The convergence is achieved when at least one of the following conditions is met:
-
a solution better than the “root” is achieved; the lower is the OBF of (1), the higher the quality of solution;
-
all paths of the tree are covered.
Besides the convergence criteria of the search in trees, there is the global convergence criteria of the MMS algorithm listed hereafter:
-
(i)
the difference between the worst and the best solutions of the adaptive memory is less than or equal to a tolerance \(\varepsilon \), or
-
(ii)
the maximum number of covered trees
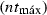 is achieved.
is achieved.
3.7 Intensification Process
After the full search in the initial tree of MMS, when the number of evaluated solutions achieves a given preestablished number \((n_\mathrm{peri})\), the algorithm obtains the multiplicative factors of the reactive supports by bus and load level—\(\alpha _{i,u}\)—of the candidate solutions stored in the adaptive memory. After that, the candidate solutions derived until the convergence maintains the factors \(\alpha _{i,u}\) and the perturbation mechanism only changes the bank capacity values—\(Q_{bi}\). Therefore, from the \(n_\mathrm{peri}\) solution obtained after the initial tree, the factors \(\alpha _{i,u}\) remain the same for both solutions “A” and “B” derived from any candidate solution.
3.8 Flowchart of the Proposed MMS Algorithm
Figure 5 presents the flowchart of the MMS algorithm, whose steps are described ahead.
-
Step 1 Input Data. In this step, the distribution system data are obtained and the MMS parameters and optimization conditions are defined.
-
Step 2 Climbing up the initial tree. This step consists of exploring the initial tree from its root, which corresponds to the base case, without any capacitor bank allocation. The root is successively perturbed until the top is reached. The root and each node achieved in the tree are solutions for the optimal capacitor allocation evaluated each one through the optimization problem formulated in (1). The quality or fitness of each solution is inversely proportional to its OBF associated with the total cost of loss and investment.
-
Step 3 Initialization of the adaptive memory (memo). The n better solutions found in the initial tree are stored in memo in descending order of fitness. The first element of memo is named ibest. In the proposed algorithm, n is set to 10.
-
Step 4 Beginning of search in the subsequent tree mi. Perturbation of ibest to generate two new nodes or solutions through the perturbation mechanism described before.
-
Step 5 Choosing the new current solution. The node generated at Step 4 that presents the better fitness is chosen.
-
Step 6 Evaluation of the new current solution chosen at Step 5. Two situations can occur: (i) If the chosen solution presents fitness better than ibest, this solution replaces ibest and the convergence of tree mi is achieved; in this case, counter i is incremented and a new tree mi begins to be explored from Step 4; (ii) otherwise, the adaptive memory is updated if the new current solution is better than at least one solution of memo; in this case, the algorithm goes to Step 7.
-
Step 7 Global convergence criteria evaluation. In this step, the global convergence criteria previously described are assessed. If at least one of the presented conditions is achieved, the algorithm is ended. Otherwise, it goes to Step 8.
-
Step 8 The algorithm verifies if the top of tree mi was achieved. If the answer is ‘yes’, it means that no solution better than ibest has been found from the root to the top of mi. In this case, the algorithm returns to Step 4 to perform a new perturbation process in ibest. This procedure is the climbing down process. Otherwise, i.e., if the top has not been achieved, the algorithm remains in the climbing up process at Step 9.
-
Step 9 Perturbation of the current solution. As previously described, the perturbation mechanism generates two new solutions candidate to the new current solution. From this generation, the algorithm goes to Step 5.
4 Case Studies
Four case studies are performed to evaluate the MMS algorithm upgraded to be applied to the problem of fixed and switched capacitors banks allocation: case 1—69 buses (Baran and Wu 1989); case 2—17 buses (Su et al. 2008), case 3—85 buses (Das et al. 1995) and case 4—123 buses (Kersting 1991). The first one is a tutorial case for the MMS algorithm and presents a step-by-step description of the optimization process. The common parameters for the cases studies are: (i) height of a tree \((h) = 8\), totaling \(c = 256\) paths according to (5); (ii) tolerance \(\varepsilon = 0\); (iii) maximum number of trees \(nt_{\max } = 20\); (iv) size of the adaptive memory equal to 10; (v) \(n_\mathrm{peri} = 100\); and (vi) maximum number of capacitor banks in the whole system is 15 as in (Duque et al. 2015). In case 1, there is a set of buses candidate for capacitor allocation from the literature, whereas in cases 2–4, all buses are candidate.
The MMS method applied in this paper is compared to other metaheuristics as listed hereafter:
-
(1)
Original Monkey Search (MS) of (Kammerdiner et al. 2009);
-
(2)
Genetic Algorithm (GA) which parameters obtained of (Silva et al. 2008) are: (i) crossover probability of 95 %, (ii) mutation probability of 2 %, (iii) population size of 300, (iv) number of generations of 100, (v) convergence criterion based on maximum number of generations, (vi) elitism with one individual, (vii) decimal coding, (viii) roulette selection and (ix) two-point crossover;
-
(3)
Simulated Annealing (SA) which parameters are (Su and Lee 2001b): (i) Boltzmann constant equal to 1, (ii) initial temperature equal to 30, (iii) maximum number of iterations equal to 300 and (iv) cooling rate equal to 0.95.
The tests were performed using a 3.20-GHz Intel Corei5–4200 processor with 6 GHz RAM.
4.1 Case 1: Tutorial
The 69-bus test system (Baran et al. 1989) is used as a tutorial case for the MMS algorithm. The system has a substation, 74 branches and nominal voltage at 12.66 kV.
The optimization conditions are described hereafter:
-
Total operation time of 8760 hours (1 year), divided into three load levels: light (0.5 pu during 2000 hours), medium (1.0 pu during 5260 hours) and heavy (1.6 pu during 1500 hours);
-
The cost related to the energy loss and the investment in capacitors, fixed or switched, are 0.06 $/kWh and 3.00 $/kvar, respectively;
-
The set of buses candidate for capacitor allocation is (Das 2008):
-
The objective function for this case considers only the first and the third terms of (1), related to the energy loss and investment in capacitors, as presented hereafter:

-
As the results from other works that are used for comparison in this case do not consider voltage limit constraints, such constraints are also not considered here by the proposed approach.
The MMS algorithm starts from the initial tree which “root” corresponds to the base case where there is not any capacitor. Table 1 presents the data for the base case.
The search in the initial tree is performed until all paths are covered, comprising 256 solutions. The ten best solutions initialize the adaptive memory. Vector \(memo_{m1}\) with the best objective function values for the initial tree is presented here.
The next step consists of searching in the subsequent trees, without necessarily evaluating all the possible paths. Figure 6a shows that the objective function reduces from $ 135,930.27 (base case) to $ 95,433.76 after searching the initial tree (m1). From the “root” of m2, i.e., the best solution found in m1, 17 perturbation processes is performed until a solution better than the “root” is achieved, when the convergence criterion of m2 is met. The same reasoning can be applied for the other trees. The final solution found by the MMS algorithm is found after the search in the last tree (m8) and presents a total cost of $ 94,067.69. Figure 6b presents the number of perturbations in each tree.
It can be seen in Fig. 6 that the number of perturbations in a tree increases from the second one to the last tree, because as the optimization process evolves, better quality solutions are obtained and it becomes harder to overcome the best solution, i.e., the “root” of the current tree. This reasoning does not apply to the first tree due to the full search that is performed only in this tree.
Table 2 presents the results of the MMS algorithm and the solutions of the MS, GA and SA algorithms, developed for comparison purpose, and other from the literature (Neelima and Subramanyam 2012; Ramalinga et al. 2012; Swarnkar et al. 2010; Sultana and Roy 2014). The total cost obtained by MMS ($ 94,067.69) presents a reduction of 30.80 % in relation to the base case ($ 135,930.27). Moreover, the results show that the MMS algorithm presents the lowest cost and processing time, compared to the other methods. It can also be observed that other sizes for the capacitor banks are considered in (Neelima and Subramanyam 2012; Swarnkar et al. 2010). The processing times for (Neelima and Subramanyam 2012; Ramalinga et al. 2012; Swarnkar et al. 2010) were not given.
The values obtained for the load multiplicative factors as in (3) are shown in the following matrix:
where the first, second and third lines are related to the light, medium and heavy load conditions, respectively. Table 3 presents the reactive power from the allocated capacitors in every load level for the best solution found by the MMS algorithm, after the updating process applied to the banks in order to obtain multiples of 150 kvar.
4.2 Case 2
Case 2 uses the 85-bus (Das et al. 1995) test system and considers the same optimization conditions of the previous case.
Tables 4 and 5 present the results for Case 2. From Table 4, it can be verified that the MMS algorithm presents the lower total cost, with a reduction of 50.82 % in relation to the base case. The processing time for (Ramalinga et al. 2012) was not given.
4.3 Case 3
Case 3 does the optimal capacitor allocation in the 17-bus system of (Su et al. 2008). The optimization conditions are as follows:
-
Operation time of 8760 hours (1 year), divided into three load levels—light (1000 hours), medium (6760 hours) and heavy (1000 hours);
-
Multiplicative factors of the load (light/medium/heavy)—0.3/0.7/1.0 pu;
-
Energy loss cost—2.1133 $/kWh for all load levels;
-
Costs for fixed and switched capacitors—Table 6 (Huang and Liu 2012);
-
Voltage limits—from 0.9 to 1.0 pu;
-
Objective function given by (1);
-
\(\hbox {CO}_{2}\) emission cost “\(k_{\mathrm{CO}_{2}}\)”—2,967 $/ton (Huang and Liu 2012).
Tables 7 and 8 present the results. In Table 7, column “Optimal Locations and Size”, “F” means fixed capacitor and “S” switched capacitor.
The efficiency of the MMS algorithm for this case can be shown by comparing the total costs, the \(\hbox {CO}_{2}\) emissions and the processing times, because the MMS obtains the lower values for such parameters and met the voltage limit constraint.
4.4 Case 4
Case 4 has as purpose to evaluate the MMS algorithm for a larger network that has 123 buses (Kersting 1991). The optimization conditions are:
-
Multiplicative factors of the load (light/medium/heavy)—0.5/0.8/1.0 pu;
-
Energy loss costs—0.64 $/kWh, 1.65 $/kWh and 2.76 $/kWh for the light, medium and heavy load, respectively;
-
Costs for fixed and switched capacitors—Table 9 (Huang and Liu 2012);
-
\(\hbox {CO}_{2}\) emission cost “\(k_{\mathrm{CO}_{2}}\)”—843 $/ton (Huang and Liu 2012).
The other optimization conditions are the same of the previous case.
Tables 10 and 11 present the results for Case 4, where the efficiency and applicability of the MMS algorithm for allocating fixed and switched capacitors, considering relevant objectives as the emission reduction, can be verified.
5 Conclusions
This paper presented an algorithm based on the metaheuristic optimization technique known as Monkey Search for the allocation of fixed and switched capacitors banks in energy distribution systems. The Modified Monkey Search algorithm applied to the capacitor allocation problem presents improvements in relation to the original method. An advantage of the applied method consists of the reduced set of parameters to be adjusted and the combination of local and global search strategies in the feasible solution space. Important aspects as different load levels, voltage limit constraints and contemporary objectives as the gas emission reduction are considered by the proposed approach. The results show that the proposed algorithm is efficient, achieving good quality solutions with reduced processing times.
References
Arora, J., et al. (1995). Global optimization methods for engineering applications: A review. Structural Optimization, 3–4(9), 137–159.
Baghipour, A., & Fallahian, S. (2015). Multi-objective placement of capacitor banks in distribution system using bee colony optimization algorithm. Journal of Advanced in Computer Research, 6(2), 117–127.
Baran, M. E., & Wu, F. F. (1989). Optimal capacitor placement on radial distribution systems. IEEE Transactions on Power Delivery, 4(1), 725–734.
Barukcic, M., Nikolovski, S., & Jovic, F. (2010). Hybrid evolutionary heuristic algorithm for capacitor banks allocation. Journal of Electrical Engineering, 61(6), 332–340.
Bhattacharya, S. K., & Goswami, S. K. (2009). A new fuzzy based solution of capacitor placement problem in radial distribution system. Expert Systems with Applications, 36(3), 4207–4212.
Chang, C. F. (2001). Reconfiguration and capacitor placement for loss reduction of distribution systems by ant colony search algorithm. IEEE Transactions on Power Systems, 16(4), 1747–1755.
Chiou, J. P., Chang, C. F., & Su, C. T. (2004). Ant direction hybrid differential evolution for solving large capacitor placement problems. IEEE Transactions on Power Systems, 19(4), 1794–1800.
Das, D. (2008). Optimal placement of capacitors in radial distribution system using a fuzzy-GA method. Electrical Power and Energy Systems, 30(6–7), 361–367.
Das, D., Kotharii, P., & Kalam, A. (1995). Simple and efficient method for load flow solution of radial distribution systems. International Journal of Electrical Power & Energy Systems, 17(5), 335–346.
De Souza, B. A., Alves, H. N., & Ferreira, H. A. (2004). Microgenetic algorithms and fuzzy logic applied to the optimal placement of capacitor banks in distribution networks. IEEE Transactions Power Systems, 19(2), 942–947.
Duque, F. G., Oliveira, L. W., Oliveira, E. J., Marcato, A. L. M., & Silva, I. C, Jr. (2015). Allocation of capacitor banks in distribution systems through a modified monkey search optimization technique. International Journal of Electrical Power & Energy Systems, 73, 420–432.
Eajal, A. A., & El-Hawary, M. E. (2010). Optimal capacitor placement and sizing in unbalanced distribution systems with harmonics consideration using particle swarm optimization. IEEE Transactions on Power Delivery, 25(3), 1734–1741.
Etemadi, A. H., & Fotuhi-Firuzabad, M. (2008). Distribution system reliability enhancement using optimal capacitor placement. IET Generation, Transmission & Distribution, 2(5), 621–631.
Gallego, R. A., Monticelli, A. J., & Romero, R. (2001). Optimal capacitor placement in radial distribution networks. IEEE Transactions on Power Systems, 16(4), 630–637.
Gerbec, D., Gasperic, S., Smon, I., & Gubina, F. (2005). Allocation of the load profiles to consumers using probabilistic neural networks. IEEE Transactions on Power Systems, 20(2), 548–555.
Ghadimi, N. (2012). Optimal placement of capacitor banks in order to improvement of voltage profile and loss reduction based on PSO. Research Journal of Applied Sciences, Engineering and Technology, 4(8), 957–961.
Gonen, T. (1986). Electrical power distribution system engineering. New York: McGraw-Hill.
Grainger, J. J., & Lee, S. H. (1981). Optimum size and location of shunt capacitors for reduction of losses on distribution feeders. IEEE Transactions on Power Apparatus and Systems, 100(3), 1105–1118.
Haghifam, M. R., & Malik, O. P. (2007). Genetic algorithm-based approach for fixed and switchable capacitors placement in distribution systems with uncertainty and time varying loads. IET Generation, Transmission & Distribution, 1(2), 244–252.
Huang, S. J., & Liu, X. Z. (2012). A plant growth-based optimization approach applied to capacitor placement in power systems. IEEE Transactions on Power Systems, 27(4), 2138–2145.
Humbert, A., Tuerlings, B. J., Hoofman, R. J. O. M., Tan, Z., Gravesteijn, D., Pertijs, M. A. P., et al. (2013). A low-power CMOS integrated sensor for CO\(_2\) detection in the percentage range. In International conference on solid-state sensors, actuators and microsystems: Transducers eurosensors XXVII, pp. 1649–1652.
Kammerdiner, A. R., Mucherino, A., & Pardalos, P. M. (2009). Application of monkey search meta-heuristic to solving instances of the multidimensional assignment problem. Optimization and Cooperative Control Strategies, 381, 385–397.
Kersting, W. H. (1991). Radial distribution test feeders. IEEE Transactions on Power Systems, 6(3), 975–985.
Lee, S. H., & Grainger, J. J. (1981). Optimum placement of fixed and switched capacitors on primary distribution. IEEE Transactions on Power Apparatus and Systems, 100(1), 345–352.
Levitin, G., Kalyuzhny, A., Shenkman, A., & Chertkov, M. (2000). Optimal capacitor allocation in distribution systems using a genetic algorithm and a fast energy loss computation technique. IEEE Transactions on Power Delivery, 15(2), 623–628.
Li, K., Chia-Yon, C., Jeng-Wen, L., & Yu-Hui, W. (2013). Abatement cost analysis in CO\(_2\) emission reduction costs regarding the supply-side policies for the Taiwan power sector. Energy Policy, 61, 551–561.
Mekhamer, S. F., Soliman, S. A., Moustafa, M. A., & El-Hawary, M. E. (2003). Application of fuzzy logic for reactive-power compensation of radial distribution feeders. IEEE Transactions on Power Systems, 18(1), 206–213.
Mucherino, A., & Seref, O. (2007). Monkey search: A novel metaheuristic search for global optimization. In AIP conference proceedings, Vol. 953, pp. 162–173.
Neelima, S., & Subramanyam, P. (2012). Optimal capacitor placement in distribution networks for loss reduction using differential evolution incorporating dimension reducing load flow for different load levels. In IEEE Energytech conference, pp. 1–7.
Oliveira, L. W., Oliveira, E. J., Carneiro, S, Jr, Pereira, J. L. R., Costa, J. S., & Silva, I. C, Jr. (2010). Optimal reconfiguration and capacitor allocation in radial distribution systems for energy losses minimization. International Journal of Electrical Power & Energy Systems, 32(8), 840–848.
Ramalinga, Raju M, Ramachandra Murthy, K. V. S., & Ravindra, K. (2012). Direct search algorithm for capacitive compensation in radial distribution systems. International Journal of Electrical Power & Energy Systems, 42(1), 24–30.
Salama, H. N., & Chikhani, M. M. (2000). Classification of capacitor allocation techniques. IEEE Transactions on Power Delivery, 15(1), 387–392.
Salazar, H., Gallego, R., & Romero, R. (2006). Artificial neural networks and clustering techniques applied in the reconfiguration of distribution systems. IEEE Transactions on Power Delivery, 21(3), 1735–1742.
Silva, I. C, Jr, Carneiro, S, Jr, Oliveira, E. J., Costa, J. S., Pereira, J. L. R., & Garcia, P. A. N. (2008). A heuristic constructive algorithm for capacitor placement on distribution systems. IEEE Transactions on Power Systems, 23(4), 1619–1626.
Singh, S. P., & Rao, A. R. (2012). Optimal allocation of capacitors in distribution systems using particle swarm optimization. International Journal of Electrical Power & Energy Systems, 43(1), 1267–1275.
Sirjani, R., & Hassanpour, B. (2012). A new ant colony-based method for optimal capacitor placement and sizing in distribution systems. Research Journal of Applied Sciences, Engineering and Technology, 4(8), 888–891.
Su, C. T., Lii, G. R., & Tsai, C. C. (2001a). Optimal capacitor allocation using fuzzy reasoning and genetic algorithms for distribution systems. Mathematical and Computer Modelling, 33(6–7), 745–757.
Su, C. T., & Lee, S. C. (2001b). Feeder reconfiguration and capacitor setting for loss reduction of distribution systems. Electric Power Systems Research, 58(2), 97–102.
Su, W. F., Chen, Y. C., Huang, C. W., Yang, H. P., Huang, S. J., Liu, C. W., et al. (2008). Improvement of loss analysis and performance evaluation in Taipower distribution systems. Monthly Journal of Taipower’s Engineering, 720, 41–54.
Sultana, S., & Roy, P. K. (2014). Optimal capacitor placement in radial distribution systems using teaching learning based optimization. International Journal of Electrical Power & Energy Systems, 54, 387–398.
Sundhararajan, S., & Pahwa, A. (1994). Optimal selection of capacitors for radial distribution systems using a genetic algorithm. IEEE Transactions on Power Systems, 9(3), 1499–1507.
Swarnkar, A., Gupta, N., & Niazi, K. R. (2010). Optimal placement of fixed and switched shunt capacitors for large-scale distribution systems using genetic algorithms. In Innovative smart grid technologies conference, pp. 1–8.
Tinney, W. F., & Hart, C. E. (1967). Power flow solution by Newton’s method. IEEE Transactions on Power Apparatus and Systems, 86, 1449–1460.
Viana, E. M., Oliveira, E. J., Martins, N., Pereira, J. L. R., & Oliveira, L. W. (2013). An optimal power flow function to aid restoration studies of long transmission segments. IEEE Transactions on Power Systems, 28(1), 121–129.
Acknowledgments
The authors thank the “Foundation for Supporting Research in of Minas Gerais” (FAPEMIG), “Coordination for the Improvement of Higher Education Personnel” (CAPES), “Brazilian National Research Council” (CNPq), “Electric Power National Institute” (INERGE) and the “Bio-inspired and Heuristic Optimization” research group of UFJF for supporting this work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Duque, F.G., de Oliveira, L.W. & de Oliveira, E.J. An Approach for Optimal Allocation of Fixed and Switched Capacitor Banks in Distribution Systems Based on the Monkey Search Optimization Method. J Control Autom Electr Syst 27, 212–227 (2016). https://doi.org/10.1007/s40313-015-0225-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40313-015-0225-z











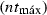 is achieved.
is achieved.