Differential evolution framework for big data optimization

Abstract

During the last two decades, dealing with big data problems has become a major issue for many industries. Although, in recent years, differential evolution has been successful in solving many complex optimization problems, there has been research gaps on using it to solve big data problems. As a real-time big data problem may not be known in advance, determining the appropriate differential evolution operators and parameters to use is a combinatorial optimization problem. Therefore, in this paper, a general differential evolution framework is proposed, in which the most suitable differential evolution algorithm for a problem on hand is adaptively configured. A local search is also employed to increase the exploitation capability of the proposed algorithm. The algorithm is tested on the 2015 big data optimization competition problems (six single objective problems and six multi-objective problems). The results show the superiority of the proposed algorithm to several state-of-the-art algorithms.

1 Introduction

Optimizing big data problems has become a significant research topic for many organizations; for instance, in August 2010, the White House announced that along with healthcare and national security big data is a national challenge and priority. The underlying complexity of big data problems is having to deal with a massive number of decision variables, different mathematical properties of the objective function(s) and/or constraints, and the computational time required for the optimization process.

The concept of big data set/matrix or big database is different from the emerging research topic “big data”. By “big data” we mean data that is too big, too fast, or too hard for existing tools to process [14]. It is also defined using 4Vs—volume, velocity, variety and veracity [38], where volume measures the amount of data that can be captured, communicated, aggregated, stored and analyzed, velocity the speed of data creation, streaming and aggregation, variety the richness of the data representation—text, images video, audio, etc. while veracity suggests that, despite data being available, its quality is a major concern [38]. Big data is assumed to be a ‘big blessing’ but comes with huge challenges. Running optimization algorithms on voluminous data sets using available processors and storage units is difficult and, with the advent of streaming data sources, the optimization process must often be performed in real time, typically without a chance to revisit past entries [25]. The problem areas that can benefit from optimizing big data are found in many industries including, but not limited to healthcare, the public sector (i.e., enabling sophisticated tax agencies to apply automated algorithms to systematically check tax returns and automatically flag those that require further examination or auditing which can reduce the gap in tax revenue by up to 10 % points [16]), cyber security (i.e., providing network managers with the means to process millions of daily attacks and identify the more serious ones), logistics, and the air traffic, retail, manufacturing, and defence sectors [23]. The problem considered in this paper is abstracted from dealing with Electroencephalographic (EEG) signals through independent component analysis (ICA) which to some extend approximate a big optimization problem, as it requires a real-time handling of EEG signals [10, 11, 37].

Evolutionary algorithms (EAs) are population-based stochastic search methods that have demonstrated great success in solving complex optimization problems, of which DE has shown its powerful search capabilities [1, 6–8, 19]. Although DE does not need to satisfy some mathematical properties, such as convexity, continuity and differentiability, of the objective function and constraints of a problem which are required by the deterministic methods [24], as it can flexibly represent knowledge, has innate parallelism behavior and performs better than many other EAs, it is not the best algorithm for all types of problems [6]. It has some basic operators (representation, mutation and crossover) and parameters (population size, mutation rate and crossover rate) but there is a research gap regarding adopting it to solve big data problems. In addition, no single operator and/or control parameter is the best for all types of test problems.

Recently, the adaptation of DE control parameters and search operators has attracted a great deal of interest among the evolutionary computation (EC) community. Based on how a DE algorithm’s control parameters are adapted, it can be classified into one of the following three classes [5]: (1) deterministic approaches—the parameters are changed based on some deterministic rules regardless of any feedback from the algorithm; (2) adaptive approaches—the parameters are dynamically updated based on learning from the evolutionary process; and (3) self-adaptive approaches—the parameters are directly encoded within individuals and undergo recombination . Also, recent studies have been proposed, which used ensemble of DE operators [1, 6–8, 19]. However, such methodologies for optimizing big data problems do not exist [11].

In this paper, an automatic integration of DE variants framework is developed and analyzed considering big data problems, both single and multi-objective. In it, three populations are initially run in parallel for a predefined number of generations (cycle), and during this cycle information regarding the performance of every DE is recorded. After that, an exponential curve is fitted and used to predict the future performance that can be achieved by each DE operator. The one with the best predicted future value is selected to optimize the best set of individuals among all populations. Also, information sharing and local search procedures are adopted. The algorithm is tested on the 2015 big data optimization problems. The objective is to decompose the obtained EEG signals into two parts, where the first part needs to be similar to the original signals to keep useful information, while the other part is used to remove as much artifacts as possible. For the problems considered in this paper, data available represent around 20 KB of data per second if the data is accessed in its binary form and 0.5 MB per second if the data is accessed in its text form. This scale requires solving an optimization problem every second. So the big optimization studied in this paper includes big volume of data and solving the problem quickly by ensuring quality of solutions. However, as the time constraint was not imposed in this version of problems as described in [10], we have demonstrated the problem solving ability for a single period. In practice, the process can be used repeatedly for multiple-period in a continuous time scale. Each optimization problem is based on a number of interdependent time series forming a dataset. The number of time series, together with the length of each time series, defines the number of variables in the problem. Each time series is of length 256; thus, each optimization problem has a multiple of 256 variables. The number of variables considered in this paper are 1024, 3072 and 4864. The solutions obtained are compared with the same several algorithms with the experimental results showing its superiority to all the algorithms considered.

This paper is organized as follows. An overview of DE is provided in Sect. 2. The proposed algorithm is then described in Sect. 3. The description of the problem and the simulation results are given in Sect. 4. Finally, the conclusions and future research directions are elaborated in Sect. 5.

2 Differential evolution

DE is as a powerful global search algorithm for real parameter optimization. DE differs from other EAs mainly in its generation of new vectors by adding the weighted difference vector (DV) between two individuals to a third individual [27]. It performs well when the feasible patches are parallel to the axes. Its main operators are briefly discussed below.

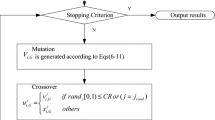
• Mutation: A mutant vector is generated by multiplying an amplification factor, F, by the difference between two random vectors and the result is added to a third random vector (DE/rand/1)

  $$\begin{aligned} \overrightarrow{v}_{z}=\overrightarrow{x}_{r_{1},j}+F. (\overrightarrow{x}_{r_{2},j}-\overrightarrow{x}_{r_{3},j}) \end{aligned}$$

  (1)

  where $r_{1},r_{2},r_{3}$ are different random integer numbers $\in [1,PS]$ and none of them is similar to z and PS the population size. As. the mutation operator has a great effect on the performance of DE, different types have been introduced in the literature, such as DE/best/1 [26], DE/rand-to-best/1 [19] and DE/current-to-best [36].

• Crossover: There are two well-known crossover schemes, exponential and binomial. In the exponential crossover, firstly, an integer index, l, is randomly selected from a range [1, D], where D is the problem dimension. This index acts as an initial position in the target vector from where an exchange of variables with the donor vector begins. An integer index, L, that defines the number of components the donor vector contributes to the target vector, is randomly selected, such that $L\in [1,D]$. Subsequently, a trial vector is calculated as follows:

  $$\begin{aligned} u_{z,j}=\left\{ \begin{array}{ll} v_{z,j} &{} for \ j=\langle l\rangle _{D},\langle l+1\rangle _{D},\ldots ,\langle l+L-1\rangle _{D}\\ x_{z,j} &{} \forall j\in [1,D] \end{array}\right. \end{aligned}$$

  (2)

  where $j=1,2, \ldots ,D$ and $\langle l\rangle _{D}$ denotes a modulo function with a modulus of D and a starting location of l. On the other hand, the binomial crossover is conducted on every variable with a predefined crossover probability, such that:

  $$\begin{aligned} u_{z,j}=\left\{ \begin{array}{l@{\quad }l} v_{z,j} &{} if(rand\le cr\,\text {or}\, j=j_{rand})\\ x_{z,j} &{} otherwise \end{array}\right. \end{aligned}$$

  (3)

  $j_{rand}\in \left\{ 1,2,\ldots ,D\right\}$ is a randomly selected index, which ensures $\overrightarrow{u_{z}}$ gets at least one component from $\overrightarrow{v_{z}}$.

• Selection The selection process is simple, in which an offspring survives to the next generation, if it is better than its parent.

As mentioned earlier, many research studies have been proposed to deal with the fact that no single DE control parameter and/or search operator is the best for all kinds of optimization problems. However, pushing such mechanisms to solve big data problems has not been explored yet. Some of existing DE algorithms are discussed below.

Caraffini et al. [2] proposed a super fit multi-adaptive DE for solving unconstrained problems. In their proposed algorithm, four DE operators with equal probability were used. Then, based on the normalized relative fitness improvement and normalized distance to the best individual, each operator’s probability was updated. Additionally, F and Cr were generated using Cauchy and normal distributions, respectively. Both parameters were then adapted during the evolutionary process. Furthermore, a covariance matrix adaptive evolution strategy was used as a local search.

Elsayed et al. [6] proposed a general framework that divided the population into four sub-populations, each of which used one combination of search operators. During the evolutionary process, the sub-population sizes were adaptively varied based on the success of each operator, which was calculated based on changes in the fitness values, constraint violations and the feasibility ratio. The algorithm performed well on a set of constrained problems. Elsayed et al. [8] also proposed two novel DE variants, each of which utilized the strengths of multiple mutation and crossover operators, to solve constrained problems. The algorithms demonstrated superior performance in comparison with the state-of-the-art algorithms.

Zamuda and Brest [35] introduced an algorithm that employed two mutation strategies in jDE [1], with population size adaptively reduced during the evolutionary process. The algorithm was tested on 22 real-world applications and performed better than two other algorithms.

Tvrdík and Polakova [31] introduced a DE algorithm for solving a set of constrained optimization problems. In it, with a predefined probability $\left( q\right)$, one set of control parameters, from 12 available, was selected and during the evolutionary process, q was updated based on its success rate in previous steps. It was evaluated using a set of unconstrained problems and showed competitive performance [32].

Wang et al. [33] introduced a composite DE algorithm (CoDE), in which at each generation a trial vector was generated by randomly combining three DE variants with three control parameter settings. The algorithm performed well on a set of unconstrained test problems.

In [15], a framework which used a mix of mutation strategies and discrete control parameters within DE was proposed for solving unconstrained problems. In it, a pool of different mutation strategies, along with a pool of values for each control parameter, coexisted during the entire evolutionary process and competed to produce new individuals.

An improved adaptive DE algorithm was introduced [3], in which a mechanism was used to reduce the population size, along with using four mutation strategies with F and Cr were adapted using the Cauchy distribution.

Qiu et al. [22] proposed an adaptive cross-generation DE (ACGDE) for solving multi-objective problems. In it, two new mutation strategies were proposed to enhance both the convergence speed and diversity maintenance. The former was the neighborhood-based cross-generation (NCG) mutation which generated mutant vectors based on the difference between two individuals from consecutive generations, while the later was the population-based cross-generation (PCG), which incorporated the use of the entire set of individuals from two consecutive generations to produce new individuals. Both the NCG and PCG mutation operators were employed in a half-half manner. In addition, a self-adaptive mechanism was used to adapt both F and Cr values. The algorithm implemented into non-dominated sorting genetic algorithm II (NSGA-II) [4] and showed its superiority to many other algorithms.

Guo et al. [12] proposed a mechanism to properly select parents to participate in the mutation and crossover processes. In it, successful solutions were stored in an archive, then parents were selected from the archive when stagnation was occurred. The algorithm was employed with many DE variants and showed its ability to improve their results. In [13], an eigenvector-based crossover operator was proposed. It utilized eigenvectors of covariance matrix of individual solutions to make the crossover rotationally invariant, that is the crossover operator exchanged information between the target and donor vectors in the eigenvector basis instead of the natural basis. The proposed crossover was employed with several algorithms and showed its effectiveness in solving 54 optimization problems.

Tang et al. [30] introduced a DE variant with an individual-dependent mechanism which incorporated an individual-dependent parameter (IDP) setting and an individual-dependent mutation (IDM) strategy. IDP setting ranked individuals based on their fitness values and then their assigned F and Cr were calculated based on each individual’s ranking. In the IDM strategy, four vectors differences mutation were used to generate new offspring. The algorithm was tested on 28 unconstrained problems, with the results demonstrated that it was superior to state-of-the-art algorithms.

3 Automated DE framework

In this section, an automated DE framework (ADEF) is described.

3.1 ADEF

As described earlier, the main goals of the proposed algorithm are (1) extending DE for optimizing big data problems; and (2) developing a DE framework to automatically configure the best set of operators to use, as no single DE operator is the best for solving all types of optimization problems [9, 34].

The main steps of the proposed framework are presented in Algorithm 1. Firstly, $\kappa$ DE variants are considered, where all of them start with the same population of individuals of size PS. Assume the population size of each DE variant is $PS_{1},PS_{2},\ldots ,PS_{\kappa }$, respectively. Subsequently, the solutions of each population are evolved by $\text {DE}{}_{1},\text {DE}{}_{2},\ldots ,\text {DE}{}_{\kappa }$, respectively. At each generation, information about each operator’s performance is recorded to be used in the automatic selection step (Sect. 3.4). Once the best DE variant is determined, an information sharing scheme is adopted, such that

• For single objective problems: all $PS_{i=1:\kappa }$ are combined and sorted based on the fitness values. Then, redundant vectors are removed, while unique vectors are kept in $x_{unique}$. Subsequently, the best PS vectors from $x_{unique}$ are selected.

• For multi-objective problems: all $PS_{i=1:\kappa }$ are combined. Then, the unique vectors are kept in $x_{unique}$. From $x_{unique}$, the non-dominated solutions are determined. Then, the first PS non-dominated solutions are selected. If the number of non-dominated solutions is less than PS, random solution vectors are selected from the remaining set of solutions from ($\overrightarrow{x}_{unique}$) to form the final PS.

Then, a local search procedure is applied to the best individual, in case of a single optimization problem, or a solution from the Pareto frontier, in case of a multi-objective problem. Subsequently, the best DE variant is used to evolve the entire population till the end of the evolutionary process.

3.2 DE variants

In this paper, three DE variants (three mutation operators with the binomial crossover) are considered

• $\text {DE}_{1}$: DE/current-to-rand/1/bin

  $$\begin{aligned} u_{z,j}={\left\{ \begin{array}{ll} x_{z,j}+F_{z}.(x_{r_{1},j}-x_{z,j}+x_{r_{2},j}-x_{r_{3},j})\\ {if(rand\le cr_{z}\,\text {or}\, j=j_{rand})}\\ x_{z,j}\quad {\text {otherwise}} \end{array}\right. } \end{aligned}$$

  (4)

• $\text {DE}_{2}$: DE/current-to-$\phi$best/1/bin

  $$\begin{aligned} u_{z,j}={\left\{ \begin{array}{ll} x_{z,j}+F_{z}.(x_{\phi ,j}-x_{z,j}+x_{r_{1},j}-x_{r_{2},j})\\ {if(rand\le cr_{z}\,\text {or}\, j=j_{rand})}\\ x_{z,j}\quad {\text {otherwise}} \end{array}\right. } \end{aligned}$$

  (5)

• $\text {DE}_{3}$: DE/rand/1/bin

  $$\begin{aligned} u_{z,j}={\left\{ \begin{array}{ll} x_{r_{1},j}+F_{z}.(x_{r_{2},j}-x_{r_{3},j})\\ {if(rand\le cr_{z}\,\text {or}\, j=j_{rand})}\\ x_{z,j}\quad {\text {otherwise}} \end{array}\right. } \end{aligned}$$

  (6)

where $\overrightarrow{x}_{\varphi }$ is a random vector selected from the range $[1,\varphi ]$, $r_{1}\ne r_{2}\ne r_{3}$ are random integer numbers and each one is different from z, while $F_{z}$ and $Cr_{z}$ are self-adaptively updated, as will be shown later.

3.3 Evolving individuals in multi-objective problems

To adapt the algorithm to handle a multi-objective problem, a multi-objective EA based on decomposition (MOEA/D) [20, 21] is considered. The main idea behind MOEA/D is to decompose a multi-objective problem into a number of single objective optimization problems. A Tchebycheff scalarization function is adopted and then ADEF is applied, as described above.

$$\begin{aligned} \text {minimize}\,\quad g(x|\lambda ,f^{*})=\text {maximize}\,\lambda |f_{z}-f_{z}^{*} \end{aligned}$$

Subject to

$$\begin{aligned} x\in \Omega \end{aligned}$$

(7)

where $\overrightarrow{\lambda }=(\lambda _{1},\ldots ,\lambda _{m})$ is a weight vector representing the weights for each of the m objectives to be optimized, such that $\sum _{z=1}^{\lambda }\lambda =1$ and $f^{*}=(f_{1}^{*},\ldots ,f_{m}^{*})$ is a vector representing the ideal objective values for m objectives. MOEA/D utilizes the relations between neighborhood among all sub-problems, optimization of a sub-problem by using the information from its neighboring sub-problems. The main steps of the adapted MOEA/D used in this paper are presented in Algorithm 2.

3.4 Selection of best DE variant

To decide the best DE variant, the following steps are conducted:

• At each iteration (t), and till the algorithm reaches CS generations, information from every DE is recorded, such that

  • For single objective problems: the average fitness value of every $PS_{i=1:\kappa }$ is recorded

    $$\begin{aligned} \text {inf}_{k,t}=\frac{\sum _{z=1}^{PS_{k}}f_{z,t}}{PS_{k}} \end{aligned}$$

    (8)

  • For multi-objective problems: information based on the quality of solutions and number of non-dominated solutions $(num_{nds})$ is recorded

    $$\begin{aligned} \text {inf}_{k,t}=\frac{\sum _{z=1}^{PS_{k}}\sum _{obj=1}^{m}\lambda _{z,obj} f_{z,obj,t}}{PS_{k}}+\left( \frac{1}{num_{nds}}\right) \end{aligned}$$

    (9)

  Note that the smaller the value of inf, the better-performing the DE variant.

• For each DE variant, the exponential curve is fitted, such that

  $$\begin{aligned} y=ae^{bt} \end{aligned}$$

  (10)

• Find a and b; then calculate the predicted values $(\widehat{y})$.

• Calculate the goodness of fit or coefficient of determination to find the likelihood of future events falling within the predicted outcomes as follows:

  $$\begin{aligned} R^{2}=\left( \frac{n\sum y\widehat{y}-\sum x\sum \widehat{y}}{\sqrt{n\sum (y^{2}) -(\sum y})^{2}\sqrt{n\sum (\widehat{y}^{2})-(\sum \widehat{y}})^{2}}\right) ^{2} \end{aligned}$$

  (11)

  where y is the actual values and $\widehat{y}$ is the predicted ones.

• For each DE variant, calculate the expected performance after the subsequent CS generations such that

  $$\begin{aligned} Efv_{i=1:\kappa }=\frac{a_{i}e^{b_{i}\times 2\times CS}}{R_{i}^{2}} \end{aligned}$$

  (12)

  It is very common that the best fitness value, within the population, improves rapidly at the early stages of the evolutionary process, while the improvement rate is too slow at later stages. From the pattern of improvement rate, one can argue that rate is decreasing exponentially, which motivated us to use an exponential function for prediction. However, other patterns can be considered which will be investigated in our future studies.

• Consequently, the one with the minimum expected value is considered the best and is selected to evolve its population till the end of the evolutionary process.

3.5 Adaptation of F and Cr

It is a fact that F and Cr have a great impact on the performance of any DE. In this paper, the mechanism proposed in [29], which is considered as an improvement of JADE [36], is adopted. There are some changes done to improve its performance on the problem on hand.

• A historical memory with H entries for both parameters ($M_{Cr}$, $M_{F}$) is initialized, where all values are set to a value of 0.5.

• Each individual $x_{z}$ is associated with its own $Cr_{z}$ and $F_{z}$, such that

  $$\begin{aligned} Cr_{z}= & {} \text {randni}(M_{Cr,r_{z}},\sigma _{cr}) \end{aligned}$$

  (13)
  $$\begin{aligned} F_{z}= & {} \text {randci}(M_{F,r_{z}},0.1) \end{aligned}$$

  (14)

  where $r_{z}$ is randomly selected from [1, H], and if a value is outside the range of [0,1], it is handled by the technique used in [36], $\text {randni}(\mu ,\sigma )$ and $\text {randci}(\mu ,\sigma )$ are values randomly selected from normal and Cauchy distributions with mean $\mu$ and variance $\sigma$, $\sigma _{cr}$ is set at a value of 0.01, while its original value was 0.1. To add to this, $F_{z}$ is set to be within [0.2–0.8].

• Similar to JADE, at the end of each generation, the $Cr_{z}$ and $F_{z}$ values used by the successful individuals are recorded in $S_{Cr}$ and $S_{F}$ , and then the contents of memory are updated as follows

  $$\begin{aligned} M_{Cr,d,iter}= & {} {\left\{ \begin{array}{ll} \text {mean}_{WA}(S_{Cr}) &{} \quad \text {if}\, S_{Cr}\ne \text {null}\\ M_{Cr,d,iter} &{} \;\;\,\text {otherwise} \end{array}\right. } \end{aligned}$$

  (15)
  $$\begin{aligned} M_{F,d,iter}= & {} {\left\{ \begin{array}{ll} \text {mean}_{WL}(S_{F}) &{} \quad \text {if}\, S_{F}\ne \text {null}\\ M_{F,d,iter} &{} \,\;\;\text {otherwise} \end{array}\right. } \end{aligned}$$

  (16)

  where $1\le d\le H$ is the the position in the memory to be updated. It is initialized to 1, and then incremented whenever a new element is inserted into the history, and if it is greater than H=6, it is set to 1. The weighted mean$(\text {mean}_{WA}(S_{Cr}))$ is computed as:

  $$\begin{aligned} \text {mean}_{WA}(S_{Cr})= & {} \sum _{zd=1}^{S_{cr}}w_{zd}.S_{cr,zd} \end{aligned}$$

  (17)
  $$\begin{aligned} w_{zd}= & {} \frac{{{\Delta }}f_{zd}}{\sum _{zd=1}^{S_{cr}} \Delta f_{zd}} \end{aligned}$$

  (18)

  where $\Delta f_{zd}=|f(u_{zd,iter})-f(x_{zd,iter})|$. The weighted Lehmer mean $(\text {mean}_{WL}(S_{F}))$ is calculated as follows:

  $$\begin{aligned} \text {mean}_{WL}(S_{F})=\frac{\sum _{zd=1}^{S_{F}}w_{zd}.S_{F,zd}^{2}}{\sum _{zd=1}^{S_{F}}w_{zd}.S_{F,zd}} \end{aligned}$$

  (19)

  and $w_{zd}$ is calculated similarly to Eq. 18.

3.6 Local search procedure

In this paper, the interior point method is applied as a local search. “The interior point methods generate one or more interesting search directions at each iteration and effectively combine these directions to ensure that sufficient progress in a suitable convergence function is made” [17]. For constrained problems, interior-point methods (1) starts with adding slack variables to make all inequality constraints into non-negativities; (2) then nonnegativity constraints are replaced with logarithmic barrier terms in the objective function. The idea of the barrier approach is to start from a point in the strict interior of the inequalities and construct a barrier that prevents any variable from reaching a boundary; (3) the equality constraints are incorporated into the objective using Lagrange multipliers; (4) solve the optimality conditions for the barrier problems using Newton’s method.

• For single objective problems, considering the optimization of Eq. 24, the interior point method is applied to the best solution obtained by of the successful DE variant a d for a predefined number of fitness evaluations.

• Similarly, in case of a multi-objective problem, a single solution from the Pareto Front is passed to the interior point to be optimized, bearing in mind the optimization of Eq. 24. The solution obtained is then evaluated based on Eqs. 22 and 23. Subsequently, the ideal reference point is updated, if required.

4 Experimental analysis

In this section, the simulation results obtained by the proposed algorithm are presented and discussed. The algorithm was coded in Matlab R2012b¹ and run on a PC with a 3.4 GHz Core I7 processor with 16 GB RAM, and Windows 7.

4.1 Problem description

The series of problems used in this paper are both single objective and multi-objective nonlinear optimization problems [10, 11]. Each optimization problem is based on a number of interdependent time series forming a dataset. The number of time series together with the length of each time series define the number of variables in the problem. For this dataset, each time series is of length 256, where the number of times series are 4, 12 and 19, hence there are 1024, 3072 and 4864 variables, respectively.

Table 1 Computational results of ADEF, DECC-DG, JADE, SHADE and NSGA-II for single objective problems

Table 2 Scores of proposed algorithm, in reference to baseline algorithm, for single objective problems

Table 3 Scores of proposed algorithm, in reference to baseline algorithm, for multi-objective problems

Assume that a matrix X is of dimension $N\times M$, where N is the number of inter-dependent time series and M is the length of each time series. Let S be a matrix of $N\times M$, with N independent time series of length M, such that, given A, an $N\times N$ linear transformation matrix

$$\begin{aligned} X=A.S \end{aligned}$$

(20)

The problem is to decompose S into two matrices: $S_{1}$ and $S_{2}$ with the same dimensionality of S, that is $S=S_{1}+S_{2}$ and $X=A.S_{1}+A.S_{2}$. Let C be the Pearson correlation coefficient between $S_{1}$ and X

$$\begin{aligned} \frac{cov(X,A.S_{1})}{\sigma (X).\sigma (A.S_{1})} \end{aligned}$$

(21)

where, cov(.) and $\sigma (.)$ are the covariance matrix and the variance, respectively. The objective is to maximize the diagonal elements of C, while minimizing off-diagonal elements to zeros. At the same time, the distance between S and $S_{1}$ should be as minimum as possible, that is $S_{1}$ needs to be similar as possible as S.

Fig. 1

Pareto frontier obtained by ADEF for D4 (first row) and D4N (second row) (figures presented in second column are for five solutions sampled uniformly from Pareto set and corresponding nearest solutions found by baseline algorithm)

Fig. 2

Pareto frontier obtained by ADEF for D12 (first row) and D12N (second row) (figures presented in second column are for five solutions sampled uniformly from Pareto set and corresponding nearest solutions found by baseline algorithm)

Fig. 3

Pareto frontier obtained by ADEF for D19 (first row) and D19N (second row) (figures presented in second column are for five solutions sampled uniformly from Pareto set and corresponding nearest solutions found by baseline algorithm)

This definition generates two formulations for the problem, one as a single objective, while the other as a multi-objective problem.

• A multi-objective optimization problem is defined as follows: Given, X, A, and S, find $S_{1}$ which optimizes the following two functions:

  $$\begin{aligned} \text {Minimize}\,\,\, f_{1}= & {} \frac{1}{(N\text {.}M)}\sum _{ij}(S_{ij}-S_{1,ij})^{2} \end{aligned}$$

  (22)
  $$\begin{aligned} \text {Minimize}\,\,\, f_{2}= & {} \frac{1}{(N^{2}-N)}\sum _{i,j\ne i}(C_{ij}^{2}) +\frac{1}{N}\sum _{i}(1-C_{ii})^{2}\nonumber \\ \end{aligned}$$

  (23)

• The single objective formulation is defined as follows:

  $$\begin{aligned}&\text {Minimize}\,\,\, f_{1}+f_{2}\nonumber \\&\text {Subject to }-8\le S_{1}\le 8 \end{aligned}$$

  (24)

4.2 Parameter settings

$\varphi$ was randomly selected within the range $[1,10~\%PS]$ and $[1,50~\%PS]$ for single and multi-objective problems, respectively. The reason for increasing this range was to maintain diversity. The maximum number of generations ($t_{max}$) was set to a value of 300, 400 and 500 iterations, for problems with 1024, 3072 and 4864 variables, respectively, and each value was increased by 100 generations for multi-objective problems. CS was equal to 25 iterations. An extra parameter of MOEA/D was the neighborhood size which was set to a value of $\frac{PS}{5}$. Lastly, 30 runs/seeds were conducted.

4.3 Results and comparison with state-of-the-art algorithms

The results obtained are discussed in this subsection and compared several algorithms from the literature.

4.3.1 Single objective problems

In this subsection, ADEF is compared with the following algorithms:

• 1. A baseline algorithm which is based on NSGA-II. As we solve single objective problem, NSGA-II was used as it is, while zeroing the second objective, as suggested by [10, 11].

• 2. A cooperative co-evolution DE with differential grouping algorithm (DECC-DG) [18], which used an automatic decomposition strategy to uncover the underlying interaction structure of the decision variables. All the parameters were set as mentioned in the published paper.

• 3. An adaptive DE algorithm with external archive (JADE) [36], where PS was set to a value of 100.

• 4. Success-history based adaptive DE (SHADE) [28], which is an improved version of JADE.

Firstly, as described in [10], the overall best solution found over 30 runs was considered as a measure of quality. Also, the stability of the algorithm was assessed using the variance of the set of best solutions found over 30 runs. The detailed results [best, average and standard deviation (Std.)] are shown in Table 1. From these results, it is clear that the proposed algorithm was much better than the other algorithms. Additionally, the standard deviation results obtained revealed that the proposed algorithm was stable.

Furthermore, the score of the proposed algorithm, in reference to the baseline algorithm, for each test function was calculated based on the procedure provided in [10]

$$\begin{aligned} score={\left\{ \begin{array}{ll} bfv_{bl}-bfv &{}\quad {\text {if }bfv<bfv_{bl}}\\ -1000(bfv_{bl}-bfv) &{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(25)

where bfv and $bfv_{bl}$ are the best fitness values obtained by any variant and the baseline algorithm, respectively.

Based on the results shown in Table 2, it is clear that the proposed algorithm was the best.

4.3.2 Multi-objective problems

To measure the quality of the proposed algorithm, five solutions were sampled uniformly from the Pareto set, including the two extreme solutions. The average distance between those five solutions and corresponding nearest solutions found in the baseline algorithm (NSGA-II, as reported in [10]) were recorded. Only those solutions found by the proposed algorithm that dominated the corresponding solution in the baseline were considered. For those solutions found which were dominated by the corresponding solutions in the baseline, a fixed distance value of $-1000$ was used. Larger distance values mean the algorithm was better. For problems with noise, the evaluation was done using the data without noise [10]. The detailed results are recorded in Table 3, which revealed that the proposed algorithm was far better than the baseline algorithm.

To give more information about the algorithm performance, the Pareto frontiers obtained, of a random seed/run, for every problem is presented in Figs. 1, 2 and 3. From these figures, it is clear that the algorithm was better.

ADEF was also compared with MOEA/D based on DE (MOEA/D-DE) [20, 21], where DE/rand/1 was employed with F and Cr were set to a value of 0.5 and the other parameters set as discussed in Sect. 4.2. Both algorithms were compared in reference to the baseline algorithm and the algorithm with a higher average score was considered the best. The results shown in Table 4 clearly reveal that ADEF was better than MOEA/D-DE. Furthermore, the Pareto frontiers obtained by both methods are depicted in Figure 4 (x-axis and y-axis are in log scales), demonstrating that solutions obtained by ADEF dominated those of MOEA/D-DE.

4.4 Parameters analysis

In this subsection, CS and $t_{max}$ are analyzed.

4.4.1 CS

Here, effects of CS on the selection of the most suitable DE, as described in Sect. 3.4, as well as the final results obtained, are analyzed. To do this, the algorithm was run with different values of CS, i.e., $CS=10$, 25 (default), and 50 generations. All other parameters were set as those described in Sect. 4.2.

Table 4 Average scores of ADEF and MOEA/D-DE for multi-objective problems

Fig. 4

Pareto frontiers obtained by ADEF and MOEA/D-D (x-axis and y-axis in log scales)

For single objective problems, considering the computational results obtained, as presented in Table 5, it was found that all variants were better than the baseline algorithm. Among them, ADEF with $CS=25$ was the best for $\text {D12}$ and $\text {D12N}$, while using $CS=50$ was the best for $\text {D19}$ and $\text {D19N}$, and no significant differences were found in solving problems with 1024 variables. For multi-objective problems, there were no significant differences in scores. The Pareto front plots are depicted in Fig. 5. From this figure, it can be concluded that when $CS=25$ the Pareto front was evenly distributed along the two objectives for D4 and $\text {D12}$, while setting CS to a value of 50 was better for $\text {D19}$ and $\text {D19N}$.

Table 5 Computational results of ADEF, using different values of CS, for single objective problems

Fig. 5

Pareto frontier for D4, D12, D19 and D19N with different values of CS

It was also interesting to know why the results changed when using different CS values. One reason for this issue was the selection of the best DE variant. In other words, a bigger CS value meant more information was captured about each DE variant, which could help fitting the exponential curve well and hence the most preferred DE was properly selected. The results are presented in Table 6. Based on this analysis, for single objective problems, it was noticed that $\text {DE}_{3}$ was not preferred for any test problem with all CS values. For a small value of CS, $\text {DE}_{2}$ was more frequently preferred followed by $\text {DE}_{1}$. However, when CS value was increased, $\text {DE}_{1}$ became first. For the multi-objective problems, it was noticed that $\text {DE}_{3}$ was selected more times than $\text {DE}_{2}$ when $CS=10$, but $\text {DE}_{2}$ was considered better than $\text {DE}_{1}$ when CS was increased. However, it was noticed that $\text {DE}_{1}$ was the most preferred algorithm for the majority of test problems.

It was also good to show the running time, consumed by ADEF with different values of CS. Table 7 summarizes the results obtained regarding this issue. Note that the code has been written in Matlab, hence the computational time could be further reduced if the code was written in C++. From Table 7, ADEF with $CS=10$ was faster than the other variants. For the multi-objective problems, the computational time was increased, in comparison with those of single objective problems. However, the results had a similar pattern to that for single objective problems.

Table 6 Number of times a DE algorithm considered the best out of 30 runs for each test problem

Table 7 Computational time, in seconds, of ADEF with different values of CS for single and multi-objective problems

4.4.2 $t_{max}$ analysis

From the previous subsection, CS was set to a value of 25 for problems with 1024 and 3072 variables, while it was 50 for 4864 variables. Subsequently, ADEF was run with different values of $t_{max}$ as presented in Table 8.

In regards to single objective problems, the best and average results are shown in Table 9. From the results obtained, it was found that in all cases the results were better than those of the baseline algorithm. Among the 3 cases, it was found that the results of case 1 were inferior to those of case 2 and case 3. Also, the results of case 3 were slightly better than those of case 2. However, using a higher number of iterations meant more computational effort.

Considering the multi-objective problems, the final sets of non-dominated solutions for $\text {D4}$, $\text {D12}$, $\text {D19}$ and $\text {D19N}$ are plotted in Fig. 6. From these plots, in general, case 2 and case 3 are better than case 1, and no much difference in the algorithm’s performance between case 1 and case 2 for solving $\text {D4}$ and $\text {D12}$. However, increasing the number of generations lead to better performance in solving $\text {D19}$ and $\text {D19N}$, but this came with the curse of computational time required.

Table 8 Different values of $t_{max}$

Table 9 Computational results of ADEF for single objective problems using different values of $t_{max}$

Fig. 6

Pareto frontier of ADEF for $\text {D4}$, $\text {D12}$, $\text {D19}$ and $\text {D19N}$ with different values of $t_{max}$

Table 10 shows the computational time of ADEF with different values of $t_{max}$, which logically revealed that ADEF based on case 1 had the smallest computational time.

4.5 Improved ADEF and discussion

From Sect. 4.4.1, it was clear that $\text {DE}_{3}$ was not preferred in solving single objective problems. However, this was not the case in solving multi-objective problems. In addition, it was noted that $\text {DE}_{1}$ was not good enough during the exploitation stage (later stages of the optimization process) compared with $\text {DE}_{2}$, as shown in Fig. 7.

Therefore, for single objective problems, two changes were undertaken: (1) $\text {DE}_{3}$ was replaced with DE/current-to-$\phi$best/1/bin with an archive [36] ($\text {DE}_{4}$), where the archive size was set to a value of 1.4PS. Note that $\text {DE}_{2}$ did not use such an archive; (2) In case that $\text {DE}_{1}$ was selected (as described in Sect. 3.4) and during the exploitation stage (here it is defined as the second half of the optimization process), it was replaced with DE/current-to-$\phi$best/1/bin with an archive. This variant was run with and without using a local search, and named IADEF and IADEF-NLS, respectively. The stopping criterion was similar case 2, with CS was 25 for problems with 1024 and 3072 variables and 50 for 4864 variables, as mentioned in Sect. 4.4.2.

For a fair comparison, ADEF was also run with and without using a local search (ADEF-NLS). The experimental results of all the variants and state-of-the-art algorithms are shown in Table 11. From these results, it is clear that IADEF was superior to all other algorithms. In addition, IADEF-NLS was better than ADEF-NLS as well as all the other algorithms. Furthermore, it was clear that IADEF and ADEF with and without using a local search were better than $\text {DE}_{1}$, $\text {DE}_{2}$, $\text {DE}_{3}$ and $\text {DE}_{4}$.

It is also important to mention that we have taken the prediction accuracy into consideration to properly select the better-performing DE variant, as described by Eqs. 11 and 12, in which the predicted value, which could be achieved by each DE, was penalized, if the prediction accuracy was low. To add to this, we calculated the average prediction rate for $\text {DE}_{1}$, $\text {DE}_{2}$ and $\text {DE}_{4}$ and found that the prediction rates were high, as depicted in Fig. 8. Also, it was noted that the function used for prediction had a great effect of the prediction accuracy. As an example, a linear function was considered for prediction, with its prediction accuracy was lower than that of the exponential function, as demonstrated in Fig. 8.

Table 10 Computational time, in seconds, of ADEF with different values of CS for single objective problems

Generally speaking, it was noticed that for better results and convergence patterns, it was better to (1) apply a powerful local search; (2) properly select the right set of operators. Here, it was useful to avoid using DE/rand/1/bin for single objective problems; (3) design or use a powerful mechanism for adapting the control parameters; (4) carefully design a framework that combines all of these components together.

Fig. 7

Convergence of $\text {DE}_{1}$, $\text {DE}_{2}$ and $\text {DE}_{3}$ for $\text {D4}$ (y-axis in log scale)

Table 11 Computational results of IADEF, IADEF-NL, ADEF, ADEF-NLS, DECC-DG, JADE, SHADE, $\text {DE}_{1},$ $\text {DE}_{2}$, $\text {DE}_{3}$ and $\text {DE}_{4}$ for single objective problems

5 Conclusions and future work

In this paper, a differential evolution framework was proposed for optimizing the big data 2015 benchmark problems with both single and multi-objective problems. In the proposed algorithm, three differential evolution variants were run in parallel, each of which used to evolve its own population of individuals. After a predefined number of generations, exponential curve was fitted to predict the future performance of each variant. The one with the best predicted value was considered the winner. At the same time, an information sharing scheme was adopted as well as a local search procedure. Subsequently, the best differential evolution was continued to evolve the new set of individuals till the end of the optimization process.

The test functions used contained 1024, 3072 and 4864 variables. Based on the results obtained, the algorithm was found better than a baseline algorithm, for single and multi-objective problems. The algorithm was also compared with state-of-the-art algorithms as well as each independent DE variant used in the proposed framework. The results showed the superiority of the proposed algorithm. In addition, some parameters were analyzed which improved the algorithm’s performance. Also, it was noted that the proper selection of operators, control parameters and local search procedure had great effects on the algorithm’s performance.

Fig. 8

Prediction accuracy of $\text {DE}_{1}$, $\text {DE}_{2}$ and $\text {DE}_{4}$ using exponential and linear functions

For future work, we intend to use feature reduction mechanisms to reduce the complexity of problems and computational time.