1 Introduction

Constrained optimization is an attractive research area in the computer science and the operation research domains, as there are a considerable number of real-world decision processes that require the solving of Constrained Optimization Problems (COPs). In COPs, the purpose is to determine the values for all of the decision variables by optimizing the objective function, while satisfying all the functional constraints and variable bounds. Formally, COP is stated as follows:

(1)

where \(\vec{X}=[x_{0}, x_{1},\ldots, x_{D}]^{T}\) is a vector with D-decision variables, \(f(\vec{X})\) is the objective function, \(g_{k}(\vec{X})\) is the kth inequality constraints, \(h_{e}(\vec{X})\) is the eth equality constraint, and where each x j has a lower limit L j and an upper limit U j .

The benefit of optimization approaches in solving practical problems can be demonstrated by using few examples. The optimization of a water management problem in South Africa has led to a 62 % reduction in the total pipe cost [1], the optimization of the Norwegian natural gas production and transport accumulated a saving of $2.0 billion in the period 1995–2008 [2], and the expected saving to optimize the US army stationing for a given set of units is $7.6 billion for 20 years [3].

Evolutionary algorithms (EAs) have a long history of successfully solving COPs. The Evolutionary algorithms (EAs) family contains a wide range of algorithms that have been used to solve COPs, such as the genetic algorithm (GA) [4], particle swarm optimization (PSO) [5], differential evolution (DE) [6, 7], evolutionary strategies (ES) [8], and evolutionary programming [9]. In this research, DE is considered for solving COPs. DE is known as an efficient EA. Due to the variability of the characteristics, and the underlying mathematical properties of problems, most EAs use specialized search operators that suit the problems on hand. Such an algorithm, even if it works well for one problem, or a class of problems, does not guarantee that it will work for another class, or range, of problems. This behavior is consistent with the no free lunch (NFL) theorem [10]. In other words, we can state that there is no single algorithm, or an algorithm with a known search operator, that will consistently perform for all classes of optimization problems. This motivates us to consider multiple strategies in DE for a better coverage of problems.

In this research, two novel self-adaptive DE algorithms that incorporate a heuristic mixing of operators (DE/HMO) are proposed. Both variants split the population into sub-populations in order to apply different evolutionary operators on each of them. In addition, to speed up the convergence pattern of the proposed algorithms, a local search procedure is applied to one random individual. To show the benefit of the local search, both variants have been run with and without the local search. The algorithms were tested by solving 60 test problems [11, 12]. They showed consistently better performance as compared to the state of the art algorithms.

This paper is organized as follows. After the introduction, Sect. 2 presents the DE algorithm with an overview of its parameters, ensemble DE and hybrid DE with local search. Section 3 describes the design of the proposed adaptive DE variants. The experimental results and the analysis of those results are presented in Sect. 4. Finally, the conclusions and future work are given in Sect. 5.

2 DE search operators

DE is known as a powerful algorithm for continuous optimization. DE usually converges fast, incorporates a relatively simple and self-adapting mutation and the same settings can be used for many different problems [6].

The remainder of this section discusses the commonly used DE operators. Some of these are later used as a basis for the operators chosen for the DE/HMO variants.

2.1 Mutation

The simplest form of this operation is that a mutant vector is generated by multiplying the amplification factor F by the difference of two random vectors, and the result is added to another third random vector as is shown in the following equation:

$$ \vec{V}_{z,t}= \vec{x}_{r_{1},t}+F. ( \vec{x}_{r_{2},t}-\vec{x}_{r_{3},t} ) $$
(2)

where r 1, r 2, r 3 are random numbers {1,2,…,PS}, r 1≠r 2≠r 3≠z, x is a decision vector, PS is the population size, the scaling factor F is a positive control parameter for scaling the difference vector, and t is the current generation. This variant is also known as: DE/rand/1 [13].

This operation enables DE to explore the search space and maintain diversity. There are many strategies for mutation, such as: DE/best/1 [13], DE/rand-to-best/1 [14], rand/2/dir [7], DE/current-to-rand/1 [15] and DE/current-to-best/1 [16]. For more details, readers are referred to [17].

2.2 Crossover

The DE family of algorithms uses two crossover schemes: exponential and binomial crossover. These crossovers are briefly discussed below.

In exponential crossover, we first choose an integer i randomly within the range [1,D]. This integer acts as a starting point in the target vector, from where the crossover or exchange of components with the donor vector starts. An integer L is chosen from the interval [1,D]. L denotes the number of components that the donor vector actually contributes to the target. After the generation of i and L, the trial vector (u z,j,t ) is obtained as:

$$ u_{z,j,t}= \left \{\begin{array}{l@{\quad }l} v_{z,j,t} & \mbox{for}\ j=\langle l\rangle_{D},\langle l+1\rangle_{D},\ldots,\langle l+L-1\rangle_{D},\\ x_{z,j,t} & \mbox{for\ all other}\ j\in [1,D]\end{array} \right . $$
(3)

where j=1,2,…,D, and the angular brackets 〈l〉 D denote a modulo function with modulus D, with a starting index l, x z,j,t is the parent vector while v z,j,t is the mutant vector.

The binomial crossover is performed on each of the jth variables whenever a randomly picked number (between 0 and 1) is less than or equal to a crossover rate (Cr). The generation number is indicated here by t. In this case, the number of parameters inherited from the donor has a (nearly) binomial distribution:

$$ u_{zj,t}=\left \{\begin{array}{l@{\quad }l} v_{zj,t}, & \mbox{if}\ (\mathit{rand}\leq \mathit{Cr}\ \mbox{or}\ j = j_{rand})\\ x_{zj,t}, & \mbox{otherwise}\end{array} \right . $$
(4)

where rand is a random number within in [0,1], and j rand ∈[1,2,…,D] is a randomly chosen index, which ensures \(\vec{U}_{z,t}\) gets at least one component from \(\vec{V}_{z,t}\).

DE has shown excellent performance for those problems with separable functions. However, DE can efficiently perform on a non-separable problem, if it must not exhibit an extreme dependency on the principle coordinate axes. Furthermore, DE can be rotationally invariant if the new generated individuals are irrespective of the orientation of the fitness landscape [15, 18]. From the literature, it is known that DE/current to-rand/1 is rotationally invariant [16].

In our work, we have considered this issue, i.e. DE/rand/3 has been used that does have ability to visit more random individuals. As will be seen later, the algorithm has the ability to consistently solve non-separable, as well as rotated problems.

2.3 A brief review and analysis

In this section, a review of DE parameters analysis, multi-strategy DE and memetic DE are presented.

In DE, there is no single fixed value for each parameter (F, Cr and PS) that will be able to solve all types of problems with a reasonable quality of solution. Many studies have been conducted on parameter selection. Storn and Price [6] recommended a population size of 5–20 times the dimensionality of the problem, and that a good initial choice of F could be 0.5. Abbass [19] proposed self-adaptive operator (crossover and mutation) for multi-objective optimization problems, where the scaling factor F is generated using a Gaussian distribution N(0, 1). Ronkkonen et al. [20] claimed that typically 0.4<F<0.95 with F=0.9 is a good first choice, and that Cr typically lies in (0,0.2) when the function is separable, while in (0.9,1) when the function’s parameters are dependent. Qin et al. [14] proposed SaDE, where the choice of learning strategy and the two control parameters F and Cr are not required being pre-specified. During evolution, the learning strategy and parameter settings are gradually self-adapted according to the learning experience. Brest et al. [21] proposed a self-adaptation scheme for the DE control parameters, known as jDE. The control parameters that have been adjusted by means of evolution were F and Cr. In jDE, a set of F and Cr values was assigned to each individual in the population, augmenting the dimensions of each vector. For more details, readers are referred to Das and Suganthan [17].

The idea of multiple strategies DE has been emerged few years ago; some of them are mentioned here. Qin et al. [14] proposed the Self-adaptive Differential Evolution algorithm (SaDE). They have used two mutation strategies (while we are using four), where each individual is assigned to one of them based on a given probability. After evaluation of all newly generated trial vectors, the numbers of trial vectors successfully entering the next generation are recorded as ns1 and ns2. Those two numbers were accumulated within a specified number of generations, called the “learning period”. Then, the probability of assigning each individual was updated. Beside this, their learning strategy is entirely different from ours, in which in their algorithm, a strategy may be totally excluded from the list if its p is equal to 0. Mallipeddi et al. [22] proposed an ensemble of mutation strategies and control parameters with DE (EPSDE) for solving unconstrained optimization problems. In EPSDE, a pool of distinct mutation strategies, along with a pool of values for each control parameter, coexists throughout the evolution process and competes to produce offspring. Mallipeddi et al. [23] also proposed an algorithm that uses an ensemble of different constraint handling techniques for solving constrained problems. The proposed algorithm has shown a good performance in comparison to other algorithms. Tasgetiren et al. [24] proposed an ensemble DE, in such a way that each individual was assigned to one of two distinct mutation strategies or a variable parameter search (VPS). VPS was used to enhance the local exploitation capability. However, no adaptive strategy was used in that algorithm. Tasgetiren et al. [25] proposed a discrete DE algorithm with mix of parameter values and crossover operators to solve a travelling salesman problem, in which parallel populations were considered. Each parameter set and crossover operator was assigned to one of the parallel populations. Furthermore, each parallel parent population competes with the same population’s offspring and the offspring populations generated by all other parallel populations. The algorithm has shown improved results in comparison to other state-of-the-art-algorithms. However, the proposed algorithm was computationally at least twice more expensive than other algorithms considered in the paper. Elsayed et al. [26] proposed a mix of four different mutation strategies within a single algorithm framework to solve constrained optimization problems. In the framework, each combination of search operators (a mutation strategy with a crossover operator) has its own subpopulation and the subpopulation size varies adaptively, as the evolution progresses, depending on the reproductive success of the search operators. However, the sum of the size of all of the sub-populations was fixed during the entire evolutionary process. In implementing the adaptive approach, they proposed a measure for reproductive success, based on fitness values and constraint violations. While running their algorithm, an operator may perform very well at an earlier stage of the evolution process and do badly at a later stage or vice-versa. To consider this fact, to effectively design their algorithm, they set a lower bound on the subpopulation size. The algorithm is known as Self Adaptive Multi Operators Differential Evolution (SAMODE). SAMODE has been tested by solving a set of small scale theoretical benchmark constrained problems.

Memetic differential evolution has appeared in the literature over the last few years, but with very limited analysis. Gao and Wang [27] introduced memetic differential evolution modified by initialization and local searching, in which the stochastic properties of a chaotic system were used to spread the individuals in search spaces as much as possible, the simplex (Nelder-Mead method) search method was employed to speed up the local exploitation and the DE operators helped the algorithm to jump to a better point. The algorithm has been tested on 13 high dimensional continuous problems with improved results. Tirronen et al. [28] proposed a hybridization of a DE framework with the Hooke-Jeeves Algorithm (HJA) and a Stochastic Local Searcher (SLS). Its local search mechanisms are coordinated by means of a novel adaptive rule which estimates the fitness diversity among the individuals of a population. Caponio et al. [29] proposed a fast adaptive memetic algorithm (FAMA) that uses DE with a dynamic parameter setting and two local search mechanisms that are adaptively launched, either one by one or simultaneously, according to the needs of the evolution. The employed local search methods are: the Hooke-Jeeves method and the Nelder-Mead simplex. The Hooke-Jeeves method is executed only on the elite individual while the Nelder-Mead simplex is carried out on 11 randomly selected individuals. This algorithm has been compared to another well-known algorithm, and obtained better results for the problem of permanent magnet synchronous motors. Caponio et al. [30] proposed the super-fit memetic differential evolution algorithm, which is a DE framework hybridized with three meta-heuristics, each having different roles and features. Particle Swarm Optimization assists the DE in the beginning of the optimization process by helping to generate a super-fit individual. The two other meta-heuristics are local search mechanisms adaptively coordinated by means of an index measuring the quality of the super-fit individual with respect to the rest of the population. The choice of the local search mechanisms and its application is then executed by means of a probabilistic scheme which makes use of a generalized beta distribution.

3 Self-adaptive differential evolution incorporating a heuristic mixing of operators

In this section, the proposed algorithms are presented, followed by the improvement scheme and the constraint handling technique that we use in this research.

3.1 DE/HMO/1

In the evolution process, for a given problem, the relative performance of the search operators may vary with the progression of generations. This means that one mutation or crossover may work well in the early stages of the search process and may perform poorly at the later stages, or vice-versa. So, it is inappropriate to give equal emphasis on all the operators throughout the entire evolution process when multiple search operators are used. To give a higher emphasis on the better performing operators, it is proposed here to change the subpopulation sizes, through dynamic adaptation, based on the relative performances of the operators. So, DE/HMO/1 starts with a random initial population, using the following equation:

$$ x_{z,j}= L_{j}+ \mathit{rand} \times(U_{j}- L_{j}). $$
(5)

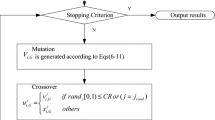
The population is then divided into four subpopulations of equal size. Each subpopulation evolves with its own mutation to generate new decision vectors. Each subpopulation is then divided into two groups of individuals. Each group uses a different crossover to modify the mutated individuals that are evaluated according to their fitness function value and/or the constraint violation of the problem under consideration. An improvement index for each subpopulation is calculated using the method as discussed below. Based on the improvement index, the subpopulation’s size and crossover group’s size are either increased or decreased or kept unchanged. As this process may abandon certain operators which may be useful at later stages of the evolution process, a minimum subpopulation size/group size of each operator is set. To speed up the convergence and to prevent the algorithm from being stuck in a local minimum due to the exponential crossover, especially in high dimensional problems [7], a random individual is selected from the whole population and a local search technique is applied to it with a given maximum number of fitness evaluations \(\mathit{FEs}_{LS}^{max}\). In the local search, a variable of the selected vector is selected randomly, and then a random Gaussian number, as a step size, is added and subtracted to decide the desired direction, according to the fitness function. If the step is successful at finding an improved point, then the value is updated. This process continues until all the variables are selected, or the maximum fitness evaluations for the local search procedure are reached. Also, after every few generations (indicated as window size—WS), the best solutions among the subpopulations are exchanged, and if an exchanged individual is redundant, then it will be replaced by a random vector. The algorithm continues until the stopping criterion is met. The basic steps of DE/HMO/1 are presented in Table 1.

Table 1 The Main steps for DE/HMO/1 algorithm
Full size table

3.2 DE/HMO/2

In DE/HMO/2 a random initial population is divided into four subpopulations of equal size. Each subpopulation evolves with its own mutation and generates new decision vectors. Also, based on the improvement index, the subpopulation’s sizes are either increased or decreased or kept unchanged, in the next generation. Then, these sub-populations are merged together to form a new single population. The new population is divided randomly into two groups of equal size, in which each group uses a different crossover to modify the mutated individuals. Like DE/HMO/1, DE/HMO/2 also sets the minimum sizes for sub-populations and groups, uses a local search, exchanges elite individuals between sub-populations at a regular interval, and replaces redundant individuals with a randomly generated vector. The basic steps of DE/HMO/1 are presented in Table 2.

Table 2 The Main steps for DE/HMO/2 algorithm
Full size table

3.3 Improvement measure

To measure the improvement of each combination in a given generation, we consider both the feasibility status and the fitness value, where the consideration of any improvement in feasibility is always better than any improvement in the infeasibility. For constrained problems, for any generation t>1, there arises one of three scenarios. These scenarios, in order from least desirable, to most desirable, are discussed below.

  • Infeasible to infeasible: For any combination i, the best solution was infeasible at generation t−1, and is still infeasible in generation t, then the improvement index is calculated as follows:

    $$ \mathit{VI}_{i,t} = \frac{\vert V_{i,t}^{best}-V_{i,t-1}^{best}\vert }{\mathit{avg}.V_{i,t}}= I_{i,t} $$
    (6)

    where \(V_{i,t}^{best}\) is constraint violation of the best individual at generation t, avg.V i,t is the average violation. Hence VI i,t =I i,t above represents a relative improvement as compared to the average violation in the current generation. As we are using the ε-constraint handling technique, we may accept a new individual that has a larger violation than its donor, if both of them are infeasible and their violations are less than ε value, in this case we set VI i,t =0 in this case.

  • Feasible to feasible: For any combination i, the best solution was feasible at generation t−1, and was still feasible in generation t, then the improvement index is:

    $$ I_{i,t}=\max_{i}(\mathit{VI}_{i,t})+ \bigl\vert F_{i,t}^{best}-F_{i,t-1}^{best} \bigr\vert \times \mathit{FR}_{i,t} $$
    (7)

    where I i,t is the improvement for combination i at generation t, \(F_{i,t}^{best}\) is the objective function for the best individual at generation t, the feasibility ratio of operator i at generation t:

    $$ \mathit{FR}_{i,t}=\frac{\mathit{Number\ of\ feasible\ solutions}}{\mathit{combination\ size\ at\ iteration}\ t}. $$
    (8)

    To assign a higher index value to the subpopulation with a higher feasibility ratio, we multiply the improvement in fitness value by the feasibility ratio. To differentiate between the improvement index of feasible and infeasible subpopulations, we add a term max i (VI i,t ) in Eq. (7). If all the best solutions are feasible, then max i (VI i,t ) will be zero.

  • Infeasible to feasible: For any combination i, the best solution was infeasible at generation t−1, and it is feasible in generation t, then the improvement index is:

    $$ I_{i,t}=\max_{i} (\mathit{VI}_{i,t})+ \bigl\vert V_{i,t-1}^{best}+F_{i,t}^{best}-F_{i,t-1}^{bv} \bigr\vert \times \mathit{FR}_{i,t} $$
    (9)

    where \(F_{i,t-1}^{bv}\) = fitness value of the least violated individual in generation t−1.

To assign a higher index value to an individual that changes from infeasible to feasible, we add \(V_{i,t-1}^{best}\) with the change of fitness value in Eq. (9). We also keep the first term as in Eq. (7).

After calculating the improvement index for each subpopulation, the subpopulation sizes are calculated according to the following equation:

$$ n_{i,t}=\mathit{MSS}+\frac{I_{i,t}}{\sum_{i=1}^{Nopt}I_{i,t}}\times (\mathit{PS} - \mathit{MSS}\times \mathit{Nopt}) $$
(10)

where, n i,t is the subpopulation size for the ith operator at generation t, MSS is the minimum subpopulation size for each operator i at generation t, PS is the population size, Nopt = number of operators

$$ \mathit{np}_{i,t}=\mathit{MSSC}+\frac{I_{i,t}}{\sum_{i=1}^{NC}I_{i,t}} \times(n_{i,t}-\mathit{MSSC} \times \mathit{NC}) $$
(11)

where MSSC is the minimum subpopulation size for each crossover operator, NC is the number of crossover operators, and n i,t is the subpopulation size. Note that previous equation is used only in DE/HMO/1.

3.4 Constraint handling

In this paper, we consider the selection of the individuals for the purposes of a tournament (Deb et al., 2000) as follows: (i) between two feasible solutions, the fittest one (according to fitness function) is better, (ii) a feasible solution is always better than an infeasible one, (iii) between two infeasible solutions, the one having the smaller sum constraint violation is preferred. The equality constraints are also transformed to inequalities of the form, where ε is a small value.

$$ \bigl\vert h_{e} (\vec{x} ) \bigr\vert -\varepsilon\leq 0,\quad \mbox{for}\ e=1,\ldots,E. $$
(12)

Although this rule is widely used for constraint handling which is implemented during the selection process and it has no influence on the search operator once the selection is done. In our algorithm, in addition to the basic rule applied in the selection process, a self-adaptive parameters selection mechanism is derived based on the feasibility status as well as the quality of fitness. These parameters influence the search operator in guiding the search in an effective manner.

3.5 Mutations operators, F and Cr parameters

As of the literature, the DE variants “rand/ */ *” perform better, because it finds the new search directions randomly [7]. The investigation, by Chuan-Kang and Chih-Hui [31], confirmed the benefit of using more than one difference vector (DV) in DE. Interestingly, two or three DV are good enough, but more than this may lead to premature convergence.

  1. 1.

    Mutation 1 (rand/ 3):

    $$ \vec{V}_{z,t}= x_{r_{1},t}+F_{z}. \bigl( (x_{r_{2},t}-x_{r_{3},t} )+ (x_{r_{4},t}-x_{r_{5},t} )+ (x_{r_{6},t}-x_{r_{7},t} ) \bigr). $$
    (13)
  2. 2.

    Mutation 2 (best/ 3):

    $$ \vec{V}_{z,t}= x_{best,t}+F_{z}. \bigl( (x_{r_{1},t}-x_{r_{2},t} )+ (x_{r_{3},t}-x_{r_{4},t} )+ (x_{r_{5},t}-x_{r_{6},t} ) \bigr). $$
    (14)
  3. 3.

    Mutation 3 (rand-to-current/ 2):

    $$ \vec{V}_{z,t}= x_{r_{1},t}+F_{z}. \bigl( (x_{r_{2},t}-x_{z,t} )+ (x_{r_{3},t}-x_{r_{4},t} ) \bigr). $$
    (15)
  4. 4.

    Mutation 4 (rand-to-best and current/ 2):

    $$ \vec{V}_{z,t}= x_{r_{1},t}+F_{z}. \bigl( (x_{best,t}-x_{r_{2},t} )+ (x_{r_{3},t}-x_{z,t} ) \bigr). $$
    (16)

The 1st mutation is well-known and is able to investigate the search space. The 2nd mutation is used because it is popular and it is good choice for both separable and non-separable unimodal test problems [7]. The 3rd variant is selected as it is able to reach the good region for the non-separable unimodal and multimodal problems [7], while the 4th variant showed encouraging results, as presented in [32].

In this research, more difference vectors than Abbass [19] and Omran [33] are used, for the same reason that has been applied to Eqs. (13)–(16). The calculation of F and Cr is described below:

  • For each individual in the population, generate two Gaussian numbers N(0.5,0.15) one for amplification factor, while the other number represents a crossover rate. The rationale behind using this Gaussian number value is to give more probability to values surrounding 0.5 and hence to provide a relatively fair chance for both the perturbed individual and the original individual to be selected as the new offspring [33].

  • To generate the new offspring, for variants mutation 1 and 2, the overall F and Cr is calculated according to formulas (17) and (18), while the same parameters are calculated according to formulas (19) and (20) for the other two variants. Note that the difference between amplification values is multiplied by a Gaussian number N (0.0, 0.5) according to [33].

(17)
(18)
(19)
(20)

4 Experimental results

In this section, the computational results and analysis for the proposed algorithms DE/HMO/1, DE/HMO/1/N (same as the DE/HMO/1, but without local search), DE/HMO/2 and DE/HMO/2/N (same as the DE/HMO/2, but without local search) are presented. The algorithm have been firstly tested on a set of 36 test instances (18 problems each with 10 and 30 dimensions) introduced in CEC2010 [11]. The properties of these test problems are shown in Table 3. In a later section, the best variants are used to solve another set of test problems. All the algorithms have been coded using visual C#, and have been run on a PC with a 3 GHz Core 2 Duo processor, 3.5G RAM, and windows XP.

Table 3 Properties of the CEC2010 test problems. D is the number of decision variables, p=|F|/|S| is the estimated ratio between the feasible region and the search space, I is the number of inequality constraints, E is the number of equality constraints
Full size table

The algorithms have been run 25 times for each test problem, where the stopping criterion is to run up to 200K fitness evaluation (FEs) for 10D instances, and 600K FEs for 30D. The parameter settings are set as follows: PS=80 individuals for 10D and 100 for 30D test problems. MSS=0.1×PS, MSSC=0.1×p i , WS=50 generation, ε=0.0001, \(m_{q}^{+}\), \(m_{q}^{-}\) are random numbers ∈[0,1] and ∈[−1,0], respectively, and \(\mathit{FEs}_{LS}^{max}= 20\). The detailed results (best, median, average, standard deviation (St. d) and the feasibility ratio) are presented in Appendix A and Appendix B, for 10D and 30D test problems, respectively. Please note that all the appendices can be found on: http://seit.unsw.adfa.edu.au/staff/sites/rsarker/Saber-COA.pdf.Footnote 1

4.1 Comparison between DE/HMO/1 and DE/HMO/1/N

In this subsection, a comparison between DE/HMO/1 and DE/HMO/1/N is provided, based on the solution quality. The difference between these two variants is that the second one does not use a local search procedure.

The detailed results are shown in Appendices A and B. The summary of comparisons, with respect to the best and average fitness values, is given in Table 4.

Table 4 Comparison of DE/HMO/1 with DE/HMO/1/N, where Dec. is the statistical decision. The numbers shown in this table are for the first algorithm in column 1
Full size table

It is also possible, to study the difference between any two stochastic algorithms in a more meaningful way. To do this, statistical significant testing has been performed. A non-parametric test, the Wilcoxon Signed Rank Test [34], has been used. This test allows us to judge the difference between paired scores when it cannot make the assumption required by the paired-samples t test, such as that the populations should be normally distributed. The best and average fitness values are presented in Table 4. As there are 18 test problems, we have 18 best and 18 average fitness values (one for each problem out of its 25 runs). In this table, the numbers for better, equal, and worse solutions are reported for the first algorithm with respect to the second algorithm. In this table, W=w − or w + is the sum of ranks based on the absolute value of the difference between the two test variables. The sign of the difference between the 2 independent samples is used to classify cases into one of samples: differences below zero (negative rank w −), above zero (positive rank w +). As a null hypothesis, it is assumed that there is no significant difference between the best and/or mean values of two samples. Whereas the alternative hypothesis is that there is significant difference in the best and/or mean fitness values of the two samples, the number of test problems N=18 for both 10D and 30D, and 5 % is the significance level. Based on the test results /rankings, one of three signs (+, −, and ≈) is assigned for the comparison of any two algorithms (shown in the last column), where the “+” sign means the first algorithm is significantly better than the second, the “−” sign means that the first algorithm is significantly worse, and the “≈” sign means that there is no significant difference between the two algorithms. Considering this non-parametric test, as is shown in Table 4, DE/HMO/1 is clearly superior to DE/HMO/1/N in regard to the average results in 10D and both the best and the average results for the 30D test problems. Note that the average solution is a better indicator to judge the performance of stochastic algorithms. From these comparisons, the addition of the local search procedure clearly improves the performance of the algorithm, especially in the 30D test problems.

4.2 Comparison between DE/HMO/2 and DE/HMO/2/N

Following the same comparison, as was described in the previous subsection, a comparison between “DE/HMO/2” and “DE/HMO/2/N” is provided. Again the difference between these two variants is that the second variant does not use the local search procedure.

Based on the best and average fitness values, the summary of comparisons, with respect to the best and average fitness values, is given in Table 5, i.e. considering the 10D test problems, DE/HMO/2 is better than DE/HMO/2/N for 1 test problem and both of them are able to obtain the same best results for the other 17 test problems.

Table 5 Comparison of DE/HMO/2 with DE/HMO/2/N, where Dec. is the statistical decision. The numbers shown in this table are for the first algorithm in column 1
Full size table

Considering the Wilcoxon test, adding the local search in (DE/HMO/2) is better than DE/HMO/2/N for the 30D test problems (as is shown in Table 5).

From these comparisons, the addition of a local search procedure is consistently improving the performance of the algorithm, specifically for high dimensional test problems.

4.3 Comparison between DE/HMO/1/N and DE/HMO/2/N

Considering the results that are obtained, the summary of comparison between DE/HMO/1/N and DE/HMO/2/N is provided in Table 6. For example, in Table 6, for the 30D test problems and considering the best results, DE/HMO/1/N is better than DE/HMO/2/N for 5 test problems and it is worse for 11 test problems, while both of them are able to obtain the same results for 2 test problems.

Table 6 Comparison of DE/HMO/1/N with DE/HMO/2/N, where Dec. is the statistical decision. The numbers shown in this table are for the first algorithm in column 1
Full size table

Based on the statistical test, there is no significant difference between DE/HMO/1/N and DE/HMO/2/N, as is shown in Table 6.

4.4 Comparison between DE/HMO/1 and DE/HMO/2

In this subsection, a comparison between DE/HMO/1 and DE/HMO/2 is provided. Based on the results that are shown in Appendices A and B, a summary of this comparison is presented in Table 7. From these results, DE/HMO/1 is marginally better.

Table 7 Comparison of DE/HMO/1 with DE/HMO/2, where Dec. is the statistical decision. The numbers shown in this table are for the first algorithm in column 1
Full size table

Furthermore, based on the non-parametric test (see Table 7); there is no significant difference between both algorithms.

4.5 More analysis

To show the convergence pattern of the proposed algorithms, some sample convergence plots are presented, for all variants, in Figs. 1 and 2. These figures reveal that the convergence pattern for DE/HMO/1 and DE/HMO/2 are faster than the same for DE/HMO/1/N and DE/HMO/2/N.

Fig. 1
figure 1

The convergence plot, only for feasible solutions, for problem “C09” and “C15” with 10D. Note that y-scale is in log scale

Full size image
Fig. 2
figure 2

The convergence plot, only for feasible solutions, for problem “C09” and “C15” with 30D. Note that y-scale is in log scale

Full size image

To this end, it is useful to show the benefit of the self-adaptive learning measure. To do this, as an example, problem “C09” with 10 dimensions is analyzed for both “DE/HMO/1” and “DE/HMO/2” regarding the changes in the subpopulation sizes. For “DE/HMO/1”, the average subpopulation sizes (p i ) are as follows: p 1 is 21 (11 for binomial crossover and 10 for exponential crossover), p 2 is 19 (11 for binomial crossover and 8 for exponential crossover), p 3 is 20 (11 for the binomial crossover and 9 for the exponential crossover), and p 4 is 21 (11 for binomial crossover and 10 for exponential crossover). For the second variant “DE/HMO/2”, the subpopulation size for each mutation type (mutation1, mutation2, mutation3, and mutation4) are 23, 21, 17 and 19, respectively, and the subpopulation size for each crossover operator (binomial and exponential) are 51 and 29, respectively.

4.6 Comparison to the-state-of-the-art algorithm

In this subsection, we compare DE/HMO/1 and DE/HMO/2 to and εDEag [35] (the CEC2010 competition winning algorithm). It should be mentioned here that “DE/HMO/1” and “DE/HMO/2” are able to reach the 100 % feasible ratio for the 10D and 30D test instances, while εDEag is able to reach 100 % and 95.11 % feasibility ratios for the 10D and 30D test instances, respectively. Note that, the “*” in Appendix B for “C11” and “C12” means that it includes infeasible solutions in calculating means and other parameters.

The summary of comparisons, with respect to the best fitness values, average fitness values and standard deviations, is given in Table 8. In this table, DE/HMO/1’s performance is firstly recorded against εDEag, then DE/HMO/2’s against εDEag. For example, in Table 6, the comparison between “DE/HMO/1” and εDEag, based on the best fitness values, show that “DE/HMO/1” obtained the best values in 3, equal fitness in 15 test problems for the 10D test instances. These numbers are 13, 1, and 4 for the 30D instances, respectively. With respect to the εDEag algorithm, from this table, it is not hard to conclude that both variants are much better than it for 30D.

Table 8 A comparison between DE/HMO/1 and DE/HMO/2 with the εDEag, where Dec. is the statistical decision. The numbers shown in this table are for the first algorithm in column 1
Full size table

Considering the non-parametric test, the results are presented in Table 8. This table reveals that both algorithms are superior to εDEag regarding the best results in 10D. Considering the best and the average results for the 30D test problems, the proposed algorithms are clearly better than εDEag.

4.7 Performance analysis of DE/HMO variants on the CEC2006 test problems

Here both DE/HMO/1 and DE/HMO/2 are tested on the CEC2006 test problems. the mathematical properties of these test problems can be found in [12]. The detailed results are provided in Appendix C along with other state-of-the-art algorithms known as: APF-GA [36], MDE [37], ATMES [38] and SMES [39]. The parameters settings are set as those in the previous section.

From Appendix C, no algorithm was able to obtain any feasible solution for problems g20 and g22. For the other 22 feasible problems, DE/HMO/1, DE/HMO/2, APF-GA, and MDE obtained the optimal solutions for 22, 22, 17, and 20 problems, respectively.

In regard to the average results, DE/HMO/1 is better than APF-GA and MDE for 4 and 2 test instances, respectively. DE/HMO/1 is inferior to APF-GA and MDE for five test problem each. For the other two algorithms, DE/HMO/1 is always able to obtain better or same results. DE/HMO/2 is better than APF-GA for 4 test problems, while it is inferior to APF-GA and MDE for 6 and 8 problems, respectively. DE/HMO/2 is also better than ATMES and SMES for 7 and 8 test problems, respectively, while it is worse for one test problem each. Finally, DE/HMO/1 is better than DE/HMO/2 for 7 test problems, while it is worse for only one test problems.

Considering the Wilcoxon test, as is shown in Table 9, in regard to the best results both DE/HMO/1 and DE/HMO/2 are superior to APF-GA, SMES, while there is no significant difference to all the other algorithms. Based on the average results, both DE/HMO/1 and DE/HMO/2 are superior to ATMES and SMES. There is no significant difference between DE/HMO/1 and APF-GA and MDE, while MDE is superior to DE/HMO/2.

Table 9 The Wilcoxon sign rank results for DE/HMO/1 and DE/HMO/2 against APF-GA, MDE, ATMES and SMES
Full size table

5 Conclusions and future work

During the last few decades, many evolutionary algorithms have been introduced to solve constrained optimization problems. Most of these algorithms were designed to use a single crossover and/or a single mutation operator. In this paper, it has been shown that the efficiency of evolutionary algorithms can be improved by adopting a concept of self-adaptation with an increased number of search operators (mutation and crossover). All of the algorithms have been used to solve a set of specialized test problems.

In the proposed algorithms, “DE/HMO/1” and “DE/HMO/2” four DE mutations and 2 crossover operators have been used. In “DE/HMO/1”, the population was divided into a number of subpopulations, each subpopulation was evolved through its own mutation, and then these subpopulation individuals have been divided into two groups of individuals, where each one was evolved through its own crossover type. In “DE/HMO/2”, the population was divided into a number of subpopulations, according to the number of mutation operators and each subpopulation is evolved through its own mutation. Then all of the new subpopulation individuals have been grouped together into a new single population. This new population has then been divided into two subpopulations to be evolved via its own crossover operator. For both algorithms, a meaningful learning strategy has been used to determine the changes of the subpopulation sizes. Those subpopulation sizes were either increased or decreased or kept unchanged, adaptively, depending on its evolutionary success. An index for measuring the evolution success was also introduced. At each generation, a random individual was selected to follow the local search procedure, up to a specified stopping criterion. Also, an important aspect for our variants was the adaptive selection for all DE parameters.

To show the benefit of using the local search procedure, the proposed two algorithms have been implemented without using the local search (these are variants DE/HMO/1/N and DE/HMO/2/N). A comparative study, based on the solution quality and a non-parametric test, showed the superiority of DE/HMO/1 and DE/HMO/2 to those without the local search. Our finding confirmed that of the literature, that the exponential crossover could affect the performance of DE algorithms on high dimensional test problems. Hence the local search played an important role in speeding up the convergence, and preventing the algorithm from becoming stuck in local minima. DE/HMO/1 and DE/HMO/2 were found superior to the best algorithm, so far, in the literature

To validate the performance of the proposed algorithm, another set of 24 test problems have been solved by DE/HMO/1 and DE/HMO/2. The results showed that these variants were competitive, if not better, to the-state-of-the-art algorithms.

For future work, we intent test these algorithms on solving real-world applications.