A novel two-level particle swarm optimization approach for efficient multiple sequence alignment

Abstract

This paper presents two-level particle swarm optimization (TL-PSO) algorithm as an effective framework for providing the solution of complex natured problems. Proposed approach is employed to solve a challenging problem of bioinformatics i.e. multiple sequence alignment (MSA) of proteins. The major challenge in MSA is the increasing complexity of the problem as soon as the number of sequences increases and average pairwise sequence identity (APSI) score decreases. Proposed TLPSO-MSA firstly maximizes the matched columns in level one followed by maximization of pairwise similarities in level two at the gbest solutions of level one. TLPSO-MSA efficiently handles the premature convergence and trapping in local optima related issues. The benchmark dataset for MSA of protein sequences are extracted from BAliBASE3.0. The special features of proposed algorithm is its prediction accuracy at very lower APSI scores. Proposed approach significantly outperforms the compared state-of-art competitive algorithms i.e. ALIGNER, MUSCLE, T-Coffee, MAFFT, ClustalW, DIALIGN-TX, ProbAlign and standard PSO algorithm. The claim is supported by the statistical significance testing using one way ANOVA followed by Bonferroni post-hoc analysis.

1 Introduction

Nature has produced several efficient processes which offer solutions for complex and dynamic real world problems. These efficient processes are the nature-inspired novel problem-solving techniques, that include evolutionary algorithms, swarm intelligence (SI), artificial neural networks and many more. One of the nature inspired process i.e. SI defines the behaviour of natural or artificial self-organized systems, in which agents interact locally with each other and with external agents. Individual agents do not show any ‘intelligent’ behaviour or centralized control structure. Despite, decentralized system of the agents shows ‘intelligent’ global behaviour known as swarm intelligence. This decentralized system of the agents is known as swarm. This self-organized system can be in the form of bird flocks, ant colonies, animal herds, bee swarm, fish schools, bacterial growth and more [1].

Population-based stochastic optimization technique particle swarm optimization (PSO) is the most popular SI approach, introduced by Kennedy and Eberhart [2]. PSO was proposed for simulating social (or collective) behaviour, as embodiment of the movement of the organisms in a bird flock. The population of the potential solution is called as swarm and each individual in the swarm is defined as particle. The particles fly in a multi-dimensional search space to search their best solution based on experience of their own and the other particles in swarm.

The reasons of astounding popularity of PSO are: its flexibility; requirement of primitive mathematical operators and very few parameters to adjust; capacity of high global convergence performance; efficiency to work at reduced memory with good computation speed [3, 4]. Therefore, PSO has been effectively implemented on several kind of problems from various fields [5]. There have been many recent reviews on PSO algorithm variants [6–8]. In past few years, PSO has been employed in numerous exigent areas of bioinformatics [9]. Multiple sequence alignment (MSA) is one of the most prominent areas and essential tool in bioinformatics which discovers functional, structural and evolutionary information of biological sequences. The challenges regarding employment of laboratory experiments and equipments for MSA are their very high expenses, time consumption and sensitiveness to experimental errors whereas classical computation approaches are not efficient enough for these kinds of problems due to the computational complexities. This creates the requirement of heuristics algorithms to generate alignments in a reasonable time with computational efficiency [10].

This paper proposes a novel two-level PSO (TL-PSO) algorithm to solve the problems that contain (or can be generated) two different objectives to be optimized, out from these one is quite complex. Proposed TL-PSO variant is employed to MSA of protein sequences with different complexities. The simulation results over the benchmark dataset BAliBASE3.0 show TL-PSO to be producing significantly accurate results over the compared state-of-art and competitive algorithms.

The work is classified as follows: Sect. 2 presents a brief literature survey of the work performed for MSA followed by Sect. 3 presenting the basics of PSO and MSA. Section 4 delineates the structure of TL-PSO algorithm followed by the details of its implementation for MSA in Sect. 5. Section 6 contains the experimental setup for benchmark dataset and algorithm parameters for TL-PSO. Section 7 discusses the results obtained, followed by the conclusions in Sect. 8.

2 Related work

The computational methods to solve MSAs are divided into four categories: Progressive approach; Exact approach; Consistency based approach and Iterative approach [11, 12]. Progressive approaches construct the alignment with most similar sequences first and then incrementally align lesser similar sequences. The most popular example of progressive approaches is ClustalW [13]. ClustalW is a deterministic, non-iterative algorithm that aims to optimize the weighted sums-of-pairs with affine gap penalties. The basic problem with progressive approaches is that they are dependent on initial pairwise alignment and require appropriate scoring schemes to measure the alignment quality. Exact approaches are different from progressive approaches, since they simultaneously align multiple sequences despite of adding them one by one to a multiple alignment [14]. These algorithms are specially useful to deal with sets of extremely divergent sequences whose pair-wise alignments are generally incorrect. To align multiple sequences, one would need to generalize the Needlman and Wunsch algorithm [15] to a multi-dimensional space. Practically (at time and memory aspects) this is only possible for a maximum of three sequences. Divide and conquer algorithm (DCA) [16] is one of the most popular example of exact algorithms. DCA first cuts the sequences in subsets of segments, then the sub-alignments are later reassembled by DCA. Despite of being quite popular in previous decades, exact approaches lack efficiency at time and memory criteria. Consistency based approaches find the maximum consensus optimal pairwise alignment within the created library of alignments of provided sequences. T-Coffee [17] and DIALIGN [18, 19] are the most popular examples of consistency based approaches. T-Coffee aligns the sequences in a progressive manner but uses a consistency-based objective function aiming to minimize potential errors, that appear specially in the early stages of the alignment assembly. Although, these approaches are quite accurate, yet are computationally quite complex [20]. Iterative approaches iteratively improve the obtained solution until the stopping criteria has met. Iterative algorithm are subdivided in two categories: stochastic iterative algorithms and non-stochastic iterative algorithms. Simulated annealing (SA) [21] was the first stochastic iterative method described for simultaneously aligning a set of sequences. The employed concept is ordered as: alignment is randomly modified; its score assessed; it is kept or discarded according to an acceptance function; the process is kept iterating until a stopping criteria is met. These techniques include hidden Markov model training [22], SA [23], evolutionary algorithms [24] and SI algorithms [25]. The examples of non-stochastic iterative algorithms include Praline [26] and IterAlign [27]. In these methods sequences are preprocessed, so that the regions get consistently conserved across the family to get their signal enhanced and tend to drive the alignment. Iterative approaches have the drawback of taking long time to converge towards solution.

Due to the certain limitations of all the above discussed state-of-art approaches including the most popular sequence alignment tools based on these approaches i.e. ClustalW and T-Coffee, there remains a scope of developing more heuristics that produce better alignments. Proposed heuristic is based on particle swarm optimization (PSO), which belongs to fourth category i.e. stochastic iterative approach, the most salient SI based approach. PSO has been proven to be a potent approach for MSA with numerous kinds of proposed variants discussed in [28].

Out from all the above mentioned approaches the population based computational approaches include genetic algorithms (GA), differential evolution, ant colony optimization (ACO), artificial bee colony algorithm and PSO. The characteristics of population based approaches include: taking population of candidate solutions; employing trial-and-error search; using graduated solution quality and performing stochastic search of solution landscape [29]. A comprehensive survey of all the stochastic optimization techniques employed for performing MSA is presented in [25]. This study regarding SA, GA, ACO and PSO based algorithms for MSA concludes that SA has the major drawbacks of getting trapped in a local optimal alignment and being too slow to converge. GA is a good alternative for finding the optimal solution for small number of sequences but the increase in number of sequences may enhance falling behind optimal solutions and exponentially growing time complexity. SI methods have the advantages of being self-organized, robust and flexible. Self-organization in SI means the cooperation of individuals to accomplish difficult tasks without any strict top-down control. Robustness means the ability of the swarms to sustain their tasks even if some individuals fail to fulfill their tasks. Flexibility means the adaptation of individuals in the changing environment [30]. These properties make SI algorithms relatively better approach for solving complex problems. Out from all the SI based approaches, PSO has achieved the most notable popularity. Present work proposes an efficient PSO based approach that addresses the complex MSA problem.

3 Problem description

3.1 Particle swarm optimization

Particle swarm optimization (PSO) started to hold the grip amongst researchers soon after getting introduced and became the most popular SI technique, due to its simple concept, easily implementable algorithm, enough robustness to control parameters and better computational efficiency over many other mathematical algorithms and heuristic optimization techniques [31]. PSO is applicable to nonlinear and non-continuous optimization problems as well. PSO is a derivative-free class of global optimization algorithm hence it neither requires the derivative of the objective function nor the bounds such as Lipschitz constant, which makes PSO very useful for complex and noisy objectives [32]. The objective function to be minimized is formulated as:

$$\begin{aligned} min \ f(x) \ s.t. \ x \in S \subseteq R^D \end{aligned}$$

(1)

where $x$ is a matrix containing decision variables, composed of $m$ vectors defined as $x=[\overrightarrow{x}^1, \overrightarrow{x}^2 \dots \overrightarrow{x}^m]$ with dimension $D$. $S$ is the feasible solution space of the problem.

For the $i$th particle $(i=1, 2, \dots ,m)$, the position can be presented by $\overrightarrow{x}^i (\overrightarrow{x}^i_1, \overrightarrow{x}^i_2 \dots \overrightarrow{x}^i_D)$, where each component of this vector denotes a decision variable of the problem. The velocity of $i$th particle can be presented by $\overrightarrow{v}^i (\overrightarrow{v}^i_1, \overrightarrow{v}^i_2 \dots \overrightarrow{v}^i_D)$, where each component of this vector presents an increment of the current position. Each particle has its own best performance in the swarm defined by personal best i.e. ${pbest}^i({pbest}^i_1, {pbest}^i_2, \dots ,{pbest}^i_D$) [33]. At $t$th iteration the previous velocity $v^i(t)$ and position $x^i(t)$ are updated by:

$$\begin{aligned} v^i(t+1)&= wv^i(t)+c_1r_1[pbest^i(t)-x^i(t)]\nonumber \\&+c_2r_2[gbest(t)-x^i(t)]\end{aligned}$$

(2)

$$\begin{aligned} x^i(t+1)&= x^i(t)+v^i(t+1) \ \text {with} \ x^i(0) { \sim \text{ U }}(x_{min}, x_{max})\nonumber \\ \end{aligned}$$

(3)

The velocity $v^i$ is monitored by employing velocity clamping over a range between lower and upper bound i.e. $[v_{min}, v_{max}]$, where $v_{min}=-v_{max}$. Inertia weight $w$ $(0 < w <1)$ is the scaling factor over the previous velocity which results in either acceleration or deceleration on trajectory of particle. A study on impact of dynamically changing inertia weights performed in [34] depicts the effect of the inertia weight over the convergence of particles. The coefficients $c_1$ as cognitive acceleration coefficient and $c_2$ as social acceleration coefficient represent their confidence in their own experience and neighborhood experience respectively, generally with the constraint $c_1+c_2 \le 4$. $r_1$ and $r_2$ are uniform random numbers in range [0 1]. The initial approximate $x_i(0)$ for $i$th particle in Eq. (3) is randomly generated within the predetermined search domain $[x_{min}, x_{max}]$. $pbest$ at iteration $(t+1)$ is updated using the following equation [35]:

$$\begin{aligned} pbest^i(t\!+\!1)\!=\! {\left\{ \begin{array}{ll} pbest ^i(t) \quad \! \text {if} \ f (x{^{i}(t\!+\!1))\!\ge \!} \ f (pbest ^i(t))\\ x{^{i}(t+1)} \quad \text {if} \ f (x{^{i}(t\!+\!1))\!<\!} \ f (pbest ^i(t)) \end{array}\right. } \nonumber \\ \end{aligned}$$

(4)

The initial approximation of $pbest^i$ is generally set equal to the initial position vector. The best of the positions i.e. $gbest$ is found among all particles from the entire swarm, is updated as follows:

$$\begin{aligned}&{ gbest}(t)=x_k \in \left\{ pbest^1(t), pbest^2(t), \dots ,pbest^m(t) \right\} \nonumber \\&\quad \text {where}\ f(x_k)= min \left\{ f(pbest^1(t)),\right. \nonumber \\&\left. \qquad f(pbest^2(t)), \dots , f(pbest^m(t))\right\} \end{aligned}$$

(5)

The social interaction between the particles follows certain structures, named as neighborhood topologies. The particle in the neighborhood can communicate and share their information; hence their neighborhood can be formed in several ways so as to depict several ways of exchanging information. The major neighborhood topologies are ring topology, fully connected topology, star topology and von neumann topology [36, 37].

3.2 Multiple sequence alignment

Multiple sequence alignment (MSA) is an extremely powerful tool for revealing the constraints imposed by structure and function on the evolution of a sequence family. MSA is crucial for phylogenetic analysis so as to determine evolutionary relationships that exist among various organisms. MSAs are key method to identify conserved motifs and domains which are preserved by evolution that play vital role in the structure and functioning of organisms. MSA are imperative in secondary and tertiary structure prediction, that envisage the role of a residue in a structure.

Sequence alignment means identifying the regions of similarity between biological sequences. Formally, MSA is a scheme of arranging two or more sequences which substitutes alike characters in the same column and places gaps in such a way that it may result in maximum number of character matches. If non-alike characters are placed in the same column then it is considered as a mismatch, whereas alike characters in same column is considered as a match. These characters are nucleotide symbols {A, C, G, T} for DNA, {A, C, G, U} for RNA and 20-letter amino acid symbols {A, R, N, D, C, E, Q, G, H, I, L, K, M, F, P, S, T, W, Y, V} for the protein sequence. The alignment of two sequences is known as pairwise alignment, whereas, the alignment of more than two sequences is MSA. The computational approaches measure the sequence similarity by employing a scoring function that assigns similarity and penalty score with the aim to maximize number of matches and minimize the number of gaps in the alignment.

3.2.1 Similarity score

A general approach to perform MSA is to perform pairwise alignment first and then construct the phylogenetic tree so as to combine those sequences first that have maximum evolutionary relationship [38]. One of the most popular method based on this scheme is similarity score (SS) method, which can be formulated as:

$$\begin{aligned} \text {SS}=\sum _{i=1}^{s-1} \ \sum _{j=i+1}^s score(S_i, S_j) \end{aligned}$$

(6)

subject to:

$$ \begin{aligned} score(S_{i}, S_{j})\!=\!{\left\{ \begin{array}{ll} a, \text { if} \ S_{i} \!=\! S_{j} \\ b, \text { if} \ S_{i} \ne S_{j} \text { and} \ S_{i}\!\ne \! \ `-' \ \& \ S_{j}\!\ne \! \ `-' \\ c, \text { if} \ S_{i} \ne S_{j} \text { and} \ S_{i}\!=\! \ `-' \ \text {or} \ S_{j} \!=\! \ `-' \end{array}\right. } \end{aligned}$$

(7)

where, $s$ is the number of sequences; $a$, $b$ and $c$ are the scores assigned to match, mismatch and gaps respectively. Scores $a$ and $b$ are determined with the score schemes whereas $c$ is obtained by the gap penalty model as discussed in Sect. 3.2.3. The most popular score schemes for match and mismatch score for protein sequence alignment are PAM and BLOSUM series.

3.2.2 Match score

Match score is the less complex score scheme which calculates the columns wise alignment score, hence the number of sequences is not a concern while employing this method [39]. The match score (MS) scheme is formulated as:

$$\begin{aligned} \text {MS}=\sum _{i=1}^{s_s} M_{i}\left\{ 1+\frac{M_i}{s}\right\} \end{aligned}$$

(8)

here $M_i$ is the number of matches in the $i$th column and $s_s$ is the length of the aligned sequence.

3.2.3 Gap penalty

The sequences are aligned by introducing some gaps at specific positions so as to obtain maximum number of matches and maximum similarity score. For each introduced and extended gap, some gap penalty is deducted from the score. The gap penalty obtained by affine gap penalty model is:

$$\begin{aligned} \eta _k=\alpha +(t_g-1)*\beta \end{aligned}$$

(9)

here, $\eta _k$ stands for the gap penalty for the $k$th series of gaps with gap length $t_g$, $\alpha$ for gap open penalty and $\beta$ for gap extension penalty. An alignment can contain several gap openings, hence can contain several gap extensions. All these penalties are added to obtain the total gap penalty $\gamma$ i.e.

$$\begin{aligned} \gamma =\sum _{k=1}^{g_p} \eta _k \end{aligned}$$

(10)

here, $g_p$ is the total number of gap openings.

The implementation of PSO for MSA could be done in several ways, as is found in literature review [28]. PSO variants or hybridization of PSO with other evolutionary strategies could be employed for: training the hidden Markov model; obtaining the suitable gap positions that may produce optimal alignment score. The details of implementation of proposed algorithm for MSA are provided in Sect. 5.

4 Two-level particle swarm optimization algorithm

Proposed algorithm TL-PSO is based on the approach of iteratively improving the solution in two different levels containing two different objective functions. It employs PSO in both the levels to improve the parameters so as to optimize respective objectives. Although proposed TL-PSO algorithm employs the same velocity and position updates as in standard PSO (SPSO) (explained in Sect. 3.1), there are several differences between SPSO and TL-PSO as described below.

• SPSO contains only one swarm, whereas TL-PSO is a multi-swarm approach.

• SPSO carrries same dimension for particles throughout the algorithm, whereas TL-PSO has two different dimensions for two levels of the algorithm.

• SPSO works with all its particles at a time, whereas TL-PSO uses all its particles and swarms in level one followed by the gbest of each swarm in level 2.

• SPSO contains a single objective function, whereas TL-PSO contains two different objectives of different complexities.

• Difference also exists in the parameter settings of SPSO and TL-PSO i.e. SPSO uses constant inertia weight, whereas TL-PSO uses exponentially decreasing inertia weight.

Proposed variant shows efficient performance for the problems that have complex parameters in the objective function requiring good amount of computational efforts. The objective may contain two levels with different complexities or it could be subdivided in two parts: one less complex objective and other as the original one. As evident from Fig. 1, level one is defined on the entire population sized $n \times d$ for each swarm $i = 1, 2, \dots ,m$, whereas level two is defined on the $x_{gbest}$ of the each swarm. The algorithm is designed to prevent premature convergence as well as to improve solution quality. The objectives for the two levels could be defined as:

$$\begin{aligned}&min \ f_1(x_1) \ s.t. \ x_1 \in S \subseteq R^{D_1} \end{aligned}$$

(11)

$$\begin{aligned}&min \ f_2(x_2) \ s.t. \ x_2 \in S \subseteq R^{D_2} \end{aligned}$$

(12)

where $x_1$ and $x_2$ are the matrices containing decision variables for first and second objective functions respectively. Here, $D_2>D_1$ because second level objective is more complex and contains more number of variables. Algorithm 1 presents the outline of the pseudocode for TL-PSO.

Fig. 1

The structure of proposed TL-PSO

The procedure followed for TL-PSO is defined as:

Step 1: Parameter determination

Set number of particles, number of swarms, number of iterations, TL-PSO parameters $(w, c_1, c_2)$

Step 2: Initialization

• (1) Generate initial positions for $n$ particles for each swarm. The $d$ dimensioned $j$th particle’s position from the $i$th swarm can be expressed as:

  $$\begin{aligned} x^i_j&= \left\{ x^i_{j1}, x^i_{j2}, \dots ,x^i_{jd} \right\} \quad \forall i=1,2, \dots ,m;\nonumber \\&\forall j=1,2, \dots ,n \end{aligned}$$

  (13)

• (2) Determine initial personal best position of $j$th particle of $i$th swarm as:

  $$\begin{aligned} x^i_{pbest(j)}=x^i_j \quad \forall i=1,2, \dots ,m;\ \forall j=1,2, \dots ,n \end{aligned}$$

  (14)

• (3) Determine global best position of the $i$th swarm for level one as:

  $$\begin{aligned} x^{gbest(i)}_{1l}=arg \ min^n_{j=1}f_1\left( x^i_{pbest(j)}\right) \quad \forall i=1,2, \dots ,m \end{aligned}$$

  (15)

Here $f_1$ is taken from Eq. (11) and each $x^{gbest(i)}_{1l}$ presents the best solution with minimum $f_1$ for $i^{\text {th}}$ swarm so far.

Level 2

• (4) Determine initial positions of particles in the level two with one swarm and $i$ particles as:

  $$\begin{aligned} x^i_{2l}=x^{gbest(i)}_{1l} \quad \forall i=1,2, \dots ,m \end{aligned}$$

  (16)

  The number of swarms of level one becomes number of particles in level two and the number of swarm in second level is one.

• (5) Determine initial personal best position of $i$th particle for level two as:

  $$\begin{aligned} x^{pbest(i)}_{2l}=x^i_{2l} \quad \forall i=1,2, \dots ,m \end{aligned}$$

  (17)

Determine global best position of the entire swarm as:

$$\begin{aligned} x^{gbest}_{2l}=arg \ min^m_{i=1}f_2\left( x^{pbest(i)}_{2l}\right) \end{aligned}$$

(18)

$x_{2l}^{gbest}$ is the best solution obtained at minimum value of $f_2$. Objective $f_2$ is determined by Eq. (12).

Step 3: Set $t =1$

Step 4: Update the velocity and position of the $j$th particle of $i$th swarm for level one by:

$$\begin{aligned} v^i_j(t+1)&= wv^i_j(t)+c_1r_1[x^i_{pbest(j)}-x^i_j(t)]\nonumber \\&+c_2r_2[x_{1l}^{gbest(i)}(t)-x^i_j(t)]\nonumber \\&\quad \forall i=1,2, \dots ,m;\ \forall j=1,2, \dots ,n \end{aligned}$$

(19)

In earlier study the exponentially decreasing weight strategy was found to be more promising and provided best results in terms of time and convergence criteria as compared to other six inertia weight strategies [34]. Hence exponentially decreasing weight strategy is employed here, as formulated below:

$$\begin{aligned} w=\theta -\frac{(\theta -\phi )}{\left\{ -exp(t/t_t)\right\} } \end{aligned}$$

(20)

here, $\theta$ = 0.9; $\phi$ = 0.4; $t$ = iteration number and $t_t$ is the total number of iterations with the condition 0.4 $\le$ $w$ $\le$ 0.9. Update the position by:

$$\begin{aligned} x^i_{j}(t+1)&= x^i_{j}(t)+v^i_{j}(t+1) \quad \forall i=1,2, \dots ,m;\nonumber \\&\forall j=1,2, \dots ,n \end{aligned}$$

(21)

Step 5: Update the personal best and global best position for $j$th particle of $i$th swarm and $i$th swarm respectively, for the objective function $f_1$ for level one [Eq. (11)] as:

$$\begin{aligned}&x^{i}_{pbest(j)}(t+1)\nonumber \\&\quad ={\left\{ \begin{array}{ll} x^{i}_{pbest(j)}(t) \quad \text { if} \ f_1( x^i_j(t+1))\ge f_1 ( x^i_{pbest(j)}(t))\\ x^i_j(t+1) \quad \text { if} \ f_1( x^i_j(t+1))< f_1 (x^i_{pbest(j)}(t)) \end{array}\right. }\nonumber \\&\qquad \qquad \qquad \forall i=1,2, \dots ,m; \forall j=1,2, \dots ,n\end{aligned}$$

(22)

$$\begin{aligned}&xl^{gbest(i)}_{1l}(t)\nonumber \\&\quad \in \left\{ x^i_{pbest(1)}(t), x^i_{pbest(2)}(t), \dots ,x^i_{pbest(n)}(t) \right\} \nonumber \\&\text{ where } \ f_1[xl^{gbest(i)}_{1l}(t)]\nonumber \\&\quad = min \left\{ f_1[x^i_{pbest(1)}(t)], f_1[x^i_{pbest(2)}(t)], \dots ,\right. \nonumber \\&\quad \left. f_1[x^i_{pbest(n)}(t)]\right\} \nonumber \\&\qquad \qquad \forall i=1,2, \dots ,m \end{aligned}$$

(23)

Here $xl^{gbest(i)}_{1l}(t)$ is the local $gbest$ of level 1. The global $gbest$ of level 1, $x^{gbest(i)}_{1l}(t)$ is obtained by:

$$\begin{aligned}&x^{gbest(i)}_{1l}(t)\nonumber \\&\quad ={\left\{ \begin{array}{ll} x^{pbest(i)}_{2l}(t) \quad \text { if} \ f_1(xl^{gbest(i)}_{1l}(t)) \ge f_1(x^{pbest(i)}_{2l}(t)) \\ xl^{gbest(i)}_{1l}(t) \quad \text { if} \ f_1(xl^{gbest(i)}_{1l}(t)) < f_1(x^{pbest(i)}_{2l}(t)) \end{array}\right. }\nonumber \\&\qquad \qquad \qquad \qquad \forall i=1,2, \dots ,m; \forall j=1,2, \dots ,n \end{aligned}$$

(24)

Move to level two

Step 6: Update the velocity and position for the $i$th particle by:

$$\begin{aligned} v^i_{2l}(t+1)&= wv^i_{2l}(t)+c_1r_1[x^{pbest(i)}_{2l}-x^{gbest(i)}_{1l}(t)]\nonumber \\&+c_2r_2[x^{gbest}_{2l}(t)-x^{gbest(i)}_{1l}(t)]\nonumber \\&\qquad \qquad \qquad \forall i=1,2, \dots ,m\end{aligned}$$

(25)

$$\begin{aligned} x^i_{2l}(t+1)&= x^{gbest(i)}_{1l}(t)+v^i_{2l}(t+1) \quad \forall i=1,2, \dots ,m \nonumber \\ \end{aligned}$$

(26)

Step 7: Update the personal best and global best position for the $i$th particle by:

$$\begin{aligned}&x^{pbest(i)}_{2l}(t+1)\nonumber \\&\quad ={\left\{ \begin{array}{ll} x^{pbest(i)}_{2l}(t) \quad \text { if} \ f_2( x^{gbest(i)}_{1l}(t))\ge f_2 (x^{pbest(i)}_{2l}(t))\\ x^{gbest(i)}_{1l}(t) \quad \text { if} \ f_2(x^{gbest(i)}_{1l}(t))< f_2 (x^{pbest(i)}_{2l}(t)) \end{array}\right. }\nonumber \\&\qquad \forall i=1,2, \dots ,m \end{aligned}$$

(27)

$$\begin{aligned}&x^{gbest}_{2l}(t) \nonumber \\&\quad \in \left\{ x^{pbest(1)}_{2l}(t), x^{pbest(2)}_{2l}(t), \dots ,x^{pbest(m)}_{2l}(t) \right\} \nonumber \\&\text{ where } \ f_2[x^{gbest}_{2l}(t)]\nonumber \\&\quad = min \left\{ f_2[x^{pbest(1)}_{2l}(t)], f_2[x^{pbest(2)}_{2l}(t)], \dots ,\right. \nonumber \\&\quad \left. f_2[x^{pbest(m)}_{2l}(t)] \right\} \end{aligned}$$

(28)

here $f_2$ is determined from Eq. (12).

Step 8: $t = t +1$ until the stopping criteria is met.

Step 9: The best solution is the final $x_{2l}^{gbest}(t)$ obtained by Eq. (28).

Since the algorithm employs exponentially decreasing inertia weight strategy, the algorithm has a good ability to explore a new area at the initial stage. At the later stages, the algorithm exploits the local area more than the beginning of the search. Hence, it balances the exploration and exploitation ability of the algorithm. The global best solution of each swarm from level one moves towards second level and then a separate PSO runs for level two, whereas the personal best from level two moves towards level one in next iteration. This process slows down the speed of convergence and increases exploitation ability of the algorithm. Due to the exploration and exploitation ability of the algorithm, TL-PSO efficiently prevents premature convergence. The algorithm gets more diversity during implementation for MSA as explained in next section.

5 Multiple sequence alignment by two-level PSO

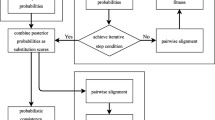
Proposed TL-PSO variant is employed to address two challenging issues of MSA, that are: aligning sequences with very small APSI score; increased complexity when a large number of sequences are to be aligned. The structure of proposed algorithm helps in reducing the problem complexity and finding optimum number of matches enhancing maximum alignment score. The sequence length gets randomly changed (within the allowed limit) at each iteration, it increases the exploration ability of the algorithm. Protein sequences with different complexities are taken so as to check the suitability of the proposed algorithm for specific kind of sequence sets. Figure 2 presents the procedure flow of proposed algorithm employed for MSA.

Fig. 2

Procedure flow of TLPSO-MSA

It is evident from Eqs. (6) and (8) that MS method is less complex than SS method because SS aligns two sequences at a time and calculates the alignment score for all $^mC_2$ pairs and then adds them, whereas MS method takes all the $m$ sequences at a time to calculate the column-wise alignment score. The maximization objectives are converted to minimization objective by strategy max($f$)=min($-f$).

The objectives of proposed TL-PSO are:

$$\begin{aligned} Max(f_1)&= \text {MS}-\gamma \end{aligned}$$

(29)

$$\begin{aligned} Max(f_2)&= \text {SS}-\gamma \end{aligned}$$

(30)

For length determination of gapped sequence for each swarm, the concept explained in [34] is adapted, which is depicted by:

$$\begin{aligned} x^i=\xi *\left\{ 1+int(0.3*rand*\rho )\right\} \quad \forall i =1,2, \dots ,m \end{aligned}$$

(31)

here $\xi$ is length of the longest sequence, int stands for output in round off form to the nearest integer value, rand stands for a random number in range [0 1] and $\rho$ is determined by:

$$\begin{aligned} \rho =\frac{(100-\chi )}{100} \end{aligned}$$

(32)

here $\chi$ is the APSI of that specific sequence set being aligned.

The procedure of implementing TL-PSO remains same as explained in Sect. 4. The position and velocity initialization phase for MSA is as explained below:

• 1. Determine sequence length for all particles of the $i$th swarm by:

  $$\begin{aligned} x^i(0)=\xi *\left\{ 1+int(0.3*rand*\rho )\right\} \quad \forall i =1,2, \dots ,m \end{aligned}$$

  (33)

• 2. Generate initial gap positions for the $j$th particle of $i$th swarm by:

  $$\begin{aligned} {x}_j^i(0)&= int(rand*x^i(0)) \quad \forall i=1,2, \dots ,m;\nonumber \\&\forall j=1,2, \dots ,n \end{aligned}$$

  (34)

• 3. Generate initial velocity for gap positions for the $j$th particle of $i$th swarm by:

  $$\begin{aligned} v_j^i(0)&= int(rand*(u^p-l^p)) \qquad \forall i=1,2, \dots ,m;\nonumber \\&\forall j=1,2, \dots ,n \end{aligned}$$

  (35)

Here $u^p$ is the upper limit of gap position which is equal to $x^i(0)$ and $l^p$ is the lower limit of gap position which is equal to 1. For gap position, velocity upper bound $v_{max}$ is ($u^p-l^p$) and lower bound $v_{min}$ is $-(u^p-l^p)$.

The gap position matrix represents the position matrix [Eq. (21)] of Sect. (4). The steps for incorporating the gap positions in the sequence are: first create a square matrix G of size $x^i(0)$ for each swarm $i=1, 2, \dots ,m$; Place 0 in G for all gaps in the gap position matrix and place 1 in G at all the other places; Now insert gaps in sequence wherever G contains 0 and amino acids wherever G contains 1; Now calculate the alignment score [by Eqs. (29) and (30)] for the obtained sequence set.

6 Experimental setup

This section presents the details of the benchmark dataset and all the experimental parameters of PSO and MSA. The performance of TL-PSO algorithm is tested on protein families extracted from the BAliBASE 3.0 database [40]. All the programming part is performed in MATLAB programming environment. One way ANOVA followed by Bonferroni post-hoc analysis is employed for determining the significance of the results. The statistical tests one way ANOVA and Bonferroni post-hoc analysis are performed in SPSS v 16.0.

6.1 Benchmark dataset

Table 1 presents the different sets of short proteins with different complexities and different APSI score used for testing. Set RV11 contains 38 sequence sets that have APSI less than 20 %, RV12 contains 44 sequence sets that have APSI between 20–40 %, whereas, RV20 contains 41 sequence sets with APSI more than 40 % containing one orphan sequence, which has less than 20 % similarity with the other sequences of the family. The details of each sequence set from each directory along with the number of sequences and minimum-maximum sequence length are provided in supplementary material as Appendix A (tables A.1, A.3, A.5).

Table 1 Benchmark dataset from BAliBASE database

6.2 Parameter settings

This subsection elucidates the details of all the parameter settings of TL-PSO and MSA. In general, all the parameter settings represent the parameter combination that has produced the best results. All the settings have been determined after testing all the possible combinations by trial and error.

6.2.1 Parameter setting for TL-PSO

The parameter setting for TL-PSO has remained same throughout the experiment for both the score schemes. The $star$ neighbourhood topology is applied as the social interaction topology among the particles. Parameters values of $c_1$ and $c_2$ are adopted from [35], since they have produced commonly better results for all sequence sets in current experiment. Further, TL-PSO parameter setting is as follows:

• Number of particles in a swarm $(n) = 20$.

• Number of swarms $(m) = 10$.

• Number of iterations $(t_t) = 1500$.

• Cognitive coefficient $(c_1) = 1.49618$.

• Social coefficient $(c_2) = 1.49618$.

For each sequence set the simulation is run 30 times. The stopping criteria is: either the maximum number of iterations has reached or the solution has not improved till 30 consecutive runs.

6.2.2 Parameter setting for MSA

The alignment score for SS method [Eqs. (6) and (7)] is obtained by BLOSUM62 matrix [41]. MS method [Eq. (8)] counts the number of matches in each column in reference to total number of sequences and sequence length, hence doesn’t need any parameters settings. The alignment quality of TLPSO-MSA is evaluated by sum-of-pairs score (SPS) and column score (CS) with respect to reference alignment [42]. Employed gap penalty values are obtained by trial and error with the aim to obtain best combination that produces maximum matches. The gap penalty score by the employed affine gap penalty model from Eq. (9) and gap-gap alignment score from Eq. (7) have following parameter values:

• Gap opening penalty $(\alpha ) = -2$.

• Gap extension penalty $(\beta ) = -1$.

• Gap-Gap alignment score $(c) = -1$.

For a test alignment of $s$ sequences consisting of $s_s$ columns the SPS is defined as:

$$\begin{aligned} \text {SPS}=\frac{\sum _{i=1}^{s_s} S_i}{\sum _{r=1}^q S_r} \end{aligned}$$

(36)

where $q$ is the number of columns in the reference alignment, $S_r$ is the score for the $r$th column in the reference alignment. $S_i$ is the score for the $i$th column of tested alignment defined as:

$$\begin{aligned} S_i=\sum _{j=1, j \ne k}^s \ \sum _{k=1}^s \ p_{ijk} \end{aligned}$$

(37)

The $i$th column in the alignment is represented by $S_{i1}, S_{i2}, \dots ,S_{in}$ with the condition:

$$\begin{aligned} p_{ijk}={\left\{ \begin{array}{ll} 1, \quad {\text {if residues}}\, S_{ij} \,\mathrm{and}\, S_{ik} \,{\text {are aligned with}}\\ \ \ \ \text{ each } \text{ other } \text{ in } \text{ the } \text{ reference } \text{ alignment }\\ 0, \quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(38)

The column score (CS) method is formulated as:

$$\begin{aligned} \text {CS}={\sum _{r=1}^{s_s} \frac{N_r}{q}} \end{aligned}$$

(39)

subject to:

$$\begin{aligned} N_r={\left\{ \begin{array}{ll} 1,\text {if all the residues in the}\, r\mathrm{th}\, \text {column are}\\ \quad \text {aligned in the reference alignment}\\ 0, \text {otherwise} \end{array}\right. } \end{aligned}$$

(40)

7 Simulation results

Performance of proposed algorithm TLPSO-MSA is compared with competitive algorithms ALIGNER [43], MUSCLE [44], T-Coffee [17], MAFFT [45], ClustalW [46], DIALIGN-TX [47], ProbAlign [48] and SPSO for CS and SPS. All the algorithms are compared for RV11, RV12 and RV20 dataset presented by Table 1. The results of compared algorithms i.e. ALIGNER, MUSCLE, T-Coffee, MAFFT, ClustalW, DIALIGN-TX and ProbAlign are adopted from [43], whereas simulating the experiment for SPSO is part of present work. Tables 2, 3 and 4 summarize the results obtained from TLPSO-MSA compared with state-of-art algorithms, competitive algorithms and SPSO for CS and SPS. Figures 3, 4, 5, 6, 7 and 8 show the sequence wise comparison between all the algorithm for CS and SPS. The detailed analysis along with numerical values of CS and SPS for each alignment by each algorithm could be found in supplementary material, Appendix A. Simulation on SPSO are performed at the objective from Eq. (8) with the same parameter settings. One way ANOVA followed by Bonferroni post-hoc analysis is applied so as to verify whether TLPSO-MSA performs significantly better than the competitive algorithms. The detailed analysis is shown in supplementary material, Appendix B. The hypothesis testing results for all datasets that presents the comparison between all algorithms are depicted by Table 4.

Fig. 3

Column score comparison for RV11 dataset

Fig. 4

Column score comparison for RV12 dataset

Fig. 5

Column score comparison for RV20 dataset

Fig. 6

Sum-of-pairs score comparison for RV11 dataset

Fig. 7

Sum-of-pairs score comparison for RV12 dataset

Fig. 8

Sum-of-pairs score comparison for RV20 dataset

Table 2 Averge column score (CS) of MSA produced by different algorithms

Table 3 Average sum-of-pairs score (SPS) of MSA produced by different algorithms

Table 4 Results of one way ANOVA followed by Bonferroni post-hoc analysis for column-score (CS) and sum-of-pairs score (SPS)

7.1 Results for column score (CS)

Table 2 presents the comparison of TLPSO-MSA with all the competitive algorithms for all the three datasets RV11, RV12 and RV20 at average CS. It is evident from this table that proposed algorithm produces better CS over all the compared algorithms. Figures 3, 4 and 5 present the sequence wise comparison of CS among all algorithms for datasets RV11, RV12 and RV20 respectively. It is evident by the figures that TLPSO-MSA has remarkable performance over compared algorithms that can be clearly observed for RV11 and RV20 datasets.

The claim is supported by the hypothesis testing results in Table 4 that for RV11 dataset, the difference of TLPSO-MSA with ALIGNER, MUSCLE, T-Coffee, MAFFT, ClustalW, DIALIGN-TX, ProbAlign and SPSO is extremely significant (p $<$ 0.001). For RV12 dataset the difference is extremely significant (p $<$ 0.001) with ClustalW and DIALIGN-TX, very significant (p $<$ 0.01) with SPSO and significant (p $<$ 0.05) with MUSCLE. TLPSO-MSA contains extremely significant difference (p $<$ 0.001) with all compared algorithms except ALIGNER for RV20 datset. The detailed quantitative analysis can be observed in supplementary material, Appendix B.

This concludes that TLPSO-MSA remains efficient enough to produces better results, even when the APSI is very small and also when the number of sequences gets increased including more complex sequences.

7.2 Results for sum-of-pairs score (SPS)

Table 3 depicts average SPS by all algorithms for datasets RV11, RV12 and RV20. Detailed result is provided in supplementary material, Appendix A. As shown by Table 3 TLPSO-MSA outperforms all the competitive algorithms for SPS. Figures 6, 7 and 8 present the sequence set wise comparison for RV11, RV12 and RV20 dataset. The figures depict the remarkable performance of TLPSO-MSA over other competitive algorithms. It can be clearly observed that for RV11 dataset, TLPSO-MSA performs far better than other competitive algorithms and performs better for RV12 and RV20 dataset.

The hypothesis testing by one way ANOVA followed by post hoc analysis results are presented in Table 4. The detailed results are provided in supplementary material, Appendix B. The results show that for RV11 dataset, the difference is extremely significant (p $<$ 0.001) from MUSCLE, T-Coffee, MAFFT, ClustalW, DIALIGN-TX, ProbAlign and SPSO, whereas significant (p $<$ 0.05) from ALIGNER. For RV12 dataset it is extremely significant for ClustalW, DIALIGN-TX and SPSO, whereas significant for ALIGNER and MUSCLE. The difference is extremely significant for ClustalW and SPSO for RV20 dataset, whereas significant for MUSCLE and DIALIGN-TX. Hence, TLPSO-MSA outperforms to all the competitive algorithms for RV11 dataset, more than 50 % of the algorithms for RV12 dataset and 50 % algorithms for RV20 dataset. The detailed quantitative analysis is provided in supplementary material, Appendix B.

It proves TLPSO-MSA an efficient performer for SPS at complex and lesser APSI score sequences also.

8 Concluding remarks and future work

Proposed work presents a novel two-level particle swarm optimization (TL-PSO) algorithm which is designed to solve complex nature problems that contain multiple decision factors i.e. complex objective with several variables. Proposed TL-PSO is employed to address an intricate and challenging area of bioinformatics i.e. multiple sequence alignment (MSA) of protein sequences. Sequence alignment is a substantial technique to discover functional, structural and evolutionary information in biological sequences. MSA plays cogent role in secondary and tertiary structure prediction, phylogenetic tree construction and conserved domain identification.

The structure of TL-PSO for MSA (TLPSO-MSA) in level one contains the aim to maximize the column-wise match score firstly and then move the gbest of first level towards second level. Second level is structured with the aim to perform pairwise alignment so as to maximize similarity score for all pairs of sequences. The quality of alignment is evaluated at the basis of column score (CS) and sum-of-pair score (SPS). The algorithm’s efficiency is tested on three kind of protein datasets i.e. RV11, RV12 and RV20 that contain 123 sequence sets of different complexities.

Proposed approach scores better at CS and SPS than compared state-of-art and competitive algorithms i.e. ALIGNER, MUSCLE, T-Coffee, MAFFT, ClustalW, DIALIGN-TX, ProbAlign and standard PSO algorithm. TLPSO-MSA shows remarkable performance for complex sequence sets from RV11 and RV20 datasets. The significance testing of the TL-PSO based results over compared approaches at the basis of CS and SPS is performed by one way ANOVA followed by Bonferroni post-hoc analysis. The statistical analysis shows that TLPSO-MSA performs significantly better than the compared approaches specially at lesser APSI score. Also it is perceived that TLPSO-MSA is capable to produce best results when all the competitive algorithm cannot i.e. when the APSI score is very small and also when the number of sequences is large with complex sequences included. It is found that the algorithm loses its efficiency when the sequence length becomes about 1000.

Although scope of proposed work is limited towards producing better alignment, in future the comparison between computational complexities between competitive algorithms could be an interesting area. Improvement in algorithm efficiency for lengthy sequences could also be a future scope for current work. Proposed TL-PSO algorithm could be employed to many problems that contain two objectives at different complexities. The two level strategy could be converted to multi-level strategy for suitable problems.