Study of forming limit diagram (FLD) prediction of anisotropic sheet metals using Gurson model in M-K method

Abstract

This study uses the Marciniak and Kuczynski (M-K) method to present an analytical forming limit diagram (FLD) for sheet metals. The procedure for the analytical FLD prediction is described in detail and step-wise manner, and an algorithm is written using MATLAB. First, an appropriate algorithm is determined to establish the theoretical analyses, and various anisotropic yield functions, such as Hill’s 48, Barlat 89, and Hosford, are considered. The predicted FLDs are compared with experiments involving a typical AA6016-T4 aluminum alloy. Second, the Gurson model that considers damage growth is implemented when Hosford is the yield function, as Hosford criterion predicts the best comparable analytical FLD with experiments among the yield functions. Third, a parametric study is performed to investigate the effects of parameters on the FLD prediction. Results indicate that an extremely low value for the initial void volume fraction in the safe and groove zones has minimal effects on the FLD prediction. Lastly, the values of void volume fractions are calculated assuming no geometrical imperfections and the imperfection is because of higher void volume fraction in groove zone than that in safe zone.

Introduction

The Marciniak and Kuczynski (M-K) method for forming limit diagram (FLD) prediction considers an extremely slight reduction in thickness of sheets in the form of a band in a certain region of a sheet specimen as a pre-existing imperfection. Such small-scale imperfections are indeed present in rolled sheet materials and can be the result of roll lines essentially small-scale surface undulation over the sheet surface. This assumption and other elements of the classical plasticity theory (e.g., yield criterion, flow rule, hardening law) and basic mechanics of sheet forming (e.g., plane stress, force equilibrium, strain compatibility, proportional tensile loading) are used thereafter to track the strain state within and outside of the imperfection. Moreover, the aforementioned ideas aim to obtain the limit strains for various biaxial tensile load paths to construct an FLD. The M-K method yields the FLD shapes for many sheet materials that are often similar to that obtained experimentally.

Given that rolled aluminum sheet materials are typically anisotropic, various anisotropic yield functions have been utilized in the literature to predict their FLDs using the M-K method. Butuc et al. [1] applied a considerably flexible mathematical framework to the M-K method, and various anisotropic yield functions on A6XXX-T4 sheets. In another study, Butuc et al. [2] performed FLD predictions for AA6016-T4 aluminum sheets using several different anisotropic yield functions, such as Hill’s 1948 [3] and 1979 [4] and Barlat Yld96 [5]. The results indicated that when the Barlat Yld96 criterion is used as the yield loci and the Voce equations considers the hardening law, the predicted FLD is compared the best to the experiments. The aforementioned study and other similar research have typically utilized a plane stress assumption within the M-K method for FLD prediction. Ganjiani and Assempour [6] utilized the M-K method by considering Hosford [7] and BBC2000 anisotropic yield functions to predict FLD for AA5XXX alloys under plane-stress condition. The algorithm developed in [1] was used in [6], and the Newton-Raphson method was modified using the globally convergence method to solve a nonlinear set of equations.

For many high-strength sheet materials, including aluminum alloys, which contain a significant amount of second phase particles, micro-voids often result in the vicinity of particles during large plastic deformation during formation. These particle-induced micro-voids are known to localize plastic flow and limit the formability of sheet materials [8,9,10,11]. One of the well-known models of ductile void growth that is often utilized in analyzing large plastic deformation of ductile metallic materials is the Gurson model [12], and its later modification called the Gurson–Tvergaard–Needleman (GTN) model, proposed by Tvergaard and Needleman [13]. These models treat voids as spherical cavities and capture their effects on material yield following a modification of the von Mises yield criterion [12]. The effect of void growth on FLDs was investigated in [14] by using the original Gurson model combined with the M-K method. This particular study showed that FLDs decrease with the increase in initial void growth. Chelovian and Kami [15] simulated the M-K method by using the finite element method to predict an FLD for AISI 304 steel material by using the GTN model. Gurson’s original model for isotropic sheets to provide the plastic flow response of metals has been extended by several studies to include anisotropy based on the Hill quadratic [16], Hosford [17, 18], and Barlat and Lian non-quadratic [19]. Hosseini et al. [20] established an algorithm to predict FLD by using the original Gurson model for anisotropic materials. Furthermore, Son et al. [21] considered the Gurson model in their M-K based FLD predictions when Barlat and Lian are the yield function with prolate-ellipsoidal void shapes. In [21], the initial void volume fraction in the groove zone is larger than that in safe zone, thereby significantly lowering FLD. Furthermore, the algorithm to predict FLD is based on applied proportional strains in [21], which is relatively complex and time-consuming to implement.

The current study uses the algorithm presented in [2], which is stress-controlled, and utilizes the Gurson model with various yield functions. FLDs for a typical aluminum alloy AA6016-T4 are predicted and compared with the experiments. Results indicate that Hosford yield function predicts the most comparable FLD. A parametric study is performed and the effect of the void volume fraction on FLD prediction is investigated. Given that extremely low values for the initial void volume fraction in the safe and groove zones are considered, FLD predicted using the Gurson model considerably approximates to the case when this model is switched off. Therefore, a high-value void volume fraction is suggested in the groove zone and consider it as the only source of imperfection in sheet metals.

M-K analysis-based analytical model for FLD prediction

This section presents and discusses all critical theoretical concepts that affect the outcome of the results of the M-K analysis in this study, as well as the framework of the M-K analysis itself. First, the analytical model developed in this research assumes the existence of a plane stress deformation state in the sheet plane. That is, no stress component in the thickness direction (σ₃ = 0) is assumed. Two types of algorithms are used to predict FLD on the basis of either applied stresses or strains during the proportional loading of specimens. Algorithms based on proportional stress loading condition (i.e., stress-controlled) is discussed in [2] and used in the present research. By contrast, algorithms based on proportional strain loading condition (i.e., strain-controlled) is discussed in [21] and implemented to compare the predicted FLDs.

The focus of the current study is to predict FLDs by using the original Gurson model and establish the best approach in this regard. Void nucleation and coalescence are not considered in the Gurson model. In this study, FLDs are predicted using the GTN model, and the effects of void nucleation and coalescence are studied briefly.

M-K method using the original Gurson model

Theoretical analysis of stress-controlled FLDs

The Gurson yield function for anisotropic porous metals is expressed as follows [12]:

$$ \varPhi ={\left(\frac{\overline{\sigma}}{{\overline{\sigma}}_M}\right)}^2+2{q}_1{C}_V\cosh \left(\frac{3{q}_2{\sigma}_m}{2{\overline{\sigma}}_M}\right)-\left(1+{q_1}^2{C_V}^2\right)=0 $$

(1)

where q₁ and q₂ are the fitting parameters, C_V is the void volume fraction, and $\overline{\sigma},{\overline{\sigma}}_M,\mathrm{and}\ {\sigma}_m$are the macroscopic effective stress, material flow stress with strain hardening, and mean stress, respectively. Yield function (Φ), which is similar to other yield functions, exhibits the following characteristics or elastic and plastic loading conditions [12]:

The symbol, Φ,is defined as follows:

$$ \varPhi =\left\{\begin{array}{c}<0\kern1.75em and\ \dot{\varPhi}<0\kern3em Linear\ elastic\ behaviour\\ {}=0\kern1.5em Linear\ elastic- strain\ hardening\ plastic\ behaviour\ \end{array}\right. $$

(2)

Swift law is used to present the following stress–strain curve of the material:

$$ {\sigma}_{Swift\ law}=B{\left(C+{\overline{\varepsilon}}^{pl}\right)}^n $$

(3)

Effective stress $\overline{\sigma}$ is defined individually for each anisotropic yield function. For the plane stress case, Hosford effective stress is expressed as follows [7]:

$$ \overline{\sigma}={\left[\frac{1}{{\left({R}_{90}\left(1.0+{R}_0\right)\right)}^{1/M}}\left\{{R}_{90}{\left|{\sigma}_1\right|}^M+{R}_0{\left|{\sigma}_2\right|}^M+{R}_0{R}_{90}{\left|{\sigma}_1-{\sigma}_2\right|}^M\right\}\right]}^{\frac{1}{M}} $$

(4)

where σ₁ and σ₂ are the two principal stress components. Meanwhile, M is an exponent and has suggested values of 6 and 8 for BCC and FCC metals, respectively [7]. Similar to Eq. (4), Barlat 89 anisotropic yield criterion for generalized plane stress case can be expressed as follows [22]:

$$ \overline{\sigma}={\left[a\left\{{\left|{k}_1+{k}_2\right|}^M+{\left|{k}_1-{k}_2\right|}^M+b{\left|2{k}_2\right|}^M\right\}\right]}^{\frac{1}{M}} $$

(5)

where,

${k}_1=\frac{\sigma_x+{h}_1{\sigma}_y}{2}$;${k}_2=\sqrt{{\left(\frac{\sigma_x-{h}_1{\sigma}_y}{2}\right)}^2+{h_2}^2{\sigma_{xy}}^2}$; ${h}_1=\sqrt{\frac{R_0}{1+{R}_0}+\frac{1+{R}_{90}}{R_{90}}}$

$$ {h}_2=\frac{\sigma_h}{\tau_h}{\left[\frac{\sqrt{\left(1+{R}_0\right)\left(1+{R}_{90}\right)}}{2\sqrt{\left(1+{R}_0\right)\left(1+{R}_{90}\right)}+\left({2}^M-2\right)\sqrt{R_0{R}_{90}}}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$M$}\right.} $$

$c=2\sqrt{\frac{R_0}{1+{R}_0}+\frac{R_{90}}{1+{R}_{90}}}$; $a=\frac{2-c}{c}$;$b=\frac{c}{2-c.}$

where σ_x, σ_y are normal and σ_xy shear stress components in the xy sheet plane and σ_h and τ_h are the yield stress and shear stress, respectively, in the rolling direction.

Hill’s 48 anisotropic yield function under plane stress condition is expressed as follows [3]:

$$ \overline{\sigma}={\left[F{\sigma_{yy}}^2+G{\sigma_{xx}}^2+H{\left({\sigma}_{xx}-{\sigma}_{yy}\right)}^2+2N{\sigma}_{xy}^2\right]}^{\frac{1}{2}} $$

(6)

For sheet materials, the constants F, G, H, L, M, and N can be obtained through three experimental planar tensile tests along the 0^o, 45^o, and 90^o orientations with respect to the sheet rolling direction in the following form [23]:

$$ F=\frac{R_0}{R_{90}\left(1+{R}_0\right)};G=\frac{1}{1+{R}_0};H=\frac{R_0}{1+{R}_0}\ \mathrm{and}\ N=\frac{\left({R}_{90}+{R}_0\right)\left(1+2{R}_{45}\right)}{2{R}_{90}\left(1+{R}_0\right)} $$

(7)

In this model, the stress component values based on the stress ratios when Hosford is the effective stress are obtained as follows:

$$ {\sigma}_1=\frac{{\overline{\sigma}}_M}{Q_{1M}} $$

(8)

where,

$$ {Q}_{1M}=\frac{1}{1-{q}_1{C}_V}\sqrt{{\left[\frac{1}{\left({R}_{90}\left(1.0+{R}_0\right)\right)}\left\{{R}_{90}+{R}_0{\left|\alpha \right|}^M+{R}_0{R}_{90}{\left|1-\alpha \right|}^M\right\}\right]}^{\frac{2}{M}}+{q}_1{C}_V{\left(1.5{q}_2\right)}^2{\left(\frac{1+\alpha }{3}\right)}^2} $$

(9)

and $\alpha =\frac{\sigma_2}{\sigma_1}$ is the stress ratio in safe zone.

Associative flow rule $\left(d{\varepsilon}_{ij}= d\lambda \frac{\partial f}{\partial {\sigma}_{ij}}\right)$ can be used to obtain the plastic strain increment, which leads to the effective strain increment using the concept of plastic work. The latter can be expressed as follows [21]:

$$ dW={\sigma}_1d{\varepsilon}_1+{\sigma}_2d{\varepsilon}_2+{\sigma}_3d{\varepsilon}_3=\left(1-{C}_V\right){\overline{\sigma}}_Md{\overline{\varepsilon}}_M $$

(10)

The following equation is obtained by substituting associative flow rule equation into Eq. (10):

$$ {\sigma}_1\ d\lambda \frac{\partial \varPhi }{\partial {\sigma}_1}+{\sigma}_2 d\lambda \frac{\partial \varPhi }{\partial {\sigma}_2}+{\sigma}_3 d\lambda \frac{\partial \varPhi }{\partial {\sigma}_3}=\left(1-{C}_V\right){\overline{\sigma}}_Md{\overline{\varepsilon}}_M $$

(11)

As σ₃ = 0 in the present work, we have:

$$ d\lambda =\frac{\left(1-{C}_V\right){\overline{\sigma}}_Md{\overline{\varepsilon}}_M}{\sigma_1\ \frac{\partial \varPhi }{\partial {\sigma}_1}+{\sigma}_2\frac{\partial \varPhi }{\partial {\sigma}_2}} $$

(12)

The major and minor strains are calculated by adding the strain increments at each step (${\varepsilon}_{ij}^{New}={\varepsilon}_{ij}^{Old}+d{\varepsilon}_{ij}$). Void volume fraction C_V for a porous metal is expressed as follows [21]:

$$ {C}_V=\frac{V_V}{V_T}=\frac{V_T-{V}_M}{V_T} $$

(13)

where V_T, V_V, and V_M are the total, void, and matrix volumes, respectively. Meanwhile, volumetric plastic strain can be expressed as follows [19]:

$$ d{\varepsilon}_V=d{\varepsilon}_1+d{\varepsilon}_2+d{\varepsilon}_3 $$

(14)

The following equation is obtained by considering that the matrix material is incompressible [21]:

$$ {C}_V=\frac{V_V}{V_T}=\frac{\left({V}_T-{V}_M\right)}{V_T} $$

(15)

$$ d{\varepsilon}_V=\frac{dV_T}{V_T}=\frac{dV_V}{V_T}=\frac{dC_V}{1-{C}_V} $$

(16)

$$ {dC}_V=\left(1-{C}_V\right)d{\varepsilon}_V=\left(1-{C}_V\right)\left(d{\varepsilon}_1+d{\varepsilon}_2+d{\varepsilon}_3\right) $$

(17)

The last equation can be integrated numerically, and the current void volume fraction can be updated using the following equation [21]:

$$ {C}_V^{New}={C}_V^{Old}+d{C}_V $$

(18)

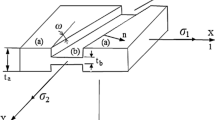
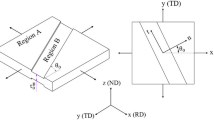
The M-K method is a commonly used approach in the literature to predict the analytical FLD of sheet materials. This method relies on a slight reduction in thickness of sheets in the form of a pre-existing imperfection band in a certain region of the sheet specimen (see Fig. 1). The imperfection factor f is defined as the ratio of the current thickness in the groove zone b and safe zone a as follows [2]:

$$ f=\frac{t^b}{t^a}={f}_o\mathit{\exp}\left({\varepsilon}_3^b-{\varepsilon}_3^a\right) $$

(19)

where f_o is the initial imperfection factor and ${\varepsilon}_3^a\ \mathrm{and}\ {\varepsilon}_3^b$ are the thickness strains in zones a and b, respectively. The stress tensors following the groove orientation using the rotation matrix are presented as follows [6]:

$$ {\sigma}^{nt}=T{\sigma}^{nt}{T}^T=\left[\begin{array}{cc}{\sigma}_{nn}& {\sigma}_{nt}\\ {}{\sigma}_{nt}& {\sigma}_{tt}\end{array}\right] $$

(20)

where

$$ T=\left[\begin{array}{cc}\cos \left(\theta \right)& \sin \left(\theta \right)\\ {}-\sin \left(\theta \right)& \cos \left(\theta \right)\end{array}\right] $$

Fig. 1

Schematic view of a sheet metal with initial thickness imperfection [24]

The strain compatibility between the regions a and b in the groove direction is expressed as follows [2]:

$$ d{\varepsilon}_{tt}^b=d{\varepsilon}_{tt}^a $$

(21)

Force equilibrium equations along and perpendicular to the groove directions are expressed as follows [2]:

$$ {F}_{nt}^a={F}_{nt}^{\mathrm{b}} $$

(22)

$$ {F}_{nn}^a={F}_{nn}^b $$

(23)

where ${F}_{nn}^a$and ${F}_{nt}^a$ are forces per unit width in the n and t directions, respectively, in zone a; and ${F}_{nn}^b$and ${F}_{nt}^b$ are forces per unit width in the n and t directions, respectively, in zone b. Therefore, the following expressions can be rewritten:

$$ \left(1-{C}_{Va}\right){\sigma}_{nn}^a\exp \left({\varepsilon}_3^a\right){t}_0^a=\left(1-{C}_{Vb}\right){\sigma}_{nn}^b\exp \left({\varepsilon}_3^b\right){t}_0^b $$

(24)

$$ \left(1-{C}_{Va}\right){\sigma}_{nt}^a\exp \left({\varepsilon}_3^a\right){t}_0^a=\left(1-{C}_{Vb}\right)\ {\sigma}_{nt}^b\exp \left({\varepsilon}_3^b\right){t}_0^b $$

(25)

By considering the imperfection factor equation (i.e., Eq. (19)), Eqs. (24) and (25) can be further written as follows:

$$ f\frac{1-{C}_{Vb}}{1-{C}_{Va}}\frac{\sigma_{nn}^b}{\sigma_{nn}^a}=1 $$

(26)

$$ f\frac{1-{C}_{Vb}}{1-{C}_{Va}}\frac{\sigma_{nt}^b}{\sigma_{nt}^a}=1 $$

(27)

For the solution of the unknown parameters in the groove region, matrix F is defined as follows:

$$ \boldsymbol{F}=\left[{F}_1\kern0.75em {F}_2\right] $$

where,

$$ {F}_1={\varPhi}_b=0 $$

(28)

$$ {F}_2=\frac{d{\varepsilon}_{tt}^b}{d{\varepsilon}_{tt}^a}-1=0 $$

(29)

The Newton–Raphson method is used to solve the preceding set of equations. Hence, the Newton–Raphson expression is as follows [2]

$$ \boldsymbol{F}\left(\boldsymbol{x}+\boldsymbol{\delta} \boldsymbol{x}\right)=\boldsymbol{F}\left(\boldsymbol{x}\right)+\boldsymbol{J}.\boldsymbol{\delta} \boldsymbol{x} $$

(30)

where, ${J}_{ij}\equiv \frac{\partial {F}_i}{\partial {x}_j}$ and unknown parameter x is defined as [2]:

$$ \boldsymbol{x}=\left[{\sigma}_{tt}^b\kern1.25em d{{\overline{\varepsilon}}_M}^b\right] $$

(31)

Values of x are obtained as follows [2]:

$$ \delta \boldsymbol{x}=-{\boldsymbol{J}}^{-\mathbf{1}}.\boldsymbol{F} $$

(32)

$$ {\boldsymbol{x}}_{\boldsymbol{new}}={\boldsymbol{x}}_{\boldsymbol{old}}+\delta \boldsymbol{x} $$

(33)

Figure 2 shows the flowchart of the algorithm to predict the stress-controlled analytical FLD. However, in every applied strain along a proportional stress in the safe zone, the stress and strain components in the algorithm are calculated in the safe zone. Thereafter, the Newton–Raphson method is used to calculate the stress and strain components in the groove zone. In every step, the total strain, imperfections and void volume fractions are updated, and necking is assumed to occur when effective strain increment in the neck exceeds the effective strain increment just outside the neck of a certain multiple of at least 10.

Fig. 2

Flow chart of the algorithm to predict the stress-controlled analytical FLD

Theoretical analysis of the strain-controlled FLD prediction

The combination of the Gurson and Barlat 89 models has been used to predict the analytical FLD in [21]. This algorithm is different from the algorithm developed in [2], which is used in the current study. Eqs. (22–23) are considered preconditions and Eqs. (28–29) are used in the Newton–Raphson method to calculate ${\sigma}_{tt}^b\ \mathrm{and}\ d{{\overline{\varepsilon}}_M}^b$ at every increment in this study when stresses are applied proportionally. In [21], Eq. (29) was used as a precondition and only Eq. (23) was used in the Newton–Raphson method to calculate the stress ratio in the groove zone when strains are applied proportionally. However, the algorithm presented in [21] has been implemented (which is not illustrated in this paper), and FLD for AA6016-T4 has been predicted by switching off the Gurson model (q₁ = q₂ = 0.0). Therefore, another FLD using the implemented algorithm in the current study has been predicted by switching off the Gurson model and considering the Barlat 89 yield function to investigate the effects of the algorithm on FLD prediction. In [21], the implementation and analysis of the algorithm to predict FLD following the constant strain paths are performed and explained in detail.

M-K method based on the GTN model

The strain-controlled void nucleation volume fraction increment is as follows:

$$ {\left(d{C}_V\right)}_{Nucleation}=\overline{A}d{\overline{\varepsilon}}_M $$

(34)

where $d{\overline{\varepsilon}}_M$ is the plastic strain increment, and the parameter $\overline{A}$ is chosen so that nucleation follows a normal distribution as suggested by Chu and Needleman [25]:

$$ \overline{A}=\frac{f_N}{S_N\sqrt{2\pi }}\mathit{\exp}\left[-\frac{1}{2}{\left(\frac{{\overline{\varepsilon}}_M-{\varepsilon}_N}{S_N}\right)}^2\right]. $$

(35)

Here, ε_N is the average void nucleating strain, f_N is the volume fraction of void nucleating particles, and S_N is the standard deviation of void nucleating strain.

In this way, the growth of existing voids and the nucleation of new voids are considered in the evolution of void volume fraction as follows:

$$ d{C}_V={\left(d{C}_V\right)}_{growth}+{\left(d{C}_V\right)}_{nucleation} $$

(36)

The function of void volume fraction (C_V^∗(C_V)) is defined to consider coalescence as follows [13]:

$$ {C_V}^{\ast }=\left\{\begin{array}{c}\kern4.75em {C}_V\kern6.75em for\ {C}_V\le {C_V}_c\\ {}{C_V}_c+\frac{{C_V}_u^{\ast }-{C}_V}{{C_V}_f-{C_V}_c}\left({C}_V-{C_V}_c\right)\kern1em for\ {C}_V>{C_V}_c\end{array}\right. $$

(37)

where C_Vc is the critical void volume fraction when coalescence happens and C_Vf is the void volume fraction at failure. The parameter ${C_V}_u^{\ast }=\frac{1}{q_1}$ is defined and C_V^∗ replaces the C_V in the Gurson yield function (Eq. (1)).

Results and Discussion

Algorithms were written using MATLAB to construct the stress- and strain-controlled analytical FLDs for the AA6016-T4 aluminum alloy sheets described in the previous section. Table 1 presents the material properties to predict FLD for the AA6016-T4 aluminum alloy. Given that the initial void volume fractions in metals is extremely low and approximates zero, ${C}_{vo}^a={C}_{vo}^a=0.001$ are considered. Moreover, q₁ = 1.5 and q₂ = 1.0 are considered for metals as suggested by Tevergaard in [26]. The remainder of the material properties that provide the elastic–plastic tensile responses (see Table 1) are as those presented in [2]. Various yield functions are used to construct the stress-controlled FLDs (see Fig. 3). The stress ratio increment to construct an FLD is 0.1. FLDs are compared with the FLD for the AA6016-T4 aluminum alloy as presented in [2]. Figure 3 shows that Hosford predicts the best theoretical FLD matched with experiments, and Hill’s 48 predicts FLD that is not considerably comparable with the experiments. Note that the initial imperfection factor (f_o) cannot be measured through physical experiments. The suggestion in [27] is to choose f_o by fitting the FLD prediction of the in-plane strain tension to the corresponding experimental limit strain. Accordingly, f_o = 0.991 is chosen for AA6016-T4 in this study. Fig. 4 shows the effects of the imperfection factor on FLD, in which the f_o value has a significant effect on FLD, which lowers with a decrease in f_o.

Table 1 Material properties to predict the analytical FLD for AA6016-T4 [2]

Fig. 3

The comparison of stress-controlled FLDs with various yield functions with experiments presented in [2]

Fig. 4

Effect of initial imperfection (f_o) factor on stress-controlled FLD prediction

The effects of the anisotropic plastic ratios on the stress- and strain-controlled predicted FLDs is investigated and shown in Fig. 5. The Barlat yield function is used, and ${C}_{vo}^a={C}_{vo}^b=0.0$ to switch off the effect of void growth. Note that in these figures, groove orientation is switched off, and FLDs are predicted when θ = 0 to investigate the direct effects of R₀, R_45, and R₉₀ on FLDs at a certain groove orientation. The results indicate that R₀, R_45, and R₉₀ have significant effects on the predicted FLDs. Note that the values of the major and minor strains at the plain strain state are the same for all cases. For the isotropic case when R₀ = R₄₅ = R₉₀ = 1.0, the predicted FLDs are the same as shown in Fig. 5(a). Given the values R₀ = R₄₅ = R₉₀ = 0.8, the right side of FLDs are the same but the left side of the strain-controlled FLD is extended substantially. Fig. 5(c) shows that the values of AA6016-T4 for R₀, R₄₅, and R₉₀ are used, and the predicted FLDs are compared. Evidently, the strain-controlled FLD is slightly extended on the right side and can be comparable with the experimental FLD. However, the left side is substantially extended and may be unsuitable for comparison with the experiments. Fig. 5(d) shows that the effect of R₉₀ is examined and that it causes the strain-controlled FLD to extend on the right and left sides compared with the stress-controlled FLD.

Fig. 5

Effect of R₀, R₄₅ and R₉₀ on predicted FLDs using the algorithm presented in [19] (strain-controlled) and [2] (stress-controlled) on FLD prediction. (a) R₀ = 1.0, R₄₅ = 1.0 and R₉₀ = 1.0 . (b) R₀ = 0.8, R₄₅ = 0.8 and R₉₀ = 0.8. (c) R₀ = 0.8, R₄₅ = 0.43 and R₉₀ = 0.61. (d) R₀ = 0.8, R₄₅ = 0.43 and R₉₀ = 1.0

This study analyzes the effects of the q₁, q₂ and void volume fractions on predicting FLDs. In Figs. 6, 7, 8 and 9, Hosford yield function is used, and the stress-controlled FLDs are predicted. The material properties are the same as presented in Table 1. Note that in these figures, groove orientation is switched off, and FLDs are predicted when θ = 0 to investigate the direct effects of each parameter on FLDs at a certain groove orientation.

Fig. 6

Effect of q₁ and q₂ on FLD prediction

Fig. 7

Effect of initial void volume fraction on FLD prediction when they are equal in both safe and groove zones

Fig. 8

Effect of initial void volume fraction on FLD prediction when they are not equal in both safe and groove zones

Fig. 9

Effect of initial void volume fraction on yield loci in Gurson model using Hosford

Figure 6 shows the sensitivity of the fitting parameters in the Gurson model (q₁ and q₂) on FLDs. The predicted FLD decreases with an increase in q₁ and q₂. Evidently, the effect of q₂ on lowering FLD is higher than the effect of q₁. However, FLD decreases drastically when the fitting parameters q₁ and q₂ change. The reason for the effects of q₁ and q₂ on FLD can be addressed from the change in yield locus. The void growth in the safe and grove zones are not equal because of thickness imperfection consideration in the groove zone, even if the initial void volume fractions are considered equal in both zones. Moreover, the void volume fraction in every applied strain step is different because of void growth. The yield locus in the Gurson model following Eq. (1) changes at every applied strain step, and q₁ and q₂ affect on the change in yield locus.

Figure 7 shows the effects of the initial void volume fractions in the safe and groove zones, and that the initial void volume fractions are the same in both zones. Clearly, FLD lowers with an increase in the initial void volume fraction. Note that the initial void volume fraction of a real material approximates zero and the value of 0.001 is an appropriate consideration for the initial void volume fraction of the safe and groove zones in aluminum alloys. The combination of the Gurson and Hosford models with 0.001 as initial void volume fraction evidently has a small change compared with FLD when the initial void volume fraction is 0.0. The plastic responses in the groove and safe zones are similar in both zones when the initial void volume fractions are the same. The FLD has a lower effect compared with the case when the initial void volume fraction in the groove zone is larger than in safe zone. Figure 8 shows the effect of latter case. Note that the same initial void volume fraction for the groove and safe zones must be considered from the metallurgical perspective.

Figure 8 also illustrates that the effect of the initial void volume fractions when the initial void volume fraction in the groove zone is twice the initial volume fraction in the safe zone. The large values of the initial void volume fraction in the groove zone play a role of imperfection factor. This case causes FLD to decrease significantly rather than the case when the initial void volume fractions are similar in the safe and groove zones. This fact can be explained with change in yield loci when the plastic responses in the groove and safe zones are not similar, and the stress–strain curve in the groove zone decreases more than that in the safe zone. When C_Vo is similar in the safe and groove zones, the behavior of the material is the same. However, when C_Vo is large in the groove zone, the yield locus in this zone shrinks (see Fig. 9), thereby lowering FLD.

The initial void volume fractions have minimal effect on the FLD prediction when they are equal in the safe and groove zones. However, this initial void volume fraction has a significant effect on FLD when the void volume fraction in the groove zone is larger than that in safe zone. From the metallurgical perspective, the void volume fractions in both zones are equal and approximates zero. In [28], FLD is predicted theoretically using the Gurson model, the safe zone is considered void-free zone, and only the groove zone has initial void volume fraction. In [21], void volume fraction in groove zone is twice the void volume fraction in safe zone to predict the FLD. Although small-scale imperfections are indeed present in the sheet metal, the initial imperfection is considered 1.0 (see Fig. 10); the assumption is that a high void volume fraction in the groove zone is the only source of imperfection. In fact, the assumption is that imperfection is a result of a high void volume fraction in the groove zone, thereby predicting FLD (see Fig. 10). When ${C}_{vo}^a=0.001\ \mathrm{and}\ {C}_{vo}^b=0.0025$ and when ${C}_{vo}^a=0.0015\ \mathrm{and}\ {C}_{vo}^b=0.003$ with f_o = 1.0, the predicted FLD is nearly comparable with FLD when ${C}_{vo}^a=0.001\ \mathrm{and}\ {C}_{vo}^b=0.001$ with f_o = 0.991.

Fig. 10

Effect of initial void volume fractions as the only source of imperfection in groove zone

Thus far, the FLDs predicted in this study were produced based on the original Gurson model. As mentioned previously, the objective of this study is to select the best approach that considers the effect of void growth on FLD prediction. The effects of void nucleation and coalescence when the GTN model is used to predict FLDs are also investigated. The results are shown in Fig. 11. The effect of void nucleation is investigated when the effect of coalescence is switched off. The parameter set of void nucleation and void coalescence for AA6016-T4 alloy is not available in literature [29]. Therefore, f_N = 0.04, S_N = 0.1, and ε_N = 0.3 are selected to show only the effect of void nucleation. These values are obtained from [13] for metals. Notably, investigation of the effect of void nucleation and coalescence on FLD prediction is the aim of this study regardless of the actual values of the mechanical properties of AA6016-T4 alloy. We observed that void nucleation exerted a significant effect on FLD prediction. Void nucleation decreased FLD because void growth increased significantly. f_c = 0.15 and f_f = 0.25 as reported in [13]. However, coalescence did not influence FLD prediction when these values were considered for void coalescence. Therefore, a small value of f_c adopted, and the predicted FLD is shown in Fig. 11. Void coalescence does not have much effect on FLD for the full range of the stress ratio (α), and FLD decreased only at high values of α. The effect of coalescence on FLD prediction when the M-K method that considers the GTN model is used for isotropic materials was studied in [30], and a similar behavior was observed.

Fig. 11

Effect of void nucleation and coalescence on an FLD

Conclusions

This study uses an analytical approach to predict FLD for sheet metals. The M-K method is utilized, and the effects of various yield functions on FLD prediction are analyzed and compared with the experiments. An appropriate algorithm is also investigated to establish the theoretical analysis. Furthermore, a parametric study was performed to understand the effects of each parameter on FLD prediction. Lastly, the salient conclusions of this study are summarized as follows:

• The stress-controlled FLD predicts the left side well and matched with the experiments for the AA6016-T4 alloy. By contrast, the strain-controlled FLD matches well with the right side of the experimental FLD.

• The Hosford yield function with M = 8 predicts the most suitable FLD compared with the experiments for a typical AA6016-T4 aluminum alloy sheet.

• Given that an extremely low value for the initial void volume fraction in the safe and groove zones are considered, FLD predicted using the Gurson model is extremely close to the case when the Gurson model is switched off.

• Accordingly, a high void volume fraction in the groove zone is assumed to result in a significant effect in predicting FLD.