1 Introduction

Permanent magnet synchronous motor (PMSM) is widely used in the field of electric vehicle drive system because of its simple structure, high power density, high reliability and small space occupation. However, PMSM is a nonlinear, multivariable and strongly coupled system, which makes it difficult to improve its dynamic and static performance due to the external disturbances, parameter disturbances and other effects (Cai et al., 2017). In recent years, some relevant scholars have proposed a variety of control strategies to suppress the uncertain interference of the system and improve the related performance of the control system; such as sliding mode control (Li et al., 2023), active disturbance rejection control (Cao et al., 2023; Xu et al., 2023; Xu et al., 2023), neural network control (Li et al., 2022; Lu et al., 2015; Yu et al., 2015), model predictive (Bai et al., 2022; Zhang et al., 2021), etc.

Sliding mode control (SMC) is widely used because of its strong robustness and insensitivity to external reactions (Wang, 2020). However, there are problems of control discontinuity and chattering, so in most cases, other control methods need to be combined to achieve better control effect. In Li et al., (2021), a back-stepping non-singular terminal sliding mode control method with finite time disturbance observer is proposed, where the load torque disturbance is assumed to change slowly and the load is bounded. In Du et al., (2022), the super-twisting sliding mode algorithm is introduced into the active disturbance rejection control by combining active disturbance rejection control and sliding mode control, and the nonlinear state error feedback control rate and tracking differentiator are optimized to improve the fast performance of the system. Li et al., (2021) designed a fractional order sliding mode surface for permanent magnet synchronous motor speed control system, through the fractional order calculus operator unique memory characteristics and genetic characteristics to suppress the chattering problem, but the dynamic response ability of the system is poor. Jin, (2021) introduced fuzzy control on the basis of fractional sliding mode, and used fuzzy algorithm to realize online adaptive adjustment of sliding mode switching term and fractional order, but the article did not consider the suppression and compensation of external disturbances. Jin and Zhao, (2019) added a complementary sliding mode surface based on the generalized sliding mode surface, and introduced Elman neural network to estimate the uncertainty interference, which can improve the position tracking accuracy of the system. In Jin and Zhao, (2020), the complementary sliding mode control and iterative learning in intelligent control are combined. This method can effectively suppress the influence of uncertainty on the system, thus accelerating the convergence speed of the controller and improving the convergence accuracy.

To further improve the anti-interference ability of the system, a control method combining neural network and fractional order complementary non-singular terminal sliding mode controller is designed in this paper. First, a non-singular terminal sliding mode is introduced to design the controller by combining the generalized sliding mode surface and complementary sliding mode surface, which can converge in finite time to solve the system singularity problem. It can shorten the time for the state trajectory to reach the sliding mode surface and also reduce the system chattering. On this basis, the fractional order calculus operator with filtering characteristics was adopted to improve the position tracking accuracy and reduce the steady-state error. Besides, the neural network is used to approximate the disturbance and un-modeled parts of the system to further improve the dynamic response ability and anti-interference ability of the system. The experimental results show that the proposed control method has the advantages of fast response speed, high tracking accuracy and small steady-state error, and it can effectively suppresses external uncertain interference.

This paper is organized as follows. The mathematical model of PMSM is reviewed in Sect. 2. The whole system control strategies are presented in Sect. 3, and fractional order complementary sliding mode and RBF neural network are designed in detail in this section. The simulation experiments are carried out and the results are analyzed with the conditions of speed step, load step and parameter change in Sect. 4. Finally, some conclusions are given in Sect. 5

2 Mathematical Model of PMSM

According to the principle of field oriented control, the dynamic model of PMSM in synchronous rotating coordinate system is established as follows:

$$\left\{ {\begin{array}{*{20}l} {u_{d} = Ri_{d} - \omega L_{q} i_{q} + L_{d} \frac{{\text{d}}}{{{\text{d}}t}}i_{d} } \hfill \\ {u_{q} = Ri_{q} + \omega L_{d} i_{q} + \omega \psi_{f} + L_{q} \frac{{\text{d}}}{{{\text{d}}t}}i_{q} } \hfill \\ \end{array} } \right.,$$
(1)

where ud and uq are stator voltages; id and iq are stator current; Ld and Lq are stator inductance; R is stator resistance; \(\omega\) is mechanical angular velocity; and \(\psi_{f}\) is permanent magnet flux linkage.

As for surface-mounted PMSM, Ld = Lq. Therefore, the electromagnetic torque in the synchronous rotating coordinate system is

$$T_{e} = \frac{3}{2}p_{n} \psi_{f} i_{q} ,$$
(2)

where Pn is the number of pole-pairs.

The motor motion equation can be described as

$$\frac{{{\text{d}}\omega }}{{{\text{d}}t}} = \frac{{T_{e} }}{J} - \frac{{T_{L} }}{J} - \frac{B}{J}\omega ,$$
(3)

where TL is load torque; Te is electromagnetic torque; B is the damping coefficient and J is the moment of inertia.

Substitute (2) into (3), it can be obtained as:

$$\left\{ {\begin{array}{*{20}l} {\dot{\omega } = a\omega + bi_{q} + c} \hfill \\ {a = - \frac{B}{J},b = \frac{{3p_{n} \psi_{f} }}{2J},c = - \frac{{T_{L} }}{J}} \hfill \\ \end{array} } \right..$$
(4)

Considering the variation of motor parameters and un-modeled uncertainty in the different working condition and external environment, Eq. (4) can be expressed as

$$\dot{\omega } = \left( {a + \Delta a} \right)\omega + \left( {b + \Delta b} \right)i_{q} + \left( {c + \Delta c} \right),$$
(5)

where \(\Delta a\),\(\Delta b\),\(\Delta c\) are uncertain disturbances of motor parameters.

The speed tracking error is defined as \(e = \omega^{ * } - \omega\), \(\omega^{ * }\) as the reference speed. Its derivation can be obtained by

$$\left\{ {\begin{array}{*{20}l} {\dot{e} = ae - bi_{q} - a\omega^{ * } - F} \hfill \\ {F = \Delta a\omega + \Delta bi_{q} + \Delta c + c} \hfill \\ \end{array} } \right.,$$
(6)

where F is the total uncertainty disturbances.

3 Design of Fractional Order Complementary Sliding Mode Controller

3.1 Fractional Calculus Theory

Fractional calculus is a generalized on the basis of integer order calculus. It can describe the dynamic characteristics of motor model more accurately. Fractional calculus operator is usually expressed by \({}_{h}D_{t}^{\alpha }\), which is defined as

$${}_{h}D_{t}^{\alpha } { = }\left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}^{\alpha } }}{{{\text{d}}t^{\alpha } }}} \hfill & {R\left( \alpha \right) > 0} \hfill \\ 1 \hfill & {R\left( \alpha \right) = 0} \hfill \\ {\int_{h}^{t} {\left( {{\text{d}}\tau } \right)^{{\left( { - \alpha } \right)}} } } \hfill & {R\left( \alpha \right) < 0} \hfill \\ \end{array} } \right.,$$
(7)

where t and h are the upper and lower bounds of the integral operator; \(\alpha\) is the order of the differential operator; \(R(\alpha )\) is the real part of \(\alpha\), and the upper and lower bounds are not considered in the following, so the fractional order is represented by \(D^{\alpha }\).

There are many definitions of fractional calculus, such as Grunwald–Letnikov, Riemann–Liouville, and Caputo. The third one (Caputo) is adopted in this paper (Podlubny, 1999)

$${}_{h}D_{t}^{\alpha } f\left( t \right) = \frac{1}{{\Gamma \left( {m - \alpha } \right)}}\int_{h}^{t} {\frac{{f^{\left( m \right)} \left( \tau \right)}}{{\left( {t - \tau } \right)^{\alpha - m + 1} }}{\text{d}}\tau } ,$$
(8)

where \(\Gamma (x)\) is the gamma function. \(0 \le m - 1 < \alpha < m\).

Lemma 1: Let \(x(t) \in R_{n}\) be a vector of a differentiable function. When \(t \ge t_{0}\), the following relation is established (Duarte-Mermoud et al., 2015):

$$\left\{ {\begin{array}{*{20}l} {\frac{1}{2}D^{\alpha } \left[ {x^{T} \left( t \right)Px\left( t \right)} \right] \le x^{T} \left( t \right)PD^{\alpha } x\left( t \right)} \hfill \\ {\forall \alpha \in \left( {0,} \right.\left. 1 \right]} \hfill \\ \end{array} } \right..$$
(9)

Since the value of fractional calculus cannot obtain an accurate numerical solution, an improved Oustaloup filter is used to approximate. And the filter formula with the filtering frequency band of \((\omega_{b} ,\omega_{h} )\) is

$$\begin{gathered} s^{\alpha } \approx \hfill \\ K\left( {\frac{{d\omega_{h} }}{l}} \right)^{\alpha } \left( {\frac{{ds^{2} + l\omega_{h} s}}{{d\left( {1{ - }\alpha } \right)s^{2} + l\omega_{h} s + d\alpha }}} \right)\prod\limits_{k = - N}^{N} {\frac{{s + \omega_{k}^{ * } }}{{s + \omega_{k} }}} . \hfill \\ \end{gathered}$$
(10)

The zero pole and gain of filter are

$$\left\{ {\begin{array}{*{20}l} {\omega_{k}^{ * } = \omega_{b} \omega_{u}^{{\left( {2k - 1 - \alpha } \right)/N}} } \hfill \\ {\omega_{k} = \omega_{b} \omega_{u}^{{\left( {2k - 1 + \alpha } \right)/N}} } \hfill \\ {K = \omega_{h}^{\alpha } } \hfill \\ {\omega_{u} = \sqrt {\omega_{h} /\omega_{b} } } \hfill \\ \end{array} } \right.,$$
(11)

where l and d are weight parameters.

Through the filter, it can output more accurate approximation of fractional calculus.

3.2 Design of Fractional Order Complementary Sliding Mode Controller

Complementary sliding mode control (CSMC) adds a complementary sliding mode surface to the traditional SMC. The added complementary sliding mode surface can make the system have higher tracking accuracy and response speed, and also improve the system robustness. Fractional order sliding mode control (FOSMC) introduces fractional order calculus on the basis of SMC. Fractional order differential operator has the advantages of slow energy transfer, memory and heredity, and it can describe the dynamic characteristics of motor model more accurately. Fractional order complementary sliding mode control (FOCSMC) combines CSMC and FOSMC to decrease the chattering and increase the degree of operation freedom; it further improves the speed tracking ability of PMSM control system.

The sliding mode surface is composed of generalized sliding mode surface \(S_{g}\) and complementary sliding mode surface \(S_{c}\), and the sliding mode control law is composed of equivalent control law \(i_{{{\text{eq}}}}\) and switching control law \(i_{v}\).

The generalized non-singular terminal sliding surface is designed as

$$S_{g} = D^{\alpha } e + 2\lambda e + \lambda^{2} D^{ - \alpha } \left( {e + c_{1} \left| e \right|^{\beta } {\text{sgn}} \left( e \right)} \right).$$
(12)

The complementary non-singular terminal sliding surface is designed as

$$S_{c} = D^{\alpha } e - \lambda^{2} D^{ - \alpha } \left( {e + c_{1} \left| e \right|^{\beta } {\text{sgn}} \left( e \right)} \right),$$
(13)

where \(\lambda\) is a positive number. \(0 < \alpha < 1\), \(0 < \beta < 1\), \(c_{1} > 0\).

Derivation of Eqs. (12) and (13) is driven as

$$\begin{gathered} D^{\alpha } S_{g} = D^{2\alpha } e + 2\lambda D^{\alpha } e + \lambda^{2} \left( {e + c_{1} \left| e \right|^{\beta } {\text{sgn}} \left( e \right)} \right) \hfill \\ D^{\alpha } S_{c} = D^{2\alpha } e - \lambda^{2} \left( {e + c_{1} \left| e \right|^{\beta } {\text{sgn}} \left( e \right)} \right). \hfill \\ \end{gathered}$$
(14)

Combining the formulas (12) and (13), the sum of the sliding surfaces is obtained

$$S_{{{\text{sum}}}} = S_{g} + S_{c} = 2\left( {D^{\alpha } e + \lambda e} \right).$$
(15)

And there are the following relationships:

$$\begin{gathered} \lambda S_{{{\text{sum}}}} = 2\lambda \left( {D^{\alpha } e + \lambda e} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;= D^{\alpha } S_{g} - D^{\alpha } S_{c} - 2c_{1} \lambda^{2} \left| e \right|^{\beta } {\text{sgn}} (e). \hfill \\ \end{gathered}$$
(16)

Let the Lyapunov function as \(V_{1} = (S_{g}^{2} + S_{c}^{2} )/2\), combining lemma 1, the \(\alpha\)th derivative of \(V_{1}\) is obtained (Liu, 2021)

$$\begin{gathered} D^{\alpha } V_{1} = \frac{1}{2}D^{\alpha } S_{g}^{2} + \frac{1}{2}D^{\alpha } S_{c}^{2} \le S_{g} D^{\alpha } S_{g} \hfill \\ \;\;\;\;\;\;\;\;\;\; + S_{c} D^{\alpha } S_{c} = S_{g} D^{\alpha } S_{g} \hfill \\ \;\;\;\;\;\;\;\;\;\; + S_{c} \left( {D^{\alpha } S_{g} - \lambda S_{{{\text{sum}}}} - 2c_{1} \lambda^{2} \left| e \right|^{\beta } {\text{sgn}} (e)} \right) \hfill \\ \;\;\;\;\;\;\;\; = S_{{{\text{sum}}}} \left( {D^{\alpha } S_{g} - \lambda S_{c} } \right) - 2c_{1} \lambda^{2} S_{c} \left| e \right|^{\beta } {\text{sgn}} (e) \hfill \\ \;\;\;\;\;\;\;\; = S_{{{\text{sum}}}} \left[ {D^{2\alpha } e + } \right.\;\lambda^{2} \left( {e + c_{1} \left| e \right|^{\beta } {\text{sgn}} \left( e \right)} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\left. { - \lambda S_{c} + 2\lambda D^{\alpha } e} \right] - 2c_{1} \lambda^{2} S_{c} \left| e \right|^{\beta } {\text{sgn}} (e) \hfill \\ \;\;\;\;\;\;\;\;{ = }S_{{{\text{sum}}}} \left[ {D^{2\alpha - 1} \left( {ae - bi_{q} - a\omega^{ * } - F} \right)} \right. \hfill \\ \left. {\;\;\;\;\;\;\;\;\;\;\, + 2\lambda D^{\alpha } e + \lambda^{2} \left( {e + c_{1} \left| e \right|^{\beta } {\text{sgn}} \left( e \right)} \right) - \lambda S_{c} } \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\, - 2c_{1} \lambda^{2} S_{c} \left| e \right|^{\beta } {\text{sgn}} (e). \hfill \\ \end{gathered}$$
(17)

The fractional order complementary sliding mode control law is composed of equivalent control law and switching control law. It can be expressed as \(i_{q}^{ * } = i_{{{\text{eq}}}} + i_{v}\).

To ensure stability, the equivalent control law can be designed as

$$\begin{gathered} i_{{{\text{eq}}}} = \frac{1}{b}\left[ { - a\omega - F + 2\lambda D^{1 - \alpha } e} \right. + \lambda D^{1 - 2\alpha } S_{g} + \hfill \\ \;\;\;\;\;\;\left. {\lambda^{2} D^{1 - 2\alpha } (e + (c_{1} - 2c_{1} \frac{{S_{c} }}{{S_{{{\text{sum}}}} }})\left| e \right|^{\beta } {\text{sgn}} (e))} \right]. \hfill \\ \end{gathered}$$
(18)

The switching control law is selected as

$$i_{v} = \frac{\rho }{b}\left[ {D^{1 - 2\alpha } sat\left( {\frac{{S_{{{\text{sum}}}} }}{\theta }} \right)} \right],$$
(19)

where \(sat\left( \cdot \right)\) is the saturation function, \(\theta > 0\) is the boundary layer thickness, and \(\rho > 0\) is the control gain

$$sat\left( {\frac{{S_{{{\text{sum}}}} }}{\theta }} \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {S_{{{\text{sum}}}} \ge \theta } \hfill \\ {\frac{{S_{{{\text{sum}}}} }}{\theta }} \hfill & { - \theta < S_{{{\text{sum}}}} < \theta } \hfill \\ { - 1} \hfill & {S_{{{\text{sum}}}} \le - \theta } \hfill \\ \end{array} } \right..$$
(20)

Substituting the above equation into Eq. (17)

$$D^{\alpha } V_{1} \le - \lambda S_{{{\text{sum}}}}^{2} - \rho S_{{{\text{sum}}}} sat\left( {\frac{{S_{{{\text{sum}}}} }}{\theta }} \right) \le 0.$$
(21)

It can be seen from formula (21) that the controller satisfies the Lyapunov stability theorem. Therefore, the control law is designed as

$$\begin{gathered} i_{q}^{ * } = \frac{1}{b}\left[ { - a\omega - \hat{F} + 2\lambda D^{1 - \alpha } e} \right. + \lambda D^{1 - 2\alpha } S_{g} \hfill \\ \;\;\;\;\;\;\; + \lambda^{2} D^{1 - 2\alpha } (e + (c_{1} - 2c_{1} \frac{{S_{c} }}{{S_{{{\text{sum}}}} }})\left| e \right|^{\beta } {\text{sgn}} (e)) \hfill \\ \;\;\;\;\;\;\;\left. { + \rho D^{1 - 2\alpha } sat\left( {\frac{{S_{{{\text{sum}}}} }}{\theta }} \right)} \right]. \hfill \\ \end{gathered}$$
(22)

3.3 Design of Fractional Order Complementary Sliding Mode Controller Based on RBF Neural Network

There are uncertain factors such as parameter changes and external disturbances during the system operation, which have adverse effects on the control performance. As for the uncertain disturbances in Eq. (22), RBF neural network is used to approximate the disturbance and un-modeled parts online and compensate them to further improve the system control performance (Liu, 2014a, 2014b). The structure of RBF neural network is shown in Fig. 1.

Fig. 1
figure 1

Neural network structure model

Full size image

The speed error and speed error change rate are used as the input of RBF neural network. Based on the above structure, \(x = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } \\ \end{array} } \right]^{\rm T} = \left[ {\begin{array}{*{20}c} e & {\mathop e\limits^{ \cdot } } \\ \end{array} } \right]^{\rm T}\).The hidden layer function of RBF neural network is selected as

$$h_{j} \left( x \right) = \exp \left( {\frac{{\left\| {x - c_{j} } \right\|^{2} }}{{2b_{j}^{2} }}} \right),$$
(23)

where \(c_{j}\) is the center vector of the jth node function; \(b_{j}\) is the base width parameter of the jth hidden layer node function.

The output of RBF neural network is the sum of the weighted product of each hidden layer neuron output value and corresponding connection weight, which is represented as

$$y = \sum\limits_{j = 1}^{n} {\omega_{j} } h_{j} \left( x \right).$$
(24)

The formula above is rewritten in vector form as

$$\hat{F} = W^{\rm T} \varphi ,$$
(25)

where \(W{ = }[\omega_{1} \cdot \cdot \cdot \omega_{j} ]^{{^{\rm T} }}\) is the RBF neural network connection weight vector; \(\varphi { = }[h_{1} \cdot \cdot \cdot h_{j} ]^{{^{\rm T} }}\)is the RBF neural network hidden layer output vector.

RBF neural network can approximate any nonlinear function. Selecting appropriate \(c_{j}\),\(b_{j}\) and \(\omega_{j}\) can improve the accuracy of approximation. The selection of \(c_{j}\) is determined according to the input value range of the network. The parameter \(b_{j}\) determines the mapping ability of the network input, which is generally designed as a moderate value. And the parameter \(\omega_{j}\) is designed by Lyapunov stability analysis.

Define \(\tilde{w} = w - \hat{w}\) as the error between the ideal optimal value and the estimated value of the weight, and select the Lyapunov function

$$V_{2} = \frac{1}{2}\left( {S_{g}^{2} + S_{c}^{2} } \right) + \frac{1}{2}\gamma D^{2\alpha - 1} \tilde{W}^{{\text{T}}} \tilde{W},$$
(26)

where \(\gamma\) is the adaptive coefficient of neural network weight.

By taking the \(\alpha\)th derivative of Eq. (26) and combining with Lemma 1, Eq. (16), Eq. (22) and Eq. (25), it can be obtained

$$\begin{gathered} D^{\alpha } V_{2} \le S_{g} D^{\alpha } S_{g} + S_{c} D^{\alpha } S_{c} + \gamma D^{2\alpha - 1} \tilde{W}^{{\text{T}}} D^{\alpha } \tilde{W} \hfill \\ \;\;\;\;\;\;\;\;\; \le S_{{{\text{sum}}}} \left[ {D^{2\alpha - 1} \left( {ae - bi_{q} - a\omega^{ * } - F} \right) + 2\lambda D^{\alpha } e} \right. \hfill \\ \left. {\;\;\;\;\;\;\;\;\;\;\, + \lambda^{2} \left( {e + c_{1} \left| e \right|^{\beta } {\text{sgn}} \left( e \right)} \right) - \lambda S_{c} } \right] \hfill \\ \;\;\;\;\;\;\;\;\;\; - 2c_{1} \lambda^{2} S_{c} \left| e \right|^{\beta } {\text{sgn}} (e) + \gamma D^{2\alpha - 1} \tilde{W}^{{\text{T}}} D^{\alpha } \tilde{W} \hfill \\ \;\;\;\;\;\;\;\; = S_{{{\text{sum}}}} \left[ {D^{2\alpha - 1} \left( {F - \hat{F}} \right) - \rho sat\left( {\frac{{S_{{{\text{sum}}}} }}{\theta }} \right)} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\; + \gamma D^{2\alpha - 1} \tilde{W}^{{\text{T}}} D^{\alpha } \tilde{W} \hfill \\ \;\;\;\;\;\;\;\; = S_{{{\text{sum}}}} \left[ {D^{2\alpha - 1} \left( {W^{{\text{T}}} - \hat{W}^{\rm T} } \right)\varphi - \rho sat\left( {\frac{{S_{{{\text{sum}}}} }}{\theta }} \right)} \right] \hfill \\ \;\;\;\;\;\;\;\;\,\,\,\, - \;\gamma D^{2\alpha - 1} \tilde{W}^{{\text{T}}} D^{\alpha } \hat{W}. \hfill \\ \end{gathered}$$
(27)

The weight adaptive law of RBF neural network is designed as

$$D^{\alpha } \hat{W} = \frac{1}{\gamma }\left( {S_{g} + S_{c} } \right)\varphi .$$
(28)

Combining Eq. (27) and Eq. (28), it can be obtained

$$\begin{gathered} D^{\alpha } V_{2} \le S_{{{\text{sum}}}} \left[ {D^{2\alpha - 1} \tilde{W}\varphi - \rho sat\left( {\frac{{S_{{{\text{sum}}}} }}{\theta }} \right)} \right] \hfill \\ \;\;\;\;\;\;\;\quad + \gamma D^{2\alpha - 1} \tilde{W}^{{\text{T}}} D^{\alpha } \tilde{W} \hfill \\ \;\;\;\;\;\;\;\; = - \rho S_{{{\text{sum}}}} sat\left( {\frac{{S_{{{\text{sum}}}} }}{\theta }} \right) \le 0. \hfill \\ \end{gathered}$$
(29)

Equation (29) satisfies the Lyapunov stability theory, which indicates the closed-loop system is asymptotically stable. Starting from any initial state, the system can reach the boundary layer in a finite time, and slide along the intersection of two sliding surfaces to the field of zero.

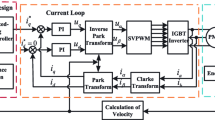
The PMSM fractional order complementary non-singular terminal sliding mode control block diagram based on RBF neural network is shown in Fig. 2.

Fig. 2
figure 2

Block diagram of RBF-FOCSMC

Full size image

4 Simulation Experiment and Analysis

The control system is built in MATLAB/Simulink to verify the effectiveness of the control strategy. Four different control methods are simulated and compared in MATLAB/Simulink environment. Scheme 1 is based on fractional order complementary sliding mode control (FOCSMC); scheme 2 is based on neural network fractional order sliding mode control (RBF-FOSMC); scheme 3 is based on neural network complementary sliding mode control (RBF-CSMC); the fourth scheme is fractional order complementary sliding mode control based on neural network (RBF-FOCSMC). To ensure the fairness, the Kp and Ki parameters of the current loop are the same during experiment. The motor parameters are shown in Table 1.

Table 1 Motor related parameters
Full size table

4.1 System Analysis of the Speed Change Response

To study the influence of the motor speed step response, the simulation time is set to 1s and the initial speed step of the motor is set from 0 to 1000 r/min, and then, it is suddenly increased to 1500 r/min at 0.4s, and reduced to 1000 r/min at 0.8s. The speed comparison curves under the four schemes are shown in Figs. 3 and 4.

Fig. 3
figure 3

Speed comparison curves of four schemes. a Speed step local amplification at start-up time. b Speed step local amplification at 0.4 s. c Speed sudden reduction local amplification at 0.8 s

Full size image
Fig. 4
figure 4

Speed mutation local amplification curves of four schemes

Full size image

To explain the dynamic response performance of the system more precisely, the system state time and overshoot of the four schemes are listed in Tables 2, 3, and 4, respectively. As for the system steady-state performance, selecting parts of steady-state speed error curves to zoom in, it is shown in Fig. 5.

Table 2 Performance analysis of four schemes when speed mutation occurs (0–1000r/min)
Full size table
Table 3 Performance analysis of four schemes when speed mutation occurs (1000–1500r/min)
Full size table
Table 4 Performance analysis of four schemes when speed mutation occurs (1500–1000r/min)
Full size table
Fig. 5
figure 5

Steady-state speed error curves of four schemes

Full size image

From Fig. 4 and Table 2, it can be seen that at the time of the motor start-up, the response time of FOCSMC, RBF-FOSMC, and RBF-CSMC is 0.0160 s, 0.0324 s, and 0.0182 s, respectively, and the speed overshoot is 0.5r/min, 50r/min, and 12r/min, respectively. The response time of RBF-FOCSMC at start-up is 0.0155 s, and there is no speed overshoot. From Fig. 4 and Table 3, it can be seen that when the motor speed increases suddenly from 1000r/min to 1500r/min at 0.4 s, the setting time of FOCSMC, RBF-FOSMC, and RBF-CSMC is 0.0134 s, 0.0240 s, and 0.0320 s respectively, and the speed overshoot is 2r/min, 20.1r/min, and 32.8r/min respectively, while the setting time of RBF-FOCSMC is 0.0119 s, and there is also no speed overshoot. From Fig. 4 and Table 4, it can be seen that when the motor speed drops suddenly at 0.8 s, the setting time of FOCSMC, RBF-FOSMC, and RBF-CSMC is 0.0070 s, 0.0250 s, and 0.0130 s, respectively, and the speed overshoot is 3.6r/min, 107r/min, and 2r/min, respectively. The setting time of RBF-FOCSMC is 0.0055 s at start-up, and there is also no speed overshoot. By comparison, RBF-FOCSMC has the fastest response time when the speed increases or decreases, besides, it is stable without overshoot.

Figure 5 is shown that when the motor entered steady state, the system speed tracking error range of the FOCSMC method is 0.05–0.25r/min, which is about 0.02% of the given speed, and the error range of the RBF-FOCSMC method is 0.08–0.57r/min, which is about 0.065% of the given speed. The system speed tracking error range of RBF-CSMC method is 0.05–0.3r/min, which is about 0.035% of the given speed. The error range of RBF-FOCSMC method is 0.02r/min ~ 0.21r/min, which is about 0.019% of the given speed, it is significantly reduced compared with the former three methods. By comparing the speed tracking error curve, it can be seen that the RBF-FOCSMC method has smaller speed tracking error and smoother control effect.

4.2 System Analysis of the Load Change Response

To further verify the anti-load disturbance ability of the proposed method, experiments are carried out for three speed situation: 500r/min, 1000r/min, and 1500r/min. The whole simulation time is 1 s, and the load with 5 \(N \cdot m\) and 10 \(N \cdot m\) is suddenly added at 0.5s for above three situation. The speed response curves under different conditions are shown in Figs. 6 and 7 (Tables 5, 6, 7, 8).

Fig. 6
figure 6

Comparison curves of four control methods under load torque disturbance of 5 \(N \cdot m\) at 0.5 s. a The speed is 500r/min. b The speed is 1000r/min. c The speed is 1500r/min

Full size image
Fig. 7
figure 7

Comparison curves of four control methods under load torque disturbance of 10 \(N \cdot m\) at 0.5 s. a The speed is 500r/min. b The speed is 1000r/min. c The speed is 1500r/min

Full size image
Table 5 Analysis of four control methods 5 \(N \cdot m\) load torque disturbance at 0.5 s (500r/min)
Full size table
Table 6 Analysis of four control methods under 5 \(N \cdot m\) load torque disturbance at 0.5 s (1000r/min)
Full size table
Table 7 Analysis of four control methods under 5 \(N \cdot m\) load torque disturbance at 0.5 s (1500r/min)
Full size table
Table 8 Analysis of four control methods under 10 \(N \cdot m\) load torque disturbance at 0.5 s (500r/min)
Full size table

Taking the speed of 1000r/min with 10 \(N \cdot m\) load torque disturbance at 0.5 s as an example, from Fig. 7b and Table 9, it can be seen that when the motor is suddenly added load disturbance, the speed of FOCSMC, RBF-FOSMC, and RBF-CSMC decreases by 13.9r/min, 7.8r/min, and 7.2r/min, respectively, and the time to restore stability are 0.0075s, 0.009s, and 0.011s, respectively. The proposed RBF-FOCSMC speed decreases by 3.8r/min, and the time to restore stability after loading is 0.0045s. The detailed experimental results at other speed and load conditions are shown in Tables 5, 6, 7, 8, 9, 10. According to the comparison, in terms of anti-load disturbance ability, the FOCSMC cannot effectively attenuate mismatch disturbance. While the RBF-FOCSMC realizes strong anti-disturbance ability by compensation, it proves that the proposed composite control method has smaller speed fluctuation and faster response.

Table 9 Analysis of four control methods under 10 \(N \cdot m\) load torque disturbance at 0.5 s (1000r/min)
Full size table
Table 10 Analysis of four control methods under 10 \(N \cdot m\) load torque disturbance at 0.5 s (1500r/min)
Full size table

To verify the tracking performance, the motor is started with a load of 3 \(N \cdot m\), and the load is suddenly increased to 10 \(N \cdot m\) at 0.5s and then reduced to 6 \(N \cdot m\) at 0.8s. The motor torque response curve is shown in Fig. 8. It can be seen that when the system is affected by the external disturbance, the proposed RBF neural network method can quickly and stably track the system load, and the disturbance estimator is fed back to the speed controller to enhance the anti-interference ability. The three-phase current curves are shown in Fig. 9, which is consistent and proportional to the motor torque.

Fig. 8
figure 8

Motor torque curve

Full size image
Fig. 9
figure 9

Three-phase current curve of motor

Full size image

4.3 System Analysis of the Parameter Change Response

To verify the robustness of proposed method with parameter changes, the values of rotor flux and inductance are changed in the experiment, and then, the performances are compared and analyzed. Specifically, the inductance and flux are increased or decreased by 30%, respectively, and the speed is setting to + 1000r/min for experiment comparison. The results under the four schemes are shown in Figs. 10, 11, 12, 13, and the data analysis are shown in Tables 11, 12, 13, 14.

Fig. 10
figure 10

Comparative curves of FOCSMC method when the parameters are changed by 30%: a 30% inductance change and b 30% flux change

Full size image
Fig. 11
figure 11

Comparative curves of RBF-FOSMC method when the parameters are changed by 30%: a 30% inductance change and b 30% flux change

Full size image
Fig. 12
figure 12

Comparative curves of RBF-CSMC method when the parameters are changed by 30%: a 30% inductance change and c 30% flux change

Full size image
Fig. 13
figure 13

Comparative curves of RBF-FOCSMC method when the parameters are changed by 30%: a 30% inductance change and b 30% flux change

Full size image
Table 11 Performance analysis of FOCSMC control method under parameter change
Full size table
Table 12 Performance analysis of RBF-FOSMC control method under parameter change
Full size table
Table 13 Performance analysis of RBF-CSMC control method under parameter change
Full size table
Table 14 Performance analysis of RBF-FOCSMC control method under parameter change
Full size table

From Fig. 10 and Table 11, it can be seen that when the motor is rotating with inductance increases or decreases, the speed of FOCSMC method changes by 0.7r/min and 1.1r/min compared with the normal condition, and the response time changes by 0.0005s; when the flux linkage increases and decreases, the speed changes by 0.9r/min and 0.6r/min compared with the normal conditions, and the response time changes by 0.0007s and 0.011s.

From Fig. 11 and Table 12, it can be seen that when the motor is rotating with inductance increases or decreases, the speed of the RBF-FOCSMC method changes by 15r/min and 15.5r/min compared with the normal condition, and the response time changes by 0.0026s and 0.0074s, respectively. When the flux linkage increases and decreases, the speed changes by 18.5r/min and 15r/min compared with normal condition, and the response time changes by 0.0056s and 0.0064s.

From Fig. 12 and Table 13, it can be seen that when the motor is rotating with inductance increases or decreases, the speed of the RBF-CSMC method changes by 0.4r/min and 0.8r/min compared with the normal condition, and the response time changes by 0.0018s and 0.0028s, respectively. When the flux linkage increases and decreases, the speed changes by 18.1r/min and 7.1r/min compared with the normal conditions, and the response time changes by 0.0042s and 0.0043s.

From Fig. 13 and Table 14, it can be seen that when the motor is rotating with inductance increases or decreases, the speed of the RBF-FOCSMC method changes by 0.1r/min and 0.2r/min compared with the normal condition, and the response time changes by 0.0006s and 0.0003s, respectively. When the flux linkage increases and decreases, the speed changes by 0.1r/min and 0.1r/min compared with the normal conditions, and the response time changes by 0.0003s and 0.0001s.

From the results of four comparative experiments, it can be seen that RBF-FOCSMC has little impact on speed tracking and response time compared with normal condition. Therefore, the designed RBF-FOCSMC has good anti-parameter disturbance ability.

5 Conclusion

In this paper, a control strategy combining RBF neural network and complementary fractional non-singular terminal sliding mode control is designed. The fractional order complementary non-singular terminal sliding mode is used to improve the static and dynamic tracking performance of the motor. While improving the tracking accuracy, the steady-state error is reduced, and finally, the effect of suppressing chattering is achieved. The RBF neural network is used to approximate the disturbance and un-modeled parts of the system, which perform feedback compensation to further improve the dynamic response ability and anti-interference ability of the system. The experimental results prove the feasibility of the proposed algorithm, which shows obvious control effect; it has higher tracking accuracy and faster response than the ordinary sliding mode control method. Therefore, the proposed method can provide an ideal method for motor control system, and also give a theoretical support for improving the PMSM control accuracy of electric vehicles. While due to the limitations of the current experimental conditions and environment, only the simulation experiment is verified in this paper, the physical experiment will be studied and focused on the future work.