Introduction

Capillary phenomena between plates appear only in channels of small size on the ground. While in the absence of gravity, channels in which capillary phenomena can happen are not limited to small scale. Therefore, capillary flow becomes a significant portion of liquid behavior in space.

Capillary driven flows in flow channels with uniform cross section have been widely studied. Lucus (1918) and Washburn (1921) derived the well-known Lucus-Washburn equation by adopting a balance between the capillary driven force, the friction force on the tube wall and the gravity forces. The dynamic equation of capillary driven flow was presented by Levine et al. (1976) with consideration of the capillary driven force and viscous force on the tube wall and the convective pressure loss in cylindrical tubes. This equation was improved by Stange et al. (2003) after adding factors of the meniscus reorientation, the dynamic contact angle, and the development of capillary driven flow. The capillary driven flow in oval tubes under microgravity was explored and a new flow model in which the entire flow process was divided into two regions was presented by Chen et al. (2021b). The oscillatory regime for liquid rise in vertical capillaries was investigated and an analytical solution was proposed by Wang et al. (2019). A theoretical model of capillary driven flow along interior corners was proposed by Weislogel and Lichter (1998), and was further extended to interior corners formed by plates with different wettability by Weislogel and Nardin (2005), as well as to rounded interior corners by Chen et al. (2006). Furthermore, capillary flows in interior corners formed by cylindrical and planar walls (Li et al. 2015), in curved interior corners (Wu et al. 2018), in narrow gaps between two vertical plates making a small angle (Higuera et al. 2008), in a narrow and tilting corner (Tian et al. 2019), and in the corner between two curved walls (Zhou and Doi 2020) were deeply analyzed and the corresponding dynamic equations of capillary rise were obtained. Dreyer et al. studied capillary driven flow between parallel plates and divided the entire flow process into three regions in 1994. Besides, capillary rise between two closely spaced, parallel planar surfaces (Bullard et al. 2009), in open channels (Klatte et al. 2008), between parallel cylindrical fibers (Charpentier et al. 2020), and in porous wire meshes (Weng et al. 2019) were investigated and the mathematical models of capillary driven flow under the above conditions were established. Different methods have been used in the study of capillary rise, such as the dimensionless scaling (by Fries and Dreyer 2009) and the Lattice-Boltzmann method (by Wolf et al. 2010). In addition, Chen et al. (2021a) used the theory of capillary driven flow to optimize tank’s propellant management device.

The flow in capillary tubes with varying diameters has also been payed great attention in recent years. Laminar fully developed flow and pressure drop in converging–diverging microtubes with linearly varying cross-sectional area was investigated and an analytical model for frictional resistance to flow was developed (Akbari et al. 2010). The nonlinear, second-order differential equation starting from the Navier–Stokes equations was derived (Liou et al. 2009). A theoretical model involving the inertia, viscosity, capillary force and gravity to describe the dynamics of capillary flow was established (Lei et al. 2021). The viscosity, capillary force and gravity was considered and an ordinary differential equation with a term that is dependent upon the shape of the capillary channel was proposed (Figliuzzi et al. 2013). However, because they all adopted some simplifications, such as ignoring the convective pressure loss in the entrance and the inertia force in the reservoir, their theoretical models couldn’t predict the meniscus height accurately in the beginning of capillary driven flow.

In this paper, a mathematical model for capillary driven flow between plates with varying widths and distances under microgravity is established. The inertia force, convective pressure loss and dynamic contact angle are also considered in this model. The model has been proven accurate in the entire process by the numerical simulation of flows between plates with small varying aspect ratios and Reynolds (Re) numbers. Effects of different forces acting on the control volume between plates are analyzed in detail. Based on this mathematical model, the optimization of channels is possible. Influences of width and distance of the plates are also discussed in detail.

Derivation of Model Equation

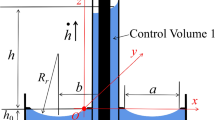
As Fig. 1 shows, the research model includes a cylindrical reservoir and two plates that are partially immersed in the liquid. Figure 2 shows side view of plates with varying width. The Cartesian coordinates (x, y, z) are used in this study. The original point is located at the center of the initial profile of free surface in the reservoir. The distance between the wetting barriers is a. The distance between the center of the meniscus in the reservoir and the central line between the plates is b. The radius of the free surface in the reservoir is Rr. The width of plates is 2c and the distance between the two plates is 2d. The plates’ width and distance in the xOy plane are 2c0 and 2d0 respectively. The liquid climbing height is h and its dynamic contact angle on the wall of plates is αd. The liquid space between the two plates and above the free surface in the reservoir is set to be Control Volume 1 (CV1).

Fig. 1
figure 1

Front view of plates with varying distance

Full size image
Fig. 2
figure 2

Side view of plates with varying width

Full size image

For a Newtonian, incompressible fluid of constant viscosity, the continuity equation and z-component Navier–Stokes equation can be written as

$$\frac{\partial {u}_{x}}{\partial x}+\frac{\partial {u}_{y}}{\partial y}+\frac{\partial {u}_{z}}{\partial z}=0$$
(1)
$$\begin{aligned}&\rho \left(\frac{\partial {u}_{z}}{\partial t}+{u}_{x}\frac{\partial {u}_{z}}{\partial x}+{u}_{y}\frac{\partial {u}_{z}}{\partial y}+{u}_{z}\frac{\partial {u}_{z}}{\partial z}\right)\\&\quad=-\frac{\partial p}{\partial z}+\rho g+\mu \left[\frac{{\partial }^{2}{u}_{z}}{\partial {x}^{2}}+\frac{{\partial }^{2}{u}_{z}}{\partial {y}^{2}}+\frac{{\partial }^{2}{u}_{z}}{\partial {z}^{2}}\right]\end{aligned}$$
(2)

At low Re number, the Hagen-Poiseuile equation remains valid, so capillary flows are laminar in nature and a parabolic profile is assumed for the axial velocity component uz, that is,

$${u}_{z}=\frac{3}{2}\frac{{c}_{h}{d}_{h}}{cd}\dot{h}\left(1-\frac{{x}^{2}}{{d}^{2}}\right)$$
(3)

where ch and dh represent plates’ half width and half distance at z = h. For flows between plates with small varying aspect ratios, it is assumed that:

$$\frac{{u}_{y}}{{u}_{x}}=\frac{y}{x}$$
(4)

For plates with a large aspect ratio, the secondary flow components are always small near the central line between the plates but can become significant near the plates. In this region, the approximation can be less satisfactory. The varying aspect ratio of plates is defined as

$$e=\sqrt{{\dot{c}}^{2}+{\dot{d}}^{2}}$$
(5)

Combining Eqs. (1), (3) and (4), it can be obtained that

$${u}_{x}=\frac{3{c}_{h}{d}_{h}x}{8{c}^{2}{d}^{4}}\dot{h}\left(2{\dot{cd}}^{3}+2c{\dot{d}d}^{2}-\dot{c}d{x}^{2}-c\dot{d}{x}^{2}\right)$$
(6)
$${u}_{y}=\frac{3{c}_{h}{d}_{h}y}{8{c}^{2}{d}^{4}}\dot{h}\left(2\dot{c}{d}^{3}+2c\dot{d}{d}^{2}-\dot{c}d{x}^{2}-c\dot{d}{x}^{2}\right)$$
(7)

Integrating Eq. (2) in CV 1 and eliminating the zero terms, it can be obtained that

$$\begin{array}{c}{\int }_{0}^{h}{\int }_{-c}^{c}{\int }_{-d}^{d}\frac{\partial {u}_{z}}{\partial t}dxdydz+{\int }_{0}^{h}{\int }_{-c}^{c}{\int }_{-d}^{d}{u}_{x}\frac{\partial {u}_{z}}{\partial x}dxdydz+{\int }_{0}^{h}{\int }_{-c}^{c}{\int }_{-d}^{d}{u}_{z}\frac{\partial {u}_{z}}{\partial z}dxdydz\\ ={\int }_{0}^{h}{\int }_{-c}^{c}{\int }_{-d}^{d}\frac{-1}{\rho }\frac{\partial p}{\partial z}dxdydz+{\int }_{0}^{h}{\int }_{-c}^{c}{\int }_{-d}^{d}v \left(\frac{{\partial }^{2}{u}_{z}}{\partial {x}^{2}}+\frac{{\partial }^{2}{u}_{z}}{\partial {z}^{2}}\right)dxdydz\end{array}$$
(8)

Equation (8), combined with Eqs. (3), (6) and (7), yields the following equations,

$${\int }_{0}^{h}{\int }_{-c}^{c}{\int }_{-d}^{d}\frac{\partial {u}_{z}}{\partial t}dxdydz=4{c}_{h}{d}_{h}h\ddot{h}$$
(9)
$${\int }_{0}^{h}{\int }_{\text{-c}}^{c}{\int }_{-d}^{d}{u}_{x}\frac{\partial {u}_{z}}{\partial x}dxdydz=-21{c}_{h}^{2}{d}_{h}^{2}{\dot{h}}^{2}{\int }_{0}^{h}\frac{c\dot{d}+\dot{c}d}{{\text{10c}}^{2}{{\text{d}}}^{2}}dz$$
(10)
$${\int }_{0}^{h}{\int }_{-c}^{c}{\int }_{-d}^{d}{u}_{z}\frac{\partial {u}_{z}}{\partial z}dxdydz=-12{c}_{h}^{2}{d}_{h}^{2}{\stackrel{*}{h}}^{2}{\int }_{0}^{h}\frac{c\dot{d}+2\dot{c}d}{5{c}^{2}{d}^{2}}dz$$
(11)
$$\begin{aligned}&{\int }_{0}^{h}{\int }_{-c}^{c}{\int }_{-d}^{d}v \left(\frac{{\partial }^{2}{u}_{z}}{\partial {x}^{2}}+\frac{{\partial }^{2}{u}_{z}}{\partial {z}^{2}}\right)dxdydz\\&\quad=-4{c}_{h}{d}_{h}v\ \dot{h}{\int }_{0}^{h}\frac{3{c}^{2}{\dot{d}}^{2}+3{c}^{2}+c\ddot{c}{d}^{2}-2{\dot{c}}^{2}{d}^{2}}{{c}^{2}{d}^{2}}dz\end{aligned}$$
(12)

The capillary driven force can be written as

$$\begin{aligned}&{\int }_{0}^{h}{\int }_{-c}^{c}{\int }_{-d}^{d}\frac{-1}{\rho }\frac{\partial p}{\partial z}dxdydz\\&\quad=\frac{-1}{\rho }\left[{\int }_{-{c}_{h}}^{{c}_{h}}{\int }_{-{d}_{h}}^{{d}_{h}}p\left(h,t\right)dxdy-{\int }_{-{c}_{0}}^{{c}_{0}}{\int }_{-{d}_{0}}^{{d}_{0}}p\left(0,t\right)dxdy\right]\end{aligned}$$
(13)

The pressure on the upper control surface is

$$p(h,t)={p}_{0}-\sigma \left[\frac{\cos\left({\alpha }_{d}+\mathrm{arctan}\ \dot{d}\right)}{d}-\frac{1}{c}\right]$$
(14)

where p0 stands for the atmosphere pressure and σ stands for the liquid surface tension. For a perfectly wetting liquid whose static contact angle is 0, there is an empirical formula for calculating the dynamic contact angle proposed by Jiang et al. (1979), which is written as

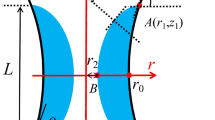
$$\cos{\alpha }_{d}=1-2\mathrm{tanh}\left[4.96*{(\frac{\mu \dot{h}}{\sigma })}^{0.702}\right]$$
(15)

where μ represents the dynamic viscosity of the liquid. To calculate the pressure at the entrance, it is necessary to build another control volume (CV 2) around the entrance in the reservoir. The radius of CV2, re, equals \(\sqrt{\frac{4{c}_{0}{d}_{0}}{\pi }}\), as shown in Fig. 3. The immersion depth of plates into the reservoir is neglected. In CV 2, we have

$${I}_{c}={I}_{e}-{I}_{l}+\Sigma F$$
(16)

where Ic stands for the rate of change of total momentum in CV 2, Ie represents the flux of momentum entering CV 2, Il represents the flux of momentum leaving CV 2, and ΣF stands for the sum of forces acting on CV 2.

Fig. 3
figure 3

An equivalent circular entrance and CV 2 around the inlet

Full size image

Combined with the continuity equation, the radial flow speed w of the fluid flowing through the hemispherical surface at r = re can be obtained as

$${\text{w}}\left(r,t\right)=\frac{{\text{c}}_{\text{h}}{{\text{d}}}_{\text{h}}{{\text{r}}}_{\text{e}}^{2}}{2{c}_{0}{d}_{0}{r}^{2}}\dot{h}$$
(17)

In CV 2, the Navier–Stokes equation in the radial direction is written as

$$\frac{\partial \mathrm{w}}{\partial t}=-\frac{1}{\rho }\frac{\partial p}{\partial r}+v\left[\frac{1}{{r}^{2}}\frac{\partial }{\partial r}\left({r}^{2}\frac{\partial w}{\partial r}\right)-\frac{2w}{{r}^{2}}\right]$$
(18)

The flow is not in the creeping flow regime. Combined with Eqs. (17), (18) is integrated with respect to r from re to \(+\infty\), pressure on the hemispherical surface at r = re can be obtained that

$${\text{p}}\left({r}_{e},t\right)={p}_{0}+{p}_{R}-\frac{1}{2}\frac{\rho {c}_{h}{d}_{h}{r}_{e}^{2}}{{c}_{0}{d}_{0}{r}^{2}}\ddot{h}$$
(19)

where pR represents the capillary pressure caused by the concave free surface in the reservoir. According to the geometric relationship, an approximate formula is given for calculating Rr as below,

$${R}_{r}=-\frac{{a}^{3}b}{24{\int }_{0}^{h}cddz}$$
(20)

So the two components of the stress tensor on the hemispheric surface at r = re are written as

$${\sigma }_{rr}=-{p}_{r={r}_{e}}+2\mu {\left(\frac{\partial w}{\partial r}\right)}_{r={r}_{e}},\ {\sigma }_{r\theta }=0$$
(21)

The force acted on the hemispheric surface at r = re in the z-direction can be derived that

$$\begin{aligned}{\text{F}}_{1}&={2}\pi {r}_{e}^{2}{\int }_{0}^{\pi /2}\left(-{\sigma }_{rr}\right)\sin\theta \cos\theta d\theta \\&=\pi {{r}_{e}}^{2}\left({p}_{0}+{p}_{R}-\frac{1{c}_{h}{d}_{h}}{2{c}_{0}{d}_{0}}\rho {r}_{e}\ddot{h}-\frac{{c}_{h}{d}_{h}}{{c}_{0}{d}_{0}}\frac{2\mu }{{r}_{e}}\dot{h}\right)\end{aligned}$$
(22)

The flux of momentum in the z-direction entering the hemisphere through the surface r = re is

$$2\pi \rho {{r}_{e}}^{2}{\int }_{0}^{\pi /2}\sin\theta {w}_{{r}_{e}}^{2}\cos\theta d\theta =\frac{1{{c}_{h}}^{2}{d}_{h}^{2}}{4{c}_{0}^{2}{d}_{0}^{2}}\pi \rho {r}_{e}^{2}{\dot{h}}^{2}$$
(23)

The flux momentum in the z-direction leaving the control surface at z = 0 is

$${\int }_{-{c}_{0}}^{{c}_{0}}{\int }_{-d}^{d}\rho {u}_{z0}^{2}dxdy=\frac{24}{5}\frac{{c}_{h}^{2}{d}_{h}^{2}}{{c}_{0}{d}_{0}}\rho {\dot{h}}^{2}$$
(24)

The flux of acceleration in the z-direction through the hemispheric surface at r = re is

$$\begin{aligned}&2\pi {r}_{e}^{2}{{\int }_{0}^{\frac{\pi }{2}}\left(\frac{Dw}{Dt}\right)}_{r={r}_{e}}{w}_{r={r}_{e}}\sin\theta \cos\theta d\theta \\&\quad=\frac{1}{4}\frac{{{c}_{h}}^{2}{d}_{h}^{2}}{{c}_{0}^{2}{d}_{0}^{2}}\pi {r}_{e}^{2}\dot{h}\left(\ddot{h}+\frac{1}{{r}_{e}}\frac{{c}_{h}{d}_{h}}{{c}_{0}{d}_{0}}{\dot{h}}^{2}\right)\end{aligned}$$
(25)

The flux of acceleration in the z-direction through the surface at z = 0 is

$${\int }_{-{c}_{0}}^{{c}_{0}}{\int }_{-d}^{d}u{a}_{z}dx=\frac{24}{5}\frac{{{c}_{h}}^{2}{d}_{h}^{2}}{{c}_{0}{d}_{0}}{\dot{h}}^{2}$$
(26)

Divided by the volume flux \(\pi {{r}_{e}}^{2}\dot{h}\), Eqs. (25) and (26) yield two accelerations which are averaged to get the mean acceleration in the hemisphere. Therefore, the mean acceleration of CV 2 is

$$\frac{2}{3}\frac{{{c}_{h}}^{2}{d}_{h}^{2}}{{{c}_{0}}^{2}{d}_{0}^{2}}\rho \pi {r}_{e}^{3}\left(\frac{29}{40}\ddot{h}+\frac{1}{8}\frac{1}{{r}_{e}}\frac{{c}_{h}{d}_{h}}{{c}_{0}{d}_{0}}{\dot{h}}^{2}\right)$$
(27)

Inserting Eqs. (19)-(27) into Eq. (16), the force at the inlet in the z-direction is

$$\begin{array}{c}{\int }_{-{c}_{0}}^{{c}_{0}}{\int }_{-{d}_{0}}^{{d}_{0}}p\left(0,t\right)dxdy=\pi {r}_{e}^{2}\left({p}_{0}+{p}_{R}\right)-\left(\frac{1}{2}+\frac{29}{60}\frac{{c}_{h}{d}_{h}}{{c}_{0}{d}_{0}}\right)\frac{{c}_{h}{d}_{h}}{{c}_{0}{d}_{0}}\pi \rho {{r}_{e}}^{3}\ddot{h}\\ -\frac{2\pi {c}_{h}{d}_{h}}{{c}_{0}{d}_{0}}{r}_{e}\mu \dot{h}-\left(\frac{19}{20}+\frac{{c}_{h}{d}_{h}}{12{c}_{0}{d}_{0}}\right)\frac{{{c}_{h}}^{2}{d}_{h}^{2}}{{{c}_{0}}^{2}{d}_{0}^{2}}\pi \rho {{r}_{e}}^{2}{\dot{h}}^{2}\end{array}$$
(28)

Inserting Eqs. (9)-(15) and Eq. (28) into Eq. (8), the dynamic equation is derived as

$$\begin{array}{c}\left[\gamma h+\left(\frac{1}{2}+\frac{29}{60}\gamma \right)\gamma {r}_{e}\right]\ddot{h}=\frac{\sigma }{\rho }\cdot \gamma \left[\frac{\mathrm{cos}\left({\alpha }_{d}+\mathrm{arctan}\ \dot{d}\right)}{d}-\frac{1}{c}\right]-\frac{\sigma }{\rho }\cdot \frac{24}{{a}^{3}b}{\int }_{0}^{h}cddz\\ +\left[\frac{21}{4}{c}_{h}{d}_{h}{\int }_{0}^{h}\frac{c\dot{d}+\dot{c}d}{10{c}^{2}{d}^{2}}dz+3{c}_{h}{d}_{h}{\int }_{0}^{h}\frac{c\dot{d}+2\dot{c}d}{5{c}^{2}{d}^{2}}dz-\left(\frac{19}{20}+\frac{\gamma }{12}\right)\right]{\gamma }^{2}{\dot{h}}^{2}\\ -\gamma v\ \dot{h}{\int }_{0}^{h}\frac{3{c}^{2}{\dot{d}}^{2}+3{c}^{2}+c\ddot{c}{d}^{2}-2{\dot{c}}^{2}{d}^{2}}{{c}^{2}{d}^{2}}dz-\frac{2\gamma }{{r}_{e}}v\ \dot{h}\end{array}$$
(29)

where γ equals chdh/c0d0. The term on the left side is the inertia force between plates (Fip). The first term on the right side is the capillary pressure between plates (Fcp), the second term on the right side is the capillary pressure in the reservoir (Fcr), the third term on the right side is the convective pressure loss between plates (Flp), the fourth term on the right side is the friction force between plates (Ffp), and the last term on the right side is the viscous force in the reservoir (Ffr).

The development of forces predicted by the flow model is shown in Fig. 4(a) and (b) under the condition of c = 7 mm and d = 1/1200z2-1/10z + 4 mm. The liquid is SF 10. Figure 4(a) shows the development of forces in the first 2 s. In this period, Fpl and Fip also play dominant roles. They are neglected in our previous study on capillary flows in tubes with varying diameters, which will cause unacceptable deviation in the beginning of the flow. Figure 4(b) shows the development of forces in the first 14 s. It can be seen that, if the flow time is long enough, the pressure loss at the entrance can be neglected. The deviation resulting from neglection of the pressure loss is acceptable. In this situation it can be considered that only Fip, Fcp and Ffp play roles. Thus Eq. (29) can be simplified as follows.

Fig. 4
figure 4

Development of forces vs time. c = 7 mm and d = 1/1200z2-1/10z + 4 mm. a In the first 2 s and b in the first 14 s

Full size image
$$4{c}_{h}{d}_{h}h\ddot{h}=\frac{\sigma }{\rho }\cdot 4{c}_{h}{d}_{h}\left[\frac{\cos\left({\alpha }_{d}+\mathrm{arctan}\ \dot{d}\right)}{d}-\frac{1}{c}\right]-4{c}_{h}{d}_{h}v\ \dot{h}{\int }_{0}^{h}\frac{3{c}^{2}{\dot{d}}^{2}+3{c}^{2}+c\ddot{c}{d}^{2}-2{\dot{c}}^{2}{d}^{2}}{{c}^{2}{d}^{2}}dz$$
(30)

This equation is similar to the one proposed by Lei et al.27, which describes the capillary flow in an undulated tube, written as

$$\begin{aligned}&\rho \frac{d\left\{{\int }_{0}^{h}{\left[1-\varepsilon \cos\left(\alpha \frac{z}{{R}_{0}}\right)\right]}^{2}dz\dot{h}\right\}}{dt}\\&\quad=\frac{2\lambda \cos\phi }{{R}_{0}}\left[1-\varepsilon \cos\left(\alpha \frac{z}{{R}_{0}}\right)\right]-\frac{8\eta {{R}_{h}}^{2}}{{\mathrm{R}}_{0}^{2}}\dot{h}{\int }_{0}^{h}\frac{1}{{R}^{2}}dz\\&\qquad-\frac{\rho g\sin\phi }{{{R}_{0}}^{2}}{\int }_{0}^{h}{R}^{2}dz\end{aligned}$$
(31)

When c and d are both constant, Eq. (29) is transformed into the capillary flow equation between parallel plates,

$$\ddot{h}=\frac{1}{h+\frac{59}{60}{r}_{e}}\left[\frac{\sigma }{\rho }\left(\frac{\cos{\alpha }_{d}}{d}-\frac{2}{c}-\frac{24cdh}{{a}^{3}b}\right)-\left(\frac{3h}{{d}^{2}}+\frac{2}{{r}_{e}}\right)v\ \dot{h}-\frac{31}{30}{\dot{h}}^{2}\right]$$
(32)

This is quite close to the equation proposed by Dreyer et al. (1994) shown as below,

$$\begin{aligned}\ddot{h}=&\frac{1}{h+0.916{r}_{e}}\left[\frac{\sigma }{\rho }\left(-\frac{1}{{R}_{1}}-\frac{1}{{R}_{2}}+\frac{1}{{R}_{3}}\right)\right.\\&\left.-\frac{3vh\dot{h}}{{c}^{2}}-\frac{1}{2}{\dot{h}}^{2}\left(1.918+\frac{8}{\mathrm{Re}}\right)\right]\end{aligned}$$
(33)

Using the following characteristic quantities:

$${t}_{c}=\frac{{{d}_{0}}^{2}}{3v}$$
(34)
$${u}_{c}=\sqrt{\frac{\sigma }{\rho {d}_{0}}}$$
(35)
$$Oh=\frac{\mu }{2\sqrt{\rho \sigma {d}_{0}}}$$
(36)

Equation (29) can be transformed into nondimensional form, which reads

$$\begin{aligned}&\left[\gamma {h}_{*}+\left(\frac{1}{2}+\frac{29}{60}\gamma \right)\gamma \frac{12}{\sqrt{\pi }}\sqrt{\frac{c}{{d}_{0}}}Oh\right]\ddot{{h}_{*}}=\gamma \left[\frac{\cos\left({\alpha }_{d}+\mathrm{arctan}\ \dot{d}\right){d}_{0}}{d}-\frac{{d}_{0}}{c}\right]\\&\quad-\frac{24{d}_{0}}{{a}^{3}b}{\int }_{0}^{h}cddz +\left[\frac{21}{4}{c}_{h}{d}_{h}\gamma {\int }_{0}^{h}\frac{c\dot{d}+\dot{c}d}{10{c}^{2}{d}^{2}}dz+3{c}_{h}{d}_{h}\gamma {\int }_{0}^{h}\frac{c\dot{d}+2\dot{c}d}{5{c}^{2}{d}^{2}}dz\right.\\&\quad\left.-\left(\frac{19}{20}+\frac{\gamma }{12}\right){\gamma }^{2}\right]{\dot{{h}_{*}}}^{2}-\gamma \frac{A\nu }{{u}_{c}}\dot{{h}_{*}}-2\sqrt{\pi }\gamma \sqrt{\frac{{d}_{0}}{c}}Oh\dot{{h}_{*}}\end{aligned}$$
(37)

where \({t}_{*}=\frac{t}{{t}_{c}},\ {h}_{*}=\frac{h}{{t}_{c}{u}_{c}},\ \dot{{h}_{*}}=\frac{\dot{h}}{{u}_{c}},\ \ddot{{h}_{*}}=\frac{{t}_{c}\dot{h}}{{u}_{c}}\) and \(A={\int }_{0}^{h}\frac{3{c}^{2}{\dot{d}}^{2}+3{c}^{2}+c\ddot{c}{d}^{2}-2{\dot{c}}^{2}{d}^{2}}{{c}^{2}{d}^{2}}dz\).

Numerical Simulation

To validate the proposed equation, capillary flows in several classical geometries are discussed in this paper. Figure 5 shows a mesh model established for the numerical simulation performed with the Volume of Fluid (VOF) method in Fluent. Establishing dozens of mesh models will take too much time. Using a square cylinder instead of a circular cylinder as the reservoir can greatly simplify the modeling process. This modification is acceptable because the influence of capillary force in the reservoir is very small compared to other forces, as Figs. 4 show. Therefore the impact of this simplification is negligible. The square cylinder with a width of 140 mm and an equivalent radius of 79.0 mm is used in the theoretical calculations. Mesh independence has been conducted and the total number of grids is chosen to be 1.1 million. Boundary layers are established near all walls. The first layer of the mesh is about 0.1 mm high and the expansion ratio between two adjacent layers is 1.2. A type of Silicone Oil named by its kinematic viscosity (SF 10) is selected as the fluid in this study. Its properties are listed in Table 1. The flow is assumed to be laminar in the simulation. Parameters settings are shown in Table 2 and the model parameters are shown in Table 3. In this study Remax is defined as

Fig. 5
figure 5

Mesh model of numerical simulation

Full size image
Table 1 Liquid properties (25 ℃)
Full size table
Table 2 Numerical settings
Full size table
Table 3 Model parameters
Full size table
$$\mathrm{Re}=\frac{2\rho {r}_{e}{\dot{h}}_{\mathrm{max}}}{\mu }$$
(38)

The meniscus height vs time is shown in Fig. 6. The yellow surface stands for the liquid–gas interface. At t = 0 s, all of the liquid is in the reservoir and the free surface in the reservoir is a flat plane. Once the simulation begins, the liquid between the plates forms a concave interface and flows upwards continuously. On the other hand, because the liquid is absorbed into the channel, a concave interface is formed in the reservoir. The meniscus height is recorded at different times and compared with theoretical results.

Fig. 6
figure 6

Meniscus height vs time. c = 7 mm, d = 1/1800z2-1/15z + 4 mm

Full size image

Results and Discussions

Figure 7 show the theoretical and numerical results of the meniscus height vs time. The abscissa represents the elapsed time, and the ordinate represents the meniscus height. Each picture shows results of two models and they are distinguished by black and blue. The solid line indicates theoretical results and the dot indicates numerical data. The triangles in Fig. 7(a) and (b) represent results calculated from the dynamic equation proposed by Dreyer et al. Because the concave-convex direction of the meniscus formed between plates and the development of the flow at the beginning are not considered, this may cause a little difference between numerical and theoretical results. Generally speaking, numerical results are in good agreement with corresponding theoretical data and the deviation is acceptable. In the case of parallel plates, theoretical results obtained in this paper are quite consistent with Dreyer’s.

Fig. 7
figure 7

Comparison between theoretical and numerical results

Full size image

Shape Optimization

This section presents a method to design plate shapes which promotes fast wicking. And the situations in which c or d is a constant are considered. Figure 8(a) shows the linear variation of the plates’ width or distance. Figure 8(b) shows the parabolic variation of the plates’ width or distance, and the parabola vertex is located in the middle of plates in the z direction. In this study the height of plates is designed to be 0.12 m.

Fig. 8
figure 8

Profiles of plates. a Linear variation and b parabolic variation

Full size image

When the width or distance of plates varies linearly, the time needed to reach the top of plates is shown in Fig. 9. The blue line represents results of plates with varying distance.In this case c = 7 mm and d0 = 3 mm. The orange line represents results of plates with varying width. In this case d = 2 mm and c0 = 5 mm. The black dots indicate results in the case of parallel plates. Positive varying aspect ratio means decrease of distance or increase of width. The height of plates is 120 mm. It can be seen that the greater the increasing aspect ratio of distance or the decreasing aspect ratio of width, the faster the flow speed. Liquid flow speed varies monotonically with the variation of plates’ width or distance. Moreover, when the width of plates continues to decrease or the distance between plates continues to increase to a certain value, the meniscus will finally reach the equilibrium height and keeps stable.

Fig. 9
figure 9

Time needed to reach the top of plates between different plate models

Full size image

When the profile of plates is parabolic, the results of the meniscus height vs time are shown in Fig. 10(a) and (b). When d is a constant and the width of plates varies parabolically, the liquid flow speed will increase as the aspect ratio increases, as shown in Fig. 10(a). When c is a constant and the distance between plates varies parabolically, it is more complicated. The parabola vertex is located in the middle of plates in the z direction. The distance between the two vertexes is defined as the neck distance. In Fig. 10(b), d0 is 4 mm for all the models. The blue line represents the results when the neck distance between plates is 1 mm, the red line represents the results when the neck distance is 2 mm, and the black line represents the results when the neck distance is 3 mm. The flow speed is faster in the beginning when the aspect ratio is larger, as shown in Fig. 10(b). However, after about 5 s, the flow speed in the case of 1 mm-wide neck distance is slower than that in the case of 2 mm-wide neck distance. After about 10.5 s, the flow speed in the case of 3 mm-wide neck distance is faster than that in the case of 2 mm-wide neck distance. In the end, the liquid between plates with a 3 mm-wide neck distance reaches the equilibrium height first. Flow speeds in the cases of 2 mm-wide and 3 mm-wide neck distances between plates are both faster than that in the case of parallel plates. The liquid flow speed won’t vary monotonically as the distance between plates varies. Too small neck distance won’t be helpful for increasing the flow speed.

Fig. 10
figure 10

Meniscus height vs time from different models. a Varying width and d = 2 mm. b Varying distance and c = 7 mm

Full size image

Conclusions

In this paper, a mathematical model for capillary driven flow between plates with varying width and distance under microgravity is established. The inertia force, convective pressure loss and dynamic contact angle are also considered in this model. Plates with linear and parabolic variations in width and distance are chosen to conduct numerical simulations. Numerical results are in good agreement with analytical data. The differential equation has been proven accurate in the entire flow process. Besides, the influences of different forces acting on the control volume between plates are discussed. For a long time period of flow, the convective pressure loss and friction force in the reservoir can be neglected and the differential equation is simplified. This dynamic equation can be extended to any plates with well-defined shapes.

Based on the mathematical model, optimization of the dimensions of flow channels is possible. The influences of the width of plates and the distance between plates on the flow speed are discussed in detail. The situations in which c or d is a constant are considered. When the width of plates or the distance between plates varies linearly, the flow speed will change monotonically with the aspect ratio. When the width of plates varies parabolically, the flow speed also varies monotonically with the aspect ratio. However, when the distance between plates varies parabolically, decreasing the distance a little is beneficial to increasing the flow speed, but too much decrease in the distance will slow down the flow speed. It is necessary to design the varying aspect ratio properly to obtain the fastest flow speed. This mathematical model will be helpful for liquid management in space and provide the theoretical foundation for the design of plate-type tanks.