List of symbol

Dimensional quantities

x′, y′, z′:

rectangular coordinate system

u′, v′, w :

velocities of x′, y′, z′-component

H :

constant height of meniscus at initial location

L :

characteristic length of the fluid column

\(R^{\prime }_{1}\) :

radius of meniscus at z-location

\(R^{\prime }_{2}\) :

radius of rounded wall

μ :

dynamic viscosity

ρ :

density

σ :

surface tension

𝜃 1 :

contact angle of straight wall

𝜃 2 :

contact angle of rounded wall

α :

angle between OO 1 and y-axis

P′:

Pressure

t′:

Time

h′:

the height of meniscus along OO 1 (the minimum distance from point O to meniscus)

k :

the slope of OA in the Oξη coordinate frame

Θ:

ε 2 σρH/μ 2

C I, i , C II, i :

the coefficient

d k :

the coefficient of h(λ) by series expansion

a j :

the coefficient of A by series expansion

c :

a constant value which is stand by z f Ż f in Eq. 25

χ :

the relative error of area A

δ :

the relative error δ of w 0II(ξ, η) in the rounded wall OB

Dimensionless quantities

x, y, z :

rectangular coordinate system, x = x′/ H, y = y′/ H, z = z′/L

ε :

ratio of length scale, ε = H/L

W :

velocity coefficient, W = εσ/ μ

u, v, w :

velocities of x, y, z-component, u = u′/ εW, v = v′/ εW, w = w′/W

P :

pressure , P = HP ′/ σ

t :

time, t = Wt ′/L

x 0 :

the value along the x-axis on the meniscus, as shown in Fig. 4

S(x, h):

the value along y-axis at a given x 0, as shown in Fig. 4

R 1 :

radius of meniscus at z-location, \(R_{1}=R^{\prime }_{1}\)/H, as shown in Fig. 4

R 2 :

radius of rounded wall\(, R_{2}=R^{\prime }_{2}\)/H, as shown in Fig. 4

A :

cross-sectional flow area

Q′:

volumetric flow rate

x 1, y 1 :

center coordinates of meniscus, as shown in Fig. 4

x 2, y 2 :

center coordinates of rounded wall, as shown in Fig. 4

x A , y A :

coordinate of intersection between meniscus and straight wall, as shown in Fig. 4

x B , y B :

the coordinate of intersection between meniscus and rounded all, as shown in Fig. 4

h :

h = h′/H

z f :

liquid’s front position at t

z f0 :

liquid’s front position at initial time

λ :

λ = z/ z f

ξ,:

local coordinates, the intersection point of η−axis and

η :

meniscus is point C, OC = h, as shown in Fig. 4

ξ 0, η 0 :

coordinate transform of (x 0, S) on local coordinate system

g 0 :

gravitational acceleration in the locality

Introduction

Capillary driven flow is common and can be observed in our surroundings from the draining of fluids via a sponge or towel to the wicking of candle wax. Although capillary phenomena are often ignored in large-scale systems considering the great Earth’s gravity, they are significant in non-gravity environments. There is the potential to displace fluids using only surface tension and wetting properties, reducing the need of intricate systems with moving parts or higher risk of failure such as centrifugal pumps. Hence, capillary driven flow has the advantages of economy and safety.

Spontaneous capillary driven flow can be used to transport fluids in places with the less influence of gravity. The amount and rate of the transported fluid strongly depends on the system geometry. As a matter of fact, due to the induced pressure gradient caused by the decrease of mean radius of curvature as it approaches the corner, interior corners can also be exploited to pump fluid passively. Research on capillary flow in interior corner can be traced back to the 1960s. Concus and Finn (1969) proposed the critical contact angle of the wetting liquid, i.e. Concus-Finn condition under non-gravity, and classified capillary flow in interior corners as steady and unsteady solutions. Weislogel (1996) simplified the three dimensional Navier-Stokes equations to one dimensional case, and got the solution by introducing the lubrication approximation. For special cases of constant height boundary condition, the length of the fluid column increases in the interior corner (L∝t 1/2). After that, Weislogel (2002) and Nardin (2005) published series of papers to extend the theory to complex geometry calculation. Mason and Morrow (1984, 1991) derived an expression for the displacement curvature of the main terminal meniscus in a regular n-sided tube with any contact angle, and later reported the general solutions for completely wetted triangular tubes of different shapes. Dong and Chatzis (1995) took the wetting area as variable to investigate the flow in square capillary tube, and obtained the nonlinear solution by using the finite element method (FEM) to solve the heat conduction equations. But the solution was only limited in the right angle and cannot be used in complex geometry for the limitation of curvature calculation. Wei and Chen (2011) extended Dong’s method to different contact angles and dihedral angles by modifying the curvature calculation algorithm and its relation with the wetting area. They also found some mistakes using FEM to solve the heat conduction equation. After the modifications, the nonlinear solution can be obtained. The proposed theory is validated by experiments of capillary tube and drop tower. Wang (2010) and Xu (2007) studied the influence of initial liquid volume on the capillary flow in interior corner systematically by microgravity experiments using drop tower, including three different conditions: satisfying, close to and dissatisfying the Concus-Finn condition. The experimental results showed that the liquid’s front position of the meniscus in the corner increased with the increase of the initial liquid volume.

In many practical applications, the interior corners are rounded instead of ideally sharp due to the manufacturing and processing. Ransohoff and Radke (1988) investigated rounded corners where the rounded portion of the corner was concentric with the free surface. The flow-resistance function was determined numerically for a selection of corner half-angles, contact angles, and degrees of roundedness, which was measured using a ratio that employs the depth of the fluid h. Concus and Finn (1990) found that the critical contact angle predicted by Concus-Finn condition decreased with the increasing of corner radius. Namely, the liquid can form stable interfacial structure easily. Chen et al. (2006, 2007) set up suitable non-dimensional flow resistance equations with appropriate non-dimensional methods, obtained the approximate analytical solution of capillary driven flow in the rounded interior corner, and verified the results with experiments in drop tower. The results showed that the climbing velocity would be reduced in rounded corner.

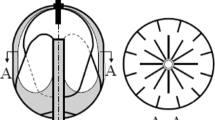
The study on the interior corner capillary flow mainly explores the interior corner made up of two straight edges with V-shape. The container is relatively complicated in practical engineering, such as the structure of the actual vane-type surface tension tank (2005) shown in Fig. 1. The capsule is of hemispherical shape in its upper and lower parts, and the intermediate portion is cylindrical. The inside and outside of the vane are fixed on the fixed pole which is in the middle of the tank. The outside of the vane is perpendicular to the wall of the tank. The interior corner formed by the adjacent inside of the vane is V-shaped. Due to the wall of the tank is curved, the interior corner between the wall and the outside of the vane is not V-shaped, which is defined as an interior corner of rounded wall in this article.

Fig. 1
figure 1

Schematic model of heavily vaned VTRE tank showing fluid location in low-gravity environment. Tank is partially liquid filled as shown at left with fluid occupying shaded region. Nardin and Weislogel (2005)

Full size image

In this paper, the capillary driven flow satisfying Concus-Finn condition in interior corner of rounded wall under microgravity environment has been investigated. Based on Navier-Stokes equations established by Davis (1983) and the capillary driven flow in interior corner of regular polygon researched by Weislogel, the governing equation for capillary driven flow is established and the approximate analytical solution is derived. Moreover the influence of different parameters in interior corner flow is analyzed.

Navier-stokes Equations and Boundary Conditions of Capillary Flow

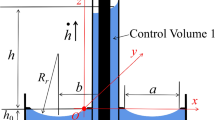
The model of capillary flow in an isolated interior corner is shown in Fig. 2. The length of container is L, with straight wall along the radial direction of container and at 45° to y axis. The lowest height of meniscus is H at z = 0. H keeps the same as time goes by when the contact angle is less than 30°. Dotted line represents the liquid location at the initial time t = 0, z f and z f0 is liquid’s front position at any time and initial time, respectively. The cross section of fluid is marked by shaded area at any z-location. x, y, z is non-dimensional rectangular coordinate system, where x = x′/ H, y = y′/ H, z = z′/L.

Fig. 2
figure 2

A fluid column in an isolated interior corner of rounded wall. The coordinate system is aligned such that the z-axis is along the corner. The characteristic height and length of the fluid column are Hand L, respectively.

Full size image

Initial meniscus height is an important parameter for the capillary flow in an interior corner of rounded wall under microgravity. Weislogel (1996) found that the capillary flow in V-type interior corner has a constant meniscus height by drop tower experiments, namely initial meniscus height. The capillary flow in an interior corner of rounded wall is numerically simulated using FLOW-3D; the results show that like capillary flow in an interior corner of V-type, the rounded wall also has the initial meniscus height, which is the H as shown in Fig. 3. Figure 3 displays the capillary rise curves at t = 0.5s, 1.0s, 1.5s, 2.0s, 2.5s, 3.0s, 3.5s, 4.0s, 4.5s, 5.0s; and curves have a intersection point A at different time, which corresponds to the initial meniscus height H.

Fig. 3
figure 3

Capillary rise at different time, which are results from the FLOW-3D simulations. xis the radial direction of the vessel and z is the axial direction. (a 𝜃 1 = 𝜃 2 = 0°b 𝜃 1 = 0°, 𝜃 2 = 10°)

Full size image

The cross-flow section is sketched in Fig. 4, where 𝜃 1, 𝜃 2 are the contact angles, A and B are intersections between the meniscus and straight, rounded wall, respectively. O 1, O 2 are the corresponding centers for circular curve of A and B, respectively. S is the meniscus height as measured from the x-z plane at a given x 0; point C is the intersection point of meniscus AB and the line OO 1. The minimum distance from point O to meniscus AB is h′, namely OC = h′, which is called meniscus height, where the dimensionless is h = h′/H. Figure 4 shows that the line OO 1 and y-axis are not coincide, the angle between them is α. If rounded wall OB transforms to straight wall, the interior corner of rounded wall transforms to perfectly sharp interior corner, and the angle α = 0∘, the line OO 1 and y-axis coincide, namely x = 0, S x = 0 = h. But for rounded wall, S x = 0≠h on x = 0 because of angle α. To be convenient, this paper constructed local coordinate system O ξη, and set η-axis along the line OO 1. η-axis divides cross-section into two areas, area I where ξ> 0 and area II where ξ<0. The transformation relations between Oxy and O ξη:

$$ \left\{ {{\begin{array}{*{20}c} {x=\xi \cos \alpha +\eta \sin \alpha} \hfill \\ {y=-\xi \sin \alpha +\eta \cos \alpha} \hfill \end{array}}}\right. $$
(1)

where α = arctan(x 1/ y 1). The linear equation of OA can be expressed as η = k.ξ, in which k = tan(α+45∘). (x 0, S) can be transformed into (ξ 0, η 0).

Fig. 4
figure 4

Schematic diagram of arbitrary cross section. 𝜃 1, 𝜃 2 are the contact angles of straight wall and rounded wall respectively. O 1, O 2 are the corresponding centers of meniscus and rounded wall, R 1, R 2 are the radius respectively. The coordinates of the meniscus are described by x 0 along the x-axis and by S along the y-axis. h is the height of meniscus along OO 1

Full size image

The non-dimensional Navier-Stokes equations and the continuity equation of capillary flow in interior corner are:

$$ \left\{ {{\begin{array}{*{20}c} {\varepsilon^{2}{\Theta} \frac{Du}{Dt}=-P_{,x} +\varepsilon^{2}\nabla^{2}u}\\ {\varepsilon^{2}{\Theta} \frac{Dv}{Dt}=-P_{,y} +\varepsilon^{2}\nabla^{2}v}\\ {\Theta \frac{Dw}{Dt}=-P_{,z} +\nabla^{2}w}\\ {\nabla \cdot \text{\textbf{v}}=0} \end{array}}}\right. $$
(2)

where D/Dt = ∂/ ∂t + u∂/ ∂x + y∂/ ∂y + w∂/ ∂z, ∇2 = ∂ 2/ ∂x 2+∂ 2/ ∂y 2+ε 2 ∂ 2/ ∂z 2, v =(u, v, w). u, v, w is dimensionless velocities of x, y, z-component, P is fluid’s pressure. u = u′/ εW, v = v′/ εW, w = w′/W, P = HP ′/ σ, W = εσ/ μ, t = Wt ′/ L,Θ = ε 2 σρH/ μ 2, ε = H/L. μ is the dynamic viscosity, ρ is the density, σ is the surface tension, P , ζ = ∂P/ ∂ζ, ζ = x, y, z.

According to Weislogel (1996), the boundary condition of capillary flow in interior corner can be described as follows:

(1) No-slip condition along straight wall and rounded wall:

$$ u=v=w=0\,\,\text{on}\,\,y=x $$
(3-a)
$$ u=v=w=0\,\,\text{on}\,\,x^{2}+y^{2}=\sqrt 2 R_{2} \left( {x+y} \right) $$
(3-b)

(2) Meniscus AB is free surface, the stresses are zero:

$$\begin{array}{@{}rcl@{}} &&\left( 1+\varepsilon^{2}S_{,z}^{2}\right)^{-1/2}\left( 1+\left| {\nabla S} \right|^{2}\right)^{-1}\\ &&\left\{\left( 1-S_{,x}^{2} +\varepsilon^{2}S_{,z}^{2}\right)\right. \left.\left[u_{,y} +v_{,x} -S_{,z} \left( \varepsilon^{2}u_{,z} +w_{,x}\right)\right]\right.\\ &&{\kern8pt}\left.+2S_{,x} \left[v_{,y} -u_{,x} -S_{,z} \left( \varepsilon^{2}v_{,z} +w_{,y}\right)\right.\right.\\ &&{\kern8pt} -\left.\left.\varepsilon^{2}S_{,z}^{2} \left( u_{,x} -w_{,z}\right)\right] \right\} =0 \end{array} $$
(3-c)
$$\begin{array}{@{}rcl@{}} &&\left( 1+\varepsilon^{2}S_{,z}^{2}\right)^{-1/2}\left( 1+\left| {\nabla S} \right|^{2}\right)^{-1/2}\\ &&\left[\left( 1-\varepsilon^{2}S_{,z}^{2}\right)\left( \varepsilon^{2}v_{,z} +w_{,y}\right)\right. \left.-S_{,x} (\varepsilon^{2}u_{,z} +w_{,x}) \right.\\ &&{\kern8pt} \left.+2\varepsilon^{2}S_{,z} \left( v_{,y} -w_{,z}\right)\! -\!\varepsilon^{2}S_{,x} S_{,z} \left( u_{,y} +v_{,x} \right)\right]\! =\! 0 \end{array} $$
(3-d)

where \(\left | {\nabla S} \right |^{2}=S_{,x}^{2}+\varepsilon ^{2}S_{,z}^{2}\), () , ζ = ∂()/ ∂ζ, () , ζχ = ∂ 2()/ ∂ζ∂χ, ζ, χ = x, y, z.

(3) The normal stress condition on meniscus AB:

$$\begin{array}{@{}rcl@{}} &&-P+2\varepsilon^{2}\left[1+\left| {\nabla S} \right|^{2}\right]^{-1}\\ &&\left[v_{,y} -S_{,x} \left( u_{,y} +v_{,x}\right) {\kern10pt}-S_{,z} \left( \varepsilon^{2}v_{,z} +w_{,y}\right)\right.\\ &&{\kern2pt}\left. +S_{,x} S_{,z} \left( \varepsilon^{2}u_{,z} +w_{,x} \right)+S_{,y}^{2} u_{,x} +\varepsilon^{2}S_{,z}^{2} w_{,z}\right]\\ && =\!\left[1+\left| {\nabla S} \right|^{2}\right]^{-3 / 2}\left[S_{,xx}\! \left( 1\! +\! \varepsilon^{2}S_{,z}^{2}\right)+\varepsilon^{2}S_{,zz} \left( 1+S_{,x}^{2} \right)\right.\\ &&{\kern82pt}\left. -2\varepsilon^{2}S_{,x} S_{,z} S_{,xz}\right] \end{array} $$
(3-e)

(4) The angle with rounded wall and the outward unit normal to meniscus is equal to contact angle:

At point A, the contact line boundary condition is:

$$ (1+\left| {\nabla S} \right|^{2})^{-1/2}(1+S_{,x} )=\sqrt 2 \cos \theta_{1} $$
(3-f)

At point B, the contact line boundary condition is:

$$\begin{array}{@{}rcl@{}} &&\frac{1}{R_{2}} \left( 1+\left| {\nabla S} \right|^{2}\right)^{-1/2}\left[\frac{\sqrt 2} {2}R_{2} +S_{,x} \left( x_{B} -\frac{\sqrt 2} {2}R_{2}\right)\right.\\ &&{\kern52pt}\left.\phantom{-\frac{\sqrt 2} {2}R_{2}}-y_{B}\right]=\cos \theta_{2} \end{array} $$
(3-g)

In the process of capillary flow, we can obtain as follows by the z-direction

$$ \frac{\partial A}{\partial t}=-\frac{\partial {Q}^{\prime}}{\partial z} $$
(4)

where A is the cross-sectional area in the x-y plane and Q′ is the volumetric flow rate in the z-direction.

Q′ can be calculated by the integral of w over the cross-section:

$$ {Q}^{\prime}={\int}_{A} {w\mathrm{d}x\mathrm{d}y} $$
(5)

According to Fig. 4, cross-sectional area A can be calculated by

$$ A={\int}_{x_{B}}^{0} {\left\{ {S-\left[ {y_{2} -\sqrt {{R_{2}^{2}} -\left( {x-x_{2}} \right)^{2}}} \right]} \right\}\mathrm{d}x} +{\int}_{0}^{x_{A}} {\left( {S-x} \right)\mathrm{d}x} $$
(6)

And the variables S, x A , x B in Eq. 6 can be expressed as the function of the meniscus height h, namely

$$ S=y_{1} -\sqrt {{R_{1}^{2}} -\left( {x-x_{1}} \right)^{2}} $$
(7-a)
$$ x_{A} =\sqrt 2 \left[h^{2}+2R_{1} h+2R_{1} R_{2} \left( {\cos \theta_{2} -\sin \theta_{1}} \right) \right] \big/ \left( 4R_{2}\right) $$
(7-b)
$$ x_{B} =\left( -b_{2} -\sqrt {{b_{2}^{2}} -4b_{1} b_{3}}\right)\big/\left( 2b_{1}\right) $$
(7-c)

where: b 1 = 4[(x 2−x 1)2+(y 2−y 1)2], b 2 = 4[(x 2−x 1)h(h+2R 1)+2y 2(y 2−y 1)(x 1−y 1)],

$$\begin{array}{@{}rcl@{}} b_{3}&=&h^{2}\left( h+2R_{1}\right)^{2}+4y_{2} h\left( y_{2} -y_{1} \right)\left( h+2R_{1}\right), \\ &&x_{2} =y_{2} ={\sqrt 2 R_{2}} / 2,\\ x_{1}&=&\sqrt 2 \left[h^{2}+2R_{1} h-2R_{1} R_{2} \left( \cos \theta_{1} -\cos \theta_{2}\right)\right]/ \left( {4R_{2}} \right),\\ y_{1}&=&\sqrt 2 \left[h^{2}+2R_{1} h+2R_{1} R_{2} \left( {\cos \theta_{1} +\cos \theta_{2}} \right) \right]/ \left( 4R_{2}\right), \end{array} $$
$$\begin{array}{@{}rcl@{}} &&R_{1}=\frac{-h\left[ {h^{2}+hR_{2} \cos \theta_{2} -2{R_{2}^{2}}}\right]}{~}\\ &&\frac{+R_{2} h\sqrt {4{R_{2}^{2}} \left( {\cos^{2}\theta_{1} +\cos^{2}\theta_{2}} \right)+h\left( h\sin^{2}\theta_{1} +4R_{2} \cos \theta_{2}\right)}} {2\left[ {\left( {h+R_{2} \cos \theta_{2}} \right)^{2}-{R_{2}^{2}} \sin^{2}\theta_{1}} \right]} \end{array} $$

Substituting (7-a)–(7-c) into Eq. 6, cross-sectional area A can be expressed by the meniscus height h, namely

$$ A=F_{A} (h) $$
(8)

When 𝜃 1 = 𝜃 2 = 0∘, the relationship between curves of cross-sectional area A and meniscus height h with different R 2 as shown in Fig. 5.

Fig. 5
figure 5

The analytical relationship between curves of A and meniscus height h with different R 2 when 𝜃 1 = 𝜃 2 = 0∘. his the height of meniscus along with OO 1, and R 2 is the radius of the rounded wall. The interior corner becomes sharp as R 2 tends to infinity

Full size image

When the radius of rounded wall R 2→∞, the rounded wall transforms to the straight wall, the interior corner transforms to the sharp interior corner, where A is positive and proportional to h 2 (Weislogel 1996). Figure 5 shows the nonlinear relationship between A and h. And with the increasing of R 2, it approaches to the relationship in sharp interior corner, namely when R 2 reaches to a certain value, the interior corner of rounded wall can be regarded as sharp interior corner. The error in cross-sectional area between interior corner of rounded wall and sharp interior corner increases with the increasing of h and can be negligible when h<0.4. It shows that the rounded wall can be simplified as straight wall when h<0.4.

Considering the complication of Eq. 8, cross-sectional area A, for convenience, can be expanded as a function of h

$$ A=\sum\limits_{j=1}^{\infty} {a_{j} h^{j}} $$
(9)

where the coefficients of A by series expansion a j (j = 1,2,…, ∞) are constants related to R 2, 𝜃 1, 𝜃 2. For example, when the R 2 = 3.0, 𝜃 1 = 0′, 𝜃 2 = 0′, the a j can be obtain that a j (j = 1,2,3,4) equal to 0.0043, 1.2171, 0.0692, -0.0248, respectively, anda j approach to zero with j >4. The fitting accuracy of area A can be expressed by χ which is the relative error of Eqs. 8 and 9, that

$$\chi =\left| {\frac{\sum\limits_{j=1}^{J_{M}} {a_{j} h^{j}} -F_{A} \left( h \right)}{F_{A} \left( h \right)}} \right|\times 100~\% $$

where, J M is the maximum of j. When R 2 = 4, 𝜃 1 = 𝜃 2 = 0°, the relation curves that the relative error χ varies with h are obtained in Fig. 6.

Fig. 6
figure 6

The relation curves that the relative error χ varies with h, where J M denotes the highest order in the polynomial

Full size image

The conclusion can be drawn when the highest order of expansion in series equals to 4, the error between the approximate result and original A has become small from Fig. 6. So the non-dimensional area A can be expanded as the four order polynomial about h.

Dynamic Equation and Approximate Analytical Solution of Capillary Flow

The perturbation method is used to solve the Navier-Stokes equations of capillary flow

$$ \left\{ {\begin{array}{l} u=u_{0} +\varepsilon^{2}u_{1} +... \\ v=v_{0} +\varepsilon^{2}v_{1} +... \\ w=w_{0} +\varepsilon^{2}w_{1} +... \\ P=P_{0} +\varepsilon^{2}P_{1} +... \end{array}} \right., $$
(10)

In this research, the length of container L>>H, we can assume that ε 2<<1. Substituting (10) into Eq. 2, (3), where terms of O(ε) are absorbed into the leading order terms for convenience. The Navier-Stokes equations can be simplified as:

$$ P_{0,z} =w_{0,xx} +w_{0,yy} $$
(11)

The boundary conditions (3-a)-(3-g) may be simplified as follows; and Eqs. 12-d and 12-e represent the boundary conditions on the interface.

$$ w_{0} =0\,\,\text{on}\,\,y=x $$
(12-a)
$$ w_{0} =0\,\,\text{on}\,\,x^{2}+y^{2}=\sqrt 2 R_{2} \left( {x+y} \right) $$
(12-b)
$$\begin{array}{@{}rcl@{}} &&\left( {1-S_{,x}^{2}} \right)\left( {u_{0,y} +v_{0,x} -S_{,z} w_{0,x}} \right)\\ &&{\kern10pt}+2S_{,x} \left( {v_{0,y} -u_{0,x} -S_{,z} w_{0,y}} \right)=0 \end{array} $$
(12-c)
$$ w_{0,y} -S_{,x} w_{0,x} =0 $$
(12-d)
$$ -P_{0} =S_{,xx}^{2} \left( {1+S_{,x}^{2}} \right)^{{-3} / 2} $$
(12-e)
$$ 1+S_{,x} =\sqrt 2 \cos \theta_{1} \left( {1+S_{,x}^{2}} \right)^{1 / 2} $$
(12-f)
$$\begin{array}{@{}rcl@{}} &&\frac{1}{R_{2}} \left( {1+\left| {\nabla S} \right|^{2}} \right)^{-1/2}\left[ {y_{\mathrm{B}} -\frac{\sqrt 2} {2}R_{2}\! -\! S_{,x} \left( {x_{\mathrm{B}} -\frac{\sqrt 2} {2}R_{2}} \right)} \right]\\ &&{\kern10pt}=\cos \theta_{2} \end{array} $$
(12-g)

Substituting (7-a) into Eq. 12-d:

$$ w_{0,y} =\frac{x-x_{1}} {y_{1} -S}w_{0,x} $$
(13)

Substituting (7-a) into Eq. 12-e:

$$ P_{0} =-R_{1}^{-1} $$
(14)

Due to the radius of meniscus R 1 is a function of z, t, so is P 0. Then the w 0, xx +w 0, yy should not contain x, y from Eq. 11. Considering the transformation relations in Eq. 1, flow velocity w 0 can be set as a quadratic function of x and y. The area I in the Fig. 4 can be set as follows:

$$ w_{0} =w_{\text{0I}} \left( {\xi ,\eta} \right)=F_{\mathrm{I}} \left( {\xi ,\eta} \right)\frac{\partial P_{0}} {\partial z} $$
(15)

where F I(ξ, η) = C I,1 ξ 2+C I,2 η 2+C I,3 ξη+C I,4 ξ+C I,5 η+C I,6.

Equation 15 must satisfy (11) and boundary conditions (12-a) and Eq. 13, so

$$\begin{array}{@{}rcl@{}} C_{\mathrm{I},1}&=&\frac{k^{2}}{2\left( {1+k^{2}} \right)}, \quad C_{\mathrm{I},2} =\frac{1}{2\left( {1+k^{2}} \right)}, \\ C_{\mathrm{I},3} &=& -\frac{k}{1+k^{2}}, \quad C_{\mathrm{I},4} =\frac{\left( {\eta_{0} -\xi_{0} k} \right)k}{1+k^{2}}, \\ C_{\mathrm{I},5} & = & \frac{\xi_{0} k-\eta_{0}} {1+k^{2}}, \quad C_{\mathrm{I},6} =0 \end{array} $$
(16)

The area II can be set as

$$ w_{0} =w_{\text{0II}} \left( {\xi ,\eta} \right)=F_{\text{II}} \left( {\xi ,\eta} \right)\frac{\partial P_{0}} {\partial z}. $$
(17)

Equation 17 to satisfy the Eq. 11 and boundary condition (13) under the premise, w 0II(ξ, η) can be set as a quadratic function of ξ and η, so

$$F_{\text{II}}\! \left( {\xi ,\eta} \right)\! =\! C_{\text{II},1} \xi^{2}+C_{\text{II},2} \eta^{2}+C_{\text{II},3} \xi \eta +C_{\text{II},4} \xi +C_{\text{II},5} \eta +C_{\text{II},6} $$

Because of the continuity of flow, w 0I(ξ, η) equals to w 0II(ξ, η) along OC. For ξ = 0, w 0I(0, η) = w 0II(0, η). Equation 17 must satisfy (11) and Eq. 13, so

$$C_{\text{II},1} =\frac{k^{2}}{2\left( {1+k^{2}} \right)}\quad , \quad C_{\text{II},2} =\frac{1}{2\left( {1+k^{2}} \right)}, $$
$$\begin{array}{@{}rcl@{}} C_{\text{II},3} &=& \frac{\eta_{1} -\eta_{0}} {\xi_{0} \left( {\eta_{1} -2\eta_{0}} \right)}\left( {2C_{\text{II},1} \frac{{\xi_{0}^{2}}} {\eta_{1} -\eta_{0}} -2C_{\text{II},2} \eta_{0} -C_{II,5}} \right)\\ &&+\frac{C_{\text{II},4}} {\eta_{1} -2\eta_{0}} , \quad C_{\text{II},5} =\frac{\xi_{0} k-\eta_{0}} {1+k^{2}}, \quad C_{\text{II},6} =0 \end{array} $$
(18)

Because the boundary condition of the interface between the two areas of the corner has a higher priority than the boundary condition along the rounded wall; and Eq. 17 can only be ξ and η of the bivariate quadratic function, leads to the fact that it is impossible to find solutions for w 0II = 0 along the rounded wall. To minimize overall residual, the specific value of C II,4 can be obtained by least square method which is described as

$$ G={\int}_{OB} {\left( {C_{\text{II},1} \xi^{2}+C_{\text{II},2} \eta^{2}+C_{\text{II},3} \xi \eta +C_{\text{II},4} \xi +C_{\text{II},5} \eta \text{-0}} \right)^{\text{2}}\mathrm{d}\eta} $$
(19)

The C II,4 can be derived by dG/dC II,4 = 0. The relative error δ of w 0II(ξ, η) in the rounded wall OB can be expressed as

$$\delta =\left| {\frac{w_{0II} \left( {\xi ,\eta} \right)_{\vert OB} -0}{w_{0II} \left( {\xi ,\eta} \right)_{\max} } } \right|\times 100~\%, $$

where, w 0II(x ξ, η) |OB is values of w 0II(ξ, η) along the rounded wall OB, w 0II(ξ, η) |max is the maximum value of w 0II(ξ, η) in the region II. The point B will change with different h, R 2, 𝜃 1, consequently, the relative error δ will change. To be convenient, when we explore the relationship between δ and h, R 2 and 𝜃 1 will be fixed. In following, δ with different parameters h, R 2, 𝜃 1 are shown in Fig. 7.

Fig. 7
figure 7

δ∼ξ/ξ B curves with different structure parameters from analytical results, where ξ B is the maximum value of ξ. (a R 2 = 3.0, 𝜃 1 = 𝜃 2 = 0∘ b h = 1.0, 𝜃 1 = 𝜃 2 = 0∘ c R 2 = 3.0, h = 1.0)

Full size image

Figure 7 shows that, the value of the relative error δ is relatively little with different structural parameters, and the maximum value is near 0.06 %. The relative error δ of w 0II (ξ, η) increases with the increasing of h when R 2, 𝜃 1 and 𝜃 2 are fixed, decrease with increasing of R 2 when h, 𝜃 1, 𝜃 2 are fixed and increasing of 𝜃 1(𝜃 2) when R 2, h are fixed.

Diagram of analytical solution of F I(ξ, η) and F II(ξ, η) with different structure parameters as shown in Fig. 8.

Fig. 8
figure 8

The analytical solutions of F I(ξ, η) and F II(ξ, η) with different structure parameters, where vertical axis and horizontal axis represent ξ and η, respectively. In each graph, right is distribution map of F I(ξ, η), left is distribution map of F II(ξ, η)

Full size image

Figure 8 shows that, the wetting length along rounded wall is longer than that along the straight wall when the contact angles are equal on both walls, and the distribution area of F II(ξ, η) is larger than that of F I(ξ, η). The distribution areas of F I(ξ, η) and F II(ξ, η) decrease with the decreasing of h when R 2, 𝜃 1 and 𝜃 2 are fixed. When h→0, the distribution areas of F I(ξ, η) and F II(ξ, η) approach zero, which lead to the liquid’s tip. The wetting length along rounded wall and distribution area of F II(ξ, η) decrease with the increasing of R 2 when h, 𝜃 1 and 𝜃 2 are fixed. The wetting length along rounded wall closes to the wetting length along the straight wall, and F I(ξ, η), F II(ξ, η) tend to be symmetrical figure gradually. When R 2, h are fixed and 𝜃 1 = 𝜃 2, the wetting length along walls and distribution areas of F I(ξ, η) and F II(ξ, η) decrease with increases of 𝜃 1, and the decrease rate of F II(ξ, η) is greater that of F II(ξ, η).

Substituting (14), (15) and Eq. 17 into Eq. 5, the volumetric flow rate Q′ can be expressed as

$$ {Q}^{\prime}=\frac{1}{{R_{1}^{2}}} \frac{\partial R_{1}} {\partial z}\left( {{\int}_{A_{\mathrm{I}}} {F_{\mathrm{I}} \mathrm{d}\xi \mathrm{d}\eta} +{\int}_{A_{\text{II}}} {F_{\text{II}} \mathrm{d}\xi \mathrm{d}\eta} } \right) $$
(20)

When R 2 and 𝜃 1, 𝜃 2 are fixed, Q′ can be fitted as a function of h, namely

$$ {Q}^{\prime}=\sum\limits_{i=1}^{\infty} {b_{i} h^{i}} \frac{\partial h}{\partial z} $$
(21)

where b i (i = 1,2, … , ∞) are constants. Substituting (9), (21) into Eq. 4, the dynamic equation of capillary flow in interior corners of rounded wall can be obtained:

$$ \sum\limits_{j=1}^{\infty} {a_{j} jh^{j-1}} \frac{\partial h}{\partial t}+\sum\limits_{i=1}^{\infty} {b_{i} ih^{i-1}} \left( {\frac{\partial h}{\partial z}} \right)^{2}+\sum\limits_{i=1}^{\infty} {b_{i} h^{i}} \frac{\partial^{2}h}{\partial z^{2}}=0 $$
(22)

Considering (22) is the nonlinear partial differential equation, we transform it to the nonlinear ordinary differential equations through introducing an auxiliary variable. The h can be set as a function of λ:

$$ h=h\left( \lambda \right) $$
(23)

where λ = z/z f , λ.∈ [0,1]. Then Eq. 22 can be transformed as

$$\begin{array}{@{}rcl@{}} &&-\sum\limits_{j=1}^{\infty} {a_{j} jh^{j-1}(\lambda )\lambda z_{f} \dot{{z}}_{f}} \frac{\mathrm{d}h(\lambda )}{\mathrm{d}\lambda}\! +\!\sum\limits_{i=1}^{\infty} {b_{i} ih^{i-1}(\lambda )} \left[ {\frac{\mathrm{d}h(\lambda )}{\mathrm{d}\lambda} } \right]^{2}\\ &&{\kern15pt}+\sum\limits_{i=1}^{\infty} {b_{i} h^{i}(\lambda )} \frac{\mathrm{d}^{2}h(\lambda )}{\mathrm{d}\lambda^{2}}=0 \end{array} $$
(24)

where \(\dot {{z}}_{f} =\mathrm {d}z_{f} /\mathrm {d}t\). Equation 24 is a function of λ except for term \(z_{f} \dot {{z}}_{f} \), so \(z_{f} \dot {{z}}_{f}\) must be a constant:

$$ z_{f} \dot{{z}}_{f} =c $$
(25)

where c is a constant. z f (t) can be obtained from Eq. 25

$$ z_{f} =\sqrt {2ct+z_{f0}^{2}} $$
(26)

where z f0 is the liquid’s front position at initial time as shown in Fig. 2. h(λ) can be solved by series solution and can be set as:

$$ h(\lambda )=\sum\limits_{k=0}^{\infty} {d_{k} \lambda^{k}} $$
(27)

Since h = 1 when λ = 0 and h = 0 when λ = 1, then

$$ \left\{ {\begin{array}{l} d_{0} =1 \\ \sum\limits_{k=0}^{\infty} {d_{k} =0} \end{array}}\right. $$
(28)

Noting that \(z_{f} \dot {{z}}_{f} =c\), and substituting (27) into Eq. 24

$$\begin{array}{@{}rcl@{}} &&-c\sum\limits_{j=1}^{\infty} {a_{j} j\lambda \left( {\sum\limits_{k=0}^{\infty} {d_{k} \lambda^{k}}} \right)^{j-1}} \left( {\sum\limits_{k=1}^{\infty} {d_{k} k\lambda^{k-1}}} \right)\\ &&{\kern15pt}+\sum\limits_{i=1}^{\infty} {b_{i} i\left( {\sum\limits_{k=0}^{\infty} {d_{k} \lambda^{k}}} \right)^{i-1}} \left( {\sum\limits_{k=1}^{\infty} {d_{k} k\lambda^{k-1}}} \right)^{2}\\ &&{\kern15pt}+\sum\limits_{i=1}^{\infty} {b_{i} \left( {\sum\limits_{k=0}^{\infty} {d_{k} \lambda^{k}}} \right)^{i}} \left[ {\sum\limits_{k=2}^{\infty} {d_{k} k\left( {k-1} \right)\lambda^{k-2}}} \right]=0 \end{array} $$
(29)

Equation 29 is an algebraic equation about λ, which can be obtained by setting the coefficients in front of λ k (k = 1,2, …, ∞) to zero, namely

$$ f_{k} \left( {d_{1} ,d_{2} ,\cdots} \right)=0, k=1,2, $$
(30)

Equation 29 contains an unknown constant c that can be solved iteratively by making the volume of liquid capillary flow at any time t is equal to the integral of the volumetric flow rate Q′ at the z = 0 on [0, t], that is

$$ {\int}_{0}^{z_{f}} {A\mathrm{d}z} -{\int}_{0}^{z_{f0}} {A_{\vert t=0} \mathrm{d}z} ={{\int}_{0}^{t}} {{Q}^{\prime}_{\vert z=0} \mathrm{d}t} $$
(31)

Substituting (9), (21) and Eq. 27 into Eq. 31

$$\begin{array}{@{}rcl@{}} &&{\int}_{0}^{z_{f}} \left\{\sum\limits_{j=1}^{\infty} a_{j} \left[\sum\limits_{k=0}^{\infty} d_{k} \left( z \big/ {z_{f}}\right)^{k}\right]^{j}\right\}\mathrm{d}z\\ &&{\kern15pt}-{\int}_{0}^{z_{f0}}\left\{ \sum\limits_{j=1}^{\infty}a_{j} \left[\sum\limits_{k=0}^{\infty} {d_{k} \left( {z / {z_{f}} } \right)^{k}} \right]^{j}\right\}\mathrm{d}z\\ &&{\kern15pt}=\left( \sum\limits_{i=1}^{\infty} {b_{i}} \right)d_{1} \left( {z_{f} -z_{f0}} \right) \big/ c \end{array} $$
(32)

Make

$$ \sum\limits_{j=1}^{\infty} {a_{j} \left[ {\sum\limits_{k=0}^{\infty} {d_{k} \left( z \big/ {z_{f}} \right)^{k}}} \right]^{j}} =\sum\limits_{m=0}^{\infty} {g_{m} \left( z / {z_{f}}\right)^{m}} $$
(33)

then Eq. 32 can be simplified as

$$ \sum\limits_{m=0}^{\infty} {\frac{g_{m}} {m+1}} ={\left( {\sum\limits_{i=1}^{\infty} {b_{i}} } \right)d_{1}} \big/ c $$
(34)

The values of c and d k (k = 1,2,…) can be obtained by solving (30) and Eq. 34 iteratively, and then h can be obtained. As is shown in Fig. 9, the relationship between c and variables R 2 and 𝜃(𝜃 1 = 𝜃 2 = 𝜃) can be obtained by changing the value of R 2 and 𝜃 with the boundary condition in Eqs. 12-a–12-e. In Fig. 9, c increases with increasing R 2 when 𝜃 is fixed, and decreases with increasing 𝜃 when R 2 is fixed. Combining with Eq. 26, z f would decrease with increasing 𝜃 when other parameters are fixed.

Fig. 9
figure 9

The surface represents the analytical values of c with the changing contact angles 𝜃 and the radius of container R 2

Full size image

The Microgravity Drop Tower Verification

Microgravity experiments were conducted to verify the correctness of the proposed method. The experiments investigated the time evolution of the liquid’s front. The experimenal device and experimental container are shown in Fig. 10.

Fig. 10
figure 10

The experimental device, experimental container and the initial position of the liquid (a the experimental device b the experimental container)

Full size image

The experimental container was cylindrical with the radius of 60 mm and made of PMMA; it contains four vanes which were perpendicular to the wall of the tank. Due to radius of the chosen rounded container in experiment being much longer than that of meniscus, the effect of the other interior corner can be neglected. The experimental mediums are silicone oil fluids. Physical properties of the medium are shown in Table 1. The liquid’s front position can be observed through gauges that fixed beside the experimental container. Short-term microgravity experiments can be produced using microgravity drop-tower of key laboratory in the Chinese academy of sciences, the gravity level was 10 −3g. The distributions of liquid level in a different time are shown in Figs. 11, 12, 13 and 14. And the pixels of the observed pictures from Figs. 11 to 14 are 1920*1080.

Fig. 11
figure 11

The liquid level scatter gram of 5cs fluid at different moments

Full size image
Fig. 12
figure 12

The liquid level scatter gram of 10cs fluid at different moments

Full size image
Fig. 13
figure 13

The partial enlarged view in Fig. 11 of the liquid’s front position

Full size image
Fig. 14
figure 14

The partial enlarged view in Fig. 12 of the liquid’s front position

Full size image
Table 1 Properties of the liquids
Full size table

The FLOW-3D software was used to explore the numerical analysis of this study. With FAVOR and improved finite difference methods, the FLOW-3D software is appropriate for the models of steady/unsteady flow, Newtonian fluid/non-Newtonian fluid, free surface, porous media, et al. Different from other computational fluid dynamics software, the FLOW-3D increases the accuracy of the tracking of free surface and can be used to accurately simulate the capillary driven flow in an interior corner.

The cross section of the tank is as shown in Fig. 15. To simplify the model and shorten the calculation time in the CFD simulations, 1/8 tank has been modeled, where the dash lines represent liquid-liquid contact, and the contact angle is 90°. After computing many grids, the results have a better convergence and stability when the grids are 100×100×300.

Fig. 15
figure 15

The cross sections of tank and 1/8 tank. Dash lines represent liquid-liquid contact, and the contact angle is 90The cross sections of tank and 1/8 tank. Dash lines represent liquid-liquid contact, and the contact angle is 90°

Full size image

As shown in Fig. 16, theoretical calculation results of the liquid’s front position z f are compared with those from drop-tower experiments and numerical simulation using FLOW-3D software.

Fig. 16
figure 16

The comparisons of the liquid’s front position

Full size image

Figure 16 shows that the liquid’s front positions of theoretical calculation results are consistent with experiments and numerical results from the FLOW-3D. We can know from Eq. 26 that the liquid’s front position of capillary flow in cylindrical interior corners is proportional to t 1/2, which corresponds with the rule of capillary flow in prismatic interior corners.

When the liquid’s front position z f is determined, we can calculate the meniscus height according to Eq. 27. The comparisons of theoretical calculation of h′(h′ = h* H) and numerical results are shown in Fig. 17 when t = 1.5s.

Fig. 17
figure 17

Meniscus height h’(h’ = h* H) in different cross-section with coordinate z’ at t = 1.5s

Full size image

As shown in Fig. 17, the meniscus height of theoretical calculation is consistent with numerical simulation results using the FLOW-3D, verifying the correctness of theoretical calculation.

The Influence of Different Structure Parameters on the Capillary Flow

Figure 18 shows the relationship curves between non-dimensionalized meniscus height h and λ when the radius of rounded wall R 2 and contact angles 𝜃 1, 𝜃 2 are selected in different values. The liquid is 5cs fluid.

Fig. 18
figure 18

The curves of h−λwith different structure parameters which are the results from approximate analytical solution

Full size image

As shown in Fig. 18a, when 𝜃 1 = 𝜃 2 = 0∘, the meniscus height h increases with the radius of rounded wall R 2 increasing. When R 2→∞, the rounded wall can be regarded as straight wall, namely the meniscus height of rounded interior corner is smaller than that of perfectly sharp interior corner; Fig. 18b shows that the smaller contact angle, the higher meniscus height would be with fixed R 2. Fig. 18c shows the effect of 𝜃 2 on h with fixed R 2 and 𝜃 1; Fig. 18d shows the effect of 𝜃 1 on h with fixed R 2 and 𝜃 2. It shows that, the meniscus height hdecreases with the increase of contact angle, but the influence of decrease of the contact angle on rounded wall is greater than that on the straight wall (see Fig. 18c and Fig. 18d). The results can be applied in the space fluid management. For example, if you want to keep liquid surface smooth in the container, the climbing height of capillary flow in cylindrical interior corners should be reduced, which means that you should choose a liquid or material with a large contact angle along rounded wall. The influence of 𝜃 2 on h when 𝜃 2 changes solely is greater than that when 𝜃 1, 𝜃 2 change together, which means the influence of 𝜃 1 on h reduces the effect of 𝜃 2 when 𝜃 1, 𝜃 2 change together (see Figs. 18b and 18c). The influence of 𝜃 1 on h when 𝜃 1 changes solely is almost the same as 𝜃 1, 𝜃 2 change together (see Figs. 18b and 18d).

Conclusions

In this paper, the capillary flow in cylindrical interior corners in a microgravity environment has been investigated under the Concus-Finn condition. The governing equation of capillary driven flow in cylindrical interior corners has been established, and the approximate analytical solution has been obtained. The function that liquid’s front position is proportional to t 1/2 is derived. The influence of different parameters on the interior corner flow is explored by using a set of typical parameters. The results show that the non-dimensional meniscus height h decreases with increasing contact angle, while increases with increasing radius of rounded wall. And the influence of decrease of the contact angle on rounded wall is greater than that on straight wall. When contact angles of the two walls change together, the influence of the contact angle on straight wall inhibits that on rounded wall. Our work can be applied to design containers and choose the suitable solution in the space fluid management. For example, if you want to keep liquid surface smooth in the container, the climbing height of capillary flow in cylindrical interior corners should be reduced, which means that you can choose liquids or materials with a large contact angle along rounded wall.